Enhancing the Resolution of Blade Tip Vortices in Hover with High-Order WENO Scheme and Hybrid RANS–LES Methods
Abstract
1. Introduction
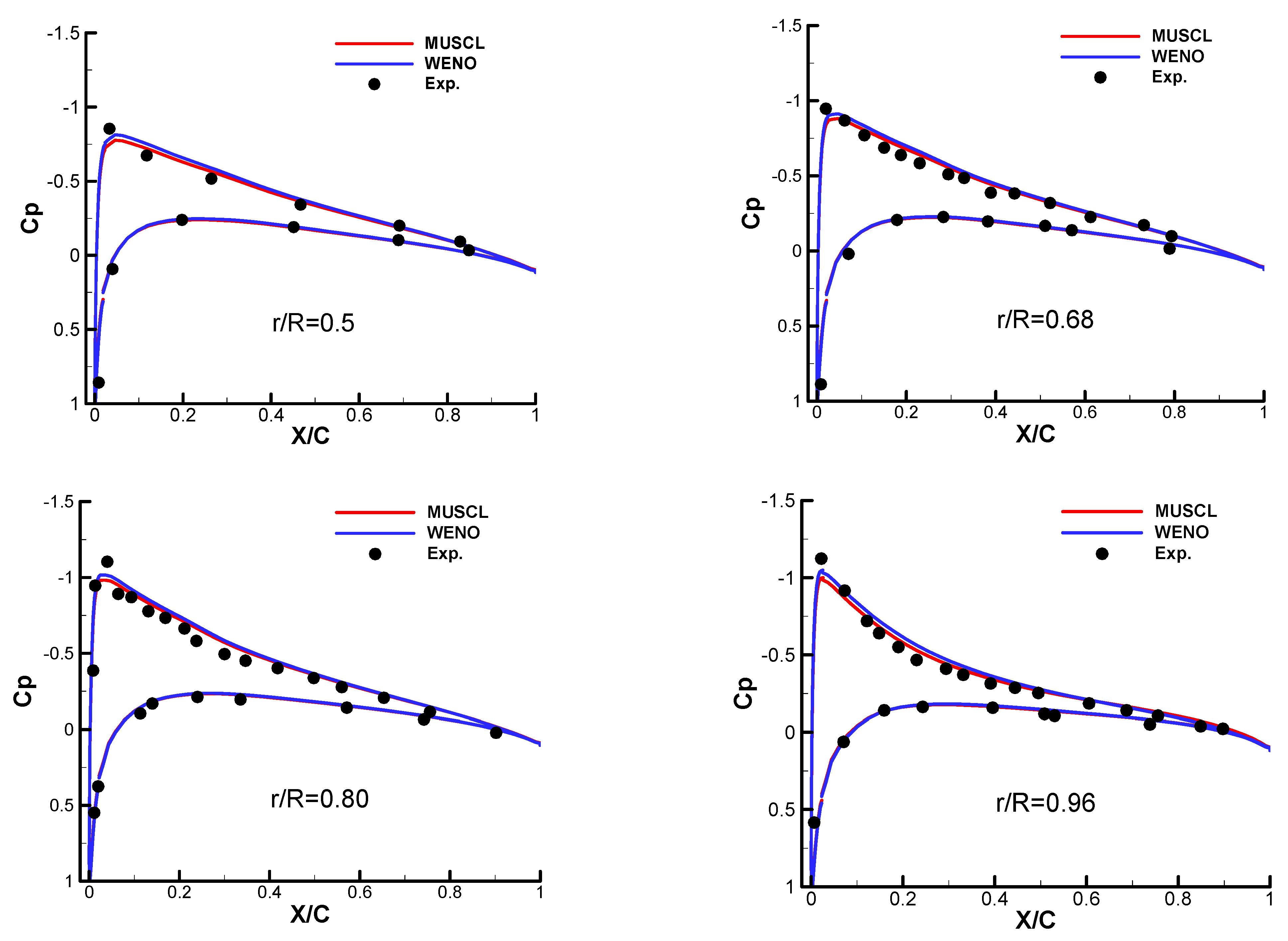
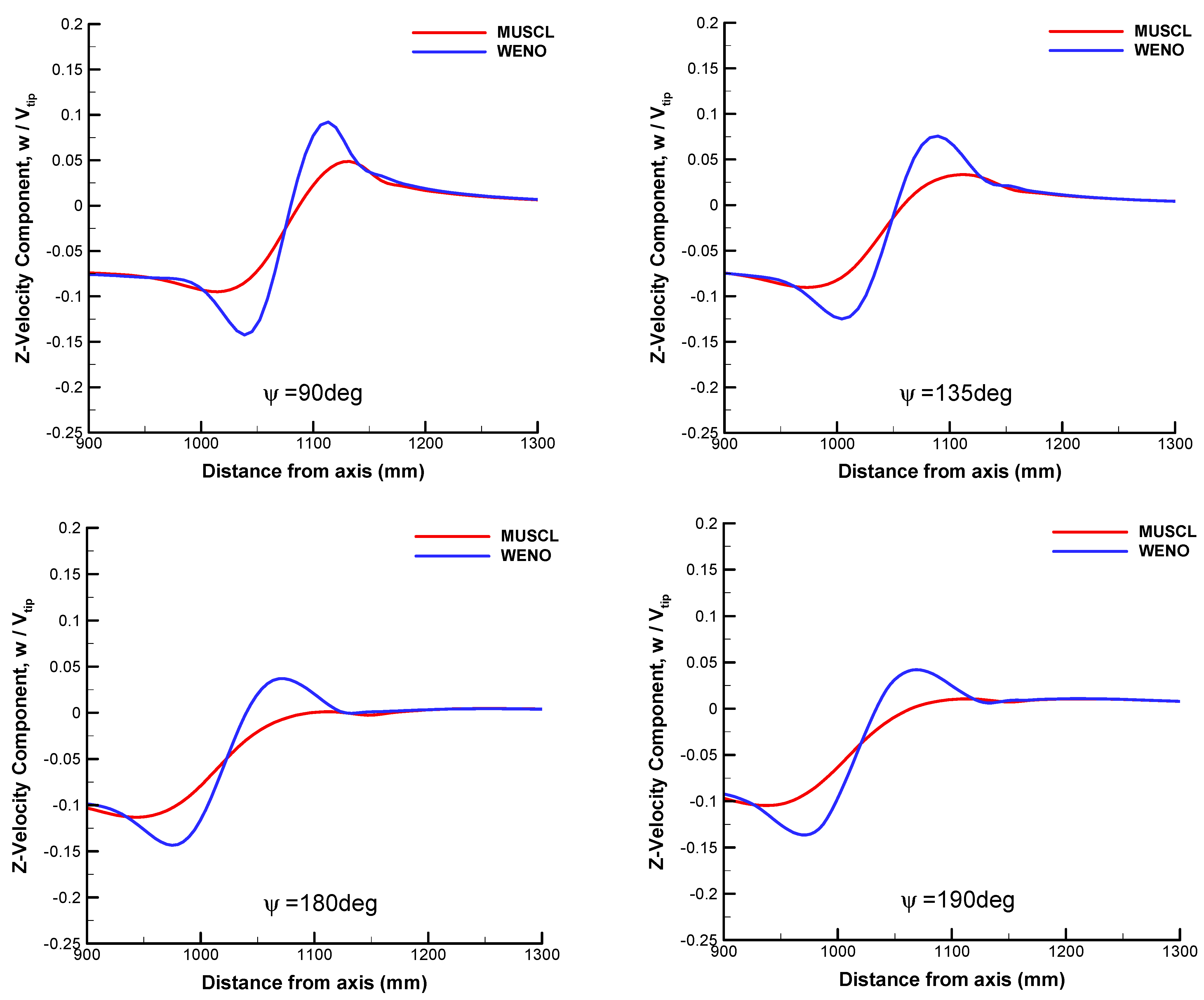
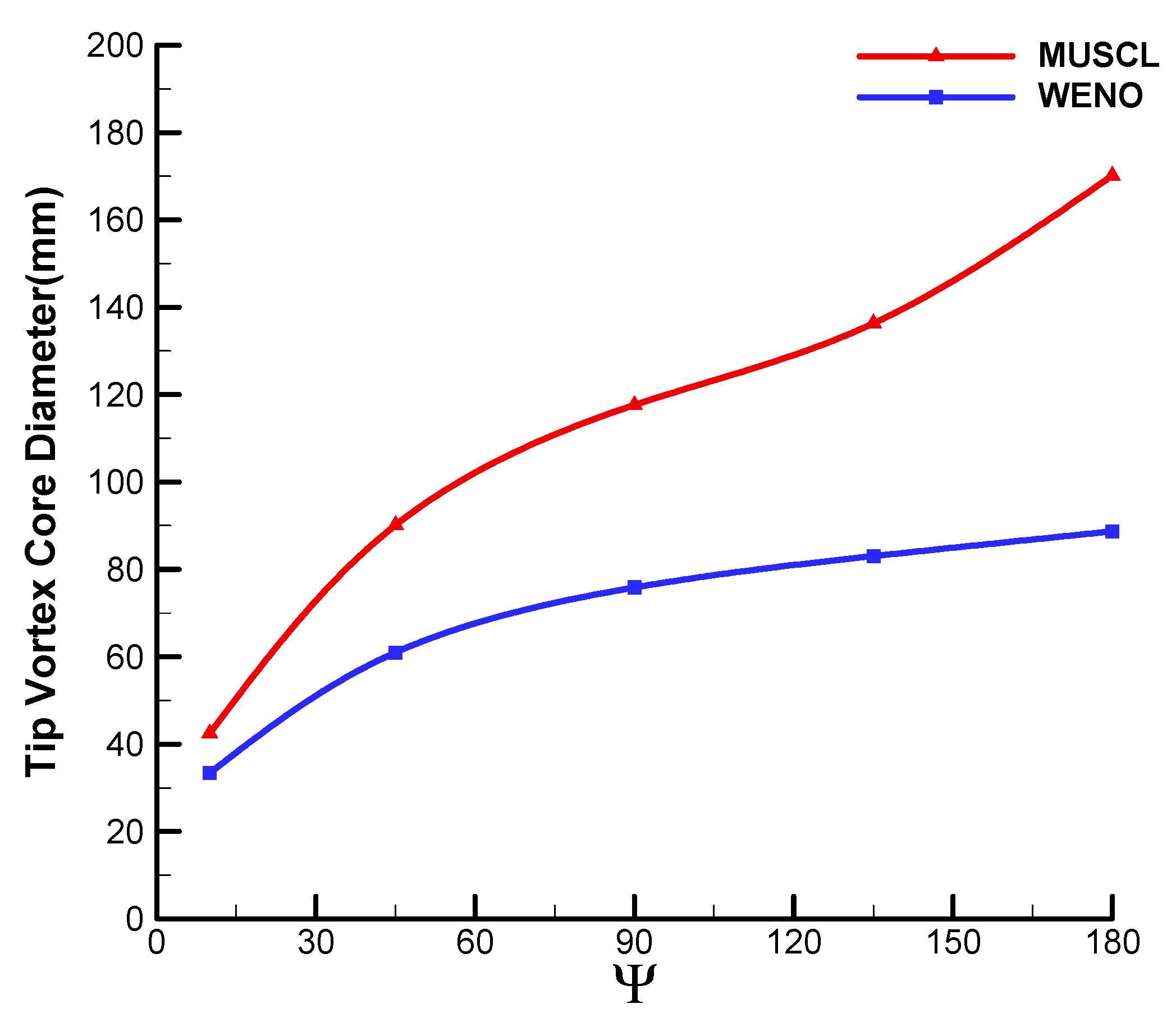
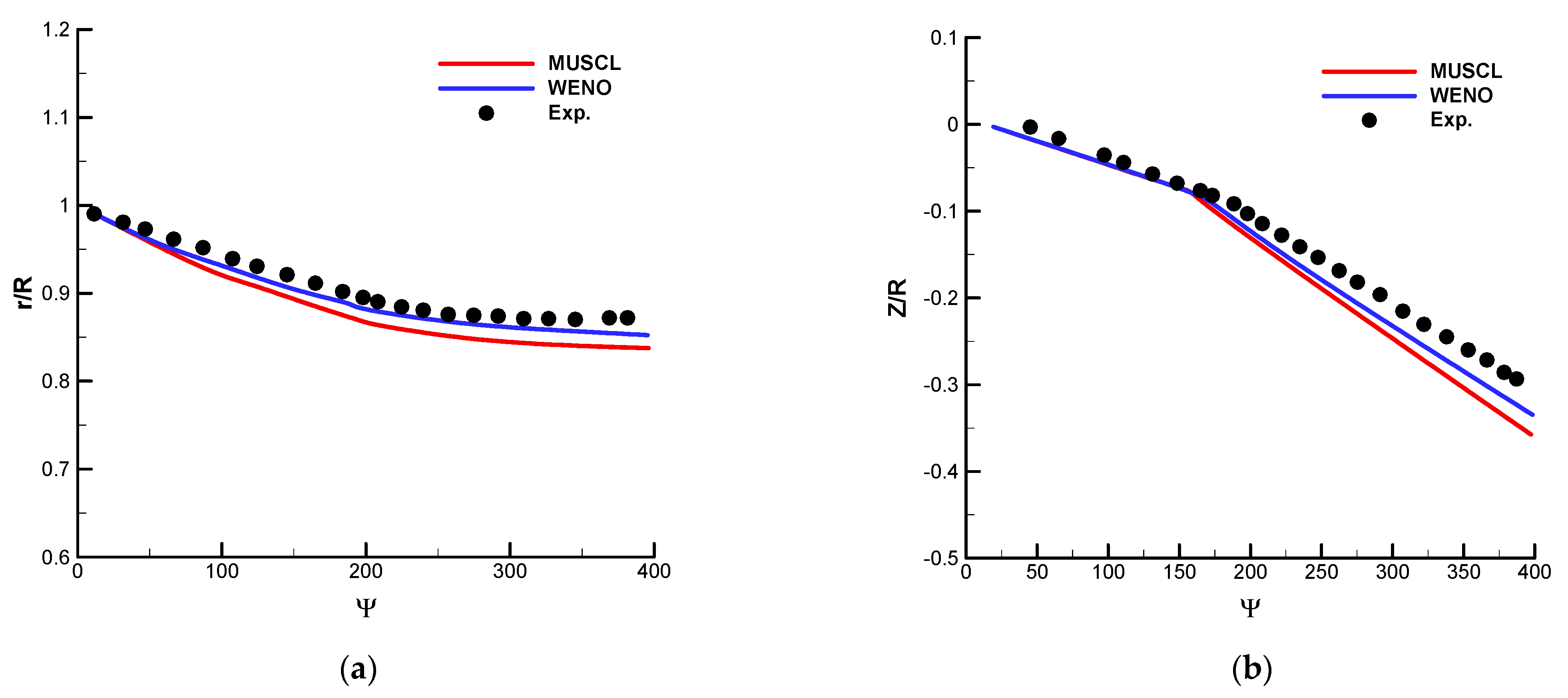
2. Efficiency of High-Order WENO Scheme
3. Efficiency of Hybrid RANS–LES Methods
3.1. The Formulation of DDES and IDDES
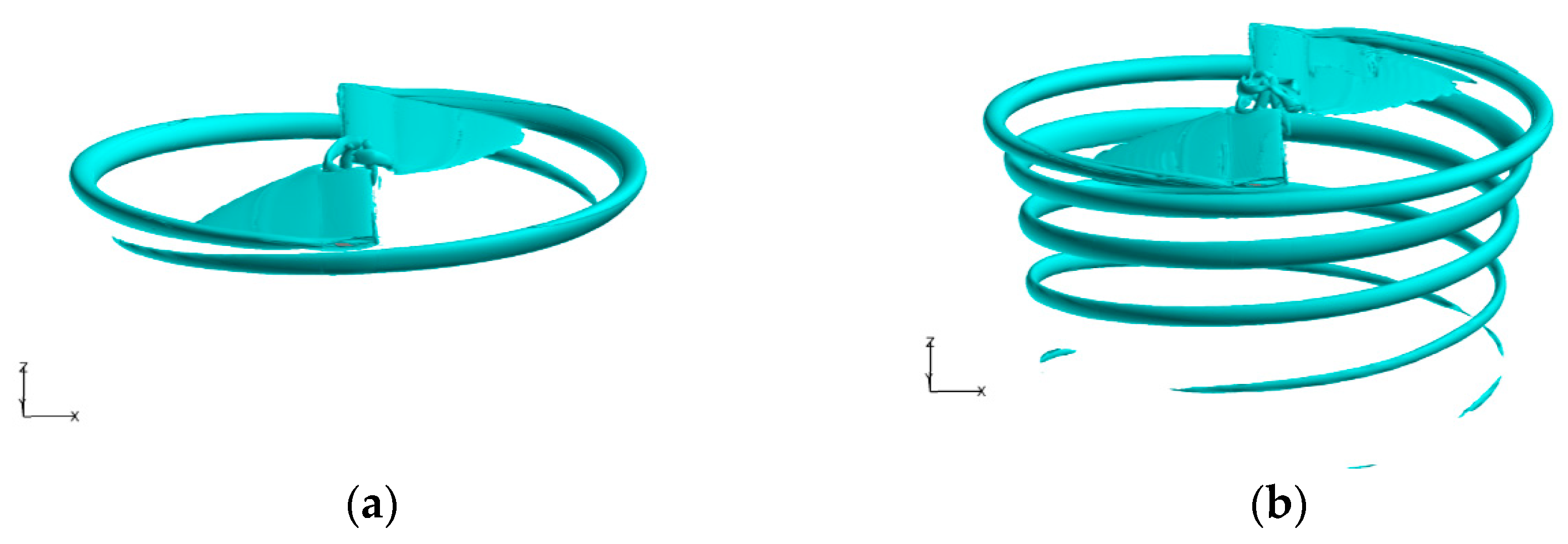
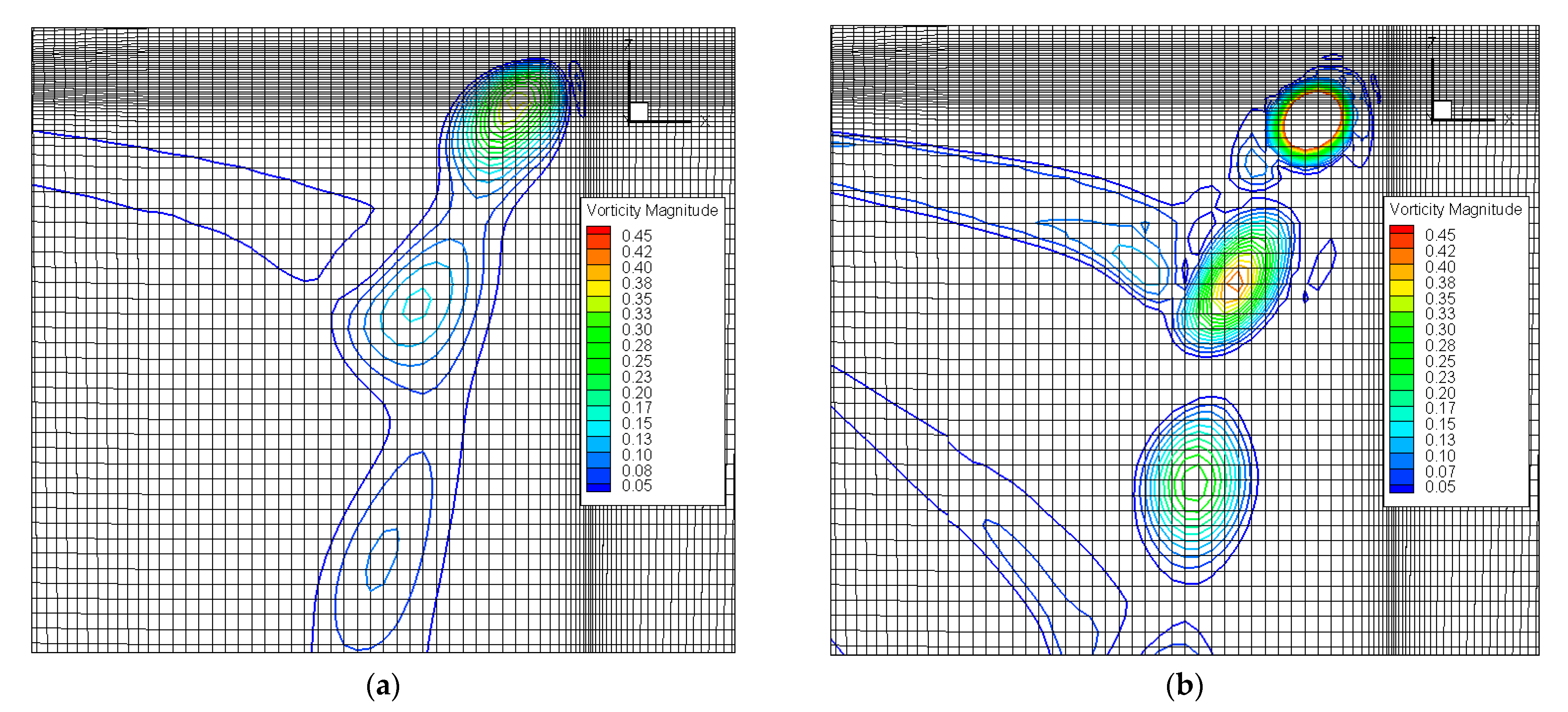
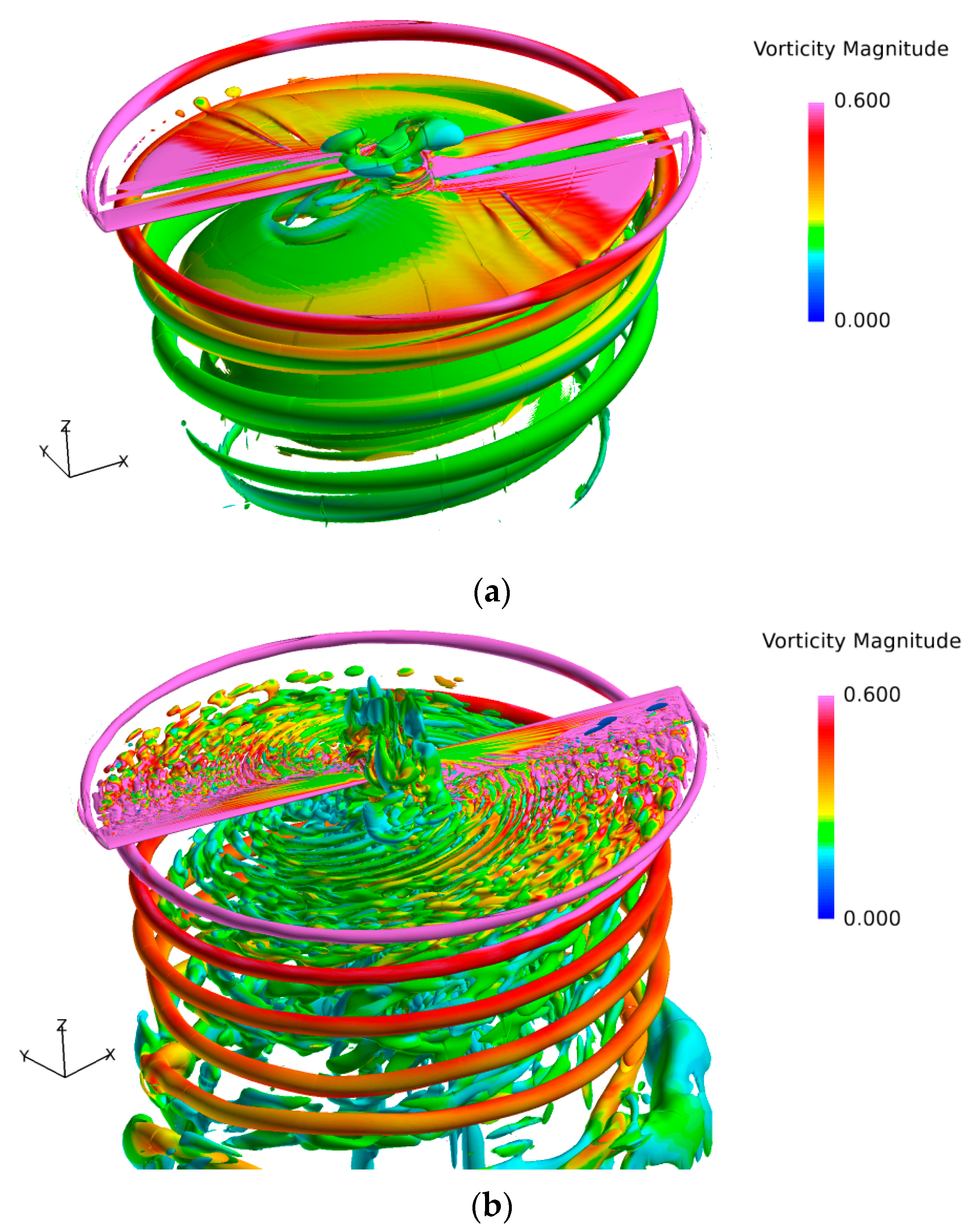
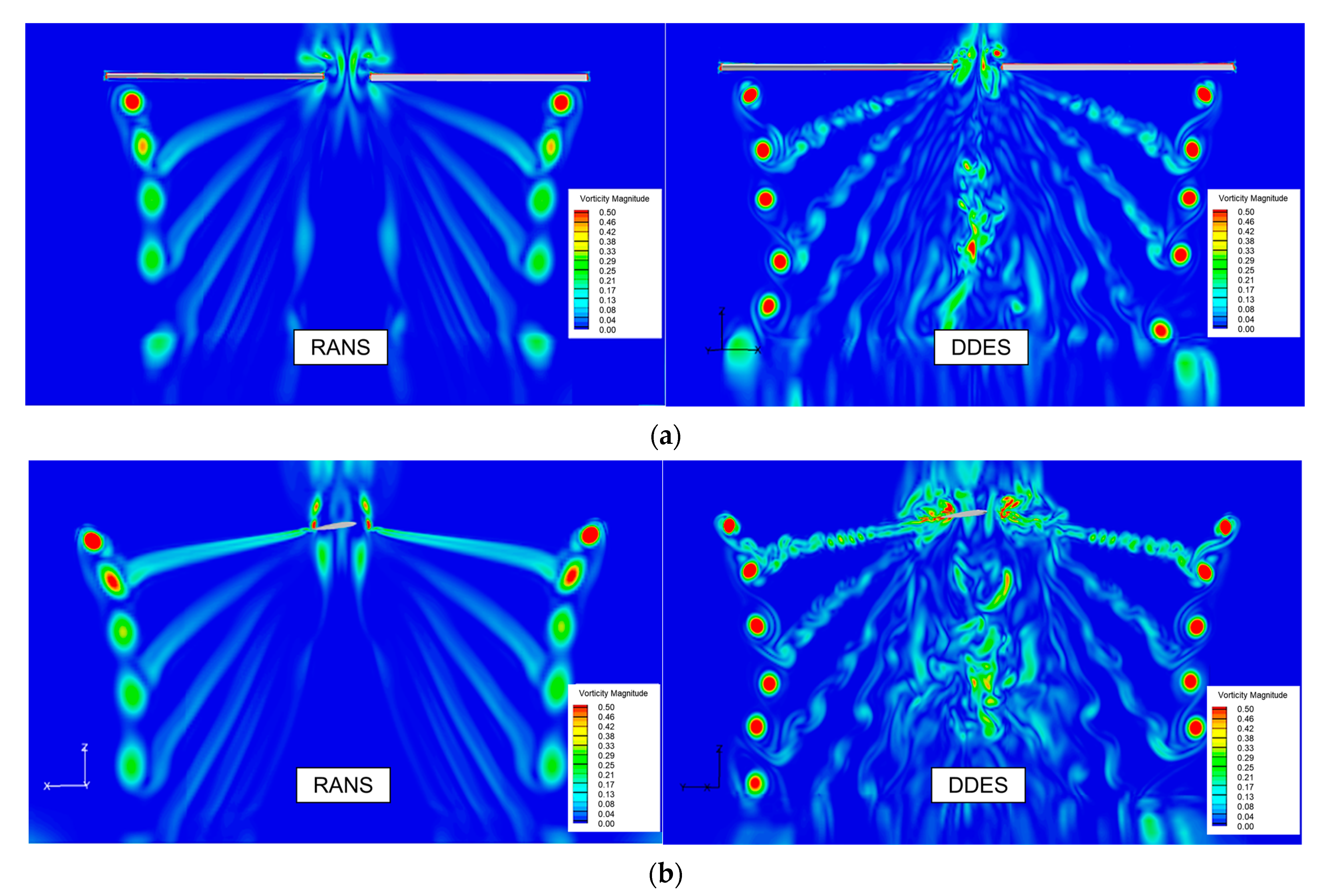
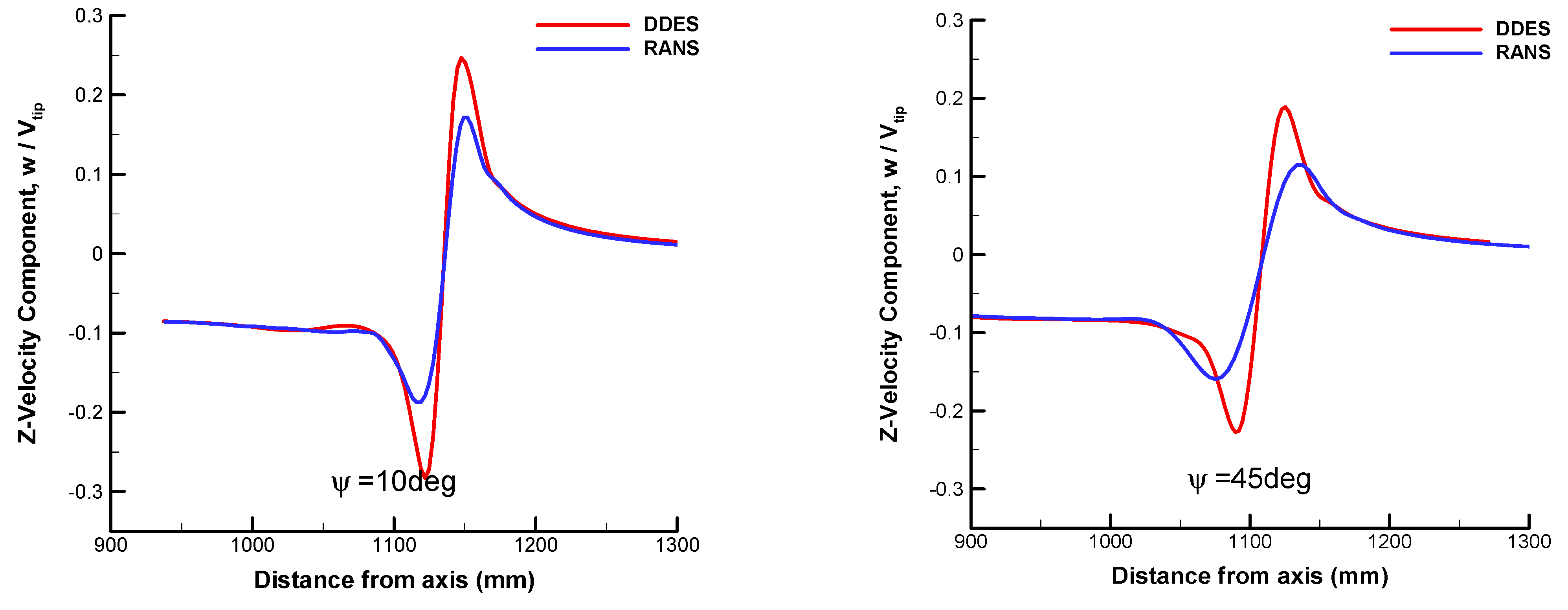
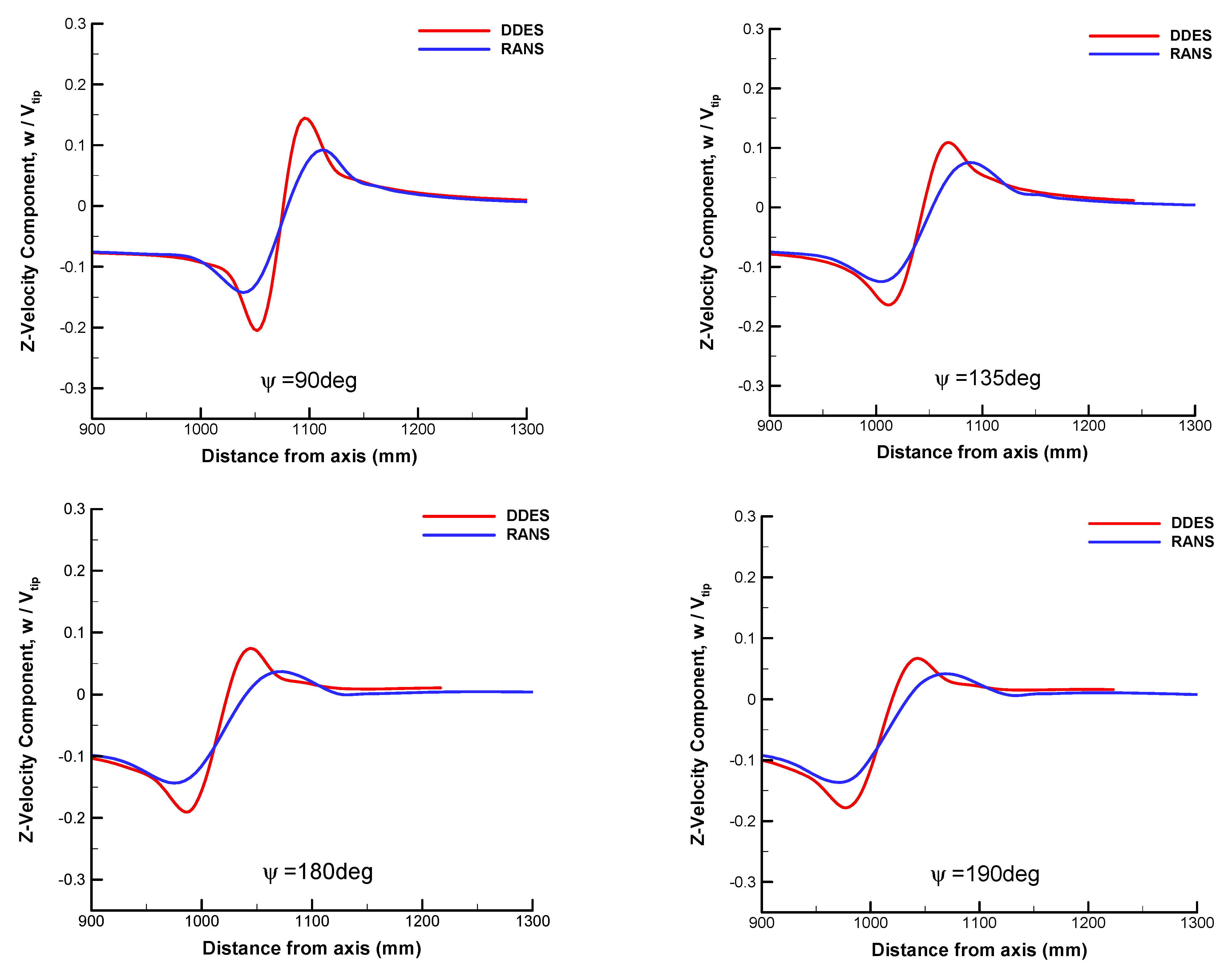
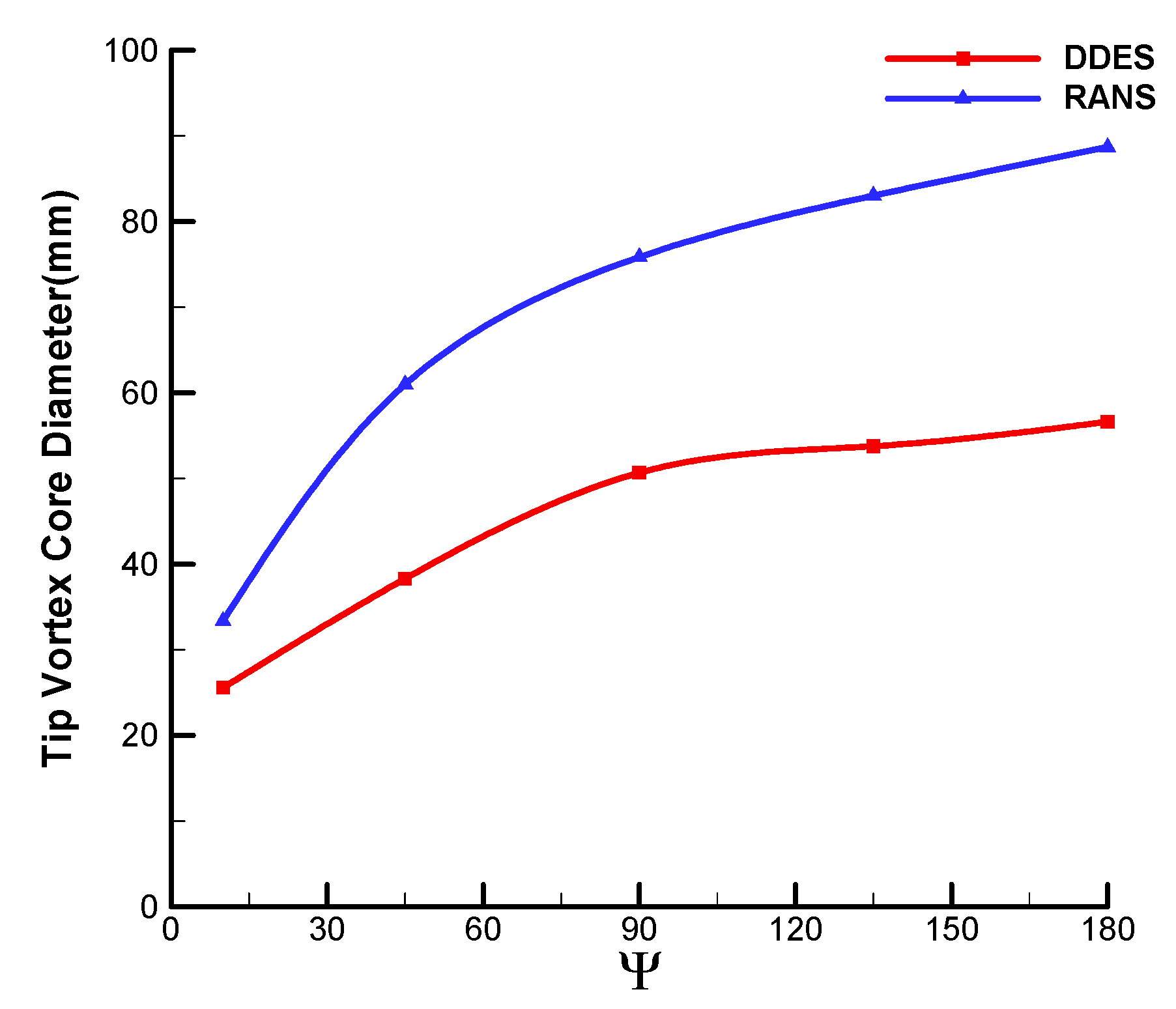
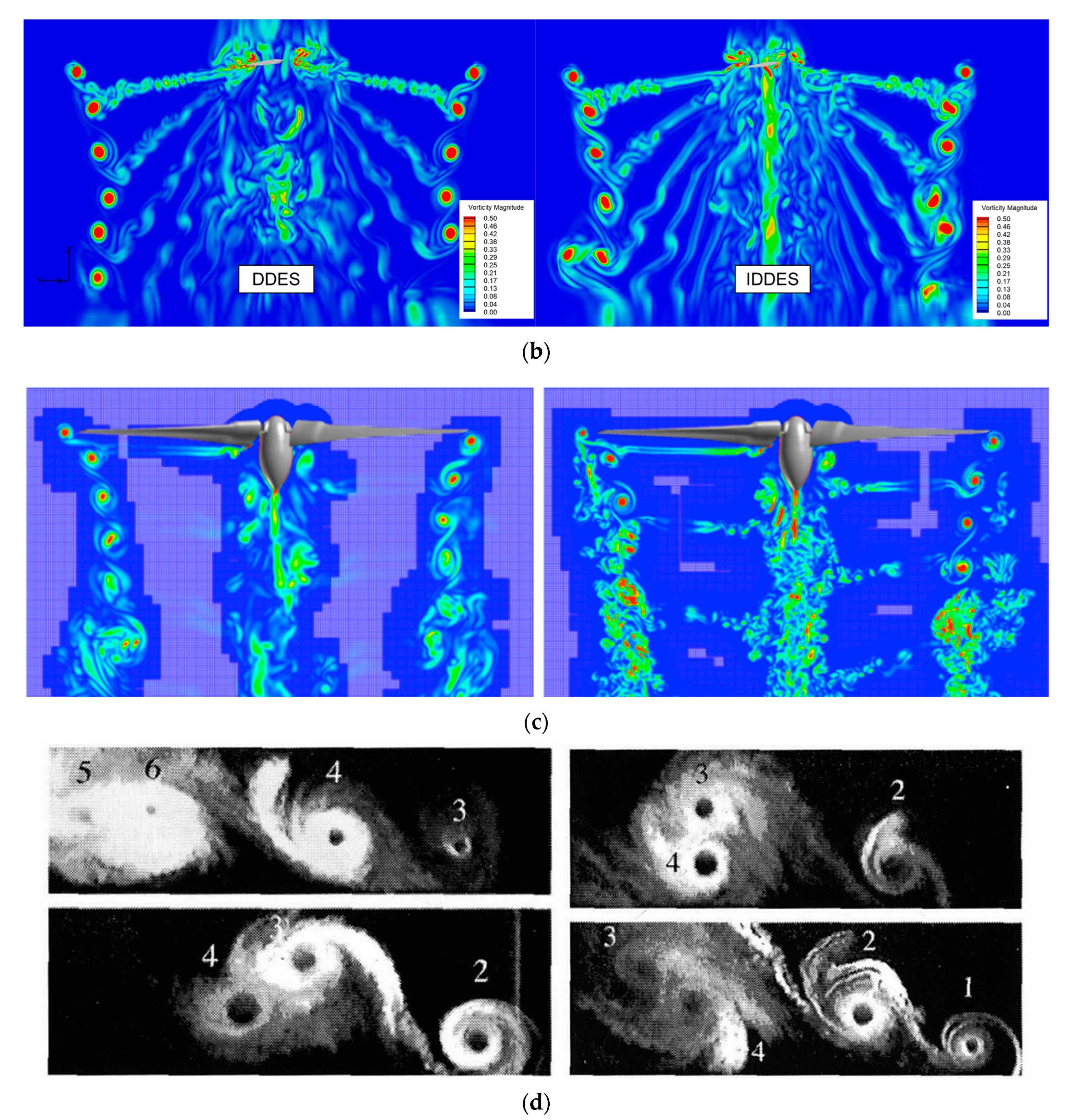
3.2. Comparison of Resolution between RANS and DDES
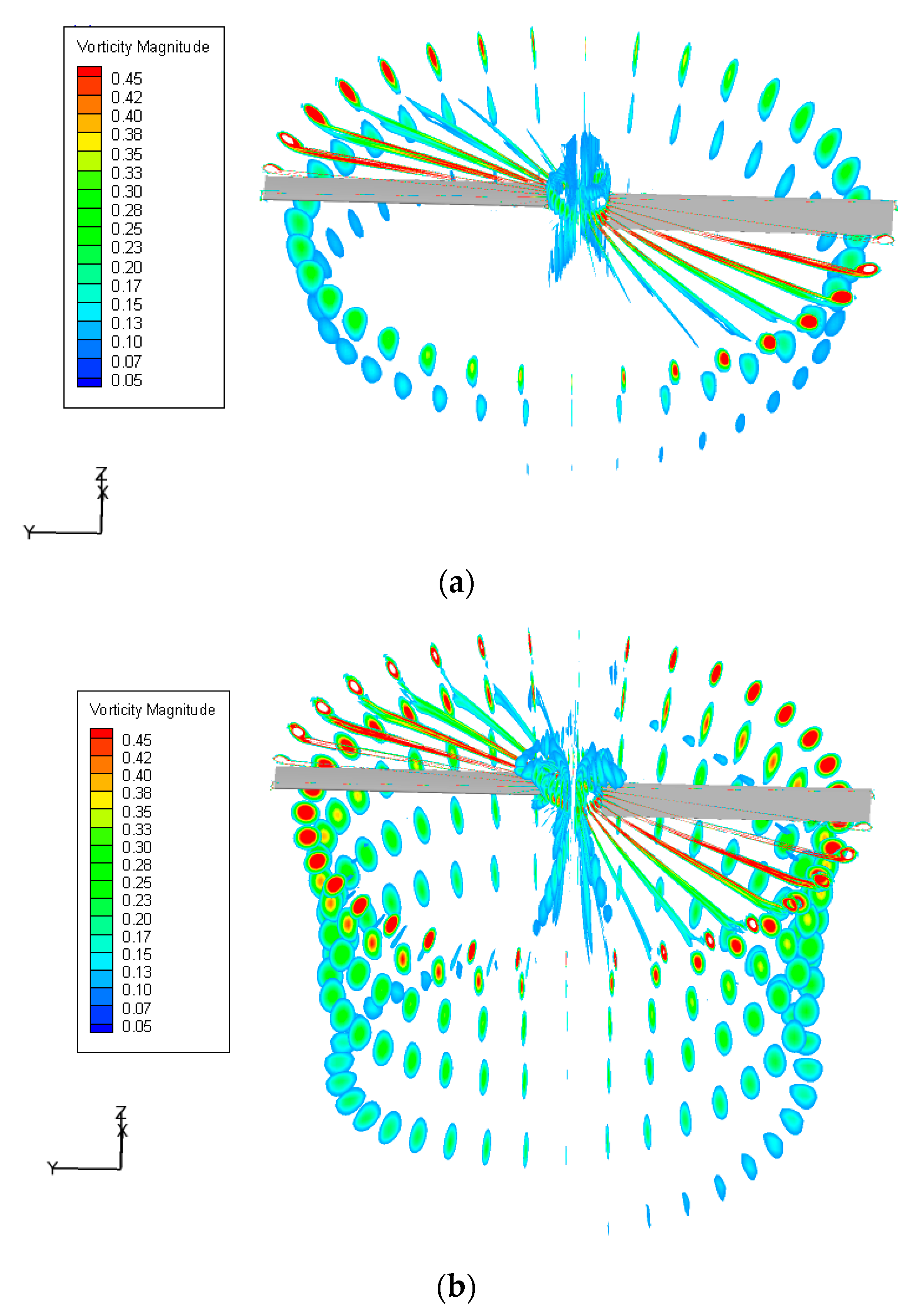
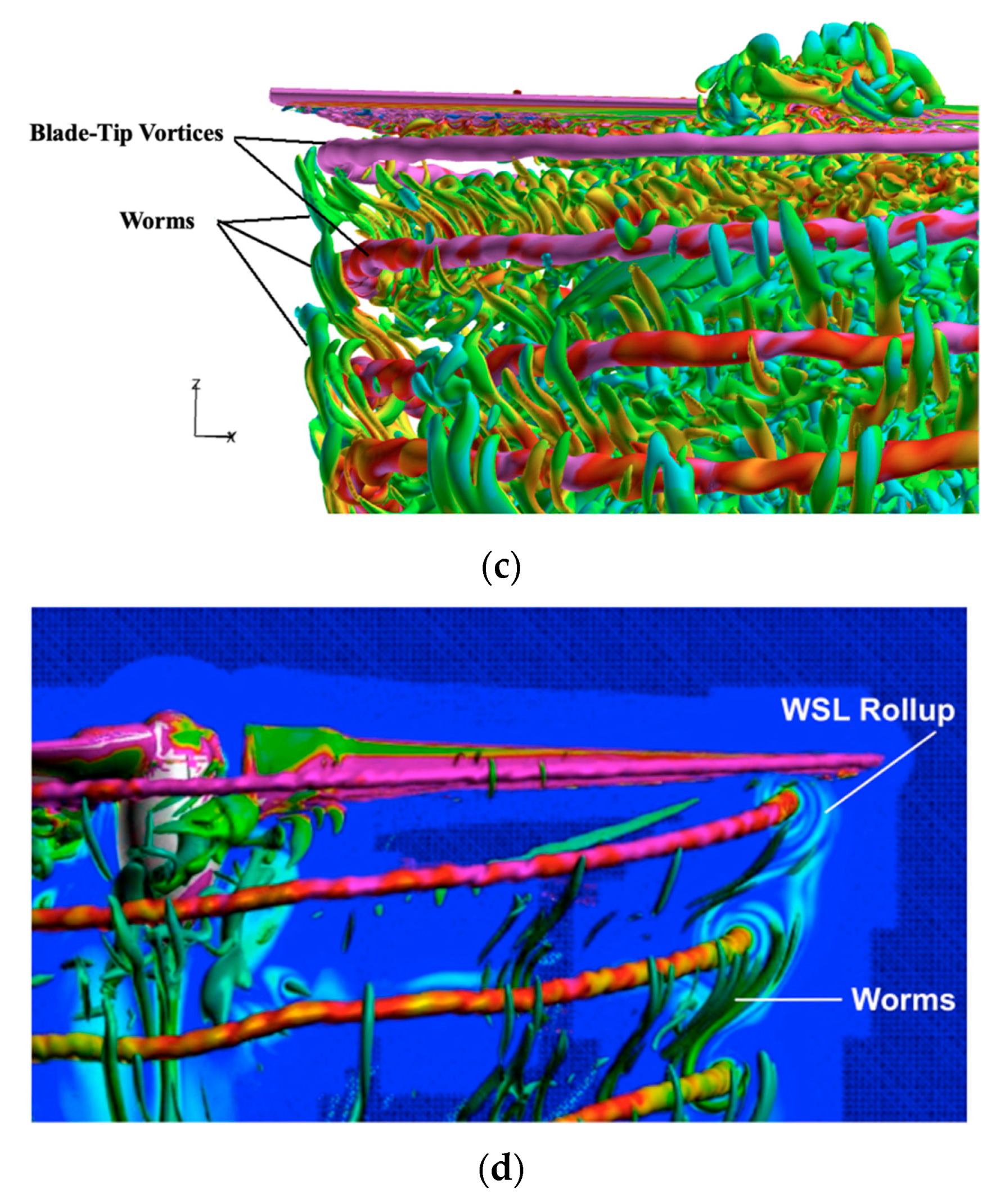
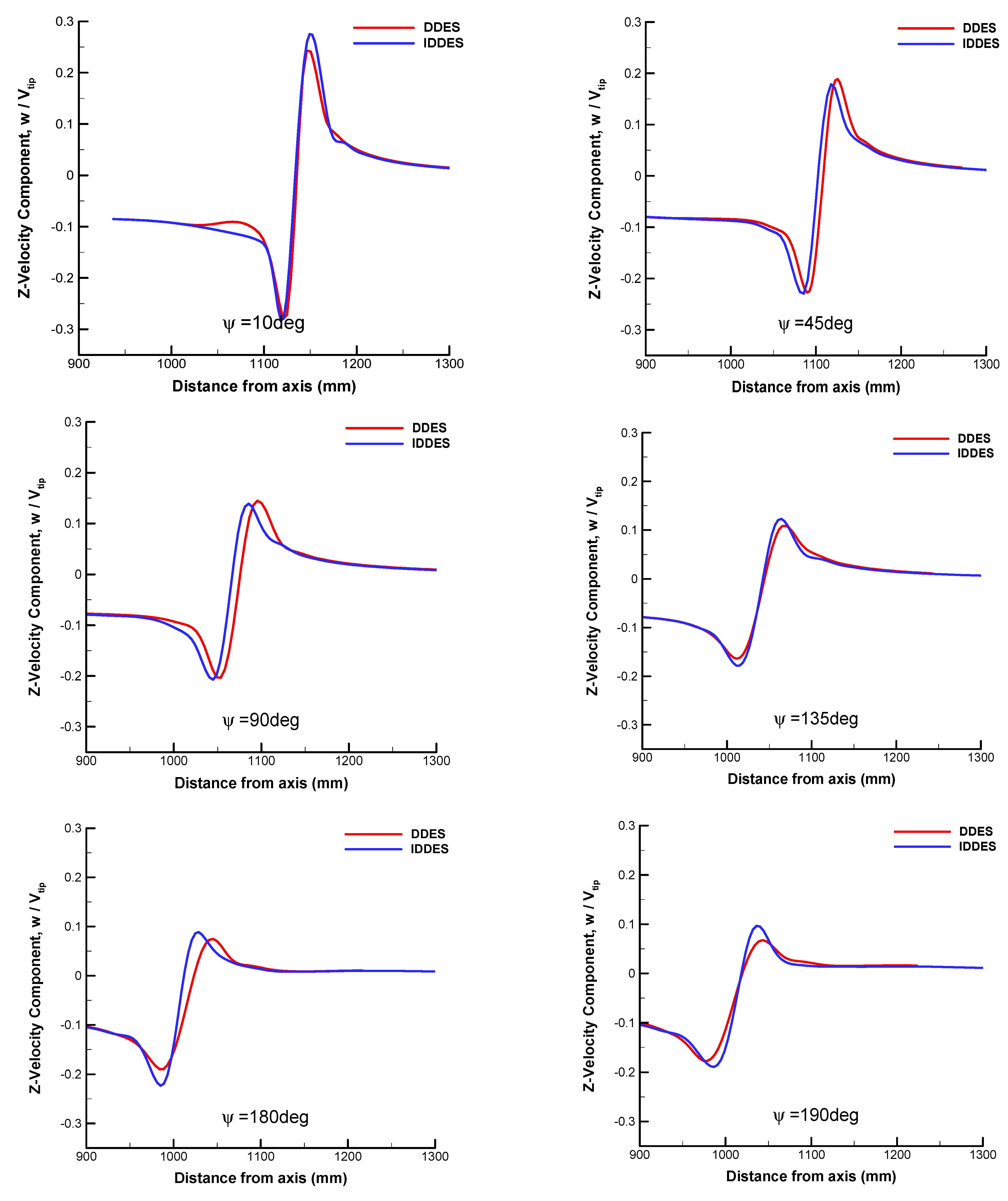
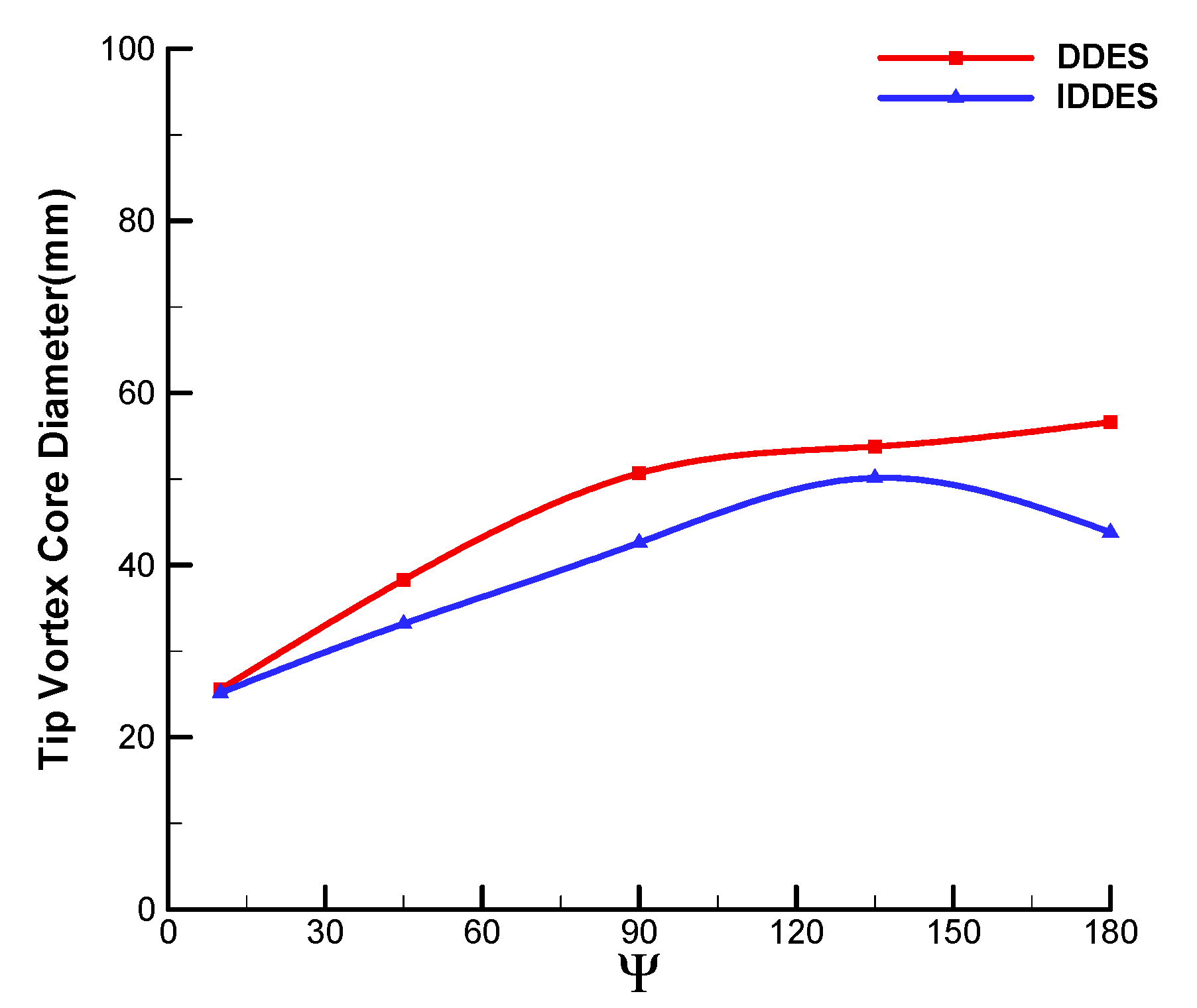
3.3. Comparison of Resolution between DDES and IDDES
4. Conclusions
- (1)
- Compared with the third-order MUSCL–Roe scheme, the fifth-order WENO–Roe scheme enhances the prediction of wake ages and vortex core diameters in the region far from the rotating plane. However, the turbulence of the flow field is totally modeled and averaged by RANS, while the time-dependent nature of the rotor flow field is not reflected properly;
- (2)
- Compared with RANS, for the well-resolving of the spatial turbulence with the switch of LES mode, the major improvement of DDES is the resolution of primary structures in the transient flow field, including blade tip vortices and vortex sheet. The asymmetrical characteristic of blade tip vortices is revealed with the release of fluctuation. The wake age of the tip vortices is prolonged with a larger vorticity value and smaller core diameter. Meanwhile, the generation and evolution of multiscale vortices are well predicted. The magnitude of peak velocity is further increased with the reduced core diameter at all wake ages.
- (3)
- With the rapid activation of WMLES mode in the focused region, the resolution of transient turbulent structures of blade tip vortices is significantly enhanced through IDDES. The behaviors of secondary turbulent structures of vortex worms around blade tip vortices are successfully predicted, including the interactions and pairing of adjacent vortices. The effects of secondary structures on the primary flow features are slight, and the statistics of velocity distributions are similar to DDES.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, Y.O.; Leishman, J.G. Investigation of Helicopter Rotor-Blade-Tip-Vortex Alleviation Using a Slotted Tip. AIAA J. 2004, 42, 524–535. [Google Scholar] [CrossRef]
- Dietz, M.; Kebler, M.; Kramer, E.; Wanger, S. Tip Vortex Conservation on a Helicopter Main Rotor Using Vortex-Adapted Chimera Grids. AIAA J. 2007, 45, 2062–2074. [Google Scholar] [CrossRef]
- Braukmann, J.N.; Schwermer, T.; Wolf, C.C. Investigation of Young Blade-Tip Vortices at a Rotor Test Facility Using Stereoscopic PIV; German Association for Laser Anemometry GALA e.V.: Karlsruhe, Germany, 2017. [Google Scholar]
- Goerttler, A.; Braukmann, J.N.; Schwermer, T.; Gardner, A.D. Tip-Vortex Investigation on a Rotating and Pitching Rotor Blade. J. Aircr. 2018, 55, 1792–1804. [Google Scholar] [CrossRef]
- Yung, H.Y. Rotor blade–vortex interaction noise. Prog. Aerosp. Sci. 2000, 36, 97–115. [Google Scholar]
- Ghias, R.; Mittal, R.; Dong, H.B.; Lund, T.S. Large-Eddy Simulation of the Tip Flow of a Rotor in Hover. In Proceedings of the 34th AIAA Fluid Dynamics Conference and Exhibit, Portland, OR, USA, 28 June–1 July 2004. [Google Scholar]
- Kao, D.L.; Smith, K.L.; Liu, Z.P. Tracking Blade Tip Vortices for Numerical Flow Simulations of Hovering Rotorcraft. In Proceedings of the AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Holst, T.; Pulliam, T. Optimization of Overset Solution Adaptive Grids for Hovering Rotorcraft Flows. In Proceedings of the 2010 AHS Specialists Meeting on Aeromechanics, San Francisco, CA, USA, 20–22 January 2010. [Google Scholar]
- Kroll, N.; Abu-Zurayk, M.; Dimitrov, D.; Franz, T.; Führer, T.; Gerhold, T.; Görtz, S.; Heinrich, R.; Ilic, C.; Jepsen, J.; et al. DLR project Digital-X: Towards virtual aircraft design and flight testing based on high-fidelity methods. CEAS Aeronaut. J. 2016, 7, 3–27. [Google Scholar] [CrossRef]
- Sankar, L.; Yeshala, N.; Hariharan, N. Application of Spatially High Order Adaptive Methods for Unsteady Flow over Rotary Wing Configurations. In Proceedings of the International Forum on Rotorcraft Multidisciplinary Technology, American Helicopter Society Specialists Meeting, Seoul, Republic of Korea, 15–17 October 2007. [Google Scholar]
- Sankaran, V.; Sitaraman, J.; Wissink, A.; Datta, A.; Strawn, R. Application of the Helios Computational Platform to Rotorcraft Flowfields. In Proceedings of the AIAA-2010-1230, 48th AIAA Aerospace Sciences Meeting, Orlando, FL, USA, 4–7 January 2010. [Google Scholar]
- Yeshala, N.; Egolf, A.; Vasilescu, R.; Sankar, L. Application of higher order spatially accurate schemes to rotors in hover. In Proceedings of the 24th AIAA Applied Aerodynamics Conference, San Francisco, CA, USA, 5–8 June 2006. [Google Scholar]
- Kowarsch, U.; Oehrle, C.; Hollands, M.; Keßler, M.; Krämer, E. Computation of helicopter phenomena using a higher order method. In High Performance Computing in Science and Engineering ’13: Transactions of the High Performance Computing Center, Stuttgart (HLRS) 2013; Springer International Publishing: Cham, Switzerland, 2013; pp. 423–438. [Google Scholar]
- Xu, L.; Weng, P.F. High order accurate and low dissipation method for unsteady compressible viscous flow computation on helicopter rotor in forward flight. J. Comput. Phys. 2014, 258, 470–488. [Google Scholar] [CrossRef]
- Kranzinger, P.P.; Kowarsch, U.; Schuff, M.; Keßler, M.; Krämer, E. Advances in parallelization and high-fidelity simulation of helicopter phenomena. In High Performance Computing in Science and Engineering’ 15: Transactions of the High Performance Computing Center, Stuttgart (HLRS) 2015; Springer International Publishing: Cham, Switzerland, 2016; pp. 479–494. [Google Scholar]
- Zhao, Q.J.; Zhang, G.Q.; Wang, B.; Wang, Q.; Shi, Y.J.; Xu, G.H. Robust Navier-Stokes method for predicting unsteady flowfield and aerodynamic characteristics of helicopter rotor. Chin. J. Aeronaut. 2018, 31, 214–224. [Google Scholar] [CrossRef]
- Frey, F.; Herb, J.; Letzgus, J.; Weihing, P.; Keßler, M.; Krämer, E. Enhancement and application of the flow solver FLOWer. In High Performance Computing in Science and Engineering’18: Transactions of the High Performance Computing Center, Stuttgart (HLRS) 2018; Springer International Publishing: Cham, Switzerland, 2019; pp. 323–336. [Google Scholar]
- Ricci, F.; Silva, P.A.; Tsoutsanis, P.; Antoniadis, A.F. Hovering rotor solutions by high-order methods on unstructured grids. Aerosp. Sci. Technol. 2020, 97, 105648. [Google Scholar] [CrossRef]
- Han, S.Q.; Song, W.P.; Han, Z.H. A novel high-order scheme for numerical simulation of wake flow over helicopter rotors in hover. Chin. J. Aeronaut. 2022, 35, 260–274. [Google Scholar] [CrossRef]
- Sun, Y.; Shi, Y.; Xu, G. Application of High-Order WENO Scheme in the CFD/FW–H Method to Predict Helicopter Rotor Blade–Vortex Interaction Tonal Noise. Aerospace 2022, 9, 196. [Google Scholar] [CrossRef]
- Busch, E.R.; Wurst, M.S.; Keßler, M.; Krämer, E. Computational aeroacoustics with higher order methods. In High Performance Computing in Science and Engineering ‘12: Transactions of the High Performance Computing Center, Stuttgart (HLRS) 2012; Springer: Berlin/Heidelberg, Germany, 2013; pp. 239–253. [Google Scholar]
- Kara, K.; Brazell, M.J.; Kirby, A.C.; Mavriplis, D.J.; Duque, E.P. Hover predictions using a high-order discontinuous Galerkin off-body discretization. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 0771. [Google Scholar]
- Genuit, F.; Keßler, M.; Krämer, E. Simulation of Flow Phenomena at a Rotor with a Discontinuous Galerkin CFD Solver. In High Performance Computing in Science and Engineering’19: Transactions of the High Performance Computing Center, Stuttgart (HLRS) 2019; Springer International Publishing: Cham, Switzerland, 2021; pp. 395–407. [Google Scholar]
- Chaderjian, N.M.; Ahmad, J.U. Detached eddy simulation of the UH-60 rotor wake using adaptive mesh refinement. In Proceedings of the AHS International 68th Annual Forum, Fort Worth, TX, USA, 1–3 May 2012. [Google Scholar]
- Chaderjian, N.M. Advances in rotor performance and turbulent wake simulation using DES and adaptive mesh refinement. In Proceedings of the Seventh International Conference on Computational Fluid Dynamics (ICCFD7), Big Island, HI, USA, 9–13 July 2012. [Google Scholar]
- Chaderjian, N.M. Navier-Stokes simulation of UH-60A rotor/wake interaction using adaptive mesh refinement. In Proceedings of the AHS International Annual Forum & Technology Display, Fort Worth, TX, USA, 9–11 May 2017. [Google Scholar]
- Yoon, S.; Pulliam, T.H.; Chaderjian, N.M. Simulations of XV-15 rotor flows in hover using OVERFLOW. In Proceedings of the Fifth Decennial AHS Aeromechanics Specialists’ Conference, San Francisco, CA, USA, 22–24 January 2014. [Google Scholar]
- Coder, J.G. OVERFLOW rotor simulations using advanced turbulence and transition modeling. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Van Leer, B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Jiang, G.S.; Shu, C.W. Efficient implementation of weighted ENO schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- Caradonna, F.X.; Tung, C. Experimental and analytical studies of a model helicopter rotor in hover. In Proceedings of the European Rotorcraft and Powered Lift Aircraft Forum, Garmisch-Partenkirchen, Germany, 8–11 September 1981. [Google Scholar]
- Jameson, A. Time dependent calculations using multigrid with applications to unsteady flows past airfoils and wings. In Proceedings of the 10th Computational Fluid Dynamics Conference, Honolulu, HI, USA, 24–26 June 1991. [Google Scholar]
- Yoon, S.; Jameson, A. Lower-upper symmetric-Gauss-Seidel method for the Euler and Navier-Stokes equations. AIAA J. 1988, 26, 1025–1026. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Shi, W.; Li, J.; Gao, H.; Zhang, H.; Yang, Z.; Jiang, Y. Numerical investigations on drag reduction of a civil light helicopter fuselage. Aerosp. Sci. Technol. 2020, 106, 106104. [Google Scholar] [CrossRef]
- Shi, W.; Li, J.; Zhao, S.; Yang, Z. Investigation and Improvement of Pusher-Propeller Installation Effect for Flying Wing UAV. Int. J. Aeronaut. Space Sci. 2021, 22, 287–302. [Google Scholar] [CrossRef]
- Yin, Z.; Zhao, Q.; Wang, B. Numerical simulations for unsteady vortex flowfield of rotors based on high-order WENO scheme. Acta Aeronaut. Astronaut. Sin. 2016, 37, 2552–2564. [Google Scholar]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.; Travin, A. A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theor. Comput. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Spalart, P.R. Detached-eddy simulation. Annu. Rev. Fluid Mech. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Caradonna, F. Performance measurement and wake characteristics of a model rotor in axial flight. J. Am. Helicopter Soc. 1999, 44, 101–108. [Google Scholar] [CrossRef]
- Young, L.A.; Warmbrodt, W. Vortex Core Size in the Rotor Near-Wake; NASA/TM-2003-212275; NASA: Washington, DC, USA, 2003.
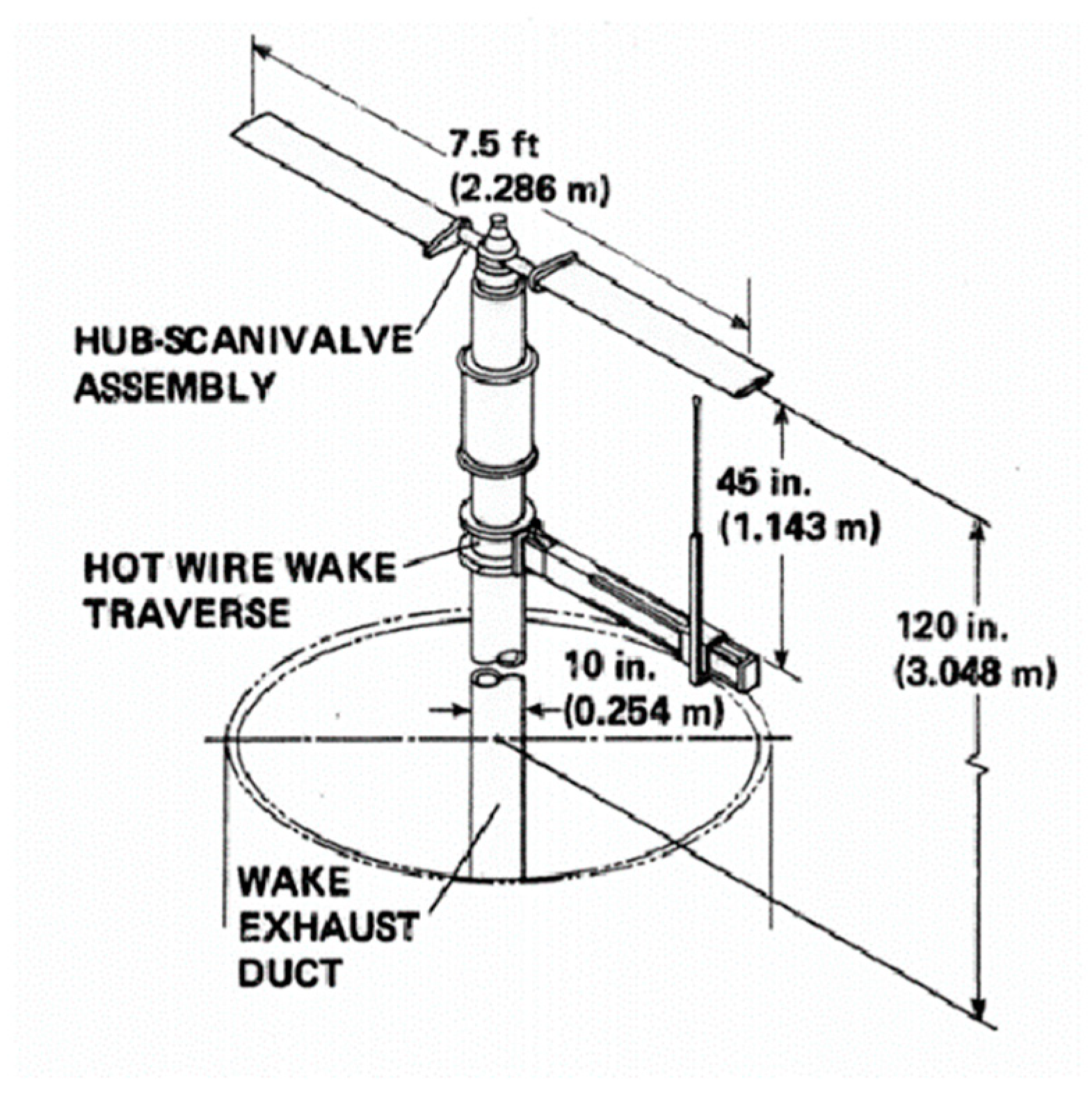
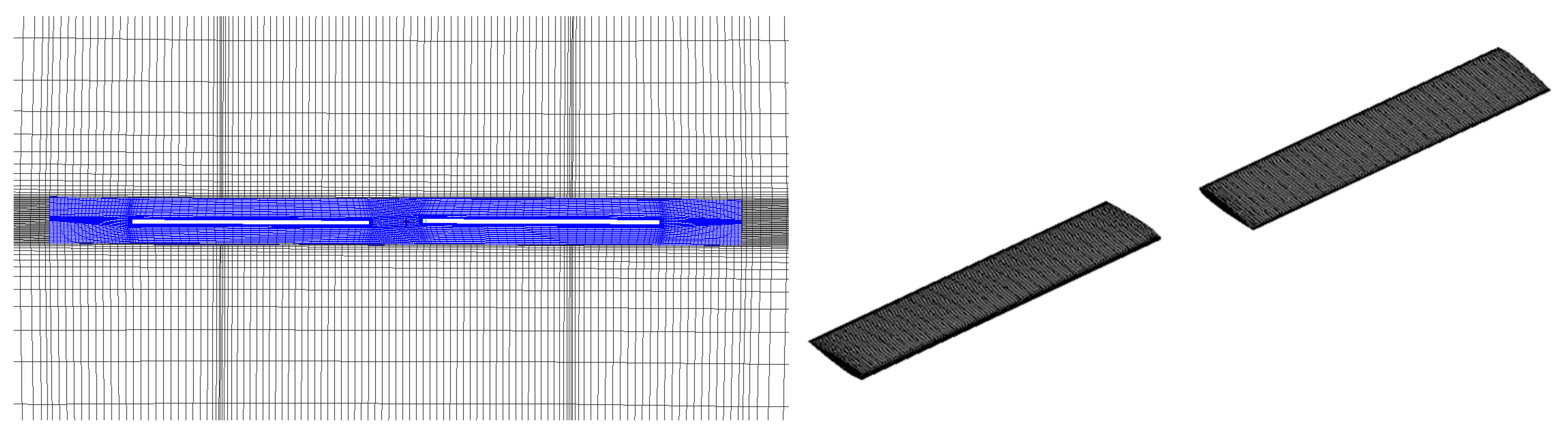
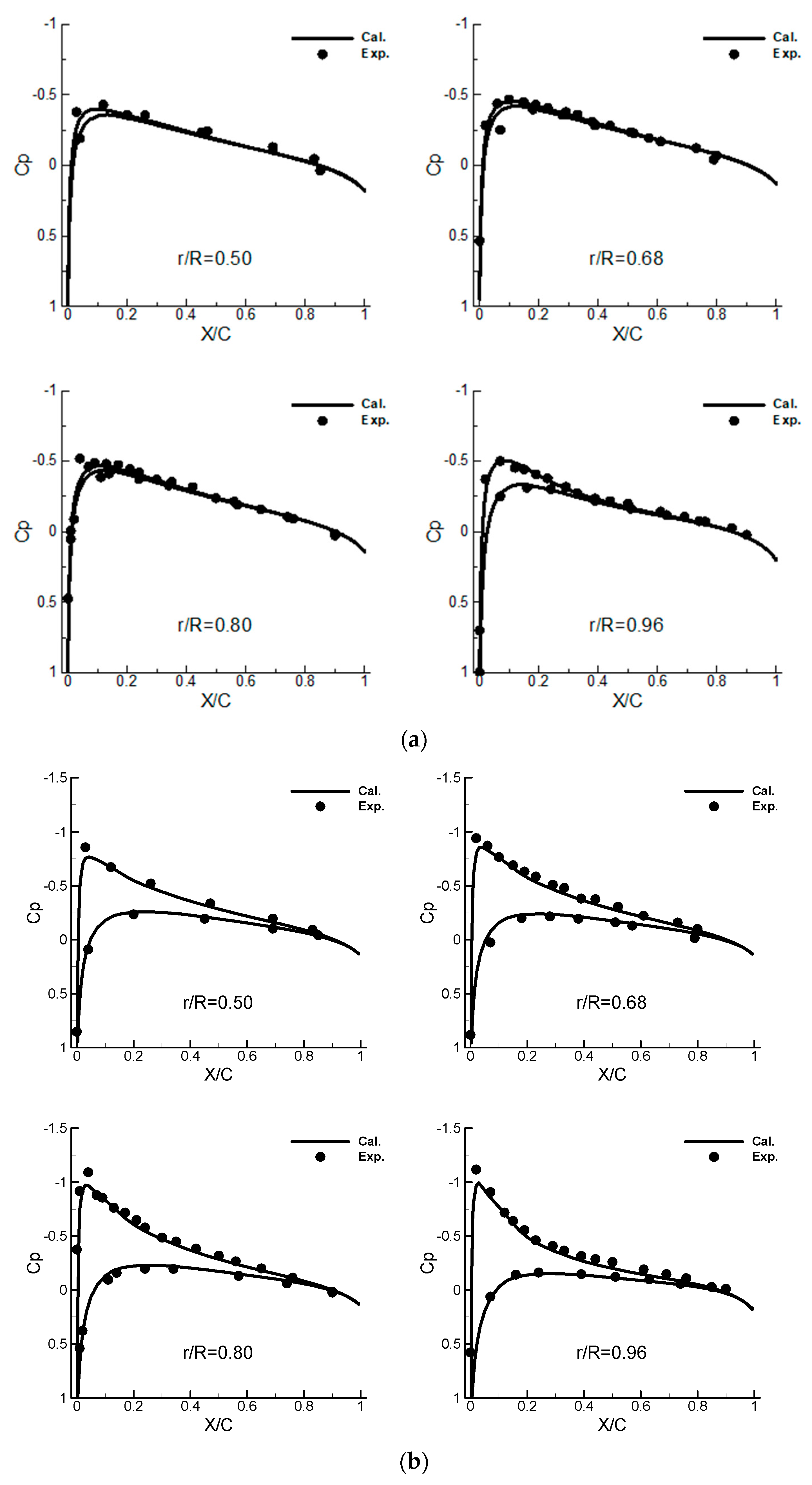
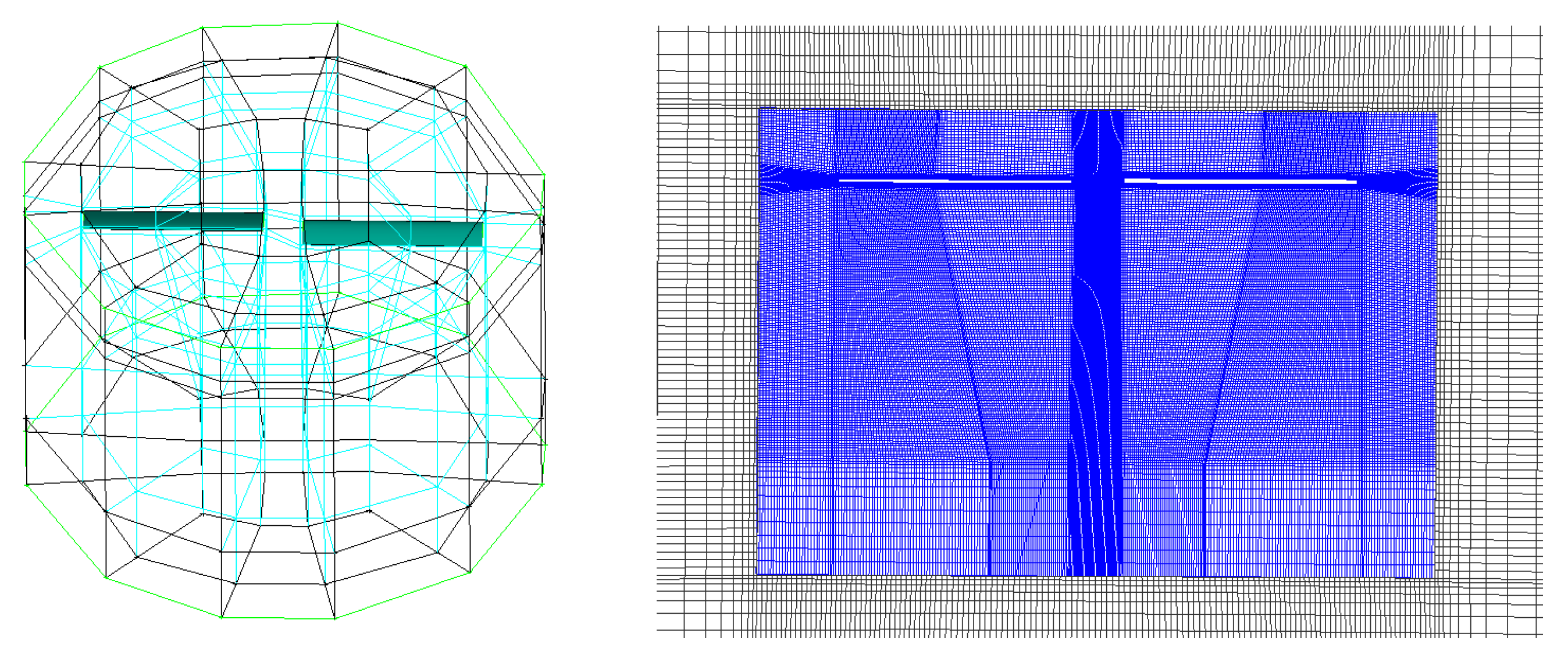
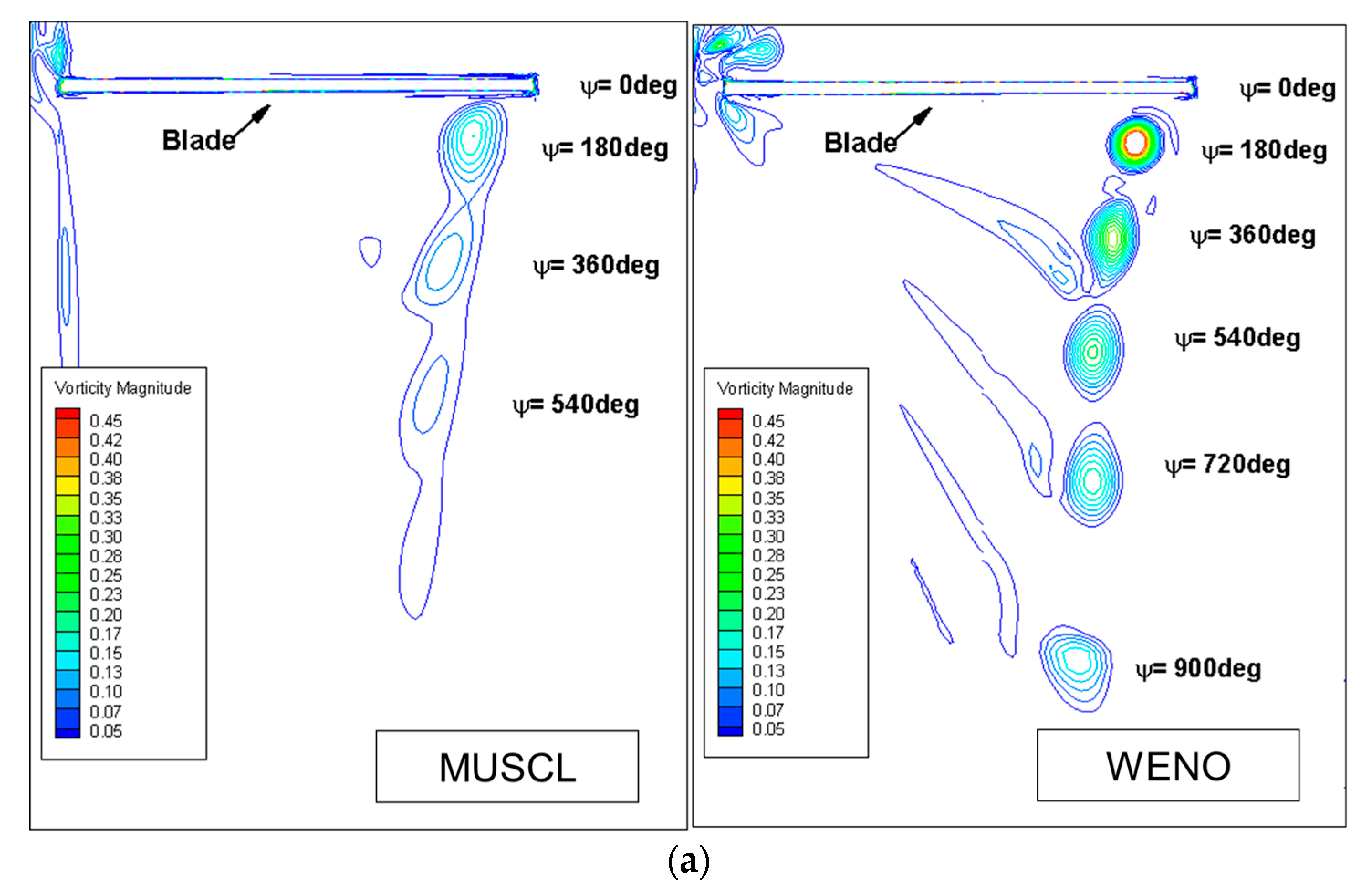
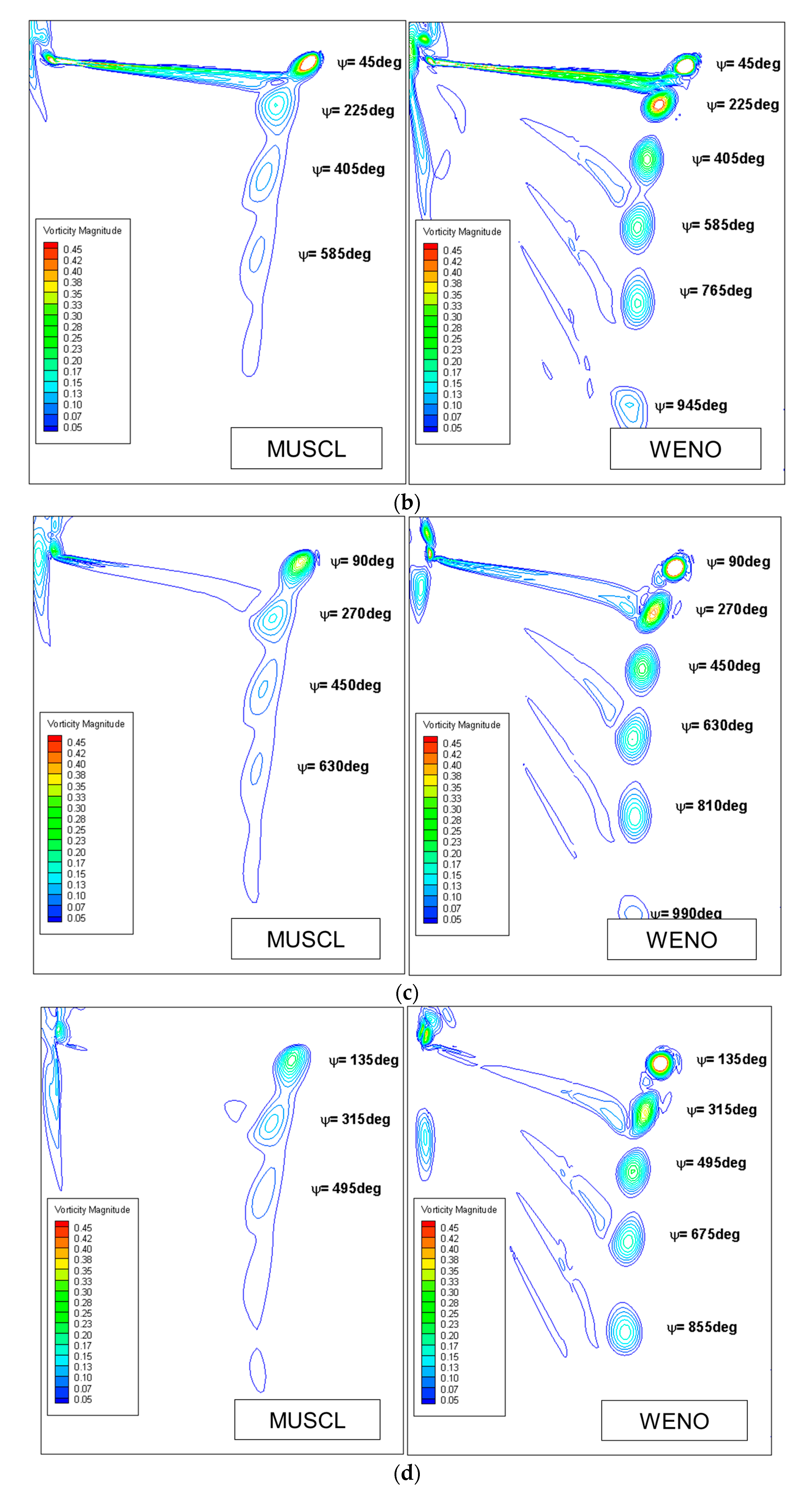
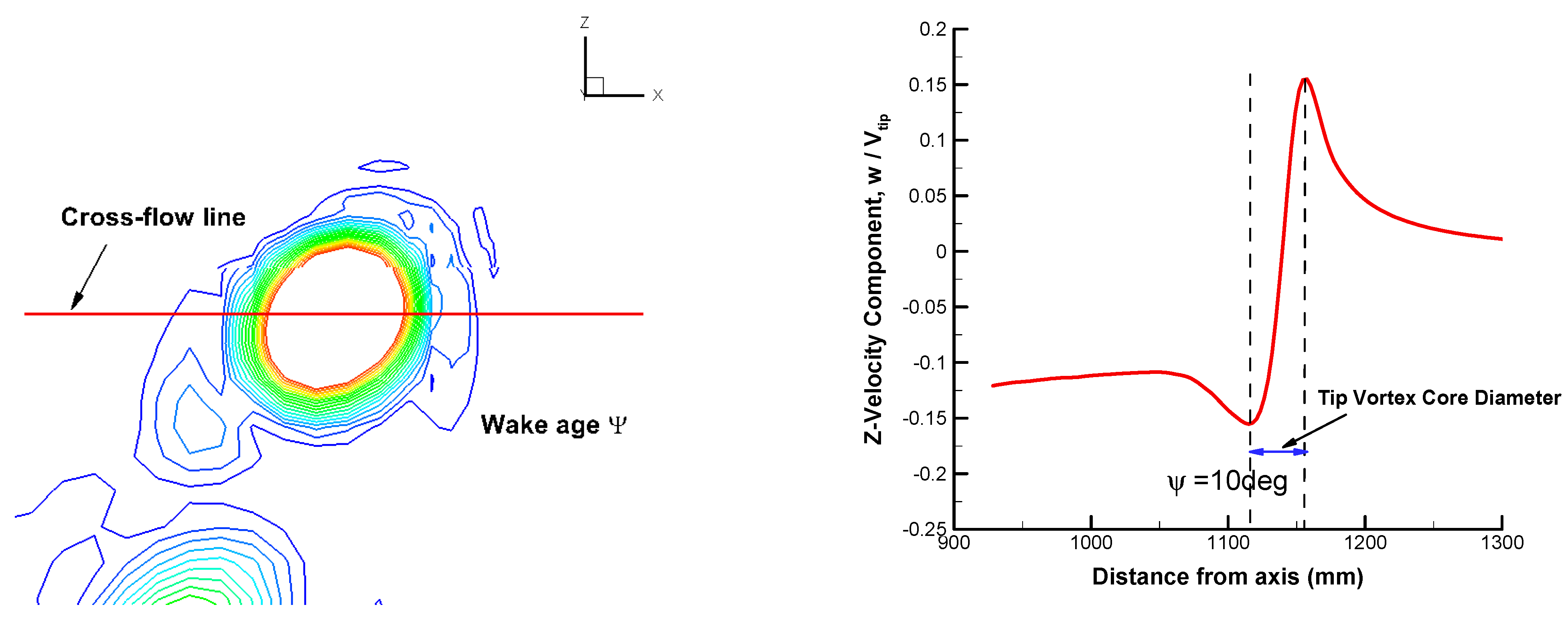
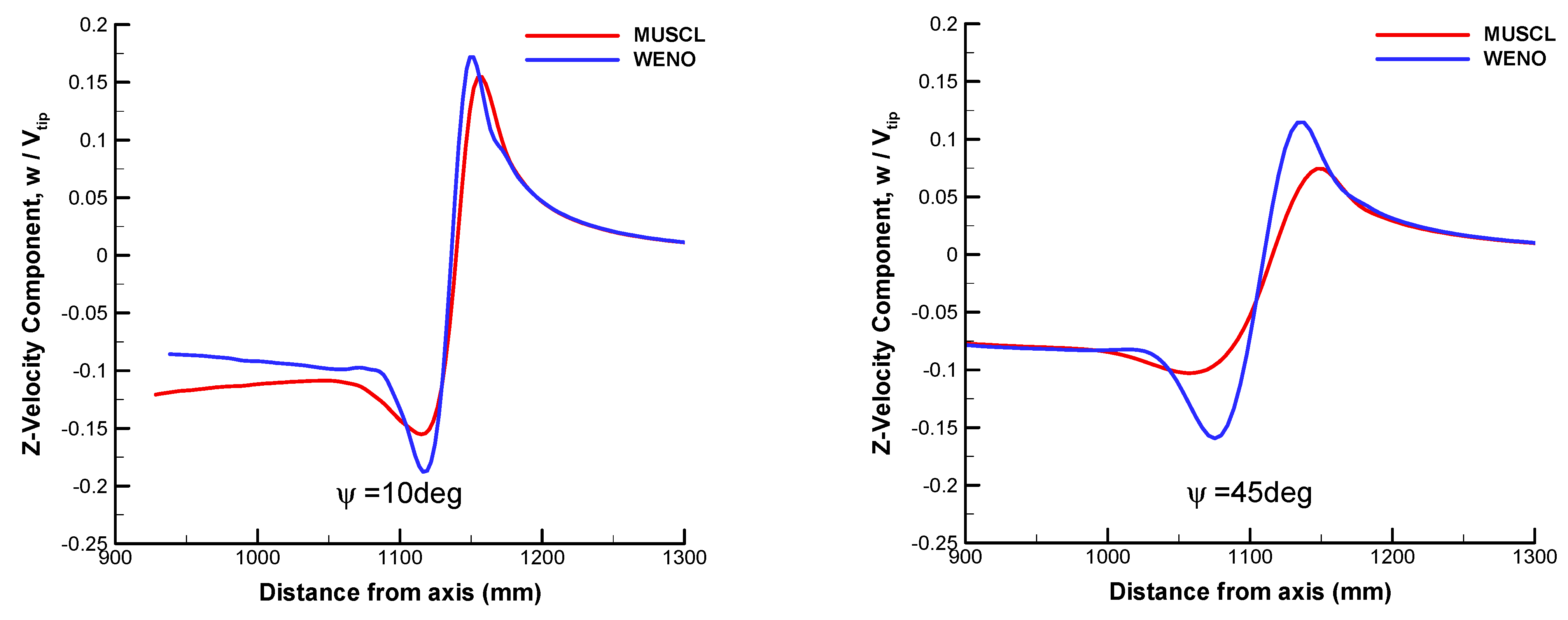



| Rotor Tip Mach Number (Mtip) | Blade Pitch Angle (θc) |
|---|---|
| 0.44 | 2 deg |
| 0.44 | 8 deg |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, W.; Zhang, H.; Li, Y. Enhancing the Resolution of Blade Tip Vortices in Hover with High-Order WENO Scheme and Hybrid RANS–LES Methods. Aerospace 2023, 10, 262. https://doi.org/10.3390/aerospace10030262
Shi W, Zhang H, Li Y. Enhancing the Resolution of Blade Tip Vortices in Hover with High-Order WENO Scheme and Hybrid RANS–LES Methods. Aerospace. 2023; 10(3):262. https://doi.org/10.3390/aerospace10030262
Chicago/Turabian StyleShi, Wenbo, Heng Zhang, and Yuanxiang Li. 2023. "Enhancing the Resolution of Blade Tip Vortices in Hover with High-Order WENO Scheme and Hybrid RANS–LES Methods" Aerospace 10, no. 3: 262. https://doi.org/10.3390/aerospace10030262
APA StyleShi, W., Zhang, H., & Li, Y. (2023). Enhancing the Resolution of Blade Tip Vortices in Hover with High-Order WENO Scheme and Hybrid RANS–LES Methods. Aerospace, 10(3), 262. https://doi.org/10.3390/aerospace10030262




