Study on Characteristics and Invulnerability of Airspace Sector Network Using Complex Network Theory
Abstract
1. Introduction
- This paper expands the research horizon of aviation networks by incorporating complex network theory into ATC sectors, offering a complementary viewpoint to existing studies on aviation networks and route networks.
- The invulnerability of various sectors under different attack strategies is evaluated, and critical sectors are identified by considering the network’s global efficiency and the relative size of its connected component.
- This research provides a perspective on alleviating air traffic congestion and improving airspace efficiency by improving the sector structure in air traffic control systems. Additionally, this research method also provides a reference for analysis in other complex network engineering projects.
2. Methods of Modeling and Topological Property Measurement
2.1. Modeling of Airspace Sector Network
2.2. Modeling of Airspace Sector Network
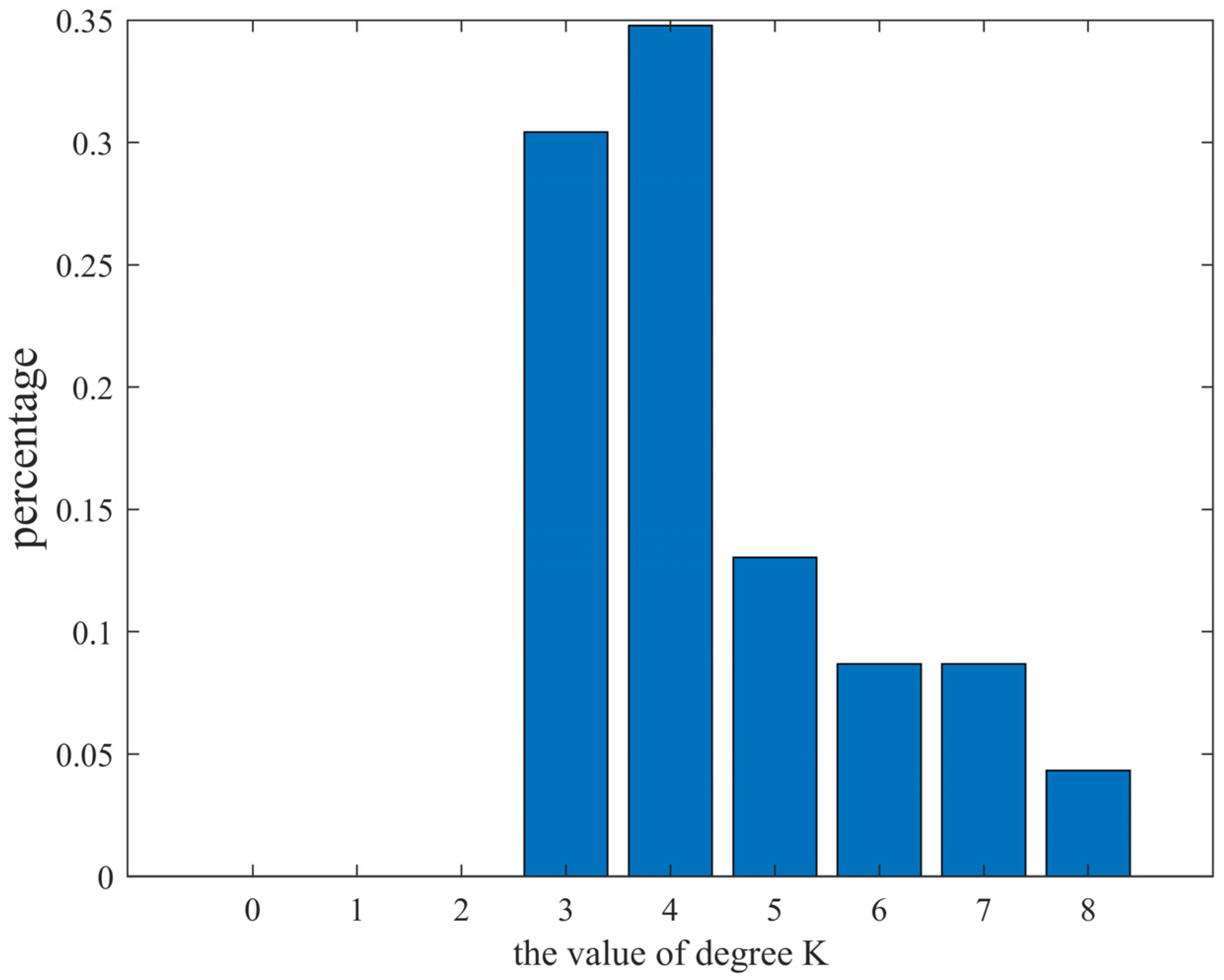
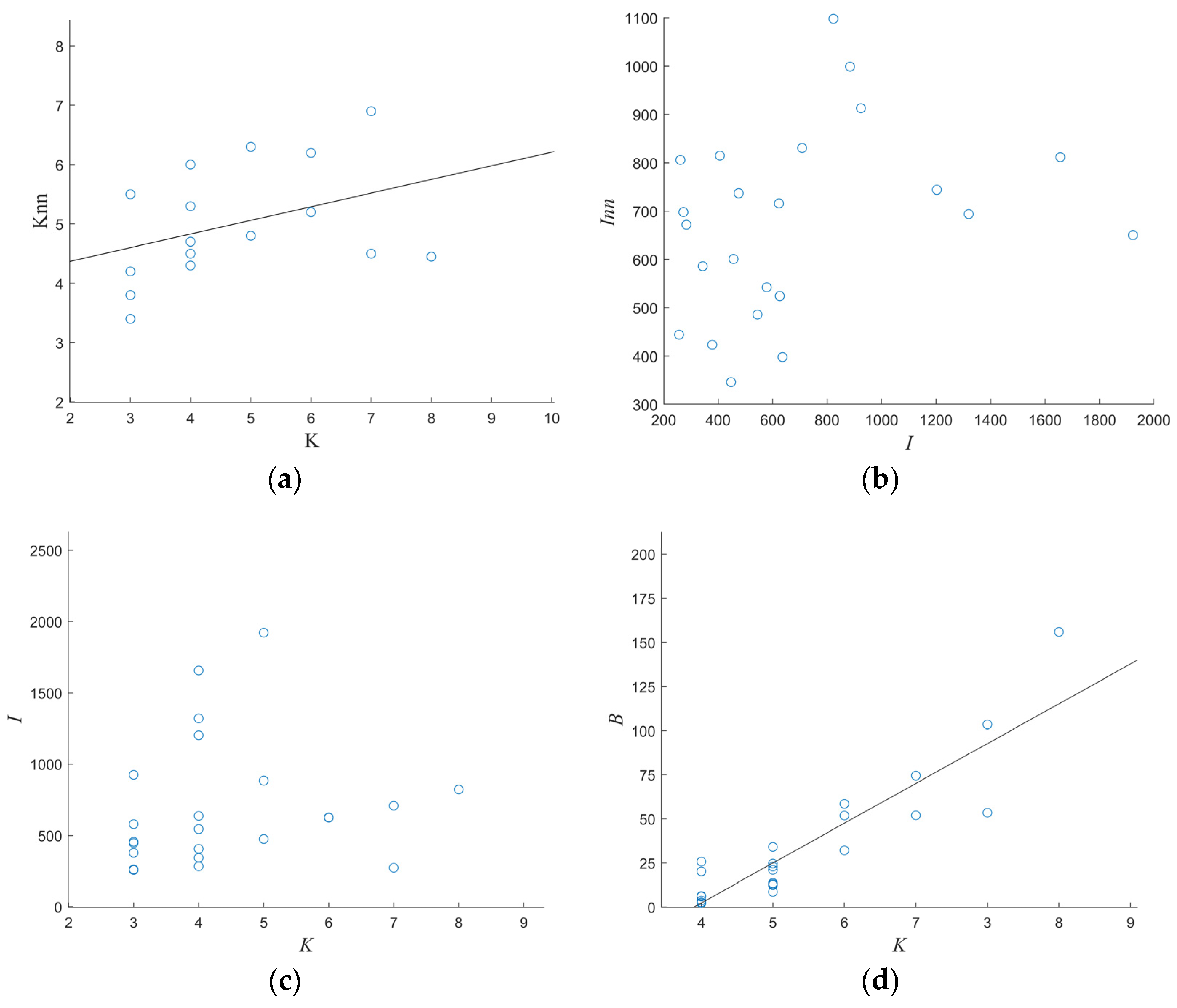
- The degree of a node, denoted as , reflects the node’s significance in the network and is defined as the number of edges connected to it. In the context of the airspace sector network, the degree of sector represents the number of sectors that are geographically adjacent and have a direct air traffic connection with sector [23]. This study expands the research scope of aviation networks by applying complex network theory to ATC sectors, providing a complementary perspective to previous studies on aviation and route networks.
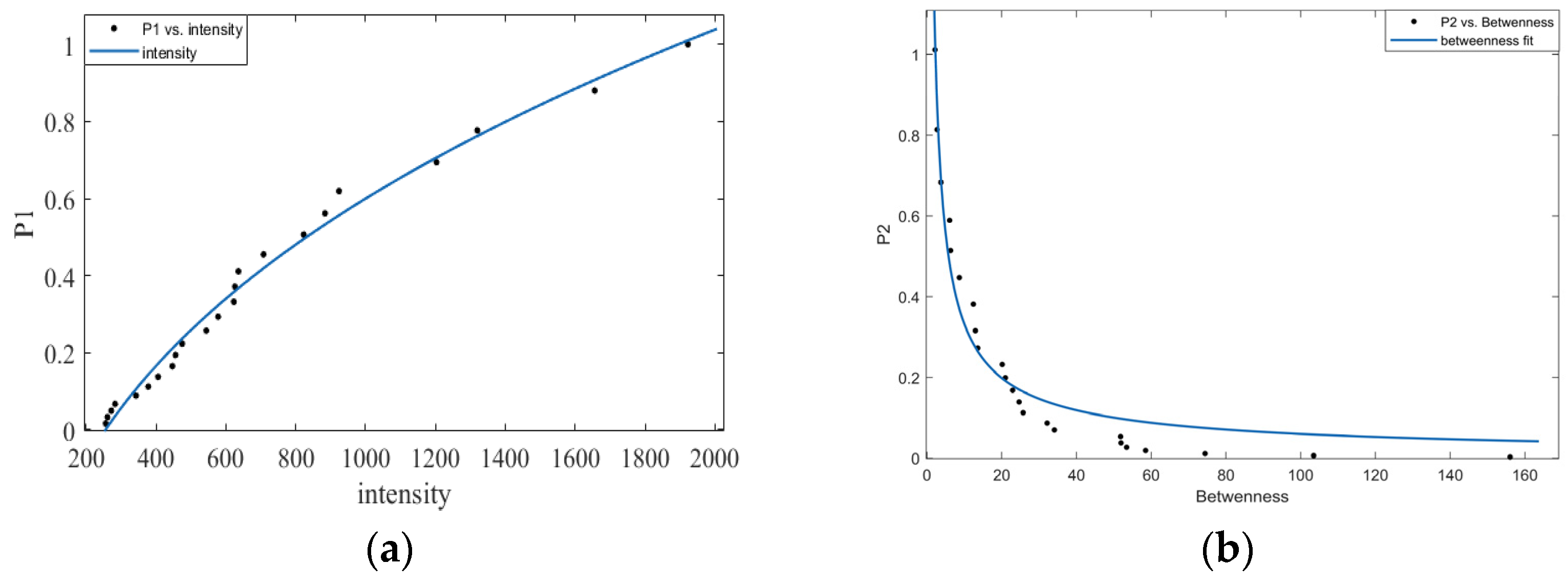
- Intensity, as expressed in Equation (1):where represents the set of sectors adjacent to sector , represents the total number of flights between sector and sector that receive ATC services within sector , and represents the overall traffic volume of sector . This last metric is considered one of the key indicators in the study of air traffic congestion [24].
- Average path length, as expressed in Equation (2):where refers to the total number of sectors in the network, and is the shortest path length between sector and sector . From an ATC perspective, represents the number of air traffic control services received by a flight traveling between sector and sector , with a value of for adjacent sectors. A smaller value of indicates that flights traverse fewer sectors and therefore require fewer control transfers. Consequently, a smaller value of suggests that the airspace sector network is better established and has higher operational efficiency [12].
- Betweenness centrality, as expressed in Equation (3):where betweenness centrality of a node , denoted as , measures the number of times node is crossed by the shortest paths in the network. This is calculated as the sum of the number of shortest paths between every pair of nodes (, ) in the network () that pass through node i () divided by the total number of shortest paths between and (). A sector with high betweenness is likely to serve as a junction for multiple shortest paths and be a structural center in the sector network [25]. In the event of a failure in such a sector, multiple shortest paths would be impacted, causing the network structure to become weaker. Hence, it is crucial to pay special attention to sectors with high betweenness when evaluating the invulnerability of the airspace sector network.
- Clustering coefficient, as expressed in Equation (4) for local clustering coefficient of node and Equation (5) for network average clustering coefficient:where the clustering coefficient of node in the airspace sector network is calculated by considering the number of neighbor nodes () and the number of edges formed by these neighbors (). This coefficient measures the connectivity between a node’s neighbors in the network [26]. In terms of air traffic control operations, represents the connection between flight routes and the coordination between controllers. A higher value of suggests that sector has better connections with neighboring sectors, leading to better collaboration between controllers. The overall connectivity of the airspace sector network can be determined by the average clustering coefficient (), which represents the tightness of connections between sectors. A higher means that the sectors in the airspace network are better connected, which can facilitate joint decision making in dealing with air traffic congestion [27].
2.3. Modeling of Airspace Sector Network
- The global efficiency of the network is a measure of its connectivity, which is represented as the average of the inverse of the distances between sectors [29]. It is expressed in Equation (6).where represents the number of connected sectors in the network, and represents the shortest path length between sector and sector . If there is no direct flight flow between two sectors, then is set to . The value of ranges from 0 to 1 and represents the connectivity and compactness of nodes in the network. A higher value of indicates better connectivity, with a shorter average length between nodes. When is close to 1, the average distance between nodes in the sector network is short and the network connectivity is well established. On the other hand, when is close to 0, most sectors are disconnected from each other and the network structure is loose, with isolated nodes.
- The relative size of the connected component is a metric that measures the proportion of nodes that remain connected after a set of nodes or edges have been removed from the network. This is expressed as a ratio of the number of nodes in the remaining connected component to the total number of nodes in the original network, as shown in Equation (7).where represents the number of sectors of the connected component when the air space sector network is affected by an attack, represents the total number of sectors in the airspace sector network before the attack, and reflects the integrity of the network after being attacked with a value ranging from 0 to 1 [30]. When is close to 1, the sector network is similar to the complete network. The number of isolated airspace sectors in the network is small, and the airspace available for air traffic control is large. When is close to 0, the distribution of the sector is scattered, and the airspace available for air traffic control is small.
3. Analysis of Sector Network Characteristics
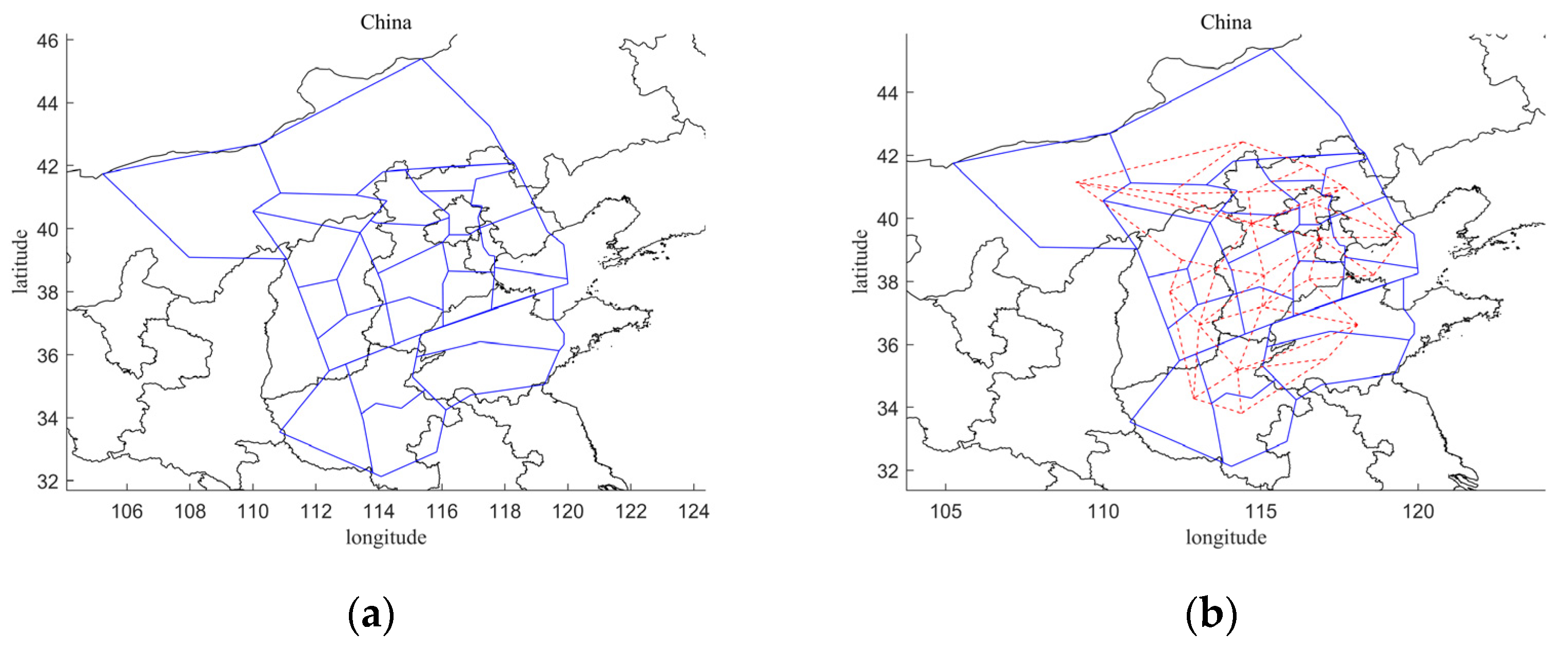
3.1. Construction of Airspace Sector Network
3.2. Topological Properties of Sector Network
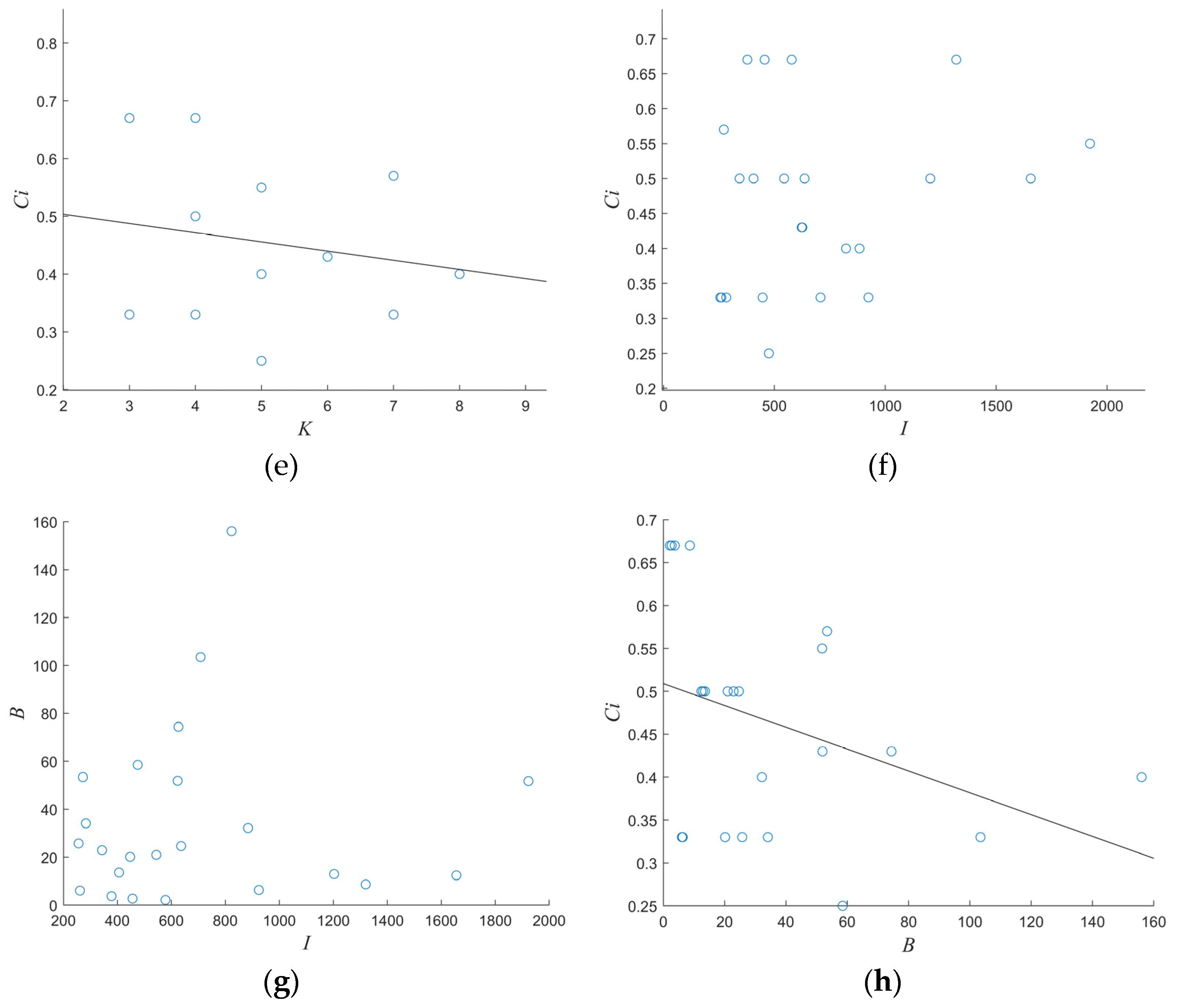
3.3. Analysis of Network Structural Characteristics
4. Invulnerability of Sector Network
4.1. Attack Strategies
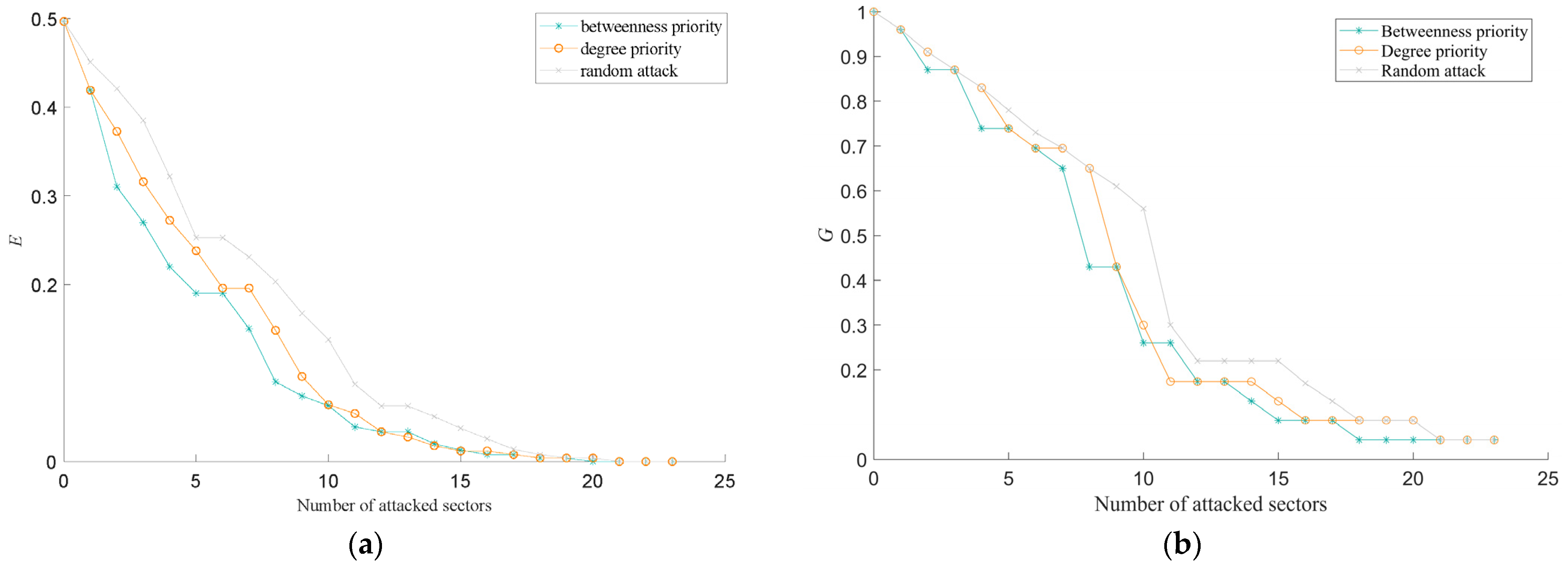
4.2. Results of Invulnerability Assessment
4.3. Impact of Attacks on Critical Sectors
5. Conclusions
- The study reveals that the airspace sector network in North China exhibits a compact and well-established structure, as indicated by its small average path length and clustering coefficient. However, the connections between adjacent sectors are scattered, posing challenges for efficient air traffic control coordination and collaboration. The sector degree distribution is relatively even, and the workload of controllers in different sectors varies significantly, as evidenced by the power-law distribution of intensity and betweenness. Therefore, optimizing sector management to balance controller workload is crucial for efficient air traffic control.
- We evaluated the invulnerability of the airspace sector network by analyzing two key measurement indices: network global efficiency and the relative size of connected components. The results indicate that the sector network is more resilient to random attacks but less so to intentional attacks. In the case of intentional attacks, degree and betweenness are crucial indices that can help identify critical sectors and potential critical sectors. Since betweenness has a higher impact than degree in intentional attacks, it was chosen as the primary critical index to analyze the effect of critical sectors and identify potential critical sectors. Critical sectors play a pivotal role in the overall invulnerability of the sector network. If critical sectors are targeted, it could significantly increase the flight traffic of potential critical sectors, leading to traffic congestion and further damage to other sectors.
- This study utilized complex network theory to investigate the airspace network, specifically analyzing the ATC sector network in North China using historical air traffic data. The study obtained a comprehensive understanding of the topological characteristics and invulnerability of the sector network from the perspective of air traffic control. This provides insights for alleviating air traffic congestion and lays the foundation for future planning of sector selection in airspace.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Sector Code | Degree Priority | Betweenness Priority | Random Attack |
|---|---|---|---|
| 0 | 0.4969 | 0.4969 | 0.4969 |
| 1 | 0.4193 | 0.4193 | 0.4510 |
| 2 | 0.3728 | 0.3102 | 0.4210 |
| 3 | 0.3159 | 0.2700 | 0.3851 |
| 4 | 0.2724 | 0.2200 | 0.3219 |
| 5 | 0.238 | 0.1900 | 0.2529 |
| 6 | 0.1958 | 0.1900 | 0.2529 |
| 7 | 0.1958 | 0.1500 | 0.2309 |
| 8 | 0.1481 | 0.0900 | 0.2031 |
| 9 | 0.0960 | 0.0740 | 0.1673 |
| 10 | 0.0640 | 0.0630 | 0.1376 |
| 11 | 0.0542 | 0.0390 | 0.0873 |
| 12 | 0.0336 | 0.0336 | 0.0626 |
| 13 | 0.0277 | 0.0336 | 0.0626 |
| 14 | 0.0178 | 0.0200 | 0.0507 |
| 15 | 0.0119 | 0.013 | 0.0375 |
| 16 | 0.0119 | 0.0079 | 0.0257 |
| 17 | 0.0079 | 0.0079 | 0.0138 |
| 18 | 0.0040 | 0.0040 | 0.0079 |
| 19 | 0.0040 | 0.0040 | 0.0040 |
| 20 | 0.0040 | 0 | 0.0040 |
| 21 | 0 | 0 | 0 |
| 22 | 0 | 0 | 0 |
| 23 | 0 | 0 | 0 |
| Sector Coding | Degree Priority | Betweenness Priority | Random Attack |
|---|---|---|---|
| 0 | 1 | 1 | 1 |
| 1 | 0.96 | 0.96 | 0.96 |
| 2 | 0.91 | 0.87 | 0.91 |
| 3 | 0.87 | 0.87 | 0.87 |
| 4 | 0.83 | 0.739 | 0.83 |
| 5 | 0.739 | 0.739 | 0.78 |
| 6 | 0.695 | 0.695 | 0.73 |
| 7 | 0.695 | 0.65 | 0.695 |
| 8 | 0.65 | 0.43 | 0.65 |
| 9 | 0.43 | 0.43 | 0.61 |
| 10 | 0.3 | 0.26 | 0.56 |
| 11 | 0.174 | 0.26 | 0.3 |
| 12 | 0.174 | 0.174 | 0.22 |
| 13 | 0.174 | 0.174 | 0.22 |
| 14 | 0.174 | 0.13 | 0.22 |
| 15 | 0.13 | 0.087 | 0.22 |
| 16 | 0.087 | 0.087 | 0.17 |
| 17 | 0.087 | 0.087 | 0.13 |
| 18 | 0.087 | 0.04348 | 0.087 |
| 19 | 0.087 | 0.04348 | 0.087 |
| 20 | 0.087 | 0.04348 | 0.087 |
| 21 | 0.04348 | 0.04348 | 0.04348 |
| 22 | 0.04348 | 0.04348 | 0.04348 |
| 23 | 0.04348 | 0.04348 | 0.04348 |
References
- Çolak, S.; Lima, A.; González, M.C. Understanding congested travel in urban areas. Nat. Commun. 2016, 7, 10793. [Google Scholar] [CrossRef]
- Brittain, M.; Wei, P. Autonomous air traffic controller: A deep multi-agent reinforcement learning approach. arXiv 2019, arXiv:1905.01303. [Google Scholar]
- Rehman, A. Machine learning based air traffic control strategy. Int. J. Mach. Learn. Cybern. 2021, 12, 2151–2161. [Google Scholar] [CrossRef]
- Ren, G.; Lu, C.; Zhu, J.; Liu, X. Analyzing the topological characteristic and key nodes of Chinese air sector network. Int. J. Mod. Phys. B 2019, 33, 1950100. [Google Scholar] [CrossRef]
- Isufaj, R.; Omeri, M.; Piera, M.A.; Saez Valls, J.; Verdonk Gallego, C.E. From Single Aircraft to Communities: A Neutral Interpretation of Air Traffic Complexity Dynamics. Aerospace 2022, 9, 613. [Google Scholar] [CrossRef]
- Angeloudis, P.; Fisk, D. Large subway systems as complex networks. Phys. A Stat. Mech. Its Appl. 2006, 367, 553–558. [Google Scholar] [CrossRef]
- Porta, S.; Crucitti, P.; Latora, V. The network analysis of urban streets: A primal approach. Environ. Plan. B Plan. Des. 2006, 33, 705–725. [Google Scholar] [CrossRef]
- Sharifi, A. Resilient urban forms: A review of literature on streets and street networks. Build. Environ. 2019, 147, 171–187. [Google Scholar] [CrossRef]
- Sen, P.; Dasgupta, S.; Chatterjee, A.; Sreeram, P.; Mukherjee, G.; Manna, S. Small-world properties of the Indian railway network. Phys. Rev. E 2003, 67, 036106. [Google Scholar] [CrossRef] [PubMed]
- Bombelli, A.; Santos, B.F.; Tavasszy, L. Analysis of the air cargo transport network using a complex network theory perspective. Transp. Res. Part E Logist. Transp. Rev. 2020, 138, 101959. [Google Scholar] [CrossRef]
- Lordan, O.; Sallan, J.M.; Simo, P. Study of the topology and robustness of airline route networks from the complex network approach: A survey and research agenda. J. Transp. Geogr. 2014, 37, 112–120. [Google Scholar] [CrossRef]
- Zanin, M.; Lillo, F. Modelling the air transport with complex networks: A short review. Eur. Phys. J. Spec. Top. 2013, 215, 5–21. [Google Scholar] [CrossRef]
- Amaral, L.A.N.; Scala, A.; Barthelemy, M.; Stanley, H.E. Classes of small-world networks. Proc. Natl. Acad. Sci. USA 2000, 97, 11149–11152. [Google Scholar] [CrossRef]
- Kaiquan, C.; Jun, Z.; Wenbo, D.; Xianbin, C. Analysis of the Chinese air route network as a complex network. Chin. Phys. B 2012, 21, 028903. [Google Scholar]
- Hossain, M.; Alam, S.; Rees, T.; Abbass, H. Australian airport network robustness analysis: A complex network approach. In Proceedings of the 36th Australasian Transport Research Forum (ATRF), Brisbane, Australia, 2–4 October 2013. [Google Scholar]
- Albert, R.; Jeong, H.; Barabási, A.-L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef]
- Janssen, M.A.; Schoon, M.L.; Ke, W.; Börner, K. Scholarly networks on resilience, vulnerability and adaptation within the human dimensions of global environmental change. Glob. Environ. Chang. 2006, 16, 240–252. [Google Scholar] [CrossRef]
- Qian, B.; Zhang, N. Topology and Robustness of Weighted Air Transport Networks in Multi-Airport Region. Sustainability 2022, 14, 6832. [Google Scholar] [CrossRef]
- Başpınar, B.; Gopalakrishnan, K.; Koyuncu, E.; Balakrishnan, H. An empirical study of the resilience of the US and European air transportation networks. J. Air Transp. Manag. 2023, 106, 102303. [Google Scholar] [CrossRef]
- Chicco, G.; Mancarella, P. Matrix modelling of small-scale trigeneration systems and application to operational optimization. Energy 2009, 34, 261–273. [Google Scholar] [CrossRef]
- Sergeeva, M.; Delahaye, D.; Mancel, C.; Vidosavljevic, A. Dynamic airspace configuration by genetic algorithm. J. Traffic Transp. Eng. (Engl. Ed.) 2017, 4, 300–314. [Google Scholar] [CrossRef]
- Zhang, X.; Miller-Hooks, E.; Denny, K. Assessing the role of network topology in transportation network resilience. J. Transp. Geogr. 2015, 46, 35–45. [Google Scholar] [CrossRef]
- Bin, J.; Claramunt, C. Topological analysis of urban street networks. Environ. Plan. B Plan. Des. 2004, 31, 151–162. [Google Scholar]
- Barrat, A.; Barthelemy, M.; Pastor-Satorras, R.; Vespignani, A. The architecture of complex weighted networks. Proc. Natl. Acad. Sci. USA 2004, 101, 3747–3752. [Google Scholar] [CrossRef] [PubMed]
- Mahyar, H.; Hasheminezhad, R.; Ghalebi, E.; Nazemian, A.; Grosu, R.; Movaghar, A.; Rabiee, H.R. Compressive sensing of high betweenness centrality nodes in networks. Phys. A Stat. Mech. Its Appl. 2018, 497, 166–184. [Google Scholar] [CrossRef]
- Said, A.; Abbasi, R.A.; Maqbool, O.; Daud, A.; Aljohani, N.R. CC-GA: A clustering coefficient based genetic algorithm for detecting communities in social networks. Appl. Soft Comput. 2018, 63, 59–70. [Google Scholar] [CrossRef]
- Berahmand, K.; Bouyer, A.; Samadi, N. A new centrality measure based on the negative and positive effects of clustering coefficient for identifying influential spreaders in complex networks. Chaos Solitons Fractals 2018, 110, 41–54. [Google Scholar] [CrossRef]
- Roy, S.; Xue, M.; Sridhar, B. Vulnerability metrics for the airspace system. In Proceedings of the 2017 FAA/Eurocontrol Air Traffic Management Research and Development Seminar, Seattle, WA, USA, 29 June 2017. [Google Scholar]
- Hébert-Dufresne, L.; Allard, A.; Young, J.-G.; Dubé, L.J. Global efficiency of local immunization on complex networks. Sci. Rep. 2013, 3, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Veremyev, A.; Prokopyev, O.A.; Boginski, V.; Pasiliao, E.L. Finding maximum subgraphs with relatively large vertex connectivity. Eur. J. Oper. Res. 2014, 239, 349–362. [Google Scholar] [CrossRef]
- Saleh, M.; Esa, Y.; Mohamed, A. Applications of Complex Network Analysis in Electric Power Systems. Energies 2018, 11, 1381. [Google Scholar] [CrossRef]
- Du, W.B.; Liang, B.Y.; Hong, C.; Lordan, O. Analysis of the Chinese provincial air transportation network. Phys. A Stat. Mech. Its Appl. 2016, 465, 579–586. [Google Scholar] [CrossRef]
- Wang, I.L.; Johnson, E.L.; Sokol, J.S. A multiple pairs shortest path algorithm. Transp. Sci. 2005, 39, 465–476. [Google Scholar]
- Zaidi, F. Small world networks and clustered small world networks with random connectivity. Soc. Netw. Anal. Min. 2013, 3, 51–63. [Google Scholar] [CrossRef]
- Yazdani, A.; Otoo, R.A.; Jeffrey, P. Resilience enhancing expansion strategies for water distribution systems: A network theory approach. Environ. Model. Softw. 2011, 26, 1574–1582. [Google Scholar] [CrossRef]
- Nie, T.; Guo, Z.; Zhao, K.; Lu, Z.-M. New attack strategies for complex networks. Phys. A Stat. Mech. Its Appl. 2015, 424, 248–253. [Google Scholar] [CrossRef]
- Cohen, R.; Havlin, S. Complex Networks: Structure, Robustness and Function; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Zanin, M.; Sun, X.; Wandelt, S. Studying the topology of transportation systems through complex networks: Handle with care. J. Adv. Transp. 2018, 2018, 3156137. [Google Scholar] [CrossRef]
- Xia, Y.; Hill, D.J. Attack vulnerability of complex communication networks. IEEE Trans. Circuits Syst. II Express Briefs 2008, 55, 65–69. [Google Scholar] [CrossRef]
- Perea, F.; Puerto, J. Revisiting a game theoretic framework for the robust railway network design against intentional attacks. Eur. J. Oper. Res. 2013, 226, 286–292. [Google Scholar] [CrossRef]
- Cook, A.; Blom, H.A.; Lillo, F.; Mantegna, R.N.; Micciche, S.; Rivas, D.; Zanin, M. Applying complexity science to air traffic management. J. Air Transp. Manag. 2015, 42, 149–158. [Google Scholar] [CrossRef]
- Muñiz, A.S.G.; Raya, A.M.; Carvajal, C.R. Key sectors: A new proposal from network theory. Reg. Stud. 2008, 42, 1013–1030. [Google Scholar] [CrossRef]
- Boccaletti, S.; Buldú, J.; Criado, R.; Flores, J.; Latora, V.; Pello, J.; Romance, M. Multiscale vulnerability of complex networks. Chaos Interdiscip. J. Nonlinear Sci. 2007, 17, 043110. [Google Scholar] [CrossRef]
- Ash, J.; Newth, D. Optimizing complex networks for resilience against cascading failure. Phys. A Stat. Mech. Its Appl. 2007, 380, 673–683. [Google Scholar] [CrossRef]
- Dobson, I.; Carreras, B.A.; Lynch, V.E.; Newman, D.E. Complex systems analysis of series of blackouts: Cascading failure, critical points, and self-organization. Chaos Interdiscip. J. Nonlinear Sci. 2007, 17, 026103. [Google Scholar] [CrossRef] [PubMed]
- Bellingeri, M.; Bevacqua, D.; Scotognella, F.; Cassi, D. The heterogeneity in link weights may decrease the robustness of real-world complex weighted networks. Sci. Rep. 2019, 9, 10692. [Google Scholar] [CrossRef] [PubMed]
- Bellingeri, M.; Bevacqua, D.; Scotognella, F.; Alfieri, R.; Cassi, D. A comparative analysis of link removal strategies in real complex weighted networks. Sci. Rep. 2020, 10, 3911. [Google Scholar] [CrossRef]
- Wandelt, S.; Lin, W.; Sun, X.; Zanin, M. From Random Failures to Targeted Attacks in Network Dismantling. Reliab. Eng. Syst. Saf. 2021, 218, 108146. [Google Scholar] [CrossRef]
| No. | Sector | Degree | Intensity | Betweenness | Clustering Coefficient |
|---|---|---|---|---|---|
| 1 | Hohhot01 | 4 | 283 | 34.08 | 0.33 |
| 2 | Hohhot02 | 3 | 261 | 6.07 | 0.33 |
| 3 | Taiyuan01 | 3 | 447 | 20.15 | 0.33 |
| 4 | Taiyuan02 | 5 | 475 | 58.50 | 0.25 |
| 5 | Taiyuan03 | 3 | 256 | 25.75 | 0.33 |
| 6 | Taiyuan04 | 7 | 272 | 53.43 | 0.57 |
| 7 | Beijing01 | 8 | 823 | 156.03 | 0.4 |
| 8 | Beijing02 | 5 | 1923 | 51.81 | 0.55 |
| 9 | Beijing03 | 6 | 626 | 74.43 | 0.43 |
| 10 | Beijing04 | 7 | 708 | 103.47 | 0.33 |
| 11 | Beijing05 | 4 | 343 | 22.93 | 0.5 |
| 12 | Beijing06 | 4 | 406 | 13.59 | 0.5 |
| 13 | Beijing07 | 3 | 378 | 3.74 | 0.67 |
| 14 | Beijing08 | 3 | 924 | 6.33 | 0.33 |
| 15 | Beijing09 | 5 | 884 | 32.16 | 0.4 |
| 16 | Beijing10 | 4 | 636 | 24.66 | 0.5 |
| 17 | Beijing11 | 6 | 623 | 51.92 | 0.43 |
| 18 | Beijing12 | 3 | 456 | 2.72 | 0.67 |
| 19 | Beijing13 | 4 | 544 | 20.99 | 0.5 |
| 20 | Beijing14 | 3 | 578 | 2.16 | 0.67 |
| 21 | Beijing15 | 4 | 1203 | 12.96 | 0.5 |
| 22 | Beijing16 | 4 | 1656 | 12.42 | 0.5 |
| 23 | Beijing17 | 4 | 1320 | 8.67 | 0.67 |
| Type of Intentional Attack | Description |
|---|---|
| Degree priority | Sort the network nodes by degree from high to low, and sequentially remove the nodes and associated edges from the network. |
| Betweenness priority | Sort the network nodes by betweenness from high to low, and sequentially remove the nodes and associated edges from the network. |
| Critical Sector | Network Efficiency | Potential Critical Sector | Betweenness | Betweenness Change Rate (%) |
|---|---|---|---|---|
| Beijing01 | 0.4454 | Hohhot01 | 54.42 | 159.7 |
| Beijing04 | 0.435 | Beijing02 | 81.67 | 157.62 |
| Beijing03 | 0.4437 | Beijing05 | 46.78 | 204.01 |
| Taiyuan02 | 0.4193 | Taiyuan01 | 220.62 | 1094.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, H.; Zhang, S.; Kong, J. Study on Characteristics and Invulnerability of Airspace Sector Network Using Complex Network Theory. Aerospace 2023, 10, 225. https://doi.org/10.3390/aerospace10030225
Liang H, Zhang S, Kong J. Study on Characteristics and Invulnerability of Airspace Sector Network Using Complex Network Theory. Aerospace. 2023; 10(3):225. https://doi.org/10.3390/aerospace10030225
Chicago/Turabian StyleLiang, Haijun, Shiyu Zhang, and Jianguo Kong. 2023. "Study on Characteristics and Invulnerability of Airspace Sector Network Using Complex Network Theory" Aerospace 10, no. 3: 225. https://doi.org/10.3390/aerospace10030225
APA StyleLiang, H., Zhang, S., & Kong, J. (2023). Study on Characteristics and Invulnerability of Airspace Sector Network Using Complex Network Theory. Aerospace, 10(3), 225. https://doi.org/10.3390/aerospace10030225






