On the Self-Similarity in an Annular Isolator under Rotating Feedback Pressure Perturbations
Abstract
1. Introduction
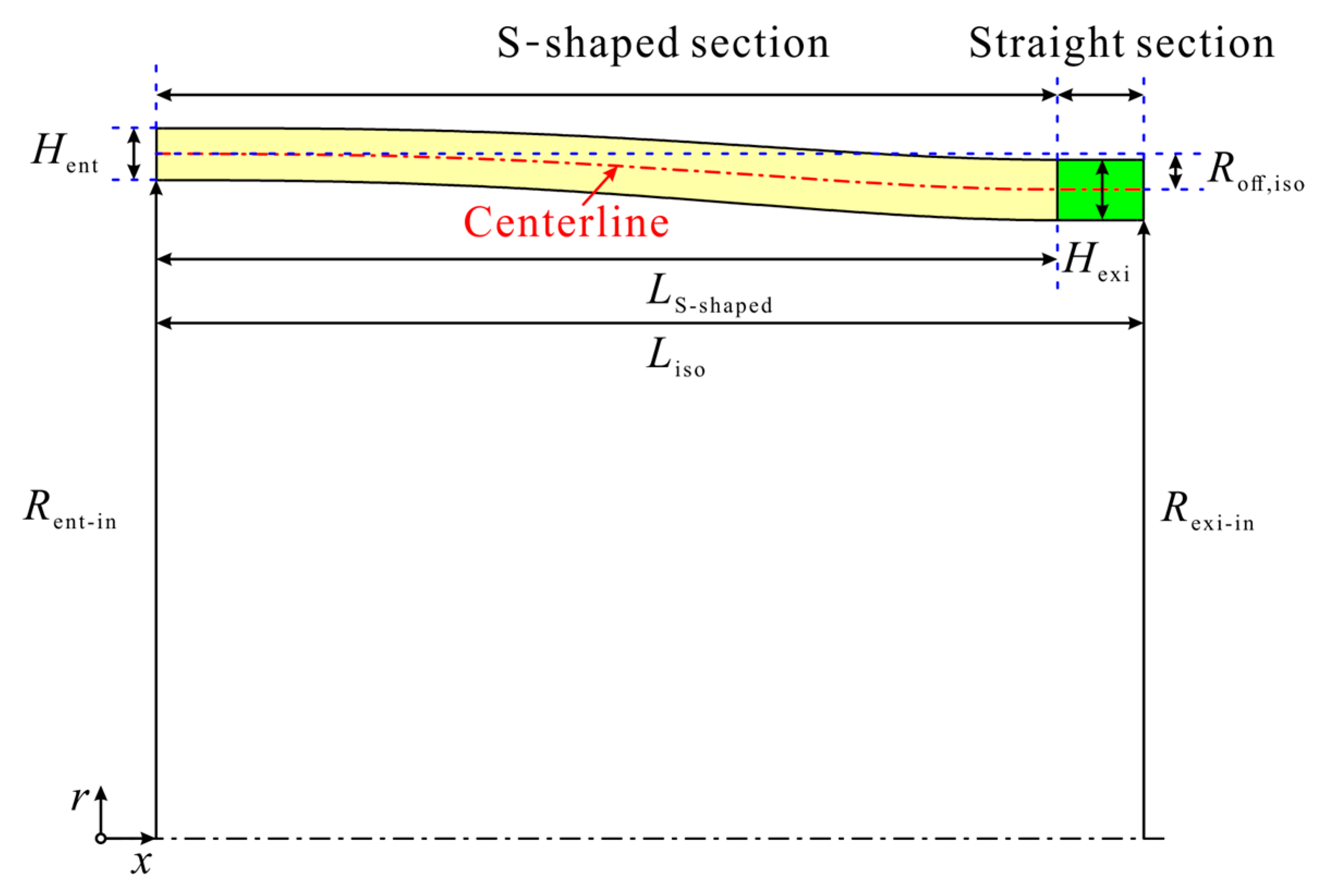
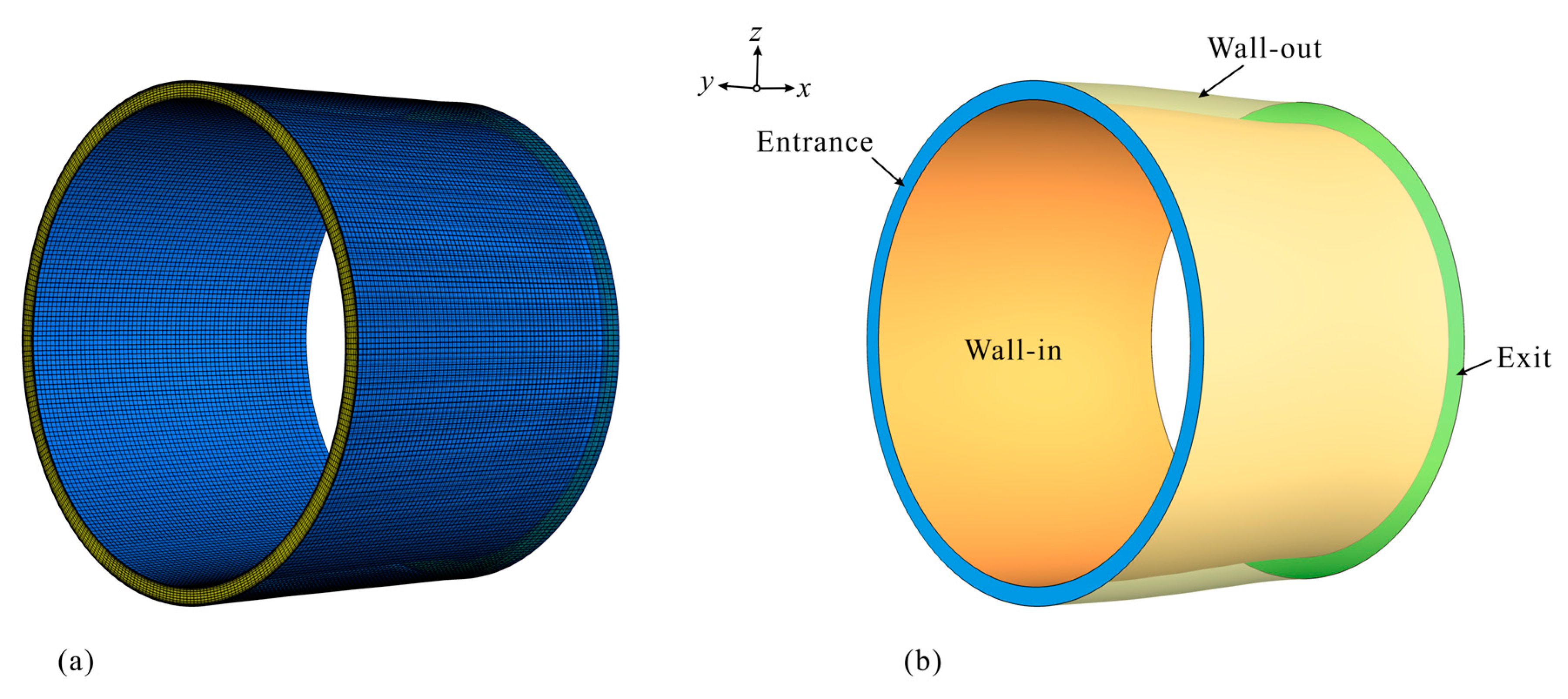
2. Physical Model of the Isolator
3. Methodology
3.1. Numerical Methods
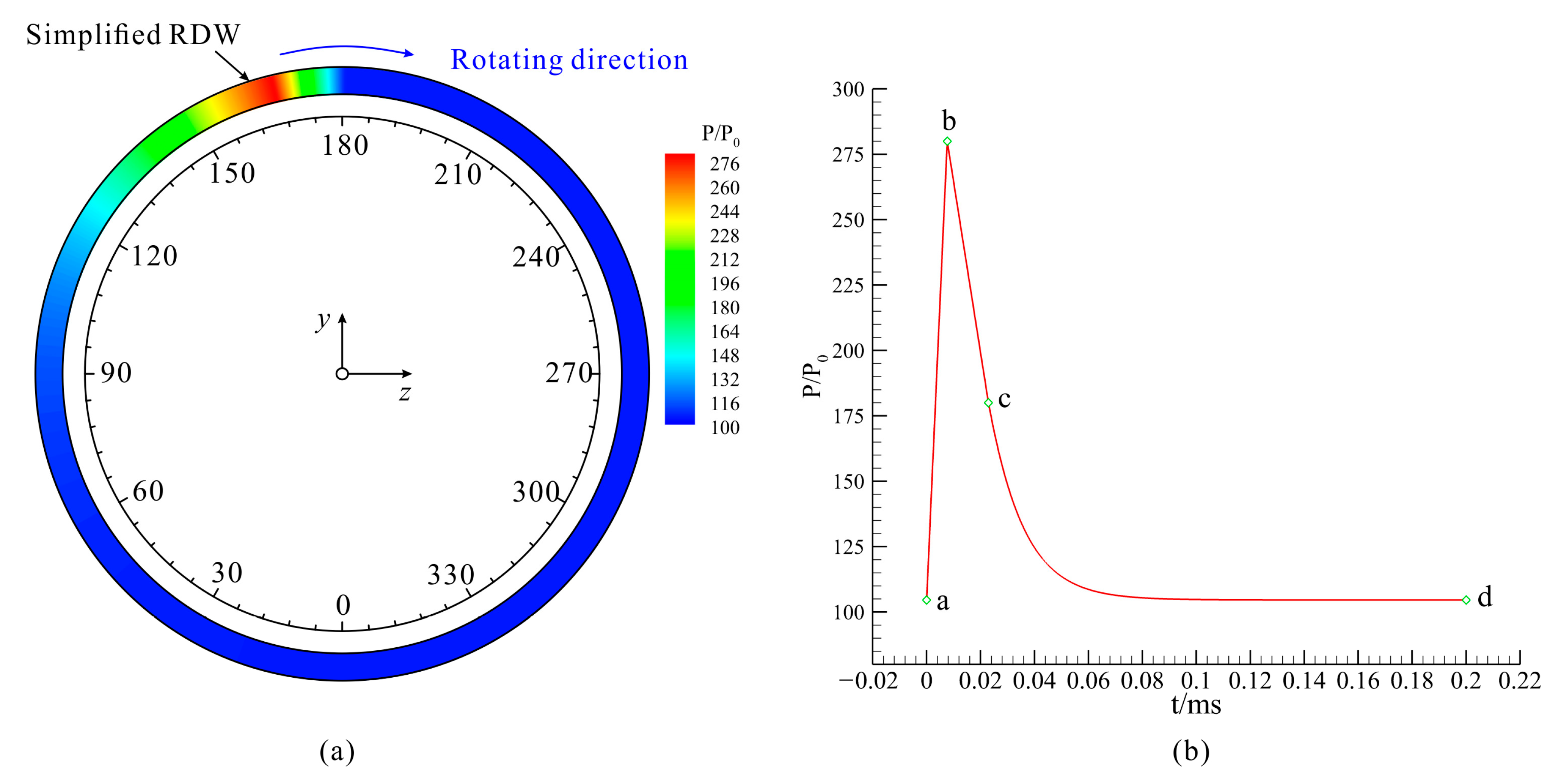
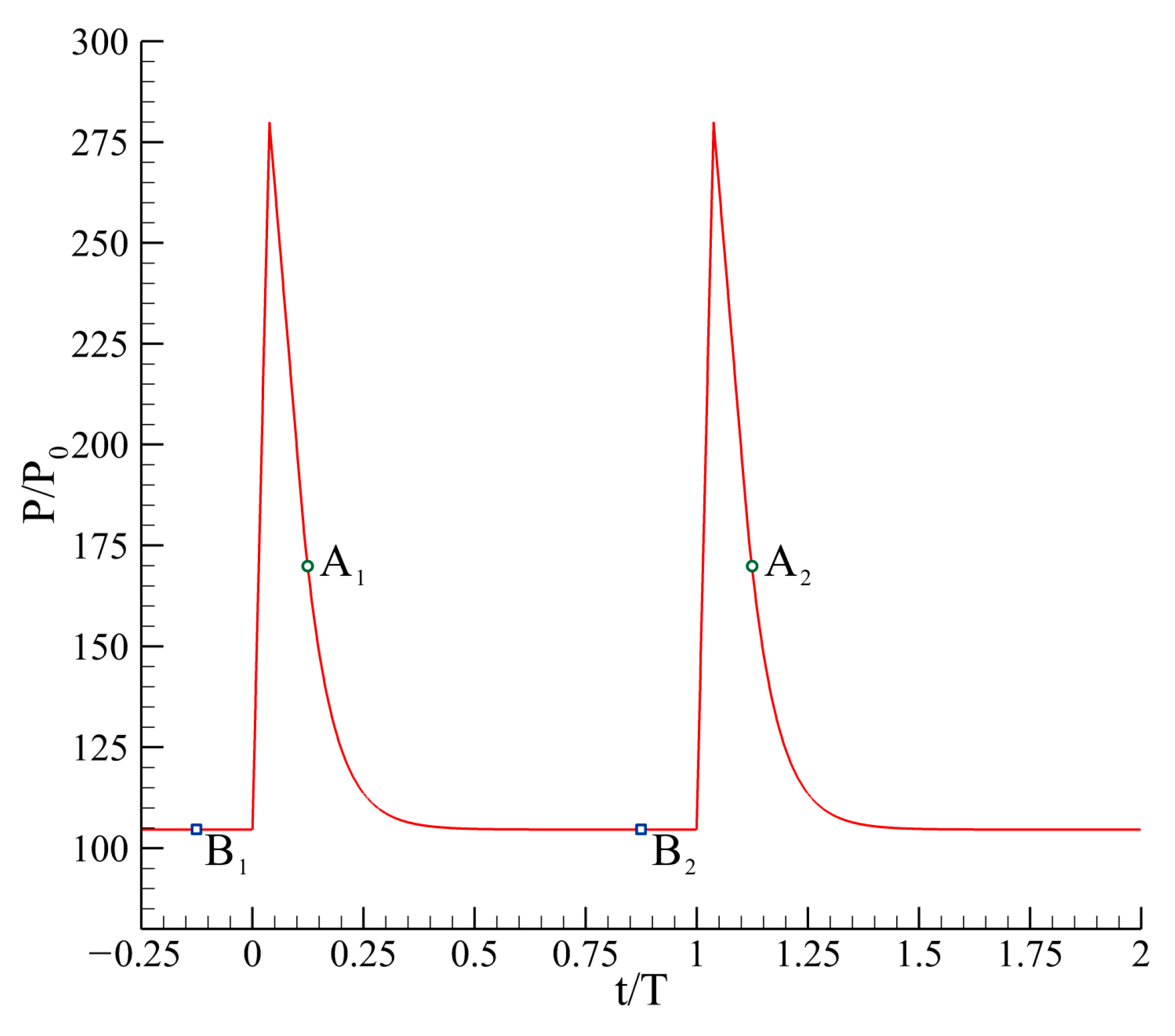
3.2. Implementation of Rotating Feedback Pressure Perturbations
3.3. Validation of the Numerical Method and Grid Sensitivity Verification
4. Transient Flow Characteristics in the Isolator Affected by the Rotating Feedback Pressure
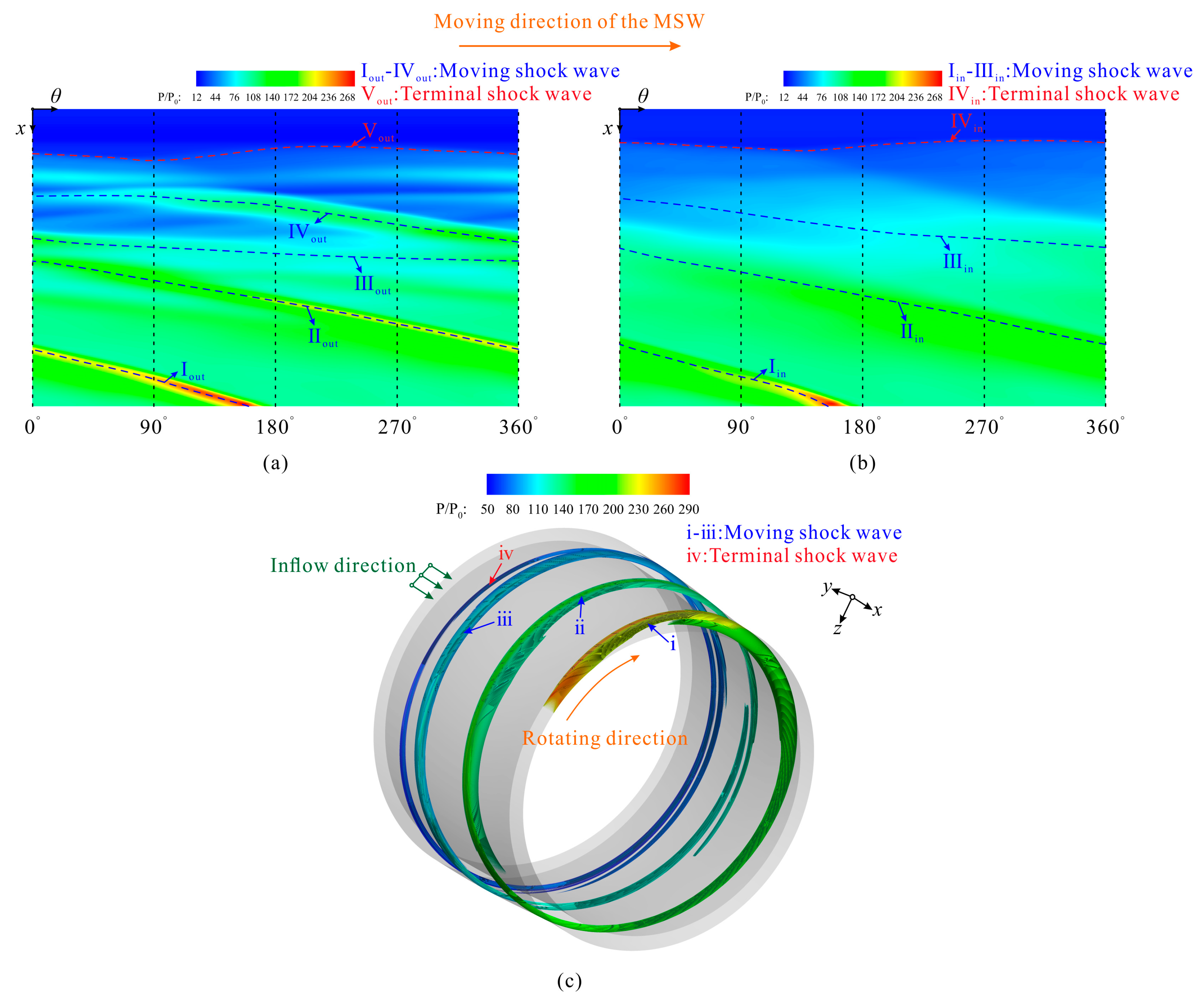
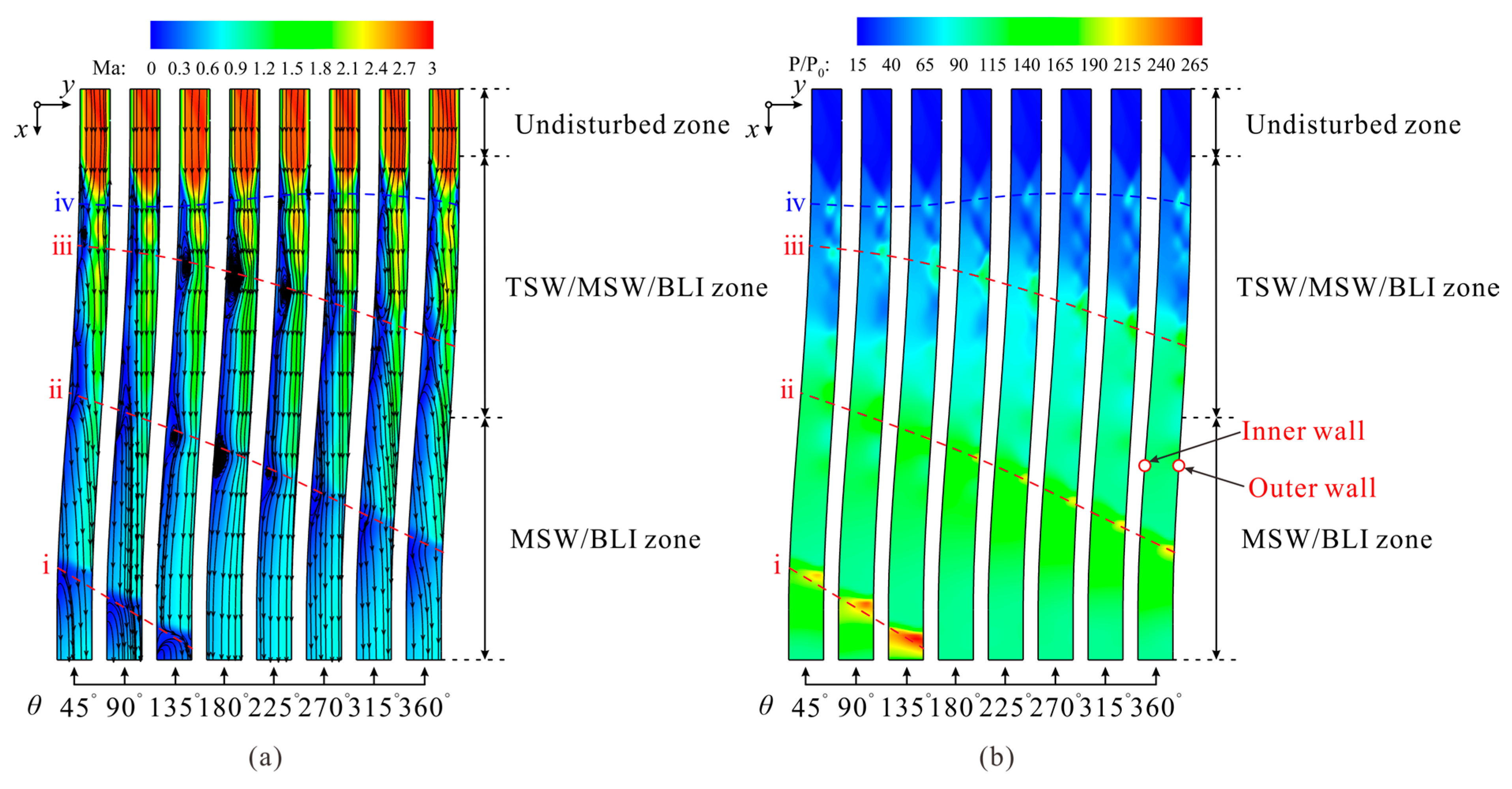
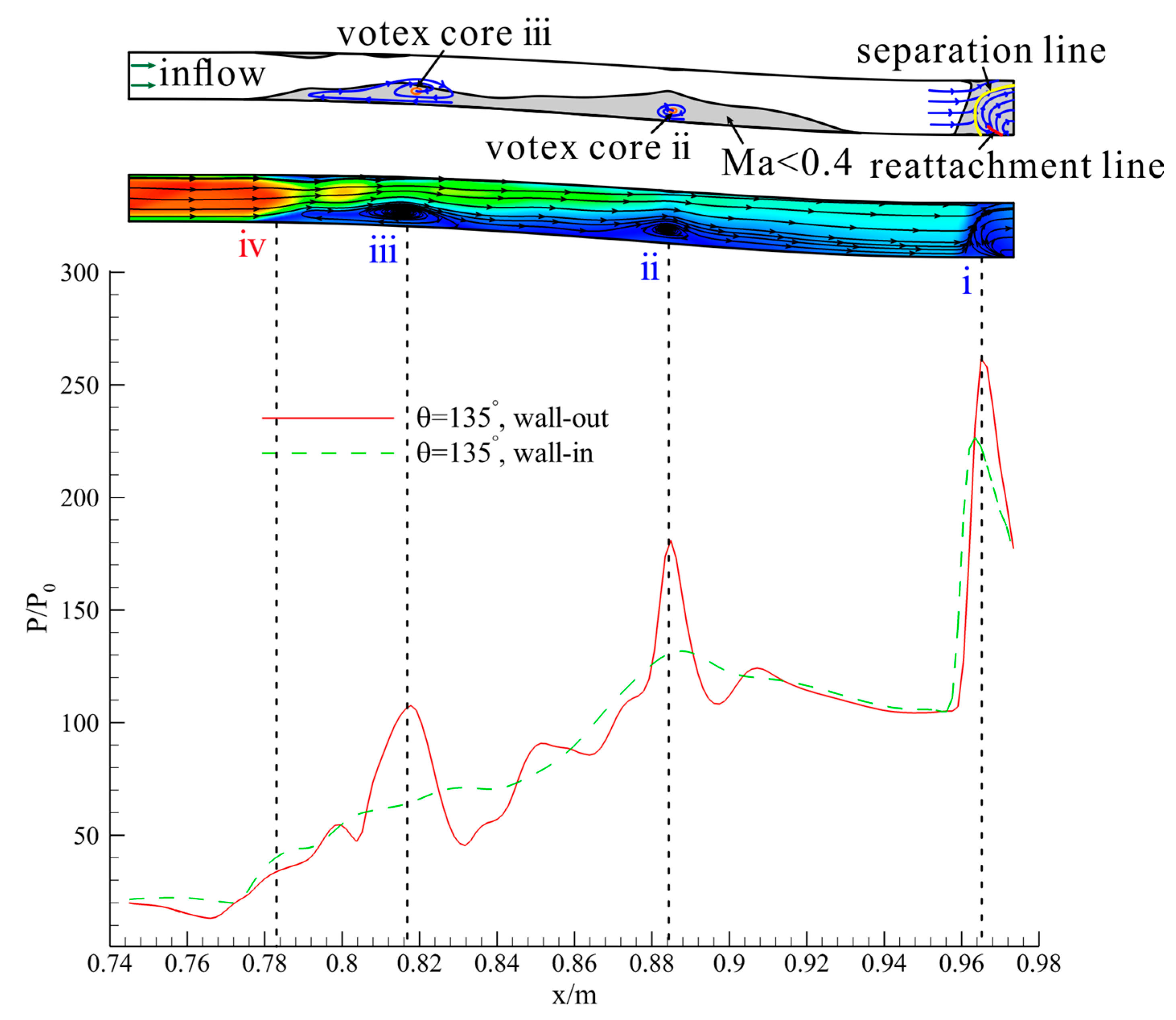
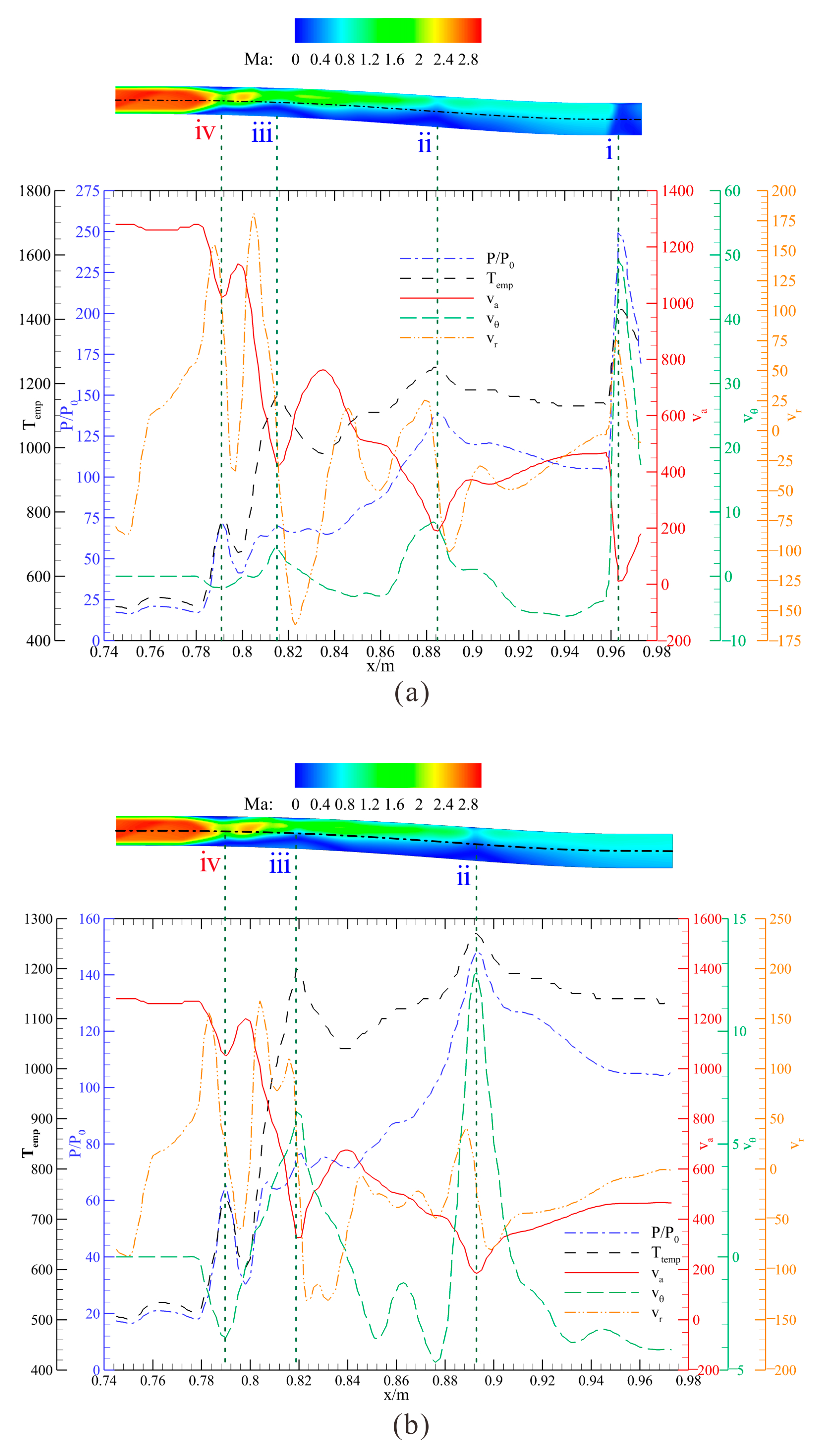
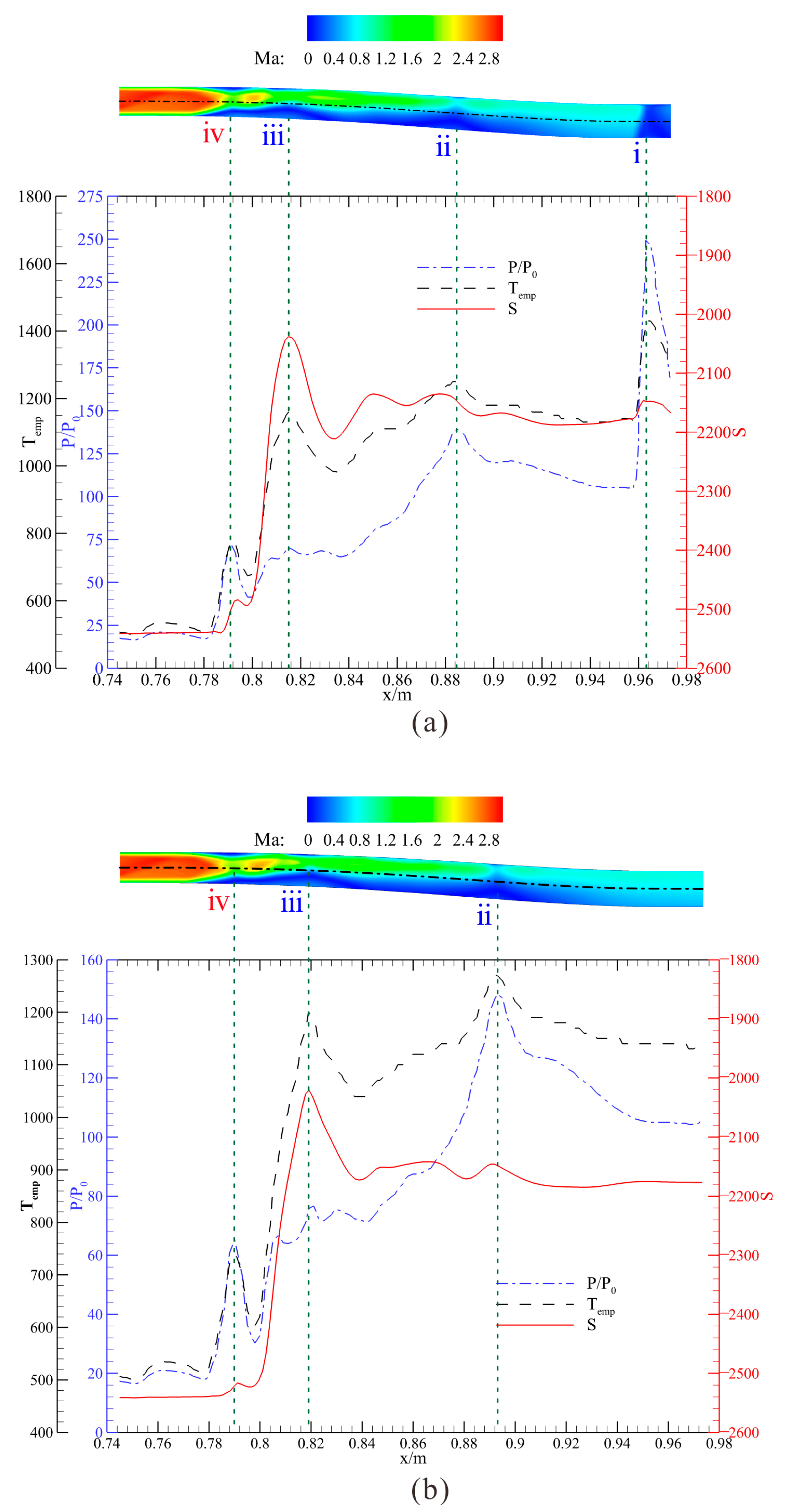
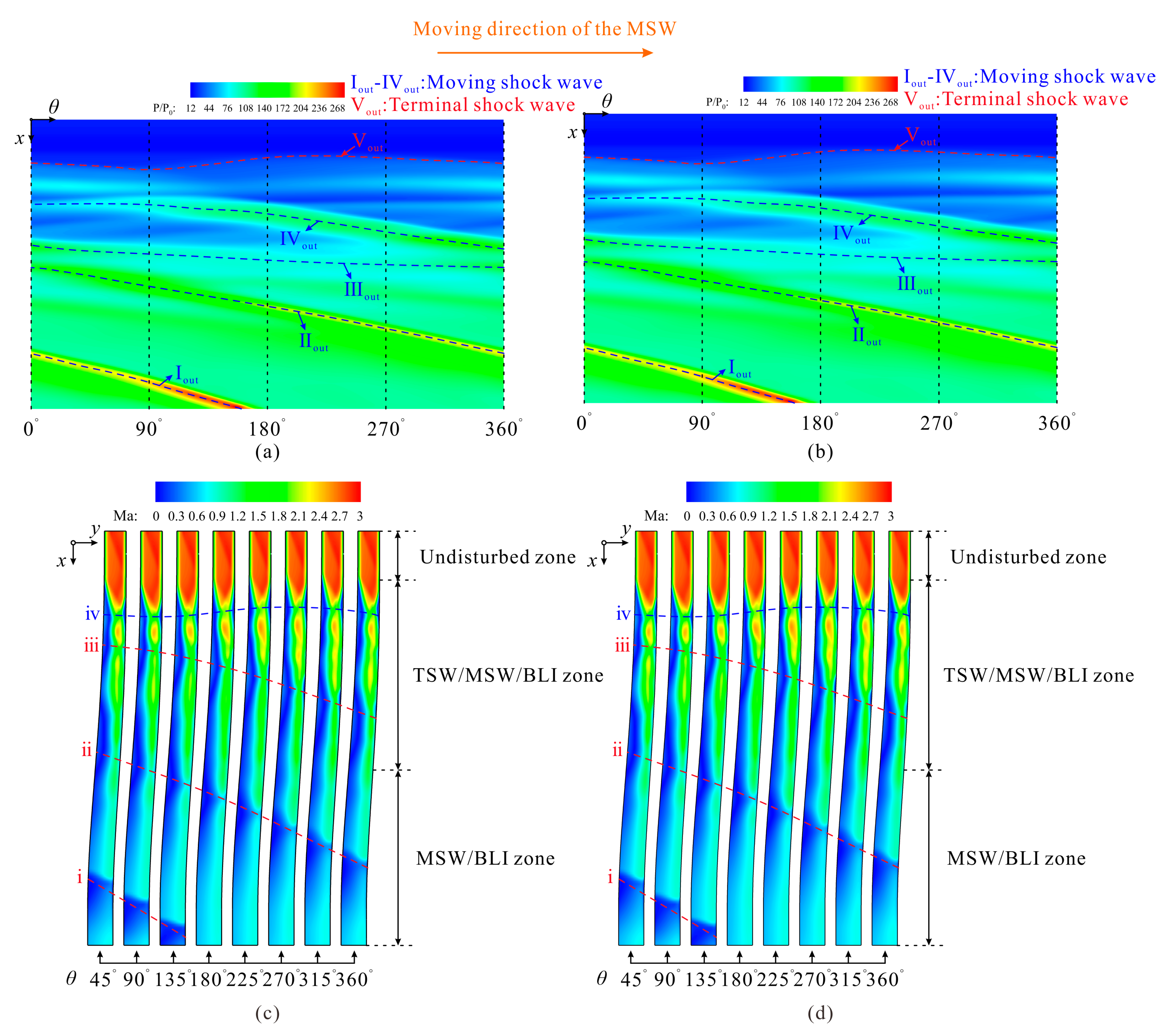
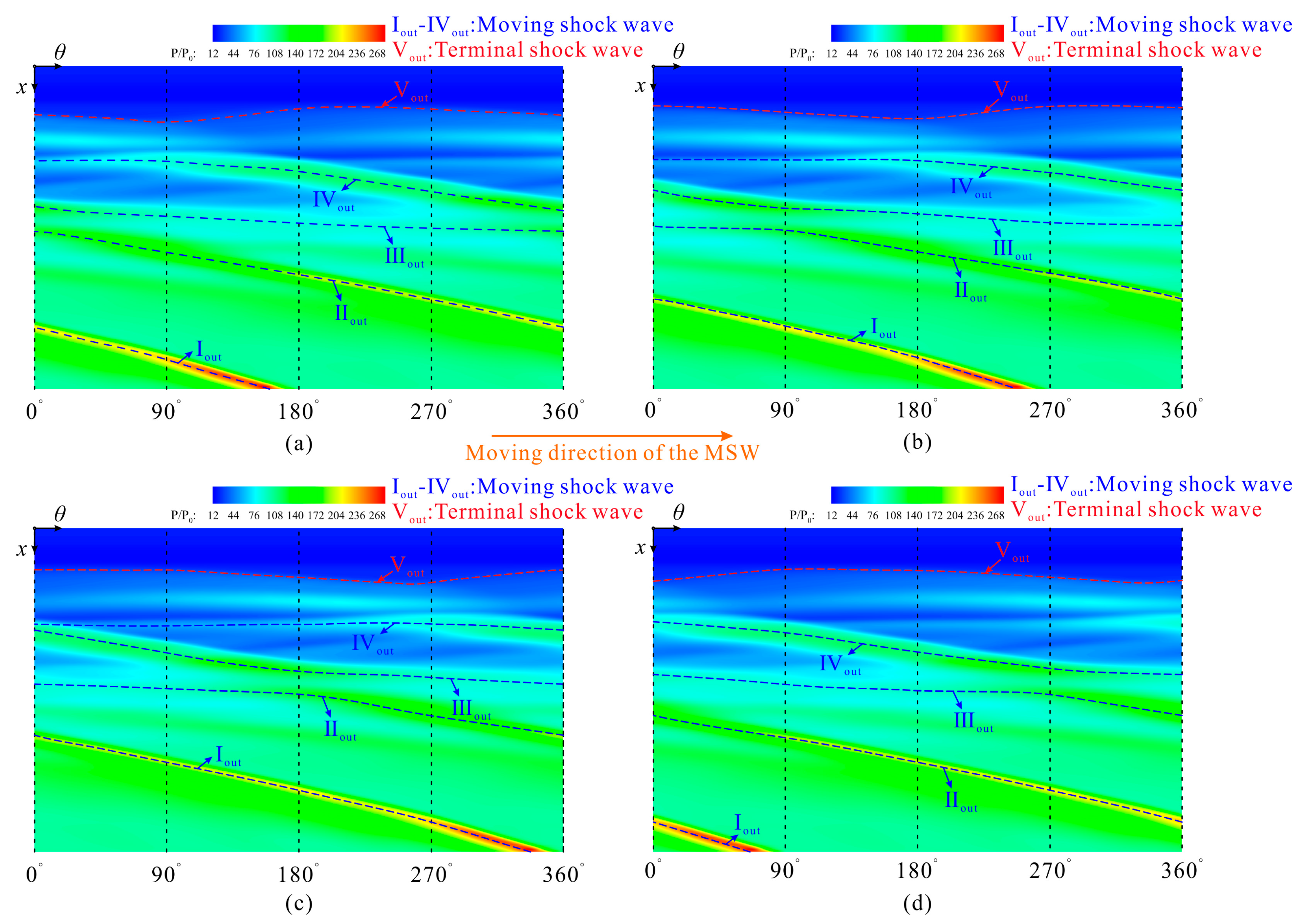
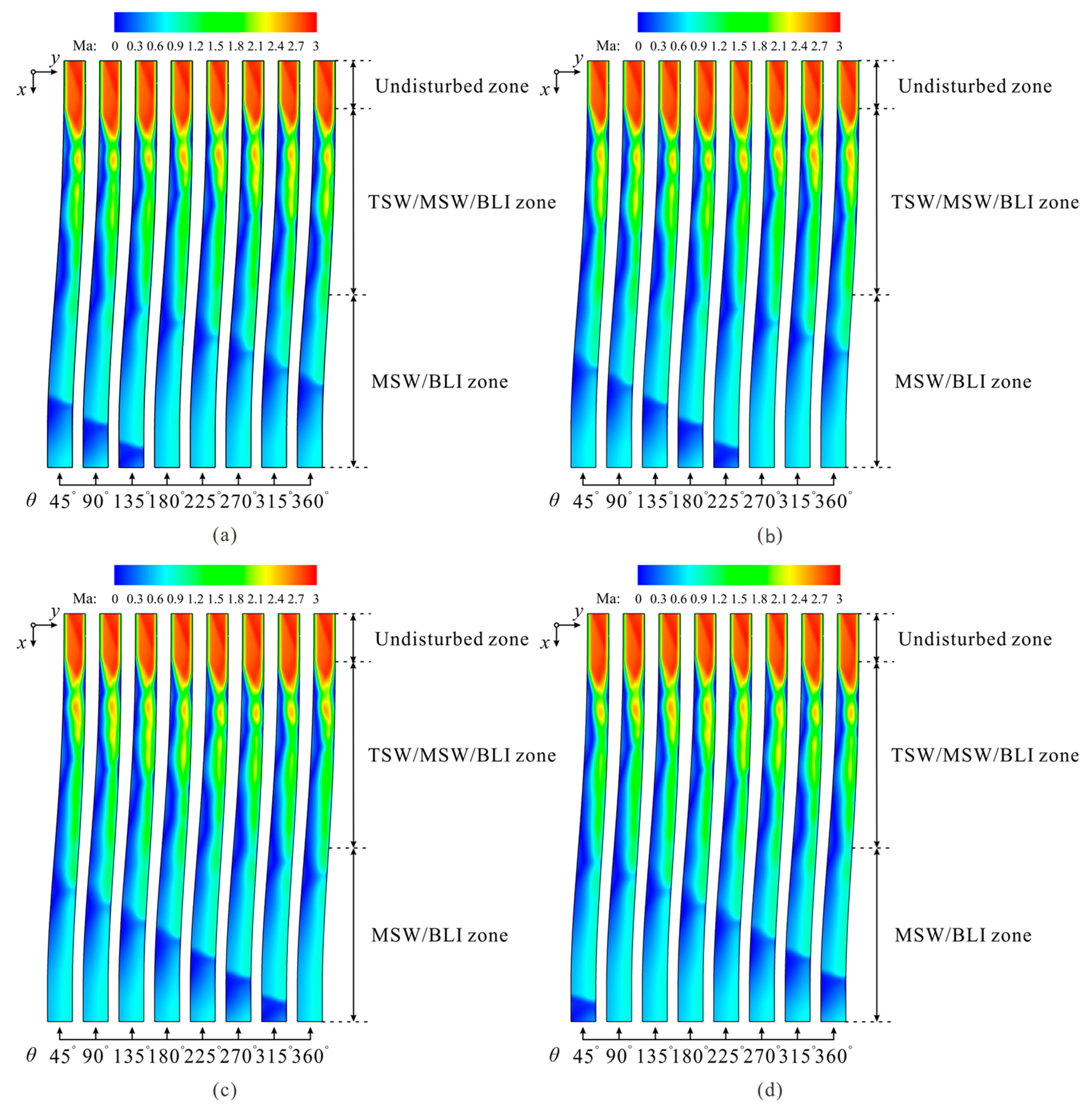
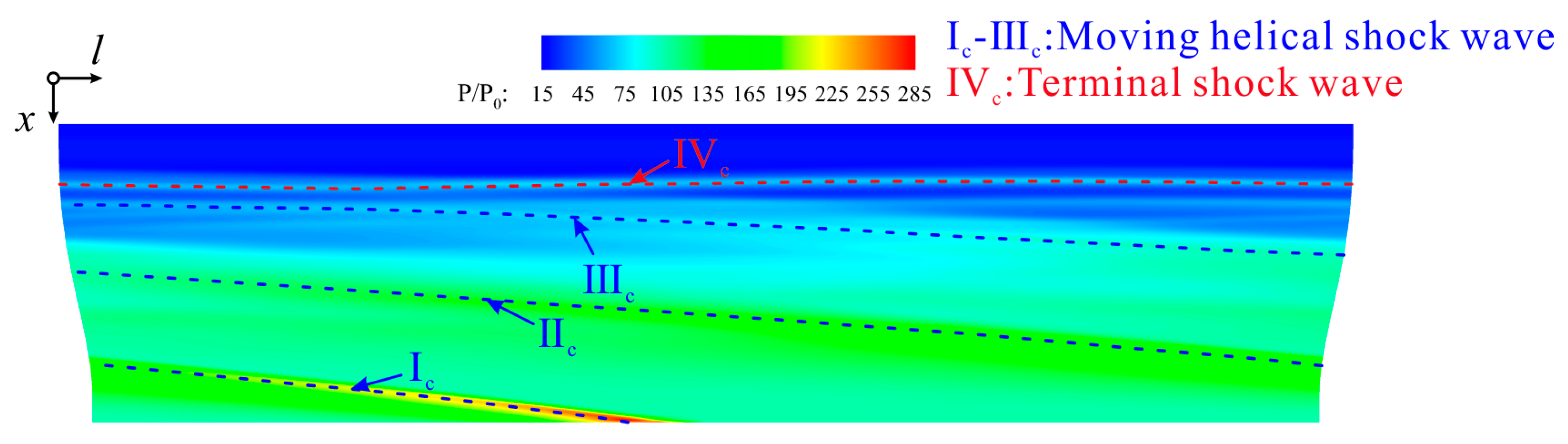
4.1. Terminal Shock Wave/Moving Shock Wave/Boundary Layer Interaction
4.2. Impact of the Shock Wave System on the Main Flow
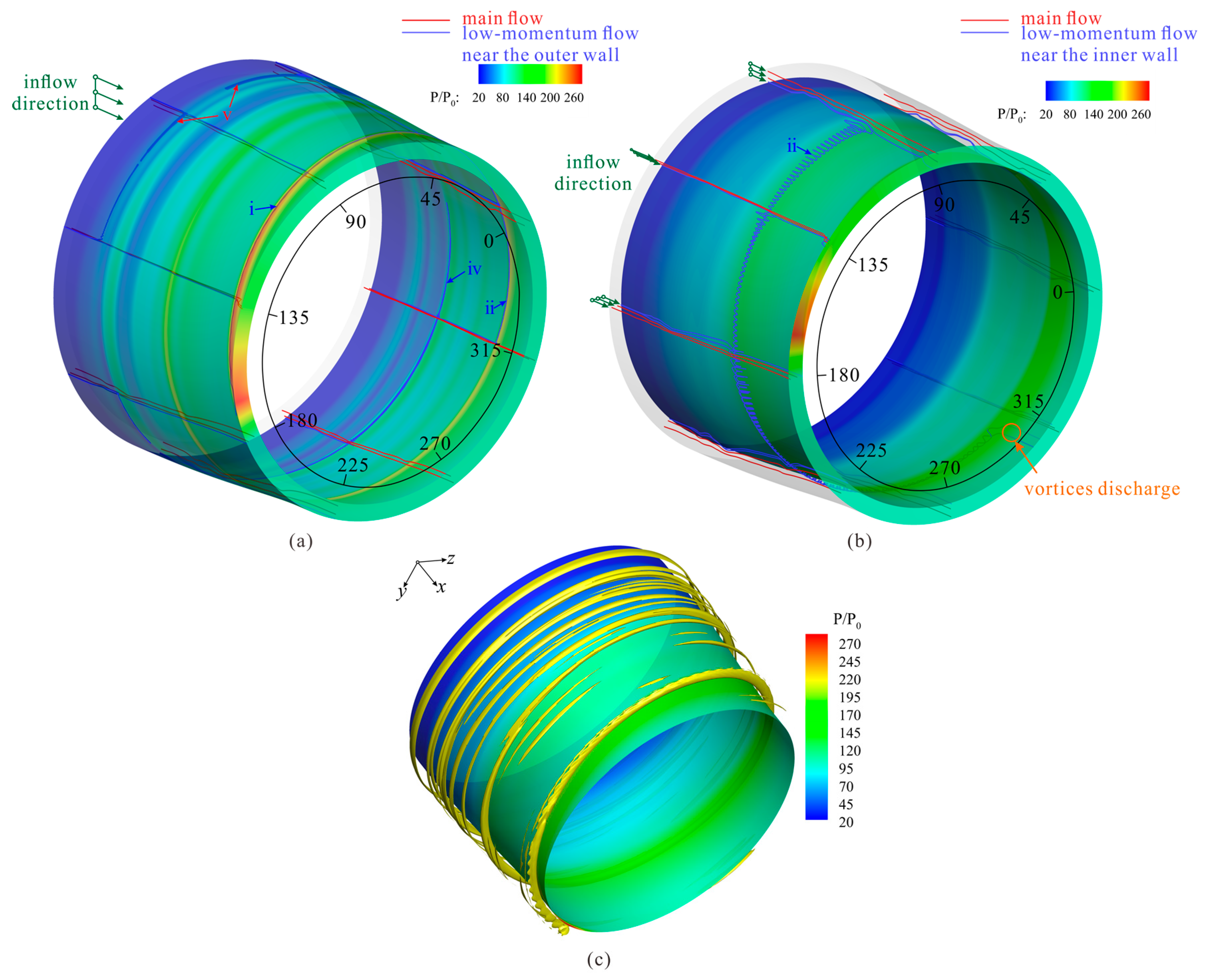
4.3. Flow Patterns at the Exit
5. Self-Similarity in the Isolator Affected by the Rotating Feedback Pressure
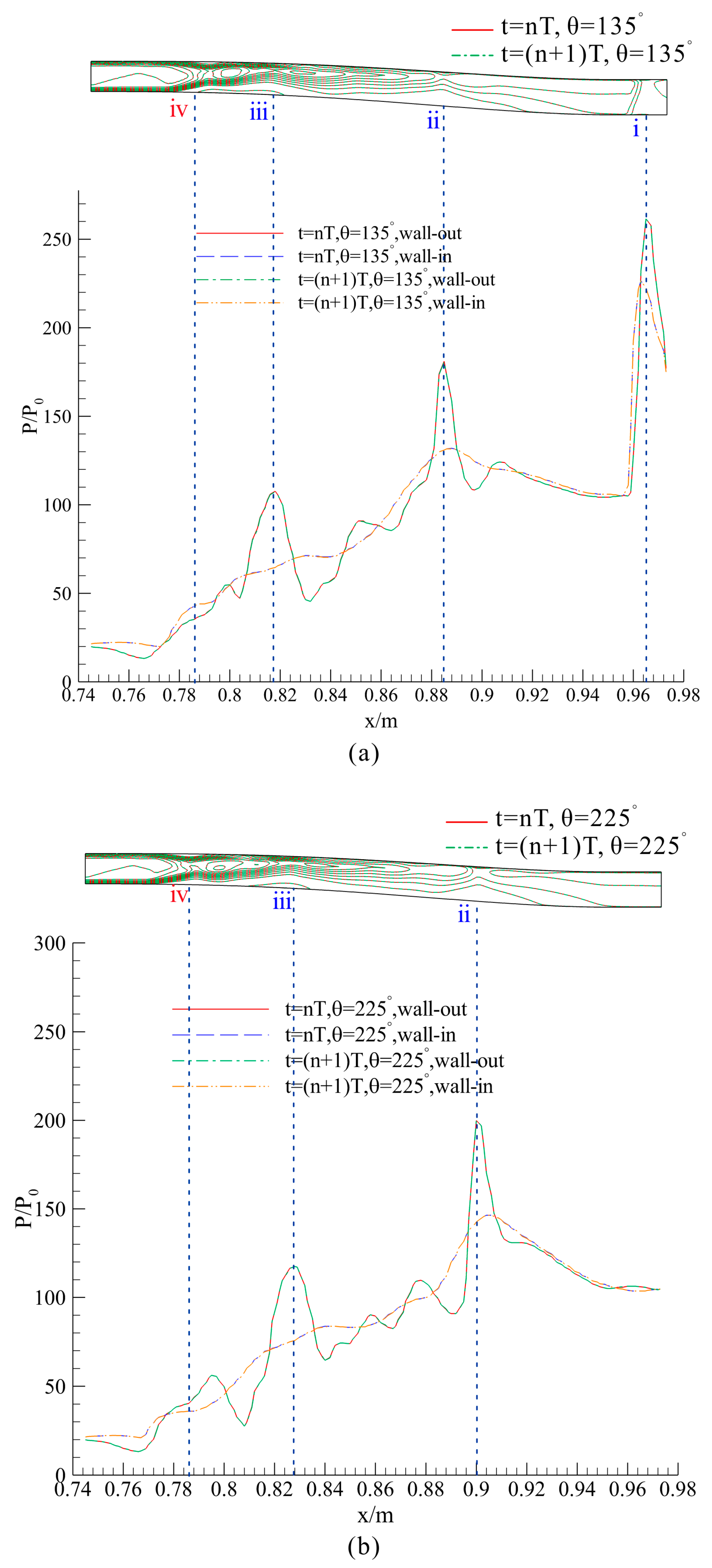
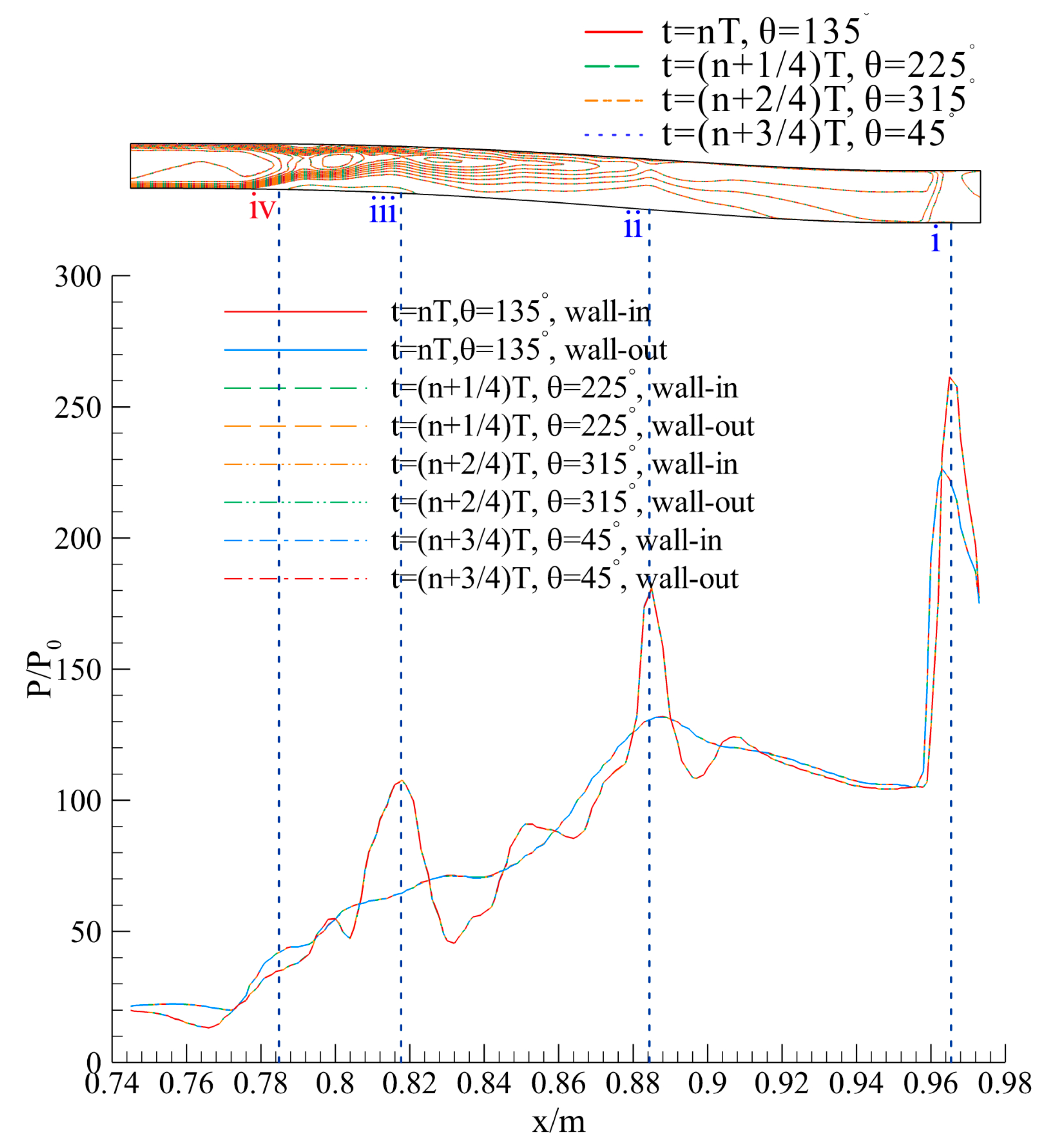
5.1. Similarity of the Flow Patterns between Adjacent Cycles
5.2. Comparison of the Flow Patterns at Different Moments in One Cycle
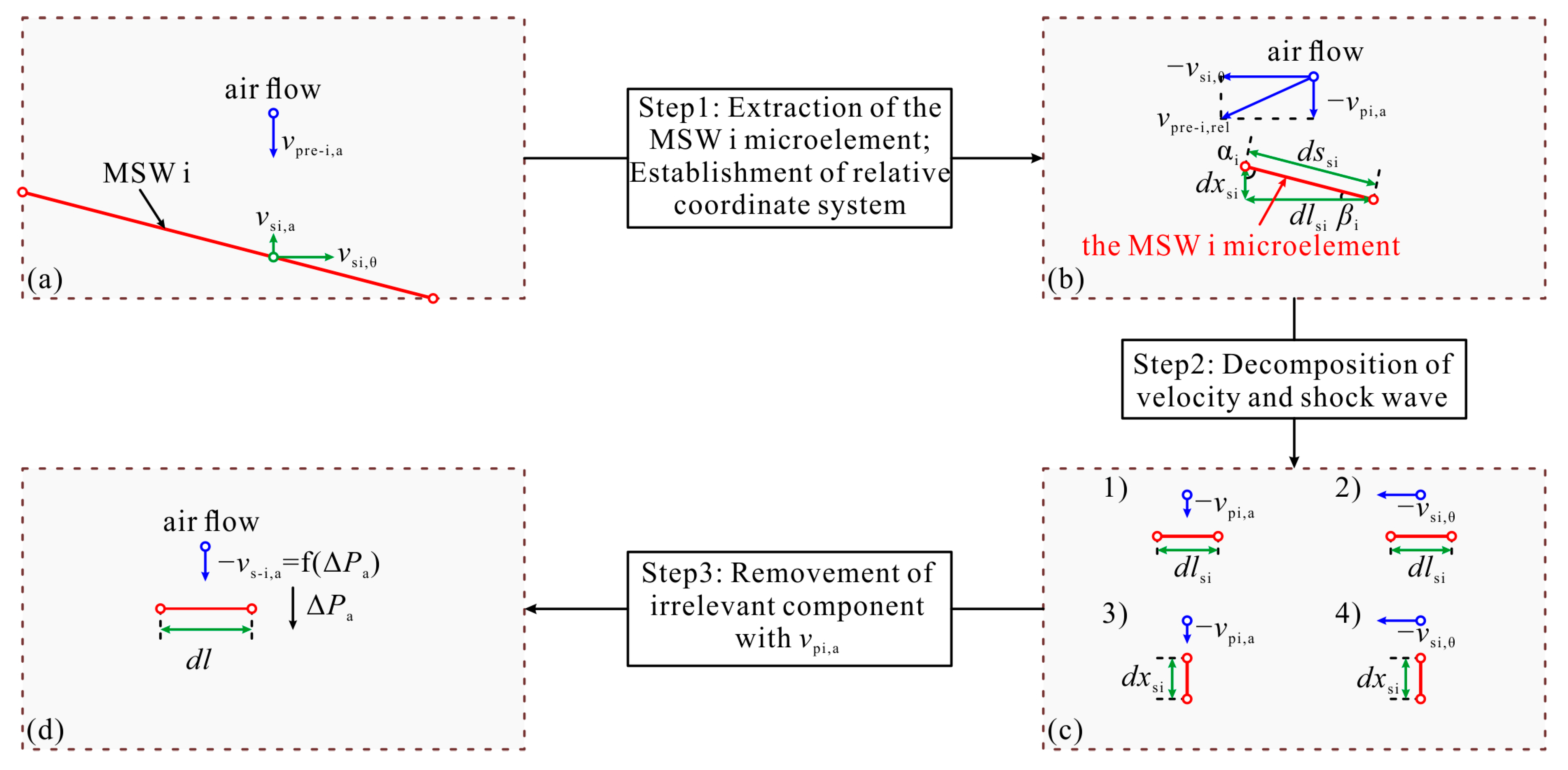
6. Theoretical Model of the Inclination Angles of the Moving Shock Wave, Based on Velocity Decomposition
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, F.K.; Braun, E.M. Rotating detonation wave propulsion: Experimental challenges, modeling, and engine concepts. J. Propul. Power 2014, 30, 1125–1142. [Google Scholar] [CrossRef]
- Wolanski, P. Detonative propulsion. Proc. Combust. Inst. 2013, 34, 125–158. [Google Scholar] [CrossRef]
- Anand, V.; Gutmark, E. Rotating detonation combustors and their similarities to rocket instabilities. Prog. Energy Combust. Sci. 2019, 73, 182–234. [Google Scholar] [CrossRef]
- Rong, G.; Cheng, M.; Sheng, Z.-H.; Liu, X.-Y.; Zhang, Y.-Z.; Wang, J.-P. Investigation of counter-rotating shock wave and wave direction control of hollow rotating detonation engine with Laval nozzle. Phys. Fluids 2022, 34, 056104. [Google Scholar] [CrossRef]
- Hexia, H.; Huijun, T.; Wang, J.; Le Ning, S.S. A fluidic control method of shock train in hypersonic inlet/isolator. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014. [Google Scholar]
- Matsuo, K.; Miyazato, Y.; Kim, H.D. Shock train and pseudo-shock phenomena in internal gas flows. Prog. Aerosp. Sci. 1999, 35, 33–100. [Google Scholar] [CrossRef]
- Bykovskii, F.A.; Zhdan, S.A.; Vedernikov, E.F. Continuous spin detonations. J. Propul. Power 2006, 22, 1204–1216. [Google Scholar] [CrossRef]
- Voitsekhovskii, B. Stationary spin detonation. Sov. J. Appl. Mech. Tech. Phys. 1960, 3, 157–164. [Google Scholar]
- Zhdan, S.A. Mathematical model of continuous detonation in an annular combustor with a supersonic flow velocity. Combust. Explos. Shock Waves 2008, 44, 690–697. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, Y.; Wang, J. Flow field of a rotating detonation engine fueled by carbon. Phys. Fluids 2022, 34, 073311. [Google Scholar] [CrossRef]
- Uemura, Y.; Hayashi, A.K.; Asahara, M.; Tsuboi, N.; Yamada, E. Transverse wave generation mechanism in rotating detonation. Proc. Combust. Inst. 2013, 34, 1981–1989. [Google Scholar] [CrossRef]
- Zhou, R.; Wang, J.P. Numerical investigation of flow particle paths and thermodynamic performance of continuously rotating detonation engines. Combust. Flame 2012, 159, 3632–3645. [Google Scholar] [CrossRef]
- Smirnov, N.; Nikitin, V.; Stamov, L.; Mikhalchenko, E.; Tyurenkova, V. Rotating detonation in a ramjet engine three-dimensional modeling. Aero. Sci. Technol. 2018, 81, 213–224. [Google Scholar] [CrossRef]
- Smirnov, N.; Nikitin, V.; Stamov, L.; Mikhalchenko, E.; Tyurenkova, V. Three-dimensional modeling of rotating detonation in a ramjet engine. Acta Astronaut. 2019, 163, 168–176. [Google Scholar] [CrossRef]
- Liu, S.-J.; Lin, Z.-Y.; Liu, W.-D.; Lin, W.; Zhuang, F.-C. Experimental realization of H2/air continuous rotating detonation in a cylindrical combustor. Combust. Sci. Technol. 2012, 184, 1302–1317. [Google Scholar] [CrossRef]
- Lin, W.; Zhou, J.; Liu, S.; Lin, Z.; Zhuang, F. Experimental study on propagation mode of H2/Air continuously rotating detonation wave. Int. J. Hydrogen Energy 2015, 40, 1980–1993. [Google Scholar] [CrossRef]
- Wang, C.; Liu, W.; Liu, S.; Jiang, L.; Lin, Z. Experimental investigation on detonation combustion patterns of hydrogen/vitiated air with annular combustor. Exp. Therm Fluid Sci. 2015, 66, 269–278. [Google Scholar] [CrossRef]
- Bluemner, R.; Bohon, M.; Paschereit, C.; Gutmark, E. Counter-rotating wave mode transition dynamics in an RDC. Int. J. Hydrogen Energy 2019, 44, 7628–7641. [Google Scholar] [CrossRef]
- Han, J.; Bai, Q.; Zhang, S.; Weng, C. Experimental study on propagation mode of rotating detonation wave with cracked kerosene gas and ambient temperature air. Phys. Fluids 2022, 34, 075127. [Google Scholar] [CrossRef]
- Naples, J.; Hoke, J.; Karnesky; Schauer, F. Flowfield Characterization of a Rotating Detonation Engine. In Proceedings of the 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Dallas, TX, USA, 7–10 January 2013. [Google Scholar]
- Anand, V.; George, A.S.; Driscoll, R.; Gutmark, E. Characterization of instabilities in a rotating detonation combustor. Int. J. Hydrogen Energy 2015, 40, 16649–16659. [Google Scholar] [CrossRef]
- Liu, Y.S.; Wang, Y.H.; Li, Y.S.; Li, Y.; Wang, J.P. Spectral analysis and self-adjusting mechanism for oscillation phenomenon in H2/O2 continuously rotating detonation engine. Chin. J. Aeronaut. 2015, 28, 669–675. [Google Scholar] [CrossRef]
- Wu, Y.X.; Ma, H.; Peng, L.; Gao, J. Experimental research on initiation characteristics of a rotating detonation engine. Exp. Therm. Fluid Sci. 2016, 71, 154–163. [Google Scholar]
- Liu, Y.; Zhou, W.; Yang, Y.; Liu, Z.; Wang, J. Numerical study on the instabilities in H2-air rotating detonation engines. Phys. Fluids 2018, 30, 046106. [Google Scholar] [CrossRef]
- Schwer, D.; Kailasanath, K. Effect of Inlet on Fill Region and Performance of Rotating Detonation Engines. In Proceedings of the 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, San Diego, CA, USA, 31 July–3 August 2011. [Google Scholar]
- Anand, V.; St George, A.; Driscoll, R.; Gutmark, E. Analysis of air inlet and fuel plenum behavior in a rotating detonation combustor. Exp. Therm. Fluid Sci. 2016, 70, 408–416. [Google Scholar] [CrossRef]
- Schwer, D.A.; Kailasanath, K.; Kaemming, T. Pressure characteristics of a ram-RDE diffuser. Aerosp. Sci. Technol. 2019, 85, 187–198. [Google Scholar] [CrossRef]
- Frolov, S.M.; Dubrovskii, A.V.; Ivanov, V.S. Three-dimensional numerical simulation of operation process in rotating detonation engine. Prog. Propuls. Phys. 2013, 4, 467–488. [Google Scholar]
- Frolov, S.M.; Dubrovsky, A.V.; Ivanov, V.S. Three-Dimensional Numerical Simulation of a Continuously Rotating Detonation in the Annular Combustion Chamber with a Wide Gap and Separate Delivery of Fuel and Oxidizer. In Proceedings of the 5th EUCASS, Munich, Germany, 1–6 July 2013. [Google Scholar]
- Dyson, R.W. Flow Diode and Method for Controlling Fluid Flow Origin of the Invention. US Patent 9169855 B1, 4 November 2015. [Google Scholar]
- Liu, S.; Liu, W.; Jiang, L.; Lin, Z. Numerical investigation on the airbreathing continuous rotating detonation engine. In Proceedings of the 25th ICDERS, Leeds (ICDERS, 2015), Leeds, UK, 2–7 August 2015; Volume 157. [Google Scholar]
- Wang, G.; Liu, W.; Liu, S.; Zhang, H.; Peng, H.; Zhou, Y. Experimental verification of cylindrical air-breathing continuous rotating detonation engine fueled by non-premixed ethylene. Acta Astronaut. 2021, 189, 722–732. [Google Scholar] [CrossRef]
- Dubrovskii, V.; Ivanov, A.; Zangiev; Frolov, S. Three-dimensional numerical simulation of the characteristics of a ramjet power plant with a continuous-detonation combustor in supersonic flight. Russ. J. Phys. Chem. B 2016, 10, 469–482. [Google Scholar] [CrossRef]
- Mengmeng, Z.; Buttsworth, D.; Gollan, R.; Jacobs, P. Simulation of a Rotating Detonation Ramjet Model in Mach 4 Flow. Simulation 2018, 10, 1321. [Google Scholar]
- Wu, K.; Zhang, S.; Luan, M.; Wang, J. Effects of flow-field structures on the stability of rotating detonation ramjet engine. Acta Astronaut. 2020, 168, 174–181. [Google Scholar] [CrossRef]
- Wu, K.; Zhang, S.; Shen, D.; Wang, J. Analysis of flow-field characteristics and pressure gain in air-breathing rotating detonation combustor. Phys. Fluids 2021, 33, 126112. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Jianhua, C. Backpressure Characteristics of Annular Isolator in CRDR; National University of Defense Technology: Changsha, China, 2017. [Google Scholar]
- Yue, S. Numerical Research on the Effects of Ramjet Rotating Detonation on the Incoming Flow; National University of Defense Technology: Changsha, China, 2019. [Google Scholar]
- Peng, H.Y.; Liu, W.D.; Liu, S.J.; Zhang, H.L. Experimental investigations on ethylene-air continuous rotating detonation wave in the hollow chamber with laval nozzle. Acta Astronaut. 2018, 151, 137–145. [Google Scholar] [CrossRef]
- Peng, H.-Y.; Liu, W.-D.; Liu, S.-J.; Zhang, H.-L.; Jiang, L.-X. Flowfield analysis and reconstruction of ethylene–air continuous rotating detonation wave. AIAA J. 2020, 58, 5036–5045. [Google Scholar] [CrossRef]
- Rentao, Z. Study of Flow Characteristics of Rotating Detonation Engine Inlet; Nanjing University of Aeronautics and Astronautics: Changsha, China, 2019. [Google Scholar]
- Igra, O.; Wang, L.; Palcovitz, J.; Heilig, W. Shock wave propagation in a branched duct. Shock Waves 1998, 8, 375–381. [Google Scholar] [CrossRef]
- Mazor, G.; Igra, O.; Ben-Dor, G.; Mond, M.; Reichenbach, H.; Smith, F.T. Head-on collision of normal shock waves with a rubber-supported wall. Philos. Trans. R. Soc. Lond. Ser. A Phys. Eng. Sci. 1992, 338, 237–269. [Google Scholar] [CrossRef]
- Chao, W. Self-Sustaining and Propagation Mechanism of Airbreathing Continuous Rotating Detonation Wave; National University of Defense Technology: Changsha, China, 2016. [Google Scholar]
- Yuan, H.; Liu, F.; Wang, X.; Zhou, Z. Design and analysis of a supersonic axisymmetric inlet based on controllable bleed slots. Aerosp. Sci. Technol. 2021, 118, 107008. [Google Scholar] [CrossRef]
- Liu, J.; Liu, C. Modified normalized Rortex/vortex identification method. Phys. Fluids 2019, 31, 061704. [Google Scholar] [CrossRef]
- Dong, X.; Gao, Y.; Liu, C. New normalized Rortex/vortex identification method. Phys. Fluids 2019, 31, 011701. [Google Scholar] [CrossRef]
- Kalkhoran, M.; Smart, M.K. Aspects of shock wave-induced vortex breakdown. Prog. Aerosp. Sci. 2000, 36, 63–95. [Google Scholar] [CrossRef]
- Liang, G.; Huang, H.; Tan, H.; Luo, Z.; Tang, X.; Li, C.; Cai, J. Shock train/glancing shock/boundary layer interaction in a curved isolator with sidewall contraction. Phys. Fluids 2022, 34, 116106. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Liso, mm | 228.43 |
| LS-shaped, mm | 208.43 |
| Rent-in, mm | 152.28 |
| Hent, mm | 12.00 |
| Rexi-in, mm | 143.00 |
| Hexi, mm | 14.00 |
| Roff,iso, mm | 8.28 |
| Parameter | Value |
|---|---|
| Mean Mach number Ment | 2.67 |
| Total pressure Pt,ent, kPa | 1423.07 |
| Static pressure Pent | 18.94 P0 |
| Static temperature Tent, K | 554.45 |
| Nominal boundary layer thickness δent, mm | 1.09 |
| Parameter | Value |
|---|---|
| Peak value | 280 P0 |
| Valley value | 104.6 P0 |
| Variation period T, s | 2 × 10−4 |
| Variation frequency f, Hz | 5000 |
| Parameters | Value | ||
|---|---|---|---|
| MSW i | MSW ii | MSWb iii | |
| , m/s | 657.50 | 485.44 | −3.75 |
| , m/s | 4716.84 | 4797.93 | 4932.15 |
| , ° | 82.07 | 84.22 | 90.04 |
| , ° | 83.94 | 85.99 | 87.77 |
| δα, % | −2.23 | −2.06 | 2.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Z.; Huang, H.; Tan, H.; Liang, G.; Lv, J.; Wu, Y.; Li, L. On the Self-Similarity in an Annular Isolator under Rotating Feedback Pressure Perturbations. Aerospace 2023, 10, 188. https://doi.org/10.3390/aerospace10020188
Luo Z, Huang H, Tan H, Liang G, Lv J, Wu Y, Li L. On the Self-Similarity in an Annular Isolator under Rotating Feedback Pressure Perturbations. Aerospace. 2023; 10(2):188. https://doi.org/10.3390/aerospace10020188
Chicago/Turabian StyleLuo, Zhongqi, Hexia Huang, Huijun Tan, Gang Liang, Jinghao Lv, Yuwen Wu, and Liugang Li. 2023. "On the Self-Similarity in an Annular Isolator under Rotating Feedback Pressure Perturbations" Aerospace 10, no. 2: 188. https://doi.org/10.3390/aerospace10020188
APA StyleLuo, Z., Huang, H., Tan, H., Liang, G., Lv, J., Wu, Y., & Li, L. (2023). On the Self-Similarity in an Annular Isolator under Rotating Feedback Pressure Perturbations. Aerospace, 10(2), 188. https://doi.org/10.3390/aerospace10020188







