Ground Test and Numerical Simulation of Aerodynamic Interference of the Marsupial UAS
Abstract
:1. Introduction
2. Methodology and Research Models
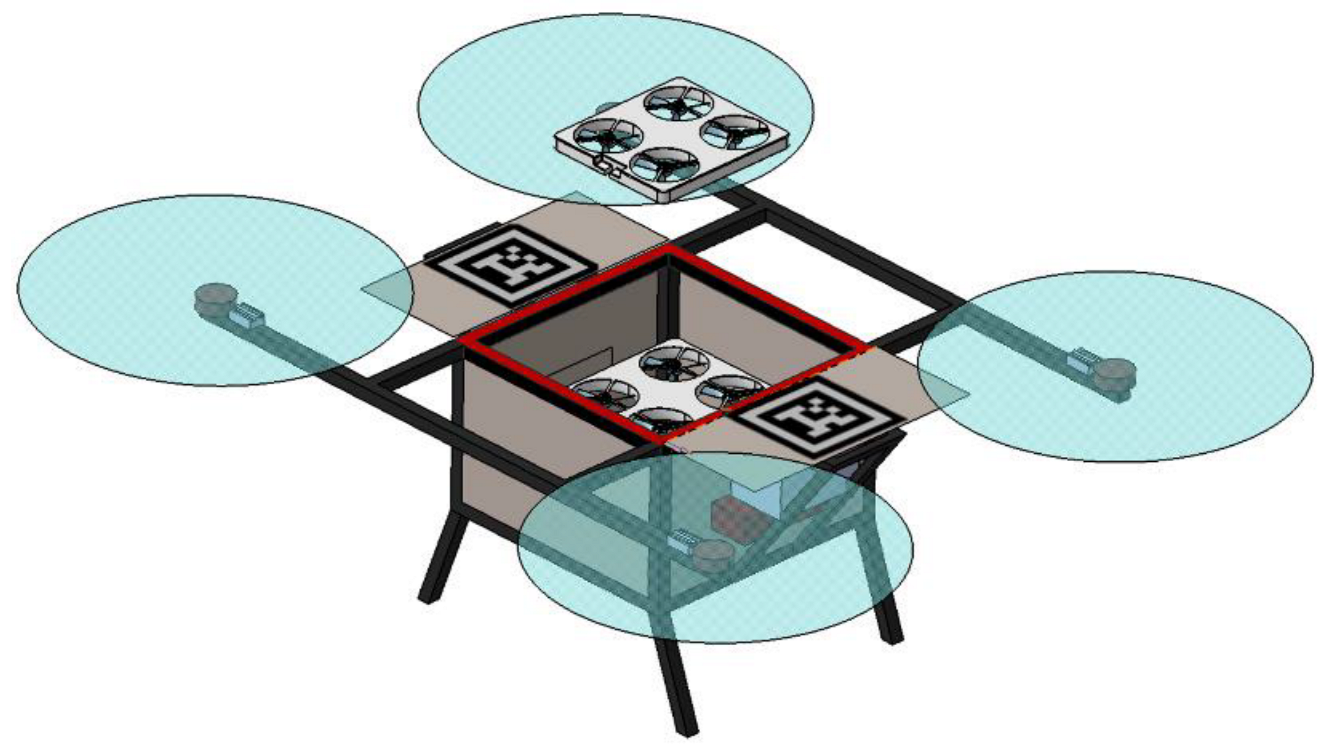
2.1. Ground Test Experiment
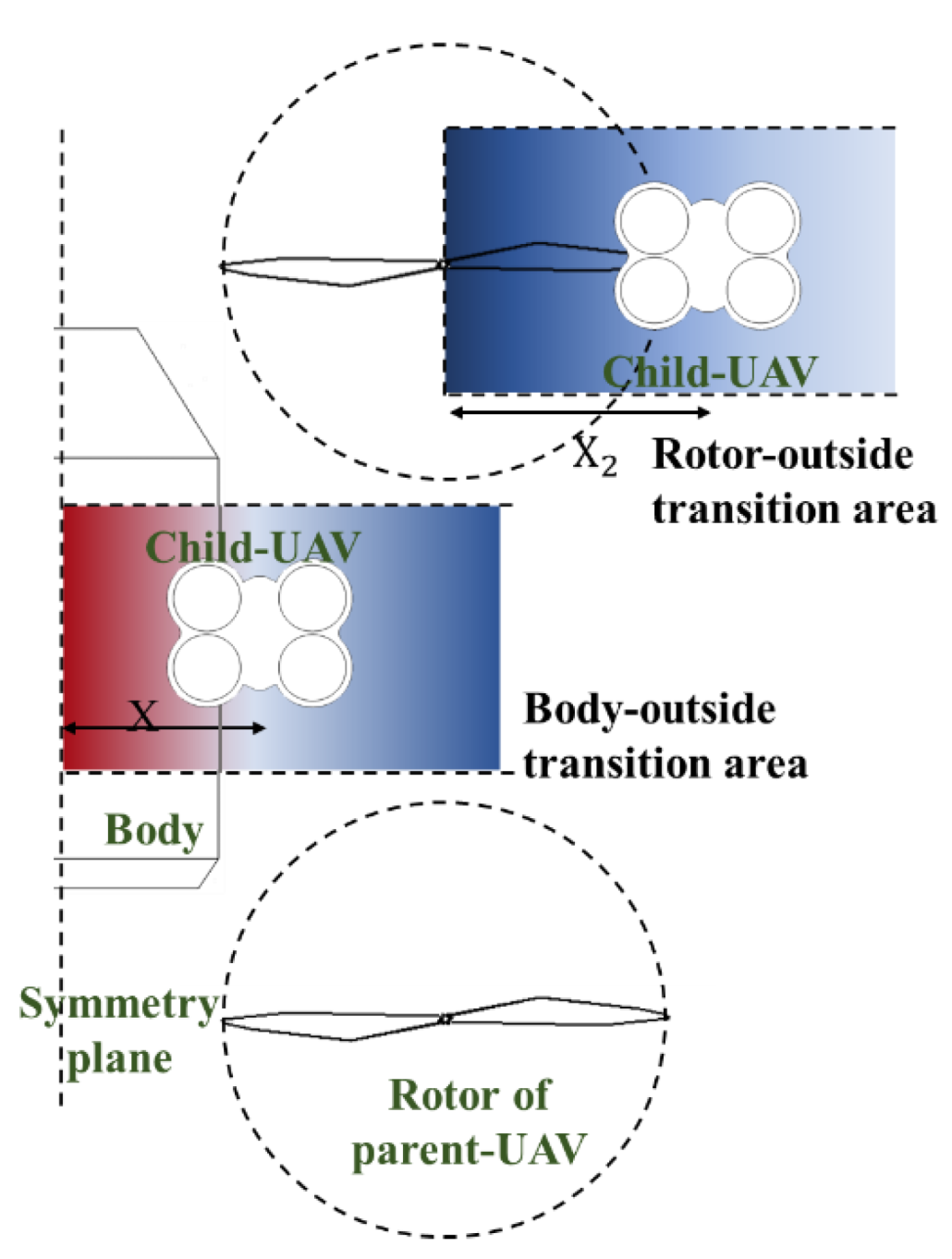
2.1.1. Research Models
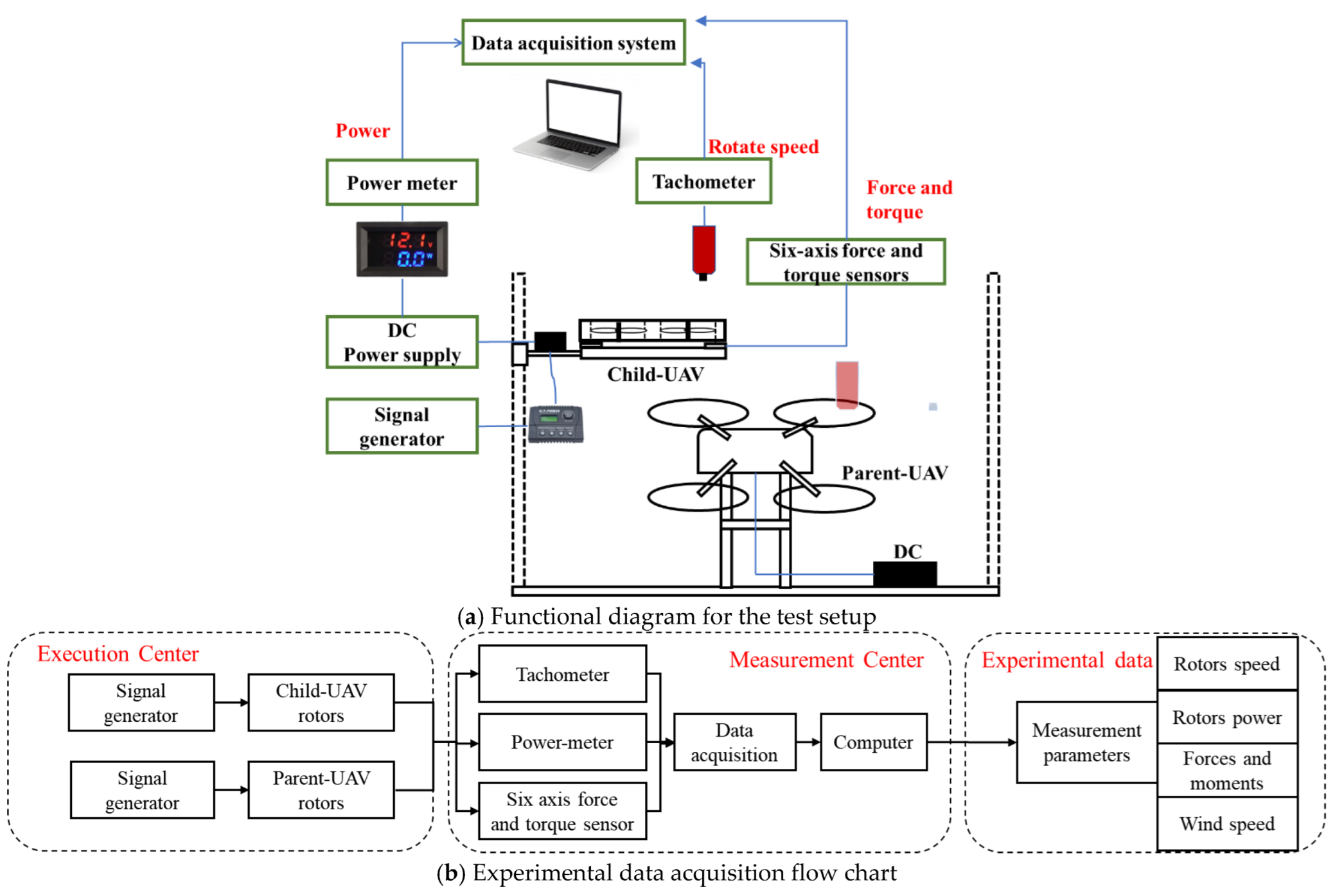
2.1.2. Experimentation Setup
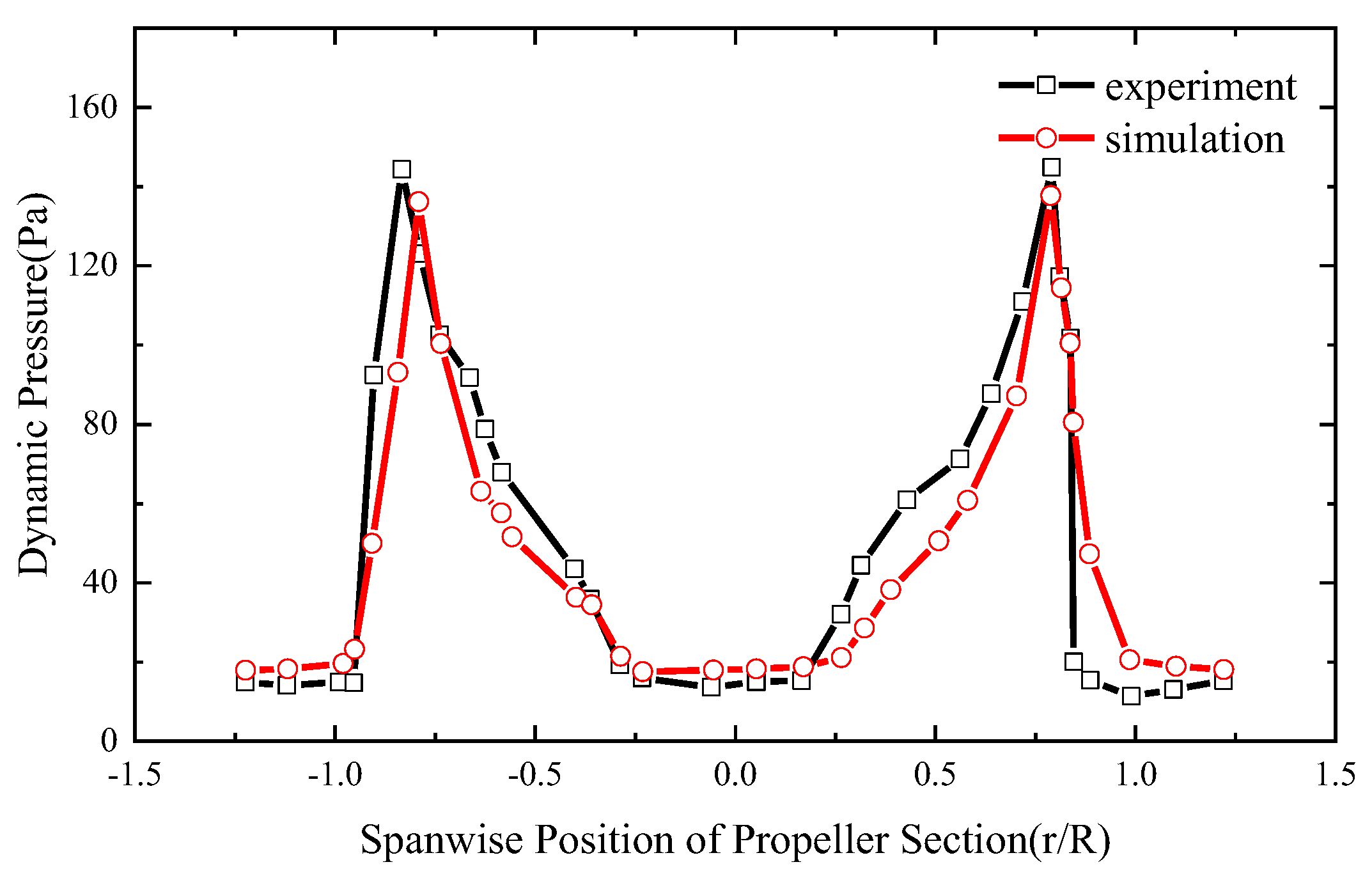
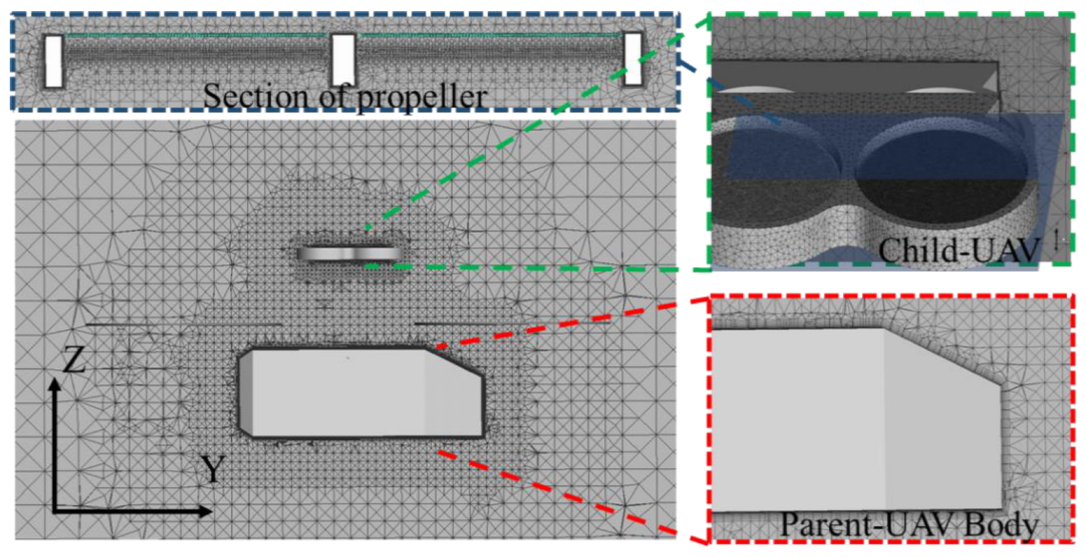
2.2. CFD Numerical Method
3. Results and Discussions
3.1. The Aerodynamic Interference in the Launch and Recovery Process
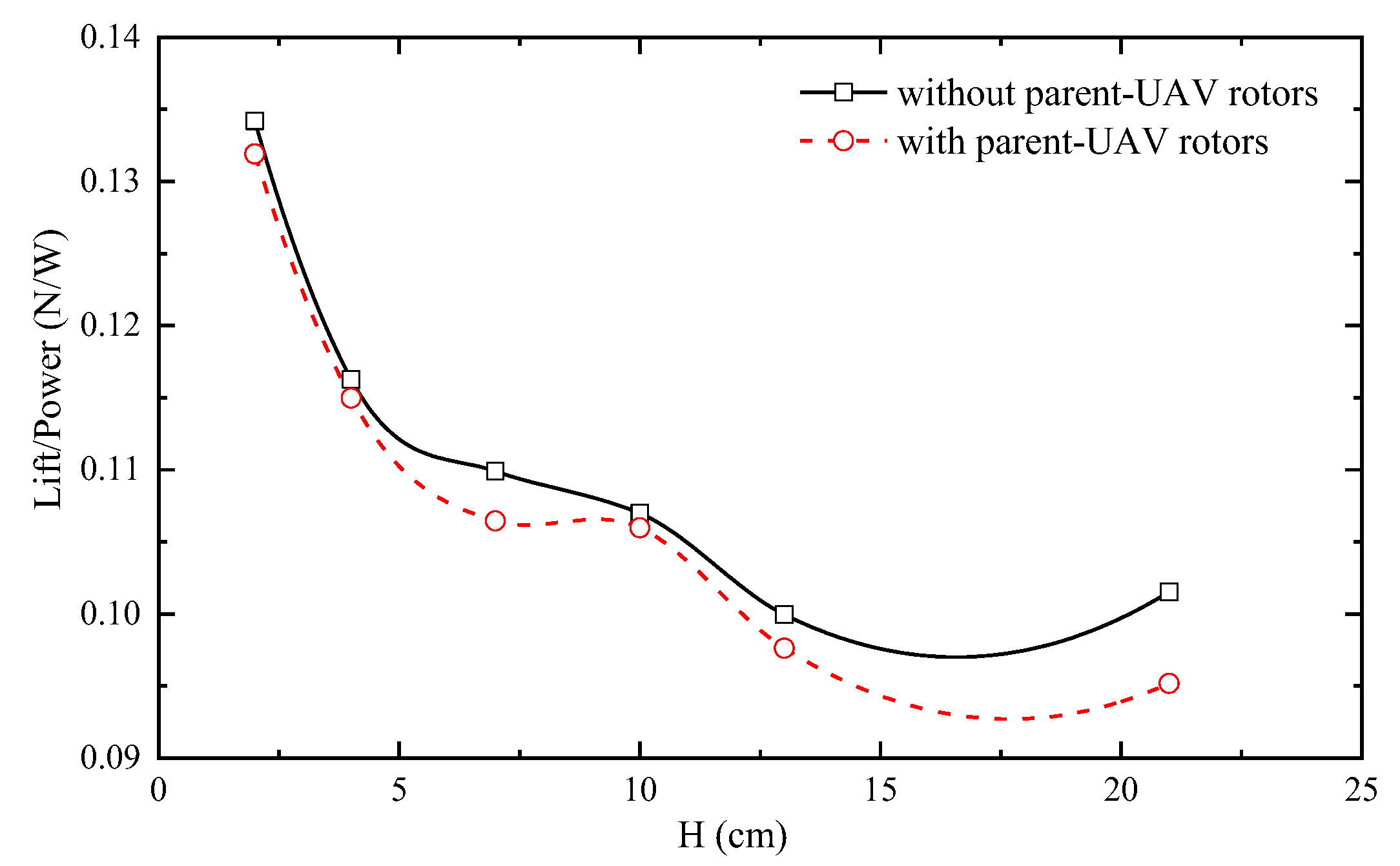
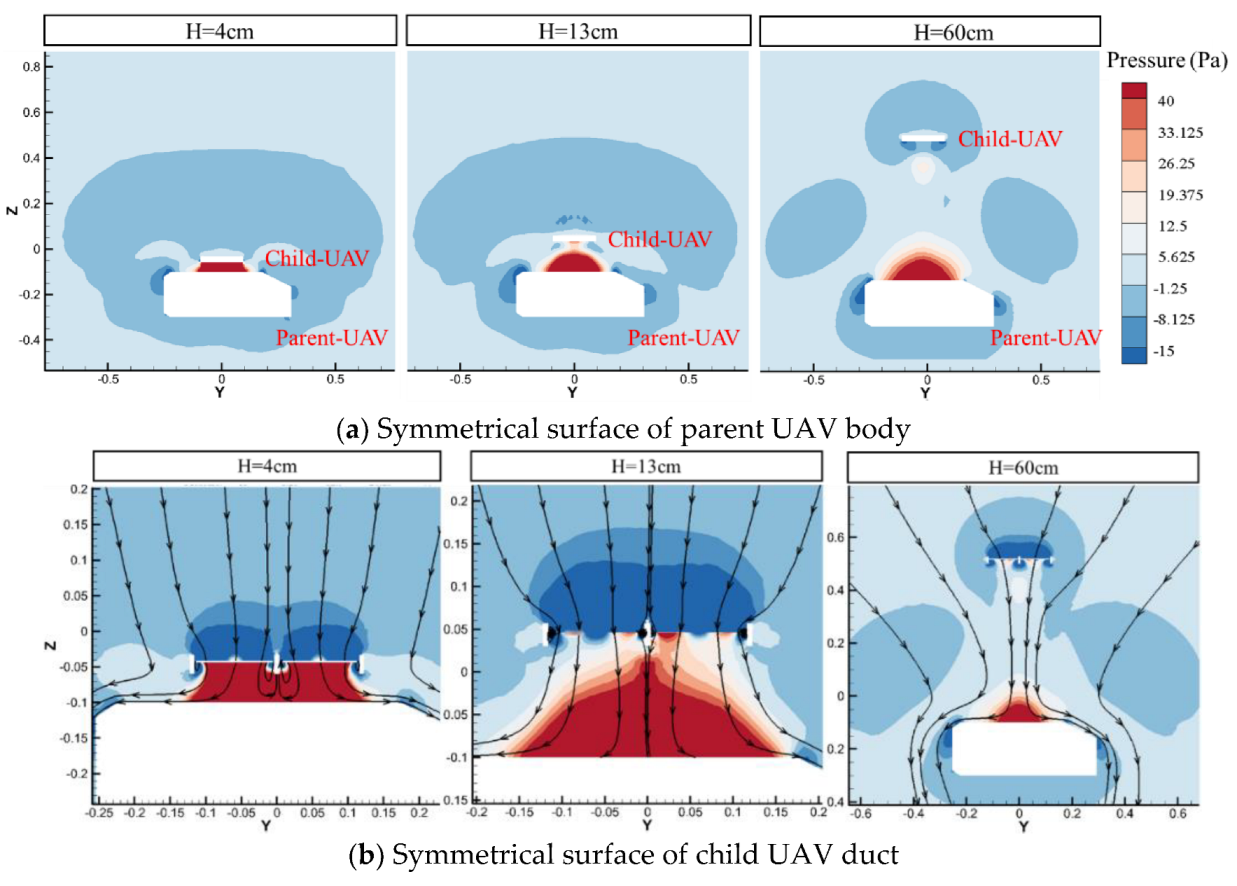
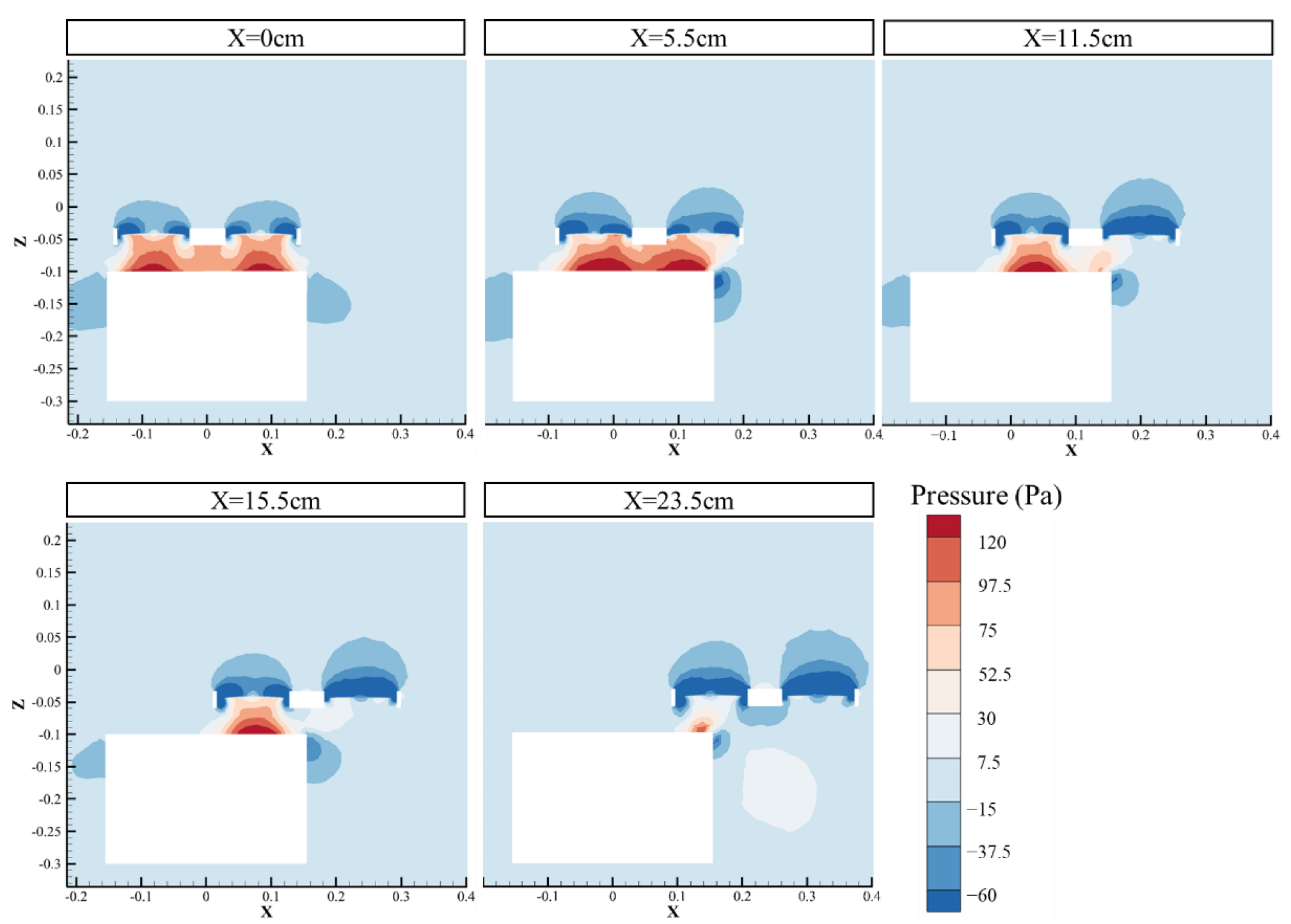
3.1.1. The Interference Area above the Body
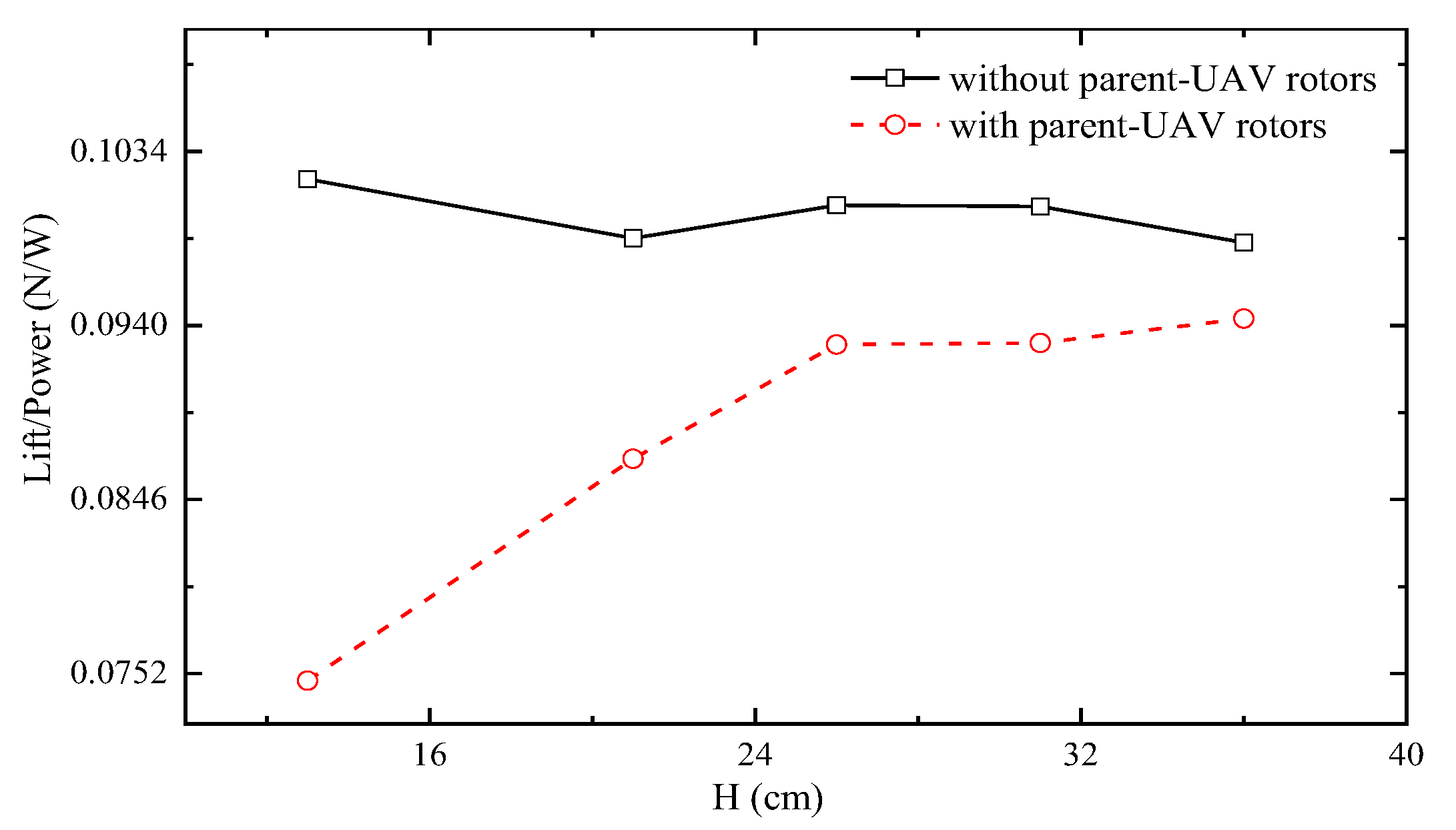
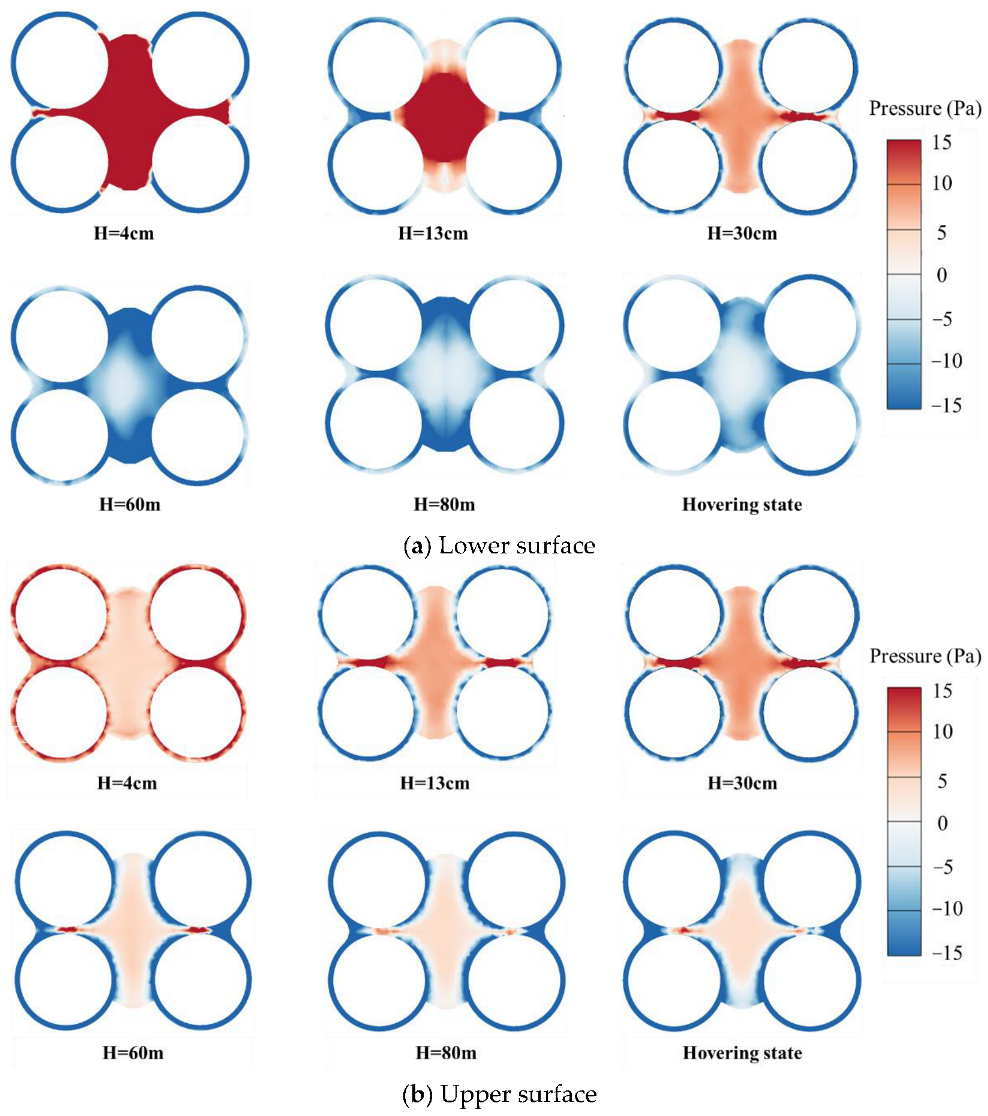
3.1.2. The Interference Area above Rotors
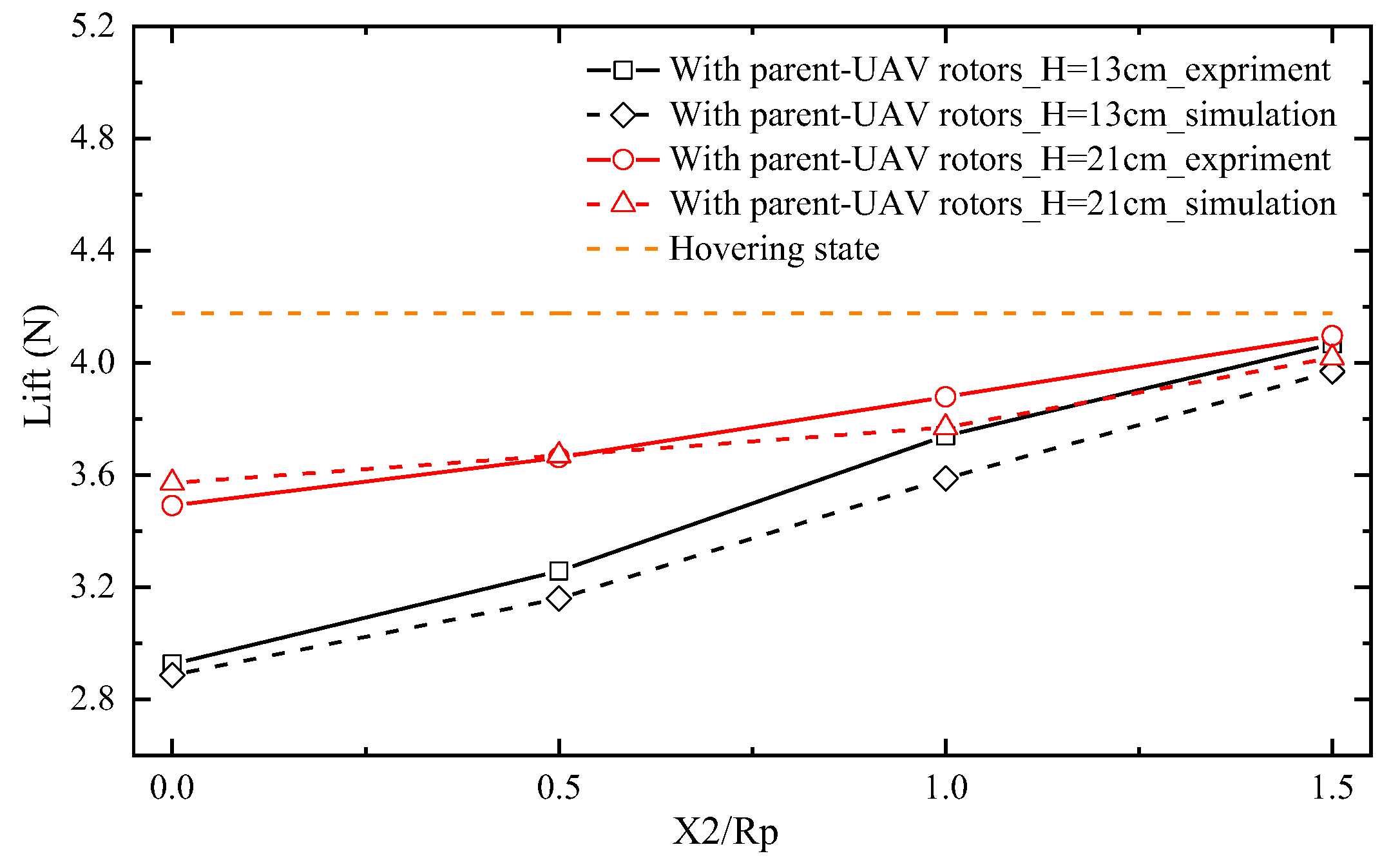
3.1.3. The Transition Area
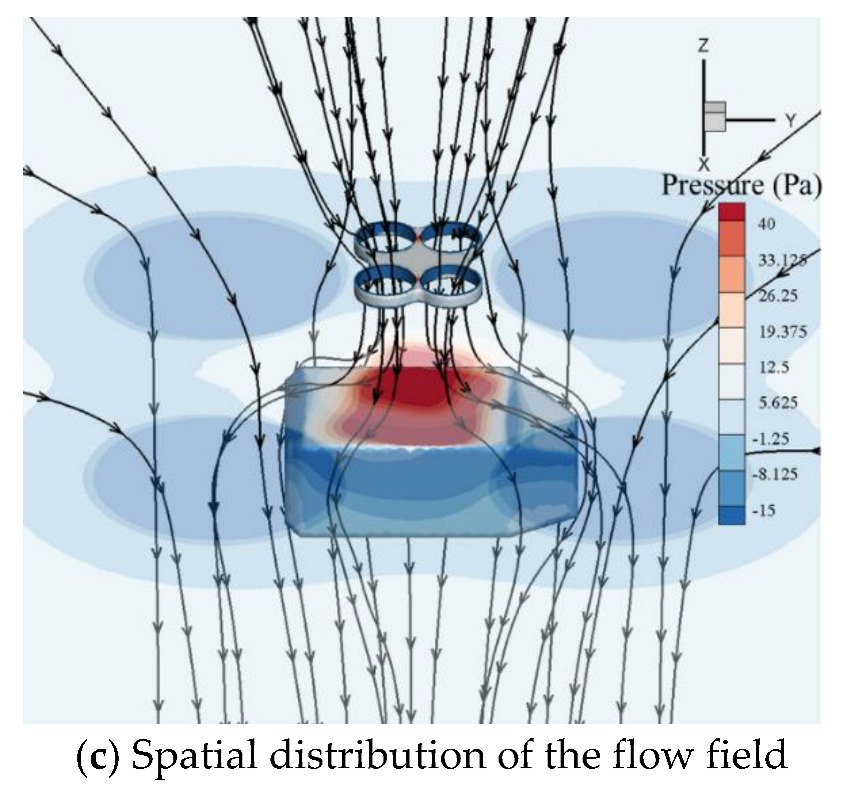
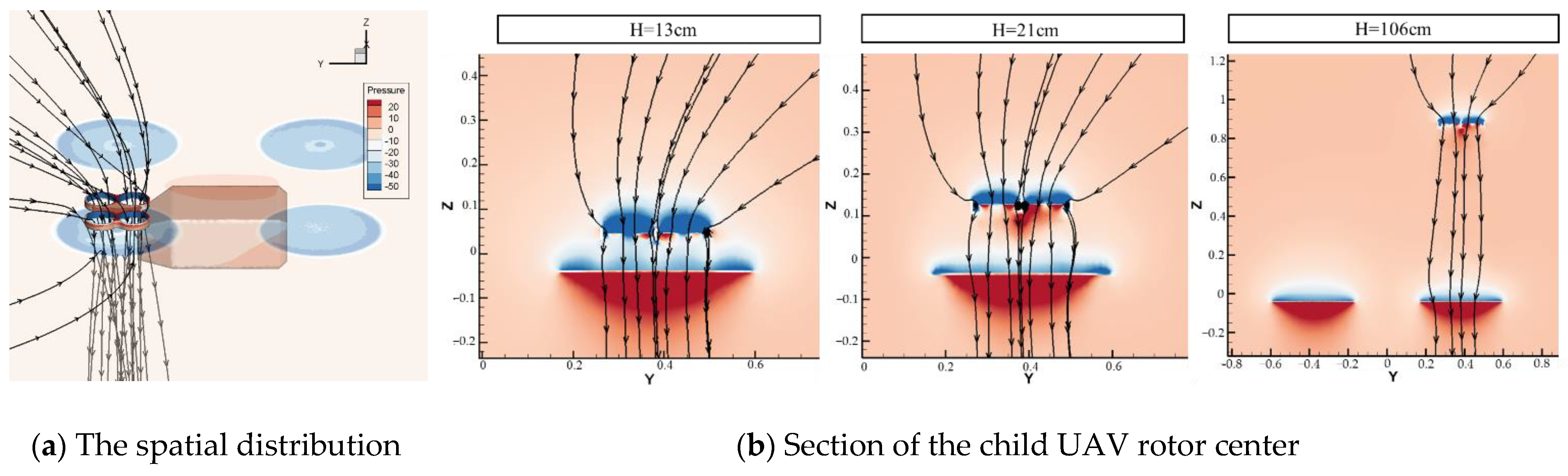
3.2. Mechanism Analysis of Aerodynamic Interference
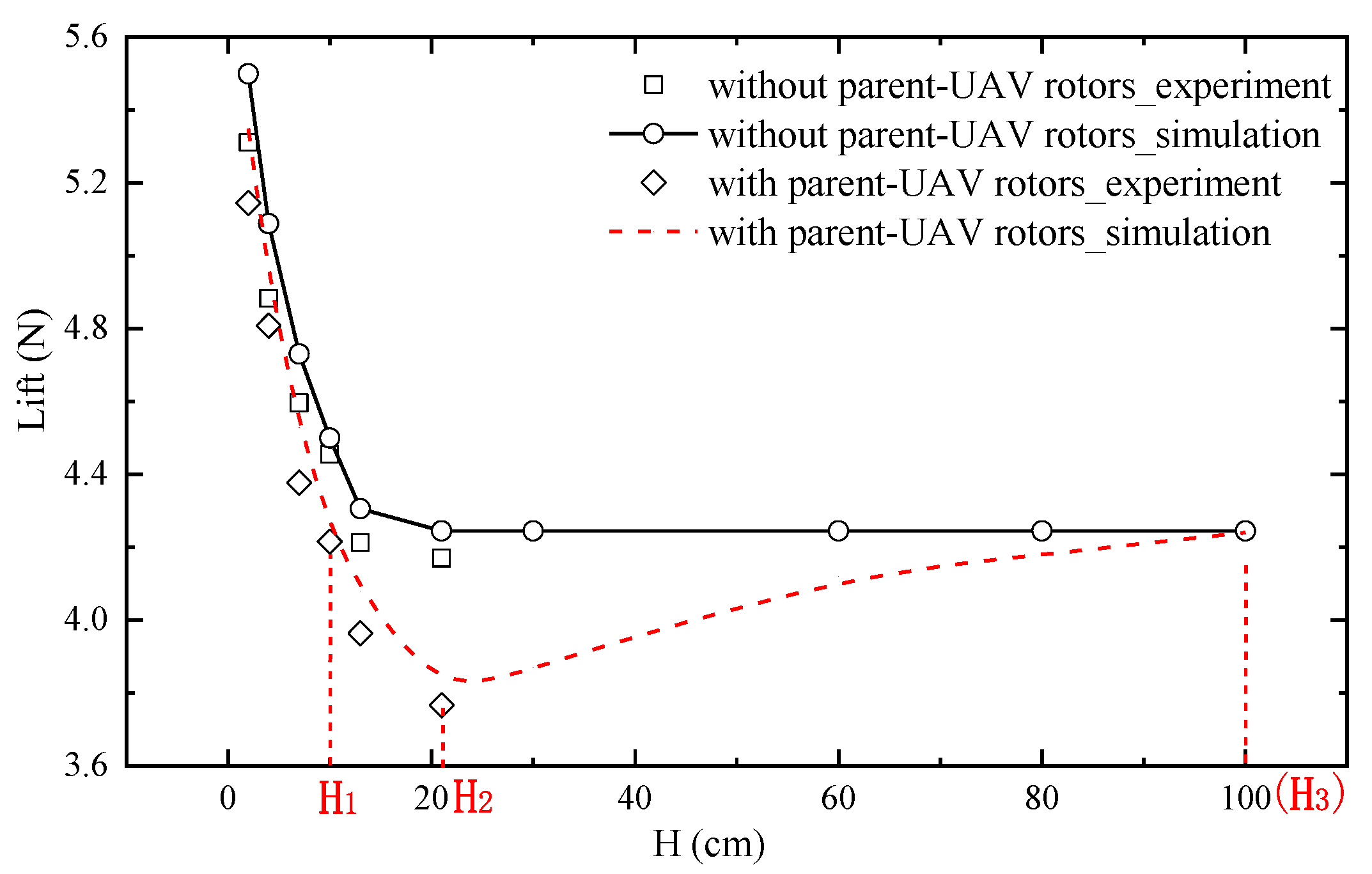
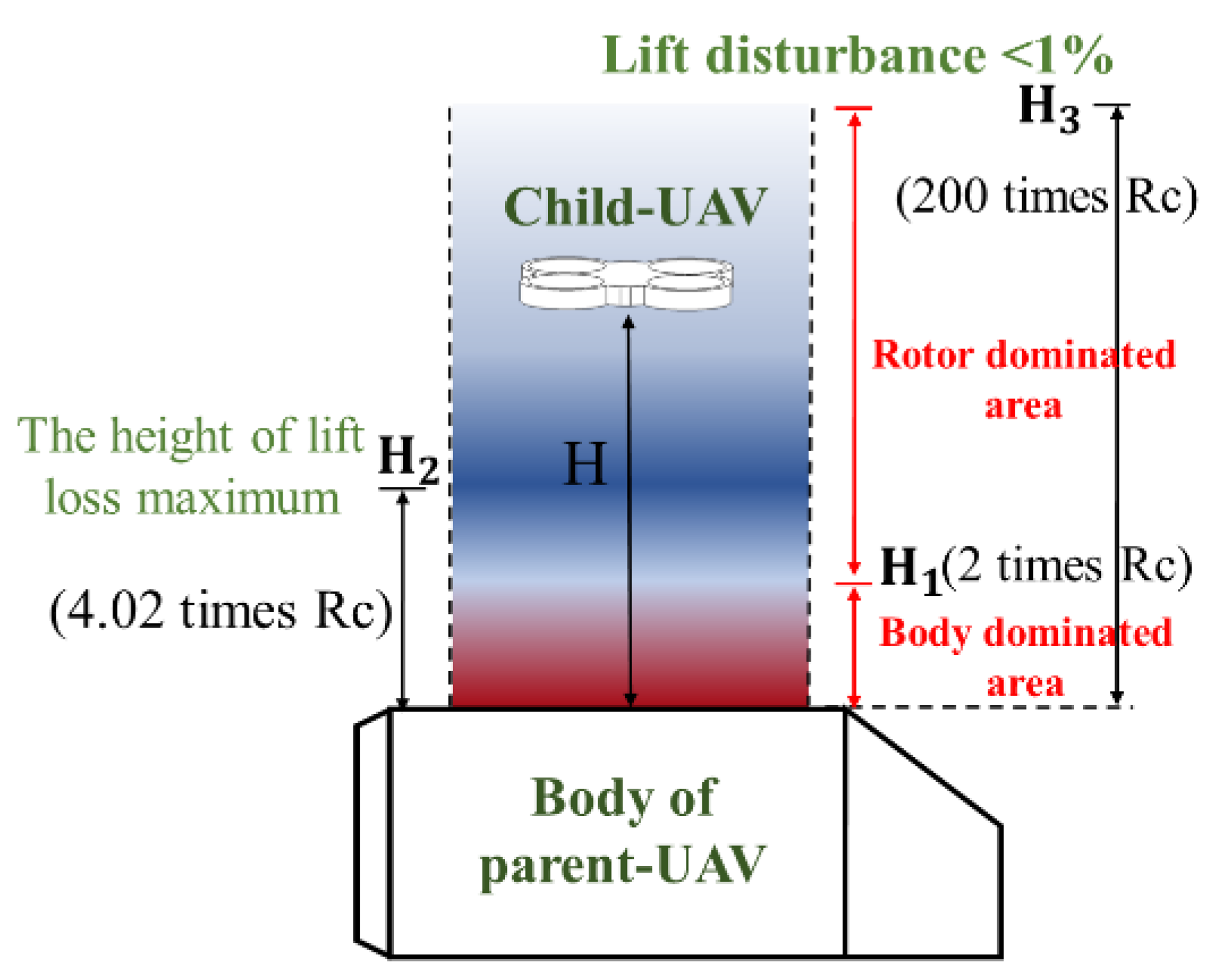
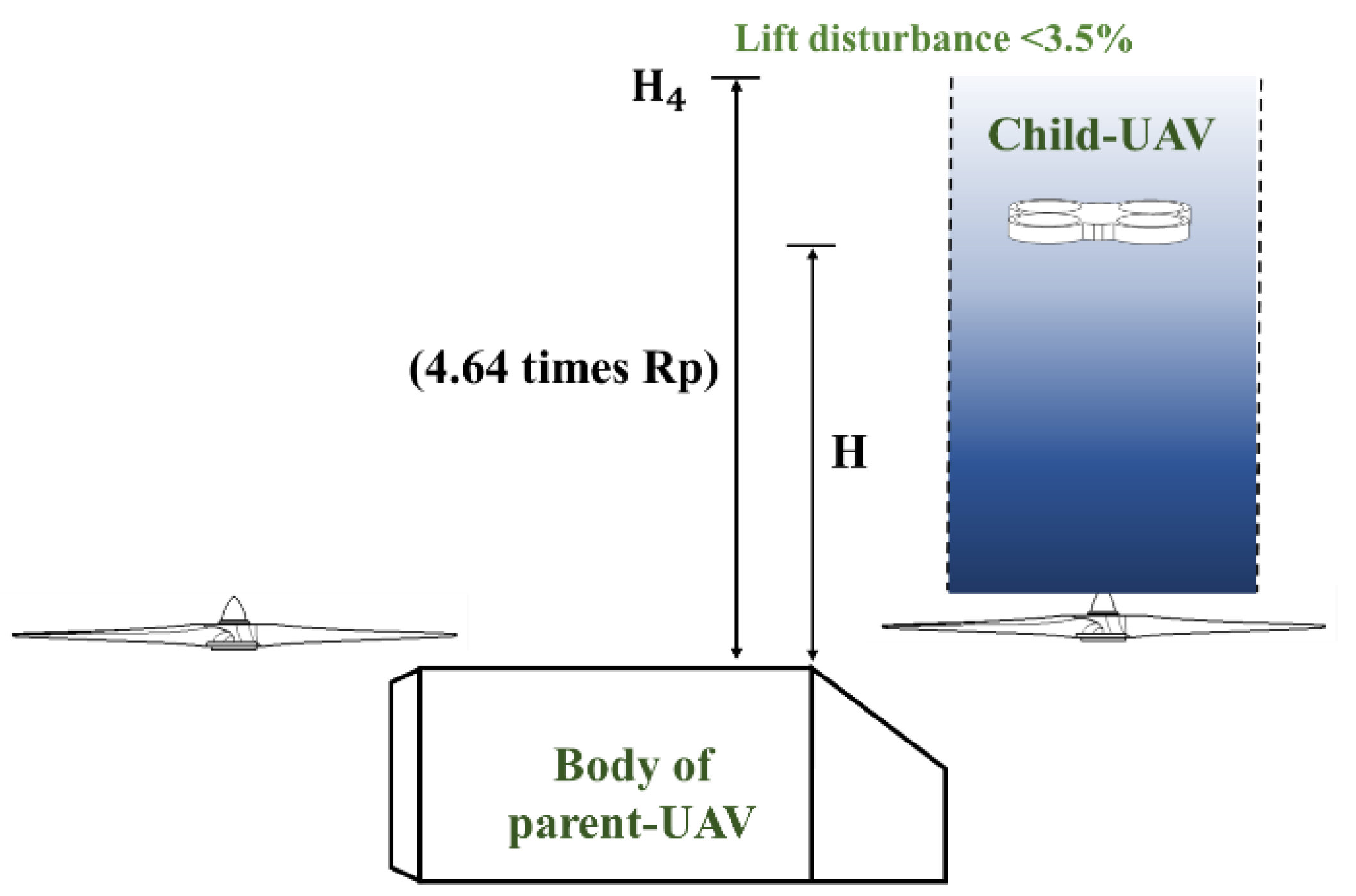
3.3. Analysis of the Safe Flight Boundary of the Child UAV
4. Conclusions
- (1)
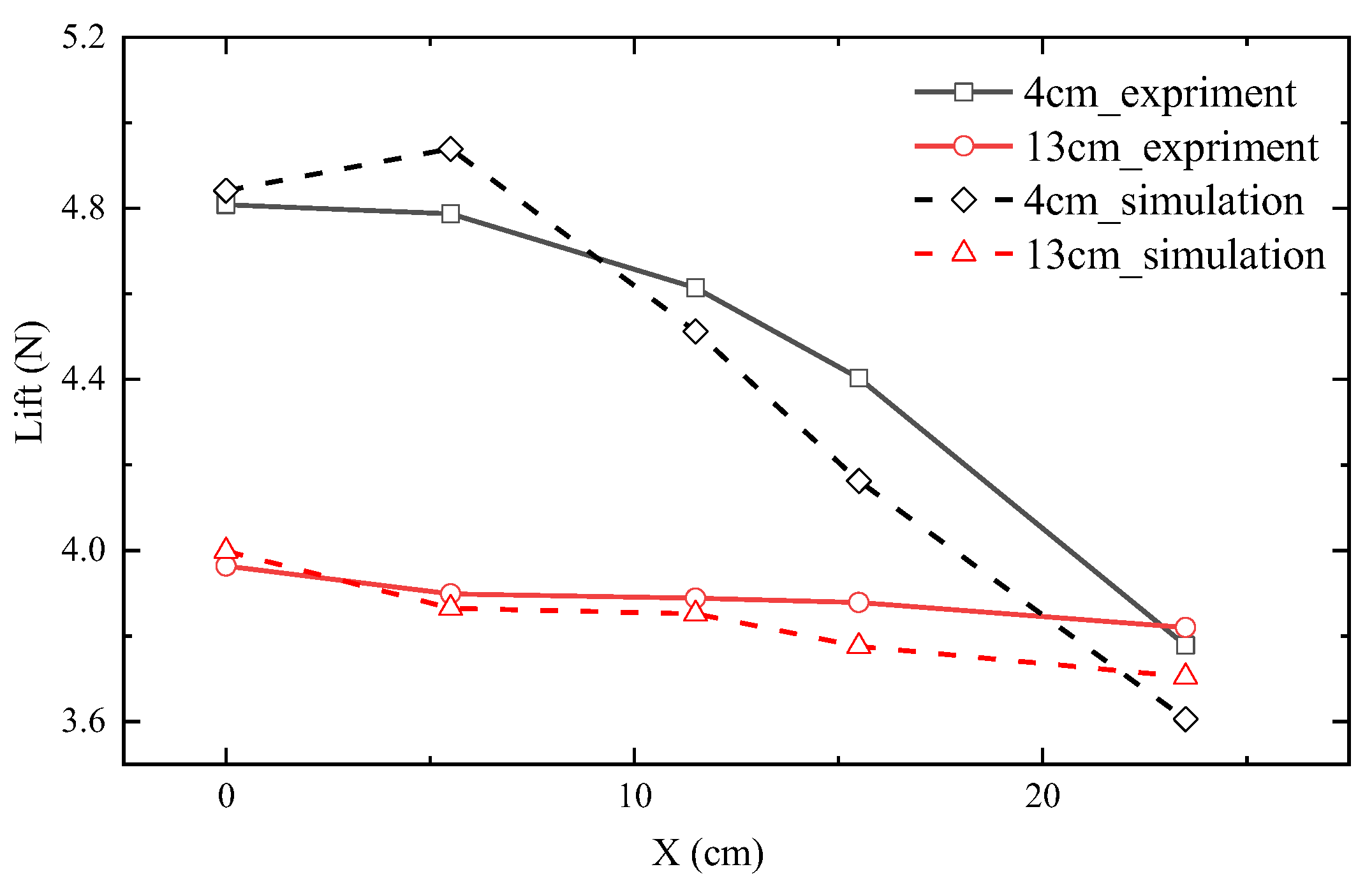
- The momentum source simulation method used in this paper is in good agreement with the experimental results. It can be used as a quasi-steady method to calculate the effects of multi-UAV aerodynamic disturbances.
- (2)
- The results show that the influence of the lower parent UAV on the upper child UAV cannot be ignored. In the longitudinal direction, there is a strong aerodynamic disturbance above the parent rotors, with a maximum lift loss of 33% of the child UAV. In the aera above the body of parent UAV, the lift of child UAV changes rapidly, from a 27.4% increment to a 10% lift loss. In the horizontal direction, the lift of the child UAV decreases significantly, and there is an asymmetric moment pointing to the nearest parent UAV rotor. These interferences may lead to instability of the child UAV, and this may even lead to collision between the child UAV and the parent UAV when the system does not respond properly.
- (3)
- A static safe flight boundary and recommended paths in the launch and recovery progress have been concluded in this paper. This research of aerodynamic interference between multi-UAVs provides a reference for the safe flight strategy in the progress of air launch and recovery.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAS | unmanned aircraft system |
| UAVs | unmanned aerial vehicles |
References
- Calhoun, M.P. DARPA Emerging Technologies. Strateg. Stud. Q. 2016, 10, 91–114. [Google Scholar]
- Throneberry, G.; Hocut, C.M.; Abdelkefi, A. Multi-Rotor Wake Propagation and Flow Development Modeling: A Review. Prog. Aerosp. Sci. 2021, 127, 100762. [Google Scholar] [CrossRef]
- Savkin, A.V.; Huang, H. A Method for Optimized Deployment of a Network of Surveillance Aerial Drones. IEEE Syst. J. 2019, 13, 4474–4477. [Google Scholar] [CrossRef]
- Cacace, J.; Finzi, A.; Lippiello, V.; Furci, M.; Mimmo, N.; Marconi, L. A Control Architecture for Multiple Drones Operated via Multimodal Interaction in Search & Rescue Mission. In Proceedings of the 2016 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Lausanne, Switzerland, 23–27 October 2016; pp. 233–239. [Google Scholar] [CrossRef]
- Ruwaimana, M.; Satyanarayana, B.; Otero, V.; Muslim, A.M.; Muhammad Syafiq, A.; Ibrahim, S.; Raymaekers, D.; Koedam, N.; Dahdouh-Guebas, F. The Advantages of Using Drones over Space-Borne Imagery in the Mapping of Mangrove Forests. PLoS ONE 2018, 13, e0200288. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, S.; Emelogu, A.; Marufuzzaman, M.; Nurre, S.G.; Bian, L. Drones for Disaster Response and Relief Operations: A Continuous Approximation Model. Int. J. Prod. Econ. 2017, 188, 167–184. [Google Scholar] [CrossRef]
- Gecgel, M. Modeling and Simulation of Coaxial-Rotor Helicopter Aerodynamics in Hover and Forward Flight. In Proceedings of the 7th Ankara International Aerospace Conference, Ankara, Turkey, 13–15 September 2018. [Google Scholar]
- Misiorowski, M.; Gandhi, F.; Oberai, A.A. Computational Study on Rotor Interactional Effects for a Quadcopter in Edgewise Flight. AIAA J. 2019, 57, 5309–5319. [Google Scholar] [CrossRef]
- Hwang, J.Y.; Jung, M.K.; Kwon, O.J. Numerical Study of Aerodynamic Performance of a Multirotor Unmanned-Aerial-Vehicle Configuration. J. Aircr. 2015, 52, 839–846. [Google Scholar] [CrossRef]
- Kang, N.; Sun, M. Simulated Flowfields in Near-Ground Operation of Single- and Twin-Rotor Configurations. J. Aircr. 2000, 37, 214–220. [Google Scholar] [CrossRef]
- Chiew, J.J.; Aftosmis, M.J. Efficient Simulation of Multi-Rotor Vehicles with Low Reynolds Number Propellers. In Proceedings of the 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar] [CrossRef]
- Bardera Mora, R.; Matías García, J.C. Helicopter Rotor Ground Effect and Frigate Interaction Investigated by Particle Image Velocimetry. AIAA J. 2021, 1–15. [Google Scholar] [CrossRef]
- Nakata, T.; Phillips, N.; Simões, P.; Russell, I.J.; Cheney, J.A.; Walker, S.M.; Bomphrey, R.J. Aerodynamic Imaging by Mosquitoes Inspires a Surface Detector for Autonomous Flying Vehicles. Science 2020, 368, 634–637. [Google Scholar] [CrossRef] [PubMed]
- Pasquali, C.; Serafini, J.; Bernardini, G.; Milluzzo, J.; Gennaretti, M. Numerical-Experimental Correlation of Hovering Rotor Aerodynamics in Ground Effect. Aerosp. Sci. Technol. 2020, 106, 106079. [Google Scholar] [CrossRef]
- Cheeseman, I.C.; Bennett, W.E. The Effect of the Ground on a Helicopter Rotor in Forward Flight. Aeronaut. Res. Counc. Rep. Memo. 1955, 3021, 12. [Google Scholar]
- Aich, S.; Ahuja, C.; Gupta, T.; Arulmozhivarman, P. Analysis of Ground Effect on Multi-Rotors. In Proceedings of the 2014 International Conference on Electronics, Communication and Computational Engineering (ICECCE), Hosur, India, 17–18 November 2014; pp. 236–241. [Google Scholar] [CrossRef]
- Raza, S.A.; Sutherland, M.; Etele, J.; Fusina, G. Experimental Validation of Quadrotor Simulation Tool for Flight within Building Wakes. Aerosp. Sci. Technol. 2017, 67, 169–180. [Google Scholar] [CrossRef]
- Paz, C.; Suárez, E.; Gil, C.; Baker, C. CFD Analysis of the Aerodynamic Effects on the Stability of the Flight of a Quadcopter UAV in the Proximity of Walls and Ground. J. Wind Eng. Ind. Aerodyn. 2020, 206. [Google Scholar] [CrossRef]
- Casalino, D.; van der Velden, W.C.P.; Romani, G. Community Noise of Urban Air Transportation Vehicles. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Casalino, D.; van der Velden, W.C.P.; Romani, G.; Gonzalez-Martino, I. Aeroacoustic Analysis of Urban Air Operations Using the Lb/Vles Method. In Proceedings of the 25th AIAA/CEAS Aeroacoustics Conference 2019, Delft, The Netherlands, 20–23 May 2019. [Google Scholar] [CrossRef]
- Khromov, V.; Rand, O. Ground Effect Modeling for Rotary-Wing Simulation. In Proceedings of the 26th International Congress of the Aeronautical Sciences, Anchorage, Ak, USA, 14–19 September 2008; Volume 6, pp. 511–520. [Google Scholar]
- Jain, K.P.; Fortmuller, T.; Byun, J.; Makiharju, S.A.; Mueller, M.W. Modeling of Aerodynamic Disturbances for Proximity Flight of Multirotors. In Proceedings of the 2019 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 11–14 June 2019; pp. 1261–1269. [Google Scholar] [CrossRef]
- Gennaretti, M.; Bernardini, G. Novel Boundary Integral Formulation for Blade-Vortex Interaction Aerodynamics of Helicopter Rotors. AIAA J. 2007, 45, 1169–1176. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, M.; Hu, A. Numerical Simulation of Rotor-Fuselage-Cylinder Interaction in Forward Flight. J. Aircr. 2010, 47, 1426–1430. [Google Scholar] [CrossRef]
- Guntupalli, K.; Rajagopalan, R.G. Development of Discrete Blade Momentum Source Method for Rotors in an Unstructured Solver. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012; pp. 1–23. [Google Scholar] [CrossRef]
- Guntupalli, K.; Helitek, S. Development, Validation and Verification of the Momentum Source Model for Discrete Rotor Blades. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 2011. [Google Scholar]
- Kakimpa, B.; Hargreaves, D.M.; Owen, J.S.; Martinez-Vazquez, P.; Bakers, C.J.; Sterling, M.; Quinn, A.D. CFD Modelling of Free-Flight and Auto-Rotation of Plate Type Debris. Wind. Struct. Int. J. 2010, 13, 169–189. [Google Scholar] [CrossRef]
- Joo, S.; Choi, H.; Lee, J. Aerodynamic Characteristics of Two-Bladed H-Darrieus at Various Solidities and Rotating Speeds. Energy 2015, 90, 439–451. [Google Scholar] [CrossRef]
- Mohamed, O.S.; Ibrahim, A.A.; Etman, A.K.; Abdelfatah, A.A.; Elbaz, A.M.R. Numerical Investigation of Darrieus Wind Turbine with Slotted Airfoil Blades. Energy Convers. Manag. X 2020, 5, 100026. [Google Scholar] [CrossRef]
- McKee, W.; Naeseth, R.L. Experimental Investigation of the Drag of Flat Plates and Cylinders in the Slipstream of a Hovering Rotor; NASA: Washington, DC, USA, 1958; Volume NACA TN 4239. [Google Scholar]
- Yoon, S.; Chan, W.M.; Pulliam, T.H. Computations of Torque-Balanced Coaxial Rotor Flows. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; pp. 1–12. [Google Scholar] [CrossRef]
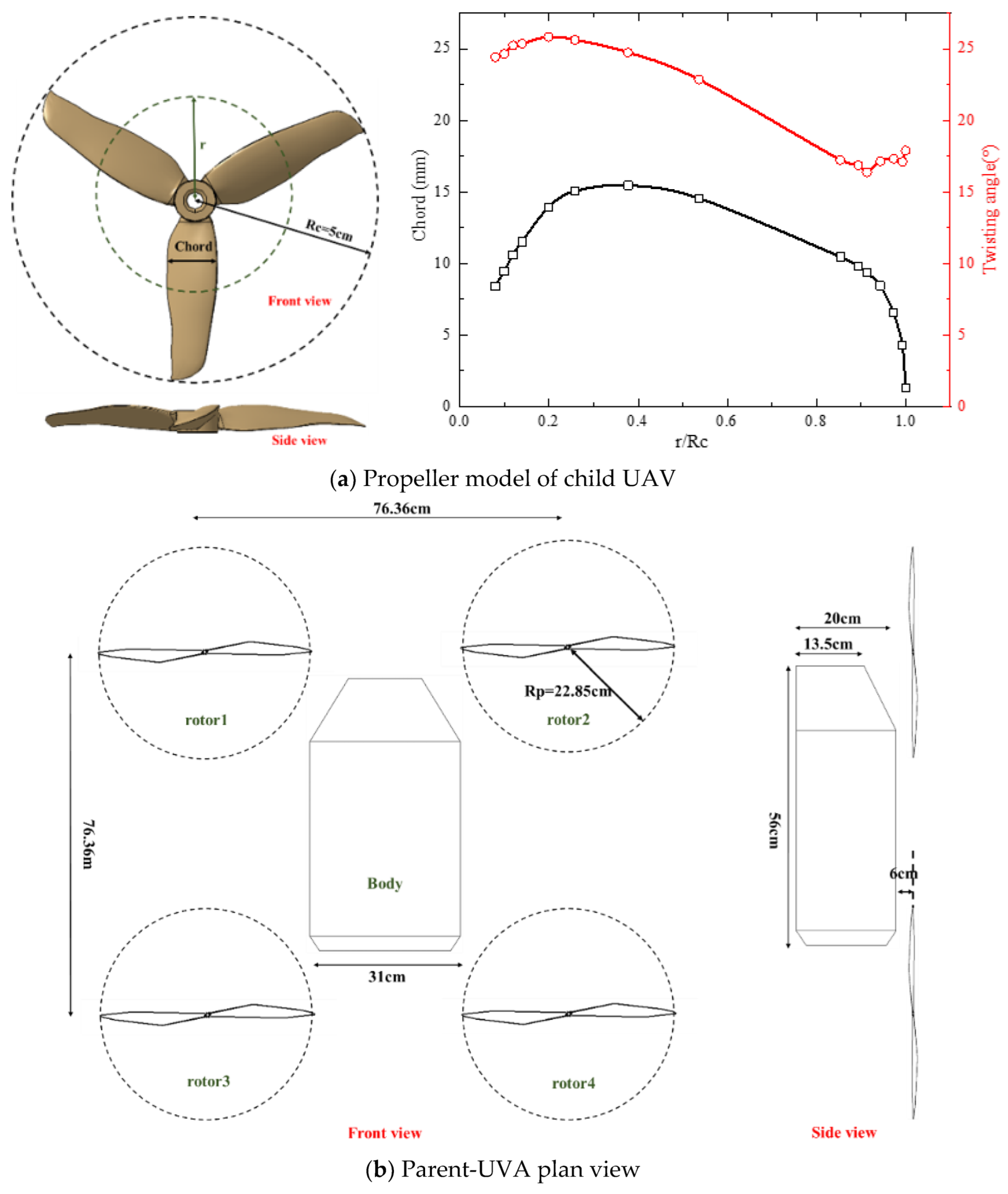

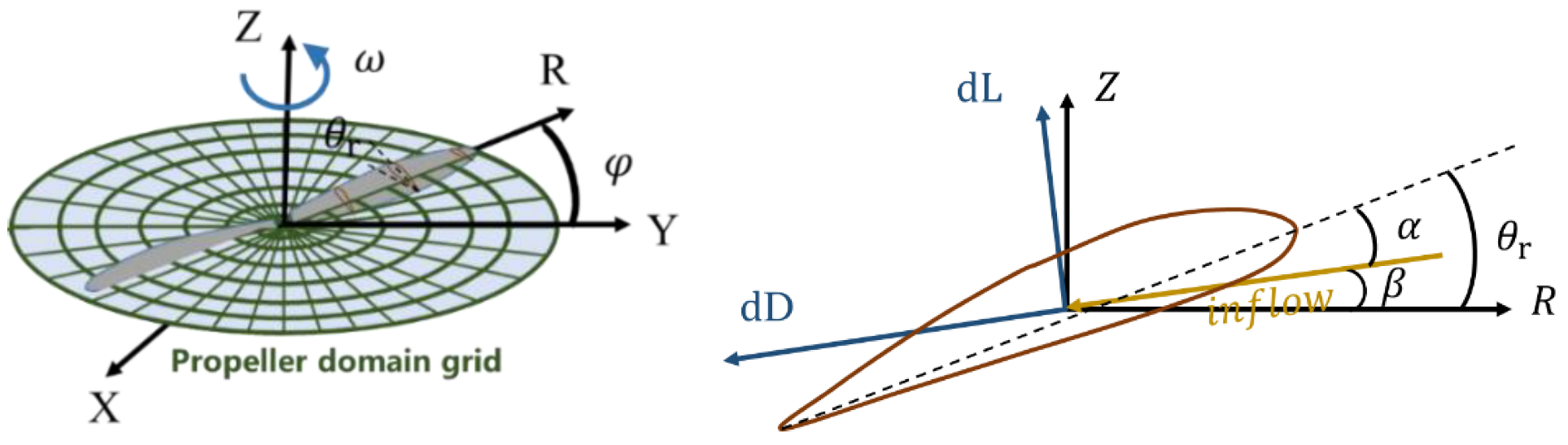






| Parameters | Data |
|---|---|
| Rotor radius of child UAV(Rc)/cm | 5.0 |
| Rotor radius of parent UAV(Rp)/cm | 22.85 |
| Diagonal size of child UAV/cm | 20.4 |
| Diagonal size of parent UAV/cm | 108.0 |
| Size of child UAV/cm | 29.0 × 27.0 × 2.7 |
| Size of parent UAV/cm | 122.0 × 122.0 × 45.0 |
| Weight of child UAV/kg | 0.418 |
| Weight of parent UAV/kg | 6.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Liu, Y.; Li, D.; Bie, D.; Kan, Z. Ground Test and Numerical Simulation of Aerodynamic Interference of the Marsupial UAS. Aerospace 2023, 10, 175. https://doi.org/10.3390/aerospace10020175
Li H, Liu Y, Li D, Bie D, Kan Z. Ground Test and Numerical Simulation of Aerodynamic Interference of the Marsupial UAS. Aerospace. 2023; 10(2):175. https://doi.org/10.3390/aerospace10020175
Chicago/Turabian StyleLi, Huadong, Yiliang Liu, Daochun Li, Dawei Bie, and Zi Kan. 2023. "Ground Test and Numerical Simulation of Aerodynamic Interference of the Marsupial UAS" Aerospace 10, no. 2: 175. https://doi.org/10.3390/aerospace10020175
APA StyleLi, H., Liu, Y., Li, D., Bie, D., & Kan, Z. (2023). Ground Test and Numerical Simulation of Aerodynamic Interference of the Marsupial UAS. Aerospace, 10(2), 175. https://doi.org/10.3390/aerospace10020175







