Figure 1.
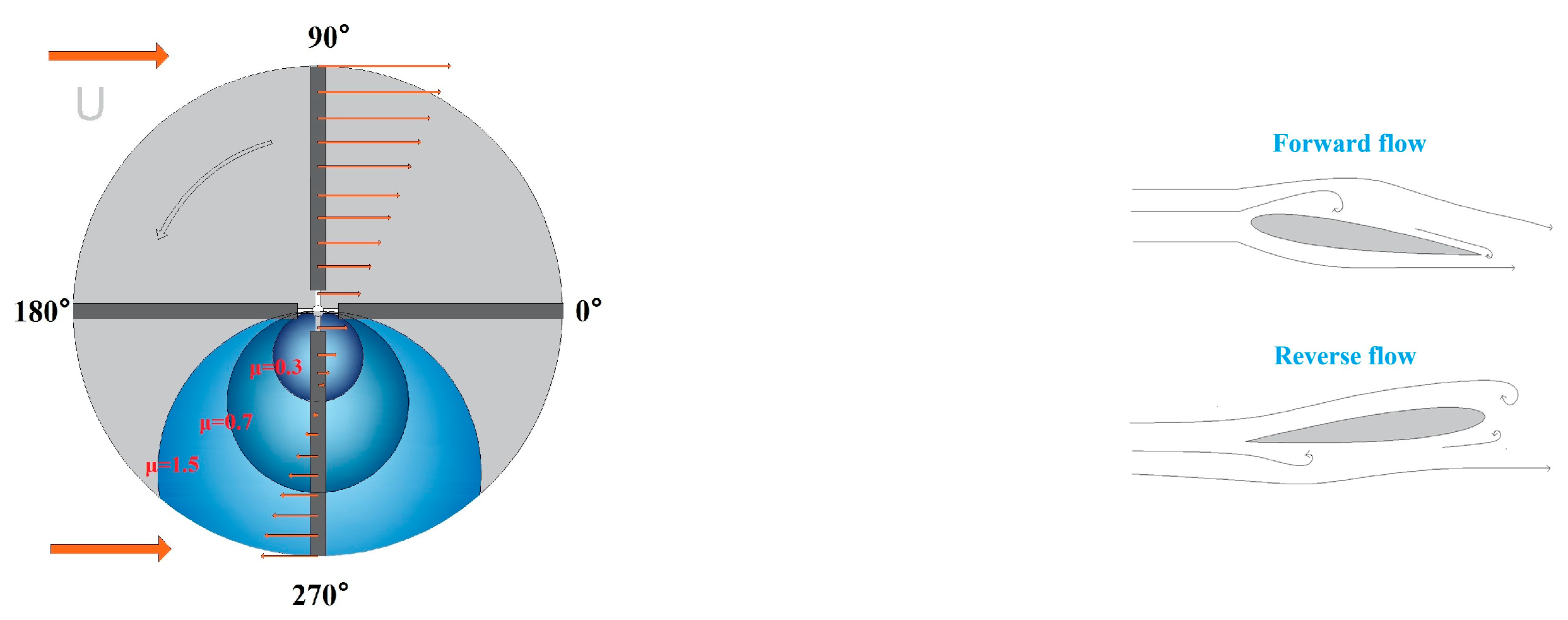
Rotor reverse flow region at different advance ratios.
Figure 1.
Rotor reverse flow region at different advance ratios.
Figure 2.
Schematic diagram of the experimental platform and experimental mode.
Figure 2.
Schematic diagram of the experimental platform and experimental mode.
Figure 3.
Miniature pressure sensors. (a) Miniature Dynamic Pressure Sensor Physical Drawing, (b) Pressure measuring probe form factor.
Figure 3.
Miniature pressure sensors. (a) Miniature Dynamic Pressure Sensor Physical Drawing, (b) Pressure measuring probe form factor.
Figure 4.
Schematic diagram of the chordal installation position of pressure sensors.
Figure 4.
Schematic diagram of the chordal installation position of pressure sensors.
Figure 5.
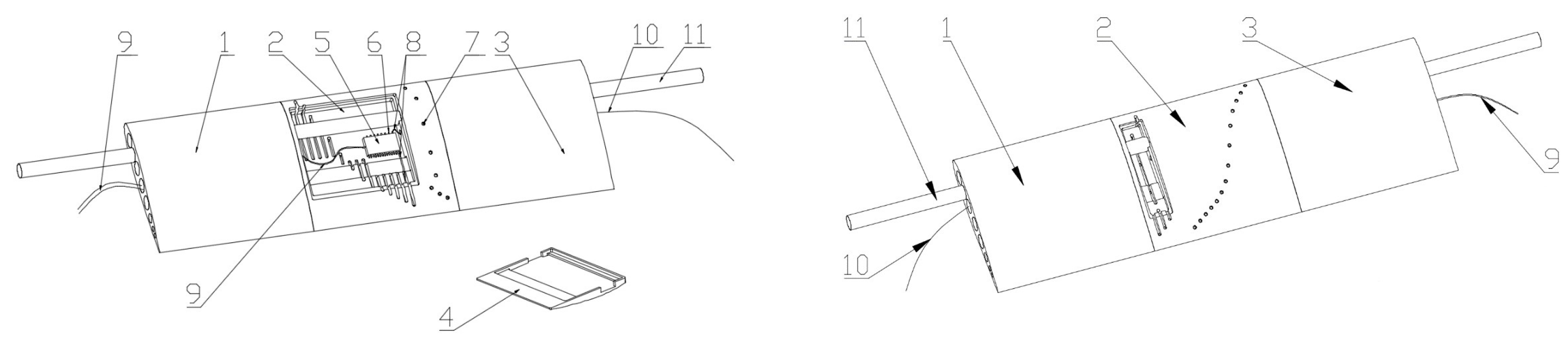
Model structure.
Figure 5.
Model structure.
Figure 6.
Data acquisition system. (a) NI9220 Data Acquisition Card, (b) NI CompactDAQ Chassis.
Figure 6.
Data acquisition system. (a) NI9220 Data Acquisition Card, (b) NI CompactDAQ Chassis.
Figure 7.
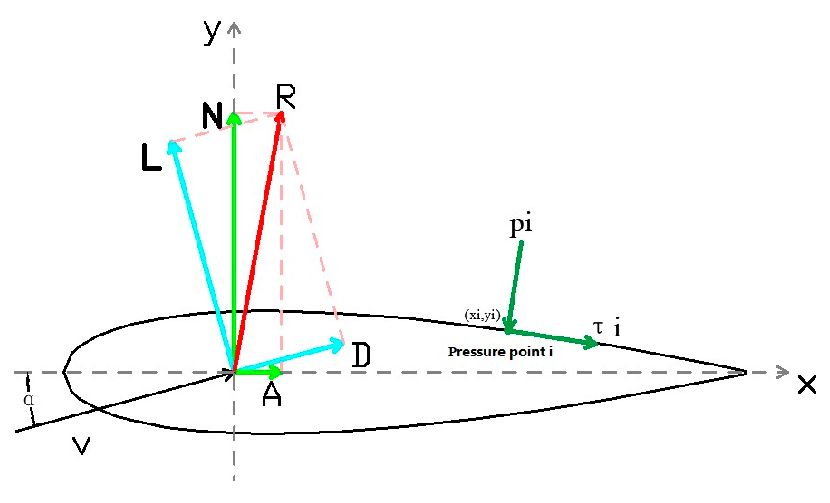
Aerodynamic forces on airfoil surface and their components.
Figure 7.
Aerodynamic forces on airfoil surface and their components.
Figure 8.
Definition of lift coefficient and moment coefficient in positive and negative directions. (a) Forward-blowing, (b) reverse blowing.
Figure 8.
Definition of lift coefficient and moment coefficient in positive and negative directions. (a) Forward-blowing, (b) reverse blowing.
Figure 9.
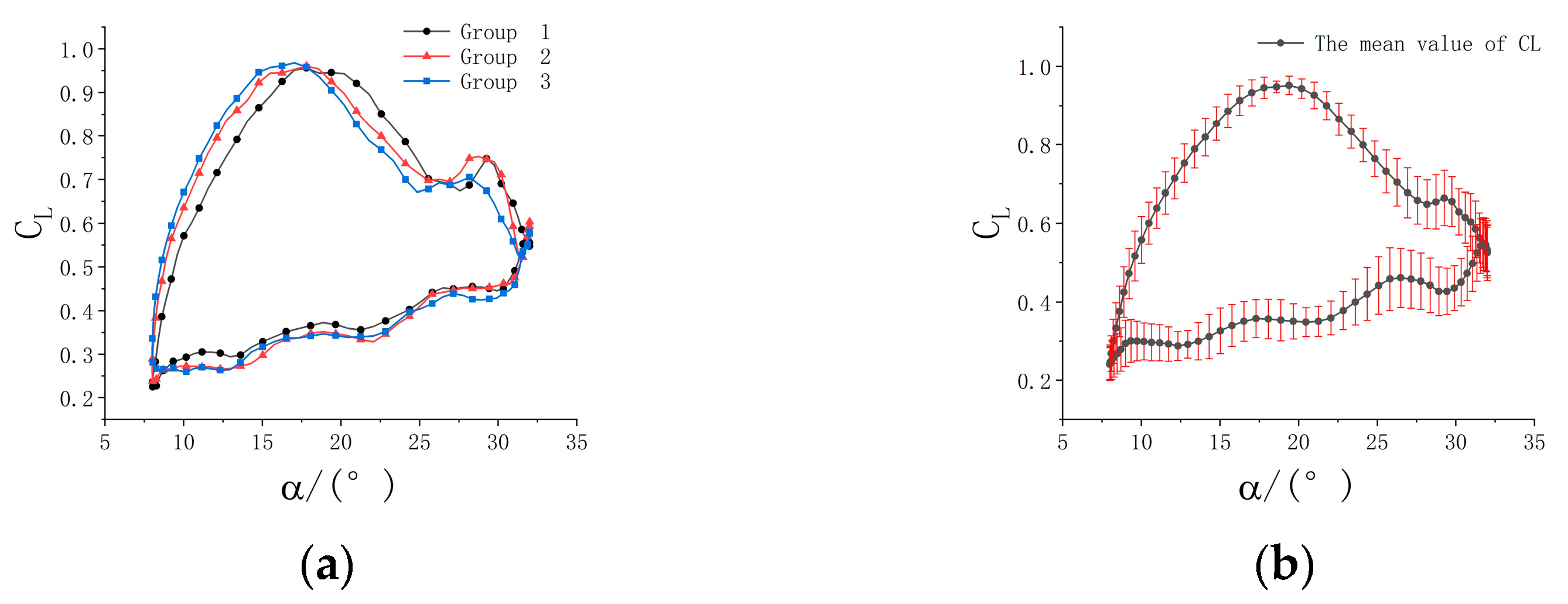
Comparison of three static experimental lift coefficients at reverse-blowing. (a) Three sets of lift coefficient curves, (b) lift factor error bars.
Figure 9.
Comparison of three static experimental lift coefficients at reverse-blowing. (a) Three sets of lift coefficient curves, (b) lift factor error bars.
Figure 10.
Comparison of three sets of dynamic experimental data at reverse-blowing. (a) Three sets of lift coefficient curves, (b) lift factor error bars, (c) three sets of moment coefficient curves, and (d) moment coefficient error bars.
Figure 10.
Comparison of three sets of dynamic experimental data at reverse-blowing. (a) Three sets of lift coefficient curves, (b) lift factor error bars, (c) three sets of moment coefficient curves, and (d) moment coefficient error bars.
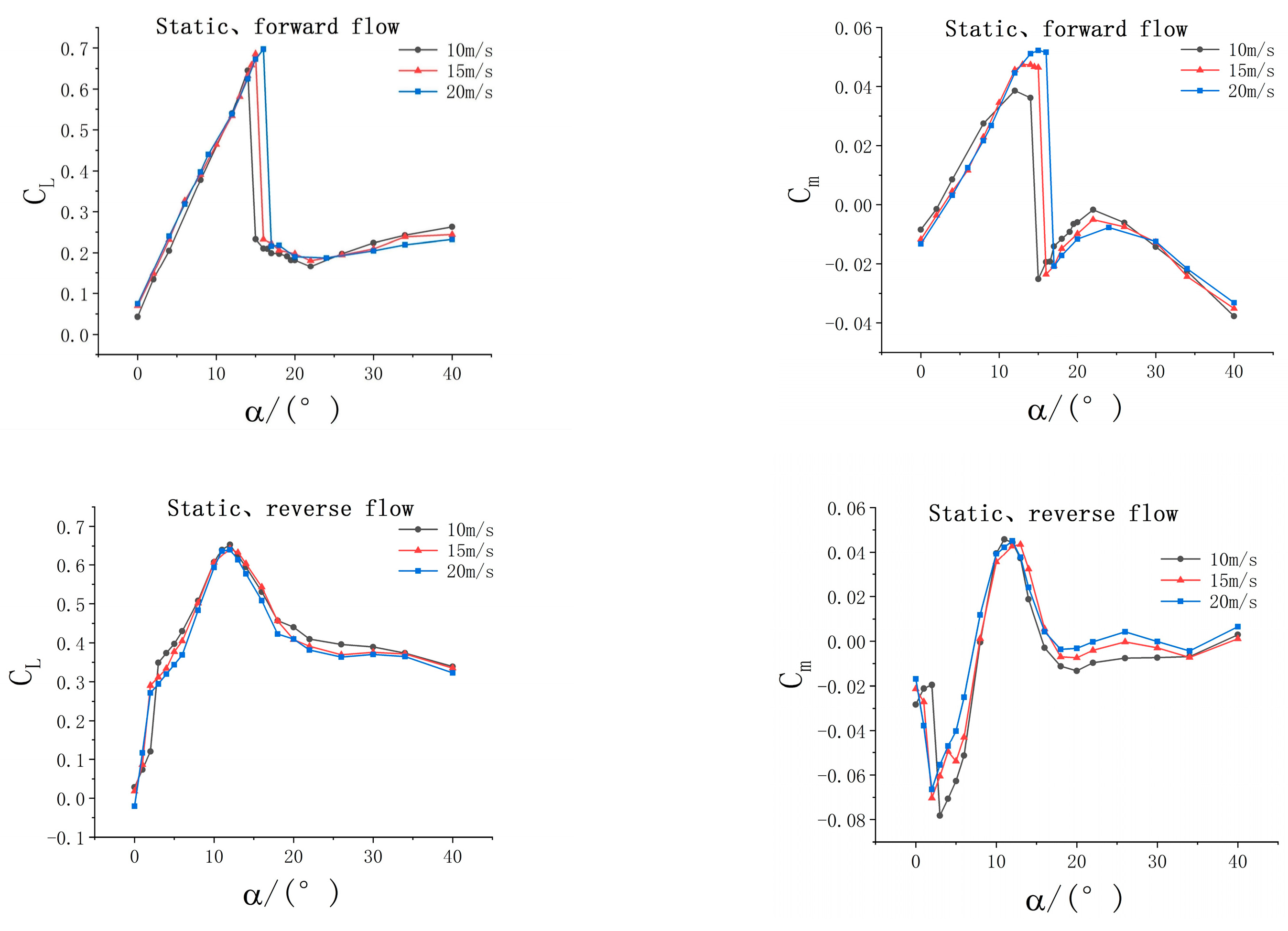
Figure 11.
Lift coefficient and moment coefficient of static airfoil under forward-blowing and reverse-blowing.
Figure 11.
Lift coefficient and moment coefficient of static airfoil under forward-blowing and reverse-blowing.
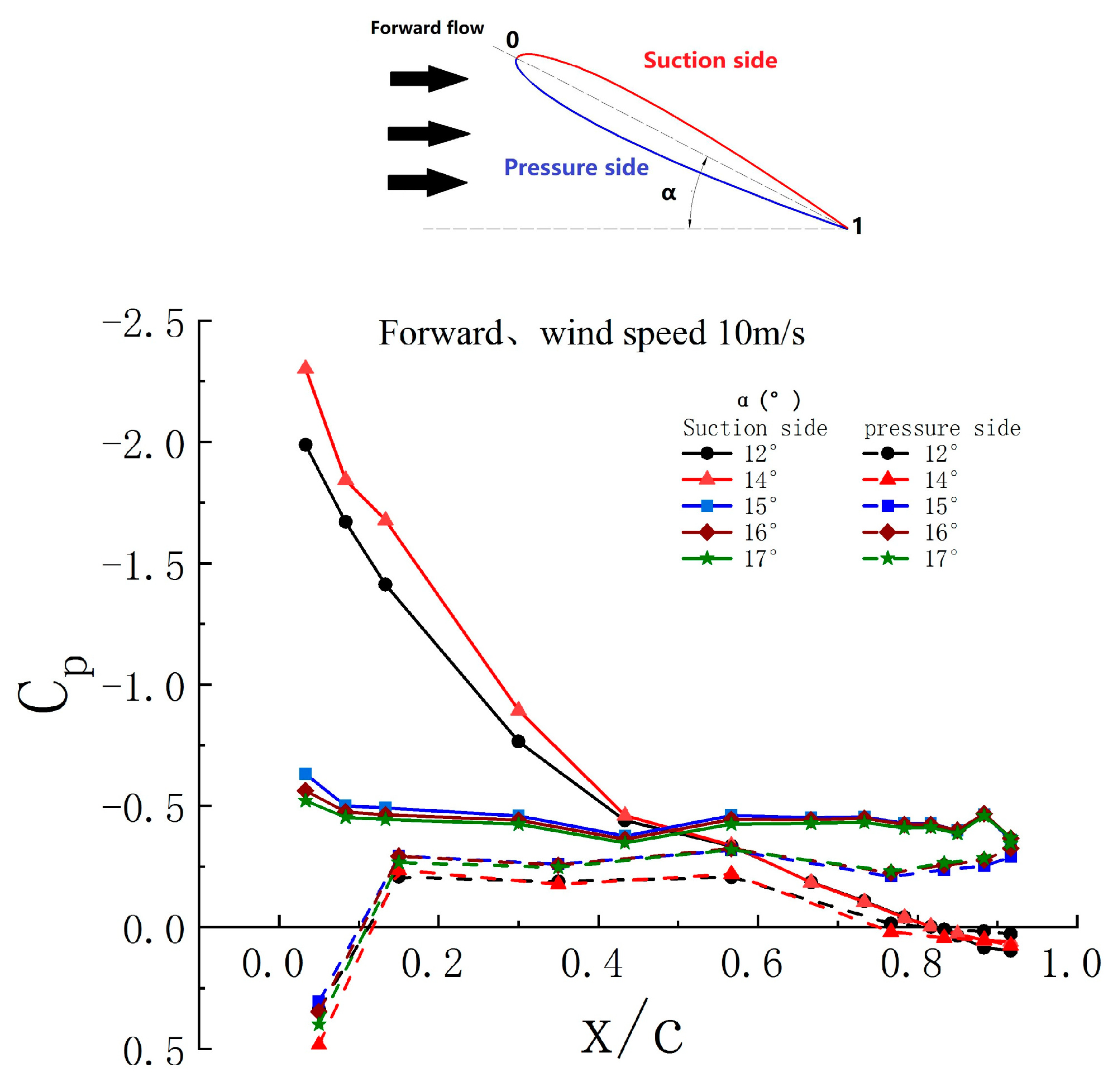
Figure 12.
Pressure coefficient of suction and pressure sides of airfoil under forward-blowing.
Figure 12.
Pressure coefficient of suction and pressure sides of airfoil under forward-blowing.
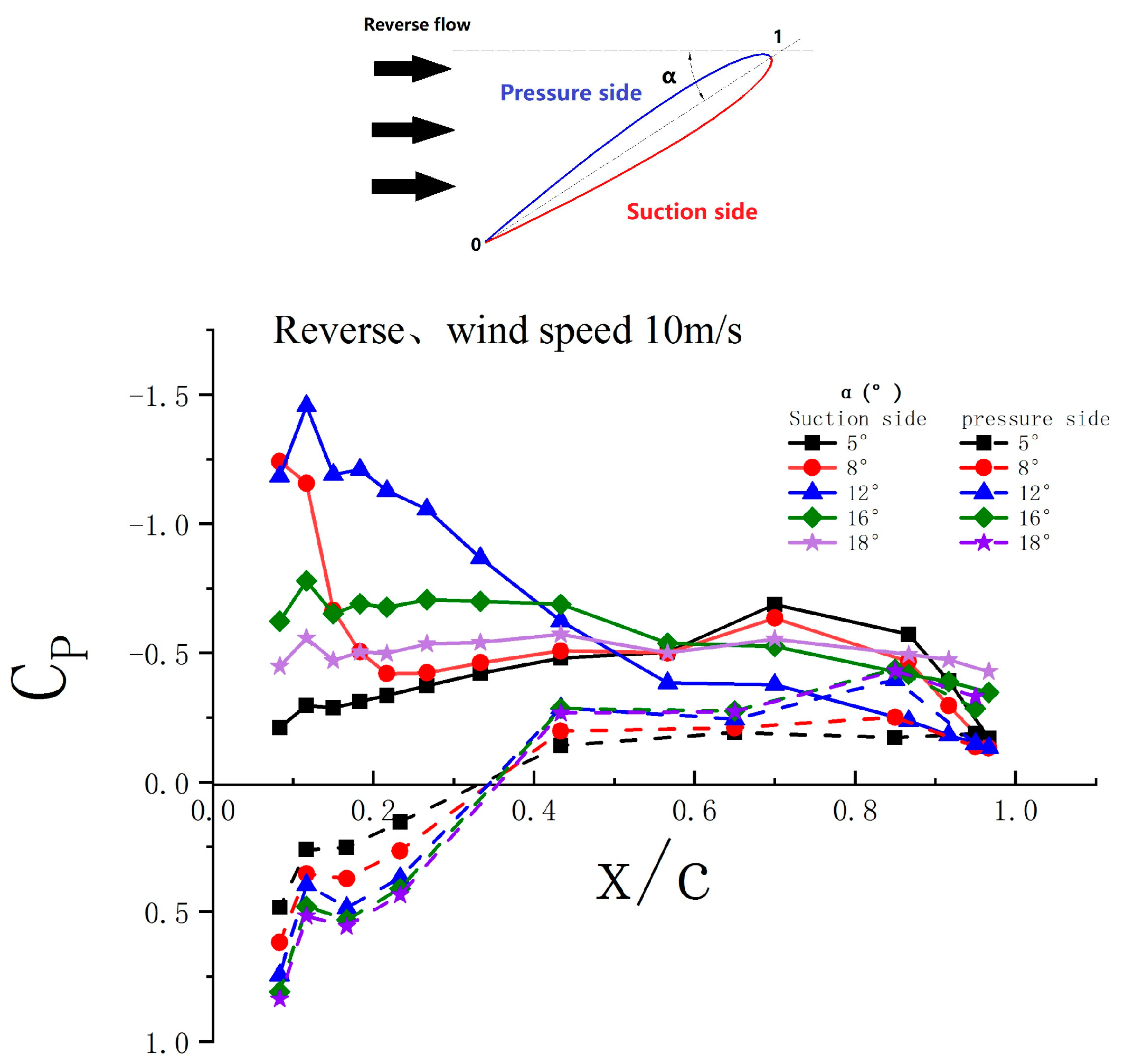
Figure 13.
Pressure coefficient of suction and pressure sides of airfoil under reverse-blowing.
Figure 13.
Pressure coefficient of suction and pressure sides of airfoil under reverse-blowing.
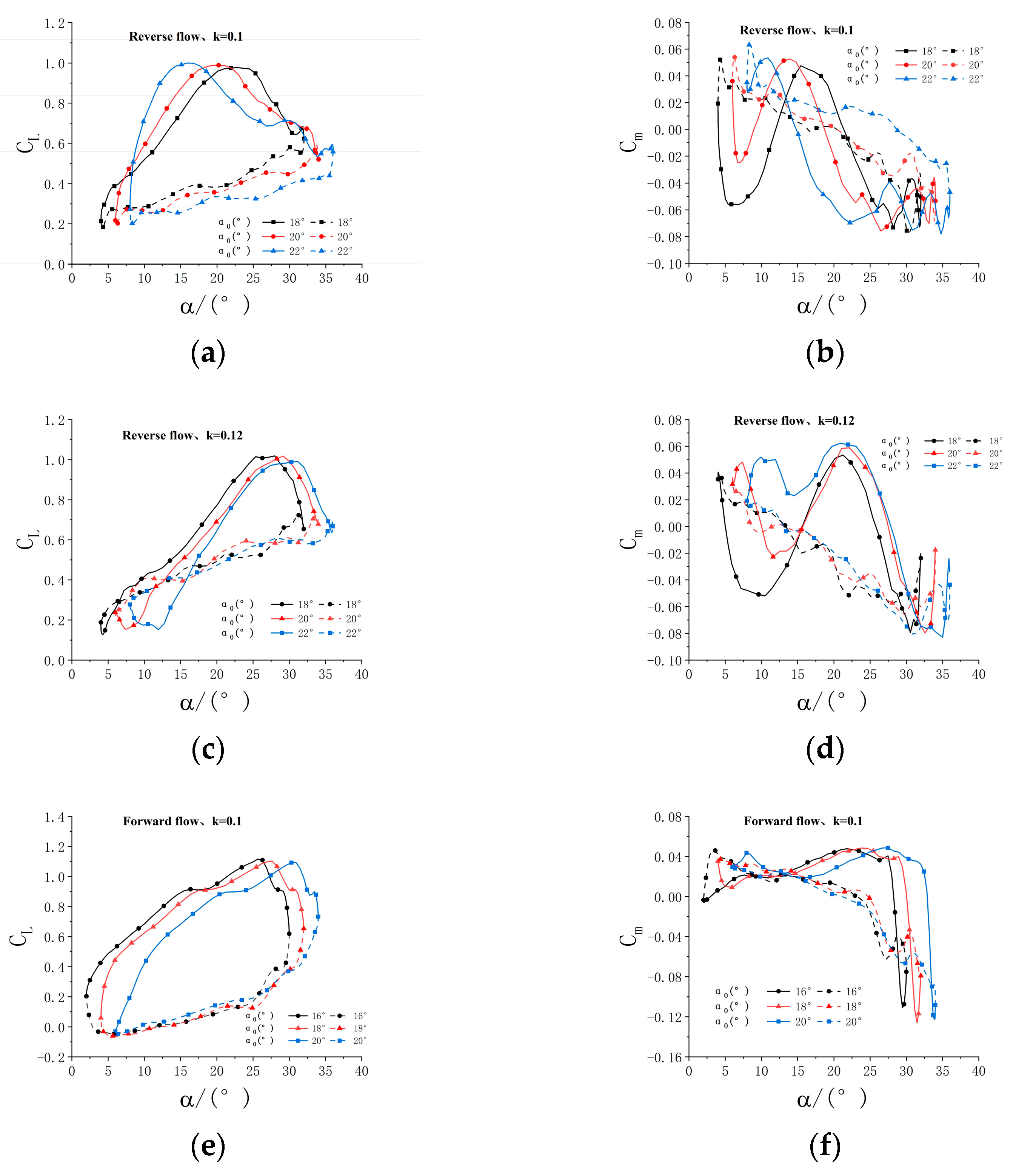
Figure 14.
Effect of the mean angle of pitch at different K. (a) K = 0.1, CL, (b) K = 0.1, Cm, (c) K = 0.12, CL, (d) K = 0.12, Cm, (e) K = 0.1, CL, (f) K = 0.1, Cm, (g) K = 0.12, CL, (h) K = 0.12, Cm.
Figure 14.
Effect of the mean angle of pitch at different K. (a) K = 0.1, CL, (b) K = 0.1, Cm, (c) K = 0.12, CL, (d) K = 0.12, Cm, (e) K = 0.1, CL, (f) K = 0.1, Cm, (g) K = 0.12, CL, (h) K = 0.12, Cm.
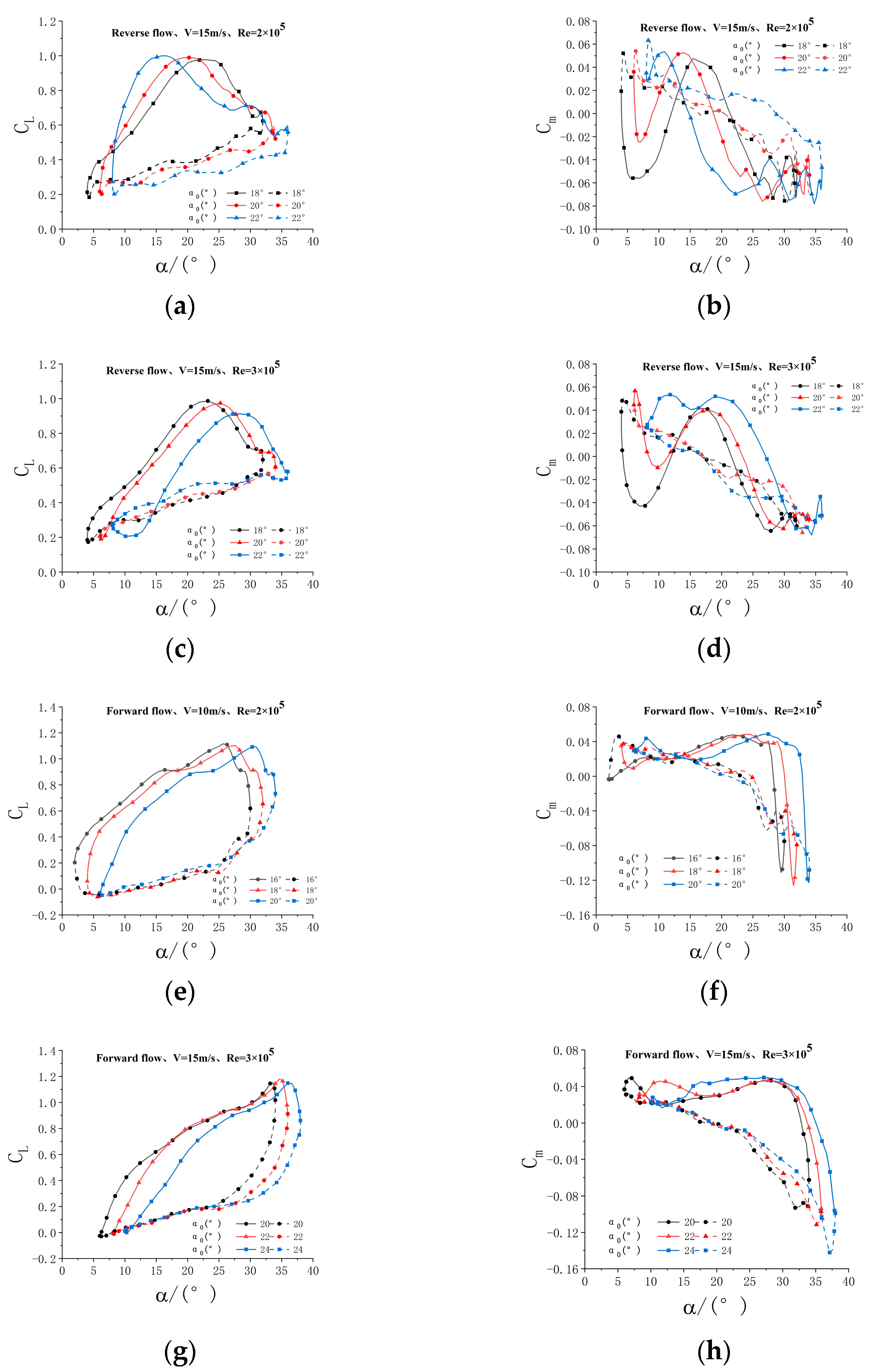
Figure 15.
Effect of the mean angle of pitch at different Reynolds numbers. (a) Re = 2 × 105, CL, (b) Re = 2 × 105, Cm, (c) Re = 3 × 105, CL, (d) Re = 3 × 105, Cm, (e) Re = 2 × 105, CL, (f) Re = 2 × 105, Cm, (g) Re = 3 × 105, CL, (h) Re = 3 × 105, Cm.
Figure 15.
Effect of the mean angle of pitch at different Reynolds numbers. (a) Re = 2 × 105, CL, (b) Re = 2 × 105, Cm, (c) Re = 3 × 105, CL, (d) Re = 3 × 105, Cm, (e) Re = 2 × 105, CL, (f) Re = 2 × 105, Cm, (g) Re = 3 × 105, CL, (h) Re = 3 × 105, Cm.
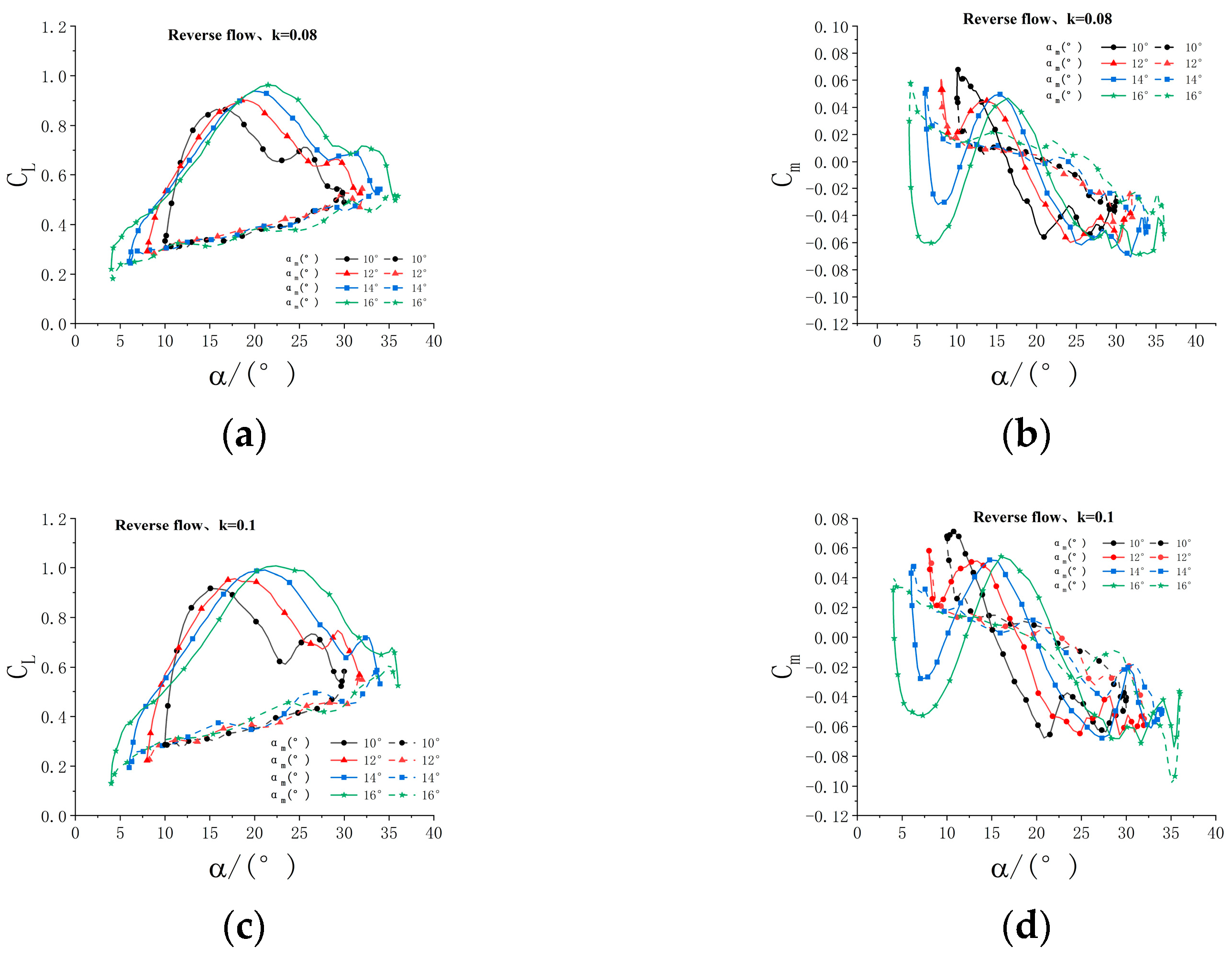
Figure 16.
Effect of the oscillation amplitude at different reduced frequencies. (a) K = 0.08, CL, (b) K = 0.08, Cm, (c) K = 0.10, CL, (d) K = 0.10, Cm, (e) K = 0.12, CL, (f) K = 0.12, Cm.
Figure 16.
Effect of the oscillation amplitude at different reduced frequencies. (a) K = 0.08, CL, (b) K = 0.08, Cm, (c) K = 0.10, CL, (d) K = 0.10, Cm, (e) K = 0.12, CL, (f) K = 0.12, Cm.
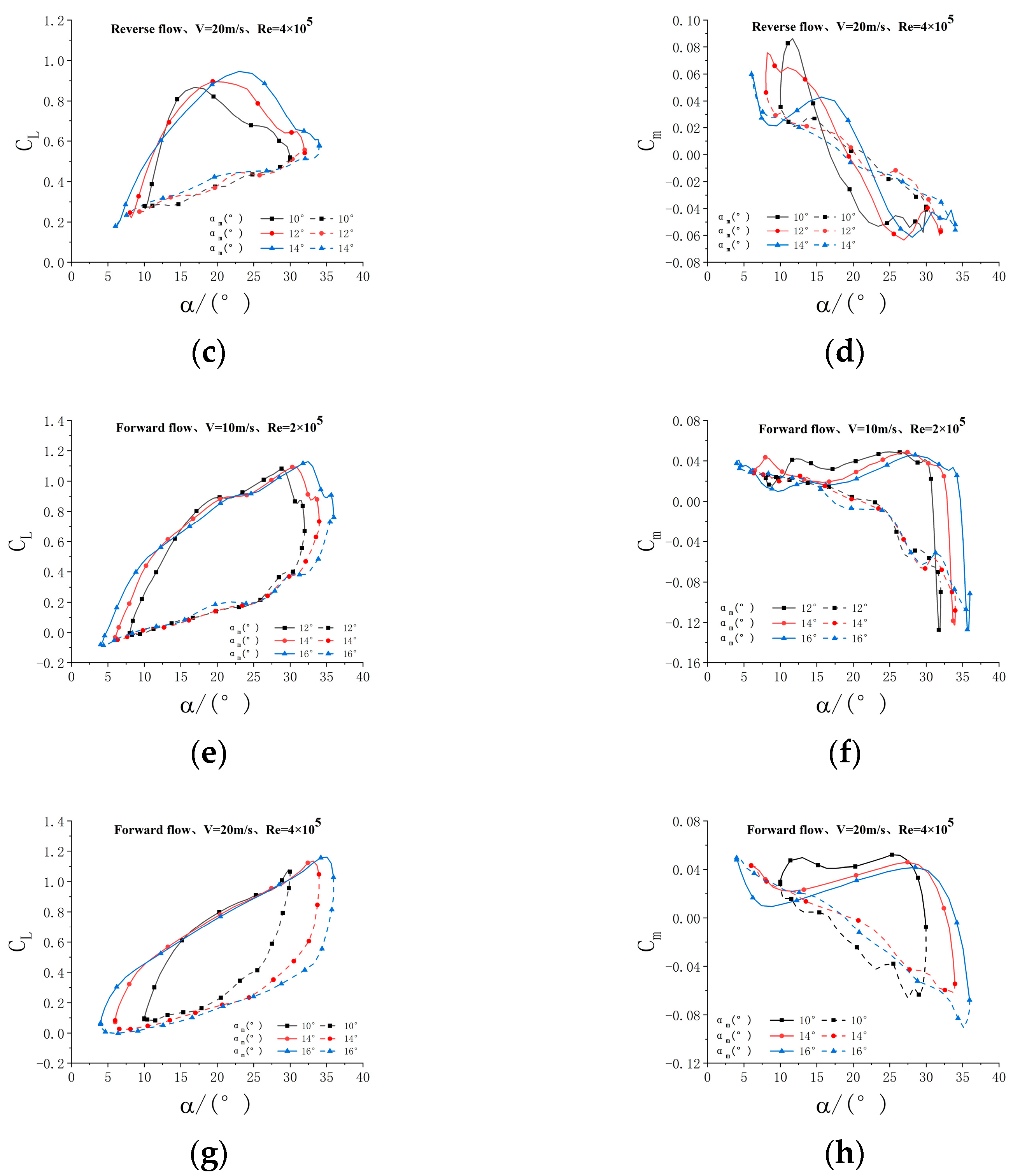
Figure 17.
Effect of the oscillation amplitude at different Reynolds numbers. (a) Re = 2 × 105, CL, (b) Re = 2 × 105, Cm, (c) Re = 4 × 105, CL, (d) Re = 4 × 105, Cm, (e) Re = 2 × 105, CL, (f) Re = 2 × 105, Cm, (g) Re = 4 × 105, CL, (h) Re = 4 × 105, Cm.
Figure 17.
Effect of the oscillation amplitude at different Reynolds numbers. (a) Re = 2 × 105, CL, (b) Re = 2 × 105, Cm, (c) Re = 4 × 105, CL, (d) Re = 4 × 105, Cm, (e) Re = 2 × 105, CL, (f) Re = 2 × 105, Cm, (g) Re = 4 × 105, CL, (h) Re = 4 × 105, Cm.
Figure 18.
Effect of the reduced frequencies. (a) CL, (b) Cm, (c) CL, (d) Cm.
Figure 18.
Effect of the reduced frequencies. (a) CL, (b) Cm, (c) CL, (d) Cm.
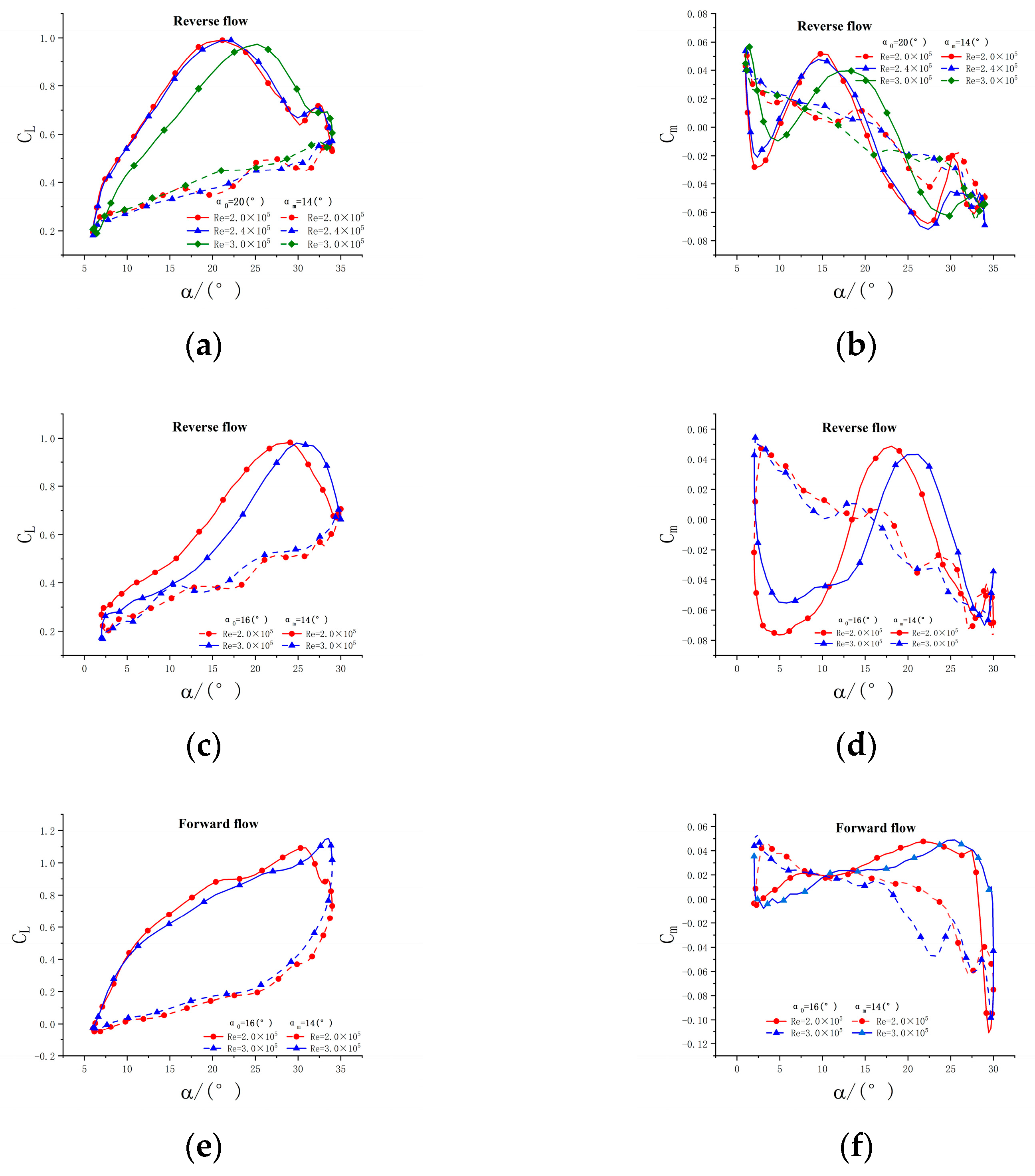
Figure 19.
Effect of the Reynolds numbers. (a) CL, (b) Cm, (c) CL, (d) Cm, (e) CL, (f) Cm.
Figure 19.
Effect of the Reynolds numbers. (a) CL, (b) Cm, (c) CL, (d) Cm, (e) CL, (f) Cm.
Figure 20.
Lift coefficient, 1/4 chord moment coefficient during forward and reverse flow switching.
Figure 20.
Lift coefficient, 1/4 chord moment coefficient during forward and reverse flow switching.
Table 1.
Main technical indicators of the wind tunnel.
Table 1.
Main technical indicators of the wind tunnel.
| Technical Indicator | Data |
|---|
| Wide × high | 1.5 m × 1 m |
| Length of the test section | 1.7 m |
| Maximum wind speed | 40 m/s |
| Degree of turbulence | ε ≤ 0.08% |
Table 2.
Main performance parameters of pressure sensors.
Table 2.
Main performance parameters of pressure sensors.
| Main Performance Parameters | Data |
|---|
| Measuring range | 0~2 KPa |
| Stress | Surface pressure |
| Full range output | 0~5 V |
| Voltage | ±15 V |
| Natural frequency | ≥3 KHz |
| Zero voltage | <±0.2%FS |
| Nonlinear | <±0.2%FS |
| Hysteresis | <±0.2%FS |
| Operating temperature | 0~70° |
Table 3.
Chord-wise installation position of pressure sensors.
Table 3.
Chord-wise installation position of pressure sensors.
| Sensor Number | x/c | Sensor Number | x/c |
|---|
| 1 | 0.0333 | 12 | 0.8500 |
| 2 | 0.0833 | 13 | 0.8833 |
| 3 | 0.1333 | 14 | 0.9167 |
| 4 | 0.2000 | 15 | 0.0500 |
| 5 | 0.3000 | 16 | 0.1500 |
| 6 | 0.4333 | 17 | 0.3500 |
| 7 | 0.5667 | 18 | 0.5667 |
| 8 | 0.6667 | 19 | 0.7667 |
| 9 | 0.7333 | 20 | 0.8333 |
| 10 | 0.7833 | 21 | 0.8833 |
| 11 | 0.8167 | 22 | 0.9167 |
Table 4.
The main performance parameters of the data collection card.
Table 4.
The main performance parameters of the data collection card.
| Main Performance Parameters | Data |
|---|
| Voltage | ±10 V |
| Sampling Rate | 100 kS/s/ch |
| Resolution | 16 |
| Number of channels | 16 |
Table 5.
Static test conditions.
Table 5.
Static test conditions.
| α (°) | v (m/s) | Re (×105) |
|---|
| 0~40 | 10 | 2 |
| 15 | 3 |
| 20 | 4 |
Table 6.
Experimental conditions of changing the mean angle of pitch at different reduced frequencies.
Table 6.
Experimental conditions of changing the mean angle of pitch at different reduced frequencies.
| K | f (Hz) | v (m/s) | α0 (°) | αm (°) |
|---|
| 0.1 | 1.06 | 10 | 16, 18, 20, 22 | 14 |
| 0.12 | 1.27 | 10 | 16, 18, 20, 22 | 14 |
Table 7.
Experimental conditions of changing the mean angle of pitch at different Reynolds numbers.
Table 7.
Experimental conditions of changing the mean angle of pitch at different Reynolds numbers.
| v (m/s) | Re (×105) | f (Hz) | α0 (°) | αm (°) |
|---|
| 10 | 2 | 10 | 16, 18, 20, 22 | 14 |
| 15 | 3 | 10 | 16, 18, 20, 22 | 14 |
Table 8.
Experimental conditions of varying pitch amplitude at different reduced frequencies.
Table 8.
Experimental conditions of varying pitch amplitude at different reduced frequencies.
| K | f (Hz) | v (m/s) | α0 (°) | αm (°) |
|---|
| 0.08 | 0.85 | 10 | 20 | 10, 12, 14, 16 |
| 0.1 | 1.06 | 10 | 20 | 10, 12, 14, 16 |
| 0.12 | 1.27 | 10 | 20 | 10, 12, 14, 16 |
Table 9.
Experimental conditions of varying pitch amplitude at different reduced frequencies.
Table 9.
Experimental conditions of varying pitch amplitude at different reduced frequencies.
| v (m/s) | Re (×105) | f (Hz) | α0 (°) | αm (°) |
|---|
| 10 | 2 | 1.06 | 20 | 10, 12, 14, 16 |
| 20 | 4 | 2.12 | 20 | 10, 12, 14, 16 |
Table 10.
Experimental conditions for changing the reduced frequency.
Table 10.
Experimental conditions for changing the reduced frequency.
| k | Re | f (Hz) | α0 (°) | αm (°) |
|---|
| 0.08 | 2 | 0.85 | 20 | 16 |
| 0.12 | 2 | 1.27 |
Table 11.
Experimental conditions for changing the Reynolds numbers.
Table 11.
Experimental conditions for changing the Reynolds numbers.
| v (m/s) | Re | f (Hz) | α0 (°) | αm (°) |
|---|
| 10 | 2 | 1.06 | 20 | 14 |
| 12 | 2 | 1.27 |
| 15 | | 1.59 |
| 10 | 2 | 1.06 | 16 | 14 |
| 15 | | 1.59 |
Table 12.
Experimental conditions of forward and backward flow switching of the airfoil.
Table 12.
Experimental conditions of forward and backward flow switching of the airfoil.
| K | f (Hz) | v (m/s) | Re (×105) | α0 (°) | αm (°) | α (°) |
|---|
| 0.10 | 1.19 | 10 | 2 | 90 | 70 | 20~160 |
| 75 | 15~165 |
| 80 | 10~170 |