Enhanced Starting Control Scheme for PMM-Based Starter/Generator System for MEA
Abstract
:1. Introduction
- In starting mode, torque or speed control is required to accelerate the engine to a self-sustaining speed
- In generator mode, the main objective is to regulate the DC link bus power, with the engine controlling the speed.
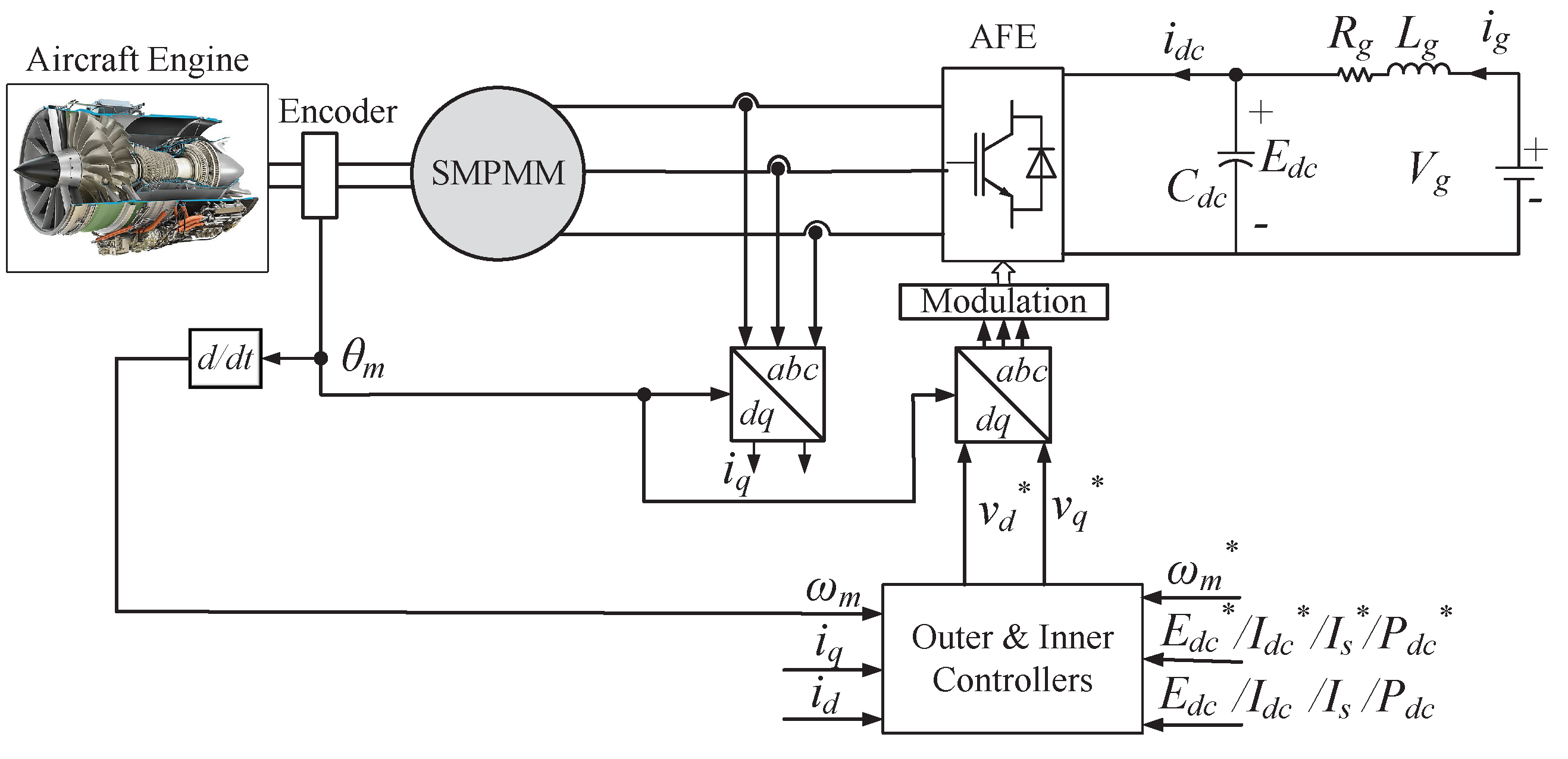
2. Electric Power System Analysis
- and represent the stator voltage of the machine in the dq frame
- and represent the stator current of the machine in the dq frame
- represents the machine stator resistance
- represents the machine’s electrical speed
- and represents the machine stator inductance in the dq frame
- represents the flux produced by the machine
- represents the voltage of the DC link capacitor
- represents the DC bus current
- is the DC bus capacitance
- represents the current of the grid
3. Capabilities and Limitations of the S/G System
- The maximum current limit defined by the machine rated current and converter device rated current .
- The inverter maximum phase voltage, , is limited by the over modulation limit and can be defined by the voltage of the DC link, , and the type of the modulation scheme.
4. Analysis of Variable Voltage Bus Method
Limitations of VVB Method
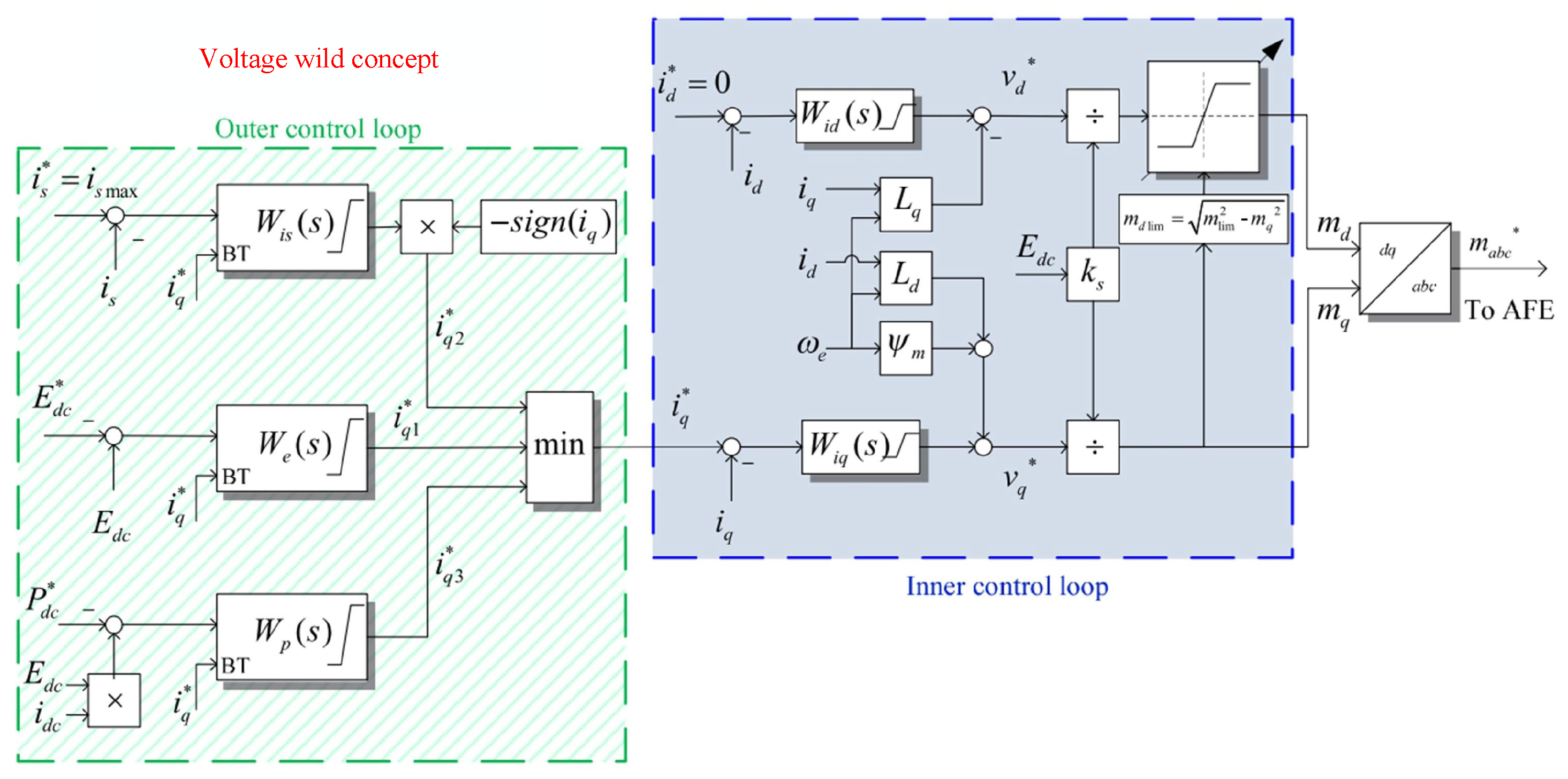
5. Proposed Control Scheme
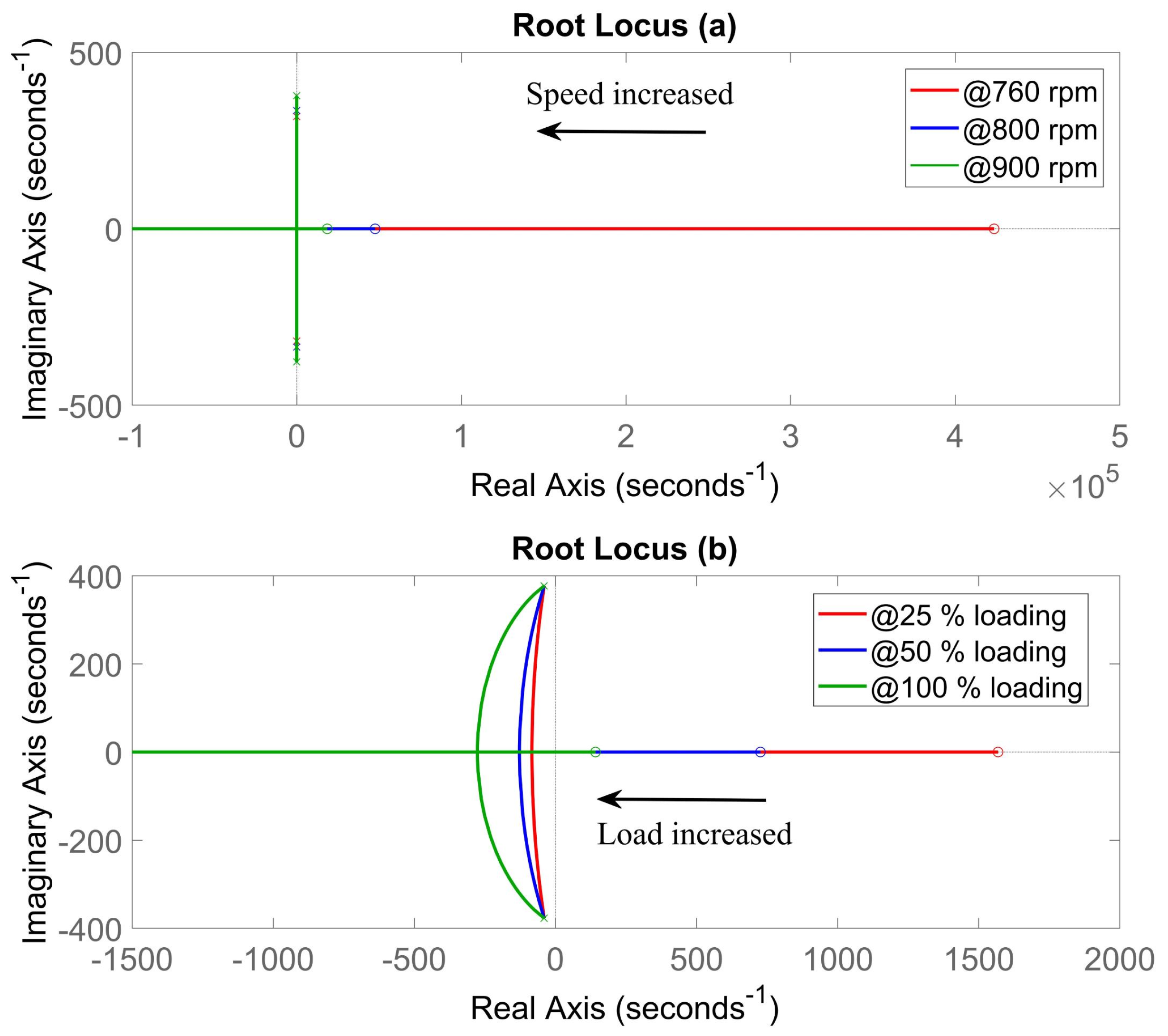
Small Signal Analysis
6. Design of the Proposed Controllers
6.1. Design of Current Controller for Starter Mode
6.2. Speed Controller Design
7. Controller Design Using the VVB Method
8. Simulation Results
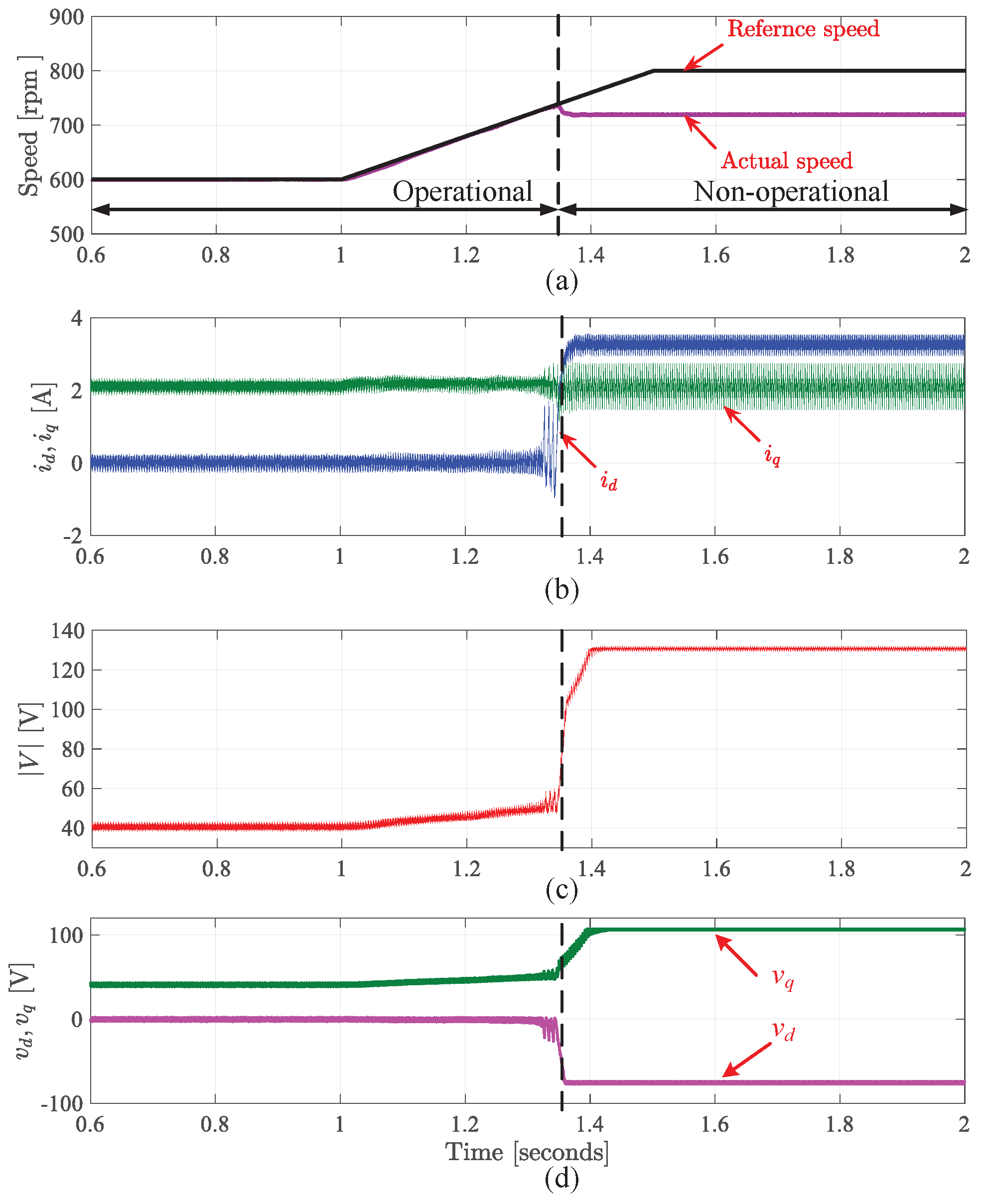
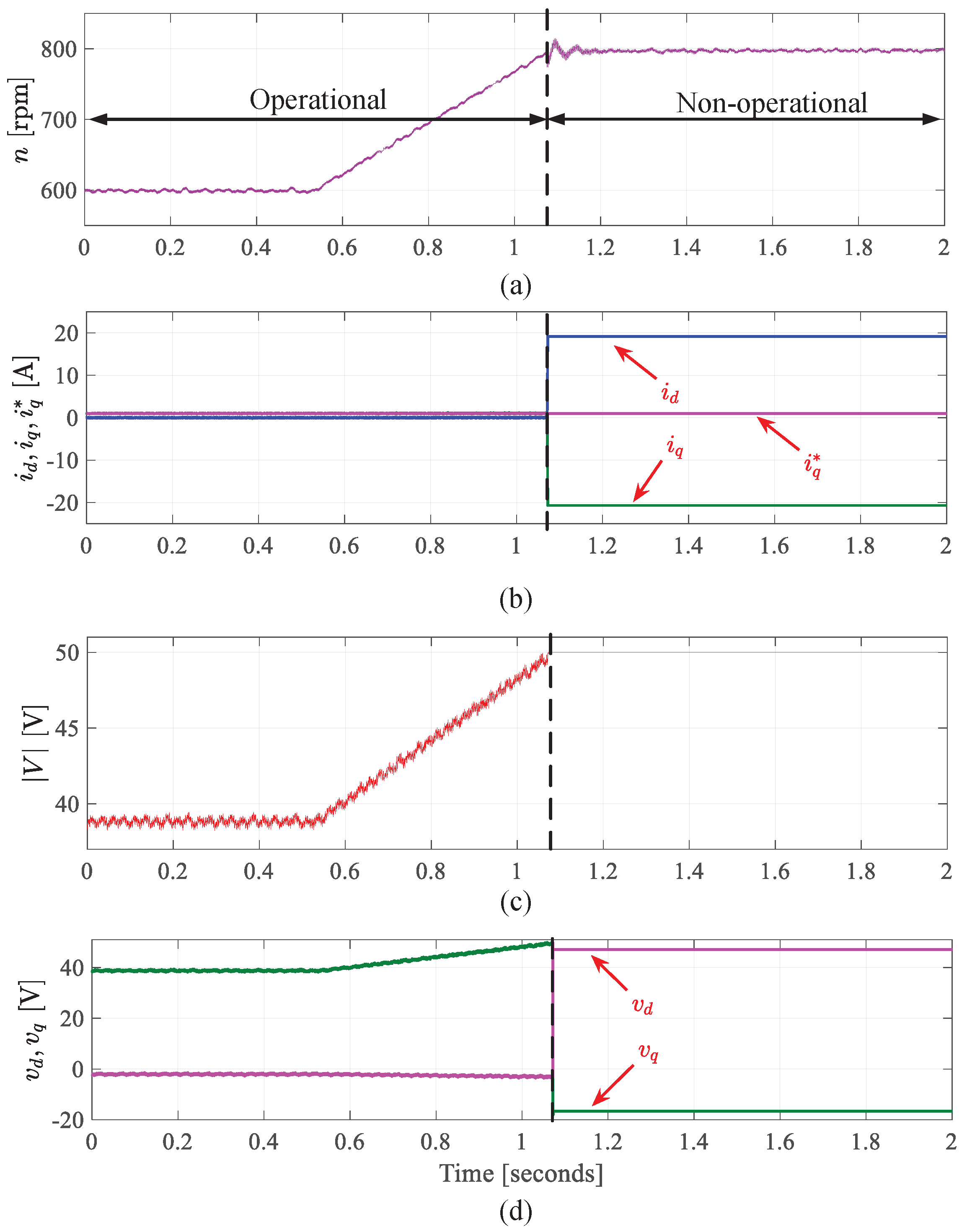
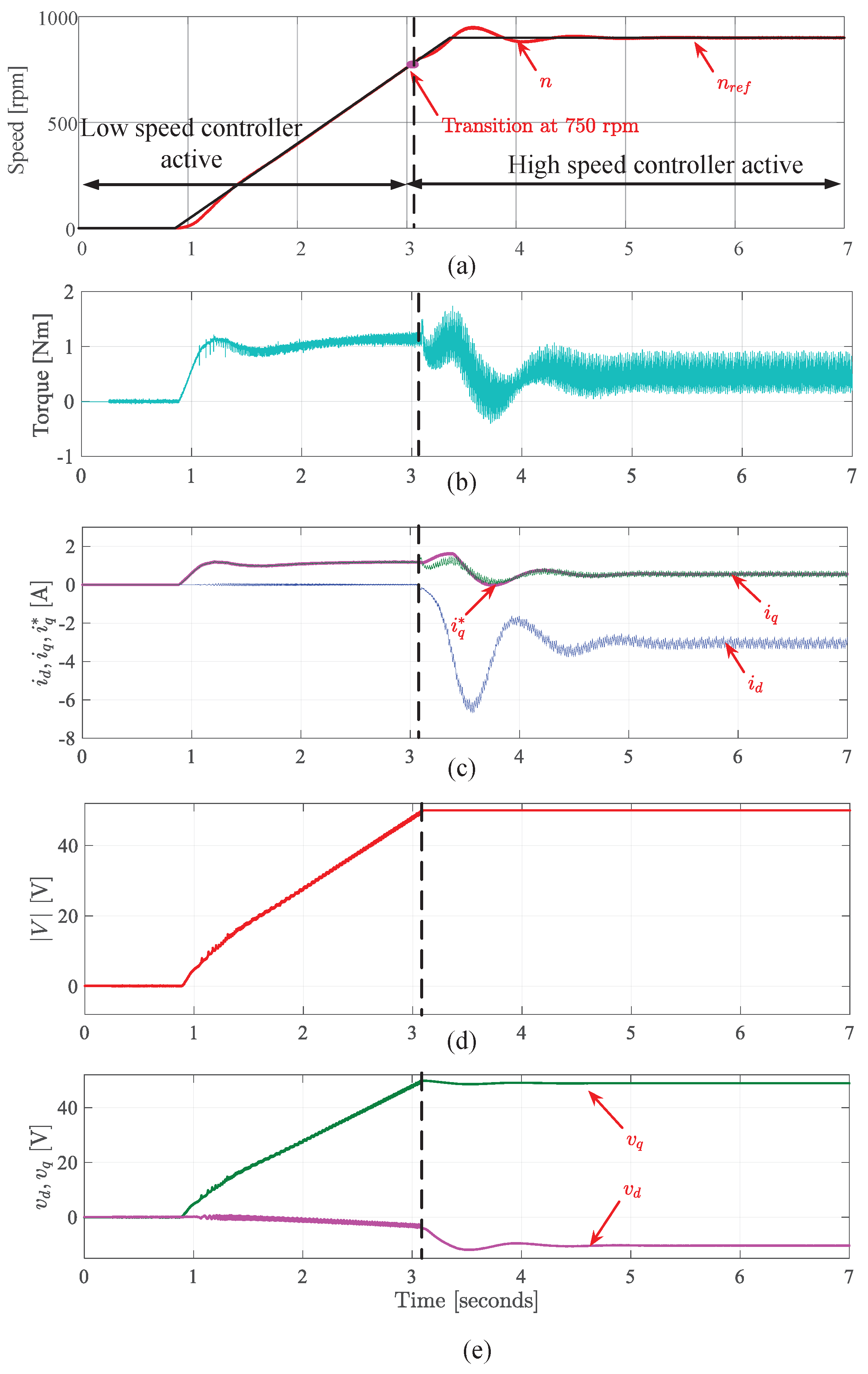
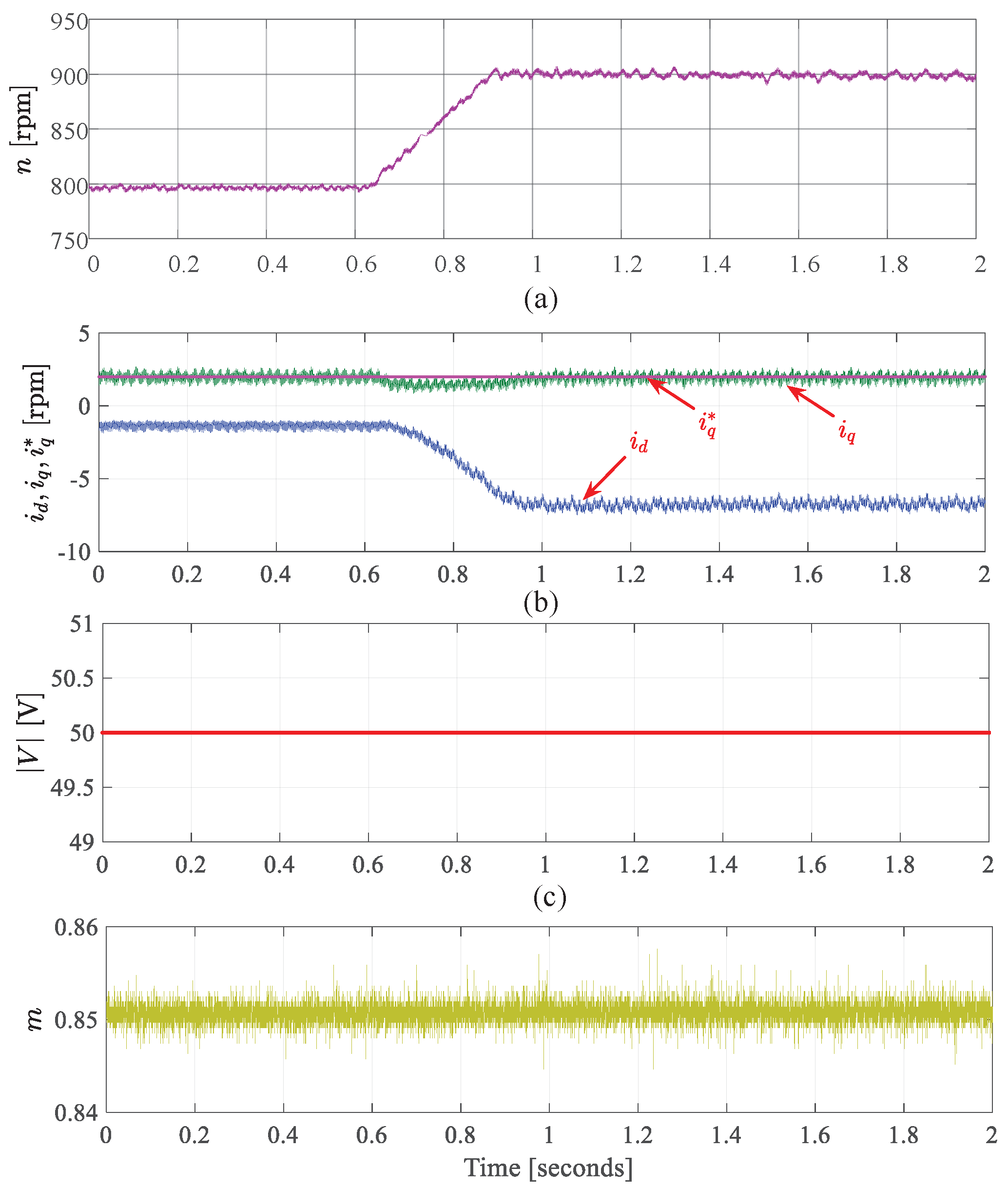
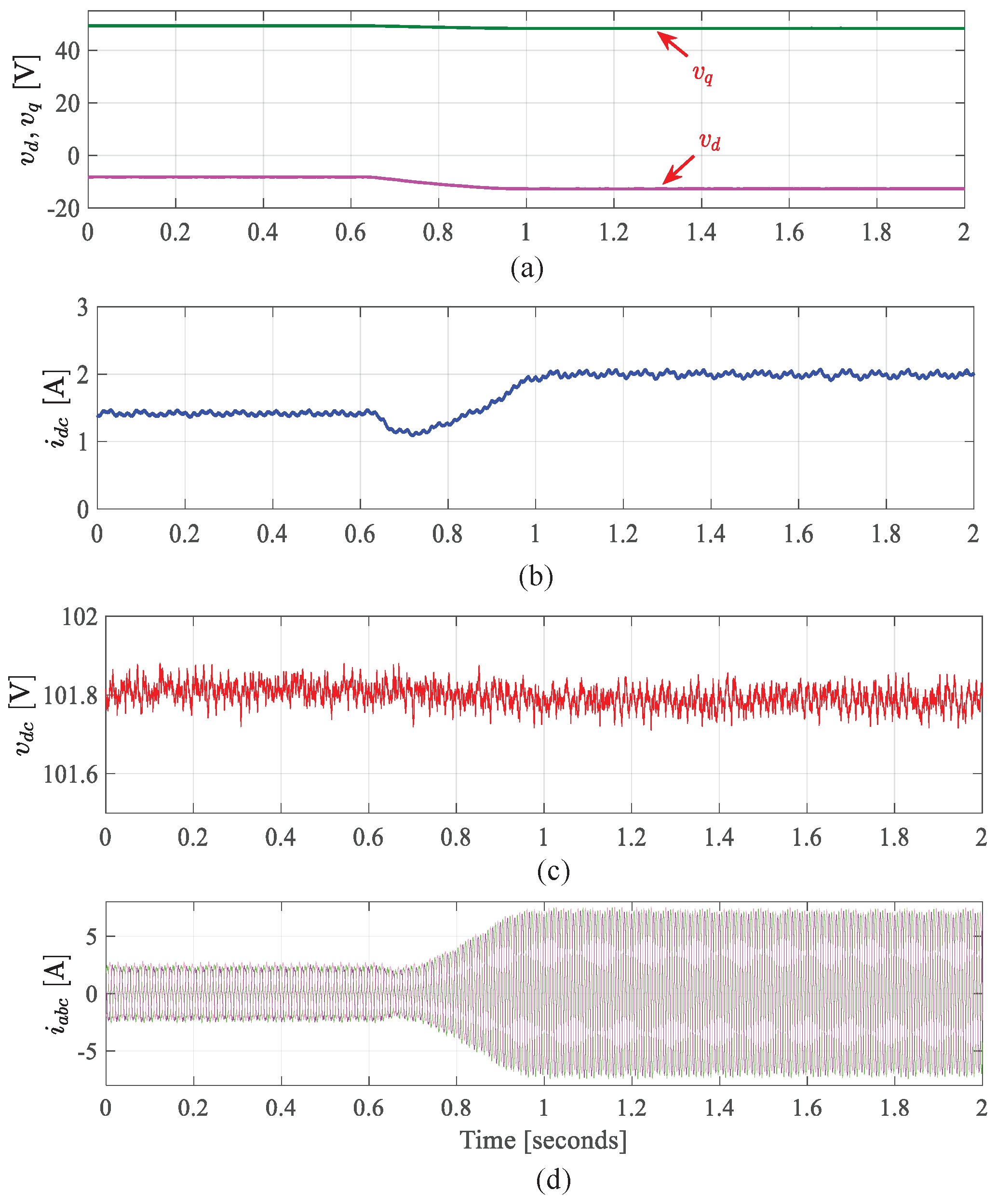
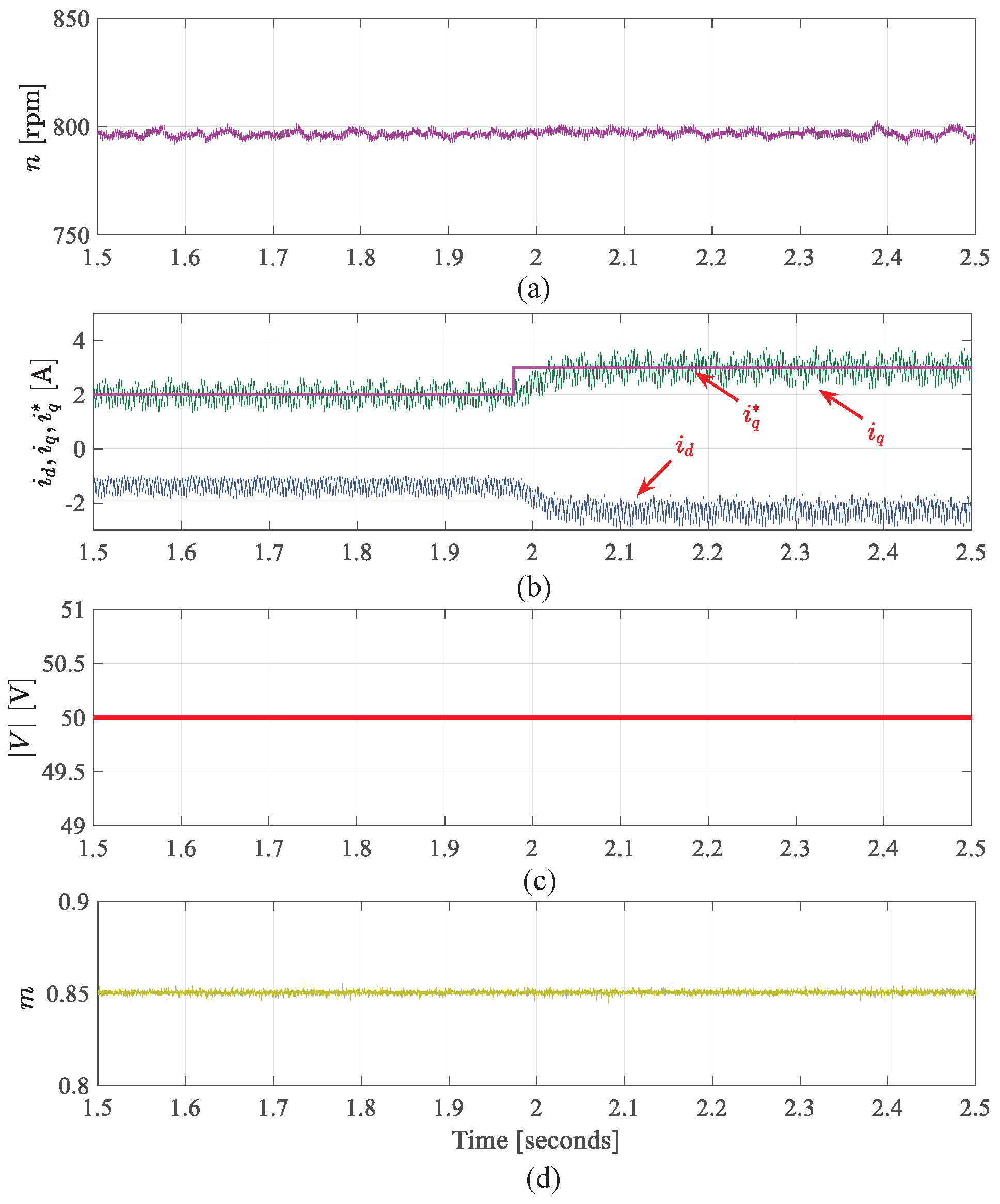
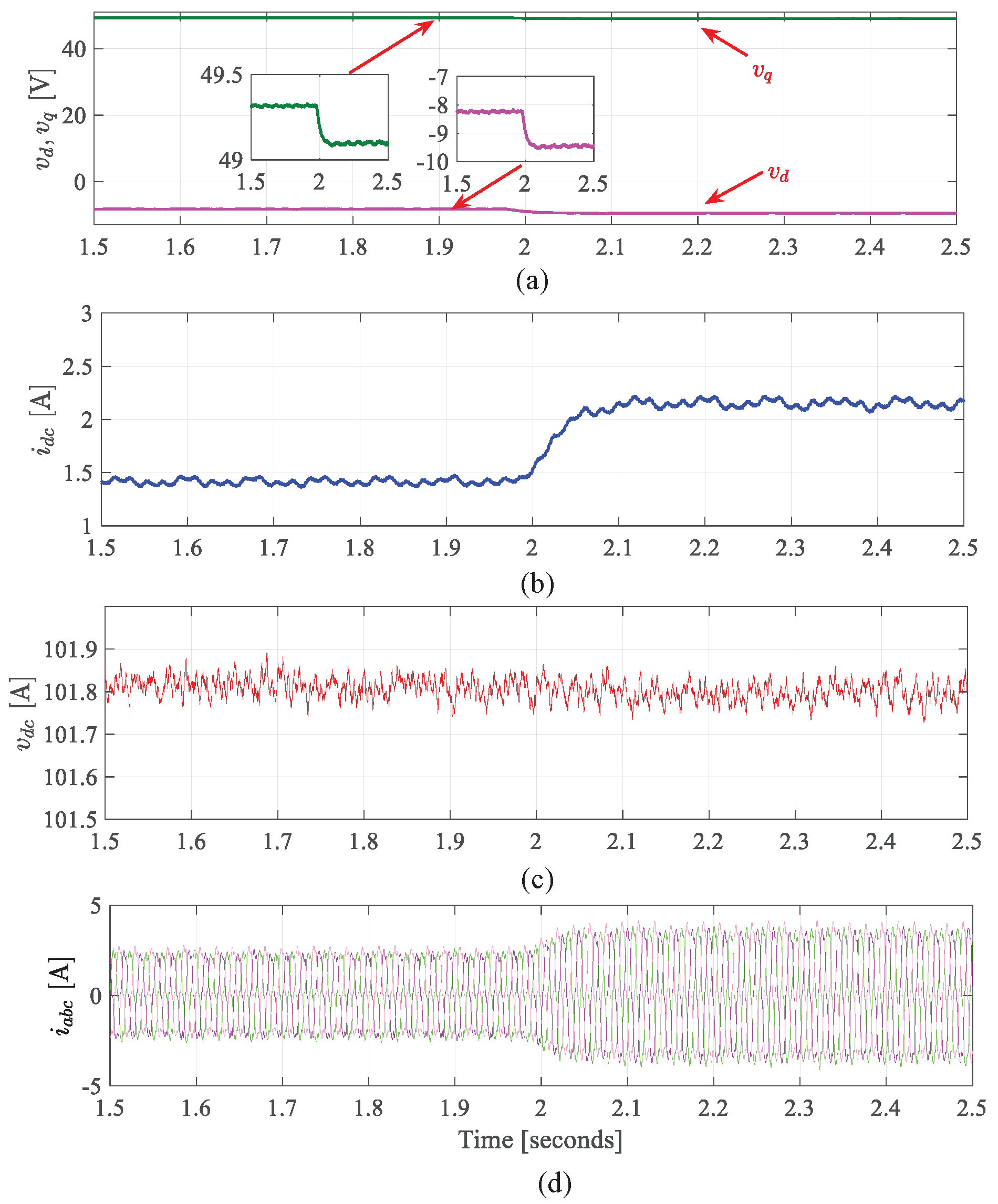
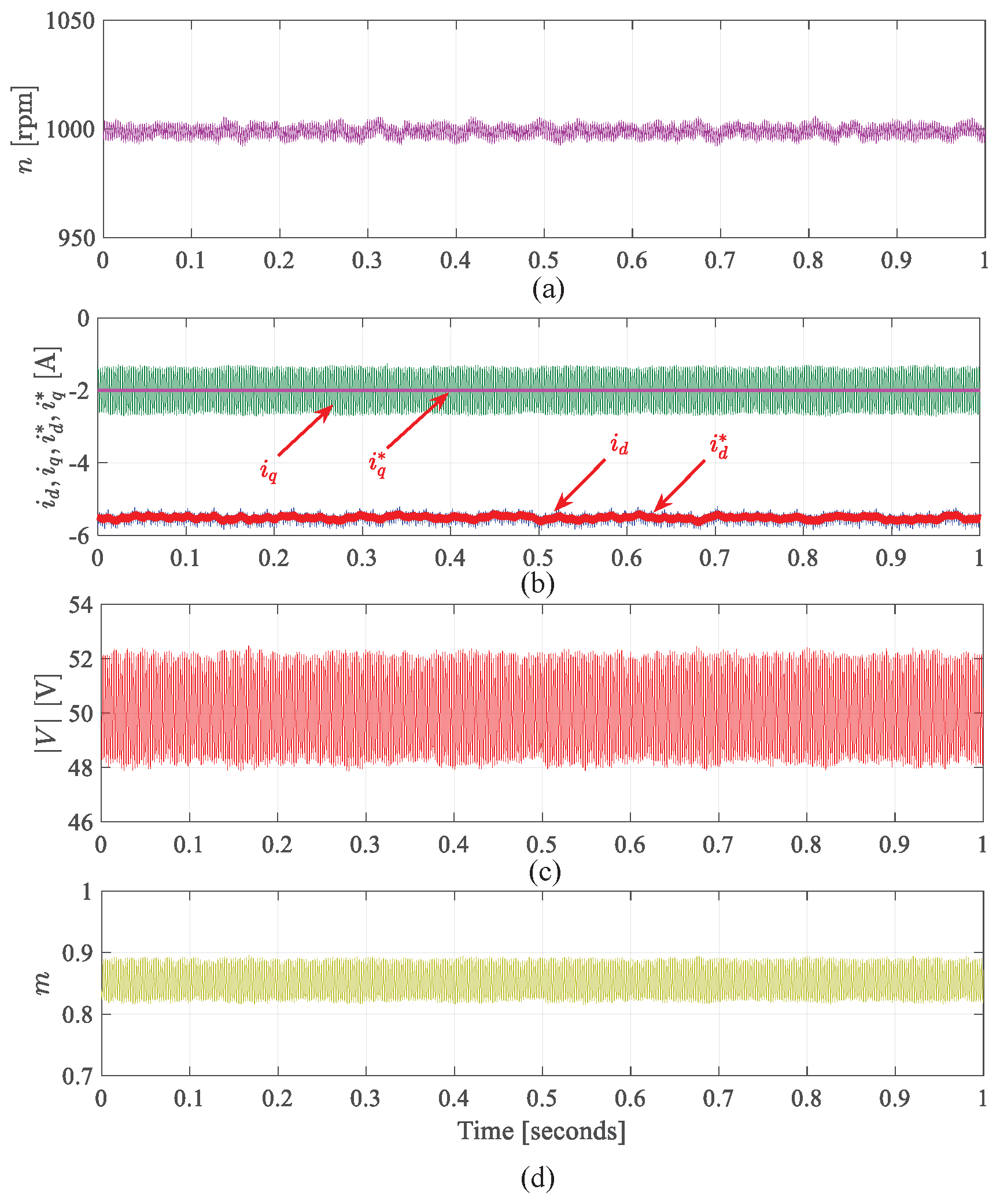
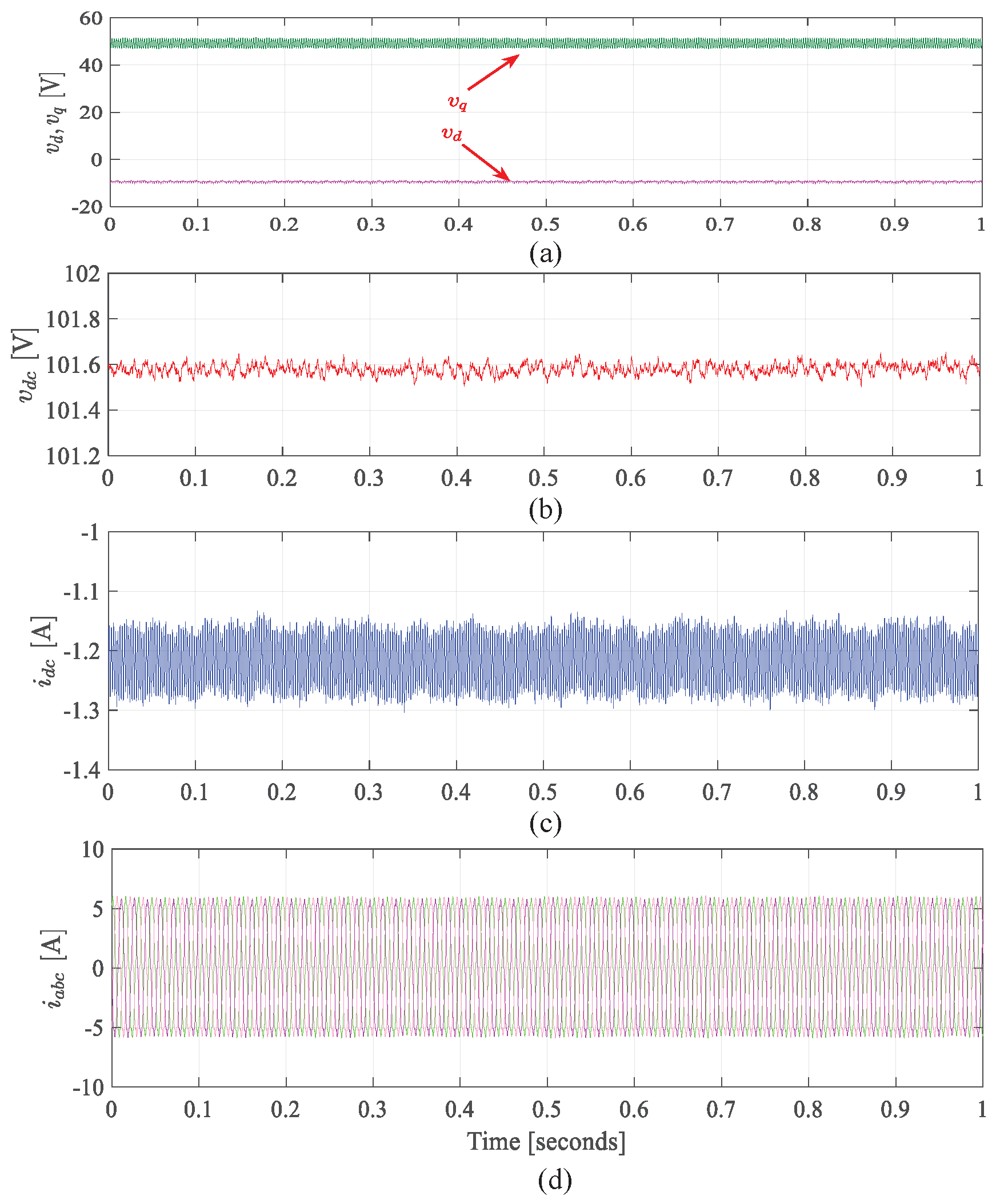
9. Experimental Validation
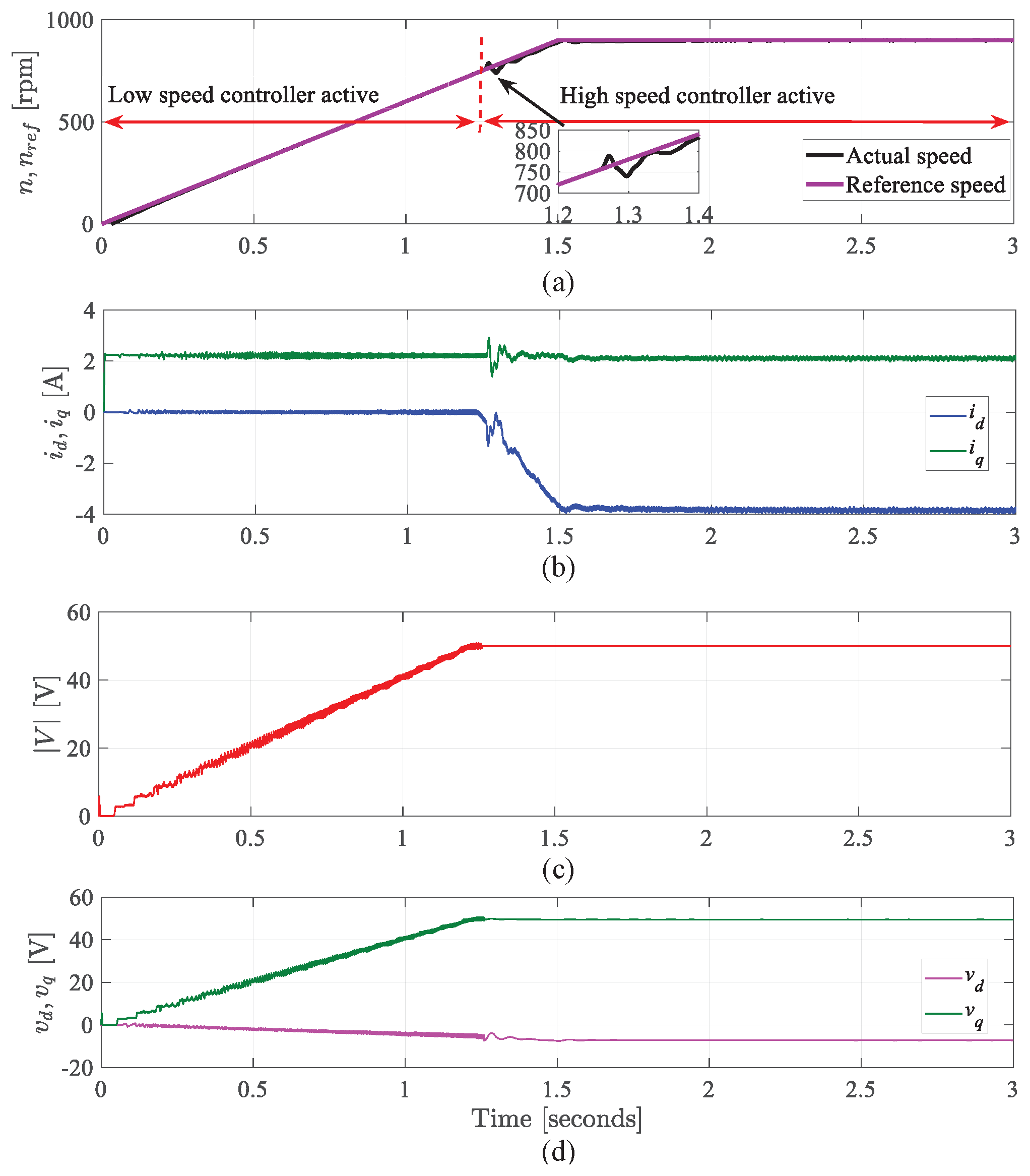
- Starting process from standstill to above FW speed
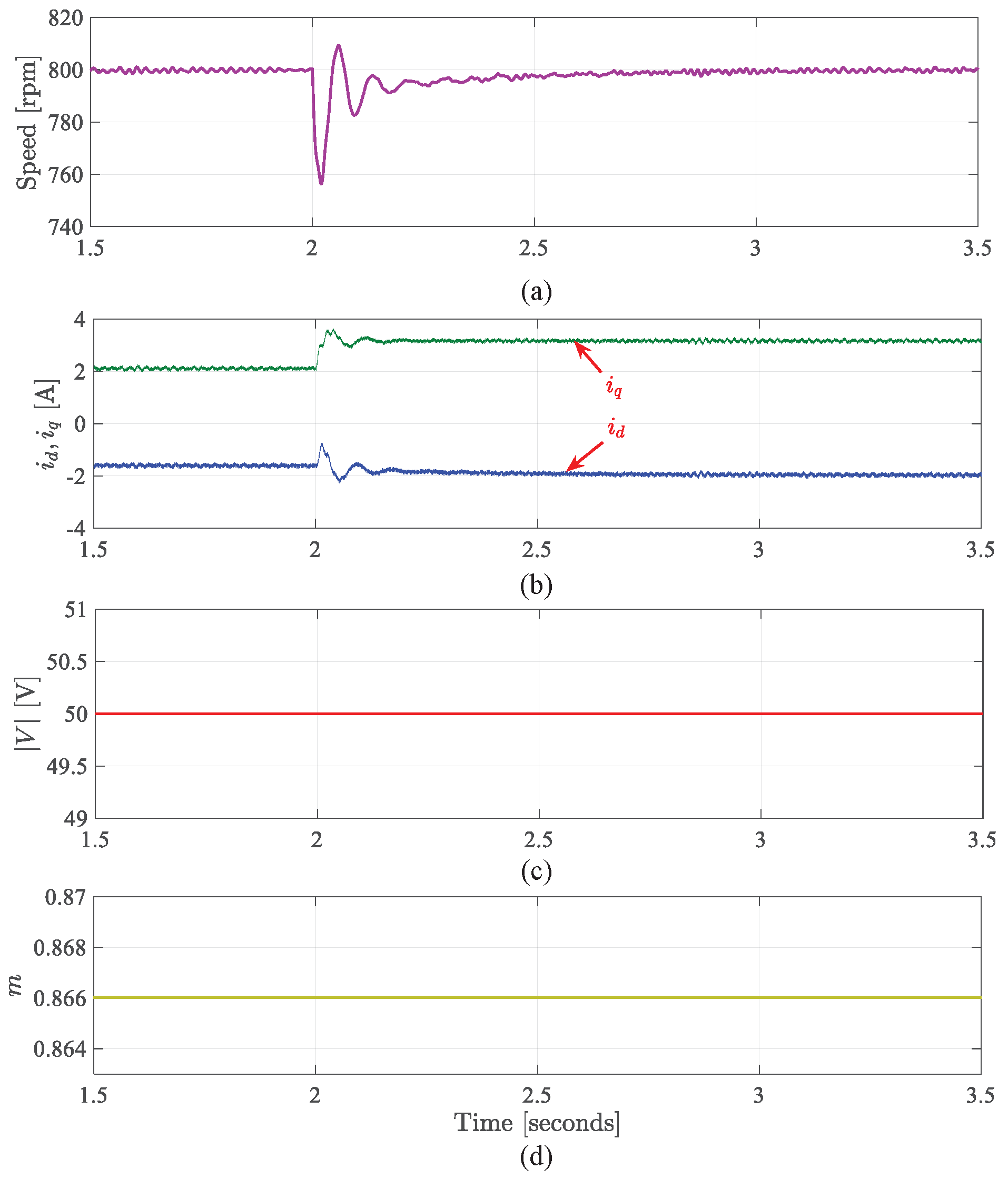
- Torque load change within FW region
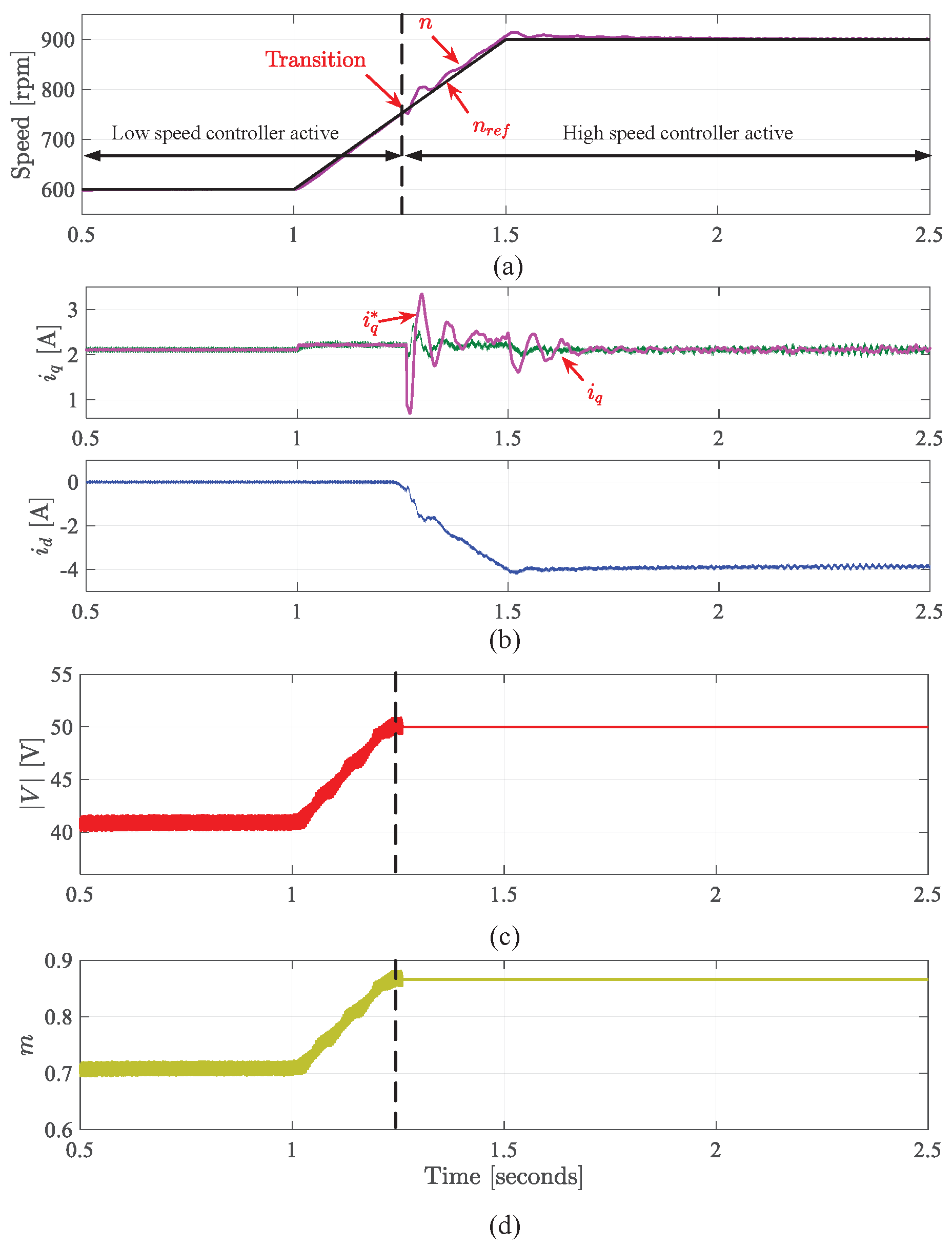
- Operation mode switching between different controllers (low and high-speed controllers)
- Speed change in FW mode
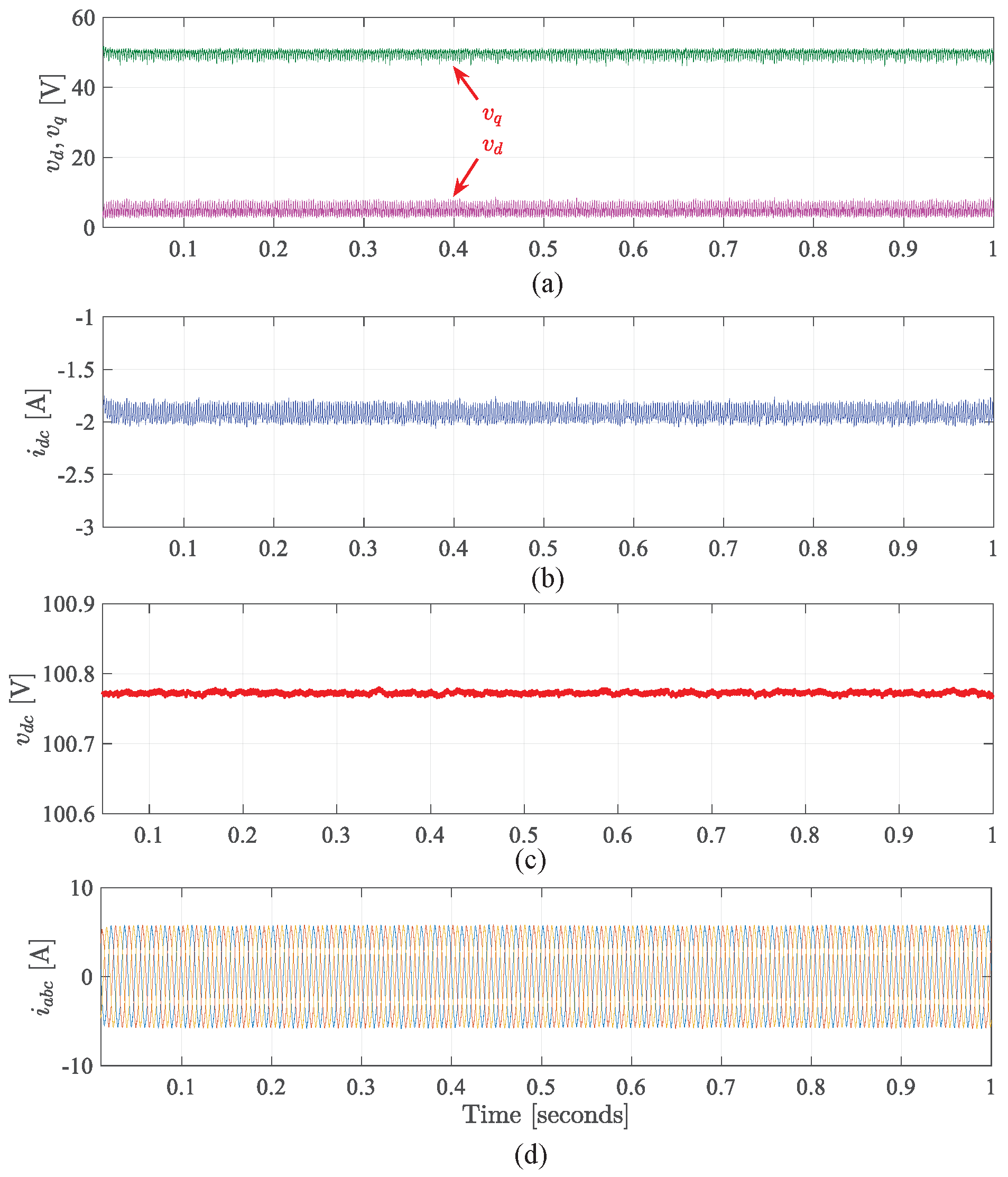
- Generation mode for VVB method
9.1. Results for VVB Method
9.2. Results for Starting Mode Using Proposed Method
9.3. Results for Generating Mode Using VVB Method
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ian Moir, A.S. Aircraft Systems: Machanical, Electrical and Avoionics Subsystems Integeration; Willey: Hoboken, NJ, USA, 2008. [Google Scholar]
- Mohamed, M.A.A.; Rashed, M.; Bozhko, S. Enhanced Flux Weakening Control of PMM-Based Starter-Generator System in More Electric Aircraft. In Proceedings of the 10th International Conference on Power Electronics, Machines and Drives (PEMD 2020), Online, 15–17 December 2020; Volume 2020, pp. 249–254. [Google Scholar]
- Ni, K.; Liu, Y.; Mei, Z.; Wu, T.; Hu, Y.; Wen, H.; Wang, Y. Electrical and Electronic Technologies in More-Electric Aircraft: A Review. IEEE Access 2019, 7, 76145–76166. [Google Scholar] [CrossRef]
- Madonna, V.; Giangrande, P.; Galea, M. Electrical Power Generation in Aircraft: Review, Challenges, and Opportunities. IEEE Trans. Transp. Electrif. 2018, 4, 646–659. [Google Scholar] [CrossRef]
- Buticchi, G.; Bozhko, S.; Liserre, M.; Wheeler, P.; Al-Haddad, K. On-Board Microgrids for the More Electric Aircraft—Technology Review. IEEE Trans. Ind. Electron. 2019, 66, 5588–5599. [Google Scholar] [CrossRef]
- Bozhko, S.; Rashed, M.; Hill, C.I.; Yeoh, S.S.; Yang, T. Flux-Weakening Control of Electric Starter/Generator Based on Permanent-Magnet Machine. IEEE Trans. Transp. Electrif. 2017, 3, 864–877. [Google Scholar] [CrossRef]
- Zhu, L.; Jiang, D.; Qu, R.; Tolbert, L.M.; Li, Q. Design of Power Hardware-in-the-Loop Simulations for Integrated Starter–Generator Systems. IEEE Trans. Transp. Electrif. 2019, 5, 80–92. [Google Scholar] [CrossRef]
- Bozhko, S.; Yang, T.; Le Peuvedic, J.M.; Arumugam, P.; Degano, M.; La Rocca, A.; Xu, Z.; Rashed, M.; Fernando, W.; Hill, C.I.; et al. Development of Aircraft Electric Starter–Generator System Based on Active Rectification Technology. IEEE Trans. Transp. Electrif. 2018, 4, 985–996. [Google Scholar] [CrossRef]
- Yeoh, S.S.; Yang, T.; Tarisciotti, L.; Hill, C.I.; Bozhko, S.; Zanchetta, P. Permanent-Magnet Machine-Based Starter/Generator System With Modulated Model Predictive Control. IEEE Trans. Transp. Electrif. 2017, 3, 878–890. [Google Scholar] [CrossRef]
- Morimoto, S.; Takeda, Y.; Hirasa, T.; Taniguchi, K. Expansion of operating limits for permanent magnet motor by current vector control considering inverter capacity. IEEE Trans. Ind. Appl. 1990, 26, 866–871. [Google Scholar] [CrossRef]
- Morimoto, S.; Sanada, M.; Takeda, Y. Wide-speed operation of interior permanent magnet synchronous motors with high-performance current regulator. IEEE Trans. Ind. Appl. 1994, 30, 920–926. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, J.; Jiang, Y.; Geng, W.; Xu, Y. Overview and analysis of PM starter/generator for aircraft electrical power systems. CES Trans. Electr. Mach. Syst. 2017, 1, 117–131. [Google Scholar] [CrossRef]
- Lang, X.; Yang, T.; Bai, G.; Bozhko, S.; Wheeler, P. Active Disturbance Rejection Control of DC-Bus Voltages within a High-Speed Aircraft Electric Starter/Generator System. IEEE Trans. Transp. Electrif. 2022, 8, 4229–4241. [Google Scholar] [CrossRef]
- Yeoh, S.S.; Rashed, M.; Sanders, M.; Bozhko, S. Variable-Voltage Bus Concept for Aircraft Electrical Power System. IEEE Trans. Ind. Electron. 2019, 66, 5634–5643. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.; Zhou, M.; You, X. Flux-Weakening in PMSM Drives: Analysis of Voltage Angle Control and the Single Current Controller Design. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 437–445. [Google Scholar] [CrossRef]
- Stojan, D.; Drevensek, D.; Plantic, A.; Grcar, B.; Stumberger, G. Novel Field-Weakening Control Scheme for Permanent-Magnet Synchronous Machines Based on Voltage Angle Control. IEEE Trans. Ind. Appl. 2012, 48, 2390–2401. [Google Scholar] [CrossRef]
- Shi, J.; Liu, T.; Yang, S. Nonlinear-controller design for an interior-permanent-magnet synchronous motor including field-weakening operation. IET Electr. Power Appl. 2007, 1, 119–126. [Google Scholar] [CrossRef]
- Rahman, M.A.; Vilathgamuwa, D.M.; Uddin, M.N.; Tseng, K.-J. Nonlinear control of interior permanent-magnet synchronous motor. IEEE Trans. Ind. Appl. 2003, 39, 408–416. [Google Scholar] [CrossRef]
- Kwon, T.; Choi, G.; Kwak, M.; Sul, S. Novel Flux-Weakening Control of an IPMSM for Quasi-Six-Step Operation. IEEE Trans. Ind. Appl. 2008, 44, 1722–1731. [Google Scholar] [CrossRef]
- Lin, P.Y.; Lai, Y.S. Voltage Control Technique for the Extension of DC-Link Voltage Utilization of Finite-Speed SPMSM Drives. IEEE Trans. Ind. Electron. 2012, 59, 3392–3402. [Google Scholar] [CrossRef]
- Diab, A.M.; Bozhko, S.; Galea, M.; Gerada, C. Stable and Robust Design of Active Disturbance-Rejection Current Controller for Permanent Magnet Machines in Transportation Systems. IEEE Trans. Transp. Electrif. 2020, 6, 1421–1433. [Google Scholar] [CrossRef]
- Yeoh, S.S. Control Strategies for the More Electric Aircraft Starter-Generator Electrical Power System. Ph.D. Thesis, Nottingham University, Nottingham, UK, 2016. [Google Scholar]










| Parameter | Value |
|---|---|
| Rated line voltage | 230 Vrms |
| Stator resistance, | 0.30 |
| d-axis inductance, | 7.5 mH |
| q-axis inductance, | 7.5 mH |
| Mutual flux, | 0.158 Vs |
| Combined AC and DC inertia, J | 0.0016 kgm2 |
| Viscous damping, B | 0.00024 Nms |
| Mechanical friction, | 0.453 Nm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, M.A.A.; Shen Yeoh, S.; Atkin, J.; Diab, A.M.; Khalaf, M.; Bozhko, S. Enhanced Starting Control Scheme for PMM-Based Starter/Generator System for MEA. Aerospace 2023, 10, 168. https://doi.org/10.3390/aerospace10020168
Mohamed MAA, Shen Yeoh S, Atkin J, Diab AM, Khalaf M, Bozhko S. Enhanced Starting Control Scheme for PMM-Based Starter/Generator System for MEA. Aerospace. 2023; 10(2):168. https://doi.org/10.3390/aerospace10020168
Chicago/Turabian StyleMohamed, Mohamed A. A., Seang Shen Yeoh, Jason Atkin, Ahmed M. Diab, Mohsen Khalaf, and Serhiy Bozhko. 2023. "Enhanced Starting Control Scheme for PMM-Based Starter/Generator System for MEA" Aerospace 10, no. 2: 168. https://doi.org/10.3390/aerospace10020168
APA StyleMohamed, M. A. A., Shen Yeoh, S., Atkin, J., Diab, A. M., Khalaf, M., & Bozhko, S. (2023). Enhanced Starting Control Scheme for PMM-Based Starter/Generator System for MEA. Aerospace, 10(2), 168. https://doi.org/10.3390/aerospace10020168








