An Experimental Study on Rotor Aerodynamic Noise Control Based on Active Flap Control
Abstract
1. Introduction
2. Experimental Principle and Scheme
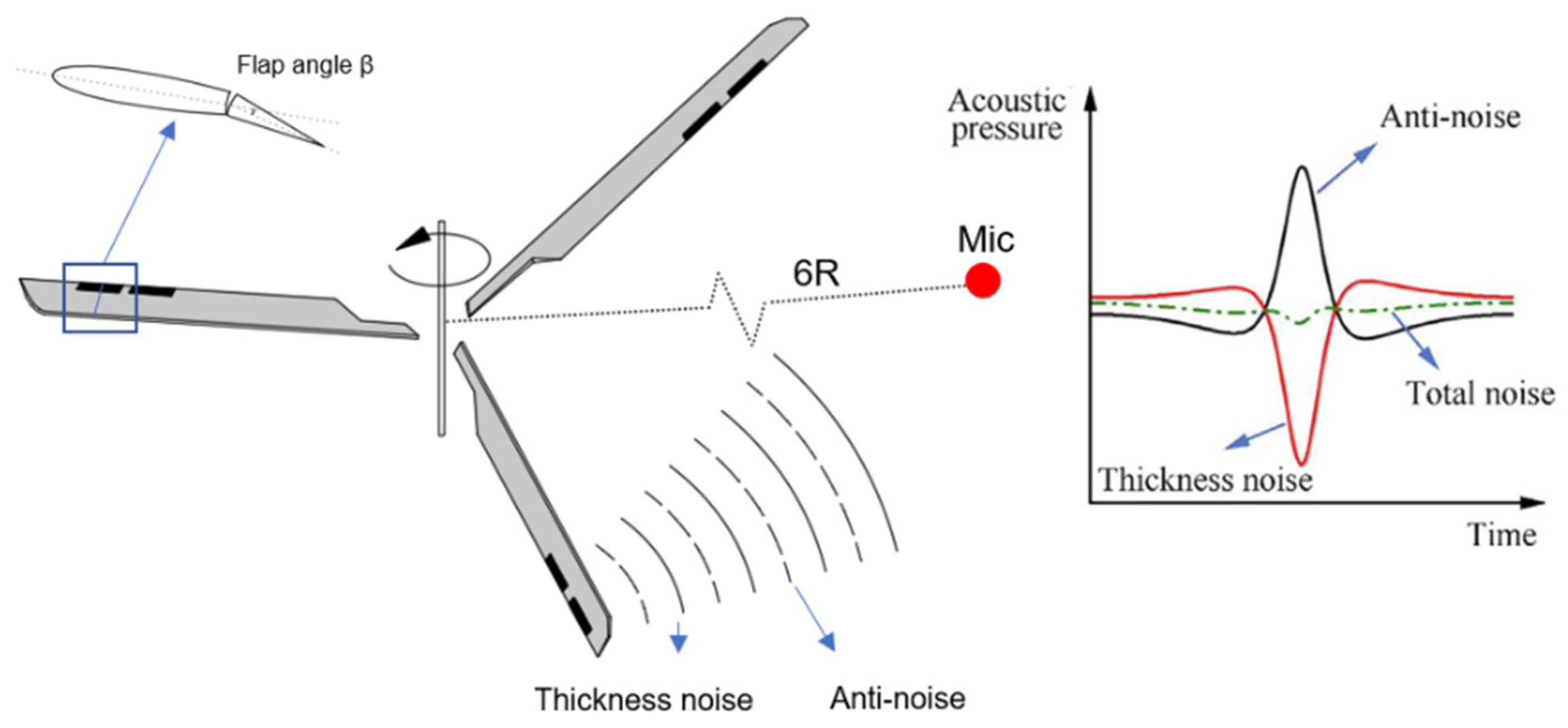
2.1. The Principle of AFC Noise Reduction
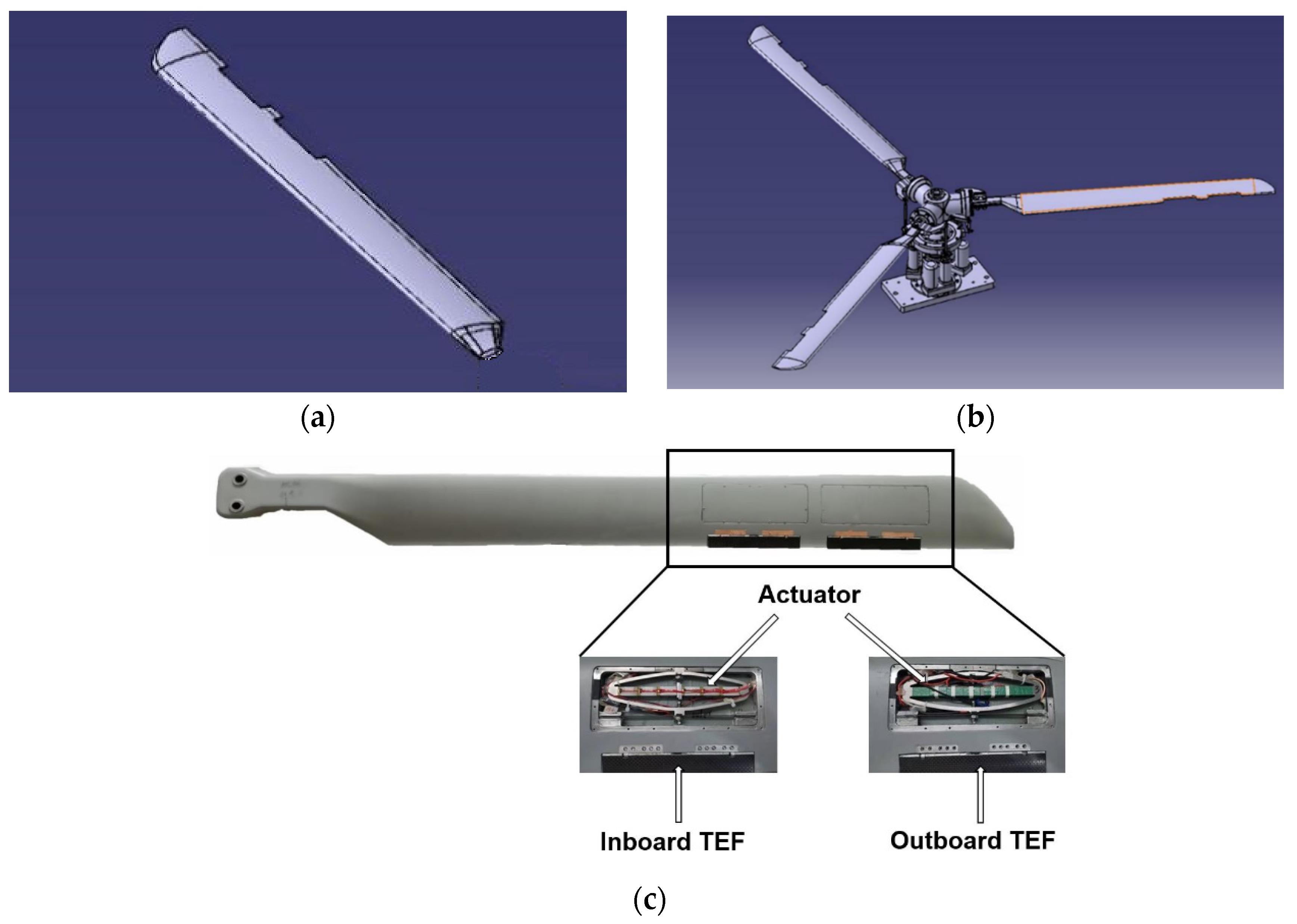
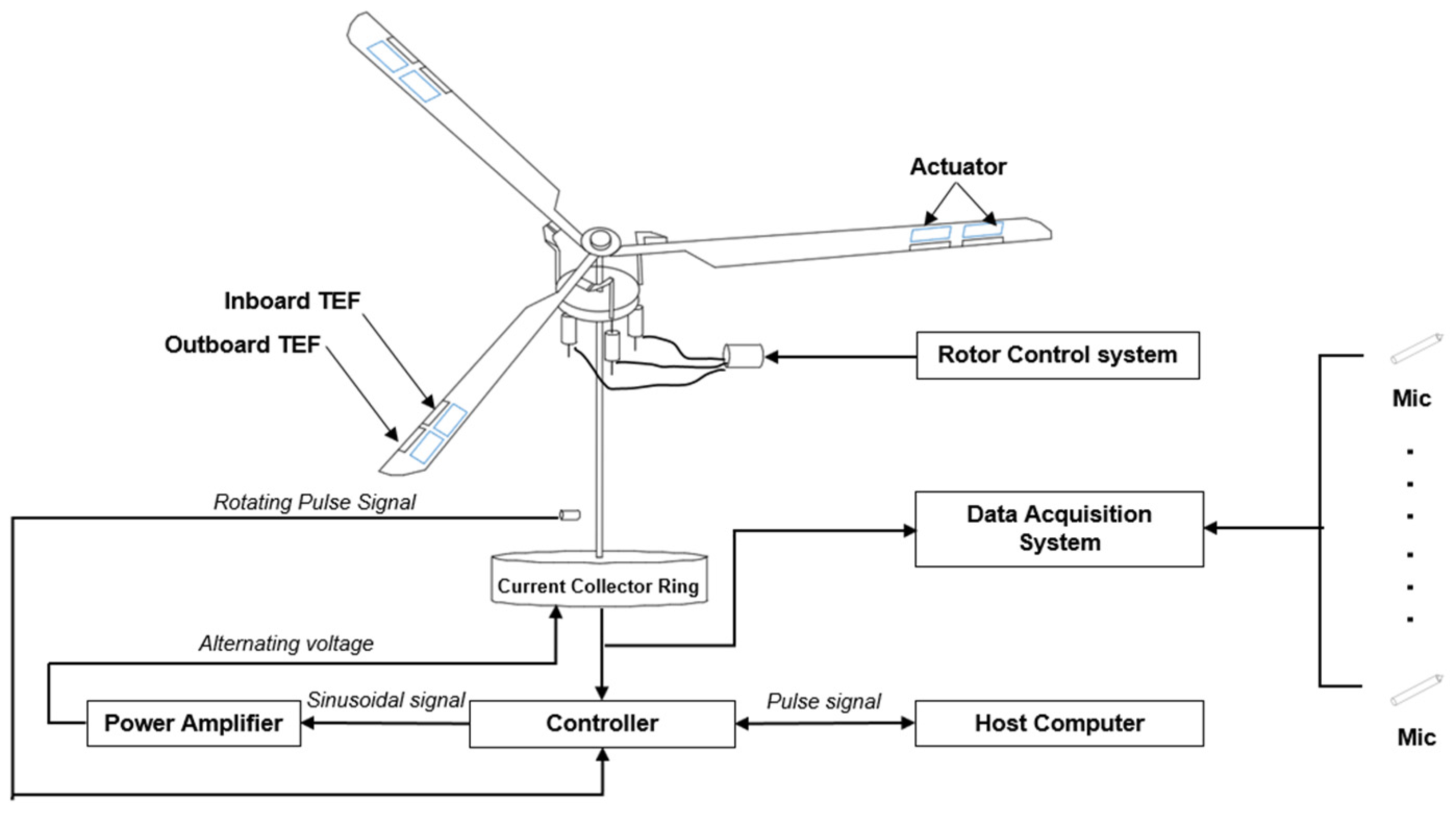
2.2. Test Platform and Scheme
2.3. Processing and Verification of the Test Data
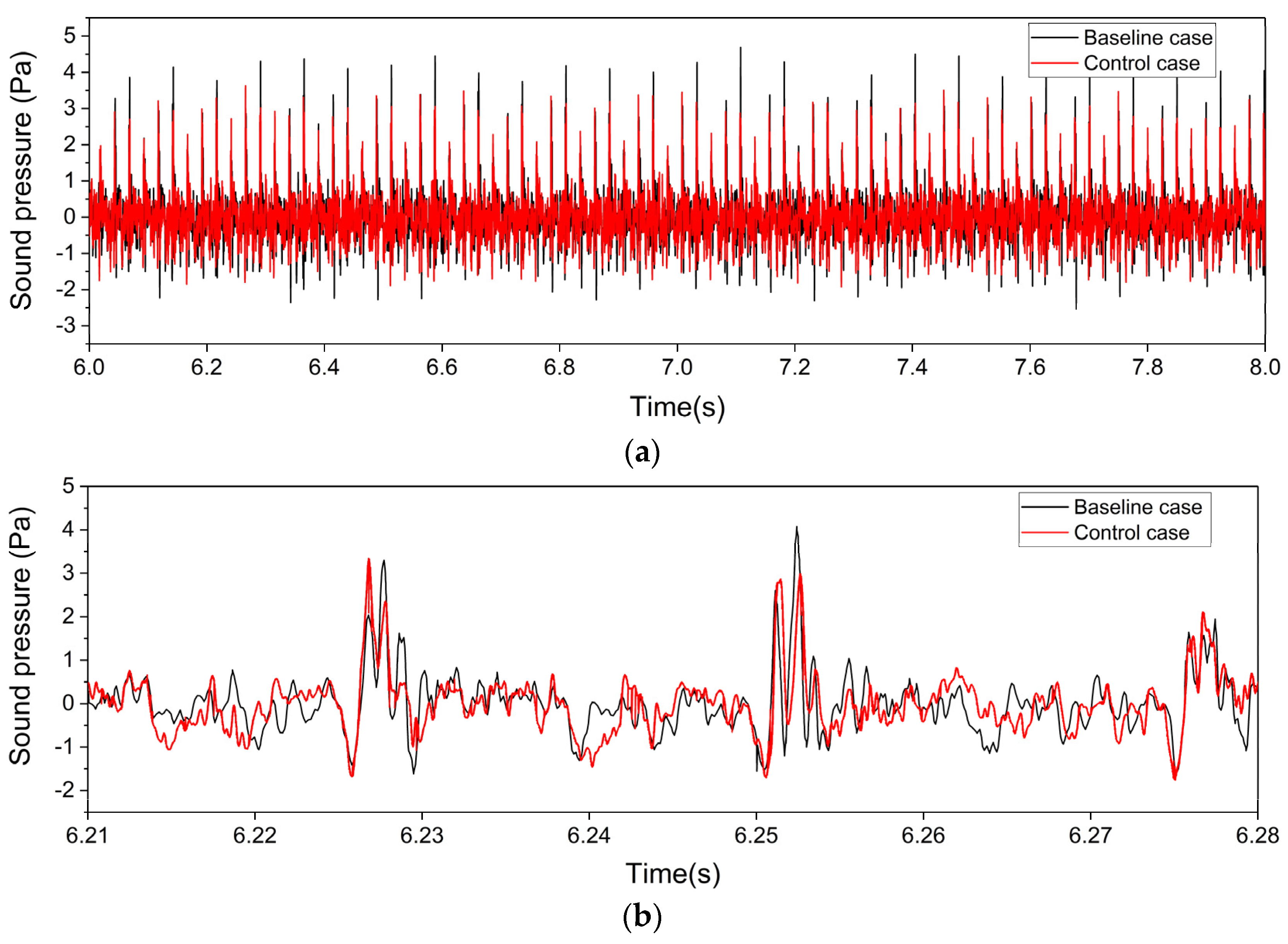
2.3.1. Acquisition and Processing of Test Data
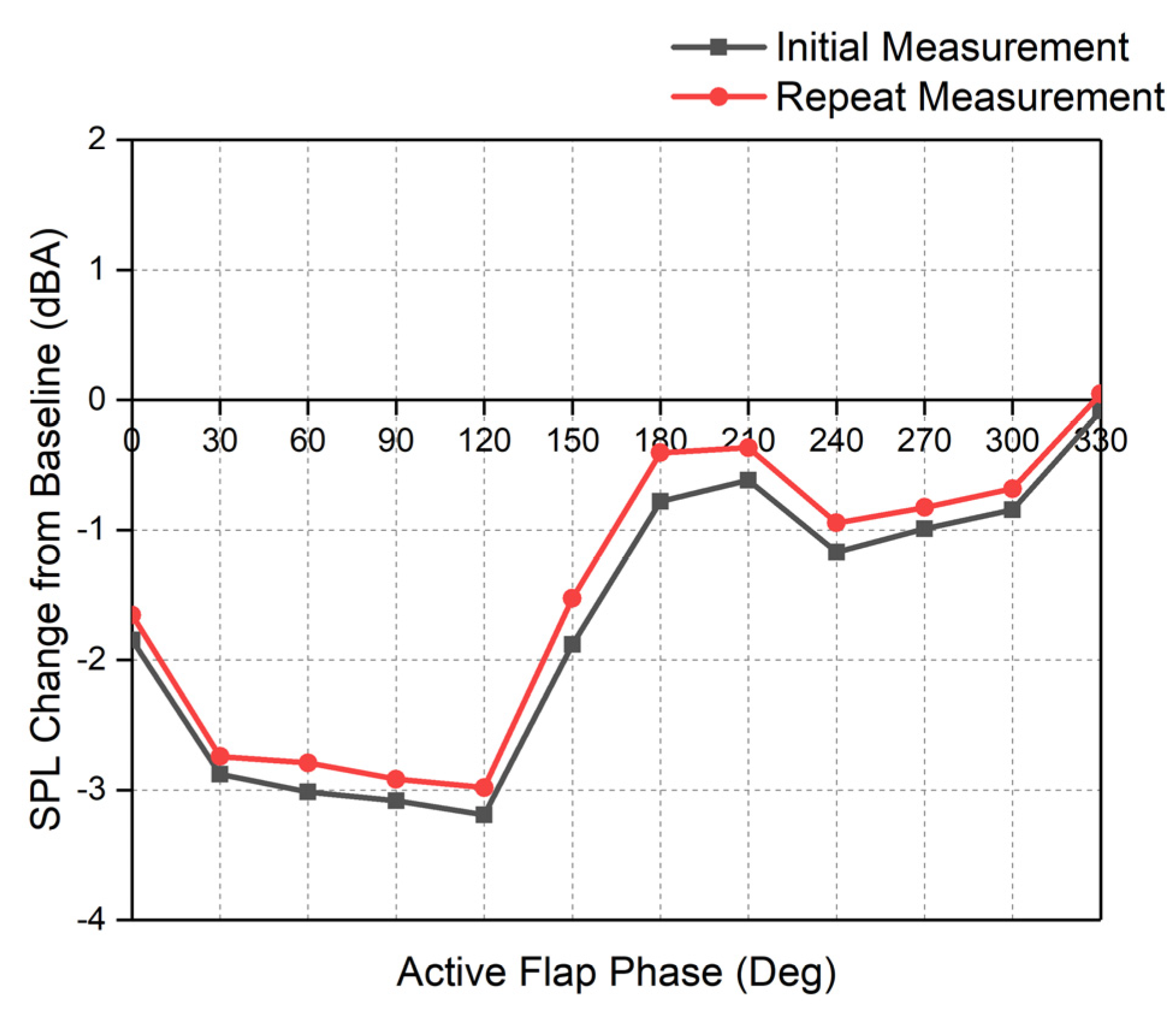
2.3.2. The Consistency of Repeated Tests
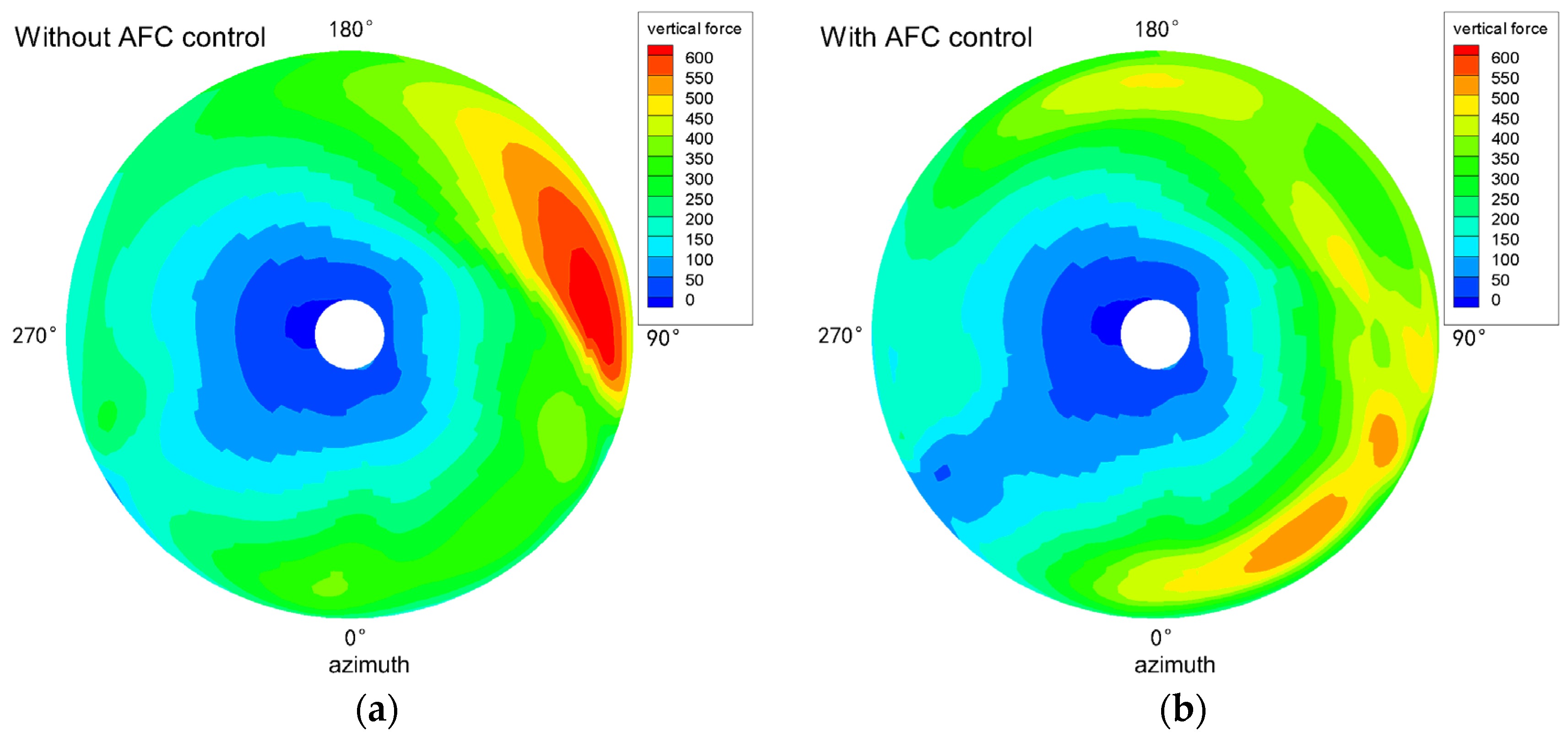
3. Results and Discussion
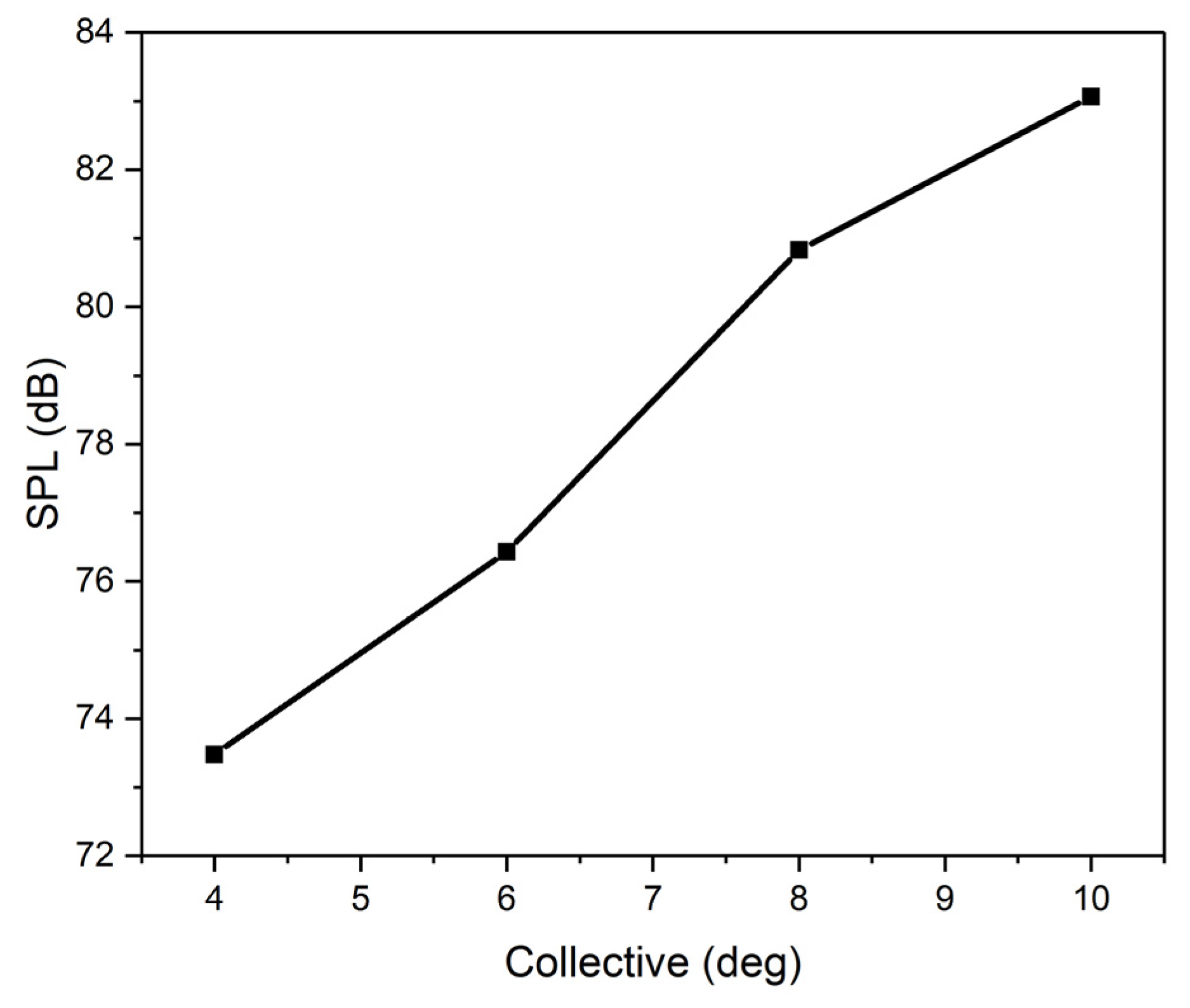
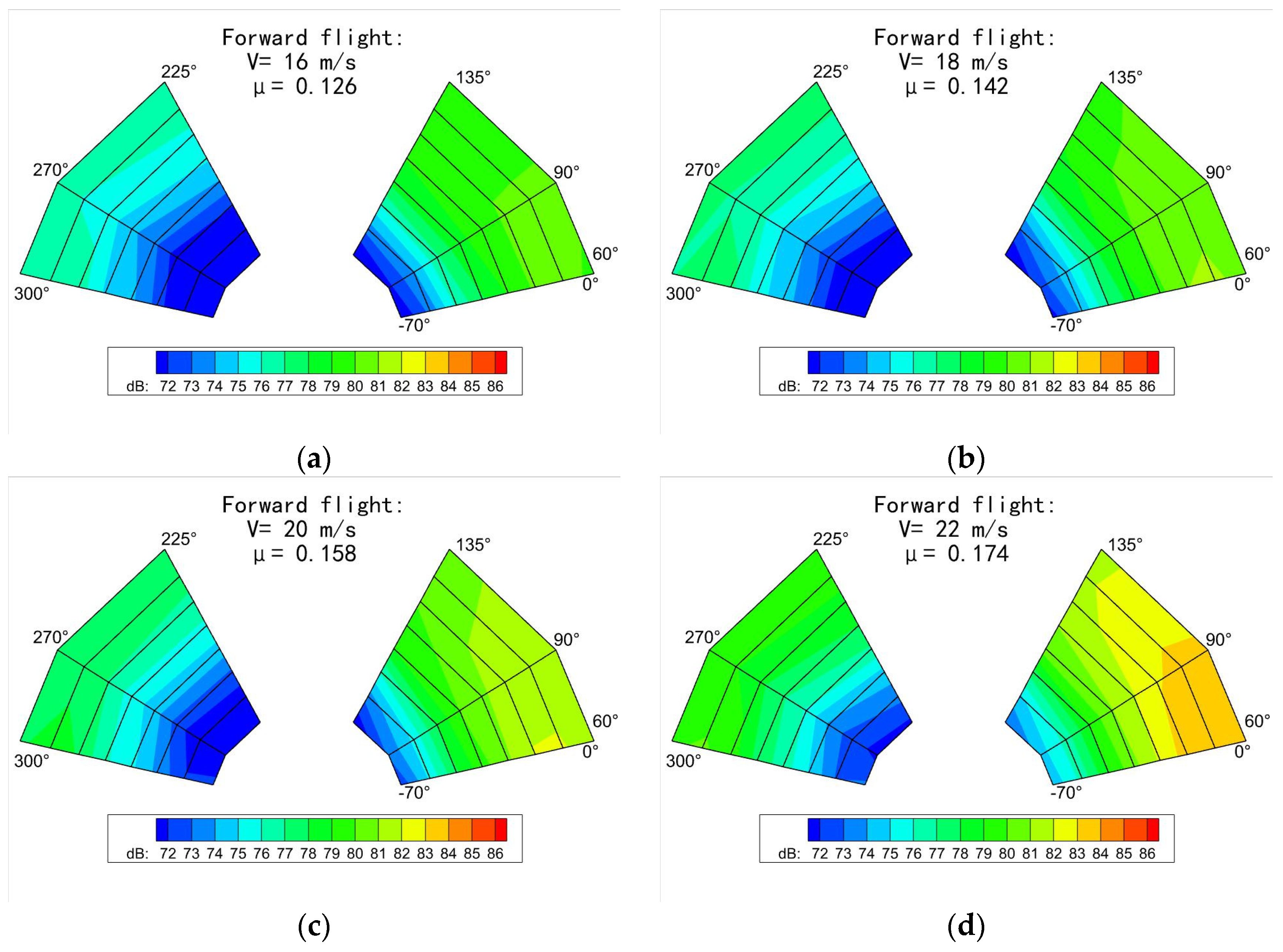
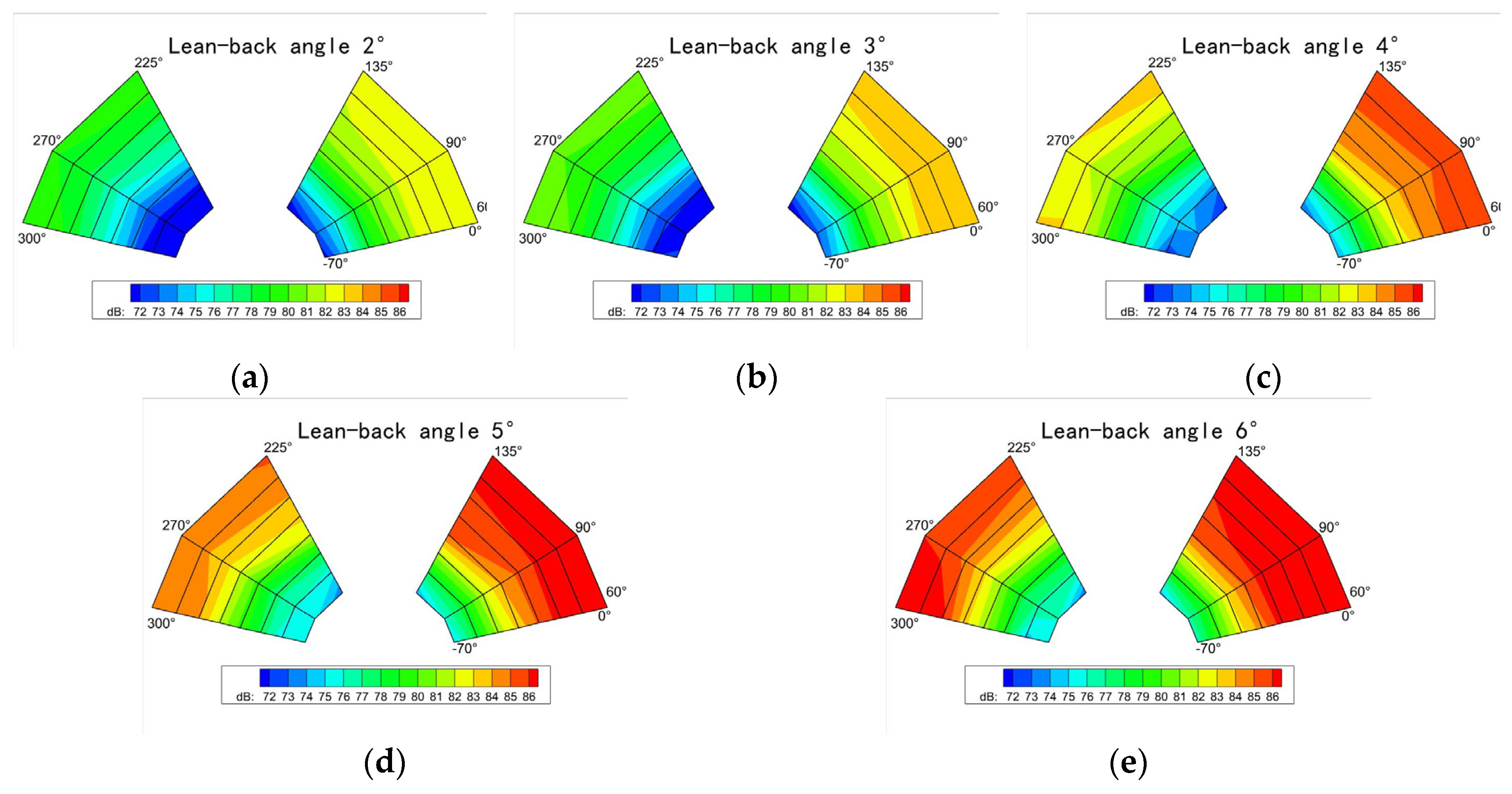
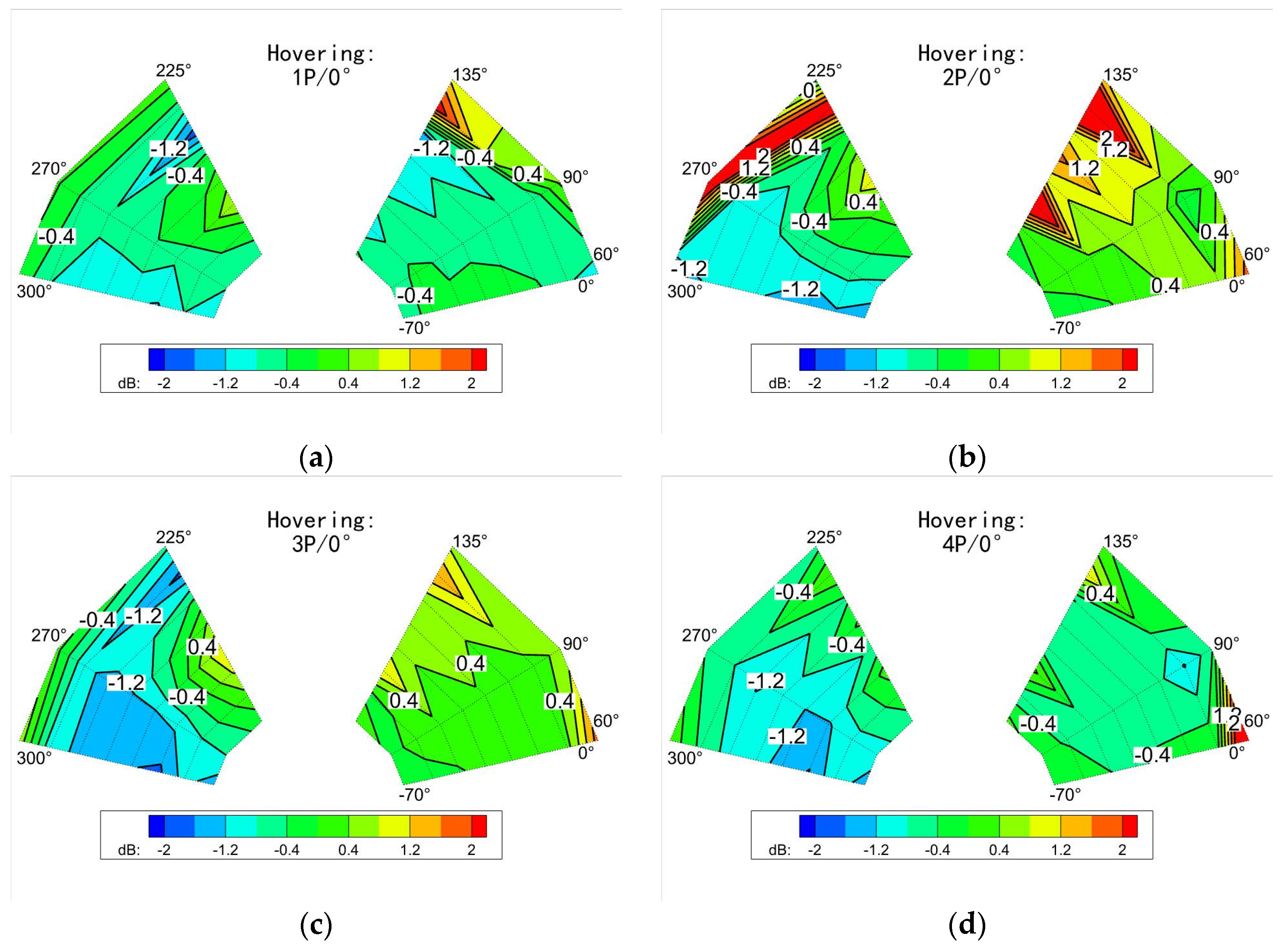
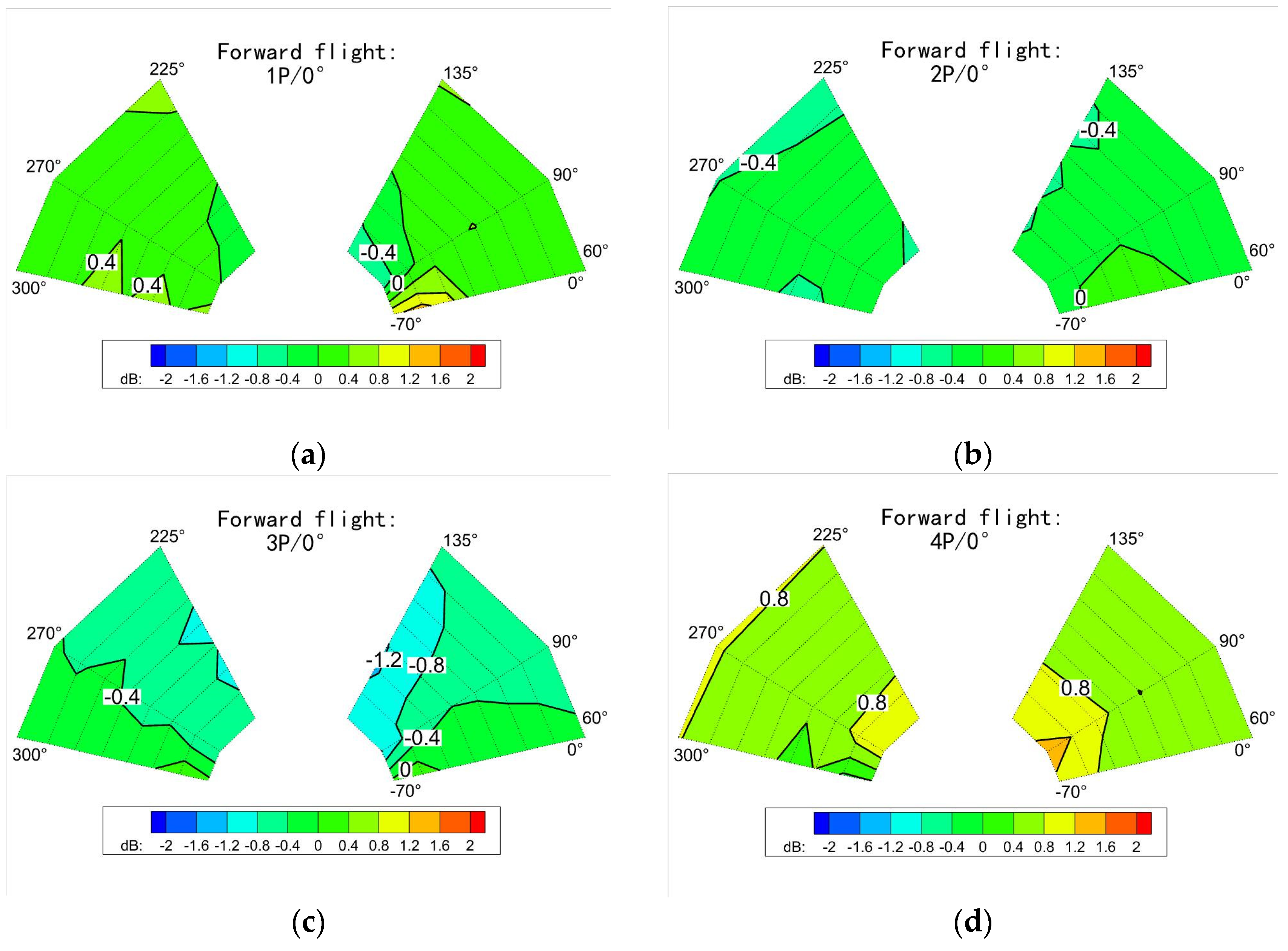
3.1. The Influence of Flight State
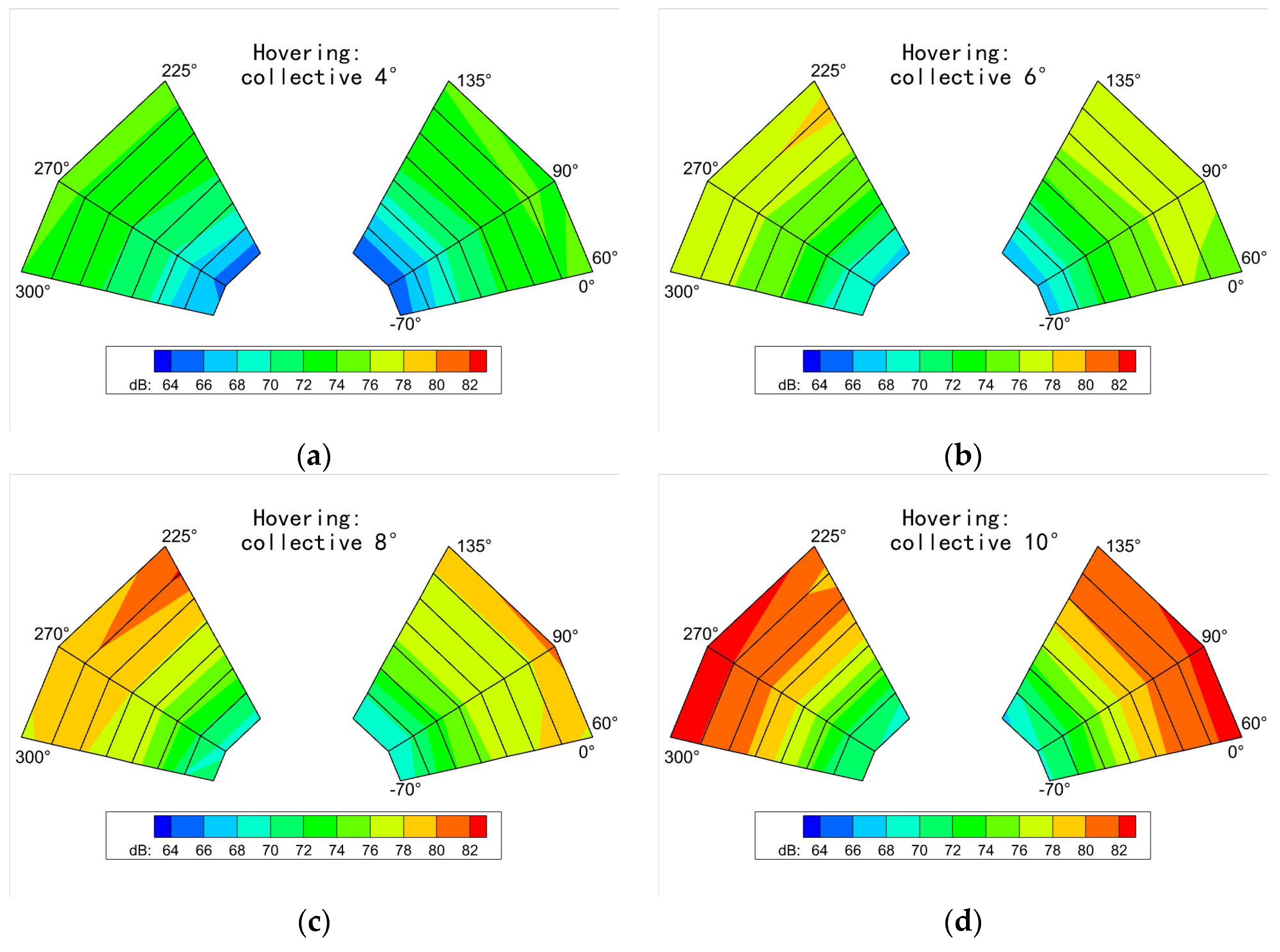
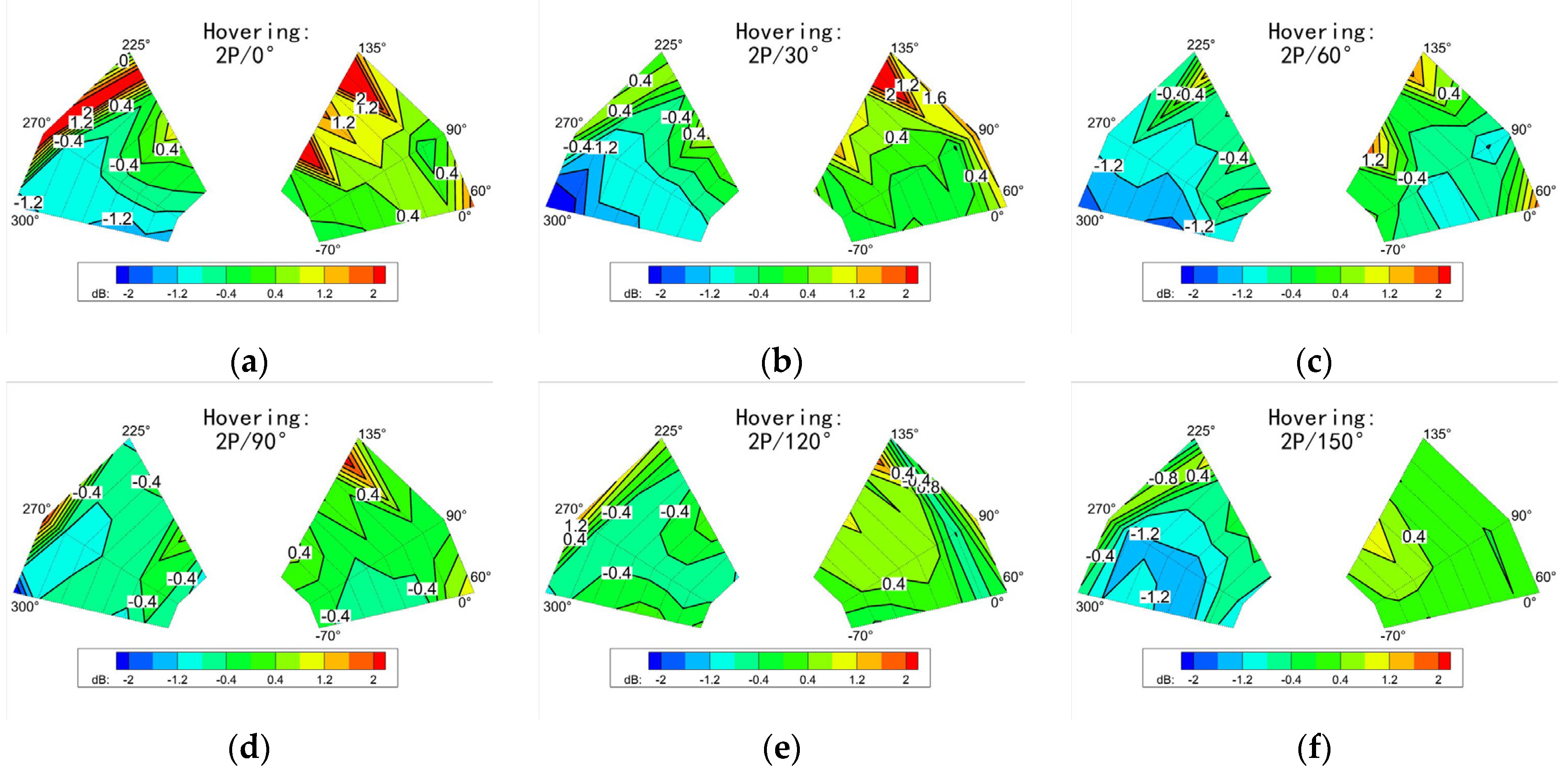
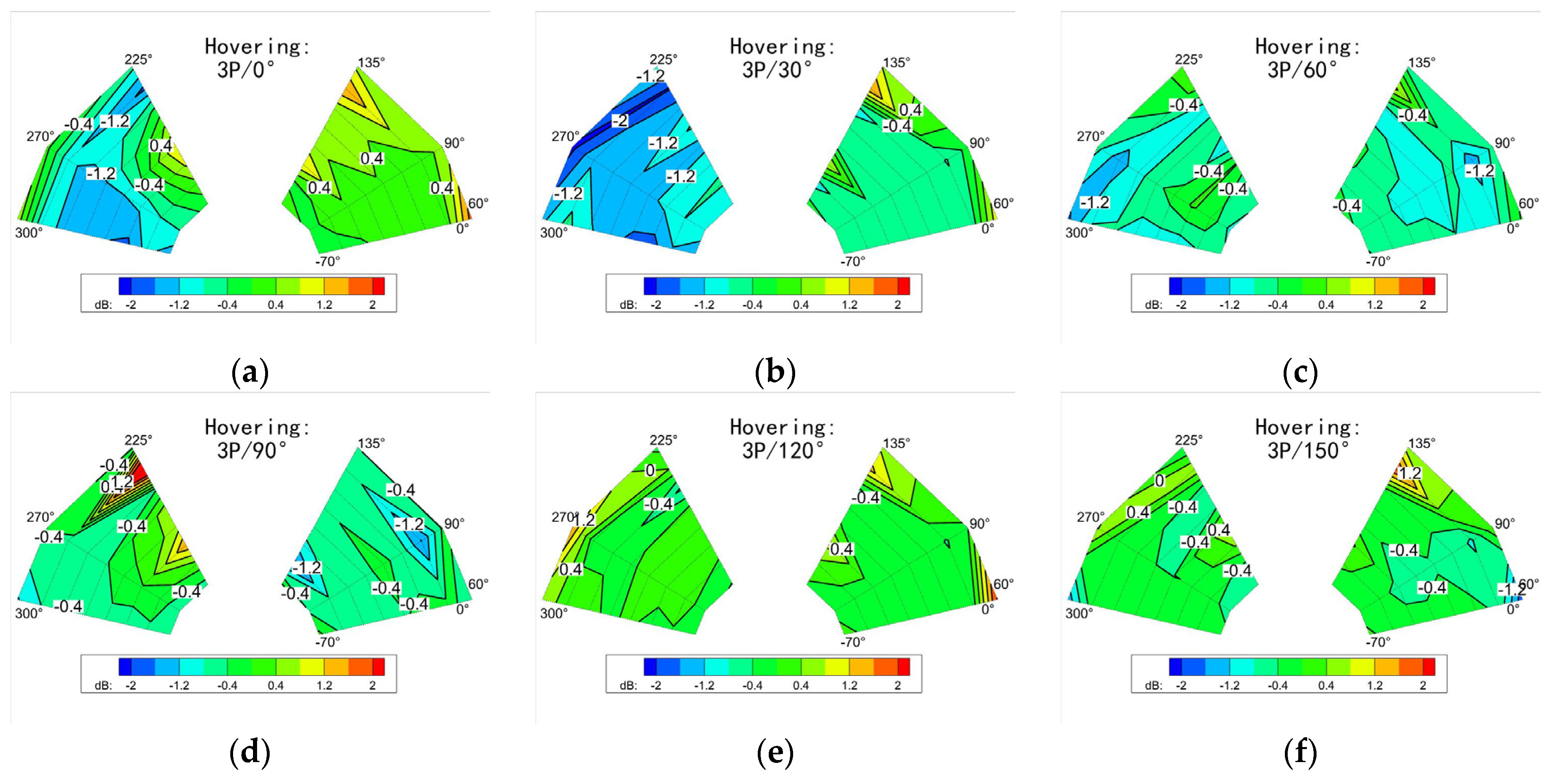
3.1.1. Hover Flight
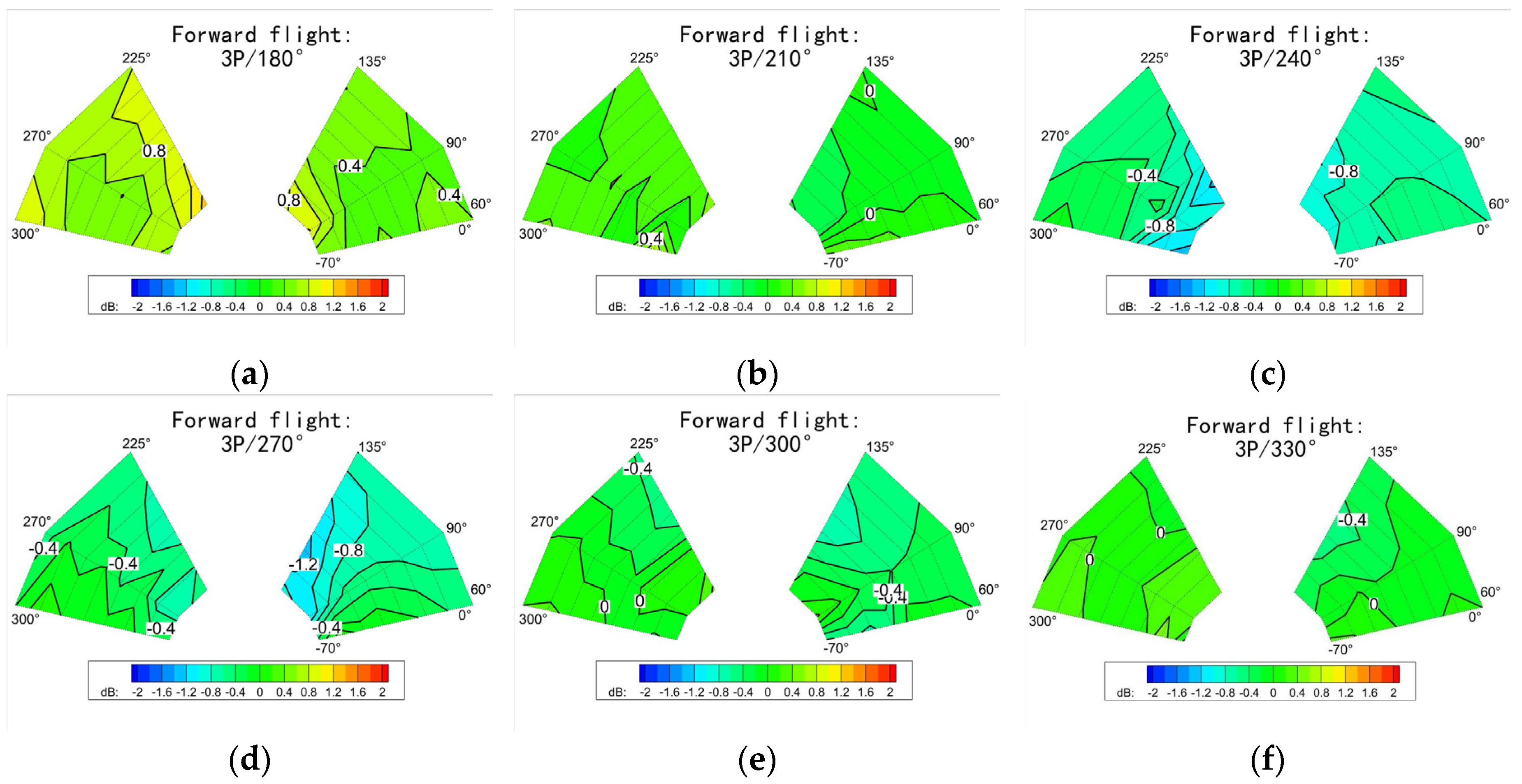
3.1.2. Forward Flight
3.1.3. Oblique Descent
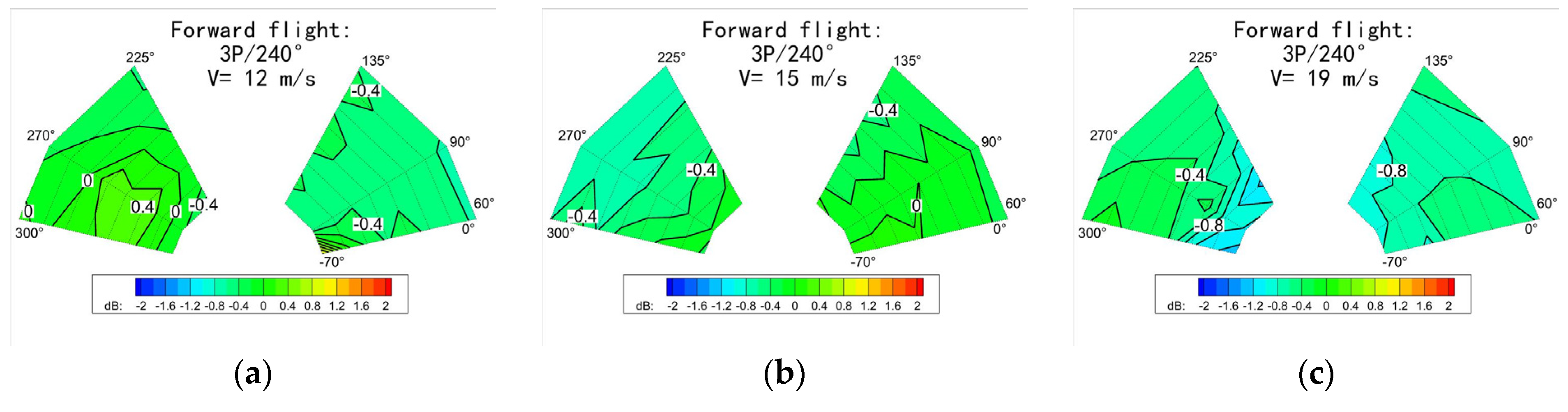
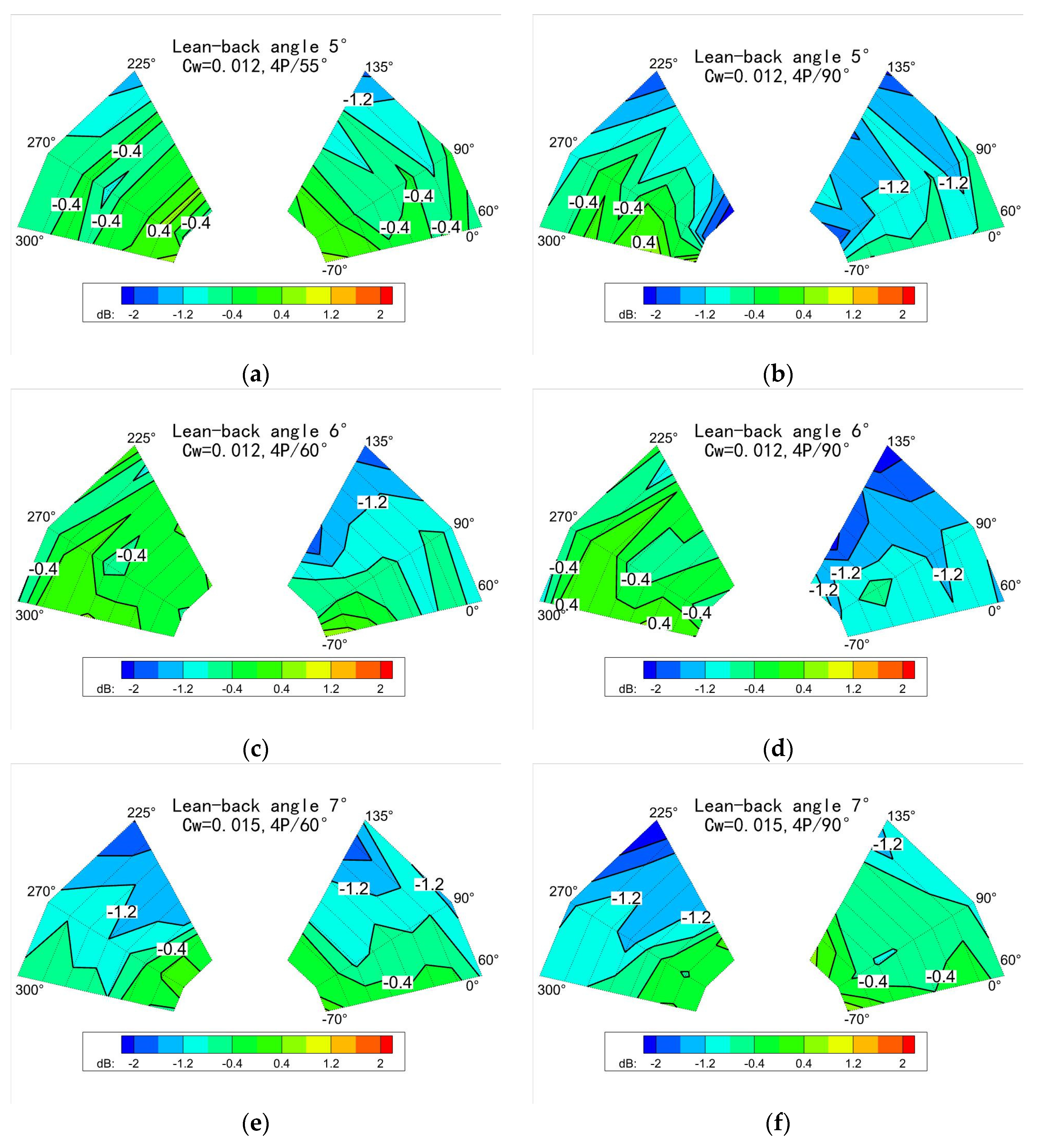
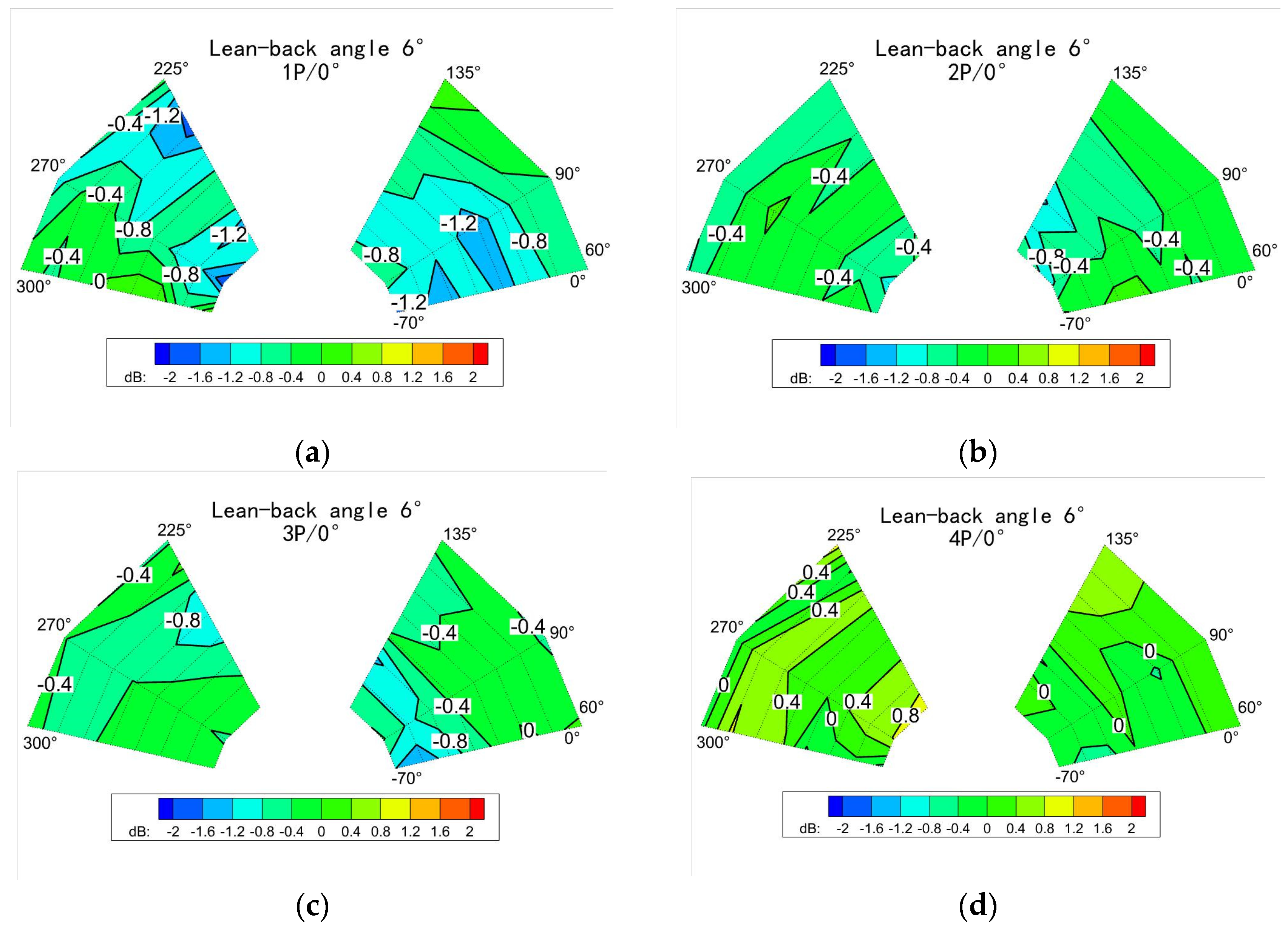
3.2. The Influence of the Control Law
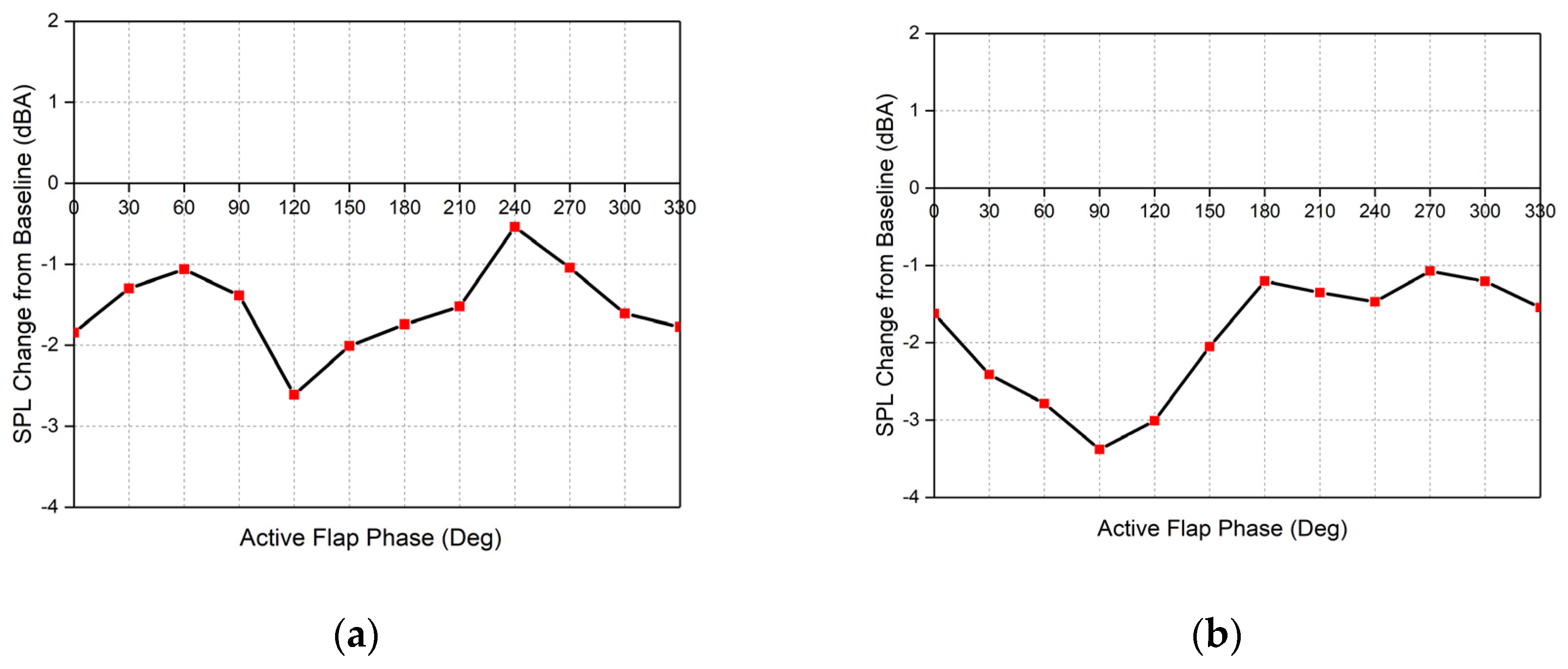
3.2.1. Frequency
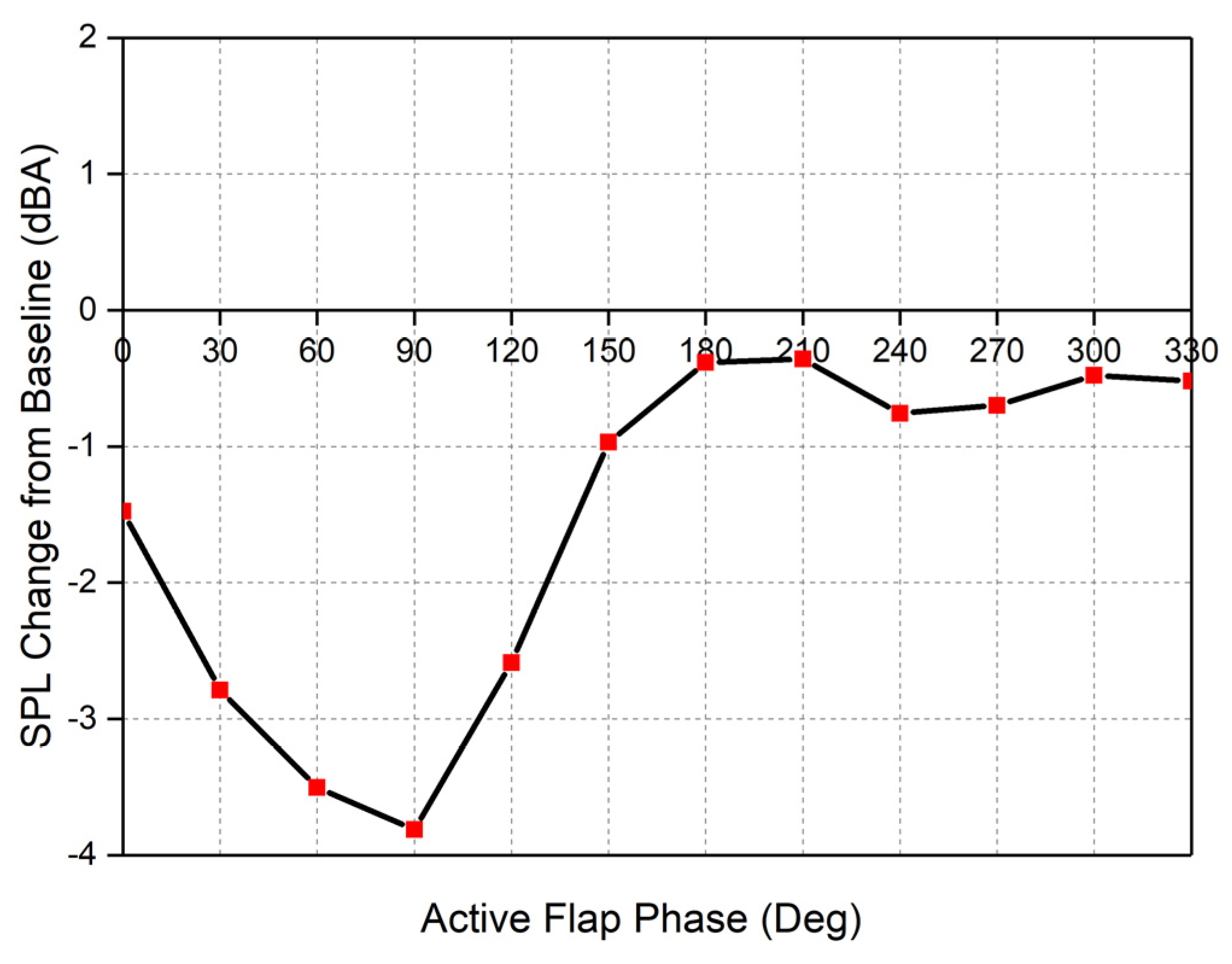
3.2.2. Combination of Frequency and Phase
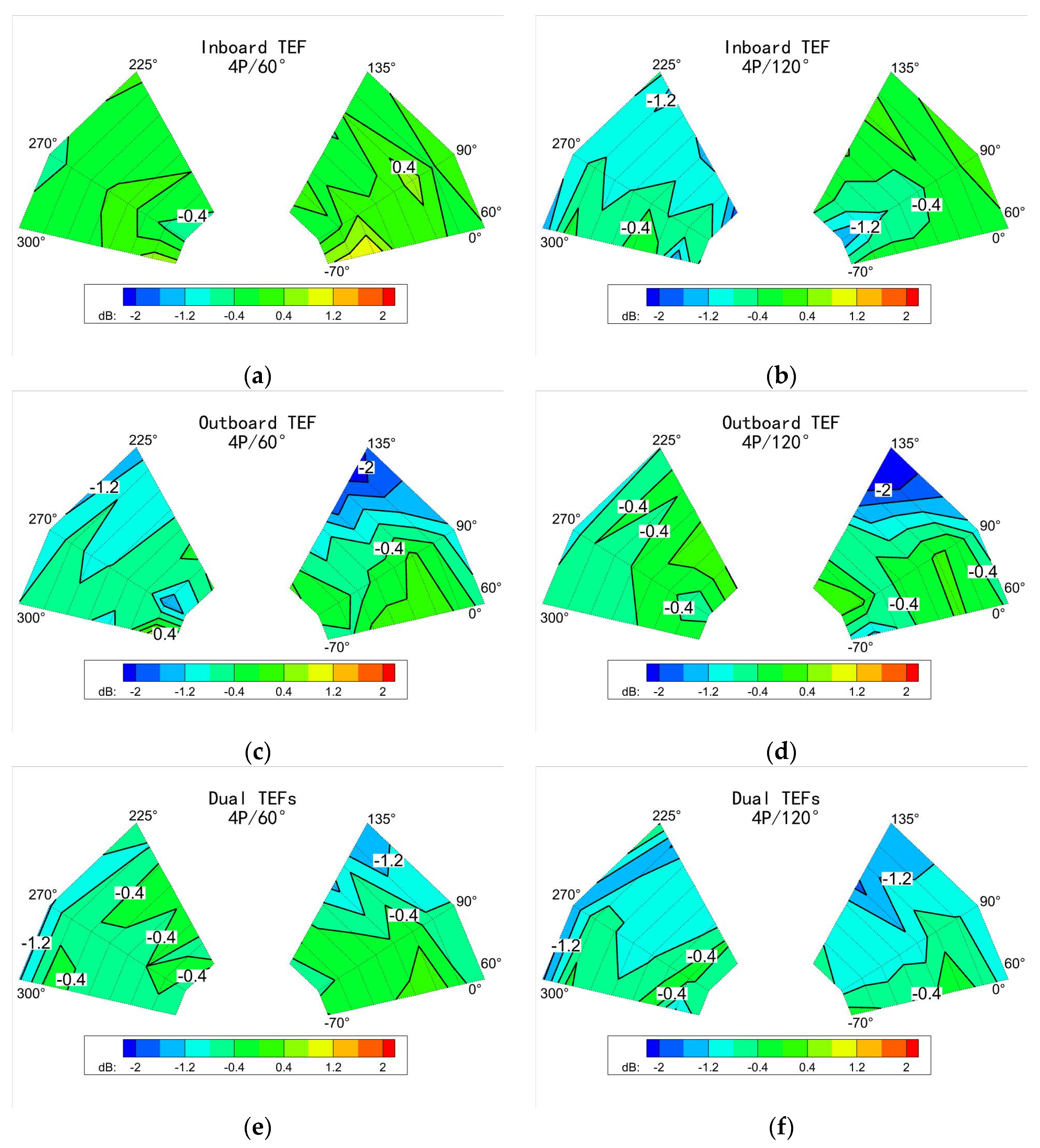
3.3. The Influence of Single/Dual-TEF Control
3.4. The Influence of Noise Statistical Period
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- George, A.R. Helicopter Noise: State-of-the-Art. J. Aircr. 1978, 15, 707–715. [Google Scholar] [CrossRef]
- Yung, H.Y. Rotor Blade–Vortex Interaction Noise. Prog. Aerosp. Sci. 2000, 36, 97–115. [Google Scholar]
- Baeder, J.D.; Gallman, J.M.; Yu, Y.H. A Computational Study of the Aeroacoustics of Rotors in Hover. J. Am. Helicopter Soc. 1997, 42, 39–53. [Google Scholar] [CrossRef]
- Hares, H.; Mebarki, G.; Brioua, M.; Naoun, M. Aerodynamic Performances Improvement of Naca 4415 Profile by Passive Flow Control Using Vortex Generators. J. Serb. Soc. Comput. Mech. 2019, 13, 17–38. [Google Scholar] [CrossRef]
- van der Wall, B.G.; Kessler, C.; Delrieux, Y.; Beaumier, P.; Gervais, M.; Hirsch, J.F.; Pengel, K.; Crozier, P. From Erato Basic Research to the Blue Edge Rotor Blade. In Proceedings of the AHS 72nd Annual Forum, West Palm Beach, FL, USA, 17–19 May 2016; American Helicopter Society, Inc. [Google Scholar]
- Buck, S.; Oerlemans, S.; Hernandez Mascarell, O.; Joseph, P.; Alexander, W.N.; Letica, S. Active Control of Trailing Edge Noise. In Proceedings of the Aiaa Aviation 2021 Forum, Online, 2–6 August 2021. [Google Scholar]
- Kessler, C. Active Rotor Control for Helicopters: Individual Blade Control and Swashplateless Rotor Designs. CEAS Aeronautical J. 2011, 1, 23–54. [Google Scholar] [CrossRef]
- Milgram, J.; Chopra, I.; Straub, F. Rotors with Trailing Edge Flaps: Analysis and Comparison with Experimental Data. J. Am. Helicopter Soc. 1998, 43, 319–332. [Google Scholar] [CrossRef]
- Millott, T.A.; Friedmann, P.P. Vibration Reduction in Helicopter Rotors Using an Actively Controlled Partial Span Trailing Edge Flap Located on the Blade; NASA: Washington, DC, USA, 1994.
- Liu, L.; Friedmann, P.P.; Kim, I.; Bernstein, D.S. Rotor Performance Enhancement and Vibration Reduction in Presence of Dynamic Stall Using Actively Controlled Flaps. J. Am. Helicopter Soc. 2008, 53, 338–350. [Google Scholar] [CrossRef]
- Sim, B.W.; JanakiRam, R.D.; Lau, B.H. Reduced in-Plane, Low-Frequency Noise of an Active Flap Rotor. J. Am. Helicopter Soc. 2014, 59, 1–17. [Google Scholar] [CrossRef]
- Aoyama, T.; Yang, C.; Kondo, N.; Saito, S. Comparison of Noise Reduction Effect between Afc and Conventional Ibc by Moving Overlapped Grid Method. In Proceedings of the 12th AIAA/CEAS Aeroacoustics Conference (27th AIAA Aeroacoustics Conference), Cambridge, MA, USA, 8–10 May 2006. [Google Scholar]
- Su, T.; Lu, Y.; Ma, J.; Guan, S. Aerodynamic Characteristics Analysis of Electrically Controlled Rotor Based on Viscous Vortex Particle Method. Aerosp. Sci. Technol. 2020, 97, 105645. [Google Scholar] [CrossRef]
- Zhou, Z.X.; Huang, X.C.; Tian, J.J.; Hua, H.X.; Tang, M.; Wang, C. Numerical and Experimental Analysis on the Helicopter Rotor Dynamic Load Controlled by the Actively Trailing Edge Flap. Smart Mater. Struct. 2022, 31, 35023. [Google Scholar] [CrossRef]
- Yung, H.Y.; Gmelin, B.; Splettstoesser, W.; Philippe, J.J.; Prieur, J.; Brooks, T.F. Reduction of Helicopter Blade-Vortex Interaction Noise by Active Rotor Control Technology. Prog. Aerosp. Sci. 1997, 33, 647–687. [Google Scholar]
- Noboru, K.; Saito, S.; Fuse, H. A Study of Closed Loop Control for Bvi Noise Reduction by Multiple Pressure Sensors. In Proceedings of the 33rd European Rotorcraft Forum, Kazan, Russia, 11–13 September 2007; pp. 2315–2356. [Google Scholar]
- Ma, J.; Lu, Y.; Su, T.; Guan, S. Experimental Research of Active Vibration and Noise Control of Electrically Controlled Rotor. Chin. J. Aeronaut. 2021, 34, 106–118. [Google Scholar]
- DeSalvo, M.; Whalen, E.; Glezer, A. High-Lift Performance Enhancement Using Active Flow Control. AIAA J. 2020, 58, 4228–4242. [Google Scholar] [CrossRef]
- Ma, Y.Y.; Zhao, Q.J.; Zhao, G.Q. New Combinational Active Control Strategy for Improving Aerodynamic Characteristics of Airfoil and Rotor. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 234, 977–996. [Google Scholar] [CrossRef]
- Zhou, J.; Dong, L.; Yang, W. Experimental Study on Transfer Functions of an Active Rotor under Different Flight Conditions. Chin. J. Aeronaut. 2022, 35, 107–120. [Google Scholar]
- Konstanzer, P.; Enenkl, B.; Aubourg, P.; Cranga, P. Recent Advances in Eurocopter’s Passive and Active Vibration Control. In Proceedings of the AHS 64th Annual Forum, Montréal, QC, Canada, 29 April–1 May 2008; American Helicopter Society, Inc. [Google Scholar]
- Woods, B.; Bubert, E.; Kothera, C.; Sirohi, J.; Wereley, N. Experimental Testing of Pneumatic Artificial Muscles for Trailing Edge Flap Actuation. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007. [Google Scholar]
- Altmikus, A.; Dummel, A.; Heger, R.; Schimke, D. Actively Controlled Rotor: Aerodynamic and Acoustic Benefit for the Helicopter Today and Tomorrow. In Proceedings of the 34th European Rotorcraft Forum, Liverpool, UK, 16–19 September 2008. [Google Scholar]
- Lau, B.H.; Straub, F.; Anand, V.R.; Birchette, T. Smart Rotor Development and Wind-Tunnel Test. In Proceedings of the 35th European Rotorcraft Forum, Hamburg, Germany, 22–25 September 2009. [Google Scholar]
- Bartholomay, S.; Wester, T.T.; Perez-Becker, S.; Konze, S.; Menzel, C.; Hölling, M.; Spickenheuer, A.; Peinke, J.; Nayeri, C.N.; Paschereit, C.O.; et al. Pressure-Based Lift Estimation and Its Application to Feedforward Load Control Employing Trailing-Edge Flaps. Wind. Energy Sci. 2021, 6, 221–245. [Google Scholar] [CrossRef]
- Nakao, M.; Uchiyama, N.; Yoshimoto, M.; Saito, S.; Kondo, N. Research for the Bvi Noise Reduction Using the Blade Active Control. In Proceedings of the 30th European Rotorcraft Forum, Marseille, France, 2014. [Google Scholar]
- Kody, F.; Corle, E.; Maughmer, M.D.; Schmitz, S. Higher-Harmonic Deployment of Trailing-Edge Flaps for Rotor-Performance Enhancement and Vibration Reduction. J. Aircr. 2016, 53, 333–342. [Google Scholar] [CrossRef]
- Padthe, A.K.; Friedmann, P.P. Simultaneous Blade–Vortex Interaction Noise and Vibration Reduction in Rotorcraft Using Microflaps, Including the Effect of Actuator Saturation. J. Am. Helicopter Soc. 2015, 60, 1–16. [Google Scholar] [CrossRef]
- Hu, Z.; Xu, G.; Shi, Y. A Robust Overset Assembly Method for Multiple Overlapping Bodies. Int. J. Numer. Methods Fluids 2020, 93, 653–682. [Google Scholar] [CrossRef]
- Xia, R.; Shi, Y.; Li, T.; Xu, G. Numerical Study of the Rotor Thickness Noise Reduction Based on the Concept of Sound Field Cancellation. Chin. J. Aeronaut. 2022, 35, 214–233. [Google Scholar]
- Zhou, J.; Dong, L.; Yang, W. A Double-Acting Piezoelectric Actuator for Helicopter Active Rotor. Actuators 2021, 10, 247. [Google Scholar] [CrossRef]
- Shi, Y.; Li, T.; He, X.; Dong, L.; Xu, G. Helicopter Rotor Thickness Noise Control Using Unsteady Force Excitation. Appl. Sci. 2019, 9, 1351. [Google Scholar] [CrossRef]
- Farassat, F. Derivation of Formulations 1 and 1a of Farassat; The NASA Scientific and Technical Information: Washington, DC, USA, 2007; p. 20.
- Shi, Y.J.; Zhao, Q.J.; Xu, G.H. An Analytical Study of Parametric Effects on Rotor—Vortex Interaction Noise. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2011, 225, 259–268. [Google Scholar] [CrossRef]
- Viswamurthy, S.; Ranjan, G. Effect of Piezoelectric Hysterisis Nonlinearity on Helicopter Vibration Control Using Trailing Edge Flaps. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Austin, TX, USA, 18–21 April 2005. [Google Scholar]
- Houser, D.S.; Yost, W.; Burkard, R.; Finneran, J.J.; Reichmuth, C.; Mulsow, J. Review of the History, Development and Application of Auditory Weighting Functions in Humans and Marine Mammals. J. Acoust Soc. Am. 2017, 141, 1371. [Google Scholar] [CrossRef] [PubMed]
- Atia, A.E.; Williams, A.E. Narrow-Bandpass Waveguide Filters. IEEE Trans. Microw. Theory Tech. 1972, 20, 258–265. [Google Scholar] [CrossRef]
- Prieur, J.; Rahier, G. Comparison of Ffowcs Williams-Hawkings and Kirchhoff Rotor Noise Calculations. In Proceedings of the 4th AIAA/CEAS Aeroacoustics Conference, Toulouse, France, 2–4 June 1998. [Google Scholar]


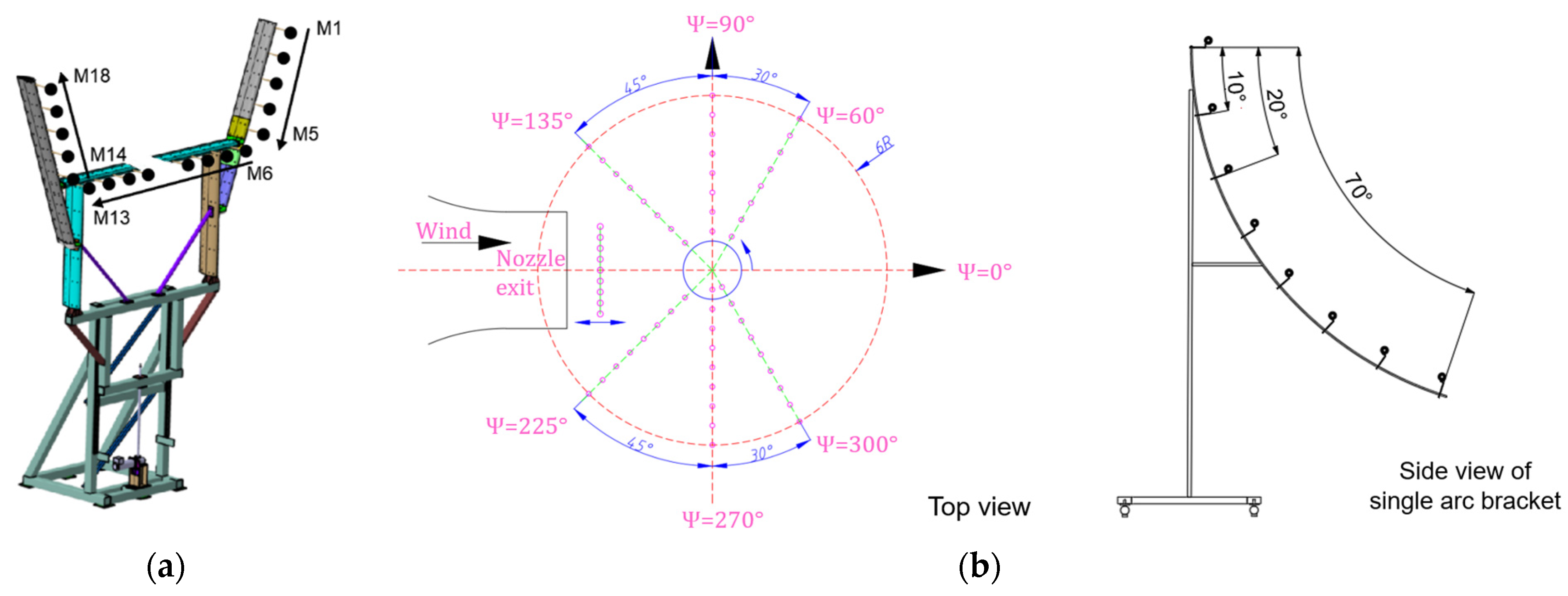

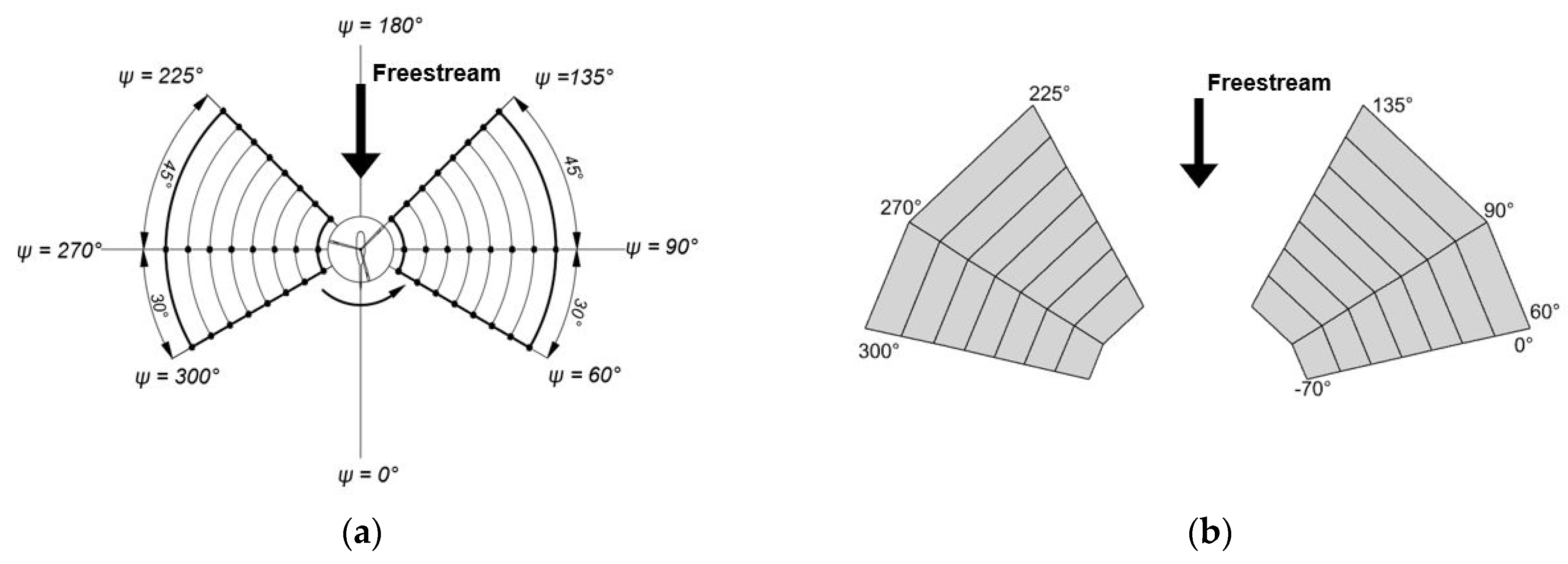



| Rotor | |
|---|---|
| Hub type | hingeless |
| Rotor radius, R | 1.5 m |
| Blade chord length, c | 0.13 m |
| Airfoil | OA312 |
| Tip Taper | 1:3, from 0.941R |
| Twist | 10° at 0.25R, −2° at 0.933R |
| Solidity | 0.1013 |
| Rotation speed | 808 rpm |
| Collective range | 0~15° |
| Lateral cyclic range | −10~10° |
| Long cyclic range | −10~10° |
| TEFs | |
| Chord length | 0.154c |
| Span length | 0.1R |
| Mid-span locations | Inboard: 0.737R Outboard: 0.85R |
| Frequency | 0~4 rev |
| Amplitude | 0~5.5° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Liu, Y.; Shi, Y.; Xu, G. An Experimental Study on Rotor Aerodynamic Noise Control Based on Active Flap Control. Aerospace 2023, 10, 121. https://doi.org/10.3390/aerospace10020121
Hu Z, Liu Y, Shi Y, Xu G. An Experimental Study on Rotor Aerodynamic Noise Control Based on Active Flap Control. Aerospace. 2023; 10(2):121. https://doi.org/10.3390/aerospace10020121
Chicago/Turabian StyleHu, Zhiyuan, Yang Liu, Yongjie Shi, and Guohua Xu. 2023. "An Experimental Study on Rotor Aerodynamic Noise Control Based on Active Flap Control" Aerospace 10, no. 2: 121. https://doi.org/10.3390/aerospace10020121
APA StyleHu, Z., Liu, Y., Shi, Y., & Xu, G. (2023). An Experimental Study on Rotor Aerodynamic Noise Control Based on Active Flap Control. Aerospace, 10(2), 121. https://doi.org/10.3390/aerospace10020121







