Abstract
In this paper, a novel flow perturbation model meant to investigate the effects of incoming wind shear on a hypersonic inlet/isolator is presented. This research focuses on the transient shock/boundary layer interaction and shock train flow evolution in a hypersonic inlet/isolator with an on-design Mach number of 6.0 under incoming wind shear at high altitudes, precisely at an altitude of 30 km with a magnitude speed of 80 m/s. Despite the low intensity of wind shear at high altitudes, the results reveal that wind shear significantly disrupts the inlet/isolator flowfield, affecting the shock wave/boundary layer interaction in the unthrottled state, which drives the separation bubble at the throat to move downstream and then upstream. Moreover, the flowfield behaves as a hysteresis phenomenon under the effect of wind shear, and the total pressure recovery coefficients at the throat and exit of the inlet/isolator increase by approximately 10% to 12%. Furthermore, this research focuses on investigating the impact of wind shear on the behavior of the shock train. Once the inlet/isolator is in a throttled state, wind shear severely impacts the motion of the shock train. When the downstream backpressure is 135 times the incoming pressure (p0), the shock train first moves upstream and gradually couples with a cowl shock wave/boundary layer interaction, resulting in a more significant separation at the throat, and then moves downstream and decouples from the separation bubble at the throat. However, if the downstream backpressure increases to 140 p0, the shock train enlarges the separation bubble, forcing the inlet/isolator to fall into the unstart state, and it cannot be restarted. These findings emphasize the need to consider wind shear effects in the design and operation of hypersonic inlet/isolator.
1. Introduction
The hypersonic inlet/isolator, an essential component of the scramjet engine, plays a significant role in the stable and safe operation of aircraft [1,2,3,4,5,6,7]. During flights, because of the complex wind field environment [8,9,10,11], aircraft frequently encounter atmospheric disturbances, such as gusts, wind shear, three-dimensional wind, vortices, and continuous turbulence. While vortex and gust disturbances are common at low altitudes, hypersonic vehicles typically operate at high altitudes exceeding 20 km, where the impact of gusts is negligible. The primary wind perturbation at these altitudes is wind shear, changes in the wind vector (wind direction and wind speed) in the horizontal and/or vertical directions [12,13]. When an aircraft encounters wind shear, it experiences temporary changes in flight attitude, which may subsequently alter the internal flow characteristics of the hypersonic inlet, including historical effects and hysteresis phenomena.
Presently, most studies on the impact of wind field disturbances on inlet/isolators concentrate predominantly on low-altitude disturbances, including gusts and wind shear. Kozakiewicz et al. analyzed the influence of changes in gust speed and direction on the development of vortices in the pitot subsonic inlet of an F-16, finding that gusts could potentially result in compressor stalls and unstable engine operations [14]. Wu et al. performed a simulation study on the flowfield and aerodynamic responses of a serpentine inlet exposed to non-stationary horizontal sinusoidal gusts and found that the gusts not only significantly change the flow structure but also play an unfavorable role in the total pressure distortion of the serpentine inlet [15]. Hussei et al. focused on the impact of side gusts (with an intensity of 56 m/s) on the supersonic inlet and discovered that they significantly affect the shock wave and airflow characteristics within the inlet, potentially leading to unstable flow phenomena such as shock wave oscillation [16]. Etkin et al. proposed a wind shear model and analyzed the flight characteristics of an aircraft in wind shear conditions [17,18,19]. Xie et al. developed a dynamic model of an aircraft to simulate the impact of wind fields on its flight state, considering atmospheric disturbances, discontinuous gusts, and wind shear and specifically examined parameters such as angle of attack, sideslip angle, aerodynamic force, and aerodynamic moment [20]. Zhao conducted research on the effect of high-altitude wind shear on the flight of a rocket and found that wind shear significantly increased the wind attack angle [21]. Based on results from Zhao et al. [21], Yang et al. developed a wind shear model at an altitude ranging from 20 km to 78 km and obtained changes in the angle of attack regarding aircraft affected by wind shear [22].
While most current studies focus on the effect of low-altitude wind shear on low-speed aircraft, wind shear also exists when hypersonic vehicles fly at high altitudes. To be exact, the magnitudes of wind shear in the near space (altitude > 20 km) are in the order of O(~100 m/s) with a time scale in the order of O(~100 ms) [22]. The equivalent angle of attack can be as high as 3 degrees for a hypersonic vehicle operating at Mach 6, and the time scale is so short that it induces flow response problems. Thus, it is essential to further study the effect of wind shear perturbation on the flowfield and performance of hypersonic inlet/isolators. This paper is organized as follows: Section 2 introduces the wind shear perturbation model and the hypersonic inlet/isolator model. Section 3 delineates the details of the numerical simulation setup and validates the reliability of the simulation method. Based on this, Section 4 provides a detailed discussion on the transient flow evolution of shock wave/boundary layer interaction and shock train under wind shear. Finally, Section 5 discusses the key results obtained from the current study.
2. Introduction of the Hypersonic Inlet/Isolator and the Wind Shear Model
2.1. Description of the Hypersonic Inlet/Isolator
In this study, a mixed-compression hypersonic inlet/isolator with a capture height, ycowl, of 334.11 mm for a design Mach number of 6.0 is described. The external compression system contains an oblique shock with a deflection angle of 8.73 degrees and a series of compression waves to decelerate the incoming hypersonic flow with minimal total pressure loss. In essence, this is a design methodology for the hypersonic inlet/isolator that emphasizes high compression efficiency. Throughout the entire compression process, the entropy of the main flow outside the boundary layer remains constant. The throat has a minimum flow area of Hth = 53 mm. The isolator has an expansion angle of 0.2 degrees and the value of Liso = 15.1Hth. The main geometrical parameters of the inlet/isolator model are listed in Table 1. Note that the coordinate origin is set at the leading point of the ramp. The X-axis and Y-axis are shown in Figure 1.

Table 1.
Model design parameters.
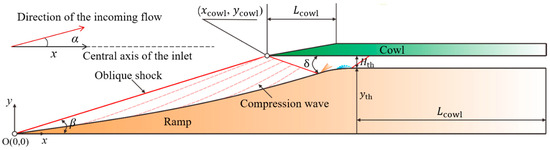
Figure 1.
Inlet/isolator model.
2.2. Model for the Wind Shear
Zhao et al. [21] proposed a statistical analysis method for high-altitude wind fields. They concluded that the primary impact of wind shear on rocket aircraft is a large angle of attack induced by wind. Based on Zhao et al.’s statistical method, Yang [22] proposed a wind shear model for near space (20–78 km) based on five-year wind field data (2009 to 2013) from the Modern-Era Retrospective Analysis for Research and Applications (MERRA) [23]. The results demonstrated that the primary impact of wind shear on aircraft is the angle of attack induced by the wind. The intensity of wind shear varies from month to month, with the largest wind shear intensity in January. Taking 30 km as an example, the magnitude speed of wind shear in January is 80 m/s, and the angle of attack can change by up to 2.65 degrees when the aircraft flies at Mach 6. Based on this, the variation in the angle of attack (α) due to wind shear over time (t) in January is shown by Equation (1), drawn in the form of a normal distribution, with the change plotted in Figure 2.
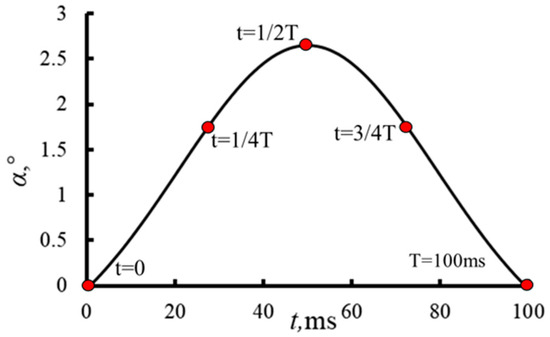
Figure 2.
Distribution of wind angle of attack, α.
3. Numerical Method
This section discusses the numerical method, which includes the governing equations, the turbulence model, the boundary conditions, and the computational grid.
3.1. Computational Method
All the calculations are performed by the commercial computational fluid dynamics (CFD) software ANSYS FLUENT 18.0. It has demonstrated robust applicability in subsonic, supersonic, and hypersonic flow simulations, particularly in research related to hypersonic inlets, and been widely used by researchers globally.
Computational fluid dynamics (CFD) methods used to predict hypersonic flows include Reynolds-Averaged Navier–Stokes (RANS), Large Eddy Simulations (LES), Direct Numerical Simulation (DNS), etc. RANS demonstrates good accuracy in predicting macroscopic flows and strongly separated flows, but it has not consistently been accurate in capturing small-scale turbulence and predicting aerothermodynamic loading over the surface of hypersonic vehicles [24]. On the other hand, LES is suitable for capturing small-scale vortices, but it requires a large number of grids and has a lengthy computation cycle for unsteady simulation calculations [25]. DES is a suitable method for a genuinely time-dependent problem, but the accuracy is very dependent on the number of grids [26]. DNS excels in predicting the laminar–turbulent transition of boundary layers, which is particularly relevant in research focusing on aerodynamic heating, drag, and vehicle operation [27]. In our paper, we mainly focus on macroscopic large-scale flow, such as the shock wave/boundary layer interaction, shock train, etc., which differs from vortices in the turbulent boundary layer. Since these flow structures result from the inertial and macroscopic motion of fluid, the RANS method was chosen for simulation given the requirements of computation and accuracy.
This study utilizes the k-ω SST turbulence model developed by Menter [28]. The control equation is discretized using an upwind scheme with second-order accuracy. Molecular viscosity is calculated using Sutherland’s formula. For the numerical calculation of the unsteady flowfield with dynamic changes in angle of attack, a steady flowfield was first calculated with an angle of attack of 0°, an incoming Mach number of 6, a static pressure of 1197 Pa, and a static temperature of 225.51 K. This served as the initial flowfield for unsteady numerical simulations. In these simulations, the dynamic changes in α are achieved using User-Defined Functions (UDFs), where the incoming flow conditions changed according to the wind shear model described in Equation (1). The time step for unsteady numerical simulations was set as 1 μs. The number of time intervals was determined by the period of the wind shear model, so the maximum number of iterations in each time interval was set to 250 steps.
3.2. Grid Generation
The model shown in Figure 1 was filled by hexahedral grids using the ICEM CFD software 21.0, as depicted in Figure 3. The grids are refined near the wall, ensuring a wall surface, y+, of less than or equal to one. Given the complexity of the flows at the lip and throat, the grid in these regions was also refined to clearly capture the shock waves and separation flow.
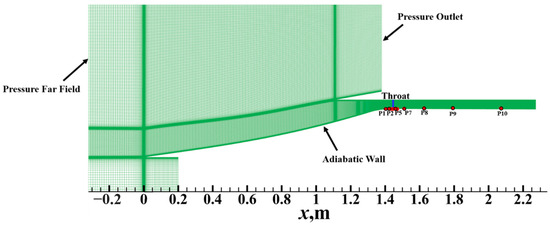
Figure 3.
Computational grid and domain.
3.3. Boundary Conditions
In the simulations, the pressure far-field boundary was applied for the incoming freestream, and the wall surface condition was set to a non-slip adiabatic wall. In addition, the wind shear model mentioned above was applied to the incoming direction and loaded using User-Defined Functions (UDFs). The pressure and temperature at the pressure far field were set to correspond to the atmospheric pressure and temperature, respectively, at an altitude of 30 km.
The static pressure outside the inlet/isolator, including the static pressure at the inlet/isolator exit, was designated as the far-field static pressure to achieve an unthrottled state. Table 2 shows the freestream conditions used in the simulations. To monitor the transient flow evolution of the hypersonic inlet/isolator, ten monitoring points, labeled P1–P10, were set during the simulation, as shown in Figure 3, and the positions are listed in Table 3.

Table 2.
Inlet/isolator data for the design conditions.

Table 3.
Position of the monitoring points.
3.4. Inlet/Isolator Performance Parameters
The inlet/isolator performance is characterized in terms of the following parameters:
- (1)
- The total pressure recovery coefficient (TPR) is the ratio of total pressure at the inlet/isolator exit (Pout*) to the freestream total pressure (P∞*). The total pressure loss is the sum of shock and viscous losses. The total pressure at the exit is calculated with the mass-weighted average.
- (2)
- The pressurization rate (PR) is one of the main indicators that characterize the compression characteristics of the inlet/isolator. It is defined as the ratio of inlet/isolator exit static pressure (Pout) to inlet/isolator static pressure (P∞). The static pressure at the exit is calculated with the mass-weighted average.
3.5. Validation of the Numerical Method and Grid Sensitivity
This paper primarily focuses on the shock system and the shock train phenomenon in the hypersonic inlet/isolator. Consequently, this section validates the numerical method. The ability of the numerical method employed in this study to capture shock waves and separation flow is validated by comparing numerical results with experimental results. In the experiment, a hypersonic inlet with an isolator under Mach 4.92 conditions was investigated. The flow region was filled with structured quadrilateral meshes, with the mesh refined near the wall. To more clearly capture the shock wave and separation structure of the duct, the mesh of the duct was further refined. The incoming flow conditions in the simulation are identical to the experimental conditions [29]. Figure 4 compares the numerical Schlieren images obtained with different turbulence models provided by FLUENT and experimental Schlieren images of the inlet/isolator. As shown in Figure 4, only the SST κ-ω can predict such large-scale separation precisely; therefore, the turbulence model is selected to model the turbulence flow in the inlet/isolator.
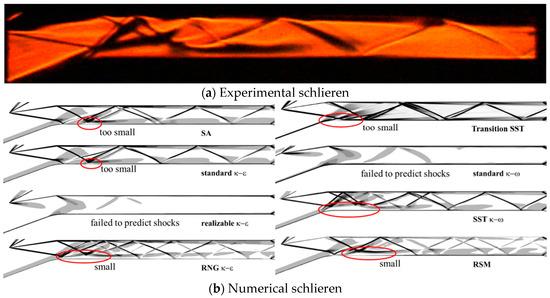
Figure 4.
Comparison of flow structures in the inlet and the isolator, where red circles indicate the separation zones.
The numerical flow structures, including the two cowl-induced shocks, the cowl-shocks/boundary layer interactions on the ramp, the reflected shocks, and the reattachment shocks in the isolator, are almost identical to the experimental results. Figure 5, furthermore, compares the numerical wall static pressure distributions with the experimental results. Generally, the numerical wall pressure values and the overall distribution pattern are in good agreement with the experimental results. Therefore, the numerical method introduced in this paper is suitable for the flow simulation of a hypersonic inlet/isolator.
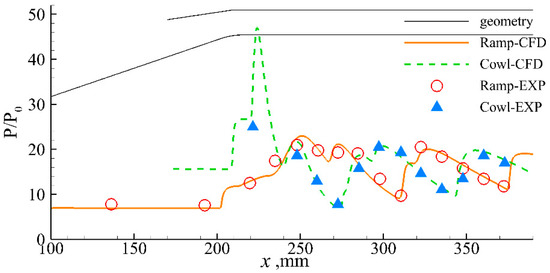
Figure 5.
Comparison of pressure distribution on walls.
To ascertain grid dependencies and determine the optimal mesh in the numerical simulation, two-dimensional structured grids of the inlet/isolator were generated with six different grid numbers: 60,000, 100,000, 120,000, 150,000, 170,000, and 200,000. The y+ distribution curves corresponding to different grids are shown in Figure 6, and it can be seen that the y+ values meet the requirement of the turbulence model [30]. Figure 7 shows the pressure distribution curves corresponding to different grids. After reaching a grid quantity of 150,000, noticeable changes in the positions of flow structures, such as separation and shock waves, can be observed compared with the coarser grid quantities. Figure 8 illustrates that, when the grid number is below 100,000, the separation bubble does not exhibit a triangular shape. Figure 9 compares the total pressure recovery (TPR) and pressurization rate (PR) results for the inlet/isolator with the six different grids. Only when the grid number exceeds 150,000 is the predicted shock wave structure insensitive to the grid number. While finer meshes require higher computational costs, the mesh with a grid number of 150,000 was selected for subsequent wind shear simulation calculations.
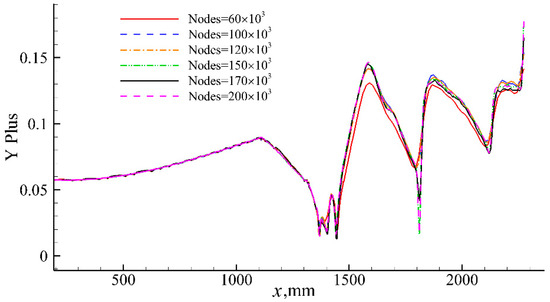
Figure 6.
y+ distribution with different grids.
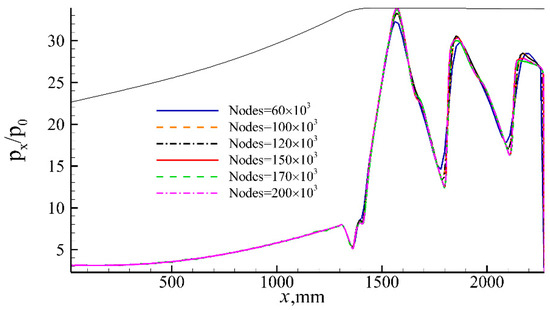
Figure 7.
Pressure distribution with different grids.
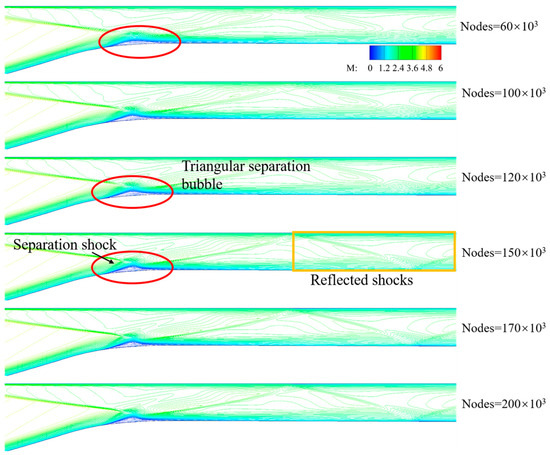
Figure 8.
Mach number contours with different grids.
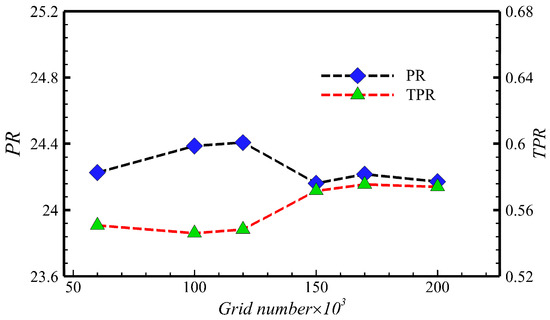
Figure 9.
Performance parameters with different grids.
3.6. Numerical Dissipation Verification
It is important to note the numerical dissipation and numerical viscosity at each time step in a simulation using a computational fluid dynamics (CFD) solver. In this section, a sufficiently long computational domain is established, as depicted in Figure 10, to verify whether numerical dissipation will reduce the perturbation in the simulation process. The wind shear in January is applied as an incoming perturbation.
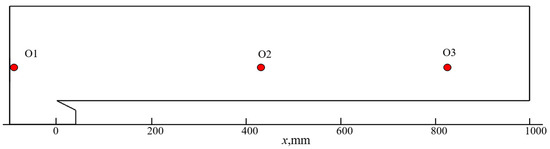
Figure 10.
Numerical dissipation verification model.
The perturbation model is introduced in Section 2, and the details are shown in Figure 3. The changes in the angle of attack, α, at three points located at different positions along the flow direction are monitored. As can be seen in Figure 11, the overall change in α remains constant along the flow direction, which indicates that the perturbation of the incoming flow is not dissipated, but there is a lag due to the propagation. Therefore, this unsteady numerical method proves to be feasible for this study.
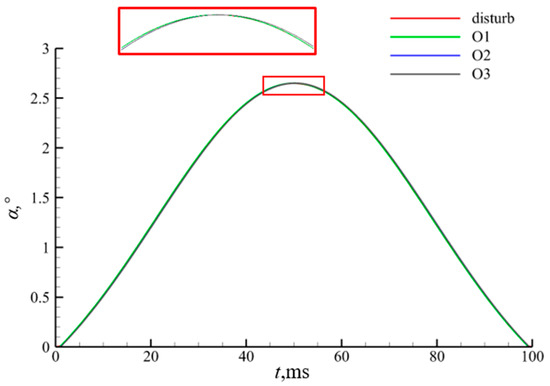
Figure 11.
Perturbation dissipation of the monitoring points.
4. Results and Discussion
4.1. Effect of Wind Shear on Hypersonic Inlet/Isolator under Unthrottled Conditions
In order to investigate the effect of wind shear on the inlet/isolator shock/boundary layer interference, an unsteady calculation of the inlet/isolator in the through flow state was conducted as a basis for the subsequent study of the shock train.
The Mach number contour of the inlet/isolator at t = 0 ms is shown in Figure 12. In the flowfield, it can be seen that the external compression system contains an oblique shock and a series of compression wave systems. The cowl shock separates the flow on the ramp surface. Because of the separation bubble, a separation shock forms and interacts with the reflected oblique shock. The separated flow re-attaches downstream, and a triangular separation bubble is formed. An expansion fan and a reattachment shock are also produced. Multiple shocks are reflected in the isolator, which corresponds to the pressure on the ramp in Figure 13. The Mach number contours near the throat, with incoming wind shear, are depicted in Figure 14, and it can be seen that the separation at the throat moves downstream and then upstream. From t = 0 ms to 50 ms, the strength of the compression wave system and the cowl shock decreases, as evidenced by the pressure on the ramp decreasing during this period in Figure 13. Although the intensity of the cowl shock decreases, the separation bubble at the throat grows as the reattachment point moves downstream. This might be due to the weakening effect of the shoulder expansion fan on the separation bubble as the impingement point of the cowl shock moves downstream [31,32]. Furthermore, as shown in Figure 15, the pressure at P2 changes the most because P2 is located near the reattachment shock. Hence, as the separation bubble moves, the pressure value of P2 changes significantly. The time scale of the wind shear is 100 ms, as shown in Figure 2, and the incoming flow of the inlet/isolator returns to the initial state at t = 100 ms. However, Figure 12 and Figure 13 reveal that the pressure distribution and separation at t = 100 ms differ from those at t = 0 ms, even though the incoming flow conditions at these two moments are identical. In particular, while the positions of the reattachment point and the peak vertex of the separation bubble change little, the separation point moves upstream at t = 100 ms. This could be because the hysteresis effect is more pronounced in low-velocity flows as the perturbation intensity recovers to zero. The inflection points of the pressure at the monitoring points vary at different moments and are delayed compared with the inflection point of the incoming flow perturbation. This observed phenomenon can be attributed to the presence of a hysteresis effect.
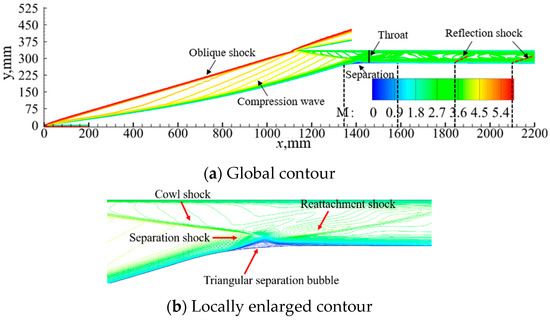
Figure 12.
Mach number contour of the inlet/isolator at t = 0 ms.
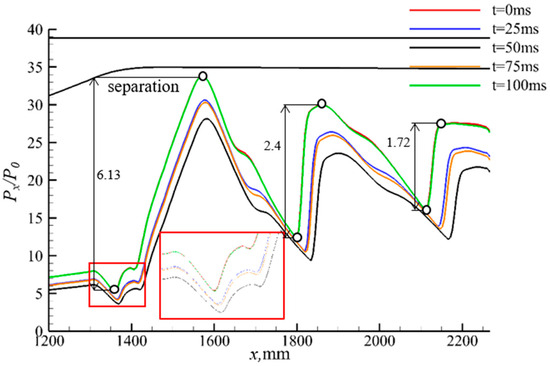
Figure 13.
The pressure distribution along the ramp at different moments.
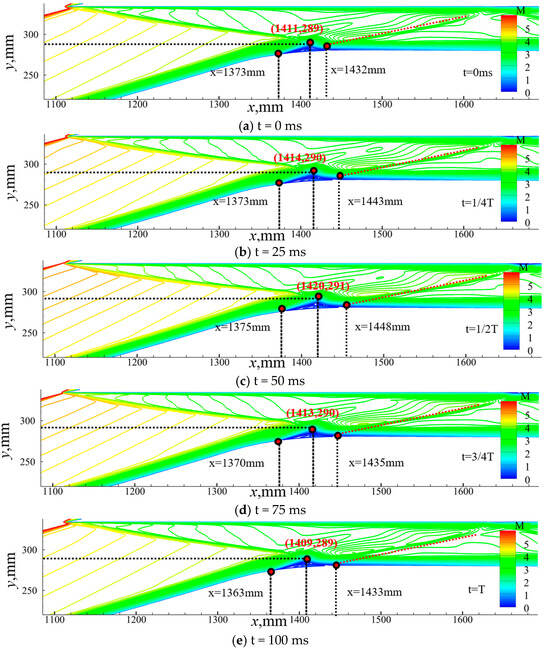
Figure 14.
Enlarged Mach number contours at different moments.
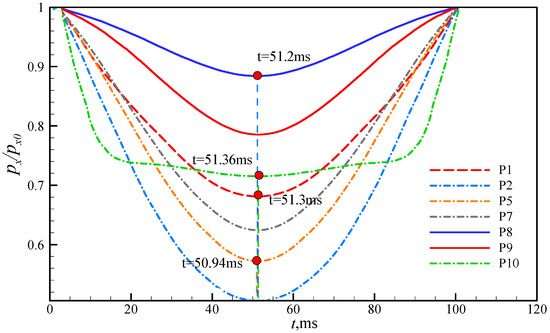
Figure 15.
Pressure variations in monitor points over time.
Figure 16 compares the changes in various parameters at the inlet/isolator throat with incoming wind shear, indicating a lag time of about 0.96 ms between results from the two of them. Figure 17 provides pressure variation at different heights of the throat, with the dotted lines indicating the times corresponding to the inflection points of the three pressure curves. The pressure variation of the monitored points near the upper and lower walls exceeds that of the mainstream. Moreover, the time corresponding to the inflection points is delayed by 0.96 ms, corroborating the lag time observed in Figure 16a. This is because the flow velocity in the boundary layer is slower than that of the mainstream, resulting in a slower perturbation propagation speed and a longer propagation time.
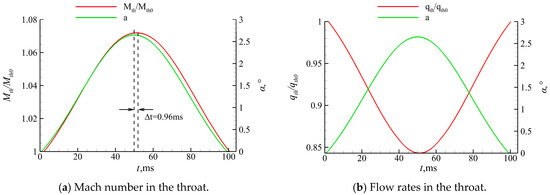
Figure 16.
Variations in Mach numbers and flow rates in the throat.
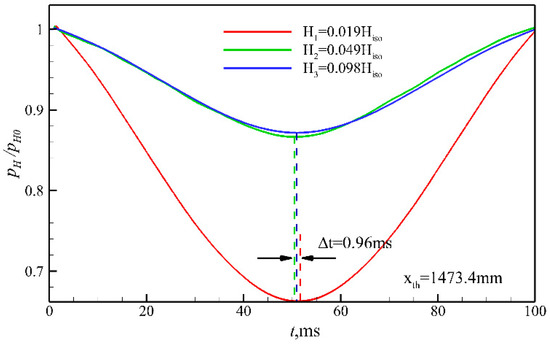
Figure 17.
Pressure changes at different heights of the throat.
Figure 18 illustrates the pressure of the throat along the y direction, indicating that the pressure decreases with y. In the pressure distribution, there are three characteristic points, i.e., CP1, CP2, and CP3. Based on the pressure contours in Figure 19, the three feature points can be analyzed in detail. From the wall to y = 330 mm, the pressure is almost constant, corresponding to the thickness of the boundary layer on the upper wall surface. The expansion wave originating from the shoulder leads to a pressure decrease as y decreases to about 315 mm. The first characteristic point (CP1) at y = 315 mm is due to the shock wave generated after the interaction between the cowl shock and the separation shock, causing the pressure to increase as y decreases. The second characteristic point (CP2) appears at y = 310 mm, which is due to the expansion wave resulting from the separation of the bubble, leading the pressure to decrease as y decreases. The third characteristic point (CP3) appears at y = 295 mm, where the pressure begins to increase because of the reattachment shock generated downstream of the separation bubble. From y = 290 mm to the wall, the pressure is almost constant, corresponding to the thickness of the boundary layer on the lower wall surface. In addition, as time passes, the y-value of the third feature point decreases significantly, which can also be observed from the Mach number contour at the shoulder in Figure 14. This is because the separation bubble gradually develops downstream over time, driving the reattachment shock to move downstream.
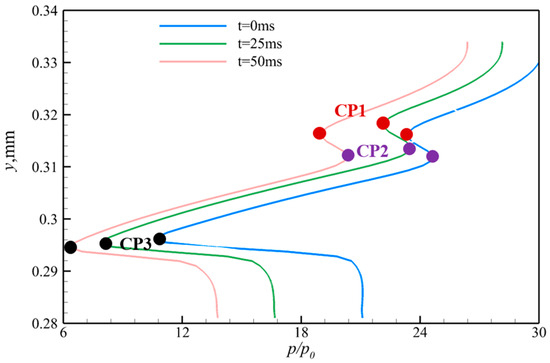
Figure 18.
Pressure distribution inside the throat area at different times.
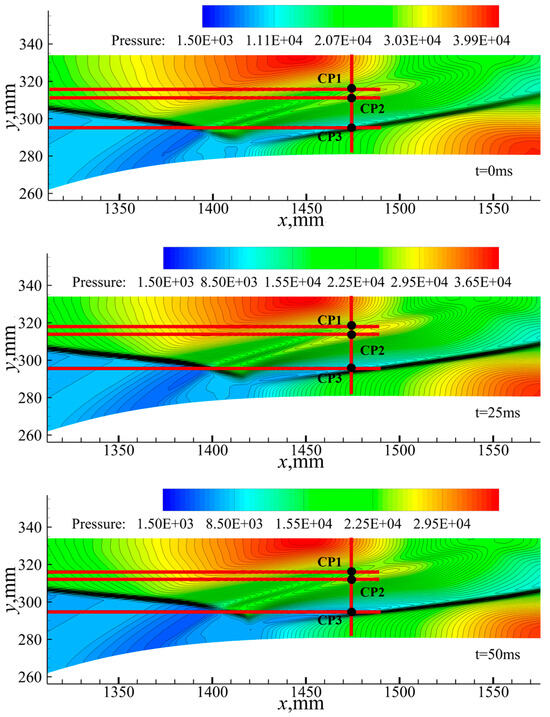
Figure 19.
Pressure contours at different moments.
It can be seen in Figure 20 that, under the influence of wind shear, the total pressure recovery coefficient of the inlet/isolator increases, which is mainly due to the weakening of the cowl shock. The total pressure recovery coefficient of the exit and throat change by about 11.5% and 10.7%. This indicates that the impact of wind shear on the inlet/isolator performance needs to be considered when a hypersonic inlet/isolator operates in near space.
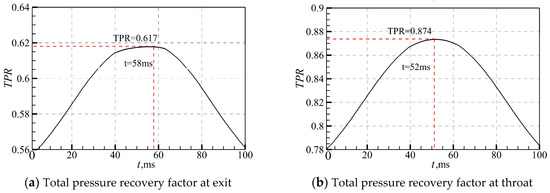
Figure 20.
Variations in the total pressure recovery factor.
4.2. Effect of Wind Shear on Shock Train
The inlet/isolator’s maximum sustainable backpressure is a crucial characteristic. Moreover, the throttling process often results in complex shock train phenomena [33,34,35]. For the inlet/isolator in this study, the maximum sustainable backpressure ratio is 195 times the incoming static pressure (p0) without wind shear. Once the backpressure exceeds this value, the shock train will be expelled out of the duct, and the inlet/isolator will fall into the unstart state. This section analyzes the impact of wind shear on the shock train under various throttling conditions.
When the backpressure is 135 p0, under incoming wind shear, the transient flowfield within the inlet/isolator is numerically analyzed. Figure 21 and Figure 22 present the Mach number and X-velocity contours of the inlet/isolator at different times. Wind shear induces the downstream shock train to continuously approach the throat, while the throat’s separation moves downstream. The reason is the compression strength of the external compression system decreases with wind shear. For the duct, the pressure at the entrance becomes smaller, while the exit remains unchanged, which eventually leads to the shock train being pushed upstream. At t = 45 ms, the lower wall separation zone of the shock train couples with the throat’s separation bubble. As the shock train moves upstream, the separation at the upper wall expands. This phenomenon happens because, as the shock train moves upstream, the shock causing separation changes from the right-running reflected shock to the left-running reflected shock [36].
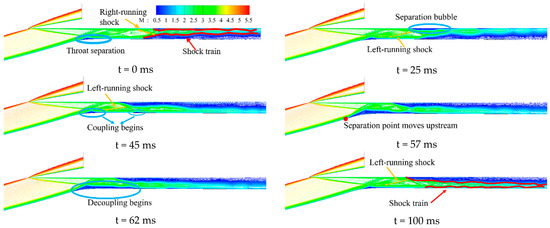
Figure 21.
Changes in Mach number contours.
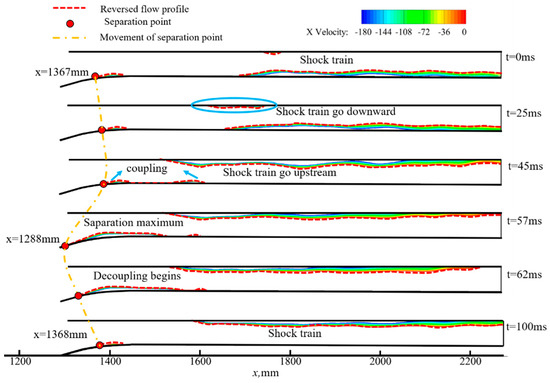
Figure 22.
Reversed flow in the inlet/isolator.
The change in the angle of attack induced by wind shear starts to decrease after t = 50 ms. The change in the angle of attack progressively recovers to 0°, the coupling separation bubble at the throat begins to decouple, and the shock train moves downstream. However, because of the hysteresis effect, it becomes evident that the shock train will not return to its initial state. Figure 23 illustrates the surface pressure distribution along the lower wall at different times. Figure 24 and Figure 25 show the distributions of the surface friction coefficient (Cf) along the upper and lower walls at different times. The pressure and Cf values both change significantly from x = 1300 mm, indicating that the cowl shock/boundary layer interaction changes. At t = 57 ms, the first rising point of the pressure is located at the furthest upstream position, as is the zero-value position of the Cf curve of the lower wall. As the separation at the throat at this moment is at maximum, which can be seen from the instantaneous Mach number contour, the separation begins further upstream than the expansion wave. In the region downstream of x = 1500 mm, the change in surface pressure is substantial, which is induced by the upstream movement of the shock train. Simultaneously, the direction of the friction drag of the upper and lower walls changes, as does the separation in the isolator on the upper wall, which is also reflected in the change in the exit Mach number distribution in Figure 26. This is because the shock train moves upstream and downward at the same time, suggesting that wind shear alters the reverse pressure gradient.
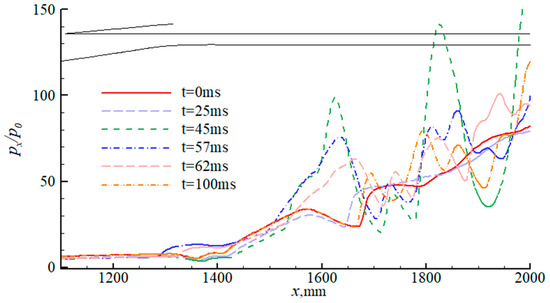
Figure 23.
Pressure changes along the lower wall.
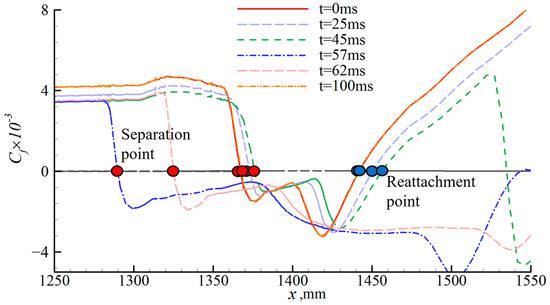
Figure 24.
Distribution of frictional resistance coefficients on the lower wall.
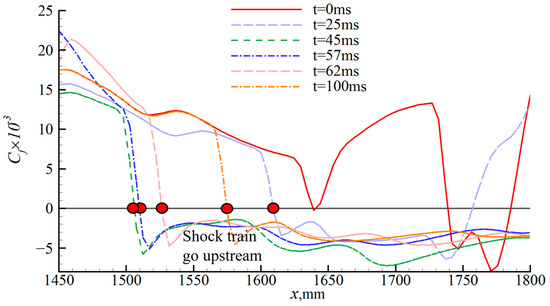
Figure 25.
Distribution of frictional resistance coefficients on the upper wall.
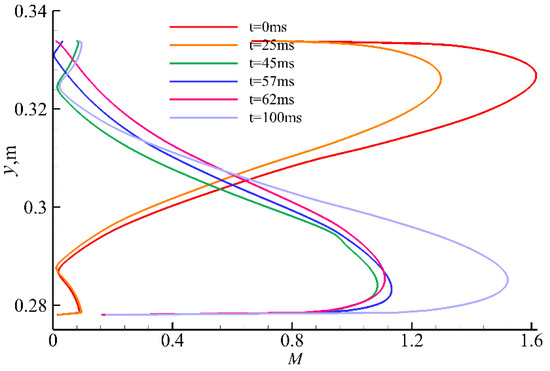
Figure 26.
Distribution of Mach numbers at the exit.
Figure 27 presents the Mach number contours of the inlet/isolator at different times when the downstream backpressure is 140 p0, clearly showing that wind shear causes the shock train to move upstream and ultimately causes the unstart state. It can be seen that the separation point of the separation bubble at the throat moves upstream, which is further demonstrated in Figure 28. Moreover, the Cf value changes for the upper and lower walls, as shown in Figure 29 and Figure 30. This occurs because, as the shock train moves upstream, it approaches the upper wall, leading to a lower exit Mach number in Figure 31. At t = 40.6 ms, the downstream separation zone and separation bubble couple at the throat, and the separation bubble at the throat enlarges rapidly over time. The angle of attack change caused by wind shear begins to decrease after t = 50 ms, and the separation bubble at the throat starts to decouple from the downstream separation zone at t = 50.6 ms. However, unlike the condition when the backpressure is 0.675 times the limit back pressure, the Mach number contour at 52.2 ms clearly shows that the decoupling has failed, forcing the inlet/isolator to fall into the unstart state. Obviously, under this condition, the influence of wind shear on the inlet/isolator is profound, directly causing the inlet/isolator to fall into the unstart state, and it cannot be restarted.
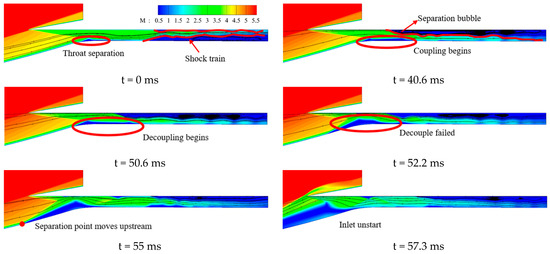
Figure 27.
Changes in Mach number contours.
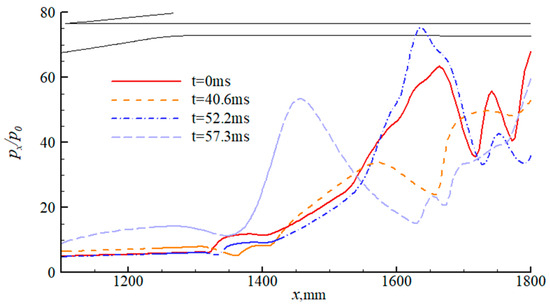
Figure 28.
Pressure changes along the lower wall.
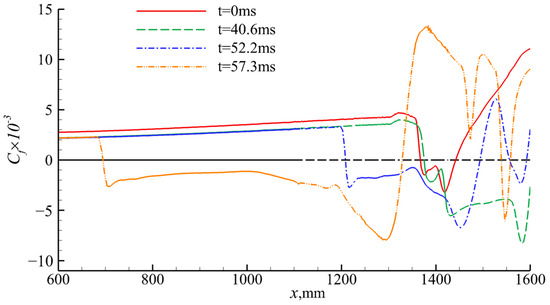
Figure 29.
Distribution of frictional resistance coefficients on the lower wall.
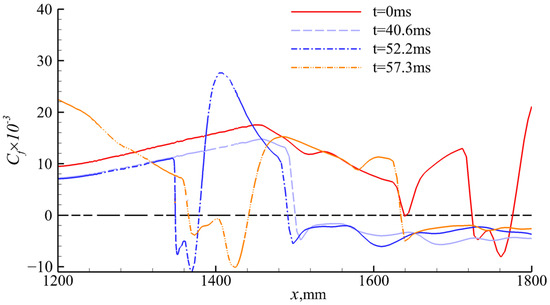
Figure 30.
Distribution of frictional resistance coefficients on the upper wall.
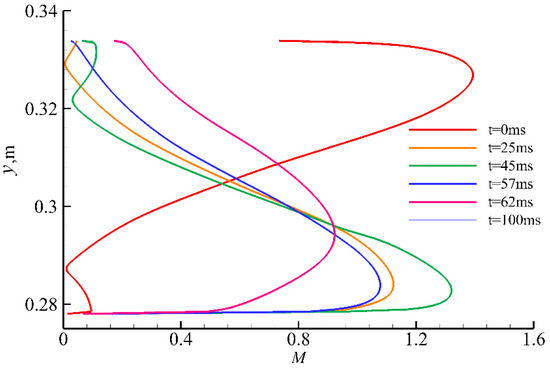
Figure 31.
Distribution of Mach numbers at the exit.
Based on the above analysis, it is evident that wind shear substantially affects the inlet/isolator’s ability to resist back pressure, weakening it by about 30%. Therefore, the presence of wind shear needs to be considered when designing an inlet/isolator.
5. Conclusions
Herein, the unsteady simulations of a hypersonic inlet/isolator with an on-design Mach number of 6.0 under incoming wind shear at an altitude of 30 km with a magnitude speed of 80 m/s are performed. The transient flow characteristics of the shock wave/boundary layer interaction (SWBLI) and shock train are investigated in detail.
A mixed-compression hypersonic inlet/isolator with an oblique shock and a series of compression waves is designed. The incoming wind shear perturbation is modeled as a variation in the angle of attack. Under the unthrottled state, wind shear significantly disrupts the flowfield of the inlet/isolator, affecting the interaction between the shock wave and the boundary layer. It drives the continuous movement of the separation bubble at the throat, both downstream and upstream, exhibiting hysteresis phenomena, which are also demonstrated by the pressure variation in the different positions of the inlet/isolator. Regarding the performance of the inlet/isolator, the total pressure recovery coefficients at the throat and exit increase by approximately 10% to 12%, respectively. Under throttled conditions, wind shear significantly impacts the isolator’s shock train. When the downstream backpressure is 135 times the incoming pressure (p0), the shock train first moves upstream and gradually interacts with the cowl shock wave/boundary layer, apparently enlarging the separation bubble at the throat. As the shock train moves upstream, the separation at the upper wall expands because the shock that interacts with the shock train switches from the right-running reflected shock to the left-running reflected shock. Then, the shock train moves downstream and decouples from the separation bubble at the throat. Though the perturbation amplitude reduces to zero, because of the hysteresis effect, the flowfield in the inlet/isolator cannot fully recover to the initial state. When the downstream backpressure increases to 140 p0, the shock train expands the separation zone in both the upper and lower walls, ultimately forcing the inlet/isolator to fall into the unstart state, and it cannot be restarted. Therefore, it is necessary to pay more attention to the adverse effects of wind shear on inlet/isolator performance, which directly affects the internal flow.
Author Contributions
Conceptualization, S.G. and H.H.; methodology, S.G., H.T. and H.H; validation, S.G., K.G. and H.H.; formal analysis, S.G.; investigation, S.G.; resources, S.G. and Y.M.; data curation, S.G. and H.H; writing—original draft preparation, S.G. and M.L.; writing—review and editing, H.H., H.T. and S.G.; visualization, S.G.; supervision, H.H. and H.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant Nos. 12272177, 12025202, and U20A2070), the National Science and Technology Major Project (No. J2019-II-0014-0035), the Young Talent Lift Project (2021-JCJQ-QT-064), the 1912 Project (No. 2019-JCJQ-DA-001-164), the Advanced Jet Propulsion Innovation Center, AEAC (Project ID. HKCX202-02-005), the Key Laboratory of Inlet and Exhaust System Technology (Grant No. CEPE2020012), and the Defense Industrial Technology Development Program (JCKY2019605D001).
Data Availability Statement
The data within the article are available upon request.
Acknowledgments
The authors would like to thank the High-Performance Computing Platform of Nanjing University of Aeronautics and Astronautics for providing the computing platform. The authors are grateful to Li Xin and Qin Yuan for their assistance in facilitating valuable discussions and providing suggestions. The manuscript greatly benefited from the helpful and constructive comments of three anonymous reviewers.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could appear to influence the work reported in this paper.
References
- Van Wie, D.M.; D’Alessio, S.M.; White, M.E. Hypersonic Airbreathing Propulsion. Johns Hopkins APL Tech. Dig. 2005, 26, 430–437. [Google Scholar]
- Ferri, A. Review of scramjet propulsion technology. J. Aircraft. 1968, 5, 3–10. [Google Scholar] [CrossRef]
- McClinton, C.; Rausch, D.; Sitz, J.; Reukauf, P. Hyper-X program status. In Proceedings of the 10th AIAA/NAL-NASDA-ISAS International Space Planes and Hypersonic Systems and Technologies Conference, Kyoto, Japan, 24–27 April 2001. [Google Scholar]
- Moses, P. X-43C Plans and Status. In Proceedings of the 12th AIAA International Space Planes and Hypersonic Systems and Technologies, Norfolk, VA, USA, 15–19 December 2003. [Google Scholar]
- Huang, H.X.; Tan, H.J.; Li, F.B.; Tang, X.B.; Qin, Y.; Xie, L.B.; Xu, Y.Y.; Li, C.M.; Gao, S.M.; Zhang, Y.; et al. A review of the shock-dominated flow in a hypersonic inlet/isolator. Prog. Aerosp. Sci. 2023, 2023, 100952. [Google Scholar] [CrossRef]
- Rozario, D.; Zouaoui, Z. Computational Fluid Dynamic Analysis of Scramjet Inlet. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno NV, USA, 8–11 January 2007. [Google Scholar]
- Van Wie, D.; Kwok, F.; Walsh, R. Starting characteristics of supersonic inlets. In Proceedings of the 32nd Joint Propulsion Conference and Exhibit, Lake Buena Vista, FL, USA, 1–3 July 1996. [Google Scholar]
- Ma, R.P.; Liao, H.Z. The characteristics of winds at height of 20-80 km in the Chinese area. Chin. J. Space Sci. 1999, 19, 334–341. [Google Scholar] [CrossRef]
- Fleming, E.L.; Chandra, S.; Barnett, J.J.; Corney, M. Zonal mean temperature, pressure, zonal wind and geopotential height as functions of latitude. Adv. Space Res. 1990, 10, 11–59. [Google Scholar] [CrossRef]
- Fleming, E.L.; Chandra, S.; Burrage, M.D.; Skinner, W.R.; Hays, P.B.; Solheim, B.H.; Shepherd, G.G. Climatological mean wind observations from the UARS high-resolution Doppler imager and wind imaging interferometer: Comparison with current reference models. J. Geophys. Res. Atmos. 1996, 101, 10455–10473. [Google Scholar] [CrossRef]
- Johnson, D.; Roberts, B.; Vaughan, W.; Justus, C. Atmospheric Models For Engineering Applications. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003. [Google Scholar]
- Luers, J. A Model of Wind Shear and Turbulence in the Surface Boundary Layer; NASA: Washington, DC, USA, 1973. [Google Scholar]
- Smith, O.E. Vector Wind and Vector Wind Shear Models 0 to 27 km Altitude for Cape Kennedy, Florida, and Vandenberg AFB, California; NASA: Washington, DC, USA, 1976. [Google Scholar]
- Kozakiewicz, A.; Frant, M. Analysis of the gust impact on inlet vortex formation of the fuselage-shielded inlet of an jet engine powered aircraft. J. Theor. Appl. Mech. 2013, 51, 993–1002. [Google Scholar]
- Sun, S.; Wu, Z.; Huang, H.; Bangga, G.; Tan, H. Aerodynamic Response of a Serpentine Inlet to Horizontal Periodic Gusts. Aerospace 2022, 9, 824. [Google Scholar] [CrossRef]
- Halwas, H.K.; Aggarwal, S. Effect of Side Gust on Performance of External Compression Supersonic Inlet. J. Aircr. 2019, 56, 569–582. [Google Scholar] [CrossRef]
- Etkin, B. Effect of Wind Gradient on Glide and Climb. J. Aeronaut. Sci. 1947, 14, 365–367. [Google Scholar] [CrossRef]
- Etkin, B. Turbulent Wind and Its Effect on Flight. J. Aircr. 1981, 18, 327–345. [Google Scholar] [CrossRef]
- Etkin, B.; Hughes, P.C.; Zhu, S. Equivalent deterministic inputs for random processes. J. Guid. Control Dyn. 1984, 7, 477–482. [Google Scholar] [CrossRef]
- Xie, R.; Wang, X.M.; Gong, J.Y. Dynamic Modeling and Simulation for a Supermaneuverable Aircraft in Disturbance of Wind Field. In Proceedings of the 2012 Fifth International Conference on Intelligent Computation Technology and Automation, Zhangjiajie, China, 12–14 January 2012; pp. 147–150. [Google Scholar]
- Zhao, R.L.; Chen, Z.G.; Fu, W.X. Wind shear and rocket design. J. Astronaut. 1998, 19, 106–109. [Google Scholar]
- Yang, J.F.; Xiao, C.Y.; Hu, X.; Cheng, X. Wind shear characteristics in near space and their impacts on air vehicle. J. Beijing Univ. Aeronaut. Astronaut. 2019, 45, 57–65. [Google Scholar] [CrossRef]
- Woollen, J.; Sienkiewicz, M.; Ruddick, A.G.; Robertson, F.R.; Reichle, R.; Redder, C.R.; Pegion, P.; Pawson, S.; Owens, T.; Molod, A.; et al. MERRA: NASA’s Modern-Era Retrospective Analysis for Research and Applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Soltania, M.R.; Daliria, A.; Younsib, J.S. Effects of shock wave/boundary-layer interaction on performance and stability of a mixed-compression inlet. Sci. Iran. 2016, 23, 1811–1825. [Google Scholar] [CrossRef]
- Kianvashrad, N.; Knight, D. Large Eddy Simulation of Hypersonic Turbulent Boundary Layers. Fluids 2021, 6, 449. [Google Scholar] [CrossRef]
- Trapier, S.; Deck, S.; Duveau, P. Delayed Detached-Eddy Simulation of Supersonic Inlet Buzz. AIAA J. 2012, 46, 118–131. [Google Scholar] [CrossRef]
- Zhong, X.L.; Wang, X.W. Direct Numerical Simulation on the Receptivity, Instability, and Transition of Hypersonic Boundary Layers. Annu. Rev. 2012, 44, 527–561. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Simeonides, G.; Haase, W.; Manna, M. Experimental, analytical, and computational methods applied to hypersonic compression ramp flows. AIAA J. 1994, 32, 301–310. [Google Scholar] [CrossRef]
- Mansour, A.; Laurien, E. Numerical error analysis for three-dimensional CFD simulations in the tworoom model containment THAI+: Grid convergence index, wall treatment error and scalability tests. Nucl. Eng. Des. 2018, 326, 220–233. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, H.J.; Zhuang, Y.; Wang, D.P. Influence of Expansion Waves on Cowl Shock/Boundary Layer Inte8action in Hypersonic Inlets. J. Propuls. Power 2014, 30, 1183–1191. [Google Scholar] [CrossRef]
- Huang, H.X.; Sun, S.; Tan, H.j.; Ning, L.; Wang, J. Characterization of Two Typical Unthrottled Flows in Hypersonic Inlet/Isolator Models. J. Aircr. 2015, 52, 1715–1721. [Google Scholar] [CrossRef]
- Huang, H.X.; Tan, H.J.; Zhuang, Y.; Sheng, F.J.; Sun, S. Progress in Internal Flow Characteristics of Hypersonic Inlet/Isolator. J. Propuls. Technol. 2018, 39, 2252–2273. [Google Scholar] [CrossRef]
- Huang, H.X.; Tan, H.J.; Sun, S.; Wang, Z.Y. Behavior of Shock Train in Curved Isolators with Complex Background Waves. AIAA J. 2018, 56, 329–341. [Google Scholar] [CrossRef]
- Tan, H.J.; Sun, S.; Huang, H.X. Behavior of shock trains in a hypersonic inlet/isolator model with complex background waves. Exp. Fluids 2012, 53, 1647–1661. [Google Scholar] [CrossRef]
- Huang, H.X.; Tan, H.J.; Sun, S.; Sheng, F.J. Unthrottled Flows with Complex Background Waves in Curved Isolators. AIAA J. 2017, 55, 2942–2955. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).