Abstract
Tiltrotor aircrafts have both fixed-wing control surfaces and helicopter rotors for attitude control. The redundancy of control surfaces provides the possibility for the control system to reconfigure the control law when actuator faults occur during flight. Possible actuator faults have been classified into two categories: predictable and unpredictable faults, and a different strategy has been adopted to deal with each kind of fault. Firstly, the predictable faults are handled by a multiple-model switching adaptive scheme. These kinds of faults are modeled, and their corresponding controllers are derived offline. Secondly, since the degree of drop in aerodynamic effectiveness cannot be predicted a priori, unpredictable faults are handled by a simple adaptive control scheme, to force the plant with faults to track the prescribed reference model. The presented methodology has been verified by nonlinear full-envelope flight simulation for both categories of actuator faults. The predictable fault is represented by the elevator floating. Elevator damage causing an aerodynamic effectiveness drop by 80% is chosen as the example of unpredictable fault. Both faults are simulated at the late stage of the tiltrotor conversion mode. Results show that the presented strategy of reconfiguration is able to detect the fault rapidly and stabilize the aircraft when a fault occurs, while the aircraft motion diverges without the reconfiguration scheme. The aircraft also presents a relatively good performance under controller reconfiguration with a well-tracked conversion path.
1. Introduction
The tiltrotor aircraft has three flight modes: helicopter mode, conversion mode, and airplane mode. Compared with conventional fixed-wing aircraft, the rotor nacelle system is installed at each end of the wing, which can drive the rotor to make a 90-degree tilt in the longitudinal plane. When the rotor axis is located in the vertical position, its configuration is equivalent to the tandem helicopter. When the rotor shaft is in a horizontal position, it is equivalent to a conventional fixed-wing propeller aircraft. The rotor serves as the main lift surface in the helicopter mode and also as the main control surface and the propeller of the aircraft mode. Because the helicopter rotors and the fixed-wing control surfaces of tiltrotor aircraft can provide forces and moments along the three axes of the body, forming a certain redundancy in the control, tiltrotor aircraft has the ability to reconfigure the flight control law under its transition mode intrinsically. When the aircraft is in the conversion mode and some control surfaces fail, the flight control law is expected to be reconstructed/reorganized by changing the parameters or structure of the flight control law, so that the tiltrotor aircraft can continue to complete the mission in the case of actuator failure.
Due to the distinctiveness of the tilting rotor mechanism, the tiltrotor is a nonlinear time-varying system in conversion mode, which has obvious nonlinear characteristics and a large number of control surfaces. The design methods of classical control theory have made it difficult to meet the requirements of control law design for complex multivariable nonlinear systems. With continuous in-depth research all over the world, the multi-variable control design method of modern control theory has been gradually applied to the control law design of complex configuration aircraft.
R. T. Rysdyk and A. J. Calise [1] proposed an adaptive model inversion control method for tiltrotor aircraft. Based on the neural network and model inversion control, the flight control law of tiltrotor aircraft under all of its flight modes is designed, and the Attitude Command Attitude Hold (ACAH) mode of the longitudinal channel is realized. The traditional design methodology of flight control law requires a wide range of gain scheduling with nacelle tilting angle and flight speed. This method reduces the need to gain scheduling of control law to a great extent, thus reducing the time and cost of control system development. The control law of neural network combined with model inverse design can meet the requirements of flight quality and compensate for limited system failure to a certain extent, which is characterized by the ability to adapt to the uncertainty of the controller and the aircraft state and the ability to learn and control at the same time. Other applications of rotorcraft control law design involving neural networks include haptic support systems [2], operating mode classification [3], attitude control [4], trajectory optimization [5], and model predictive control [6].
G. D. Francesco et al. [7] designed the flight control law of tiltrotor aircraft using the nonlinear dynamic inversion control distribution method. The tiltrotor aircraft is modeled by a modular method to calculate the flight dynamics response of the aircraft. The controller adopts the inner and outer loop structure: the inner loop is for the fast variable, and the outer loop is for the slow variable to control the aircraft. The control distribution of tiltrotor aircraft is carried out through the redundancy of the rudder surface. The control logic of the flight control system is realized and tested. The inner loop mixes the first- and second-order errors dynamically. The outer ring uses a first- and second-order reference model and a dynamic inversion control algorithm. The system shows good tracking performance. For adaptive control, direct uncertainty minimization has been applied to the fin-controlled projectile [8,9]. Mooij [10] adopted simple adaptive control to the unpowered winged reentry vehicle and performed the sensitivity analysis. Hsu and Liu [11] applied a nonlinear hierarchical adaptive control framework to an aquatic tiltrotor UAV.
Among recent works on the fault-tolerant control (FTC) of flight vehicles, both fixed-wing aircrafts [12,13,14,15,16,17,18] and rotorcrafts [19,20,21,22,23,24,25,26,27,28] have been taken into account. In [12], FTC systems are presented for vectored thrust aircraft with a robust fault detection and identification mechanism. Reference [13] presented a control allocation scheme for overactuated aircrafts, with reference trajectory being tracked by an adaptive super twisting sliding mode controller. In [15], adaptive controller with a nonlinear reference model is utilized for the fault-tolerant control of systems with redundant control and uncertain input gains. The presented FTC scheme is applied to an F-18 model with a backstepping controller as the baseline. A PID-based FTC is presented in [16], incorporating a neural network and disturbance observer to deal with the nonlinearity caused by the faults. For spacecraft attitude control in the presence of external disturbances, actuator failures, and signal quantization errors, reference [17] presented a fixed-time observer-based adaptive fault-tolerant control. Other than actuator failure, other kinds of faults have also been considered. For example, reference [14] proposed the diagnosis and FTC for fixed-wing fighter aircraft considering three kinds of wing damage. Longitudinal and lateral flight control laws are derived based on the diagnostic results using dynamic inverse and LQR methodologies.
With respect to rotorcrafts, attention is paid mainly to the configuration of conventional helicopters [19], quadrotors [20,21,22,23,26,27,28], octorotors [25], and rarely to novel configurations such as hybrid helicopters [24]. Using a backstepping baseline controller to improve performance under healthy situations, a robust adaptive compensation FTC system is presented in [19]. For motor performance decline and propeller damage encountered by multirotors, thrust systems are reconfigured by optimal control, and directional control will no longer be performed if anti-torque cannot be balanced during failure [21]. Adaptive sliding mode is utilized for the FTC of a novel hybrid helicopter configuration [24]. The aircraft is incorporated with a helicopter rotor and a canard control. A high-level sliding-mode controller is used for both faulty and healthy situations for vehicle command tracking. A low-level allocator is for allocating the virtual control of the sliding-mode controller.
This work combines the multiple-model switching adaptive scheme and simple adaptive control scheme to form a hybrid adaptive scheme for tiltrotor aircraft controller reconfiguration. For a nominal small-scaled tiltrotor aircraft, the flight dynamics model is derived first. Adopting the modular modeling technique, each part of the aerodynamic component is modeled and then incorporated into the rigid body equations of motion. To derive the baseline controller under normal situations, the aircraft nonlinear model is trimmed to establish a properly prescribed conversion path. Reconfigurability is then studied by evaluating the control effectiveness of each control surface. For the baseline controller design under normal situations, a redundant control allocation method based on optimal control effectiveness is presented to implement the actuator mixing. The baseline controller design adopts the model inversion technique based on feedback linearization to acquire a relatively good performance for the inner angular rate loop rate command mode. For controller reconfiguration, this work is based on a divide-and-conquer strategy. Specifically, the problem is considered by classifying the actuator fault into two categories, i.e., predictable fault and unpredictable fault, and these different kinds of faults are handled by separate methodologies. Since the degree of damage is known for predictable faults, these faults are modeled offline with their corresponding controller. Fault model set and controller set are incorporated by the multiple-model switching adaptive control technique. When a certain fault occurs during flight, the online supervising logic will switch to the proper controller. Predictable faults are characterized by unknown aerodynamic effectiveness loss, an example of this kind is the fixed-wing control surface damage. This category of fault is coped with by a simple adaptive controller. The fault plant will be forced to track a healthy reference model by the adaptive scheme. The positive real condition is guaranteed by the reconfigurability that the same control channel is redundant by at least two control surfaces.
2. Reconfigurability Evaluation
2.1. Flight Dynamics Model of the Tiltrotor Aircraft
This paper adopts an Euler-angle-based 6-degree-of-freedom (DoF) nonlinear model for the tiltrotor aircraft as the subject of research. In its vector form, the aircraft motion is governed by the following equations:
In the above equations, Fb and Mb denote the resultant forces and moments acting on the aircraft’s center of mass, produced by the rotors, the fuselage, the empennage, and the control deflections; is the center of mass translational velocity derivative vector; is the airframe angular velocity derivative vector; m denotes the aircraft mass; J denotes the inertia tensor; is the gravitational acceleration vector in the earth frame; and is the vector of derivatives of the Euler angles. is the transformation matrix from the earth frame to the aircraft body frame, and is that from the body frame to the Euler frame, where the Euler angles are defined:
The above set of equations can be represented by a general form of a nonlinear dynamic system state equation:
where the state vector , the control vector , including the helicopter rotor controls (rotor collective pitch, differential collective pitch, lateral and longitudinal cyclic pitch, and differential longitudinal cyclic pitch), the fixed-wing control surface deflections (aileron, elevator, and rudder), and the rotor nacelle tilting angle, explained in their order of appearance. The aircraft modeling diagram is shown in Figure 1 and will be explained in detail in subsequent subsections.
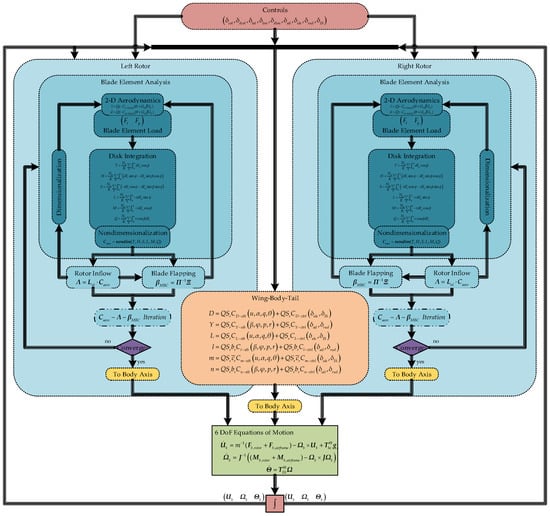
Figure 1.
Flight dynamics model diagram of the tiltrotor aircraft.
2.1.1. Rotor Forces and Moments
The two main rotors are modeled by Blade Element Momentum Theory (BEMT) with the steady-state version of a 3-state Pitt–Peters dynamic inflow model and a truncated quasi-steady flapping equation of motion. The rotor aerodynamic forces and moments can be represented as follows:
where T, H, S, L, M, and Q denote the rotor thrust, in-plane forces pair, aerodynamic rolling and pitching moments, and torque. Nb, K, r0, and r1 are the number of blades, azimuth stations, blade root cut, and tip loss. Angles and are blade flapping and azimuth angle. Components dFp and dFt are the blade element perpendicular and tangential force elements, which can be represented by the element lift and drag as follows:
where Up and Ut denote the velocity in-plane and normal components seen by the rotor. These components can be evaluated by the advance ratio and inflow ratio. The rotor dimensionless induced velocity is governed by the Pitt–Peters’ dynamic inflow model:
The above inflow model is truncated to a steady-state version by ignoring the derivative term of the base and first harmonic term, as the frequency of the time-varying behavior of the rotor inflow is much higher than that of the flight dynamics of the tiltrotor aircraft.
The rotor blade flapping motion is governed by the equation:
where denotes the second-order flapping angle derivative with respect to the blade azimuth, and variable with a bar denotes the normalization by the blade tip speed . By incorporating the dimensionless rotor hub rolling and pitching angular velocity terms, i.e., and , the influence of gyroscopic acceleration on the blade flap is also taken into account. By defining the collective flap , the longitudinal flap , and the lateral flap , the above flapping equation of motion can be transformed to the multi-blade coordinate (MBC), according to the following relations:
where flapping angles in each coordinate are and . The transformation matrix is obtained by the definition of the collective and first harmonic flapping angles. By concatenating the flapping motion equations of each blade, the rotor flapping equation in MBC takes the form:
Again, due to flapping angular velocity and accelerations being less significant in nature for flight dynamics analysis, and to reduce the amount of system states, the derivative terms are truncated from the equation, and only quasi-steady flapping motion is considered. This leaves the above equation as follows:
where is affected mainly by the rotor rotational centripetal acceleration and center-spring stiffness, while is the result of the aerodynamics and hub motion.
Rotor aerodynamic forces and moments are then converted to the airframe body axis by the rotor nacelle tilting angle . The total rotor aerodynamic forces and moments on the airframe’s center of gravity are the sum of those produced by the left and right rotors.
2.1.2. Airframe Forces and Moments
The forces and moments of the airframe are computed in the wind axis of the fuselage by the dynamic pressure , the reference area Sr, the lateral reference length br (the wingspan), the longitudinal reference length (mean aerodynamic cord, MAC), and the aerodynamic coefficients:
The aerodynamic coefficients of drag CD, side force CY, lift CL, rolling moment Cl, pitching moment Cm, and yawing moment Cn are nonlinearly interpolated by the corresponding flight state variables and control surface deflections:
2.2. Model Trimming and Control Effectiveness
This subsection conducts the evaluation of the effectiveness of the redundant controls of the tiltrotor aircraft. The purpose of this evaluation is twofold: On the one hand, the basis of the control law reconfiguration needs to be established based on the reconfigurability provided by the sufficient control effectiveness (aerodynamic moments); on the other hand, a proper conversion path is desired to be derived. As a result, a preliminarily decided control allocation scheme is conformed to perform the model trimming. This allocation scheme is listed in Table 1. The control effectiveness is the aerodynamic moment produced by each primary control and redundant control under unit control surface deflection.

Table 1.
Control allocation scheme on the main control channels.
Trimming results are shown in Figure 2. A particular conversion path is selected during the trimming process. The nacelle tilting angle is chosen as a linear function of the airspeed. The conversion mode begins at an airspeed of 15 m/s and reaches airplane mode (90 deg nacelle angle) at 24.1 m/s, see Figure 2a. As shown in Figure 2b, the longitudinal control is accomplished by both the longitudinal cyclic pitch and the elevator deflection during the conversion mode. In Figure 2c, the aircraft appears a nose up and nose down course in conversion mode, which is mainly caused by the increasing lift on the wing to compensate for the loss of lift due to nacelle forward tilting.
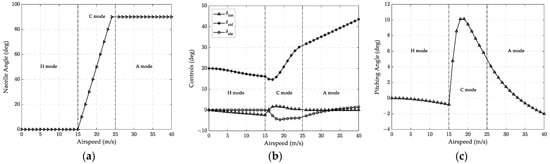
Figure 2.
Trimming results: (a) trimmed nacelle angle, (b) trimmed control deflections, and (c) trimmed pitching angle.
From the above trimming results, a feasible conversion path is established with its corresponding control strategy. The control effectiveness on each angular motion axis is then analyzed based on the trimming flight status. Each of the controls is increased by a small value with respect to its trimming value, and the control effectiveness is evaluated by the ratio of the incremental aerodynamic moment to the incremental value of control deflection. The results are shown in Figure 3, from which one can find both the redundancy and the coupling effect of the aircraft controls during conversion mode. These are summarized as follows:
- Rolling Axis. As the airspeed increases (during the conversion from the helicopter to airplane mode), the effectiveness of differential collective pitch () on rolling moment decreases rapidly. The differential collective transitions from controlling rolling to that of yawing (see Figure 3a,c). In the meantime, the rolling effectiveness of lateral cyclic pitch () also decreases with the forward tilting of the rotor nacelle. On the contrary, the rudder () contributes to an increasing rolling moment as airspeed increases, given the buildup of dynamic pressure. Also, it is worth noting the cross-coupling effect of differential longitudinal cyclic pitch (), which is the primary yawing control during helicopter mode, on both rolling and yawing channels. Coupling on the rolling axis is mainly because of the unsymmetric thrust variation during differential longitudinal flapping, which causes the difference in the effective blade element angle of attack on each rotor.
- Pitching Axis. Pitching controls are of great importance for tiltrotor aircraft conversion, during which the primary longitudinal controls are the longitudinal cyclic pitch () and the elevator (), see Figure 3b. The elevator pitching moment increases significantly with airspeed as dynamic pressure builds up, whereas the decrease in longitudinal cyclic pitching moment is much less obvious with respect to the airspeed. The collective pitch () also has some influence on the pitching moment because of the relative position of the thrust vector with respect to the aircraft’s center of gravity.
- Yawing Axis. Primary controls are differential collective pitch () and the rudder, among which the former presents a much more controlling moment than the latter, see Figure 3c. The collective pitch, however, is coupling in both heading control and lateral control.
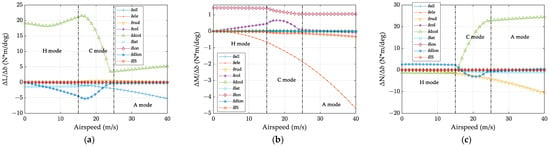
Figure 3.
Effectiveness on each of the control axes: (a) control effectiveness on the rolling axis, (b) control effectiveness on the pitching axis, and (c) control effectiveness on the yawing axis.
2.3. Redundant Control Allocation Based on Optimal Control Effectiveness
Redundant controls including five rotor controls, three fixed-wing control surfaces, and one open-loop nacelle tilting command are cooperating to perform aircraft attitude control. There are, however, only four main control channels to receive the pilot and/or autopilot input command (i.e., the roll, pitch, yaw, and vertical for ACAH mode). For each command channel, there are at least two controls providing the same control forces and moments effectiveness. It is thus desirable to mix the redundant controls to form a four-channel generalized control vector for the basic controller and then reallocate them when implementing the controller. A readily available approach to do so is according to the flight mode. Specifically, helicopter mode utilizes helicopter rotor controls primarily. During conversion mode, rotor controls are phased out and fixed-wing surfaces are phased in via a factor proportional to the nacelle angle. This consideration can be very easy for implementation but clearly not optimal. In a sense of minimizing the control effort (i.e., control surface deflection), certain mixing-and-reallocation methods should be found.
The moment components of the aircraft equations of motion can be represented as follows:
where , and are the controls of the angular channels. When the above equation is Taylor-expanded at the neighborhood of some flight condition x0, Equation (13) can be written in the linear form as follows:
Since we consider only the system’s control derivatives, which is the effect of controls on the angular derivatives (i.e., moments), the term of incremental of states x can be set to zero in the above equation. In this case, given the desired angular velocity derivatives , the linear system
is underdetermined and has an infinite number of solutions since it has a greater number of controls than angular derivatives, due to the redundant nature of the tiltrotor. The problem here would be to find, for the consistent system described above, the unique minimum norm solution umin, given s0 being the solution of:
Then
Thus, when defined umin by
the is the generalized inverse of in a minimum norm sense. The physical significance of umin is that it is composed of the minimum combined control surface deflections, which produce the desired angular derivatives .
For the controller design problem of a tiltrotor aircraft, umin is the optimal mixed close-loop control variables that affect the three angular channels, in this case, , based on the so-called optimal control effectiveness, and should be the angular velocity acceleration commands produced by the most inner-loop angular rate controller. For controller implementation, which will be discussed in the next section, the is the optimal effectiveness control transformation matrix that allocates three angular motion channel commands to actual vehicle controls. In this case, we have mixed the vehicle’s control surfaces into three generalized controls, and the angular equations of motion under change of variables of controls become
3. Basic Flight Controller for Normal Conditions
3.1. Feedback Linearization Control for the Inner Angular Rate Loop
Control design for tiltrotor aircrafts has long been a challenging task, as the system itself is intrinsically unstable due to the helicopter rotor aerodynamics. Transformation during the conversion mode forces the aerodynamics and flight dynamic characteristics to vary drastically through the conversion pathway, which in turn contributes to the system’s nonlinearity and coupling in controls. As was discussed in the previous section, during nacelle tilting, several controls shift their authorities on different control channels. Thus, an inner loop rate mode controller, providing basic functions of angular rate loop stability augmentation, linearizing, decoupling, and command tracking, plays a central role throughout the entire control system hierarchy. This work adopts the feedback linearization technique for the inner angular rate loop control of the tiltrotor aircraft under its normal conditions, i.e., without actuator malfunction. This technique involves utilizing the inversion of the system function to linearize the original multi-input multi-output (MIMO) nonlinear system to m (equals to the number of outputs) decoupled integrators. Specifically, consider a MIMO nonlinear system (the aircraft inner loop state-space equation) of a general form:
where , , and .
Differentiating the output equation along the trajectory of the autonomous system gives
where and are the Lie derivatives of h along f and g.
If the original system has a relative degree , in other words
the term of u exists in the th derivative of the output equation:
In this case, take the control input u as follows:
The original system will be decoupled into th order integrators as follows:
and thus, the th state derivative will track the reference command v.
Practically, when applying feedback linearization control directly to the inner angular rate state equations (Equation (13)) of the tiltrotor aircraft, it is usually not possible to force tracking an arbitrary angular derivative command directly. Thus, a command filter must be involved to attenuate the high-frequency signal from the previous stage of the attitude controller or from the stick input. The command filter takes the form of the reference model transfer function of the first-order system, with , , and being the characteristic frequency of each angular channel. The command filter provides angular rate commands with its rate derivative commands taken from the reference model. The inner loop controller structure can be represented in Figure 4.
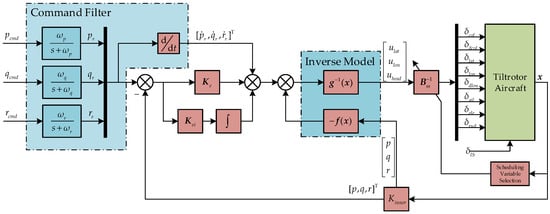
Figure 4.
Inner loop feedback linearization controller.
3.2. Mode-Conversion Controller and Forward/Vertical Speed Decoupling
With the inner loop feedback linearization controller providing angular rate command tracking, decoupling, and control surface allocation, the outer loops focus primarily on forward/vertical decoupling and velocity control. The overall control system diagram is shown in Figure 5.
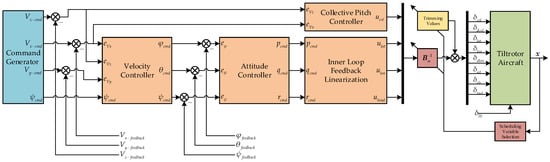
Figure 5.
Mode-conversion controller diagram.
By the analysis of Section 2.2, during the conversion process from the helicopter to airplane mode, the control of vertical speed shifts from collective pitch to the longitudinal channel control, thus causing cross-coupling between vertical and forward speed control channels. As a result, cross feedback is introduced to decouple the vertical speed and longitudinal/forward speed control in Figure 5. The forward/vertical speed decoupling scheme is shown in Figure 6. Both state errors of forward and vertical speed are fed to the collective controller and the velocity controller. Passing PI controllers for vertical and forward speed control, the corresponding control signals for the next stages are mixed by the factors of sine and cosine of the nacelle tilting angle. Specifically, at an early stage of conversion mode, the collective pitch dominates in vertical speed control and the pitching attitude, which causes the forward tilting of the thrust for forward speed control, and vice versa. Thus, the collective signal is obtained by the sum of -weighted forward speed control and -weighted vertical speed control, and the pitch attitude command for the next stage attitude controller is derived by the -weighted forward speed control and the -weighted vertical speed control.
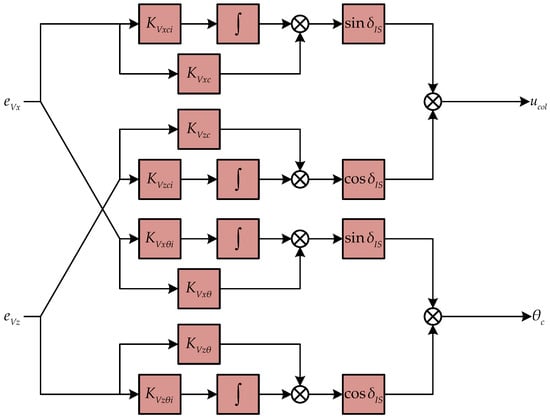
Figure 6.
Forward/vertical speed decoupling controller.
3.3. Simulation of the Mode-Conversion Flight
Mode-conversion flight simulation is performed. The results are shown in Figure 7. The simulation is started at the aircraft’s hover state. After accelerating to an airspeed of 15 m/s, the aircraft enters its conversion mode. During conversion, the rotor nacelle maintains a constant tilting angular velocity of 6 deg/s, and the conversion mode lasts 15 s. In airplane mode, the aircraft continues to accelerate to an airspeed of 40 m/s. Finally, the aircraft converts back to helicopter mode hovering via the same conversion path. From the vehicle state and command depicted in Figure 7b, the aircraft can follow the velocity command closely throughout the entire simulation path. In the meantime, the altitude during conversion flight is maintained quite well with an altitude loss of no more than 2 m. In summary, the designed controller shows a good performance in all three flight modes.
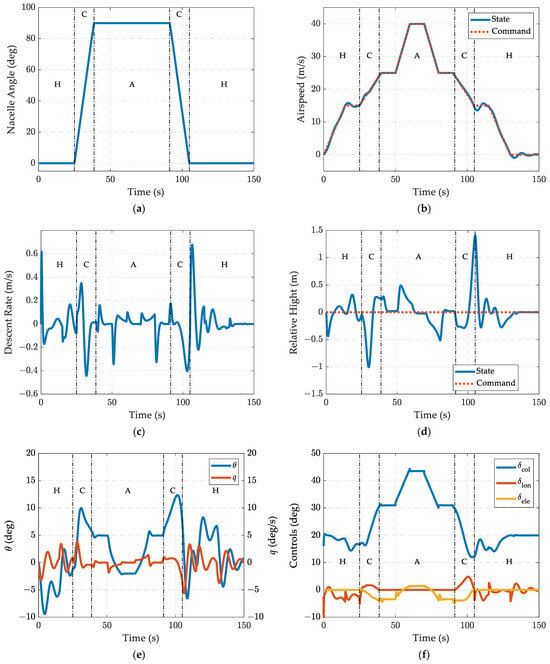
Figure 7.
Mode-conversion flight simulation results: (a) nacelle tilting angle command, (b) airspeed response, (c) descent rate response, (d) relative height response, (e) longitudinal states responses, and (f) controller outputs.
4. Fault-Tolerant Flight Control Design
The actuator malfunctions during the conversion mode of the tiltrotor aircraft can be divided into two categories, i.e., the predictable faults and the unpredictable faults. This section considers the fault-tolerant controller (FTC) design for both cases. When a predictable fault occurs, by its definition, the channel output is known a priori, such as the control surface floating and saturation. The control effectiveness can be predicted as 0% or 100% in these cases. As a result, the influence on the flight dynamics of the aircraft caused by actuator faults of this type is known and can be modeled a priori. On the contrary, for those unpredictable faults, for example, control surface damage and stuck, one cannot know the exact alteration of the aerodynamic forces and moments caused by these types of faults. This work adopts different strategies for dealing with these two types of faults and then combines the two systems as a whole to establish the so-called hybrid adaptive fault tolerant control scheme. For predictable faults, since the aircraft model of flight dynamics can be obtained offline, we utilized the multi-model switching adaptive control (MMAC) scheme, by which each of the faults is modeled a priori with its corresponding controller satisfying the desirable performance [29]. A supervisory mechanism is monitoring the error between the actual plant and each fault model online. The corresponding controller will be switched online when a certain fault occurs during the flight.
4.1. Multi-Model Switching Adaptive Control for Predictable Faults
4.1.1. Fault Model and Controller Set
Predictable faults considered here are primarily the actuator float and saturation, which can be parameterized by:
For each of the three predictable faults, an aircraft model under malfunction situation is obtained and thus constitutes the reference model set :
By the control design process discussed in the previous section, for each model in , a controller satisfying the desirable performance is derived, and these controllers are incorporated to form the controller set C:
The adaptive scheme adopted in this section is based on the supervisory mechanism. That is, for every moment during flight, the switching logic of the supervisory mechanism will choose the controller whose corresponding fault model has a minimum state error with respect to the actual aircraft states, and this controller will be the current one for flight control. The scheme of the MMAC is shown in Figure 8.
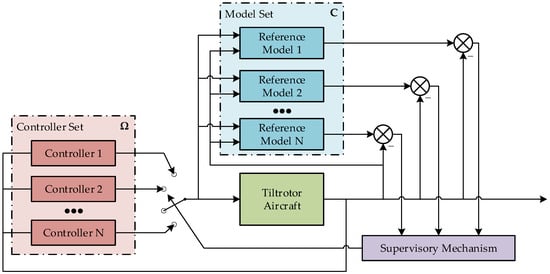
Figure 8.
MMAC scheme for predictable faults.
4.1.2. Reference Model Performance Index of the Supervisory Mechanism
Scalar functions of the model state error are adopted as performance indexes referenced by the switching logic of the supervisory mechanism:
where Ji denotes the performance index of the ith model
, is the state error between reference model and the aircraft, denotes the Euclidean norm, and and are the weights of the instant error term and the integral error term, respectively. The adopted index has the ability to balance the transient and steady performance of the switching mechanism. The integral term requires a certain amount of time until it can provide significant information about the fault system. Thus, at the beginning of the adaptation process, the instant error term is more reliable; moreover, this term is also able to reflect the transient characteristics of the adaptive system. If the transient term is used solely, however, the adaptation system will experience an excessively rapid switching and cause the close-loop system unstable. Therefore, an integral term has to be introduced. As the system reaches a steady state, the transient term approaches zero, and the integral term is able to provide accurate information about the system. The parameter is the factor of the long-term forgetting term. For engineering practice, a forgetting factor is always desirable because, with long-term integration, the state measuring error can cause the state error term quadratically non-integrable. In the meantime, the integral term can also effectively suppress the influence of the output of the previously switched-out model.
4.1.3. Mode-Conversion Flight Simulation under Predictable Fault Condition
The designed MMAC-FTC is simulated under one of the predictable fault conditions. To test the FTC performance, the actuator failure is set to be the elevator floating during the conversion from helicopter mode to airplane mode, where the primary longitudinal control of the airplane mode loses its effectiveness completely. The results are shown in Figure 9. As indicated in Figure 9f, elevator floating failure is injected at the simulation time t = 30 s. From the state responses shown in Figure 9a–d, without the MMAC-FTC, the aircraft cannot maintain stability during the late stage of the forward tilt, since the inner loop controller can no longer allocate the controller command to the longitudinal channel. In Figure 9e, the collective control also diverges without the MMAC-FTC when elevator failure occurs. With the FTC, the MMAC controller identifies the fault correctly, as shown in Figure 9g. The decision made by the supervisory mechanism performs a rapid switching from the controller of reference model (the normal model) to that of (the elevator failure model) by comparing the model performance index of the actual plant and each of the reference model. From the longitudinal controls indicated in Figure 9f, the control of the longitudinal channel is reallocated to the longitudinal cyclic pitch after losing the elevator. After the controller reallocation, the system maintains relatively good performance in tracking the airspeed command and altitude hold in the following conversion and reconversion flight, with the total altitude lost no more than 2 m during the conversion flight.
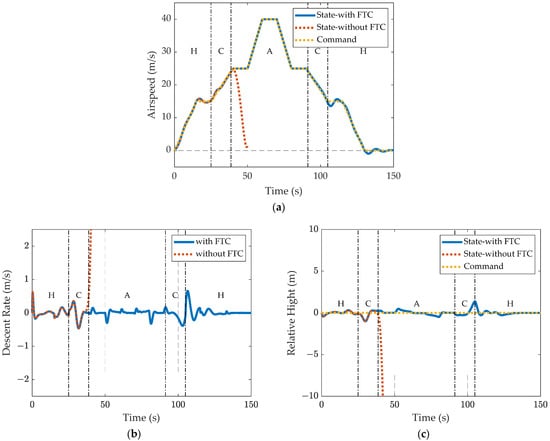
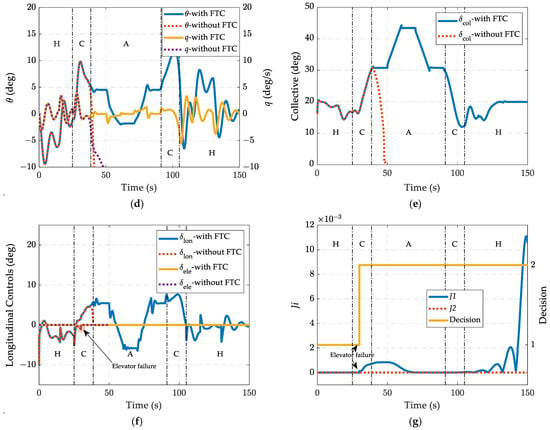
Figure 9.
Mode-conversion flight simulation results under an elevator floating condition with MMAC fault-tolerant controller: (a) airspeed responses, (b) descent rate responses, (c) relative height responses, (d) longitudinal states responses, (e) collective controller outputs, (f) longitudinal controller outputs, and (g) model indexes and switching logic decision.
4.2. Direct Adaptive FTC for Unpredictable Faults
For unpredictable faults such as control surface damage, since one cannot know the exact degree of damage, i.e., the decline of aerodynamics efficiency, the exact failure model thus cannot be derived a priori. Therefore, the strategy of MMAC will not be applicable. The model reference direct adaptive control (MRDAC) is thus chosen as the control scheme for unpredictable faults. Using MRDAC does not require an exact failure model, instead, general reference models are designed for each inner loop angular velocity channel, and the aircraft with actuator failures is forced to track the output of the channel’s reference model and to approximate the performance of the reference model. In this work, we adopt the simple adaptive control (SAC) technique [30], based on the Lyapunov stability theory and positive realness of the system.
4.2.1. Direct Adaptive Control for Unpredictable Faults
The simple adaptive control scheme is based on forcing the states of the fault plant to follow that of the reference model, as shown in Figure 10. The control law is presented as follows:
where the controller output consists of the model state feedforward, the model input, and the output tracking error between the model and the fault plant. The Kx(t), Ku(t), and Ke(t) are time-varying gain matrices, and these factors are to be adjusted online. The adaptive law of the gain matrices is
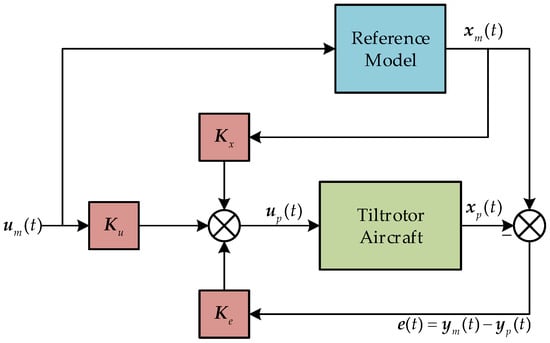
Figure 10.
Simple adaptive control scheme.
Each gain is divided into an integral term and a proportional term:
where and are time-invariant positive definite weight matrices.
During actuator malfunctioning, the reconfigurable flight controller utilizes the remaining control effectiveness and alters the controller structure and parameters to maintain the stability of the tiltrotor aircraft. Instead of relying on the damage information and the online parameter estimation, the adaptive controller under unpredictable faults adopted in this work tunes the controller parameters by the online adaptive law with the knowledge of the error between the actual aircraft and the reference model of each control channel. The controller diagram of the MRDAC for unpredictable faults is shown in Figure 11. The baseline controller is the one derived in Section 3.
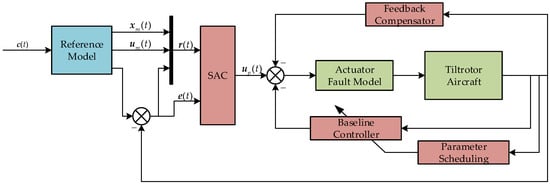
Figure 11.
MRDAC scheme for unpredictable faults.
4.2.2. Hybrid Control Scheme for Tiltrotor Aircraft Control Law Reconfiguration
For complicated problems, using a controller with a simple structure will always be inadequate. Better performance can often be reached by a combined control scheme that incorporates different strategies for solving practical problems. This work, solving the problem of the flight control law reconfiguration under both predictable and unpredictable situations, presents the MMAC-SAC scheme integrating the MMAC and SAC strategy, as shown by Figure 12. The two schemes run in parallel, operating simultaneously, awaiting actuator faults to occur and then taking over authority from the baseline controller:
- The model set of the MMAC scheme is derived a priori, and controllers are also designed for each of the failure models to maintain the flight performance to the maximum extent. When the actuator floating or saturation at minimum or maximum position occurs, the MMAC controller is switched to by the online system switching logic. Through the comparison of the actual aircraft states and each of the failure model states, the supervisory mechanism of the MMAC controller will allocate the control authority to one of the MMAC controllers corresponding to the proper fault model.
- When the aircraft encounters a failure such as control surface damage and stuck, the switching logic may not match the current fault plant to any of the modeled failures. In this case, the SAC controller for unpredictable faults is activated. Utilizing the direct adaptive methodology, the aircraft is forced to track the reference model and does not need any pre-established actuator failure model.
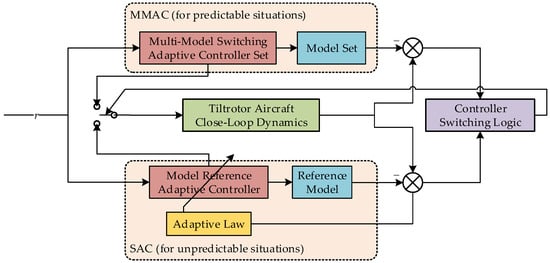
Figure 12.
MMAC-SAC fault-tolerant flight controller for tiltrotor aircrafts.
4.2.3. Simulation
The designed hybrid adaptive controller is tested by the nonlinear mode-conversion flight simulation. The simulation procedure is started in a hovering state. After reaching an airspeed of 15 m/s, the conversion mode is entered. The rotor nacelle is forward tilting under a constant angular velocity of 6 deg/s. A fault simulating the unpredictable elevator damage is injected during the conversion mode. The elevator effectiveness has declined by 80%, and the aircraft cannot maintain stable flight without any control law reconfiguration mechanism. The results are shown in Figure 13. Figure 13a–e shows the aircraft states. In the absence of the FTC, the flight states diverge shortly after the elevator failure occurs. Since the vertical speed is controlled by the elevator during the aircraft mode, the vehicle height cannot be maintained when it loses the majority of the elevator effectiveness. From the simulation results, the hybrid controller is able to deal with the unpredictable actuator failure. In Figure 13f, the helicopter rotor longitudinal cyclic pitch control takes over the control authority after fault occurrence, thus maintaining the system stability. After the controller reconfiguration, the conversion path can be tracked precisely (Figure 13a). However, vertical channel performance declined (Figure 13b,c), and this is mainly because of the relatively low pitching moment effectiveness of the rotor’s longitudinal control caused by the large axial flow encountered during airplane mode. In spite of the low pitching control effectiveness, the rotor’s longitudinal cyclic is still able to maintain the aircraft’s attitude alone, see Figure 13d.
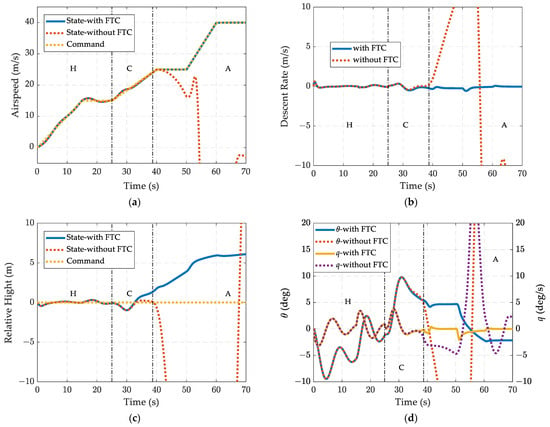
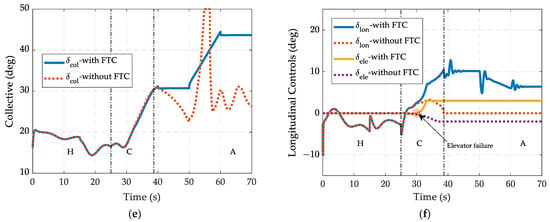
Figure 13.
Nonlinear mode-conversion flight simulation under unpredictable elevator failure: (a) airspeed responses, (b) descent rate responses, (c) relative height responses, (d) longitudinal states responses, (e) collective controller outputs, and (f) longitudinal controller outputs.
5. Conclusions and Discussion
The uniqueness and contributions of this work can be revealed by the following aspects. Firstly, this work has presented a synthetical solution in control law reconfiguration, considering various aspects in the design of a reconfigurable controller for a tiltrotor aircraft. For example, the presented controller design is applied to the actual nonlinear model of a tiltrotor, considering various aerodynamic and flight dynamic characteristics like instability and cross-coupling. It is well-known that due to its intrinsic complexity, the tiltrotor control problems cannot be solved simply by a series linear model stabilization, unless the full-state nonlinear model of flight dynamics is analyzed. The model analysis performed during reconfigurability evaluation paved the way for the subsequent optimal-effectiveness-based control allocation. In the baseline controller design, not only is the inner loop cross-axis decoupling achieved but also outer loop height/airspeed channel decoupling is taken into account. This leads to minimal height loss during the conversion, which is another major aspect of tiltrotor control design. The above work lays a foundation for the practically implementable control design for this configuration.
Secondly, the divide-and-conquer strategy presented to solve the control law reconfiguration has effectively combined the MMAC and SAC. The combined hybrid adaptive scheme exploits the advantages of both methodologies. MMAC is able to provide quick switching among the limited number of predictable faults. In the meantime, when severe unpredictable faults happen, SAC is able to guarantee system stability as long as the actual plant retains remaining control effectiveness. The advantage of this hybrid scheme is that it can take a wide variety of actuator failures into account, not just a specific one. In the meantime, not only the reconfigurable controller, but the entire synthetical approach can be readily applied to the tiltrotor, as many specific problems have already been addressed.
The conclusions drawn by this work can be summarized as follows:
- (1)
- For the baseline controller under normal situations, an inner angular rate loop controller is adopted based on the model inversion technique. Outer attitude and velocity loops are designed considering the decoupling of the height/velocity channel. During model conversion flight simulation, the aircraft is able to track the velocity command and thus the prescribed conversion path with ignorable static error. The maximum height loss during conversion is no more than 2 m. Simulation results have shown good performance of the full-envelope controller of the healthy system.
- (2)
- Predictable flight control law reconfiguration strategy is derived based on a multiple-model switching adaptive control scheme, which is the inner loop controller of the layered hybrid direct adaptive reconfigurable controller. The possible actuator faults of tiltrotor aircraft are analyzed and fault modeling is carried out. The controller of the fault model is designed and the recognition of the predictable fault and the smooth switching of the controller are implemented by using the appropriate performance index and the switching logic of the controller. Simulation is performed, taking the elevator floating as an example of a predictable fault. The elevator floating fault is injected into the system during the late phase of the conversion mode to verify the effectiveness of the MMAC-FTC. Results show that the presented scheme can detect the fault rapidly and switch to the corresponding controller. Performance during conversion can be recovered, and the aircraft is able to track the conversion path with a minimum height loss similar to that of the healthy plant.
- (3)
- The outer layer of the hybrid adaptive scheme is derived by simple adaptive control. Under unpredictable fault conditions, the degree of damage cannot be modeled a priori. Thus, a reference model of the healthy aircraft is prescribed. The fault plant is forced to track the state trajectory of the healthy reference model, as long as there is sufficient surplus control effectiveness. Simulation is performed under the condition of 80% elevator damage during the late stage of conversion. Results show that the fault can be detected and the controller is able to stabilize the aircraft and complete the conversion phase. Although performance reduction indeed exists as evidenced by a much larger height variation than in a healthy case, the aircraft can still track the correct conversion path.
Author Contributions
Conceptualization, J.W. and Y.S.; methodology, J.W.; software, J.W.; validation, J.W.; formal analysis, J.W.; investigation, J.W. and D.H.; resources, J.W. and C.Y.; data curation, J.W. and H.W.; writing—original draft preparation, J.W.; writing—review and editing, J.W., Y.S., H.W., D.H. and C.Y.; visualization, J.W.; supervision, Y.S., H.W. and D.H.; project administration, Y.S.; funding acquisition, Y.S. and C.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Jiangxi Province Key Research and Development Program: Research on Key Technologies of High-Speed VTOL Vehicles, grant number 20203ABC28W002.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The funders had no role in the design of the study, in the collection, analyses, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results. Author C.Y. is an employee of Hongdu Aviation Industry Group (AVIC). The paper reflects the views of the scientist, and not the company.
References
- Rysdyk, R.T.; Calise, A.J. Adaptive Model Inversion Flight Control for Tilt-Rotor Aircraft. J. Guid. Control Dyn. 2012, 22, 402–407. [Google Scholar] [CrossRef]
- D’Intino, G.; Pollini, L.; Buelthoff, H.H. A 2-DoF Helicopter Haptic Support System based on Pilot Intent Estimation with Neural Networks. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Swinney, C.J.; Woods, J.C. Unmanned Aerial Vehicle Operating Mode Classification Using Deep Residual Learning Feature Extraction. Aerospace 2021, 8, 79. [Google Scholar] [CrossRef]
- Wada, D.; Araujo-Estrada, S.A.; Windsor, S. Unmanned Aerial Vehicle Pitch Control under Delay Using Deep Reinforcement Learning with Continuous Action in Wind Tunnel Test. Aerospace 2021, 8, 258. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Y.; Liu, M.; Yang, M.; Liang, H. A Real-Time Trajectory Optimization Method for Hypersonic Vehicles Based on a Deep Neural Network. Aerospace 2022, 9, 188. [Google Scholar] [CrossRef]
- Jiang, B.; Li, B.; Zhou, W.; Lo, L.-Y.; Chen, C.-K.; Wen, C.-Y. Neural Network Based Model Predictive Control for a Quadrotor UAV. Aerospace 2022, 9, 460. [Google Scholar] [CrossRef]
- Francesco, G.D.; D’Amato, E.; Mattei, M. Incremental Nonlinear Dynamic Inversion and Control Allocation for a Tilt Rotor UAV. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, National Harbor, ML, USA, 13–17 January 2014. [Google Scholar]
- Gruenwald, B.C.; Bryson, J. Direct Uncertainty Minimization Adaptive Control for a Guided Projectile. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 & 19–21 January 2021. [Google Scholar] [CrossRef]
- Gruenwald, B.C.; Yucelen, T.; Muse, J.A. Direct Uncertainty Minimization in Model Reference Adaptive Control: Experimental Results. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Mooij, E. Simple Adaptive Control System Design Trades, AIAA 2017-1502. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Hsu, M.W.; Liu, H. Design of a Nonlinear Hierarchical Adaptive Controller for a Novel Tilt-Rotor VTOL AquaUAV. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 & 19–21 January 2021. [Google Scholar] [CrossRef]
- Ma, X.; Dong, W.; Li, B. A Novel RFDI-FTC System for Thrust-Vectoring Aircraft Undergoing Control Surface Damage and Actuator Faults During Supermaneuverable Flight. IEEE Access 2019, 7, 156374–156385. [Google Scholar] [CrossRef]
- Lu, B.; Ma, J.; Zheng, Z. Adaptive Closed-Loop Control Allocation-Based Fault Tolerant Flight Control for an Overactuated Aircraft. IEEE Access 2019, 7, 179505–179516. [Google Scholar] [CrossRef]
- Cui, Y.; Li, A.; Meng, X. A fault-tolerant control method for distributed flight control system facing wing damage. J. Syst. Eng. Electron. 2021, 32, 1041–1052. [Google Scholar]
- Park, H.; Kim, Y. Adaptive Fault Tolerant Flight Control for Input Redundant Systems Using a Nonlinear Reference Model. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 3337–3356. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, Y.; Jiang, B. PID-type fault-tolerant prescribed performance control of fixed-wing UAV. J. Syst. Eng. Electron. 2021, 32, 1053–1061. [Google Scholar] [CrossRef]
- Sun, R.; Shan, A.; Zhang, C.; Wu, J.; Jia, Q. Quantized Fault-Tolerant Control for Attitude Stabilization with Fixed-Time Disturbance Observer. J. Guid. Control Dyn. 2021, 44, 449–455. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, Y. Adaptive Fault-Tolerant Control Allocation of an Over-actuated Hybrid Fixed-wing UAV. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Yan, K.; Chen, M.; Wu, Q.; Zhu, R. Robust adaptive compensation control for unmanned autonomous helicopter with input saturation and actuator faults. Chin. J. Aeronaut. 2019, 32, 2299–2310. [Google Scholar] [CrossRef]
- Ortiz-Torres, G.; Castillo, P.; Sorcia-Vazquez, F.D.J.; Rumbo-Morales, J.Y.; Brizuela-Mendoza, J.A.; De La Cruz-Soto, J.; Martinez-Garcia, M. Fault Estimation and Fault Tolerant Control Strategies Applied to VTOL Aerial Vehicles with Soft and Aggressive Actuator Faults. IEEE Access 2020, 8, 10649–10661. [Google Scholar] [CrossRef]
- Chung, W.; Son, H. Fault-Tolerant Control of Multirotor UAVs by Control Variable Elimination. IEEE/ASME Trans. Mechatron. 2020, 25, 2513–2522. [Google Scholar] [CrossRef]
- Sun, S.; Wang, X.; Chu, Q.; de Visser, C. Incremental Nonlinear Fault-Tolerant Control of a Quadrotor with Complete Loss of Two Opposing Rotors. IEEE Trans. Robot. 2021, 37, 116–130. [Google Scholar] [CrossRef]
- Thanaraj, T.; Ng, B.F.; Low, K.H. Active Fault Tolerant Control on Multi-rotor UAVs using ELM-based Neuro-Fuzzy System. In Proceedings of the AIAA AVIATION 2022 Forum, Chicago, IL, USA, 27 June 27–1 July 2022. [Google Scholar]
- Wang, B.; Zhu, D.; Han, L.; Gao, H.; Gao, Z.; Zhang, Y. Adaptive Fault-Tolerant Control of a Hybrid Canard Rotor/Wing UAV Under Transition Flight Subject to Actuator Faults and Model Uncertainties. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4559–4574. [Google Scholar] [CrossRef]
- Ahmed, I.; Quinones-Grueiro, M.; Biswas, G. Adaptive fault-tolerant control of octo-rotor UAV under motor faults in adverse wind conditions. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar]
- Beyer, Y.; Steen, M.; Hecker, P. Incremental Passive Fault-Tolerant Control for Quadrotors Subjected to Complete Rotor Failures. J. Guid. Control Dyn. 2023, 46, 2033–2042. [Google Scholar] [CrossRef]
- Du, Y.; Huang, P.; Cheng, Y.; Fan, Y.; Yuan, Y. Fault Tolerant Control of a Quadrotor Unmanned Aerial Vehicle Based on Active Disturbance Rejection Control and Two-Stage Kalman Filter. IEEE Access 2023, 11, 67556–67566. [Google Scholar] [CrossRef]
- Lee, H.; Kim, J.; Kim, S.; Kim, M.; Kim, Y. Local Strong Accessibility Analysis and Fault-Tolerant Control of Multicopter Considering Actuator Failures. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar]
- Anderson, B.D.O.; Brinsmead, T.S.; Bruyne, F.D.; Hespanha, J.; Liberzon, D.; Morse, A.S. Multiple model adaptive control. Part 1: Finite controller coverings. Int. J. Robust Nonlinear Control 2000, 10, 909–929. [Google Scholar] [CrossRef]
- Kaufman, H.; Barkana, I.; Sobel, K. Direct Adaptive Control Algorithms: Theory and Applications, 2nd ed.; Springer-Verlag: New York, NY, USA, 1998. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).