Efficient Method for Heat Flux Calculations within Multidisciplinary Analyses of Hypersonic Vehicles
Abstract
:1. Introduction
2. Heat Flux Calculation
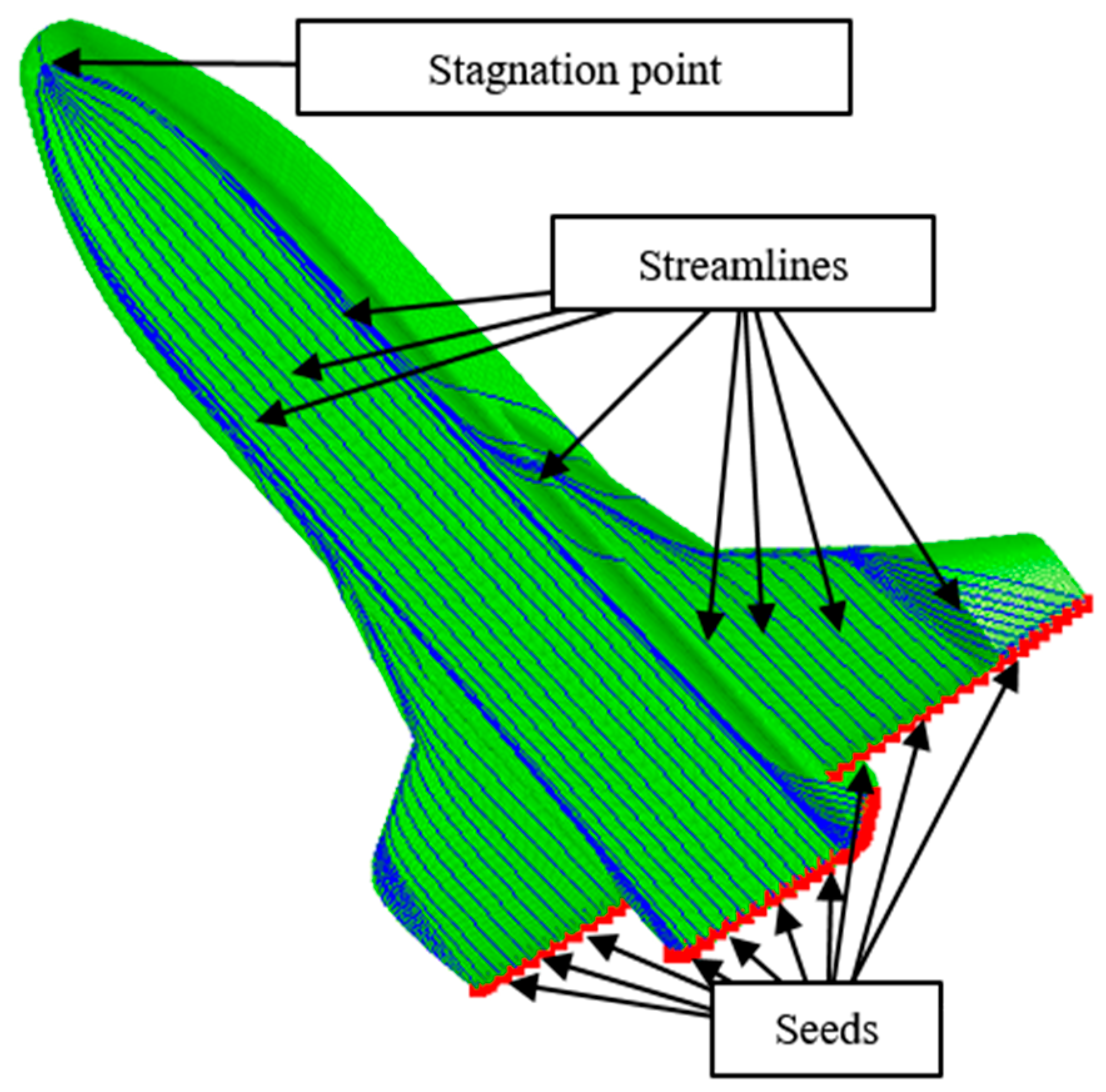
2.1. Streamline Calculation
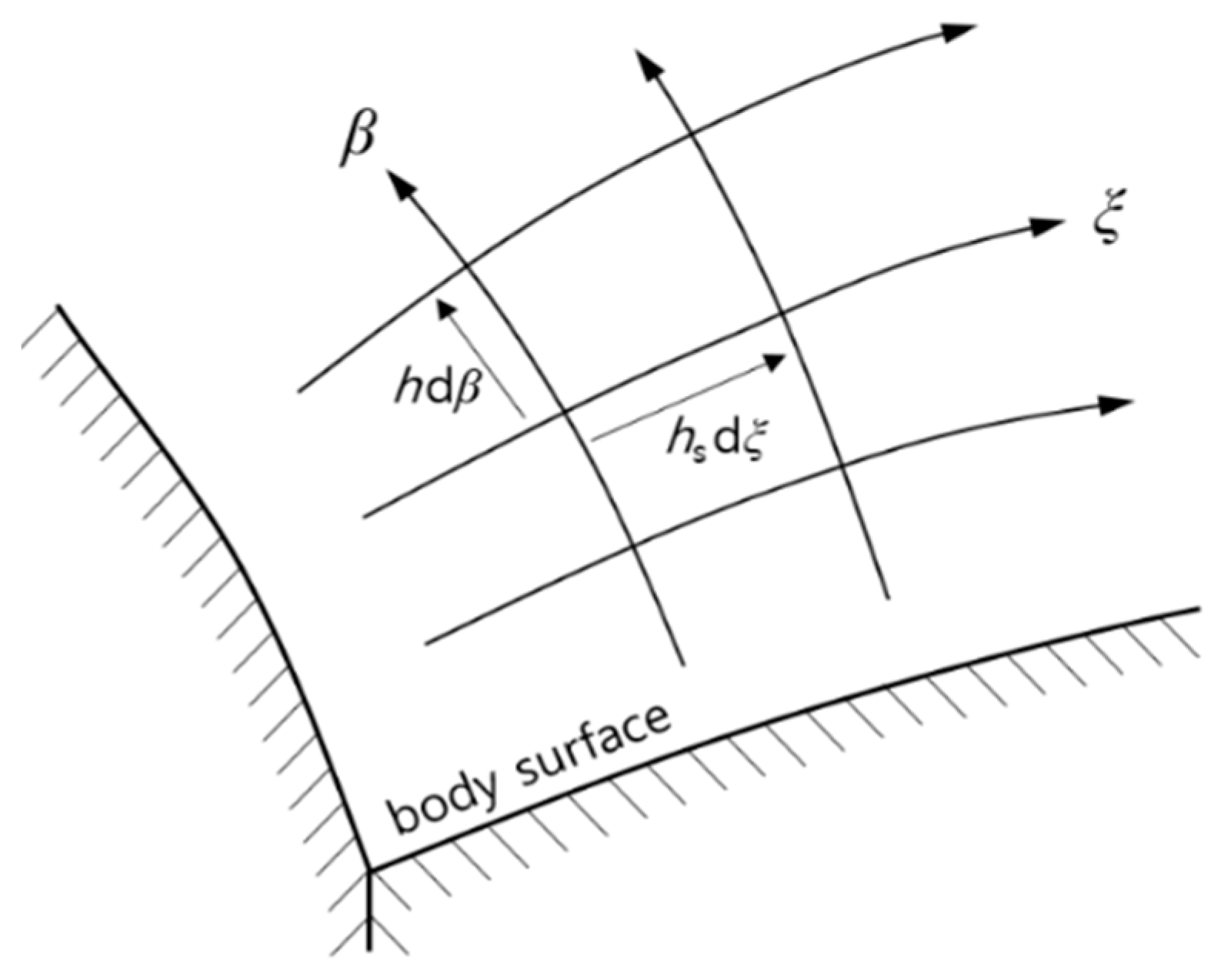
2.2. Streamline Metrics
2.3. Heating Equations
2.4. Heat Flux near the Stagnation Point
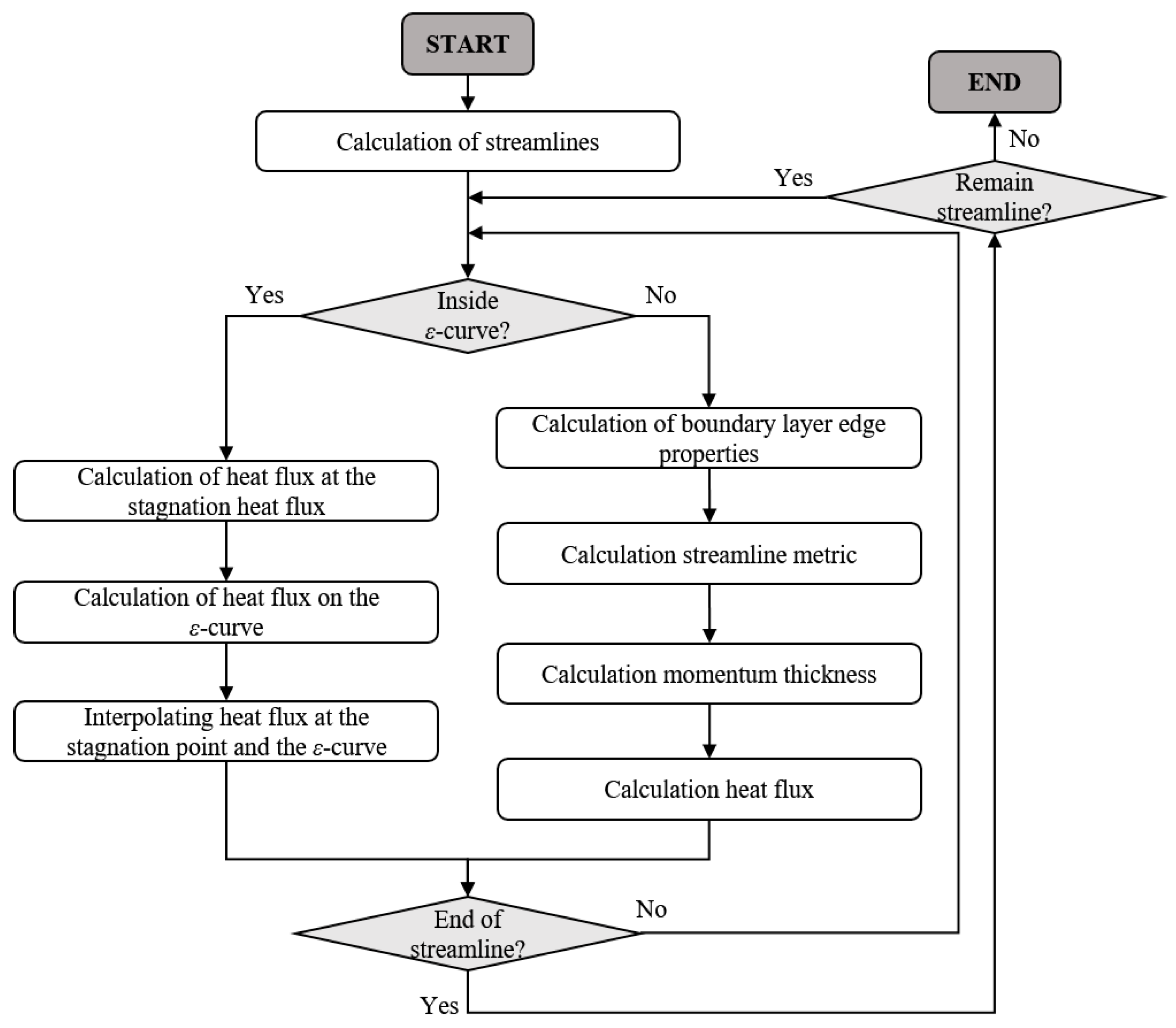
2.5. Heat Flux Calculation Procedure
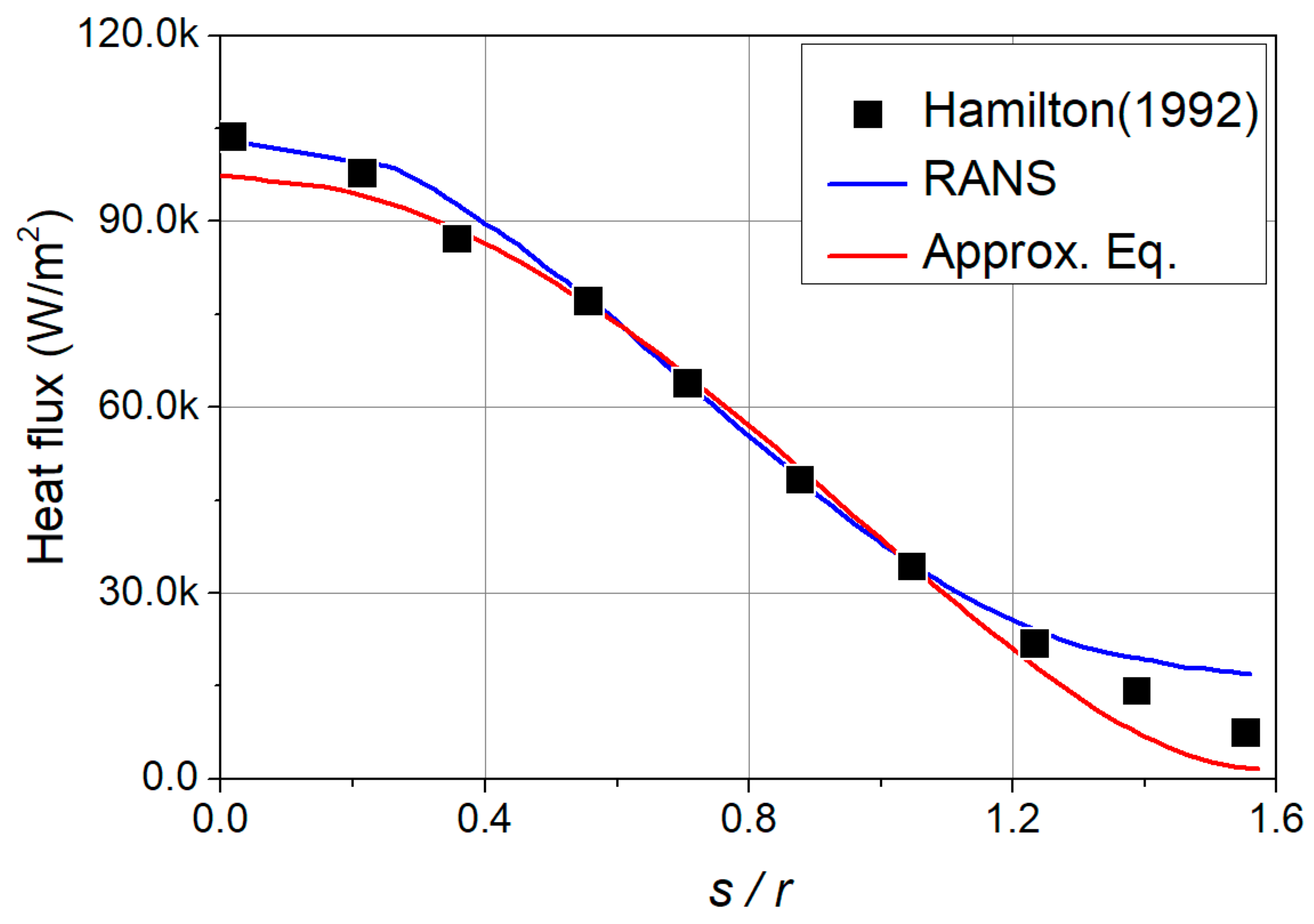
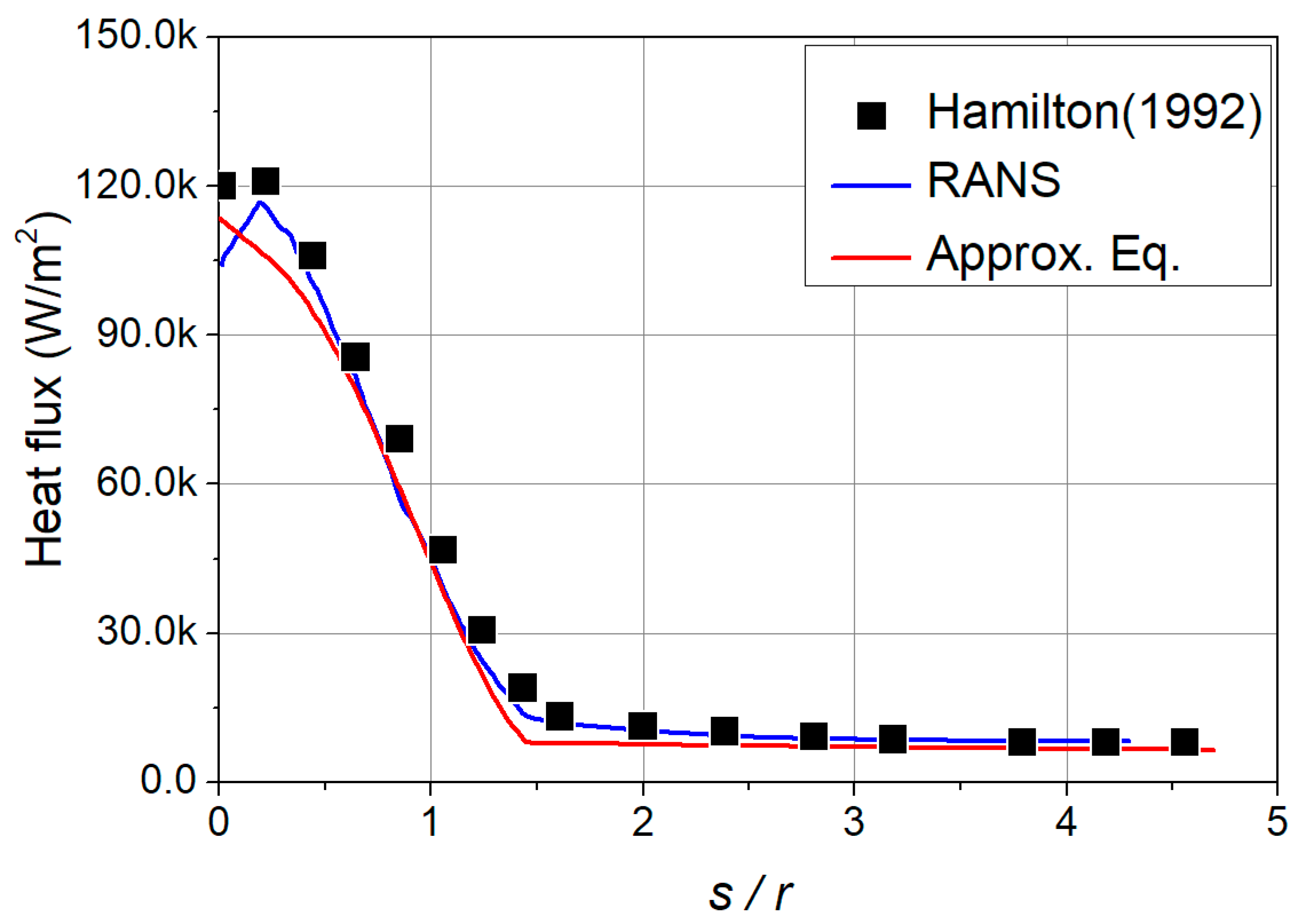
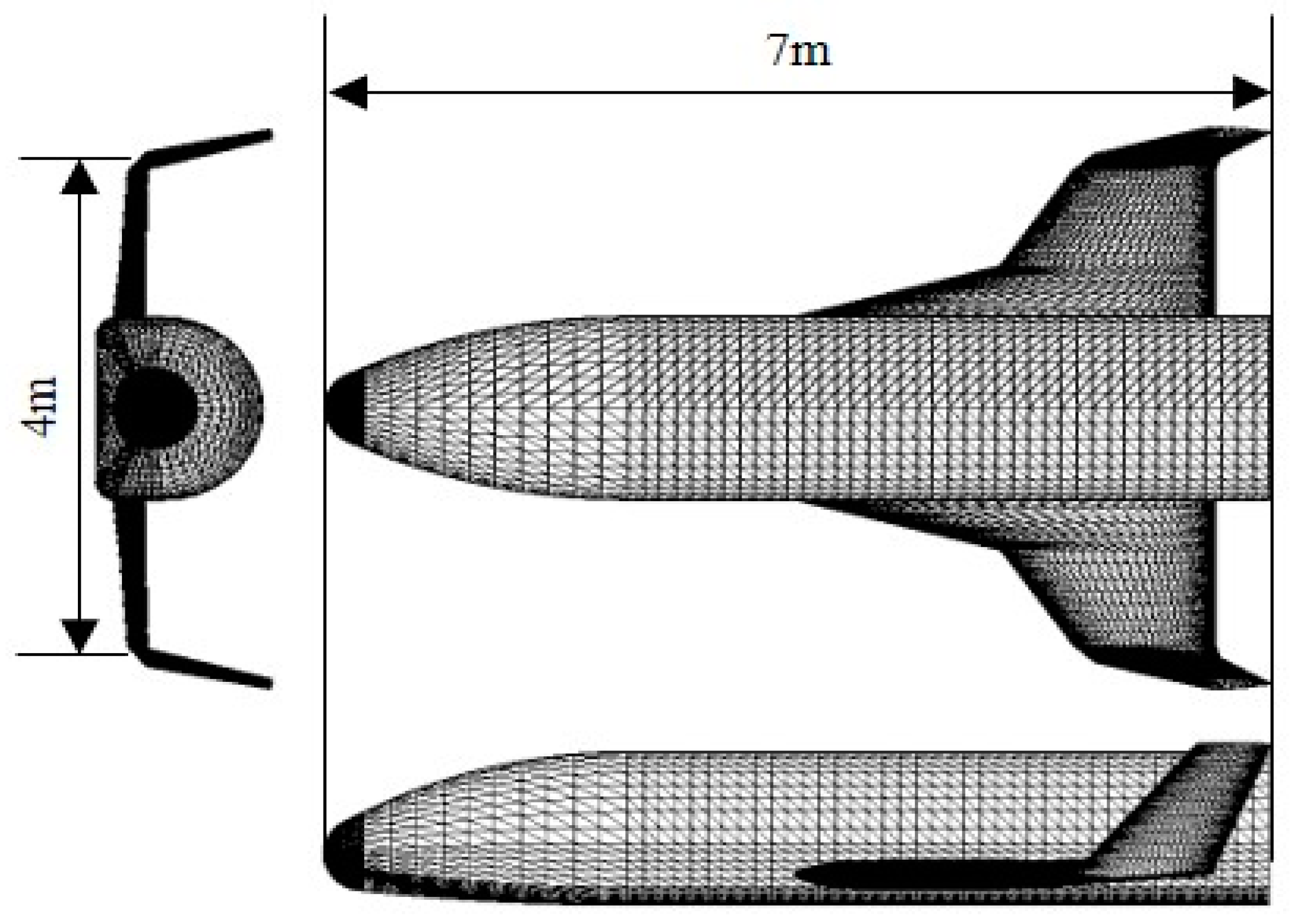
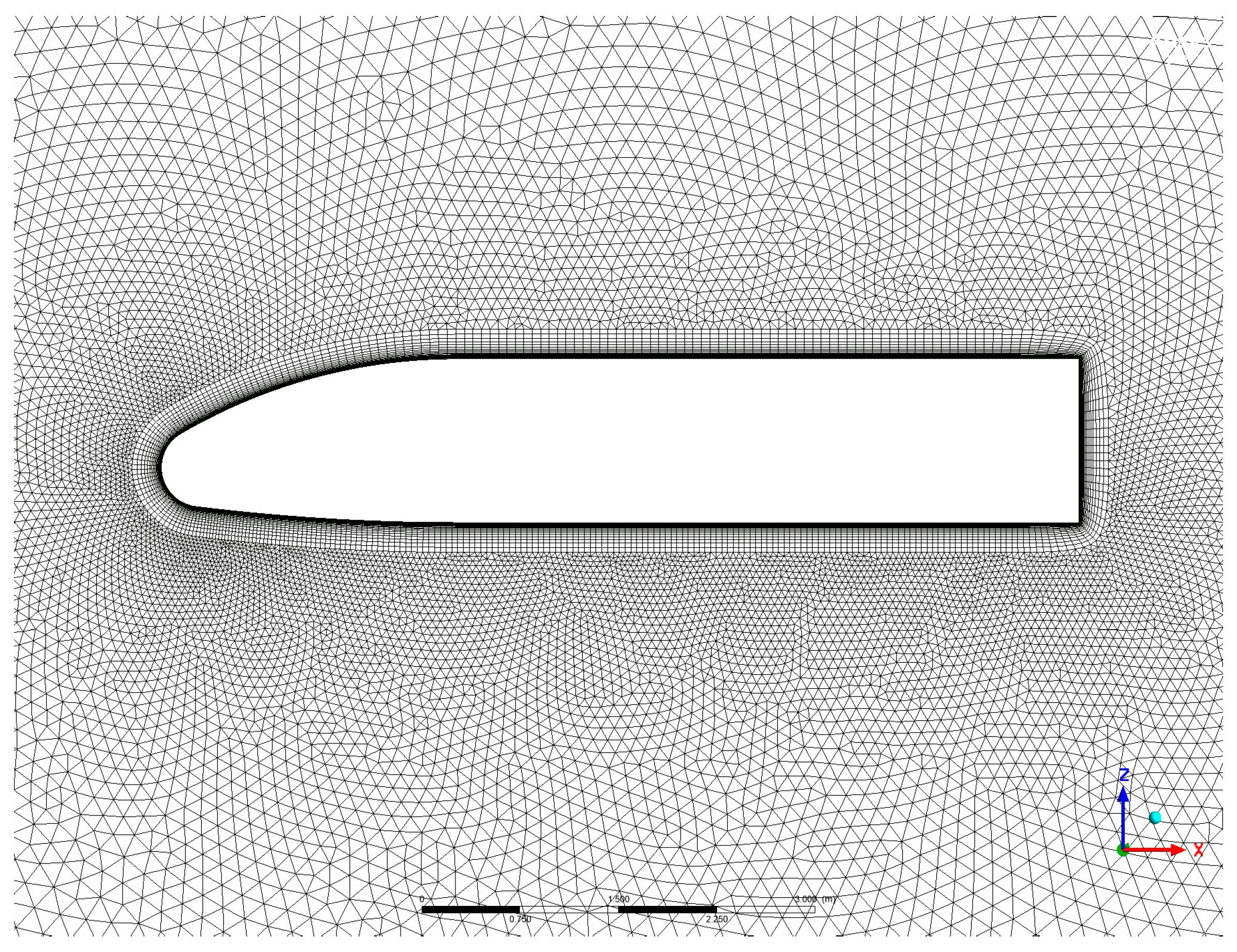
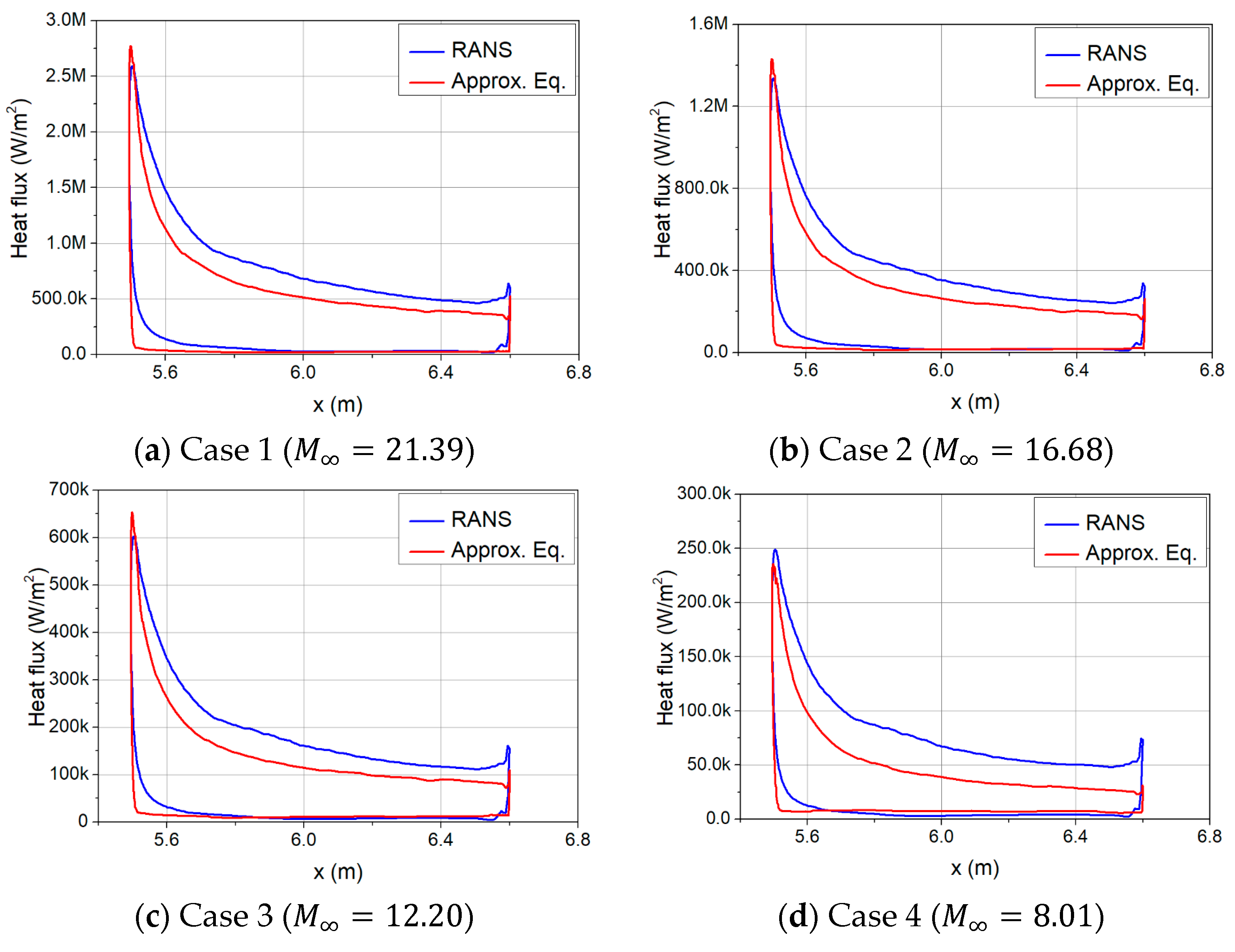
2.6. Heat Flux Calculation Validation
3. Adaptive Time Step for the Heat Flux Calculation
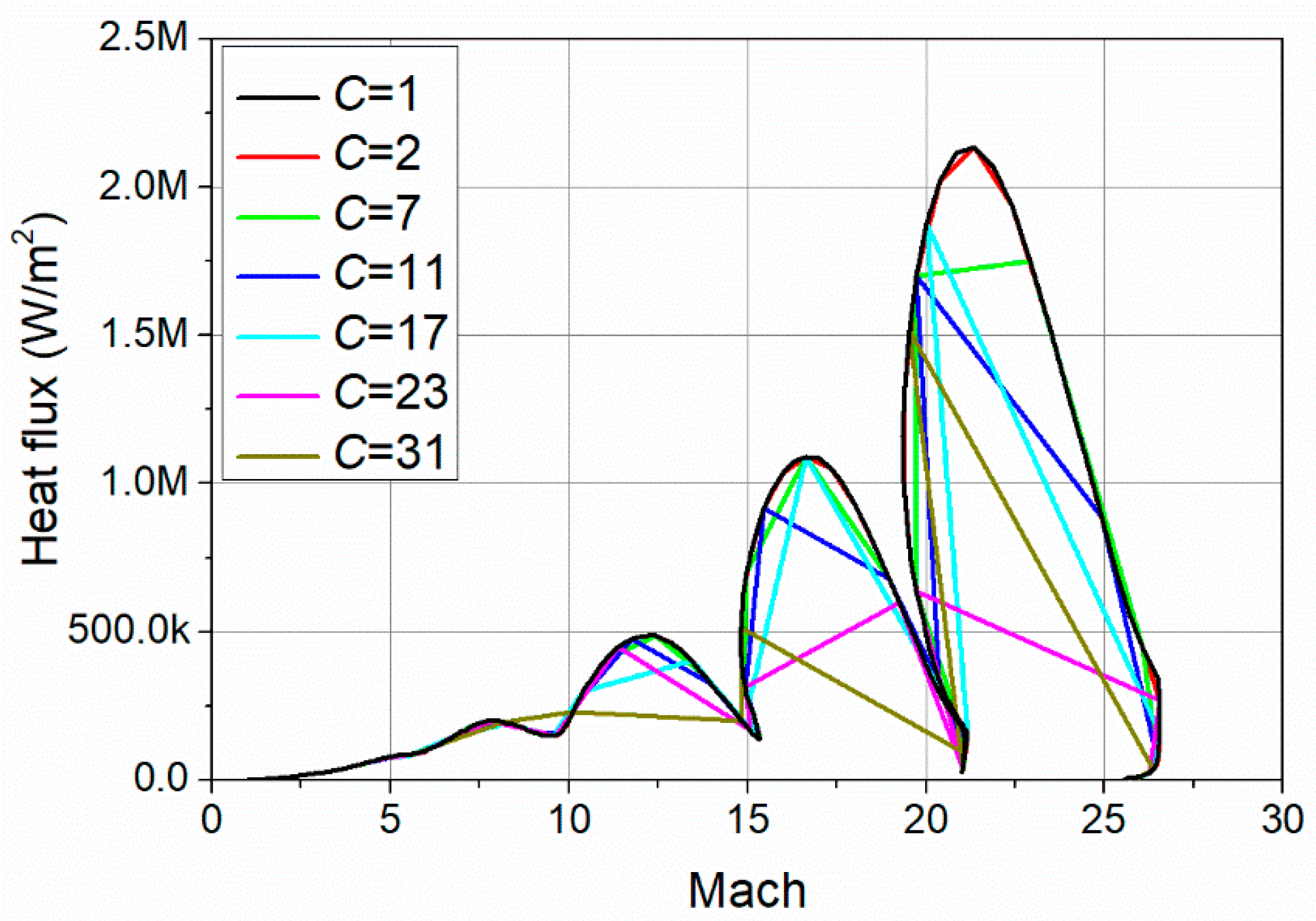
3.1. Constant
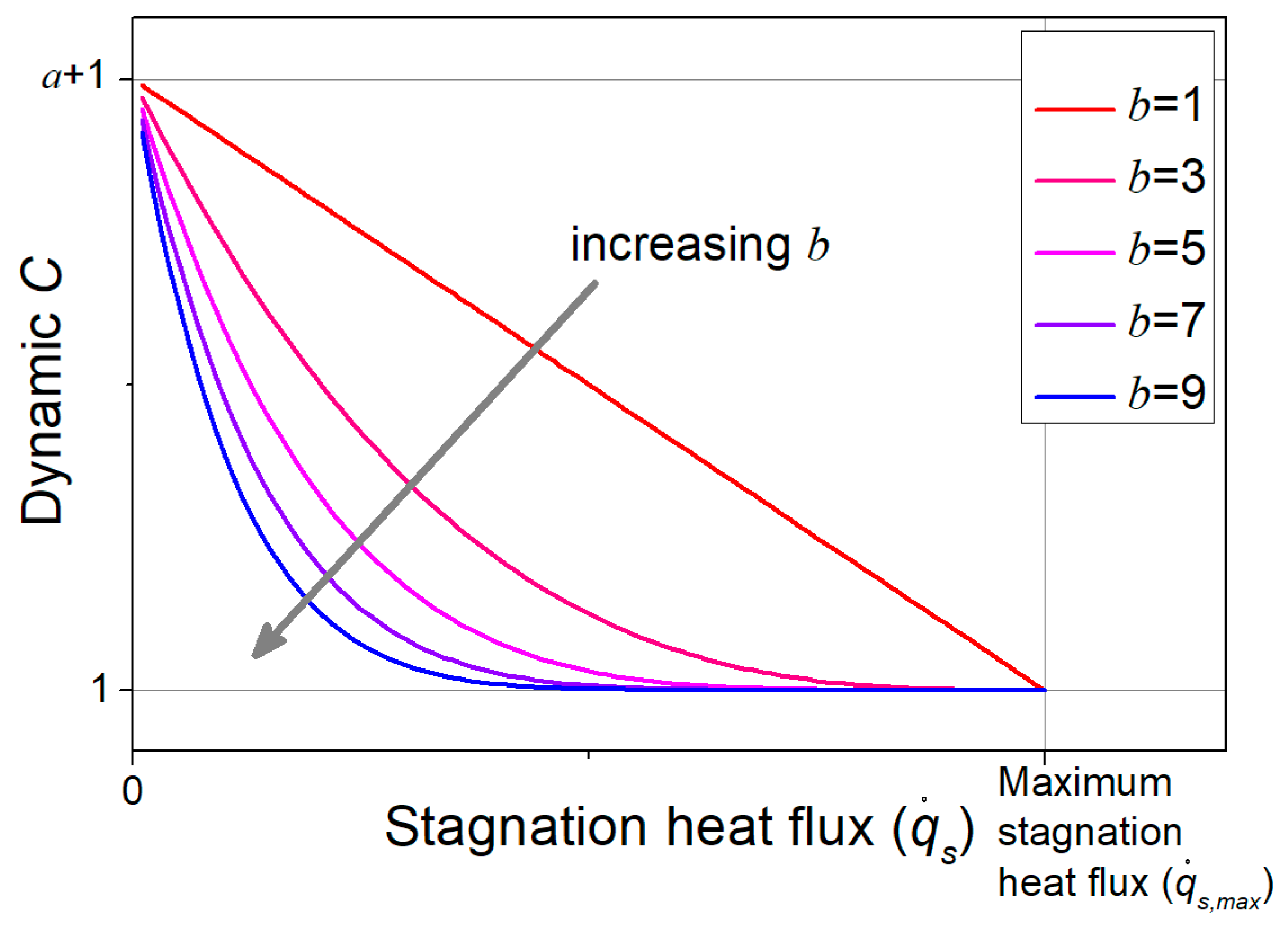
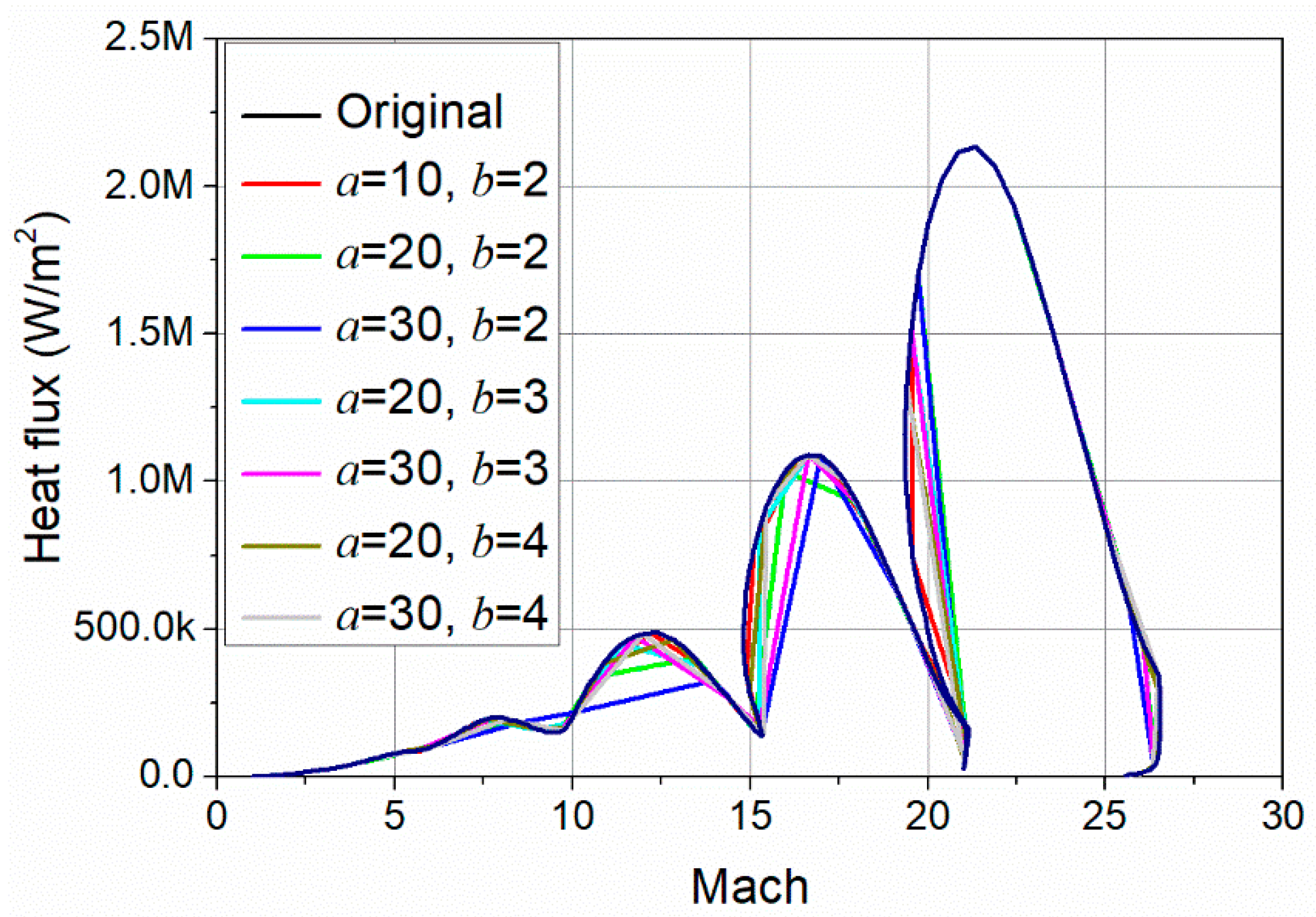
3.2. Dynamic
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, F.; Liu, H.; Zhang, S. Coupled heat transfer and thermo-mechanical behavior of hypersonic cylindrical leading edges. Int. J. Heat Mass Transf. 2018, 122, 846–862. [Google Scholar] [CrossRef]
- Seager, C.; Agarwal, R.K. Hypersonic blunt-body shape optimization for reducing drag and heat transfer. J. Thermophys. Heat Transf. 2017, 31, 48–55. [Google Scholar] [CrossRef]
- Wang, W.; Wu, Z.; Wang, D.; Yang, J.; Wang, P.; Zhang, W. Hypersonic vehicle aerodynamic optimization using field metamodel-enhanced sequential approximate optimization. Int. J. Aerosp. Eng. 2021, 2021, 8889593. [Google Scholar] [CrossRef]
- Helm, C.M.; Martin, M.P. New LES of a Hypersonic Shock/Turbulent Boundary Layer Interaction. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2016. [Google Scholar]
- Liu, X.; Shen, Z.; Lu, P. Entry trajectory optimization by second-order cone programming. J. Guid. Control. Dyn. 2016, 39, 227–241. [Google Scholar] [CrossRef]
- Tauber, M.E. A Review of High-Speed, Convective, Heat-Transfer Computation Methods; NASA TP 2914; NASA: Mountain View, CA, USA, 1989. [Google Scholar]
- Meador, W.E.; Smart, M.K. Reference enthalpy method developed from solutions of the boundary-layer equations. AIAA J. 2005, 43, 135–139. [Google Scholar] [CrossRef]
- Anderson, J.D., Jr. Hypersonic and High-Temperature Gas Dynamics; AIAA: Reston, VA, USA, 2019. [Google Scholar]
- Zoby, E.V.; Moss, J.N.; Suttont, K. Approximate convective-heating equations for hypersonic flows. J. Spacecr. Rockets 1981, 18, 64–70. [Google Scholar] [CrossRef]
- Hamilton, H.H.; Weilmuenster, K.J.; Dejarnette, F.R. Improved approximate method for computing convective heating on hypersonic vehicles using unstructured grids. In Proceedings of the 9th AIAA/ASME Joint Thermophysics and Heat Transfer Conference, San Francsico, CA, USA, 5–8 June 2006; Volume 2, pp. 1306–1326. [Google Scholar] [CrossRef]
- Hamilton, H.H.; Weilmuenster, K.J.; DeJarnette, F.R. Approximate method for computing laminar and turbulent convective heating on hypersonic vehicles using unstructured grids. In Proceedings of the 41st AIAA Thermophysics Conference, San Antonio, TX, USA, 22–25 June 2009; pp. 1–26. [Google Scholar] [CrossRef]
- Kamezawa, H.; Ruffin, S.M. Approximate convective heat flux calculation methods for hypersonic vehicles. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; pp. 1–15. [Google Scholar] [CrossRef]
- Zhao, J.; Gu, L.; Ma, H. A rapid approach to convective aeroheating prediction of hypersonic vehicles. Sci. China Technol. Sci. 2013, 56, 2010–2024. [Google Scholar] [CrossRef]
- Jung, J.; Yang, H.; Kim, K.; Yee, K.; You, K.; Park, K.; Jeong, S. Conceptual design of a reusable unmanned space vehicle using multidisciplinary optimization. Int. J. Aeronaut. Space Sci. 2018, 19, 743–750. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, Y. Integrated optimization design using improved pigeon-inspired algorithm for a hypersonic vehicle model. Int. J. Aeronaut. Space Sci. 2022, 23, 1033–1042. [Google Scholar] [CrossRef]
- Lee, D.-S.; Sung, H.-G. Performance design of a turbofan engine using multi-objective particle swarm optimization (MOPSO). Int. J. Aeronaut. Space Sci. 2022, 23, 533–545. [Google Scholar] [CrossRef]
- Arshad, A.; Rodrigues, L.B.; López, I.M. Design optimization and investigation of aerodynamic characteristics of low Reynolds number airfoils. Int. J. Aeronaut. Space Sci. 2021, 22, 751–764. [Google Scholar] [CrossRef]
- Birken, P.; Quint, K.J.; Hartmann, S.; Meister, A. A time-adaptive fluid-structure interaction method for thermal coupling. Comput. Vis. Sci. 2010, 13, 331–340. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A. Adaptive stepsize Runge-Kutta integration. Comput. Phys. 1992, 6, 188–191. [Google Scholar] [CrossRef]
- Tremblay, J.C.; Carrington, T. Using preconditioned adaptive step size Runge-Kutta methods for solving the time-dependent Schrödinger equation. J. Chem. Phys. 2004, 121, 11535–11541. [Google Scholar] [CrossRef]
- Gustafsson, K. Control theoretic techniques for stepsize selection in explicit Runge-Kutta methods. ACM Trans. Math. Softw. 1991, 17, 533–554. [Google Scholar] [CrossRef]
- Gustafsson, K. Control-theoretic techniques for stepsize selection in implicit Runge-Kutta methods. ACM Trans. Math. Softw. 1994, 20, 496–517. [Google Scholar] [CrossRef]
- Gustafsson, K.; Lundh, M.; Söderlind, G. A PI stepsize control for the numerical solution of ordinary differential equations. BIT Numer. Math. 1988, 28, 270–287. [Google Scholar] [CrossRef]
- Kushner, H.J.; Yang, J. Analysis of adaptive step-size SA algorithms for parameter tracking. IEEE Trans. Automat. Control 1995, 40, 1403–1410. [Google Scholar] [CrossRef]
- Söderlind, G. Automatic control and adaptive time-stepping. Numer. Algorithms 2002, 31, 281–310. [Google Scholar] [CrossRef]
- Walter, D.; Petrov, V.; Manera, A.; Kendrick, B.K. A control theory approach to adaptive stepsize selection for coupled CFD and crud chemistry simulations. In Proceedings of the International Topical Meeting on Nuclear Reactor Thermal Hydraulics 2015, NURETH 2015, Chicago, IL, USA, 30 August–4 September 2015; Volume 2, pp. 926–939. [Google Scholar]
- Valli, A.M.P.; Carey, G.F.; Coutinho, A.L.G.A. Control strategies for timestep selection in finite element simulation of incompressible flows and coupled reaction-convection-diffusion processes. Int. J. Numer. Methods Fluids 2005, 47, 201–231. [Google Scholar] [CrossRef]
- Valli, A.M.P.; Carey, G.F.; Coutinho, A.L.G.A. Control strategies for timestep selection in simulation of coupled viscous flow and heat transfer. Commun. Numer. Methods Eng. 2002, 18, 131–139. [Google Scholar] [CrossRef]
- Cueto-Felgueroso, L.; Peraire, J. A time-adaptive finite volume method for the Cahn–Hilliard and Kuramoto–Sivashinsky equations. J. Comput. Phys. 2008, 227, 9985–10017. [Google Scholar] [CrossRef]
- Chen, F.; Liu, H.; Zhang, S. Time-adaptive loosely coupled analysis on fluid–thermal–structural behaviors of hypersonic wing structures under sustained aeroheating. Aerosp. Sci. Technol. 2018, 78, 620–636. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, F.; Liu, H. Time-adaptive, loosely coupled strategy for conjugate heat transfer problems in hypersonic flows. J. Thermophys. Heat Transf. 2014, 28, 635–646. [Google Scholar] [CrossRef]
- Somarathne, S.; Seymour, M.; Kolokotroni, M. Dynamic thermal CFD simulation of a typical office by efficient transient solution methods. Build. Environ. 2005, 40, 887–896. [Google Scholar] [CrossRef]
- Anderson, J.D., Jr. Modern Compressible Flow with Historical Perspective, 3rd ed.; McGraw-Hill: NewYork, NY, USA, 2004; ISBN 9780071241366. [Google Scholar]
- Lo, S.H. Automatic mesh generation over intersecting surfaces. Int. J. Numer. Methods Eng. 1995, 38, 943–954. [Google Scholar] [CrossRef]
- Cooke, J.C. An Axially Symmetric Analogue for General Three-Dimensional Boundary Layers; AERADE: London, UK, 1961. [Google Scholar]
- Bertin, J.J.; Cummings, R.M. Fifty years of hypersonics: Where we’ve been, where we’re going. Prog. Aerosp. Sci. 2003, 39, 511–536. [Google Scholar] [CrossRef]
- Brchnelova, M.; Mooij, E. Re-entry shape optimisation using the axisymmetric analogue method with modified newtonian technique resolved inviscid flow field. In Proceedings of the AIAA Scitech 2021 Forum, Virtual Event, 11–15 January 2021; pp. 1–23. [Google Scholar] [CrossRef]
- Bouslog, S.; An, M.; Hartmann, L.; Derry, S. Review of Boundary Layer Transition Flight Data on the Space ShuttleOrbiter. In Proceedings of the 29th Aerospace Sciences Meeting, Reno, NV, USA, 7–10 January 1991; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1991. [Google Scholar]
- Ernst, E. Survey on Heat Transfer at High Speed; ARL 189; U.S Air Force: Wright-Patterson AFB, OH, USA, 1961. [Google Scholar]
- Kemp, N.H.; Rose, P.H.; Detra, R.W. Laminar heat transfer around blunt bodies in dissociated air. J. Aerosp. Sci. 1959, 26, 421–430. [Google Scholar] [CrossRef]
- Cohen, N.B. Boundary-Layer Similar Solutions and Correlation Equations for Laminar Heat-Transfer Distribution in Equilibrium Air at Velocities Up to 41,100 Feet Per Second; NASA TR R-118; NASA: Hampton, VA, USA, 1961. [Google Scholar]
- De Jarnette, F.R.; Hamilton, H.H.; Weilmuenster, K.J.; Cheatwood, F.M. A review of some approximate methods used in aerodynamic heating analyses. J. Thermophys. Heat Transf. 1987, 1, 5–12. [Google Scholar] [CrossRef]
- Hamilton, H.H.; Millman, D.R.; Greendyke, R.B. Finite-Difference Solution for Laminar or Turbulent Boundary Layer Flow over Axisymmetric Bodies with Ideal Gas, CF4, or Equilibrium Air Chemistry; NASA Technical Paper 3271; NASA: Hampton, VA, USA, 1992. [Google Scholar]
- Liou, M.-S. A sequel to AUSM: AUSM+. J. Comput. Phys. 1996, 129, 364–382. [Google Scholar] [CrossRef]
- Rausch, R.; Yang, H.; Batina, J. Spatial adaption procedures on unstructured meshes for accurate unsteady aerodynamic flow computation. In Proceedings of the 32nd Structures, Structural Dynamics, and Materials Conference, Baltimore, MD, USA, 8–10 April 1991; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1991. [Google Scholar]
| Value | |
|---|---|
| 9.74 | |
| 1.4 (perfect gas) | |
| 0.004272 kg/m3 | |
| 53.17 K | |
| 300.0 K |
| Value | |
|---|---|
| 5.00 | |
| 1.4 (perfect gas) | |
| 0.0500 kg/m3 | |
| 115.28 K | |
| 300.0 K |
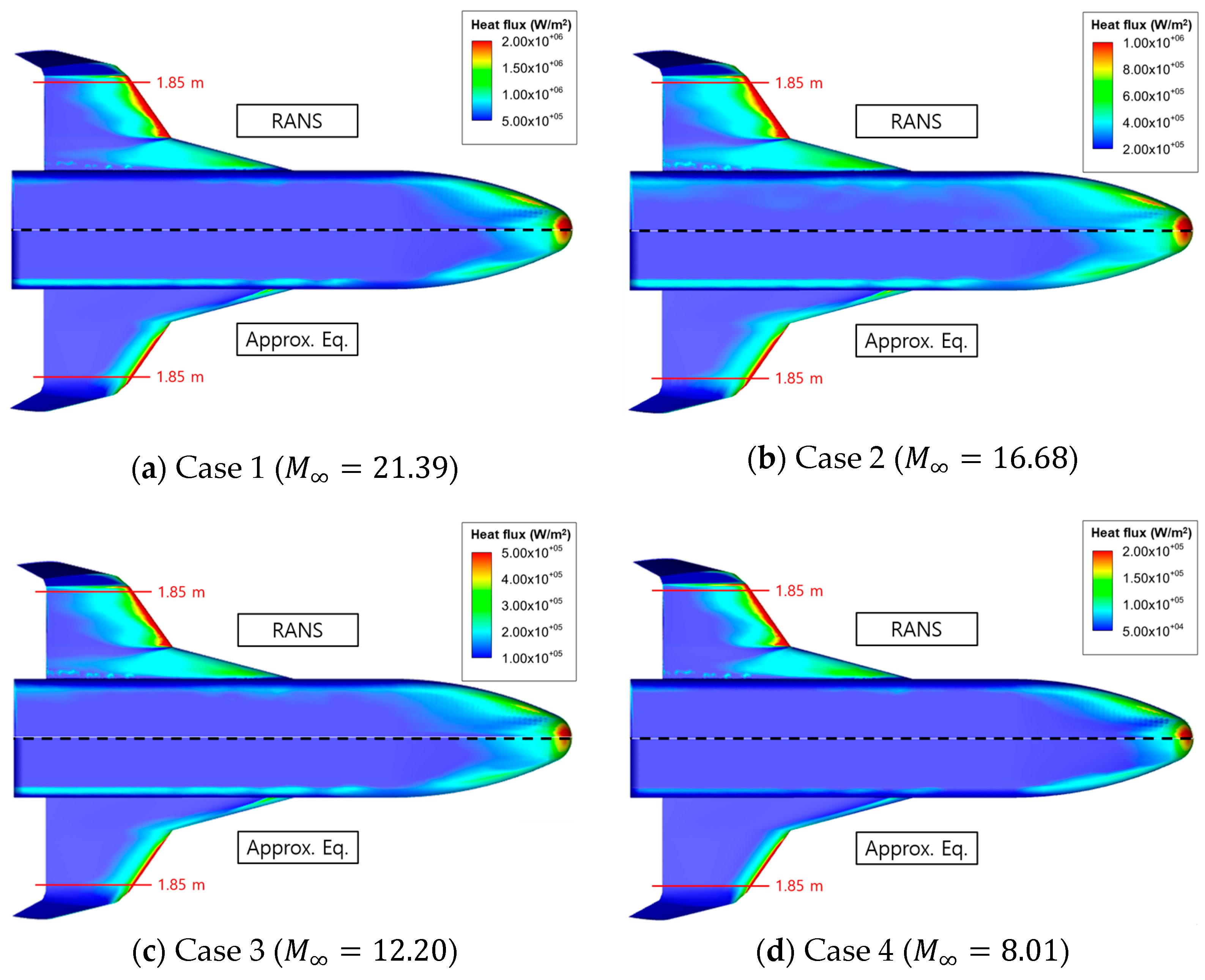
| Case 1 | Case 2 | Case 3 | Case 4 | |
|---|---|---|---|---|
| 21.39 | 16.68 | 12.20 | 8.01 | |
| 1.4 | 1.4 | 1.4 | 1.4 | |
| 40° | 40° | 40° | 40° | |
| 0.000439 kg/m3 | 0.000508 kg/m3 | 0.000645 kg/m3 | 0.001302 kg/m3 | |
| 254.83 K | 258.16 K | 263.76 K | 270.65 K | |
| 300.0 K | 300.0 K | 300.0 K | 300.0 K |
| Number of Computations | Maximum Stagnation Heat Flux (W/m2) | Total Computational Cost (s) | |
|---|---|---|---|
| 1 (original) | 1197 | 2,133,778 | 1553.9525 |
| 2 | 600 | 2,133,778 | 832.1355 |
| 7 | 174 | 1,751,234 | 272.4919 |
| 11 | 111 | 1,700,364 | 211.6848 |
| 17 | 72 | 1,875,972 | 137.2899 |
| 23 | 54 | 634,614 | 114.4419 |
| 31 | 39 | 1,513,749 | 103.5552 |
| Number of Calculations | Maximum Stagnation Heat Flux (W/m2) | Total Computational Cost (s) | ||
|---|---|---|---|---|
| Original | 1197 | 2,133,778 | 1553.9525 | |
| 20 | 1 | 75 | 2,133,778 | 125.2944 |
| 10 | 2 | 156 | 2,133,778 | 215.9298 |
| 20 | 2 | 93 | 2,133,778 | 139.2946 |
| 30 | 2 | 72 | 2,133,778 | 103.8202 |
| 40 | 2 | 57 | 2,133,778 | 81.8680 |
| 20 | 3 | 108 | 2,133,778 | 132.3144 |
| 30 | 3 | 81 | 2,133,778 | 98.2031 |
| 20 | 4 | 123 | 2,133,778 | 128.7518 |
| 30 | 4 | 96 | 2,133,778 | 85.8918 |
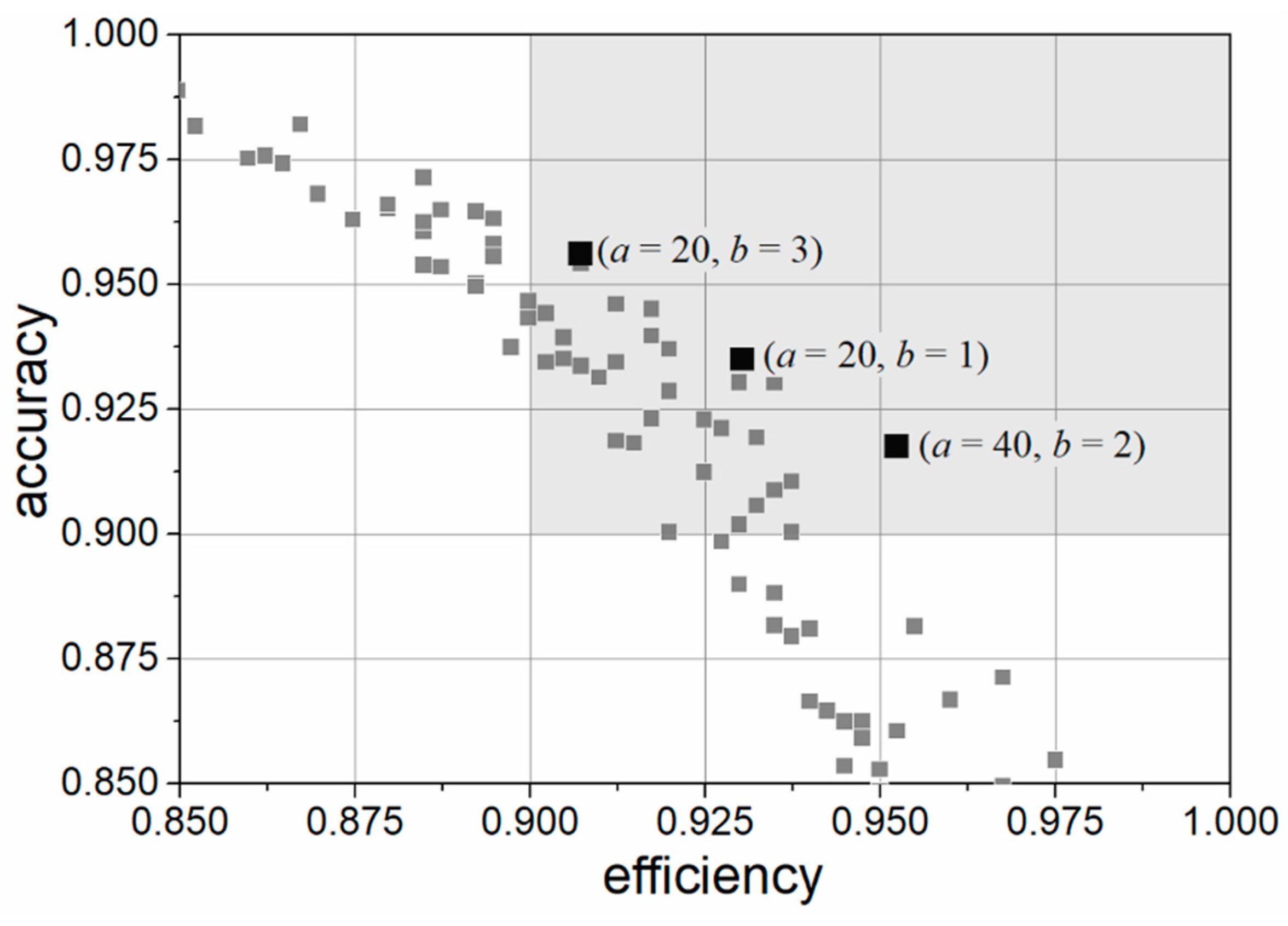
| Number of Calculations | Efficiency | Maximum Stagnation Heat Flux (W/m2) | Accuracy | ||
|---|---|---|---|---|---|
| 40 | 2 | 57 | 0.95238 | 2,133,778 | 0.91737 |
| 20 | 1 | 75 | 0.93042 | 2,133,778 | 0.93484 |
| 20 | 3 | 108 | 0.90727 | 2,133,778 | 0.95610 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, J.; Yee, K.; Jeong, S. Efficient Method for Heat Flux Calculations within Multidisciplinary Analyses of Hypersonic Vehicles. Aerospace 2023, 10, 846. https://doi.org/10.3390/aerospace10100846
Jung J, Yee K, Jeong S. Efficient Method for Heat Flux Calculations within Multidisciplinary Analyses of Hypersonic Vehicles. Aerospace. 2023; 10(10):846. https://doi.org/10.3390/aerospace10100846
Chicago/Turabian StyleJung, Jongho, Kwanjung Yee, and Shinkyu Jeong. 2023. "Efficient Method for Heat Flux Calculations within Multidisciplinary Analyses of Hypersonic Vehicles" Aerospace 10, no. 10: 846. https://doi.org/10.3390/aerospace10100846
APA StyleJung, J., Yee, K., & Jeong, S. (2023). Efficient Method for Heat Flux Calculations within Multidisciplinary Analyses of Hypersonic Vehicles. Aerospace, 10(10), 846. https://doi.org/10.3390/aerospace10100846






