A Unified Numerical Approach to the Dynamics of Beams with Longitudinally Varying Cross-Sections, Materials, Foundations, and Loads Using Chebyshev Spectral Approximation
Abstract
:1. Introduction
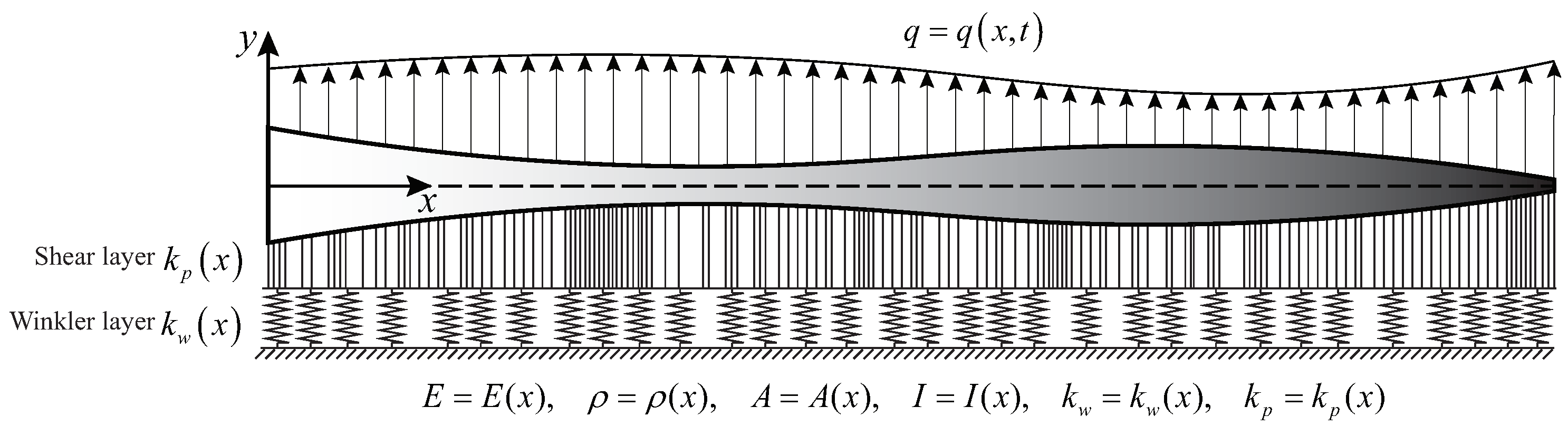
2. Problem Description
3. Theoretical Formulation
3.1. Chebyshev Spectral Approximation
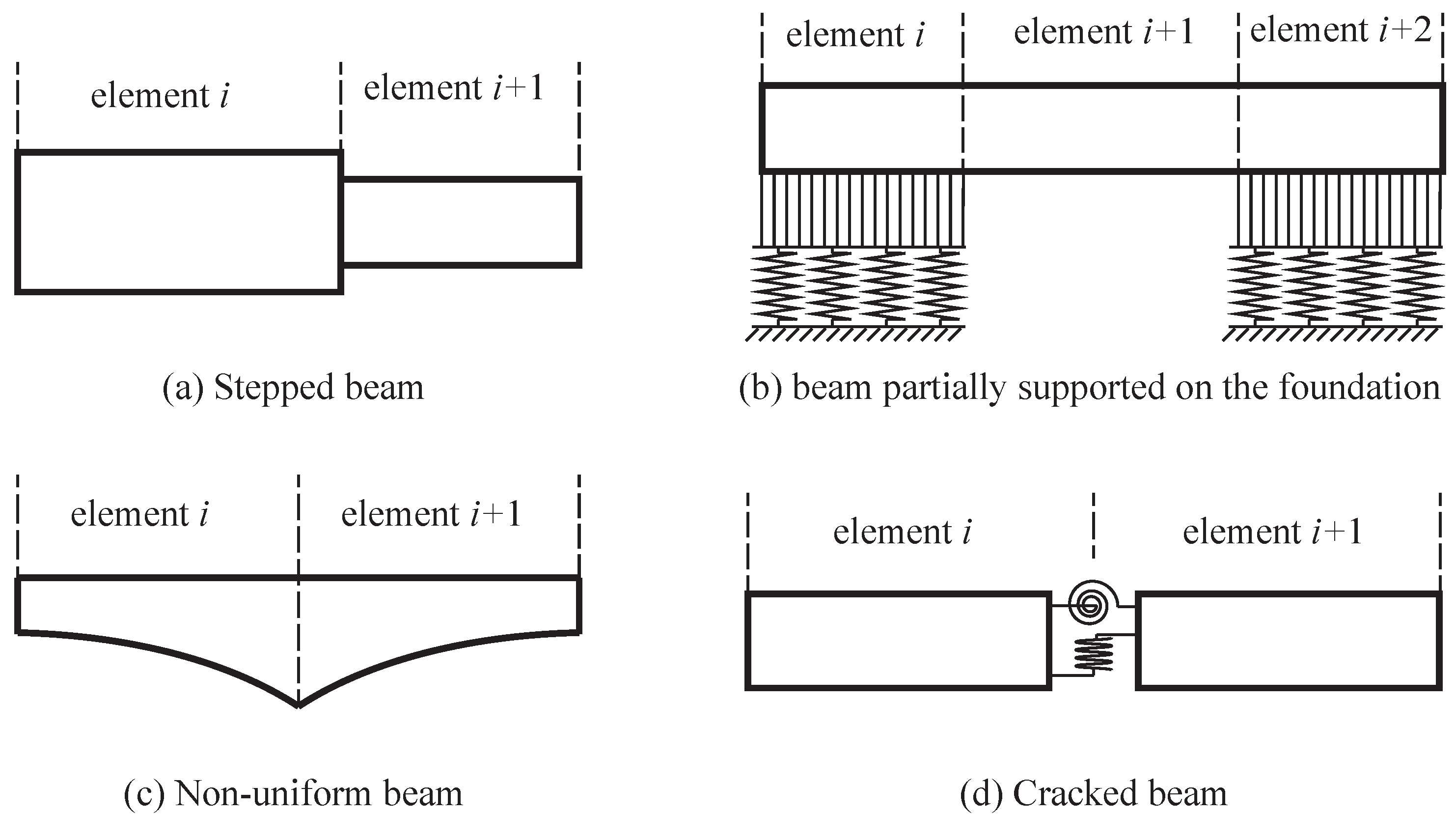
3.2. Spectral Element of Non-Uniform AFG Beams Resting on Variable Foundation
3.3. Assembling Spectral Elements and Imposing Boundary Conditions
4. Numerical Examples
- Case 1: Uniform beams on the homogeneous foundation;
- Case 2: Stepped beams made of axially functionally graded materials;
- Case 3: Non-uniform AFG beams resting on the variable foundation.
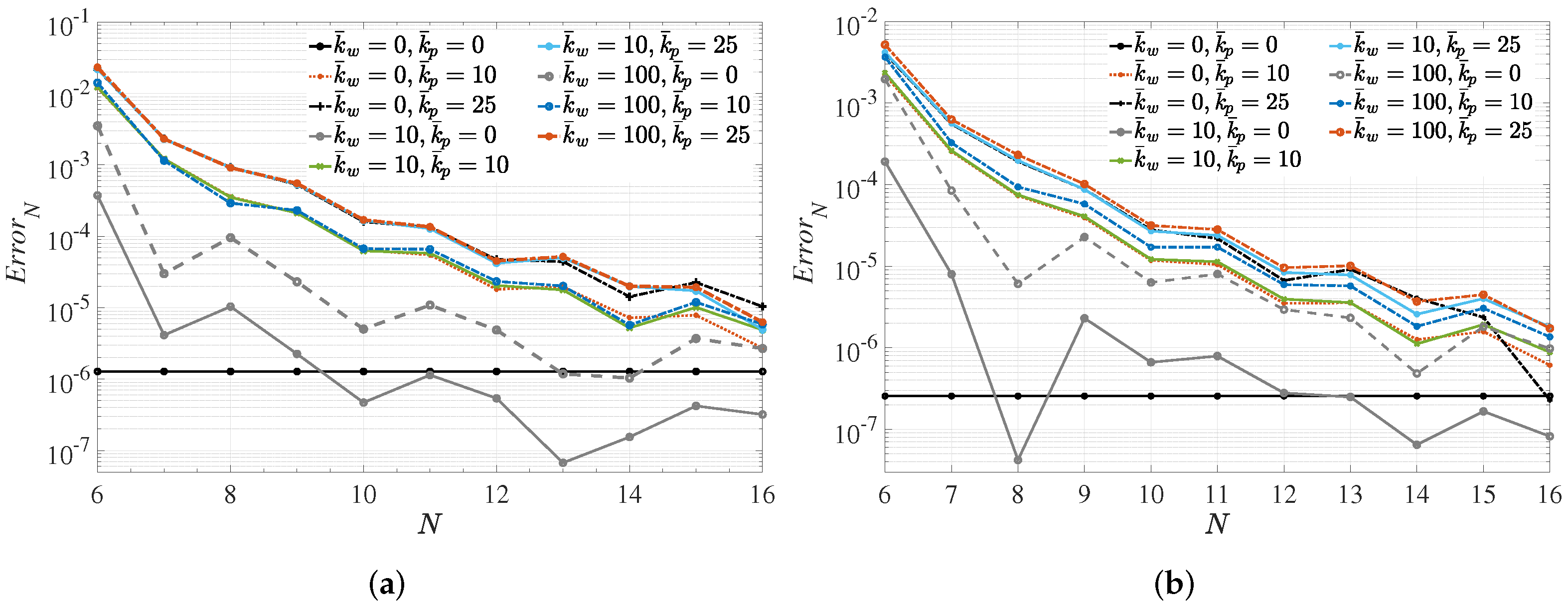
4.1. Uniform Beams on Homogeneous Foundations
4.2. AFG Stepped Beams
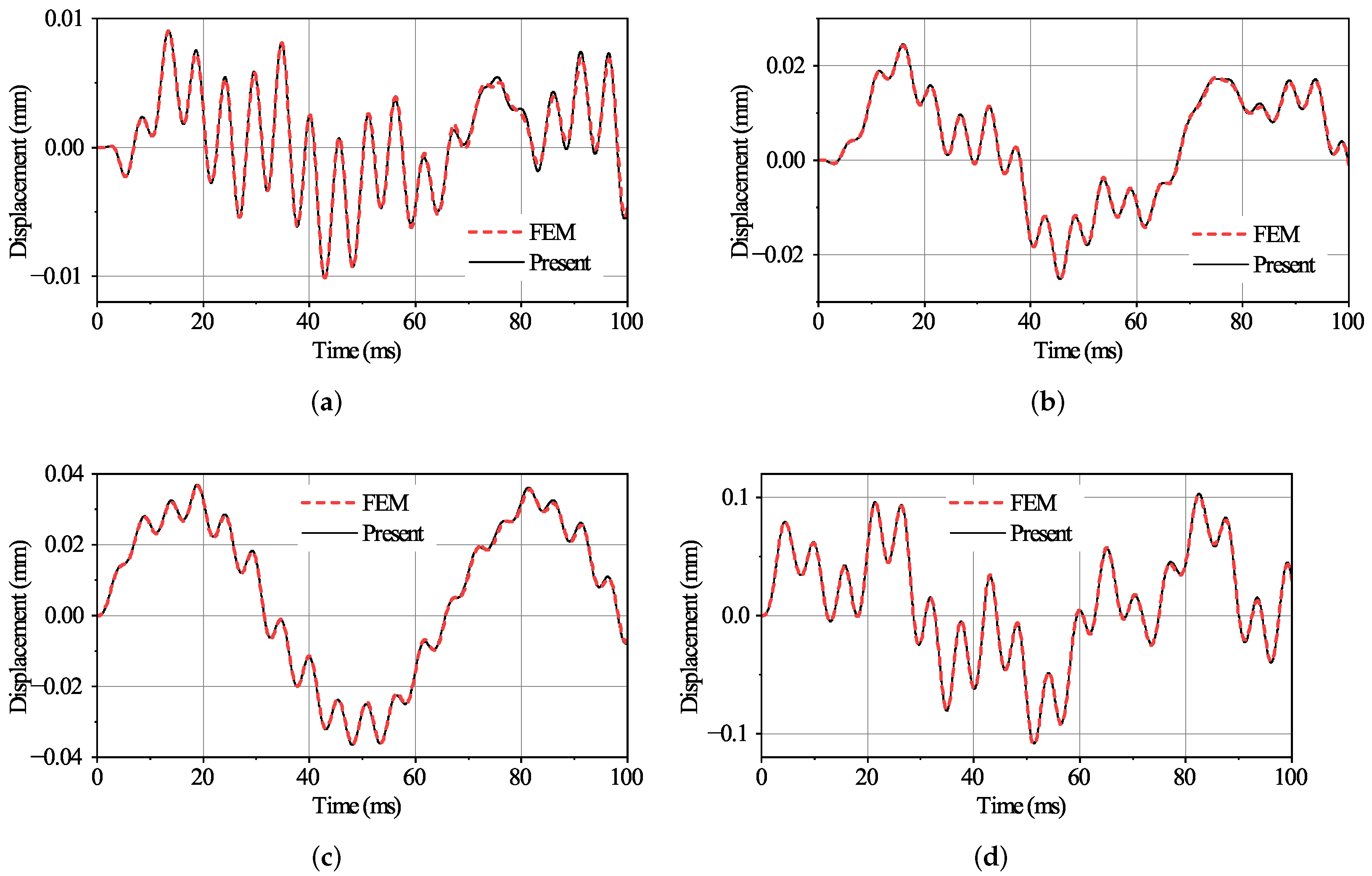
4.3. Non-Uniform AFG Beams on Variable Foundations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Birman, V.; Byrd, L.W. Modeling and Analysis of Functionally Graded Materials and Structures. Appl. Mech. Rev. 2007, 60, 195–216. [Google Scholar] [CrossRef]
- Nikbakht, S.; Kamarian, S.; Shakeri, M. A review on optimization of composite structures part II: Functionally graded materials. Compos. Struct. 2019, 214, 83–102. [Google Scholar] [CrossRef]
- Thang, P.T.; Nguyen-Thoi, T.; Lee, J. Shape and material optimization for buckling behavior of functionally graded toroidal shells. Thin-Walled Struct. 2020, 157, 107129. [Google Scholar] [CrossRef]
- Truong, T.T.; Nguyen-Thoi, T.; Lee, J. Isogeometric size optimization of bi-directional functionally graded beams under static loads. Compos. Struct. 2019, 227, 111259. [Google Scholar] [CrossRef]
- Lieu, Q.X.; Lee, J. An isogeometric multimesh design approach for size and shape optimization of multidirectional functionally graded plates. Comput. Methods Appl. Mech. Eng. 2019, 343, 407–437. [Google Scholar] [CrossRef]
- Wang, C.; Koh, J.M.; Yu, T.; Xie, N.G.; Cheong, K.H. Material and shape optimization of bi-directional functionally graded plates by GIGA and an improved multi-objective particle swarm optimization algorithm. Comput. Methods Appl. Mech. Eng. 2020, 366, 113017. [Google Scholar] [CrossRef]
- Abo-bakr, H.M.; Abo-bakr, R.M.; Mohamed, S.A.; Eltaher, M.A. Multi-objective shape optimization for axially functionally graded microbeams. Compos. Struct. 2021, 258, 113370. [Google Scholar] [CrossRef]
- Truong, T.T.; Lee, S.; Lee, J. An artificial neural network-differential evolution approach for optimization of bidirectional functionally graded beams. Compos. Struct. 2020, 233, 111517. [Google Scholar] [CrossRef]
- Ghanavati, R.; Naffakh-Moosavy, H. Additive manufacturing of functionally graded metallic materials: A review of experimental and numerical studies. J. Mater. Res. Technol. 2021, 13, 1628–1664. [Google Scholar] [CrossRef]
- Ansari, M.; Jabari, E.; Toyserkani, E. Opportunities and challenges in additive manufacturing of functionally graded metallic materials via powder-fed laser directed energy deposition: A review. J. Mater. Process. Technol. 2021, 294, 117117. [Google Scholar] [CrossRef]
- Taati, E.; Sina, N. Multi-objective optimization of functionally graded materials, thickness and aspect ratio in micro-beams embedded in an elastic medium. Struct. Multidiscip. Optim. 2018, 58, 265–285. [Google Scholar] [CrossRef]
- Huang, Y.; Li, X.F. A new approach for free vibration of axially functionally graded beams with non-uniform cross-section. J. Sound Vib. 2010, 329, 2291–2303. [Google Scholar] [CrossRef]
- Reddy, J.N.; Ruocco, E.; Loya, J.A.; Neves, A.M. Theories and Analysis of Functionally Graded Beams. Appl. Sci. 2021, 11, 7159. [Google Scholar] [CrossRef]
- Sarkar, K.; Ganguli, R. Closed-form solutions for axially functionally graded Timoshenko beams having uniform cross-section and fixed–fixed boundary condition. Compos. Part B Eng. 2014, 58, 361–370. [Google Scholar] [CrossRef]
- Abrate, S. Vibration of non-uniform rods and beams. J. Sound Vib. 1995, 185, 703–716. [Google Scholar] [CrossRef]
- Zheng, D.Y.; Cheung, Y.K.; Au, F.T.K.; Cheng, Y.S. Vibration of multi-span non-uniform beams under moving loads by using modified beam vibration functions. J. Sound Vib. 1998, 212, 455–467. [Google Scholar] [CrossRef]
- Eisenberger, M.; Clastornik, J. Vibrations and buckling of a beam on a variable Winkler elastic foundation. J. Sound Vib. 1987, 2, 233–241. [Google Scholar] [CrossRef]
- Olotu, O.T.; Gbadeyan, J.A.; Agboola, O.O. Free Vibration Analysis of Tapered Rayleigh Beams resting on Variable Two-Parameter Elastic Foundation. Forces Mech. 2023, 12, 100215. [Google Scholar] [CrossRef]
- Sayyad, A.S.; Avhad, P.V.; Hadji, L. On the static deformation and frequency analysis of functionally graded porous circular beams. Forces Mech. 2022, 7, 100093. [Google Scholar] [CrossRef]
- Hein, H.; Feklistova, L. Free vibrations of non-uniform and axially functionally graded beams using haar wavelets. Eng. Struct. 2011, 33, 3696–3701. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, Y.; Guo, M. A novel approach for free vibration of axially functionally graded beams with non-uniform cross-section based on Chebyshev polynomials theory. Compos. Struct. 2017, 168, 277–284. [Google Scholar] [CrossRef]
- Calim, F.F. Transient analysis of axially functionally graded Timoshenko beams with variable cross-section. Compos. Part B Eng. 2016, 98, 472–483. [Google Scholar] [CrossRef]
- Han, H.; Cao, D.; Liu, L. A new approach for steady-state dynamic response of axially functionally graded and non-uniformed beams. Compos. Struct. 2019, 226, 111270. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, H.; Liu, H. Dynamic response of double-FG porous beam system subjected to moving load. Eng. Comput. 2022, 38, S2309–S2328. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Y.; Huang, D. Analytical solution for vibration of functionally graded beams with variable cross-sections resting on Pasternak elastic foundations. Int. J. Mech. Sci. 2021, 191, 106084. [Google Scholar] [CrossRef]
- Kumar, S. Vibration analysis of non-uniform axially functionally graded beam resting on Pasternak foundation. Mater. Today Proc. 2022, 62, 619–623. [Google Scholar] [CrossRef]
- Ta, D.H.; Nguyen, V.T.; Chun, N.H. Eigen analysis of functionally graded beams with variable cross-section resting on elastic supports and elastic foundation. Struct. Eng. Mech. 2014, 52, 1033–1049. [Google Scholar]
- Robinson, M.T.A.; Adali, S. Buckling of nonuniform and axially functionally graded nonlocal Timoshenko nanobeams on Winkler-Pasternak foundation. Compos. Struct. 2018, 206, 95–103. [Google Scholar] [CrossRef]
- Fang, J.; Zhou, D. Free vibration analysis of rotating axially functionally graded-tapered beams using Chebyshev-Ritz method. Mater. Res. Innov. 2015, 19, 1255–1262. [Google Scholar] [CrossRef]
- Fang, J.; Zhou, D. Free Vibration Analysis of Rotating Axially Functionally Graded Tapered Timoshenko Beams. Int. J. Struct. Stab. Dyn. 2016, 16, 1550007. [Google Scholar] [CrossRef]
- Soltani, M.; Asgarian, B. New hybrid approach for free vibration and stability analyses of axially functionally graded Euler-Bernoulli beams with variable cross-section resting on uniform Winkler-Pasternak foundation. SIAM Rev. 2019, 16, e173. [Google Scholar] [CrossRef]
- Liu, T.; Liang, W.; Wang, Q.; Qin, B.; Guo, C.; Wang, A. Random vibration study of functionally graded porous curved beams with elastically restrained ends. Eng. Struct. 2022, 270, 114874. [Google Scholar] [CrossRef]
- Abdalla, H.M.A. Pseudospectral Approach to the Shape Optimization of Beams Under Buckling Constraints. Eur. J. Comput. Mech. 2022, 31, 351–386. [Google Scholar] [CrossRef]
- Wang, K.; Feng, C.; Zhou, D. An improved weak-form quadrature element (IWQE) method for static and dynamic analysis of non-homogeneous plane trusses. Eng. Struct. 2023, 277, 115410. [Google Scholar] [CrossRef]
- Boggarapu, V.; Gujjala, R.; Ojha, S.; Acharya, S.; Babu, P.; Chowdary, S.; Kumar Gara, D. State of the art in functionally graded materials. Compos. Struct. 2021, 10, 113596. [Google Scholar] [CrossRef]
- Yagci, B.; Filiz, S.; Romero, L.L.; Ozdoganlar, O.B. A spectral-tchebychev technique for solving linear and nonlinear beam equations. J. Sound Vib. 2009, 321, 375–404. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, T.; Zhao, Y.; Wang, P. Effect of axially functionally graded material on whirling frequencies and critical speeds of a spinning Timoshenko beam. Compos. Struct. 2018, 192, 355–367. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, Y.; Wang, T.; Tian, H. A new chebyshev spectral approach for vibration of in-plane functionally graded mindlin plates with variable thickness. Appl. Math. Model. 2019, 74, 21–42. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, Y.; Cao, D. Bending and free vibration analysis of orthotropic in-plane functionally graded plates using a chebyshev spectral approach. Compos. Struct. 2021, 255, 112938. [Google Scholar] [CrossRef]
- Deng, H.; Chen, K.; Cheng, W.; Zhao, S. Vibration and buckling analysis of double-functionally graded Timoshenko beam system on winkler-pasternak elastic foundation. Compos. Struct. 2017, 160, 152–168. [Google Scholar] [CrossRef]
- Doeva, O.; Masjedi, P.K.; Weaver, P.M. Closed form solutions for an anisotropic composite beam on a twoparameter elastic foundation. Eur. J. Mech. A Solids 2021, 88, 104245. [Google Scholar] [CrossRef]
- Chen, W.Q.; Lu, C.F.; Bian, Z.G. A mixed method for bending and free vibration of beams resting on a Pasternak elastic foundation. Appl. Math. Model. 2004, 28, 877–890. [Google Scholar] [CrossRef]
- Dutta, A.K.; Mandal, J.J.; Bandyopadhyay, D. Analysis of beams on Pasternak foundation using quintic displacement functions. Geotech. Geol. Eng. 2021, 39, 4213–4224. [Google Scholar] [CrossRef]
- Obara, P. Vibrations and stability of Bernoulli-Euler and timoshenko beams on two-parameter elastic foundation. Arch. Civ. Eng. 2014, 60, 421–440. [Google Scholar] [CrossRef]
- Šalinić, S.; Obradović, A.; Tomović, A. Free vibration analysis of axially functionally graded tapered, stepped, and continuously segmented rods and beams. Compos. Part B Eng. 2018, 150, 135–143. [Google Scholar] [CrossRef]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A fresh approach to numerical computing. Lat. Am. J. Solids Struct. 2017, 59, 65–98. [Google Scholar] [CrossRef]

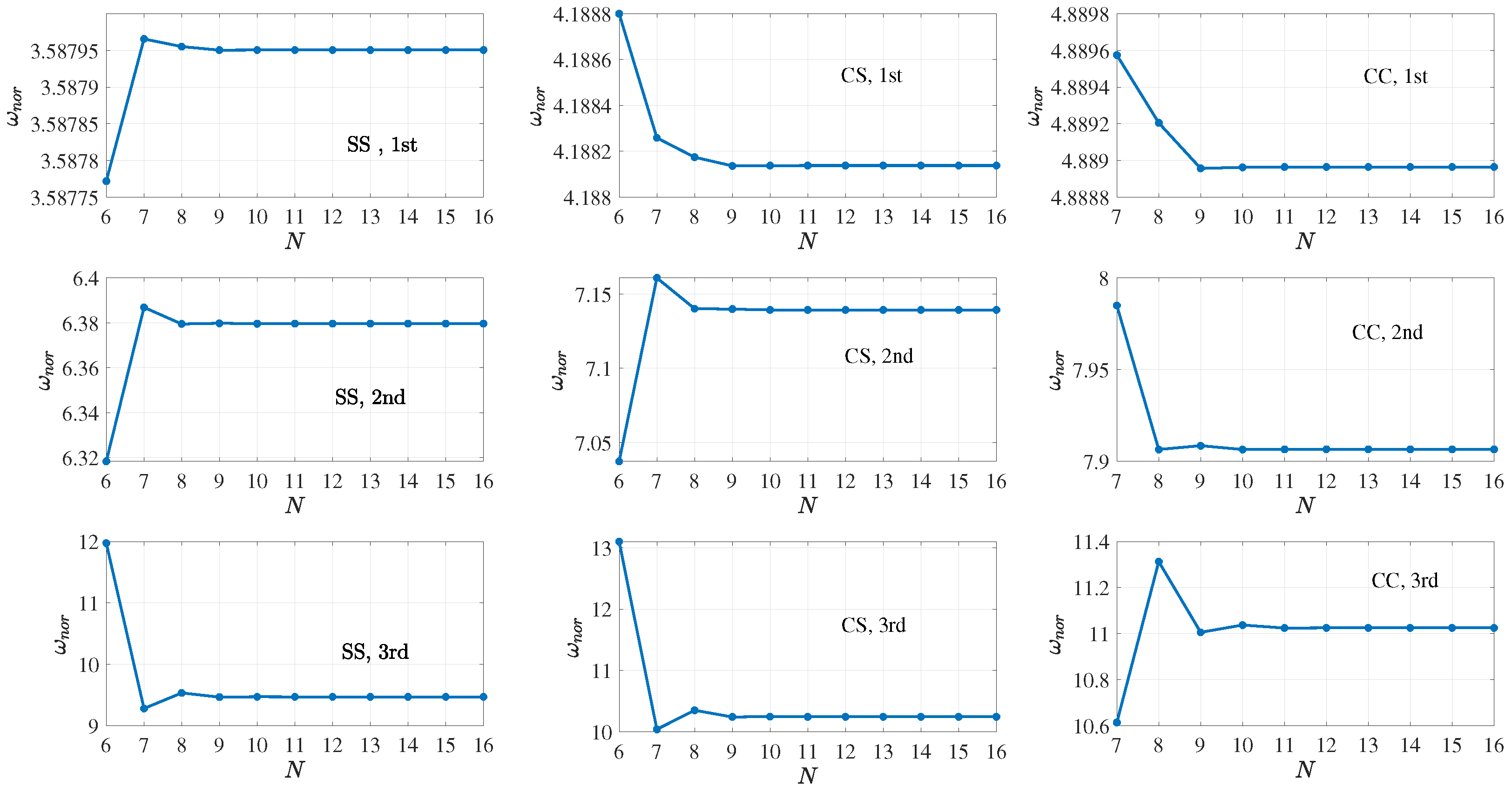

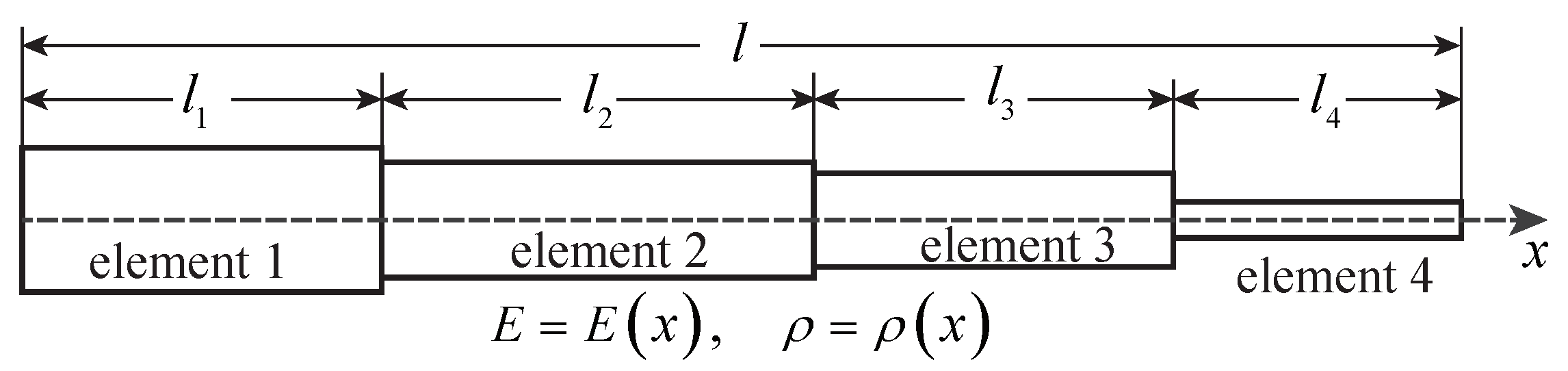


| B.C. | Foundation Parameters | DQM [42] | Exact [41] | Present | |
|---|---|---|---|---|---|
| CC | 0 | 0 | 2.6064 | 2.60417 | 2.60417 |
| 10 | 2.0862 | 2.08454 | 2.08455 | ||
| 25 | 1.6081 | 1.60687 | 1.60688 | ||
| 10 | 0 | 2.5547 | 2.55256 | 2.55256 | |
| 10 | 2.0528 | 2.05116 | 2.05116 | ||
| 25 | 1.5880 | 1.58681 | 1.58683 | ||
| 100 | 0 | 2.1670 | 2.16547 | 2.16547 | |
| 10 | 1.7935 | 1.79229 | 1.79229 | ||
| 25 | 1.4273 | 1.42633 | 1.42635 | ||
| SS | 0 | 0 | 13.02290 | 13.02083 | 13.02083 |
| 10 | 6.44827 | 6.44771 | 6.44771 | ||
| 25 | 3.66111 | 3.66091 | 3.66092 | ||
| 10 | 0 | 11.80567 | 11.80396 | 11.80396 | |
| 10 | 6.13325 | 6.13275 | 6.13275 | ||
| 25 | 3.55668 | 3.55649 | 3.55649 | ||
| 100 | 0 | 6.40074 | 6.40020 | 6.40020 | |
| 10 | 4.25582 | 4.25557 | 4.25557 | ||
| 25 | 2.82846 | 2.82834 | 2.82835 | ||
| SC | SF | CF | SC | SF | CF | SC | SF | CF | |
| FEM [43] | 3.54113 | 36.29669 | 23.01367 | 3.39874 | 25.59052 | 18.34552 | 2.82864 | 10.01332 | 8.92297 |
| Present | 3.54142 | 36.29669 | 23.01367 | 3.39903 | 25.59052 | 18.34552 | 2.82896 | 10.01332 | 8.92297 |
| 0.008% | 0% | 0% | 0.009% | 0% | 0% | 0.011% | 0% | 0% | |
| B.C. | Model Number | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | |||||||||
| [44] | FEM | Present | [44] | FEM | Present | [44] | FEM | Present | |||
| SS | 0 | 0 | 3.142 | 3.1416 | 3.14159 | 6.283 | 6.2832 | 6.28318 | 9.425 | 9.4248 | 9.42478 |
| 0 | 3.533 | 3.5333 | 3.53329 | 6.341 | 6.3413 | 6.34128 | 9.442 | 6.4422 | 9.44218 | ||
| 1 | 3.588 | 3.5880 | 3.58795 | 6.380 | 6.3796 | 6.37963 | 9.468 | 9.4685 | 9.46845 | ||
| CS | 0 | 0 | 3.927 | 3.9266 | 3.92660 | 7.069 | 7.0686 | 7.06858 | 10.210 | 10.210 | 10.2102 |
| 0 | 4.148 | 4.1484 | 4.14843 | 7.109 | 7.1096 | 7.10959 | 10.224 | 10.224 | 10.2239 | ||
| 1 | 4.188 | 4.1881 | 4.18814 | 7.139 | 7.1392 | 7.13924 | 10.246 | 10.246 | 10.2458 | ||
| CC | 0 | 0 | 4.730 | 4.7300 | 4.73004 | 7.853 | 7.8532 | 7.85320 | 10.996 | 10.996 | 10.9956 |
| 0 | 4.862 | 4.8624 | 4.86245 | 7.883 | 7.8832 | 7.88320 | 11.007 | 11.007 | 11.0066 | ||
| 1 | 4.889 | 4.8890 | 4.88896 | 7.907 | 7.9066 | 7.90659 | 11.025 | 11.025 | 11.0251 | ||
| B.C. | Mode 1 | Mode 2 | Mode 3 | |||
|---|---|---|---|---|---|---|
| [45] | Present | [45] | Present | [45] | Present | |
| CC | 3.4077 | 3.407699 | 5.72338 | 5.723375 | 8.39335 | 8.393376 |
| CS | 3.00028 | 3.000280 | 5.43323 | 5.433228 | 8.04824 | 8.047760 |
| SS | 2.08694 | 2.086939 | 4.62467 | 4.624669 | 7.38797 | 7.387968 |
| CF | 2.3605 | 2.360501 | 4.32307 | 4.323069 | 5.903 | 5.902994 |
| B.C. | Load | |||||||
|---|---|---|---|---|---|---|---|---|
| FEM | Present | FEM | Present | FEM | Present | |||
| SS | Uniform | 4.97926 | 4.99585 | 7.31450 | 7.32638 | 7.53748 | 7.52987 | 0.333% |
| Sinusoidal | 3.78410 | 3.79682 | 5.71830 | 5.72696 | 5.87506 | 5.86841 | 0.336% | |
| Exponential | 7.78435 | 7.81942 | 12.0451 | 12.0756 | 13.1182 | 13.1159 | 0.451% | |
| SC | Uniform | 4.58116 | 4.59948 | 6.42648 | 6.43455 | 6.07975 | 6.07271 | 0.400% |
| Sinusoidal | 3.51090 | 3.51966 | 5.09786 | 5.10337 | 4.85422 | 4.84952 | 0.250% | |
| Exponential | 7.0490 | 7.02686 | 10.3421 | 10.3248 | 10.2835 | 10.2878 | 0.314% | |
| CC | Uniform | 2.43342 | 2.43564 | 4.52038 | 4.52419 | 4.86512 | 4.86252 | 0.091% |
| Sinusoidal | 1.93322 | 1.93491 | 3.70152 | 3.70425 | 3.96564 | 3.96320 | 0.087% | |
| Exponential | 3.83054 | 3.83662 | 7.49591 | 7.50600 | 8.48754 | 8.48691 | 0.159% | |
| B.C. | Mode 1 | Mode 2 | Mode 3 | ||||
|---|---|---|---|---|---|---|---|
| Present | FEM | Present | FEM | Present | FEM | ||
| SS | 49.7113 | 49.7130 | 121.554 | 121.554 | 259.659 | 259.659 | 0.003% |
| CC | 61.9321 | 61.9331 | 157.299 | 157.299 | 319.936 | 319.936 | 0.002% |
| CS | 56.7793 | 56.7806 | 140.869 | 140.869 | 291.068 | 291.068 | 0.002% |
| SC | 53.3359 | 53.3372 | 135.827 | 135.827 | 285.790 | 285.790 | 0.002% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Huang, Y.; Zhao, Y. A Unified Numerical Approach to the Dynamics of Beams with Longitudinally Varying Cross-Sections, Materials, Foundations, and Loads Using Chebyshev Spectral Approximation. Aerospace 2023, 10, 842. https://doi.org/10.3390/aerospace10100842
Liu H, Huang Y, Zhao Y. A Unified Numerical Approach to the Dynamics of Beams with Longitudinally Varying Cross-Sections, Materials, Foundations, and Loads Using Chebyshev Spectral Approximation. Aerospace. 2023; 10(10):842. https://doi.org/10.3390/aerospace10100842
Chicago/Turabian StyleLiu, Haizhou, Yixin Huang, and Yang Zhao. 2023. "A Unified Numerical Approach to the Dynamics of Beams with Longitudinally Varying Cross-Sections, Materials, Foundations, and Loads Using Chebyshev Spectral Approximation" Aerospace 10, no. 10: 842. https://doi.org/10.3390/aerospace10100842
APA StyleLiu, H., Huang, Y., & Zhao, Y. (2023). A Unified Numerical Approach to the Dynamics of Beams with Longitudinally Varying Cross-Sections, Materials, Foundations, and Loads Using Chebyshev Spectral Approximation. Aerospace, 10(10), 842. https://doi.org/10.3390/aerospace10100842







