Autonomous Task Planning Method for Multi-Satellite System Based on a Hybrid Genetic Algorithm

Abstract

The increasing number of satellites for specific space tasks makes it difficult for traditional satellite task planning that relies on ground station planning and on-board execution to fully exploit the overall effectiveness of satellites. Meanwhile, the complex and changeable environment in space also poses challenges to the management of multi-satellite systems (MSS). To address the above issues, this paper formulates a mixed integer optimization problem to solve the autonomous task planning for MSS. First, we constructed a multi-agent-based on-board autonomous management and multi-satellite collaboration architecture. Based on this architecture, we propose a hybrid genetic algorithm with simulated annealing (H-GASA) to solve the multi-satellite cooperative autonomous task planning (MSCATP). With the H-GASA, a heuristic task scheduling scheme was developed to deal with possible task conflicts in MSCATP. Finally, a simulation scenario was established to validate our proposed H-GASA, which exhibits a superior performance in terms of computational power and success rate compared to existing algorithms.

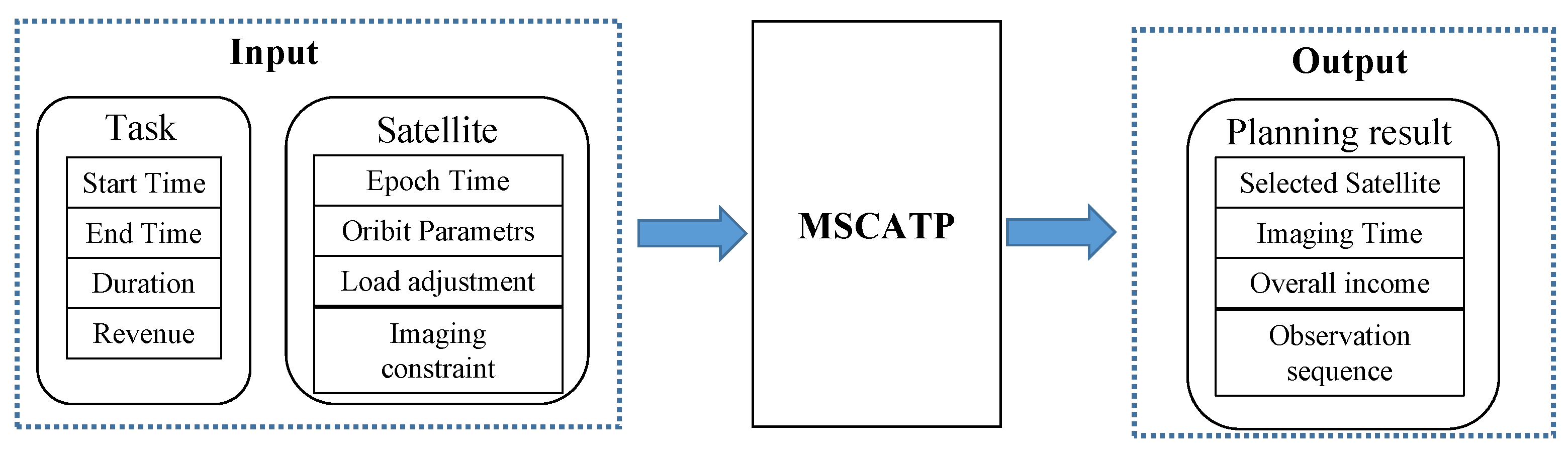
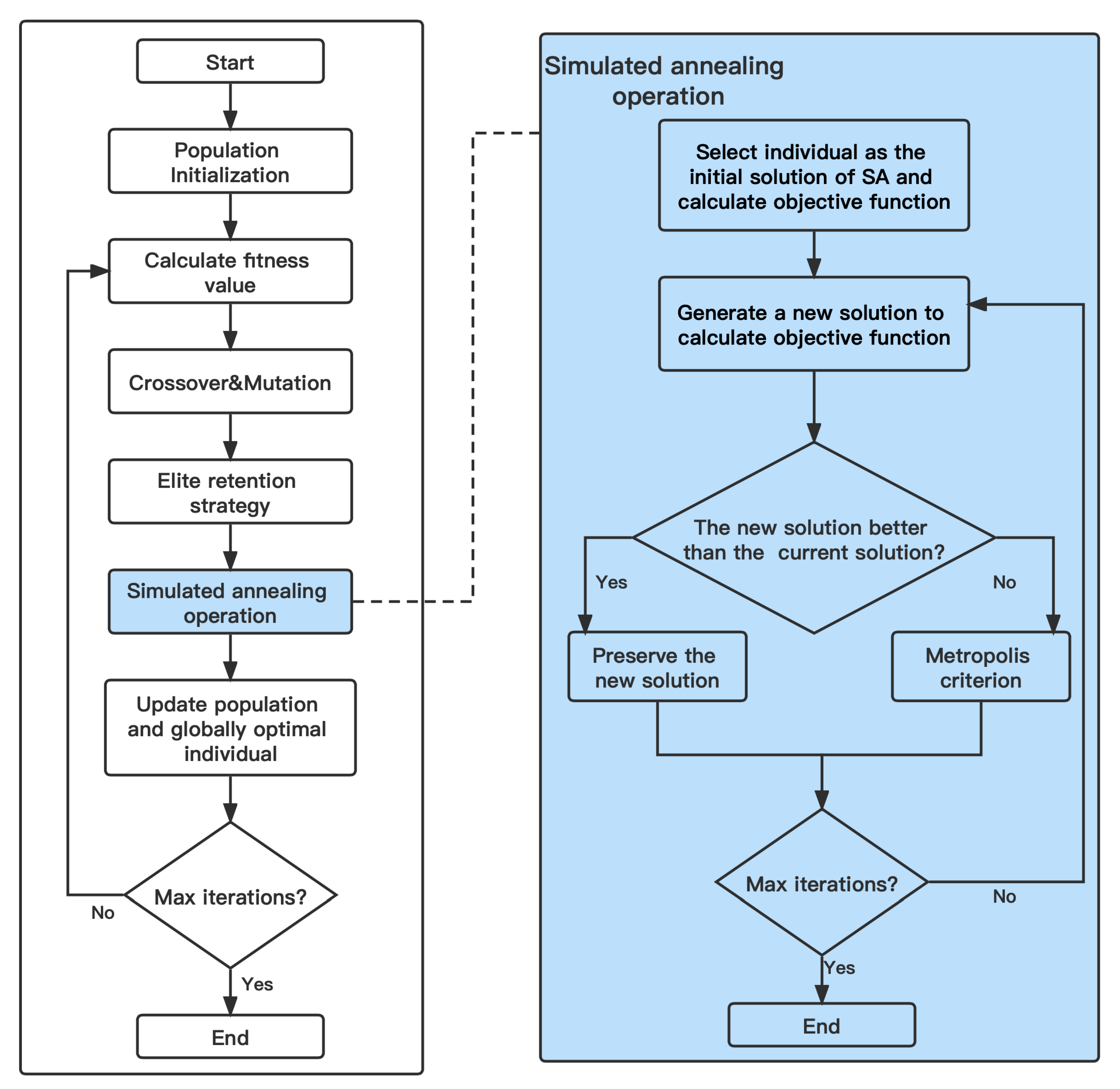
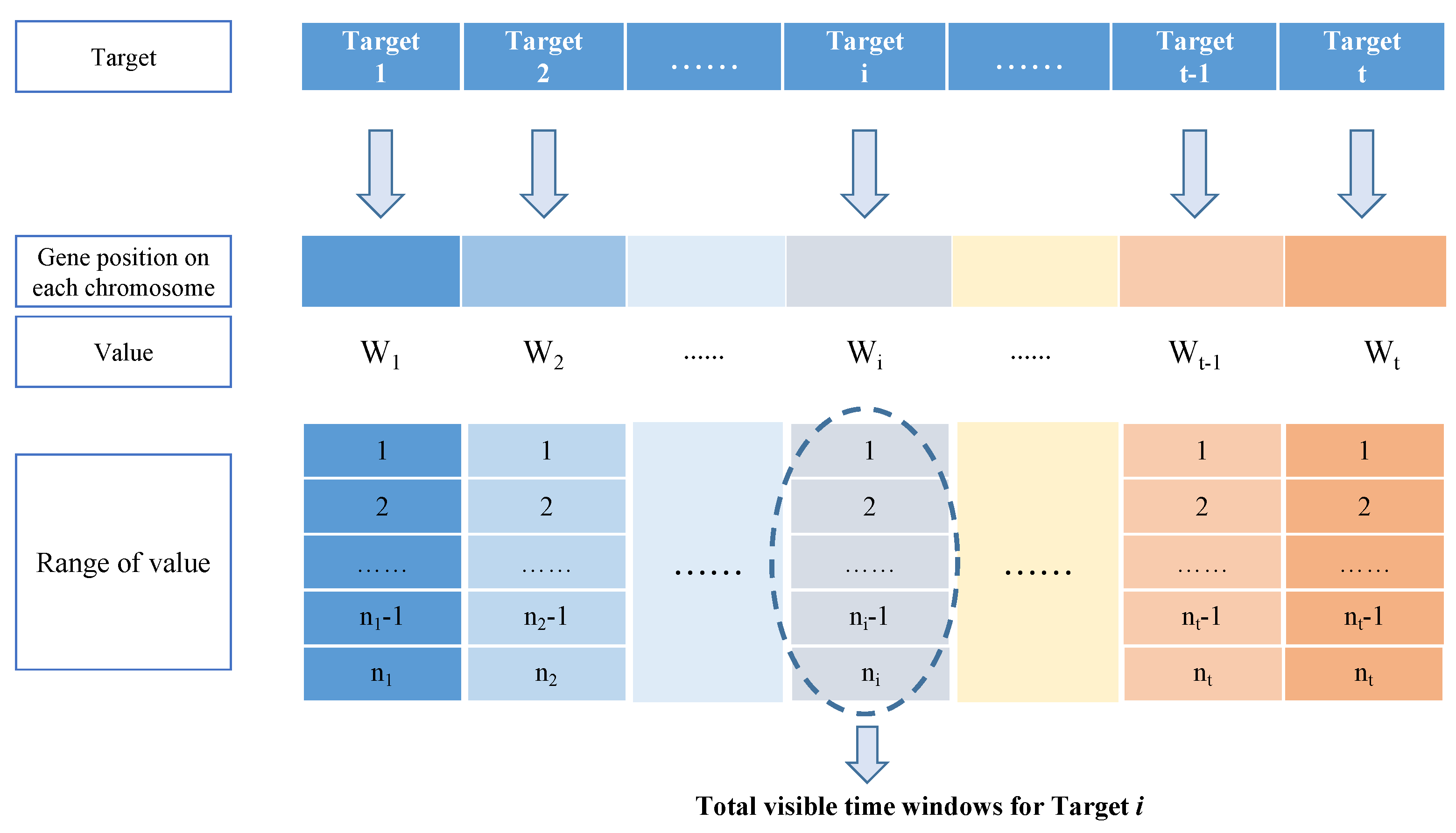
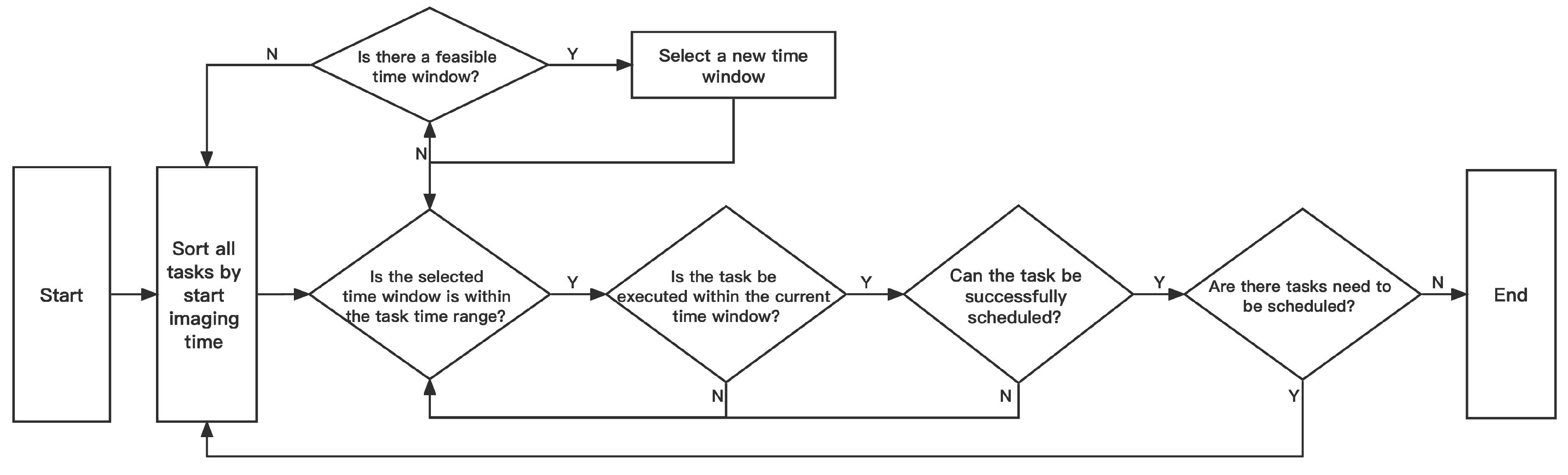
1. Introduction

Earth observation satellites (EOS) are critical for obtaining surface information resources. They can image the Earth from space within a specified time and play an important role in meteorological forecasting, emergency rescuing and environmental protecting [1]. With the development of satellite technology, the flexibility and autonomy of satellites are becoming stronger and stronger. Compared with a single satellite, a multi-satellite system (MSS) can better meet the current explosive growth of task requirements.

In the traditional satellite observation mode, satellites management mainly depends on the ground station, and all kinds of spatial information data are mostly transmitted back to the ground for unified processing [2]. The task control center receives the user’s task request and transmits it to the ground station to generate an observation plan, which is uploaded to the satellite for execution when the satellite passes over the ground station. However, this mode has a slow response and requires significant human involvement for an MSS with large numbers of satellites, which is very inefficient. The improvement of satellite autonomous management and online decision-making capabilities enables space engineers to develop on-board autonomous systems for MSS. The Multi-Satellite Cooperative Autonomous Task Planning (MSCATP) is developing in the direction of coordination and autonomy.

Multi-satellite cooperation can make up for the deficiency of a single satellite. According to the method of organization, it can be divided into the centralized and the distributed task planning. In the centralized task planning, multiple satellites perform tasks under the unified planning of the controller satellite. It treats MSCATP as an optimization problem; a constraint satisfiable problem (CSP) model [3], an integer model [4,5], and some general models such as graphs are used to model the problem [6,7,8,9,10,11]. In the solution of the centralized task planning problem, due to its NP-Hard characteristics, most are solved by heuristic methods, such as the ant colony algorithm [12,13,14,15,16,17], the particle swarm algorithm [18,19,20,21,22], and some methods based on graph theory [23,24,25,26]. These heuristic optimization algorithms are easy to implement and can obtain near-optimal solutions in an acceptable time. Although the centralized task planning can obtain the global optimal solution under a certain condition, it is highly dependent on the control center. Meanwhile, it has poor robustness and cannot provide a task planning service for an MSS when facing the single point breakdown of the controller satellite. Therefore, some works try to adopt the distributed task planning methods.

The distributed task planning focuses on how to design the organizational structure of satellite cooperative control, so as to realize independent task allocation and negotiation among multiple satellites. Hewitt systematically expounded NASA’s point of view on Agent and proposed the idea of using Agent technology to realize the autonomy of ground systems and spacecraft [27]. For an MSS, a new generation of satellites with on-board autonomous planning capabilities can make full use of the individual intelligence of agents to form a multi-agent system (MAS) and solve on-board planning problems through multi-agent collaboration [28].

The organizational model of a multi-agent system reflects the roles, interrelationships and authority structures of agents [29]. The hierarchical organization is the most commonly used model [30]. In a hierarchical organization, other agents are managed by a control center with the highest authority. Lin et al. performed job dispatch for distributed systems using a dynamic load-balancing strategy implemented on a central controller [31]. Kennedy adopted a two-layer scheduling method to solve the constellation joint planning problem but caused a serious computational load on the control center [32]. Most spatial applications use a hierarchical organization model due to its clear structure, easy control and strong universality. However, its robustness is poor, and its high reliance on the control center will result in high computational cost. Coalition-based organization is another commonly used organizational model. In the coalition-based organization, each agent is completely independent and equal, and its decision-making is based on its own favorable criteria [33]. Schetter et al. constructed a multi-satellite task negotiation and assignment method with a hierarchical structure and divides the satellites into four different levels of agents [9]. Li et al. proposed a multi-autonomous satellite cooperative mission planning framework based on JADE (Java Agent Development Framework, TILAB, State of California, United States), which consists of a single-satellite autonomous layer and a multi-satellite cooperative layer [34]. Du et al. designed a distributed multi-dimensional multi-agent task cooperation framework, which divided satellites into a management layer and a working layer, and the management layer satellites were responsible for the negotiation and distribution of observation tasks in addition to the basic functions of the working layer [10]. The advantage of this structure is strong robustness and low computational cost, but the disadvantage is that only considering what is beneficial to itself will affect the global revenue to a certain extent.

To address the above respective defects in centralized and distributed structure, a central-distributed federation architecture is proposed in this paper. In the federated architecture, agents are organized into multiple groups with complex functions, namely federation. The entire multi-agent system consists of several federations, each of which is independent of each other but internally coordinated and cooperative.

Based on the organizational model of the MAS, satellites can jointly complete tasks through negotiation on the basis of autonomous decision-making. Facing the realistic scenarios of multi-satellites and multi-tasking, it is necessary to develop an effective task allocation strategy. Based on Darwin’s theory of evolution, the genetic algorithm simulates natural selection and evolves the optimal solution of the problem through selection, crossover, mutation and inheritance. For example, Han designed a hybrid adaptive genetic algorithm combined with a large-neighborhood search process, in which “destroy” and “repair” operations are performed on elite individuals to enhance local search capabilities in each generation of the genetic algorithm [35]. In addition, other researchers improved the genetic algorithm in fitness function, coding, crossover operator and other aspects to solve the task planning problem [36,37,38,39,40]. Despite these improvements, how to develop an effective method for MSCATP remains an open question. A genetic algorithm can be applied to solve large-scale optimization problems. Although it can avoid the dilemma of local optimization to a certain extent, in the face of some complex problems, a genetic algorithm still has certain limitations, and it is difficult to accurately converge to the global optimal solution. Simulated annealing (SA) is an annealing-inspired search method in which a probabilistic approach is used to accept candidate solutions that can “jump” from a local optimum [41]. Through a new hybrid technique in which a simulated annealing process is combined with an adaptive approach to design an improved genetic algorithm, the local search capability of GA is enhanced using SA to provide proper exploration and exploitation of large solution spaces [42,43,44].

In this paper, we discuss the modeling and algorithms of MSCATP. Our work contributions are as follows:

• We built a multi-satellite collaborative federation architecture based on multi-agents for MSS, which overcomes the shortcoming that the inter-satellite resources are independent and lack cooperation, and allows the satellites to exchange information status with each other. It combines the characteristics of centralized management and distributed collaboration, and has high robustness and intellectual abilities.
• We develop a hybrid genetic algorithm with simulated annealing to solve MSCATP. Specifically, the standard of accepting new solutions is improved by introducing a simulated annealing operation, and the threshold of accepting new solutions is set, which changes the way that the algorithm jumps out of the local optimal solution. Meanwhile, the task sequence represented by the real-coding format can shorten the chromosome length and improve the search speed.
• We construct a heuristic scheduling strategy to eliminate the possibility of task time window preemption in MSCATP, which can effectively resolve task conflicts and complete tasks as much as possible.

The organization of this paper is as follows: Section 2 presents a multi-satellite task cooperation framework; on this basis, an autonomous task planning method is proposed. Section 3 establishes a simulation scenario to illustrate the effectiveness of experimental results. Section 4 discusses the advantages and disadvantages of the algorithm. Section 5 presents the summary and outlook.

2. Materials and Methods

2.1. Problem Formulation

During the satellite orbit, the payload can be imaged at the sub-satellite point trajectory corresponding to the satellite orbit. The area that the satellite payload can observe is the visible light region, and the time range in the visible light region is called the satellite’s visible time window. Due to the limited visibility of the satellite, imaging can only be performed when the satellite passes over the observation area within the visible time window. Generally speaking, the number of observation tasks is far greater than the number of satellites, and the single-satellite performing observation tasks cannot meet the observation requirements for all the objects to be observed in terms of maneuverability and imaging capabilities. Therefore, the observation results of more targets can be obtained through the coordinated observation of multiple satellites in orbit. The increased number of satellites makes it more difficult to manage the satellites, and how to effectively plan tasks and manage satellite resources has become an important issue. The input and output of multi-satellite cooperative autonomous task planning (MSCATP) are shown in Figure 1.

2.2. Multi-Agent Collaborative Framework

We decompose MSCATP into two sub-problems—satellite cooperation and task planning. In this architecture, the agent represents the Earth observation satellite. It combines the centralized task distribution capabilities of satellites with the distributed computing capabilities of constellations, and is a central-distributed federation structure. As shown in Figure 2a, the whole structure is a multi-layer management mode, which is divided into a control layer, an organization layer and a working layer. The first layer is the control layer, and the control center agent has the highest authority to manage all the agents; the second layer is the organization layer, and the agents in the organization layer are responsible for the formation and management of the federation in the system. When the agent of the organization layer obtains the task from the control layer, it can assign the task to the agent of the working layer for execution; the bottom layer is the working layer, and the agent of the working layer is mainly responsible for task reception, execution and cooperation.

On the one hand, the architecture consists of several federal structures, which is a highly centralized multi-level management architecture; on the other hand, each federal structure is relatively independent. Within each federated structure, agents can interact bi-directionally for task assignment, execution and message feedback, as shown in Figure 2b. The organization agents can communicate with each other, and the working agents can exchange information through the organization agents, thus laying the foundation for multi-agent cooperation. The specific cooperation architecture is shown in Figure 2.

In MSCATP, the ground station uploads the task information to the control satellite, and the organization satellite transmits the task information to each working satellite. Each satellite quickly calculates the observation information based on its own state and orbit information and feeds it back to the organization satellite. The organization satellite assigns tasks according to the feedback information, and each satellite schedules independently and feeds the observation results back to the organization satellite to form the final planning scheme.

2.3. Mathematical Model

Simplifying the problem to facilitate model building, this paper makes the following assumptions for MSCATP:

• When the task is determined to start observation, it will not be preempted or interrupted by other tasks;
• Each task can be observed at most once, regardless of periodic execution or repeated execution;
• Planning is limited to a certain time frame, and subsequent task planning follows our proposed method.

Multi-satellite cooperative autonomous task planning has been proved to be a time-dependent NP-Hard problem with multiple constraints. Since the time window of each task is limited, it is difficult to guarantee the successful observation of all tasks. In this paper, our goal is to meet the user’s observation needs as much as possible, that is, to maximize the revenue of the observation task sequence.

Based on the above analysis, we establish the mathematical model of MSCATP. A summary of notations is presented in

Table 1. Definitions of the notations in MSCATP.

Notations	Definitions
T	Observation tasks set, $T=\left\{{\tau }_1,{\tau }_2,\cdots ,{\tau }_{n_t}\right\}$, $n_t$ represents the number of tasks executed
S	EOS resource set, $S=\left\{s_1,s_2,\cdots ,s_{n_s}\right\}$, $n_s$ represents the number of satellites
TW	Visible time windows set
$du{r}_i$	Observation duration of task ${\tau }_i$
$es{t}_i$	The earliest observation time of task ${\tau }_i$
$ls{t}_i$	The latest observation time of task ${\tau }_i$
$tw{s}_{ijk}$	Visible start time of task ${\tau }_i$ at the k-th time window of satellite $s_j$
$tw{e}_{ijk}$	Visible end time of task ${\tau }_i$ at the k-th time window of satellite $s_j$
$s{t}_{ijk}$	Observation start time of task ${\tau }_i$ at the k-th time window of satellite $s_j$
$e{t}_{ijk}$	Observation end time of task ${\tau }_i$ at the k-th time window of satellite $s_j$
$\gamma$	Attitude adjustment duration
$p_i$	Priority of task ${\tau }_i$
$x_{ijk}$	0–1 variable, 1 denotes task ${\tau }_i$ is observed by the k-th time window of satellite $s_j$, while 0 not

.

In MSCATP, the objective is to maximize the revenue of the observation task sequence.

$$max\sum _{i\in T}^{}\sum _{j\in S}^{}\sum _{k\in TW}^{}re{v}_i·x_{ijk}.$$

(1)

Equation (1) represents the total revenue of tasks observed by satellites, and $re{v}_i$ is the priority of tasks. The constraints are shown in Equations (2)–(9).

$$es{t}_i⩽t_{ij},i\in T,j\in S$$

(2)

$$t_{ij}+du{r}_i⩽la{t}_i,i\in T,j\in S$$

(3)

$$tw{s}_{ijk}⩽t_{ij},i\in T,j\in S,k\in TW$$

(4)

$$t_{ij}+du{r}_i⩽tw{e}_{ijk},i\in T,j\in S,k\in TW$$

(5)

$$t_{ij}+du{r}_i+\gamma ⩽t_{\left(i+1\right)j},i\in T,j\in S$$

(6)

$$\sum _{j\in S}^{}\sum _{k\in TW}^{}{x}_{ijk}⩽1,i\in T,j\in S,k\in TW$$

(7)

$$x_{mjk}{x}_{njv}\left(s{t}_{njv}-e{t}_{mjk}\right)\left(e{t}_{njv}-s{t}_{mjk}\right)⩾0,m,n\in T,j\in S,k,v\in TW$$

(8)

$$x_{ijk}\in \left\{0,1\right\}.$$

(9)

Equation (2) indicates that the actual start execution time of the task should be after the earliest start time specified by the user. Equation (3) indicates that it should be completed before the latest end time specified by the user. Equations (4) and (5) show that the task should be completed within the visible time window of the satellite. Equation (6) represents that the two tasks before and after the execution need to meet the time interval requirements. Equation (7) gives that each task is executed at most once by a satellite that meets the requirements. Equation (8) defines that a single satellite resource can only complete one task at any time. Equation (9) is the value range of decision variables.

2.4. Methods

2.4.1. Algorithm Framework

The core of an evolutionary algorithm is to balance the contradiction between search ability and development ability. Among them, the search ability is to search the whole space to find the best possible areas, while the development ability is to focus on those individuals with the best fitness. A genetic algorithm (GA), as an effective bionic optimization algorithm, is widely used in various fields. If properly handled, it can obtain the optimal solution through many iterations, but its shortcomings are also obvious, such as poor local search ability, slow convergence speed, and stagnation of individual evolution in the later stage, which leads to local optimization. The advantages of simulated annealing algorithm are strong local searching ability and short running time, but the disadvantages are poor global searching ability and being easily influenced by parameters. Therefore, combining the advantages and disadvantages of the two algorithms, we propose a hybrid genetic algorithm with simulated annealing (H-GASA) to solve MSCATP.

The overall idea for the H-GASA is as follows:

Step 1: Initialize a random population, randomly generate N chromosomes to form a population;

Step 2: Evaluate the fitness of the initial population. Obtain individuals with high fitness in the population and select excellent individuals through selection operators to directly pass on to the next generation;

Step 3: Select individuals for crossover and mutation operations to generate new individuals;

Step 4: Elite retention strategy. Screen the whole population, find the individuals with high fitness and keep them directly to the next generation;

Step 5: Use a simulated annealing model to accept individuals with poor fitness with a certain probability;

Step 6: Repeat the above steps to update the population until the predefined maximum number of iterations is reached.

Based on the above design, the flowchart of our proposed H-GASA is shown in Figure 3.

2.4.2. Chromosome Design

As the number of missions and satellites increases, the number of visible time windows will obviously increase. At this time, the binary coding method will lead to the chromosome being too long, and every bit of the chromosome needs to be checked for conflicts by using constraints, which will lead to a too-long operation time and reduce the efficiency of the algorithm. For this reason, this paper proposes a real coding method, as shown in Figure 4.

As shown in Figure 4, each bit of a chromosome represents an observation task. Assuming that the total number of visible time windows for task i is $n_i$, each time window is numbered from 1 to $n_i$, which corresponds to the value range of the i-th gene on the chromosome. If the value of i-th gene is $w_i$, one of the natural numbers from 1 to $n_i$, this means that the task selects the w-th time window of task i to complete the observation.

2.4.3. Elite Retention Strategy

Genetic operators mainly include selection operators, crossover operators and mutation operators. The selection operator can effectively improve the convergence speed of the algorithm, and the crossover and mutation operators can expand the diversity of the population and prevent the algorithm from converging prematurely.

The roulette method is used to select excellent individuals. Assuming that the population size is m, the formula for calculating the selection probability of each individual is as shown in Equation (10). $Fitness\left(i\right)$ represents the fitness value of the individual i. Therefore, the greater the fitness value, the greater the probability of being selected.

$$p\left(i\right)=\frac{Fitness\left(i\right)}{{\sum }_{i=0}^{m}Fitness\left(i\right)}.$$

(10)

In order to prevent the optimal individual of the current population from being lost in the next generation, which leads to the inability of the genetic algorithm to converge to the global optimal solution, an elite retention strategy is adopted. All individuals are screened after each crossover and mutation operation, and the individuals with the highest fitness are directly copied to the next generation. The elite retention strategy plays an important role in improving the global convergence ability of the genetic algorithm.

2.4.4. Simulated Annealing Operation

After crossover and mutation, new individuals will be produced. For those individuals with high fitness, we choose to keep them directly, while for those individuals with poor fitness, we accept them as new individuals of the next generation with a certain probability through an introduced simulated annealing operation.

According to the sampling method of Metropolis in the 1950s, the most recent form is accepted by using the quantity of change, that is, the probability, which is called the Metropolis criterion. The new individual with poor fitness is used as the initial solution of the simulated annealing algorithm, a random search is carried out in the constraint interval, and its objective function is calculated. Add random disturbance to the current solution to generate a new solution and calculate the corresponding objective function value. The algorithm criterion stipulates that when the system changes from one state energy E1 to another state energy E2, the probability of energy change is shown in Equation (11). T is the simulated temperature value initially set by the algorithm.

$$p=exp\left(-\frac{E2-E1}{T}\right).$$

(11)

If the new solution is better than the current solution, the new solution generated by the change state is accepted; otherwise, the algorithm will judge whether to accept the new solution based on the Metropolis criterion. The probability that the new solution of the changing state is accepted is shown in Equation (12).

$$p=\left\{\begin{array}{cc}1,\hfill & E2<E1\hfill \\ exp\left(-\frac{E2-E1}{T}\right),\hfill & E2⩾E1.\hfill \end{array}\right.$$

(12)

The population size of GA is set to the number of SA adjacent solutions to reduce the difference between parallel GA and continuous SA processes. The specific algorithm operation is shown in Figure 3.

2.4.5. Heuristic Task Scheduling Strategy

Task conflict handling is an important part of a scheduling algorithm. When the time window conflict occurs, the task start execution time is determined. If there is time overlap with the current scheduled task, moving the current task back to the non-overlapping time segment can effectively handle the task conflict.

We design a greedy task scheduling algorithm. Firstly, we sort the tasks according to the starting imaging time and check the imaging conflict to ensure the feasibility of the observation sequence. In this process, once the imaging is completed, the corresponding download schedule is made, and if the download fails due to satellite resource shortage, the task will be abandoned.

The specific steps are as follows:

Step 1: Input task set, satellite set, time window set;

Step 2: Sort all tasks by start imaging time and arrange visible time windows in order;

Step 2.1: Determine whether the visible time window range is within the time range required by the task. If the conditions are met, go to step 2.2. Otherwise, select a new time window and repeat step 2.1. If there is no visible time window, go to step 2;

Step 2.2: Determine the inclusive relationship between the length of the visible time window and the execution time required by the current task. If it is satisfied, go to step 2.3. Otherwise, go to step 2.1;

Step 2.3: Conflict processing is performed, and whether the task can be successfully scheduled is judged according to the actual start time of the task, the latest end time of the visible time window, and the task execution duration. If satisfied, go to step 3. Otherwise, go to step 2.1;

Step 3: Determine the satellite to execute the task, the start time and end time of the execution, generate the observation sequence, and go to step 2. If no task needs to be scheduled, go to step 4;

Step 4: Output the task execution sequence.

The flowchart of the greedy task scheduling algorithm is shown in Figure 5.

3. Results

In this section, we obtain computational data through experiments to evaluate the effectiveness of our proposed method and demonstrate that it outperforms other existing methods. The coding environment of all algorithms is Matlab 2018a, and the simulation scenarios, including satellite establishment, target selection and time window calculation, are all realized by STK 11.6 simulation software. The simulation computer environment is Intel Core i3-3220 CPU @ 3.30 GHz 3.30 GHz, 8 GB RAM.

3.1. Simulation Scenario

The Satellite Tool Kit (STK) supports the entire process of space tasks; the core capabilities of STK are the generation of position and attitude data, acquisition time, and remote sensor coverage analysis. It can be applied to scenarios such as satellites, vehicles, ground stations, targets, and remote sensors.

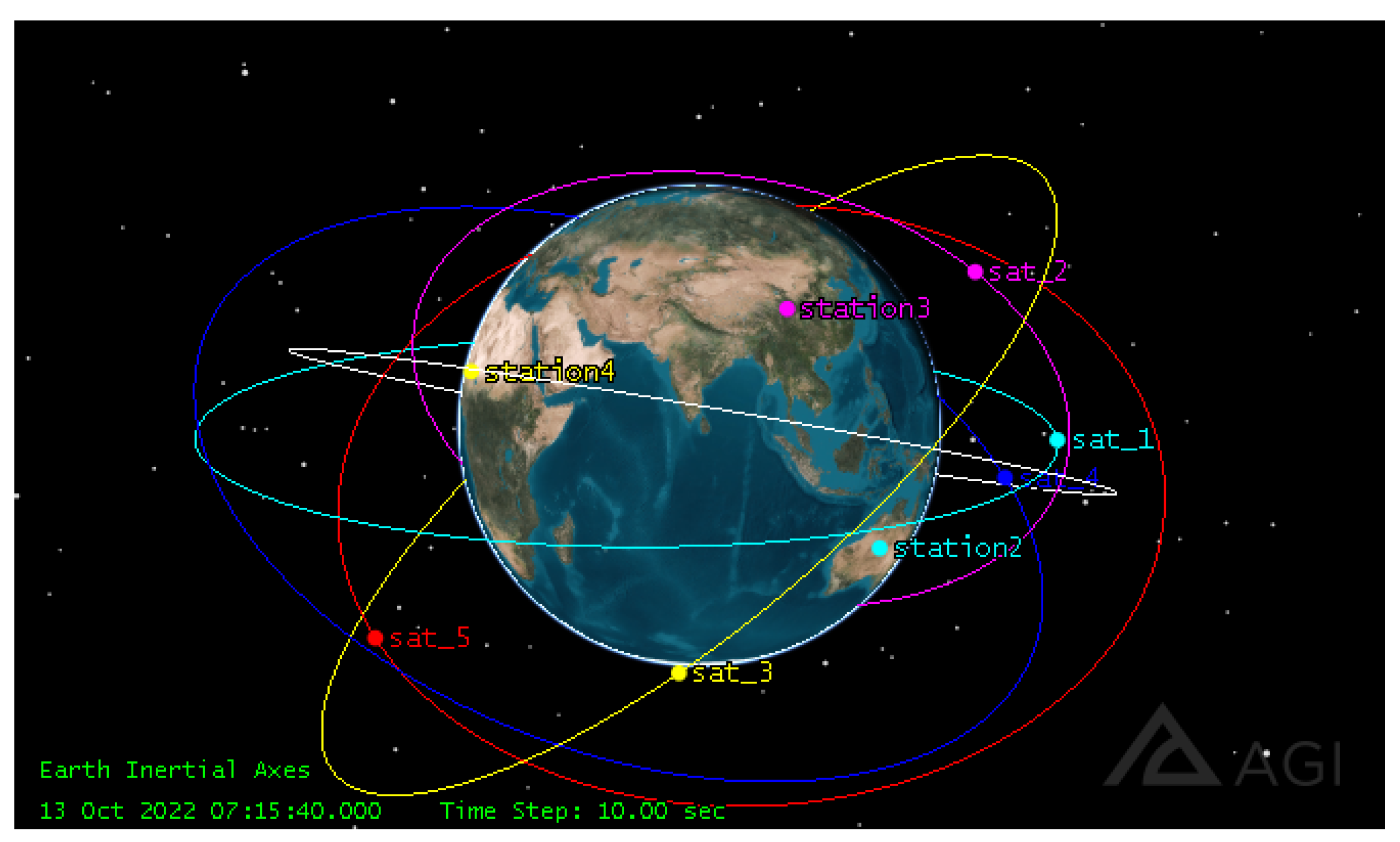
In terms of observation tasks, we use STK 11.6 software to randomly generate a certain number (25–100) of point targets as observation tasks, which randomly distribute on the Earth’s surface with latitude among (50° E, 150° E) and latitude among (40° S, 40° N). Each target is associated with a priority uniformly distributed among [1,10] and corresponding to different benefits. The time period of the scenario is (13 October 2022 00:00:00, 14 October 2022 00:00:00).

The orbital information of the satellite includes semi-major axis (a), eccentricity (e), inclination (i), ascending node right ascension ($\phi$), argument of perigee ($\omega$), true perigee angle ($\tau$). The specific orbit parameters are shown in

Table 2. Orbit paraments.

Satellite	a	e	i	$\mathit{\phi }$	$\mathit{\omega }$	$\mathit{\tau }$
Sat_1	11,451.7584	0.1812	6.3493	308.6624	328.8153	35.1145
Sat_2	8770.6311	0.1094	47.8753	105.7602	347.3599	349.4134
Sat_3	12,163.9747	0.0970	40.0140	230.4941	51.0791	329.6647
Sat_4	11,339.1766	0.1918	32.7870	337.9213	12.8562	336.2375
Sat_5	10,771.8157	0.1515	37.1566	294.5971	141.2017	61.6272
Sat_6	10,908.3704	0.0063	13.8461	75.1243	16.6217	296.4448
⋯	⋯	⋯	⋯	⋯	⋯	⋯

. Task information is collected by ground stations and uploaded to the satellites, and we simulated four ground stations in the scenario. The distribution of the ground stations and satellites in STK is shown in Figure 6.

3.2. Multi-Satellite Cooperative Autonomous Task Planning simulation Analysis

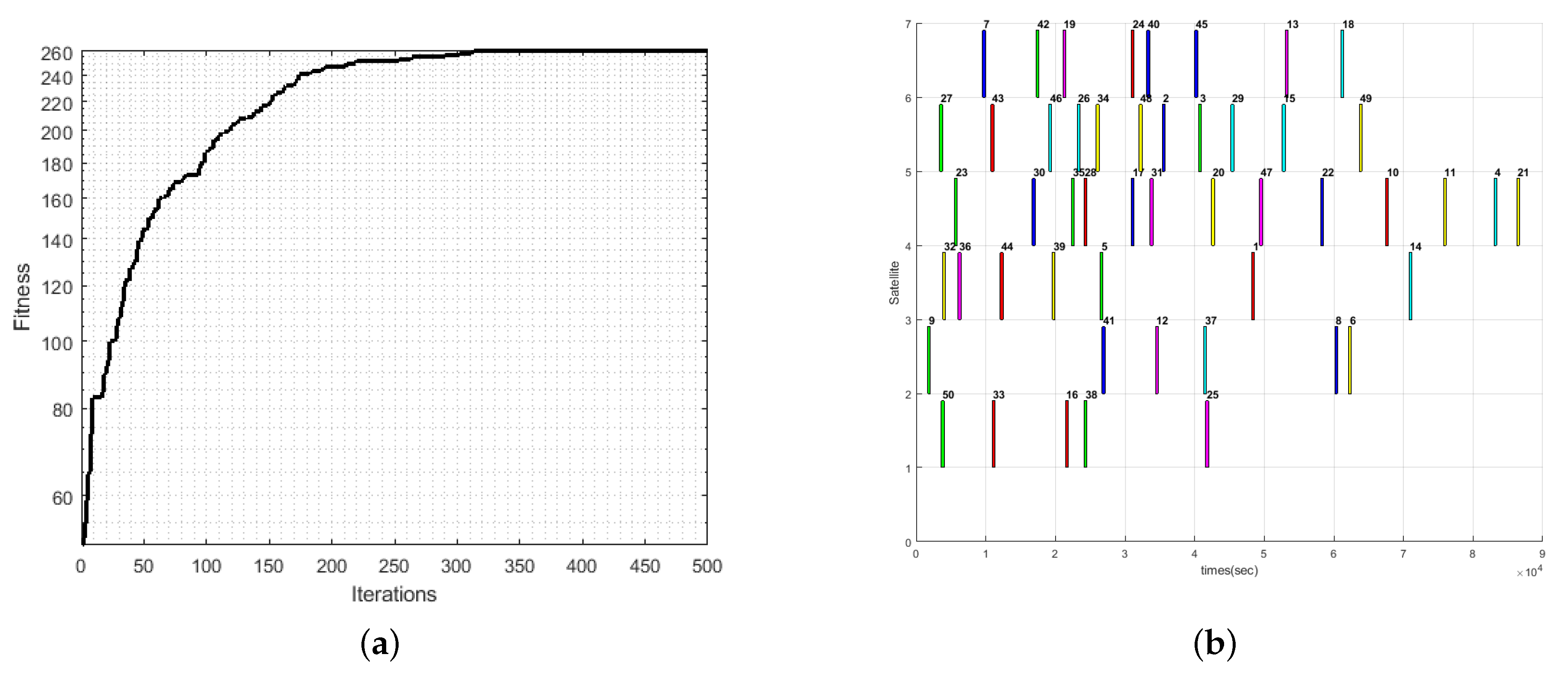
We selected 50 observation targets to conduct 10 experiments, and stipulated that the fixed observation time of each target point was 30 s. The average results are shown in

Table 3. Typical results of MSCATP based on H-GASA.

Simulation Scene Setting		Average Optimal Fitness Value
Number of Satellites	Number of Targets	Average Fitness Value	Average Running time(s)
6	50	261	204

and Figure 7, and selected two evaluation indicators: task completion revenue and running time.

As shown in the above results, H-GASA has a good effect on solving multi-satellite collaborative autonomous task planning. The fitness value rises rapidly in the first 50 generations, indicating that the algorithm has an obvious improvement effect in the early stage. As the number of iterations increases, the probability of the new solution increases, and it is more inclined to generate individuals with higher fitness values, so the individual fitness value gradually increased and stabilized, finally converging at the 300-th generation.

3.3. Analysis of Algorithm Performance

3.3.1. Different Coding Format of H-GASA

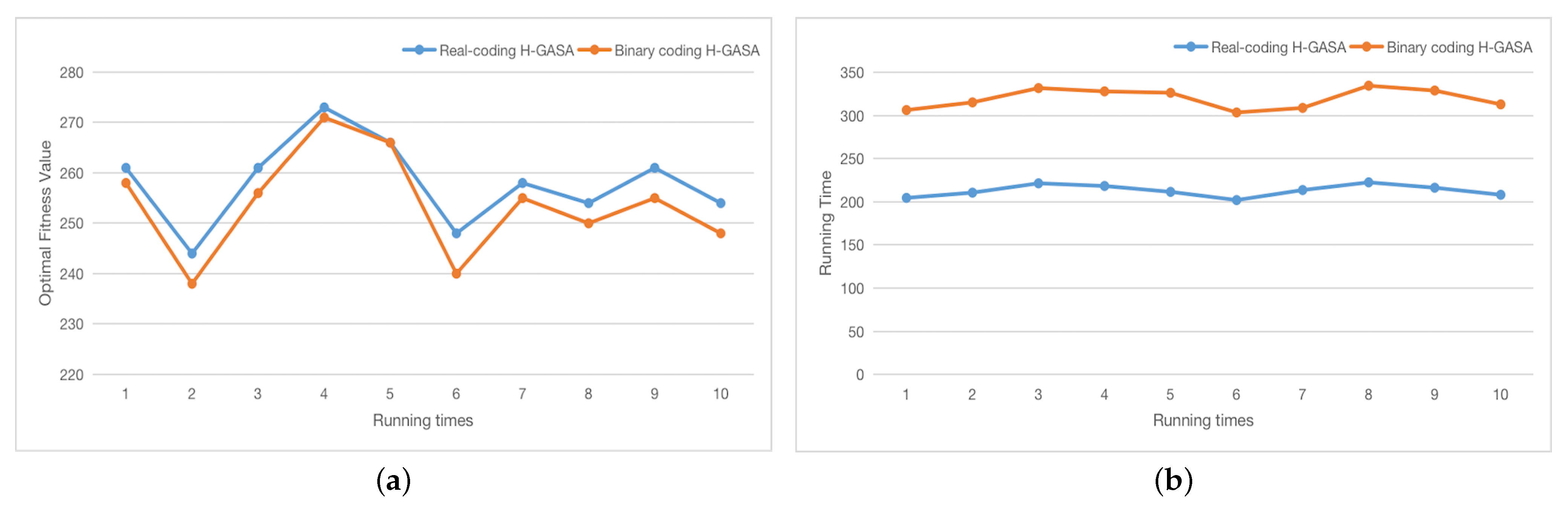
For multi-satellite multi-task scenarios, a different encoding format can usually determine the length of chromosomes and affect the efficiency of the algorithm. For our proposed real coding format and traditional binary coding format, 10 simulation experiments were carried out under the same conditions, and the results are shown in

Table 4. Statistical results of different coding format in H-GASA.

Number	Optimal Fitness Value		Running Time(s)		Encoding Length
	Real-Coding H-GASA	Binary Coding H-GASA	Real-Coding H-GASA	Binary Coding H-GASA	Real-Coding H-GASA	Binary Coding H-GASA
1	261	258	204.5	306.23	50	146
2	244	238	210.6	315.12	50	146
3	261	256	221.4	331.66	50	146
4	273	271	218.3	327.83	50	146
5	266	266	211.5	326.23	50	146
6	248	240	202.0	303.43	50	146
7	258	255	213.6	308.68	50	146
8	254	250	222.5	334.42	50	146
9	261	255	216.3	328.80	50	146
10	254	248	208.1	312.84	50	146
Max	273	271	222.5	334.42	50	146
Min	244	238	202.0	303.43	50	146
Avg	258	253.7	212.88	319.524	50	146

and Figure 8.

As can be seen from the above results, the number of tasks determines that the chromosome length of real coding is 50, while that of binary coding is the number of visible time windows of the satellite to the target in a planning period. According to the comparison between the optimal fitness value and the running time, it can be seen that the genetic algorithm based on real coding is superior to the genetic algorithm based on binary coding in terms of optimization ability and calculation speed. Among them, the average computation time of H-GASA based on binary coding is about 1.5 times that of H-GASA based on real coding, which indicates that the coding format has an important impact on the performance of H-GASA algorithm. Obviously, the chromosome length has a significant influence on the evolution process, and a shorter chromosome length can speed up the search.

3.3.2. Comparison Results Analysis

According to the optimization goal in Section 2, we carried out experiments comparing H-GASA and different algorithms for solving MSCATP under the same conditions. This paper selects GA, SA and PSO for experimental comparison. They are all widely used heuristic algorithms and are representative. The parameters of all algorithms for different task scenarios were set as shown in

Table 5. The parameters of all algorithms for different scenarios.

Parameters	H-GASA	GA	SA	PSO
Targets	25/50/75/100	25/50/75/100	25/50/75/100	25/50/75/100
Population size	20/40/60/80	20/40/60/80	20/40/60/80	20/40/60/80
Crossover probability	0.8	0.8	-	-
Mutation probability	0.01	0.01	-	-
Temperature iterations	-	-	20/40/60/80	-
Acceleration constant	-	-	-	1.457
Iterations	400/500/600/800	400/500/600/800	400/500/600/800	400/500/600/800

. The results of several heuristic algorithms involved in the experiment are shown in Figure 9 and the statistics for the results are shown in

Table 6. Results of fitness value of comparison algorithms with different target numbers.

Scenario	Optimal Fitness Value
	H-GASA	SA	PSO	GA
25-1	157	100	124	72
25-2	134	99	110	65
25-3	178	110	156	87
50-1	320	210	208	100
50-2	274	157	156	99
50-3	250	128	133	100
75-1	461	269	271	122
75-2	505	300	297	120
75-3	420	220	227	125
100-1	553	291	339	154
100-2	518	266	277	147
100-3	610	304	398	180

.

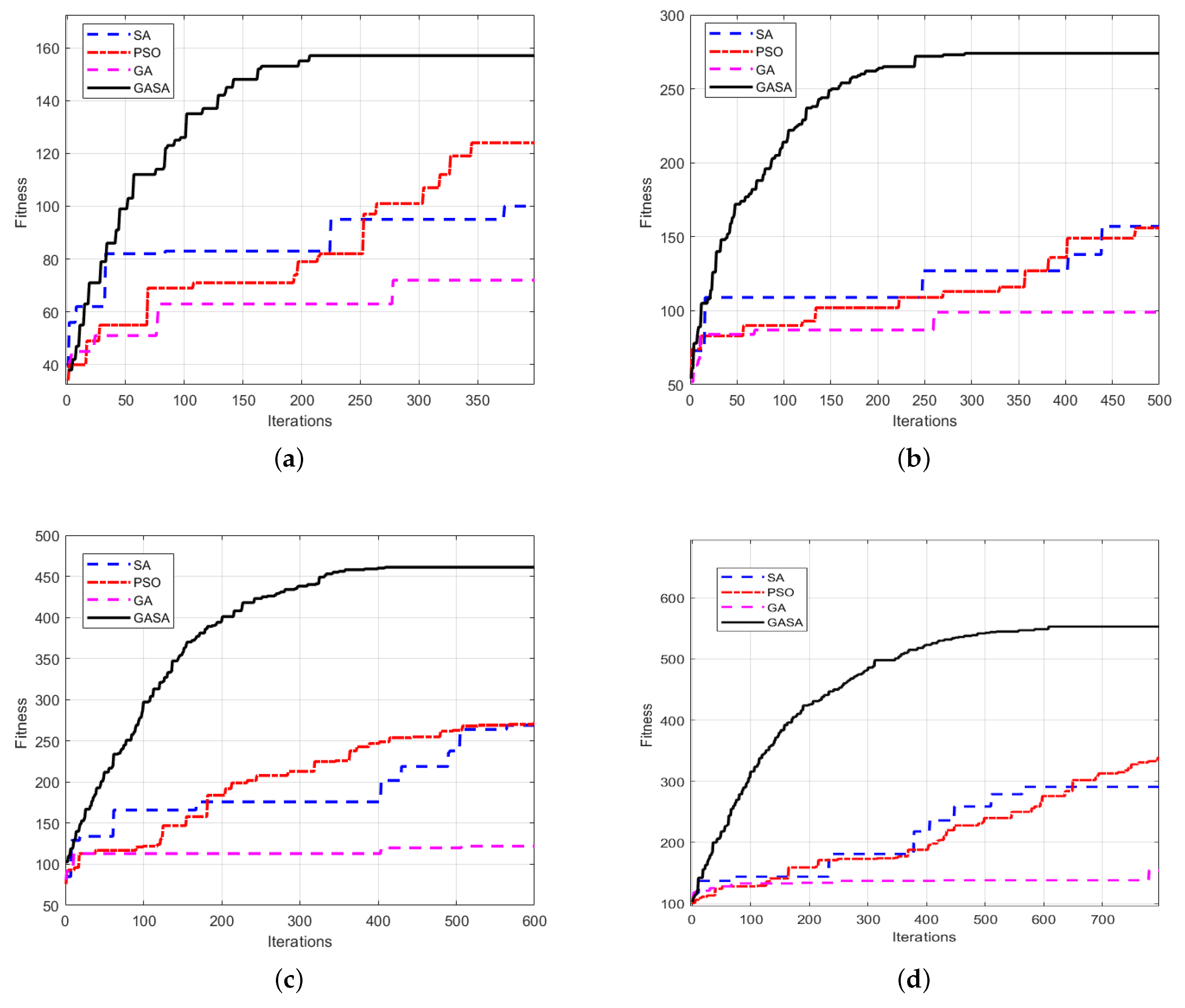
We have carried out three groups of task planning from 25 to 100 targets, respectively, and the specific values of the optimal fitness values corresponding to different target numbers are shown in Table 6. From the above results, it can be seen that the H-GASA optimization results are much better than the existing three algorithms. When the number of targets increases from 25 to 100, H-GASA still has a strong optimization ability and can keep a good stability, which indicates that H-GASA still has a good computational efficiency when it is extended to large-scale operations. The specific average evolution curve analysis is shown in Figure 9.

According to the comparison between the optimal fitness value and the convergence speed in Figure 9, GA has a faster convergence speed but cannot achieve the optimal solution. PSO and SA have better optimization capabilities than GA but cannot achieve global convergence. H-GASA has obvious advantages in terms of optimization ability and calculation speed, and has good stability. Especially in terms of optimization ability, the optimal fitness value obtained by H-GASA is much higher than the other three algorithms. This is because H-GASA combines the advantages of the two algorithms and has stronger global search and local optimization capabilities. At the same time, H-GASA can achieve global convergence more stably than other algorithms.

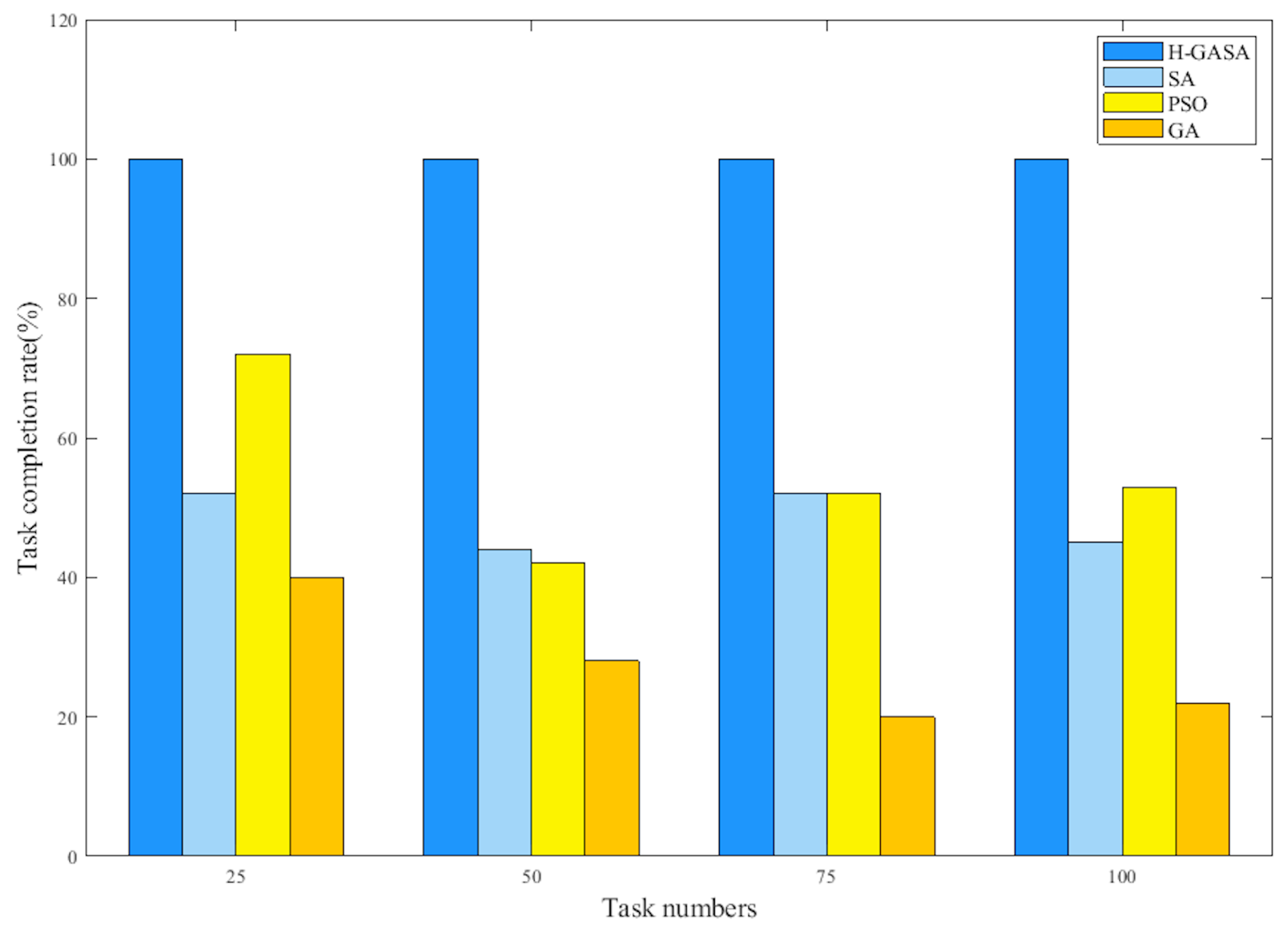
We also compared the task completion rates of several algorithms, and the results are shown in

Table 7. Results of task completion rate of comparison algorithms with different target numbers.

Scenario	Task Completion Rate
	H-GASA	SA	PSO	GA
25	1	0.52	0.72	0.40
50	1	0.44	0.42	0.28
75	1	0.52	0.52	0.20
100	1	0.45	0.53	0.22

and Figure 10.

As we can see from Figure 10, compared with other algorithms, the task completion rate of H-GASA is higher than other algorithms, and it has reached the final convergence. The phenomenon of task conflict is improved by moving tasks with time window conflicts to non-overlapping time periods, and the utilization of task time windows in the planning period is raised. Meanwhile, it is verified that our proposed greedy task scheduling algorithm is effective.

4. Discussion

Recent research has focused on developing the satellite autonomy scheme for MSS. On-board autonomy planning is more successful in terms of safety and efficiency than uploading the results to the satellite after the ground station planning. In this study, on-board autonomous task planning is divided into two stages: multi-satellite task assignment and single-satellite task scheduling. The results show that the planning method proposed in this study can effectively plan all the tasks received by MSS. Specifically, this method can coordinate multiple satellites in MSS to make autonomous on-board planning for multiple tasks, and output the best task planning scheme according to the task information and satellite orbit state. As discussed in this paper, the H-GASA developed in this study performs better in terms of search speed and optimization ability, and has obvious advantages in various applications. Table 6 and Figure 9 show the benefits of planning schemes in different scenarios, which proves that this method can be widely used to support the planning, allocation and scheduling of tasks. This suggests that on-board autonomous task planning can be a worthwhile investment, especially in the long term.

In simulation results, the main advantages of our work are: (1) Less computation time. In the comparative analysis of different coding formats, we improved the coding format to shorten the average calculation time of the algorithm by 1.5 times, and improved the search speed of the algorithm; (2) The task completion rate and planning benefits are higher. In the benefit analysis, we compared the task completion rate and the final benefit, and the results show that our method has a significant improvement. This is because the algorithm can accept the poor individual solution with a certain probability, jump out of the local optimum and reach the global optimum. Meanwhile, this study considered that possible task conflicts caused by time window preemption will have a negative impact on planning results. Therefore, adding a heuristic strategy in the task scheduling process can effectively eliminate possible task time window conflicts and complete tasks as much as possible; (3) The basic energy consumption of satellites is reduced. The method can reduce the number of communications with the ground station, improve the utilization rate of satellite resources, and reduce the energy consumption of the satellite.

There are several aspects of this study that need to be improved in future simulation methods. The benefit analysis in different scenarios shows that, even in high demand scenarios, the global optimal solution can be achieved by increasing the number of iterations of the algorithm. However, the computational complexity of the algorithm will also increase significantly. Due to the low computing power of the on-board processor, in order to ensure efficiency, it is necessary to make a trade-off between the quality of the algorithm solution and the running time, and further improve the algorithm to balance the optimization ability and convergence speed.

5. Conclusions

A realistic formulation of multi-satellite cooperative autonomous task planning in the Earth observation scenario and a solution technique were proposed in this work. To facilitate multi-satellite cooperation management, a multi-satellite task cooperation architecture based on multi-agents was formulated. The established mixed-integer optimization problem finds the optimal planning by maximizing the revenue with the realistic satellite load and orbit constraints. A hybrid genetic algorithm with simulated annealing has been proposed to solve the built mathematical model. With this algorithm, a greedy task scheduling algorithm was developed to solve task conflicts. Different simulation scenarios were established to test the performance of the algorithms. From the experimental results, the proposed algorithm is applicable to MSCATP. Moreover, through the comparison of task completion income and task completion rate, the proposed algorithm has a better effect than existing algorithms.

In the future, we will consider more uncertain factors, such as the need to respond in time to change the task observation sequence in case of emergency, and it will involve the re-planning of tasks.