An EMD-LSTM Deep Learning Method for Aircraft Hydraulic System Fault Diagnosis under Different Environmental Noises
Abstract
1. Introduction
2. Aircraft Hydraulic System Model Building and Data Collection
2.1. Aircraft Hydraulic System Definition and AMESIM Model Build
2.2. Normal State and Fault State
2.3. Data Collection
3. The EMD-LSTM Method
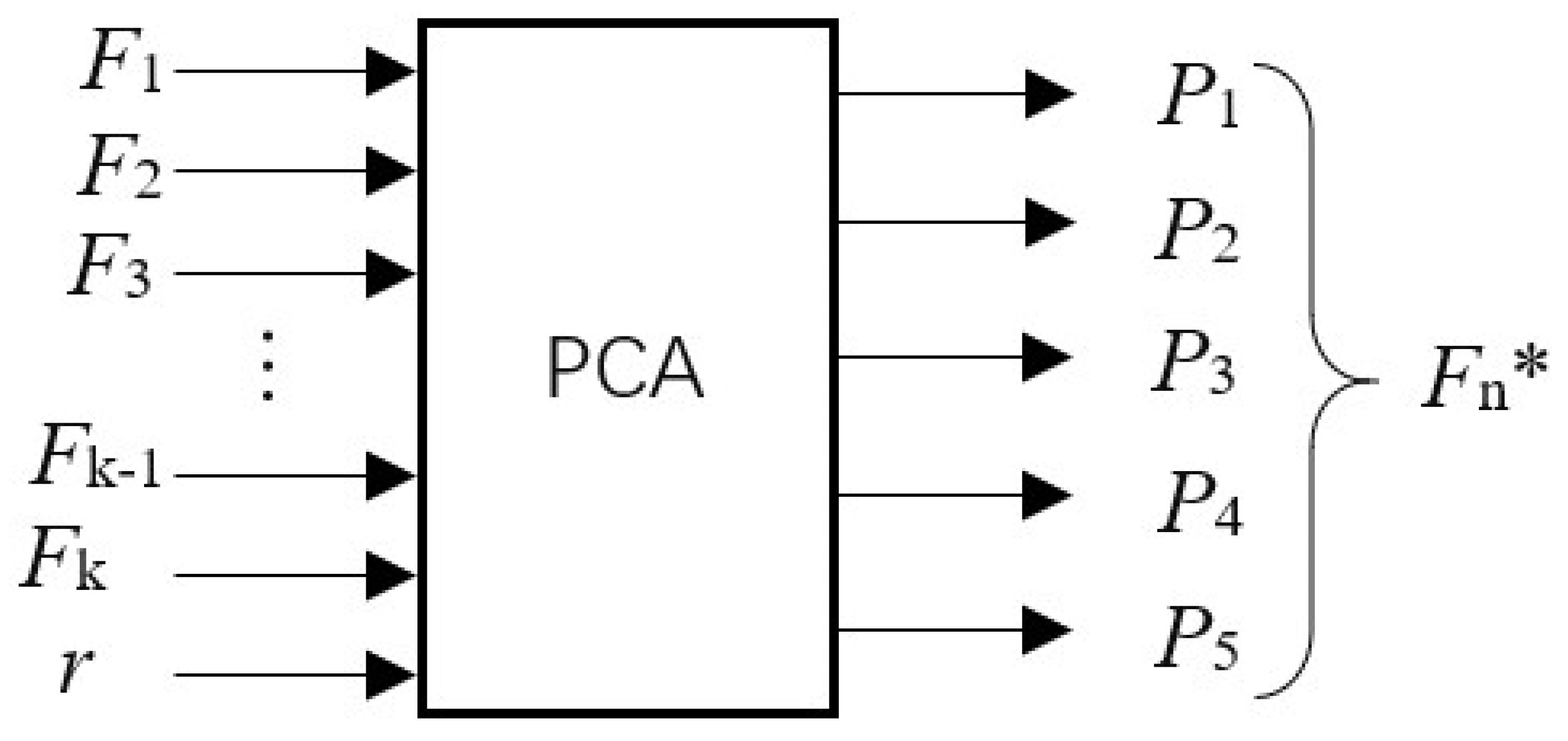
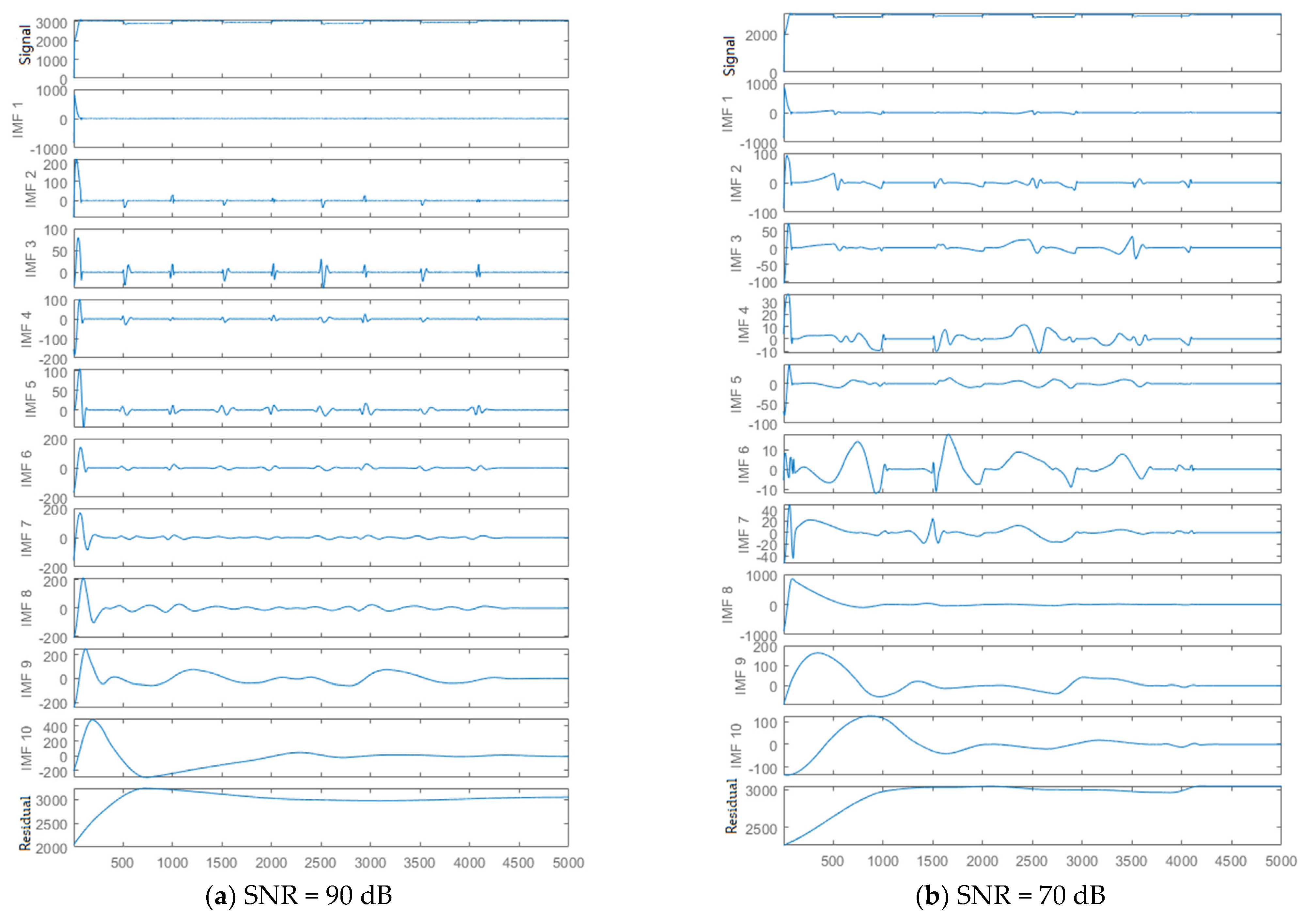
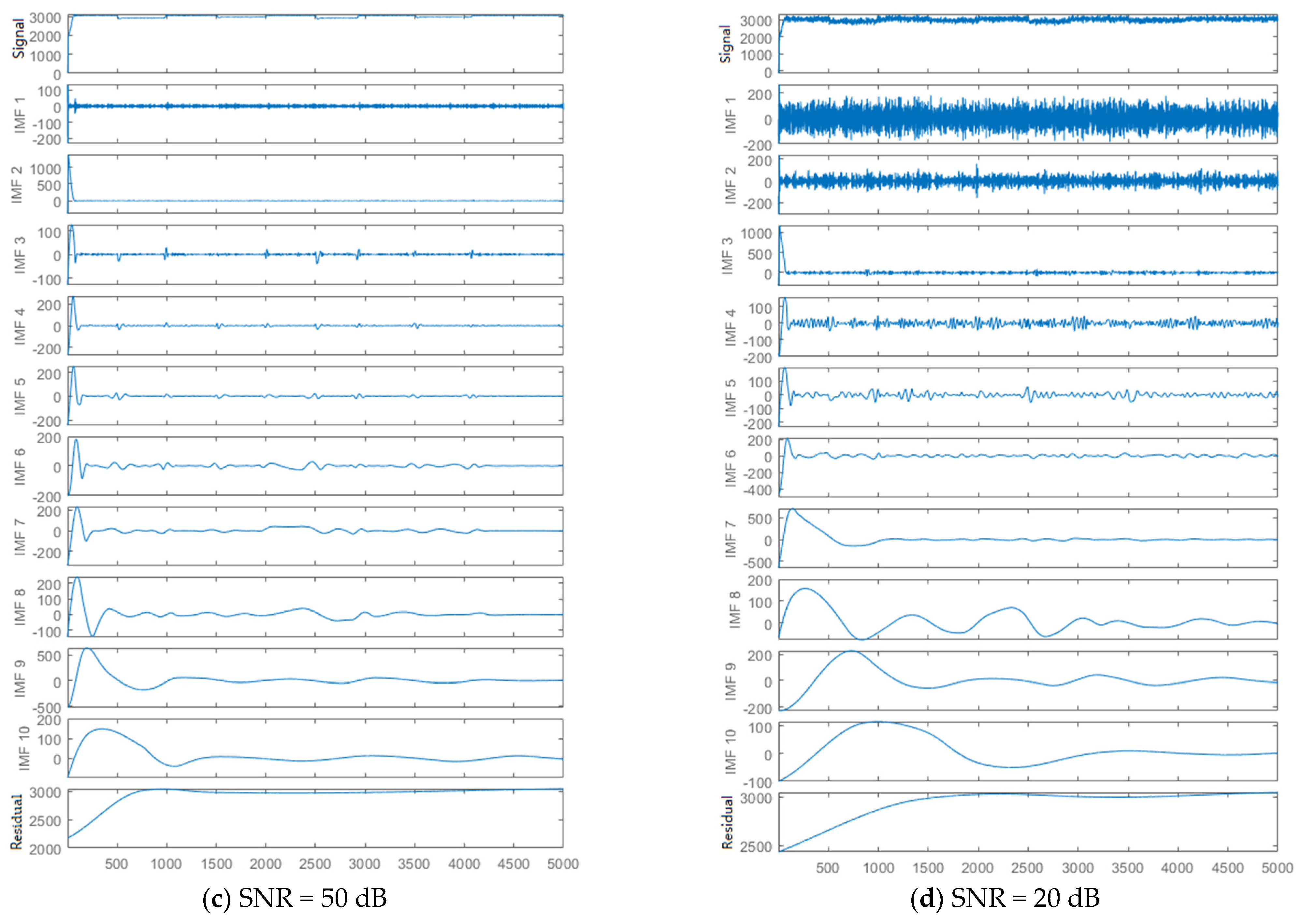
3.1. EMD and PCA Method
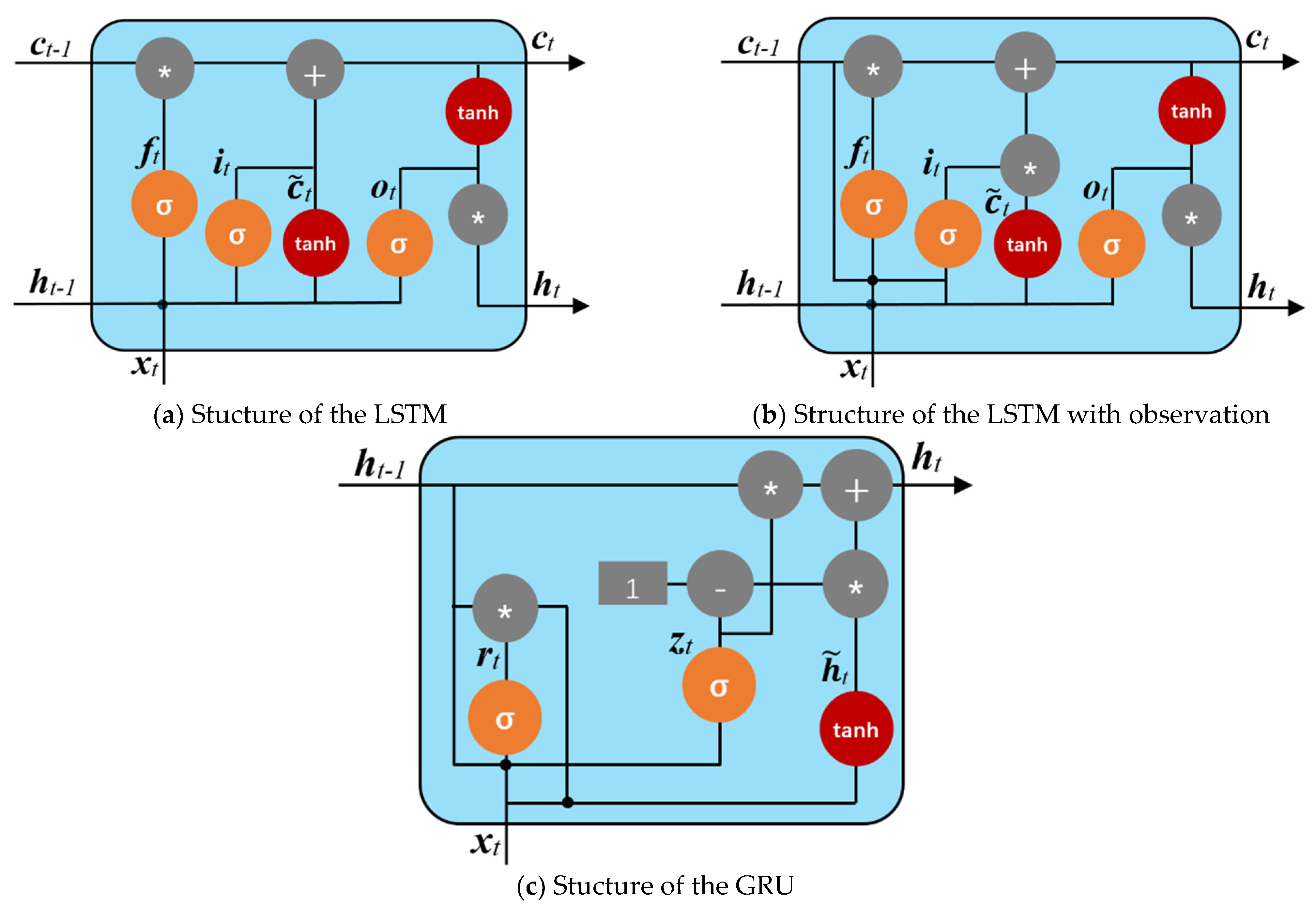
3.2. Three Inner Structure of LSTM Networks
3.3. The LSTM Network Structure Design
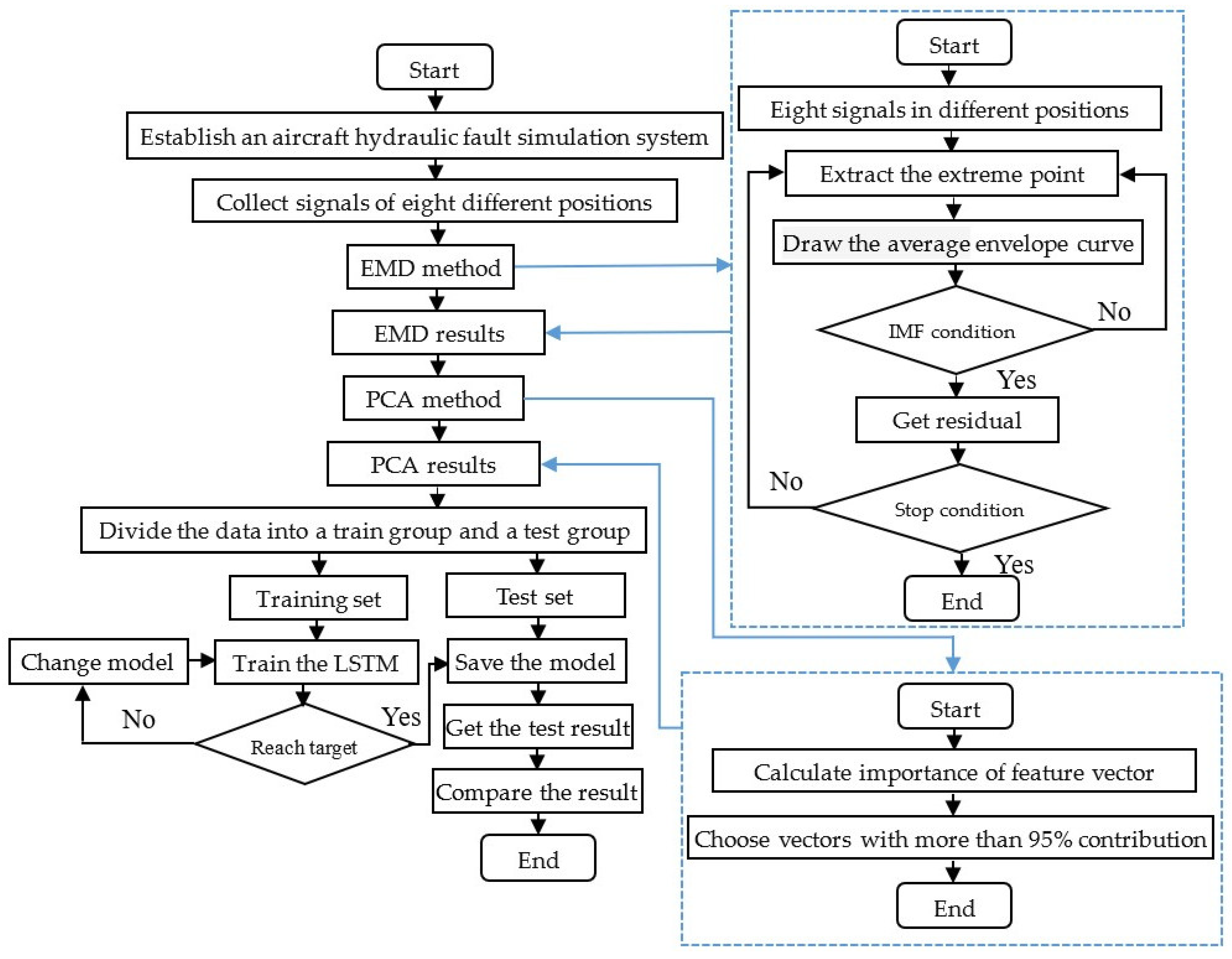
3.4. EMD-LSTM Method for the Aircraft Hydraulic System
4. The Simulation Results of the EMD-LSTM Method
4.1. Data Collection and Feature Extraction
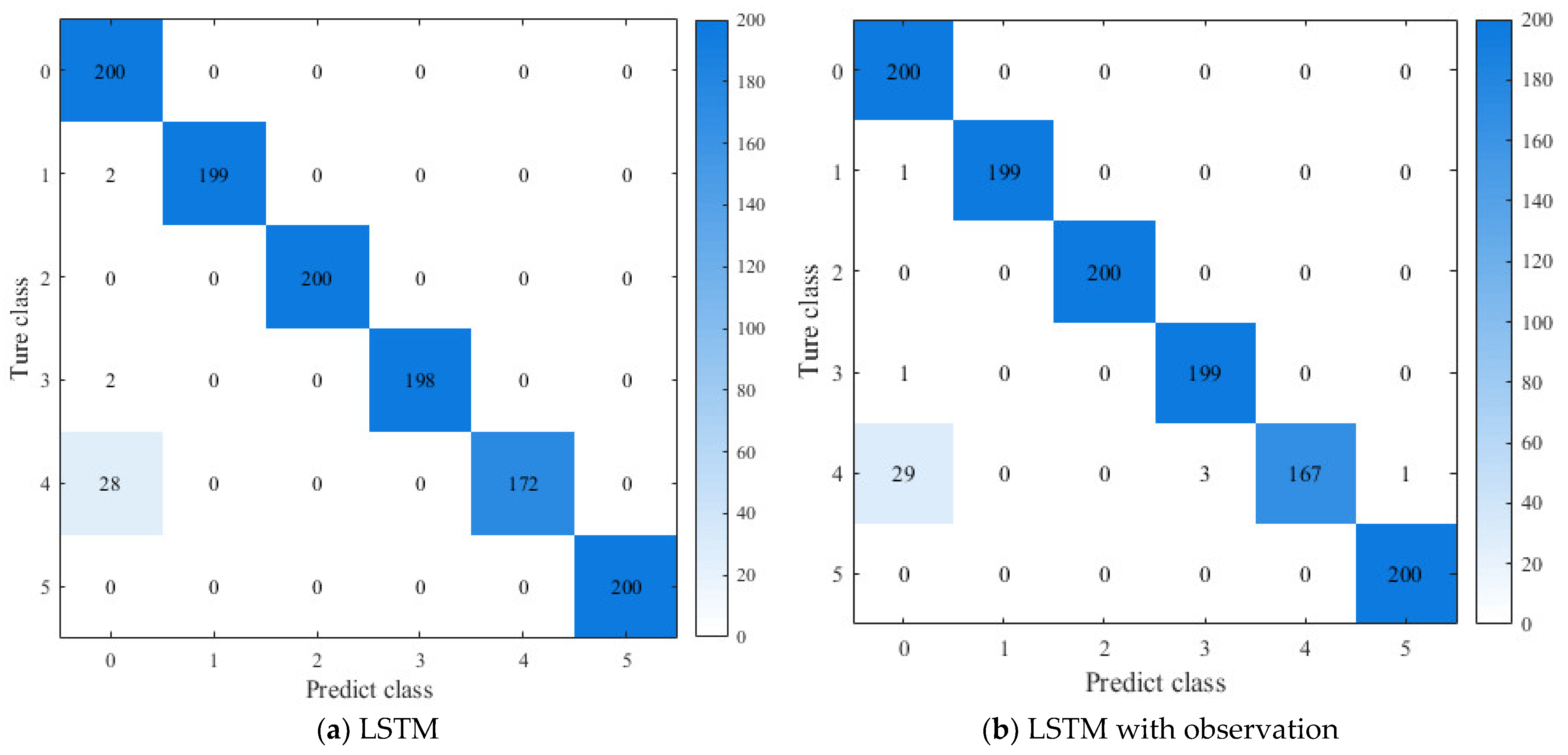
4.2. The Fault Diagnostic Results in the Comparison of Three EMD-LSTM Methods
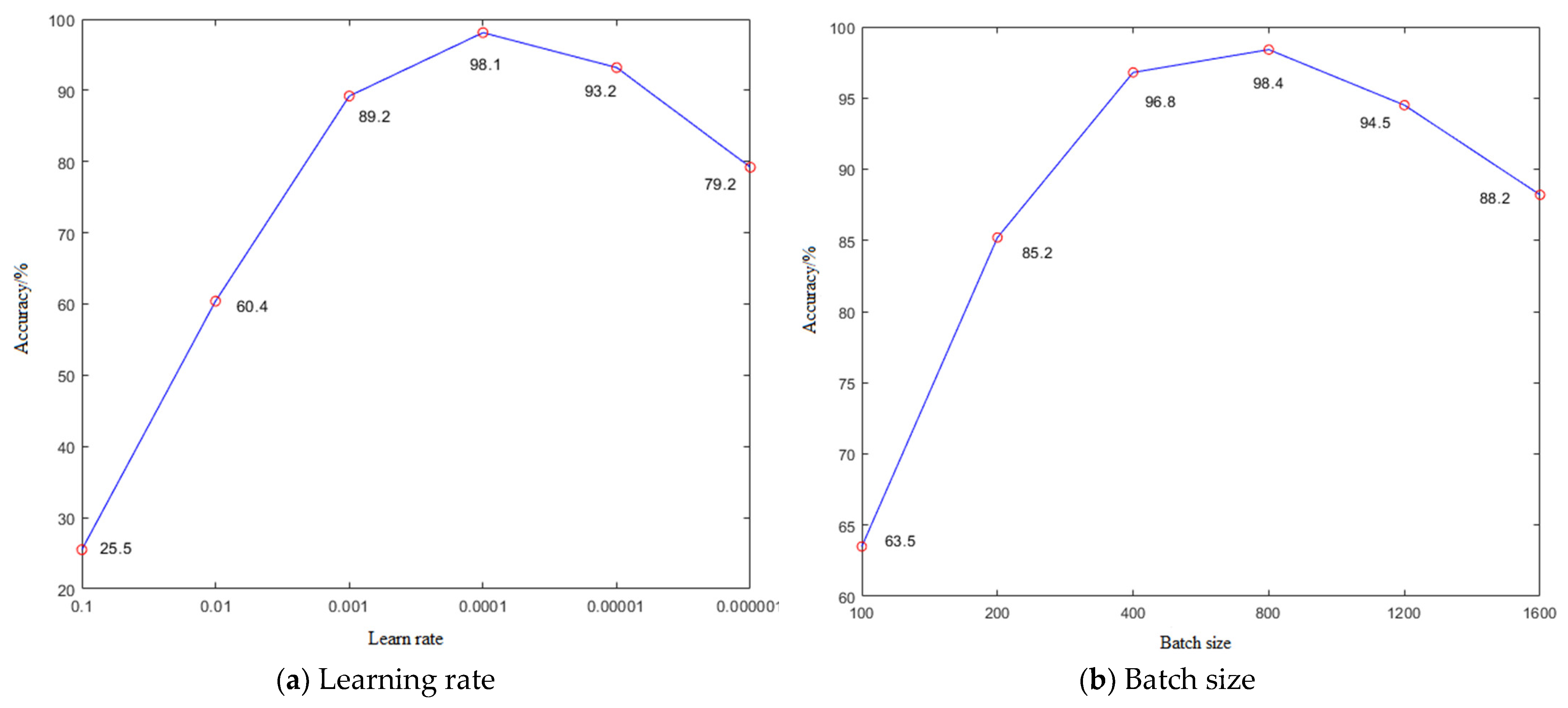
4.3. EMD-GRU Network Structure and Parameter Optimization
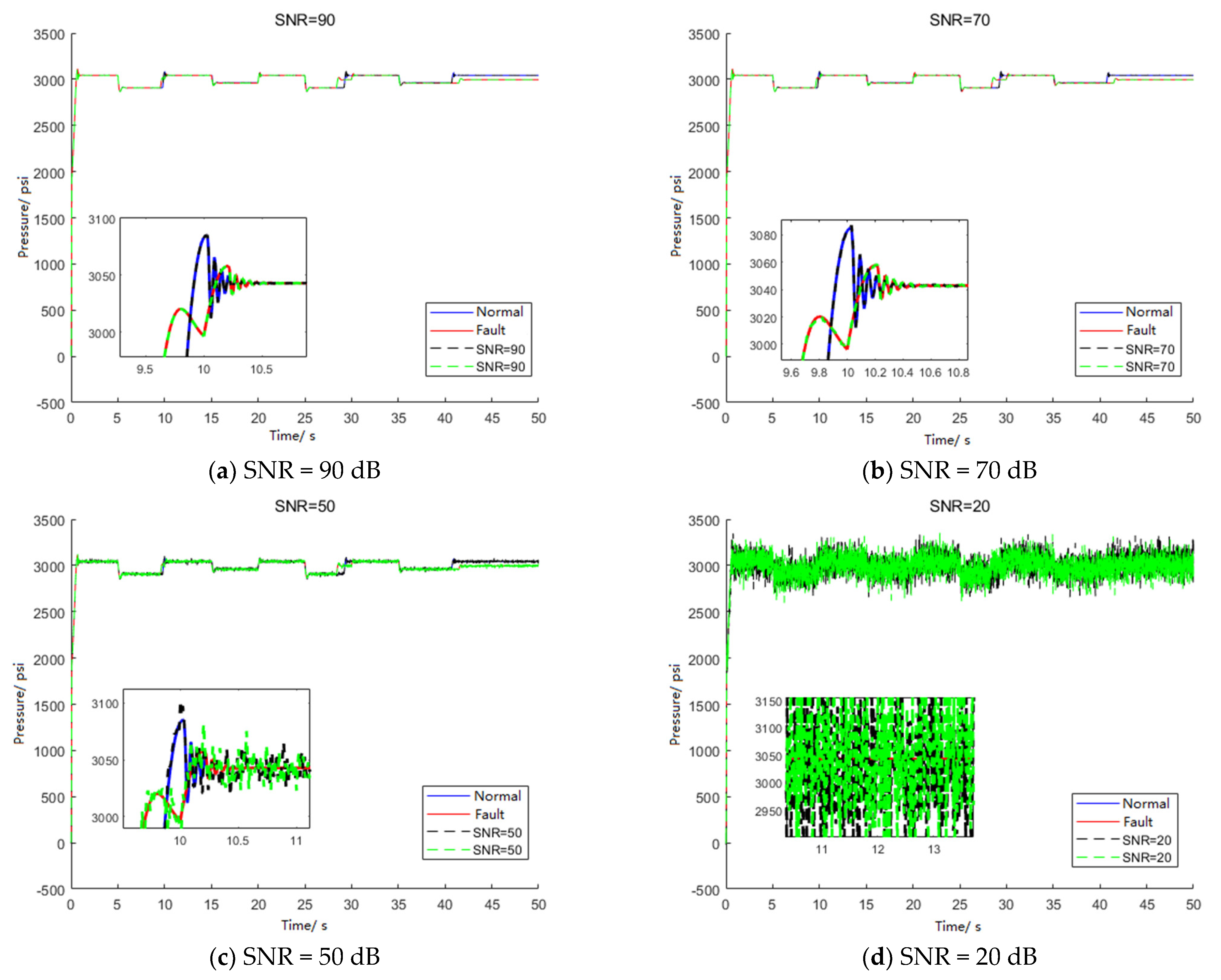
4.4. Noise Addition and EMD-GRU Fault Diagnosis under Different Noise Environments
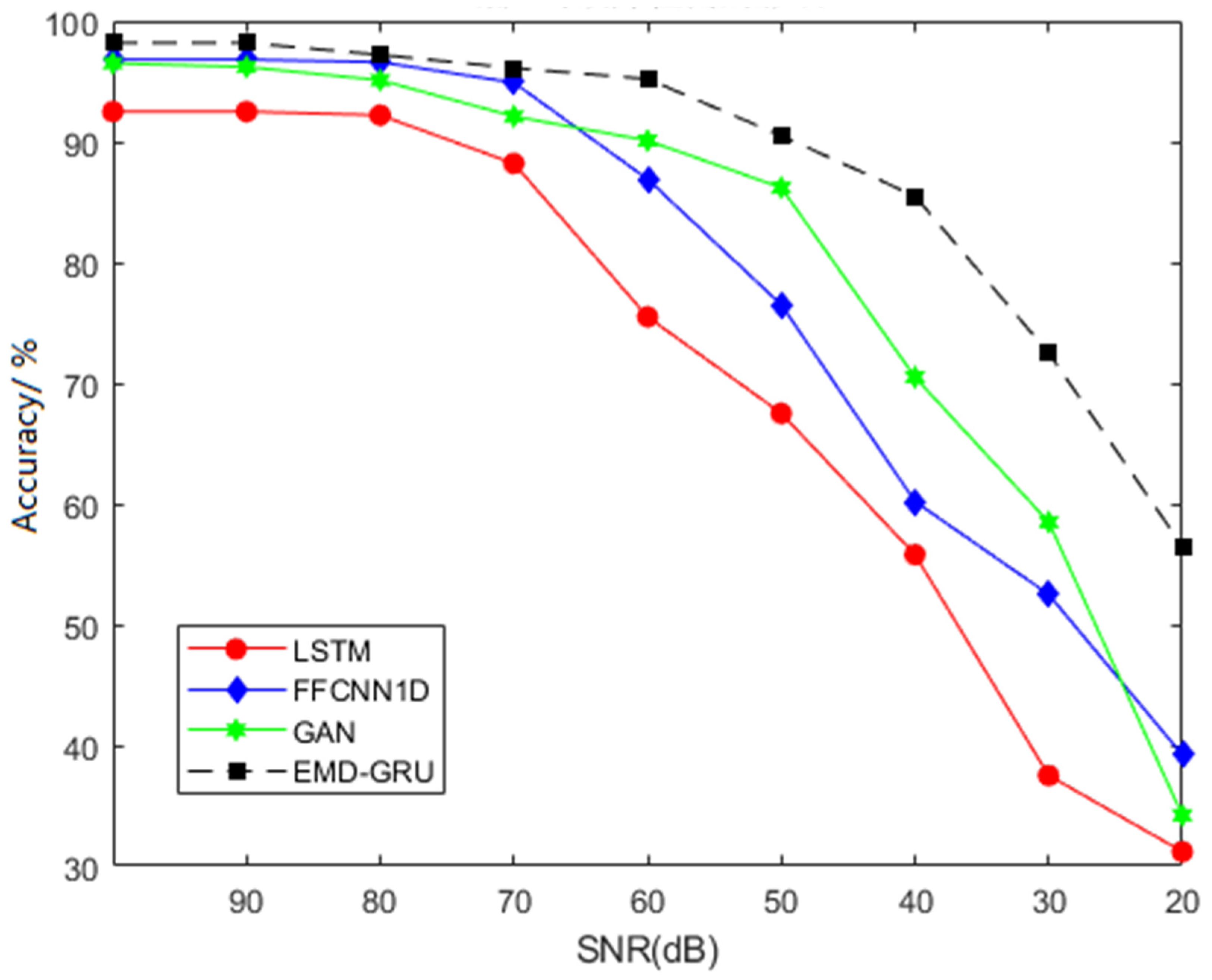
4.5. Comparison between EMD-GRU Method with Various Other Fault Diagnostic Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Reveley, M.S.; Briggs, J.L.; Evans, J.K.; Sandifer, C.E.; Jones, S.M. Causal Factors and Adverse Conditions of Aviation Accidents and Incidents Related to Integrated Resilient Aircraft Control. US: NASA/TM-216967, 1 November 2010. [Google Scholar]
- Atkinson, R.M.; Montakhab, M.R.; Pillay, K.D.A.; Woollons, D.J.; Hogan, P.A.; Burrows, C.R.; Edge, K.A. Automated Fault Analysis for Hydraulic Systems: Part 1: Fundamentals. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 1992, 206, 207–214. [Google Scholar] [CrossRef]
- Hogan, P.A.; Burrows, C.R.; Edge, K.A.; Atkinson, R.M.; Montakhab, M.R.; Woollons, D.J. Automated Fault Analysis for Hydraulic Systems: Part 2: Applications. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 1992, 206, 215–224. [Google Scholar] [CrossRef]
- Al-Baldawi, R.A. Improved Performance of Fluid Power System Using Updating Knowledge-Based System. J. Eng. Dev. 2009, 13, 1–9. [Google Scholar]
- Mehra, R.K.; Peschon, J. An Innovations Approach to Fault Detection and Diagnosis in Dynamic Systems. Automatica 1971, 7, 637–640. [Google Scholar] [CrossRef]
- Khoshzaban Zavarehi, M. On-Line Condition Monitoring and Fault Diagnosis in Hydraulic System Components Using Parameter Estimation and Pattern Classification; The University of British Columbia: Vancouver, BC, Canada, 1997. [Google Scholar]
- Chen, X.; Zhang, B.; Gao, D. Bearing fault diagnosis base on multi-scale CNN and LSTM model. J. Intell. Manuf. 2021, 32, 971–987. [Google Scholar] [CrossRef]
- Xu, J.; Luo, N.; Yang, Y.; Han, P.; Zhang, D. Reliability analysis for the hydraulic booster control surface of aircraft. J. Aircr. 2017, 54, 456–463. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, S.; Shi, J.; Li, T.; Wang, X. Fault diagnosis of an intelligent hydraulic pump based on a nonlinear unknown input observer. Chin. J. Aeronaut. 2018, 31, 385–394. [Google Scholar] [CrossRef]
- Liu, K.; Feng, Y.; Xue, X. Fault diagnosis of hydraulic retraction system based on multi-source signals feature fusion and health assessment for the actuator. J. Intell. Fuzzy Syst. 2018, 34, 3635–3649. [Google Scholar] [CrossRef]
- Li, W.; Nie, W.; Su, Y. Human action recognition based on selected spatio-temporal features via bidirectional LSTM. IEEE Access 2018, 6, 44211–44220. [Google Scholar] [CrossRef]
- Stollenga, M.F.; Byeon, W.; Liwicki, M.; Schmidhuber, J. Parallel multi-dimensional LSTM, with application to fast biomedical volumetric image segmentation. Adv. Neural Inf. Process. Syst. 2015, 28. [Google Scholar]
- Bappy, J.H.; Simons, C.; Nataraj, L.; Manjunath, B.S.; Roy-Chowdhury, A.K. Hybrid lstm and encoder–decoder architecture for detection of image forgeries. IEEE Trans. Image Process. 2019, 28, 3286–3300. [Google Scholar] [CrossRef]
- Islam, M.Z.; Islam, M.M.; Asraf, A. A combined deep CNN-LSTM network for the detection of novel coronavirus (COVID-19) using X-ray images. Inform. Med. Unlocked 2020, 20, 100412. [Google Scholar] [CrossRef]
- Cabrera, D.; Guamán, A.; Zhang, S.; Cerrada, M.; Sánchez, R.V.; Cevallos, J.; Long, J.; Li, C. Bayesian approach and time series dimensionality reduction to LSTM-based model-building for fault diagnosis of a reciprocating compressor. Neurocomputing 2020, 380, 51–66. [Google Scholar] [CrossRef]
- Khorram, A.; Khalooei, M.; Rezghi, M. End-to-end CNN+ LSTM deep learning approach for bearing fault diagnosis. Appl. Intell. 2021, 51, 736–751. [Google Scholar] [CrossRef]
- Ravikumar, K.N.; Yadav, A.; Kumar, H.; Gangadharan, K.V.; Narasimhadhan, A.V. Gearbox fault diagnosis based on Multi-Scale deep residual learning and stacked LSTM model. Measurement 2021, 186, 110099. [Google Scholar] [CrossRef]
- Ye, S.; Jiang, J.; Li, J.; Liu, Y.; Zhou, Z.; Liu, C. Fault diagnosis and tolerance control of five-level nested NPP converter using wavelet packet and LSTM. IEEE Trans. Power Electron. 2019, 35, 1907–1921. [Google Scholar] [CrossRef]
- Zou, F.; Zhang, H.; Sang, S.; Li, X.; He, W.; Liu, X. Bearing fault diagnosis based on combined multi-scale weighted entropy morphological filtering and bi-LSTM. Appl. Intell. 2021, 51, 6647–6664. [Google Scholar] [CrossRef]
- Jalayer, M.; Orsenigo, C.; Vercellis, C. Fault detection and diagnosis for rotating machinery: A model based on convolutional LSTM, Fast Fourier and continuous wavelet transforms. Comput. Ind. 2021, 125, 103378. [Google Scholar] [CrossRef]
- De Bruin, T.; Verbert, K.; Babuška, R. Railway track circuit fault diagnosis using recurrent neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 523–533. [Google Scholar] [CrossRef]
- Seilsepour, H.; Zarastvand, M.; Talebitooti, R. Acoustic insulation characteristics of sandwich composite shell systems with double curvature: The effect of nature of viscoelastic core. J. Vib. Control 2022, 10775463211056758. [Google Scholar] [CrossRef]
- Zarastvand, M.R.; Asadijafari, M.H.; Talebitooti, R. Acoustic wave transmission characteristics of stiffened composite shell systems with double curvature. Compos. Struct. 2022, 292, 115688. [Google Scholar] [CrossRef]
- Xu, G.P.; Tian, W.F.; Qian, L. EMD-and SVM-based temperature drift modeling and compensation for a dynamically tuned gyroscope (DTG). Mech. Syst. Signal Process. 2007, 21, 3182–3188. [Google Scholar] [CrossRef]
- Mohanty, S.; Gupta, K.K.; Raju, K.S. Comparative study between VMD and EMD in bearing fault diagnosis. In Proceedings of the 2014 9th International Conference on Industrial and Information Systems (ICIIS), Gwalior, India, 15–17 December 2014; IEEE: New York, NY, USA, 2014. [Google Scholar]
- Saidi, L.; Ali, J.B.; Fnaiech, F. Bi-spectrum based-EMD applied to the non-stationary vibration signals for bearing faults diagnosis. ISA Trans. 2014, 53, 1650–1660. [Google Scholar] [CrossRef]
- Yuan, J.; Jiang, H.; Zhao, Q.; Xu, C.; Liu, H.; Tian, Y. Dual-mode noise-reconstructed EMD for weak feature extraction and fault diagnosis of rotating machinery. IEEE Access 2019, 7, 173541–173548. [Google Scholar] [CrossRef]
- Beau, A.; Daniels, A. The Main Users of the Hydraulic System in an Aircraft Hydraulic System. 2010, 04. Available online: https://beaudaniels.com/info-graphics (accessed on 4 April 2010).
- Zhang, S.; Xu, F.; Hu, M.; Zhang, L.; Liu, H.; Li, M. A novel denoising algorithm based on TVF-EMD and its application in fault classification of rotating machinery. Measurement 2021, 179, 109337. [Google Scholar] [CrossRef]
- Manikumar, R.; Singampalli, R.S.; Raj, J.A. Application of EMD based statistical parameters for the prediction of fault severity in a spur gear through vibration signals. Adv. Mater. Process. Technol. 2022, 8, 2152–2170. [Google Scholar] [CrossRef]
- Malik, H.; Sharma, R. EMD and ANN based intelligent fault diagnosis model for transmission line. J. Intell. Fuzzy Syst. 2017, 32, 3043–3050. [Google Scholar] [CrossRef]
- Malik, H.; Pandya, Y.; Parashar, A.; Sharma, R. Feature Extraction Using EMD and Classifier through Artificial Neural Networks for Gearbox Fault Diagnosis. In Applications of Artificial Intelligence Techniques in Engineering; Springer: Singapore, 2019; pp. 309–317. [Google Scholar]
- Kendler, K.S. The beginnings of the debate between the Mendelians and the Biometricians in psychiatric genetics: David Heron, Karl Pearson, Abraham Rosanoff, and Charles Davenport 1913–1914. Am. J. Med. Genet. Part B Neuropsychiatr. Genet. 2022, 189, 16–25. [Google Scholar] [CrossRef]
- Ding, S.; Zhang, P.; Ding, E.; Yin, S.; Naik, A.; Deng, P.; Gui, W. On the application of PCA technique to fault diagnosis. Tsinghua Sci. Technol. 2010, 15, 138–144. [Google Scholar] [CrossRef]
- Choi, S.W.; Lee, C.; Lee, J.M.; Park, J.H.; Lee, I.B. Fault detection and identification of nonlinear processes based on kernel PCA. Chemom. Intell. Lab. Syst. 2005, 75, 55–67. [Google Scholar] [CrossRef]
- Jaffel, I.; Taouali, O.; Elaissi, E.; Messaoud, H. A new online fault detection method based on PCA technique. IMA J. Math. Control Inf. 2014, 31, 487–499. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Shen, K.N.; Zhao, D.B. Fault diagnosis for aircraft hydraulic systems via one-dimensional multichannel convolution neural network. Actuators 2022, 11, 182. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, T.; Wang, Y.; Cao, Z.; Guo, Z.; Fu, H. A novel method for imbalanced fault diagnosis of rotating machinery based on generative adversarial networks. IEEE Trans. Instrum. Meas. 2020, 70, 1–17. [Google Scholar] [CrossRef]
- Yan, K.; Zhong, C.; Ji, Z.; Huang, J. Semi-supervised learning for early detection and diagnosis of various air handling unit faults. Energy Build. 2018, 181, 75–83. [Google Scholar] [CrossRef]
- Jin, C.; Shi, F.; Xiang, D.; Jiang, X.; Zhang, B.; Wang, X.; Zhu, W.; Gao, E.; Chen, X. 3D fast automatic segmentation of kidney based on modified AAM and random forest. IEEE Trans. Med. Imaging 2016, 35, 1395–1407. [Google Scholar] [CrossRef]
- Babu, G.S.; Zhao, P.; Li, X. Deep convolutional neural network-based regression approach for estimation of remaining useful life. In Proceedings of the International Conference on Database Systems for Advanced Applications, Dallas, TX, USA, 16–19 April 2016; Springer: Berlin, Germany, 2016; pp. 214–228. [Google Scholar]
- Vlachas, P.R.; Byeon, W.; Wan, Z.Y.; Sapsis, T.P.; Koumoutsakos, P. Data-Driven Forecasting of High-Dimensional Chaotic Systems with Long Short-Term Memory Networks. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20170844. [Google Scholar] [CrossRef]
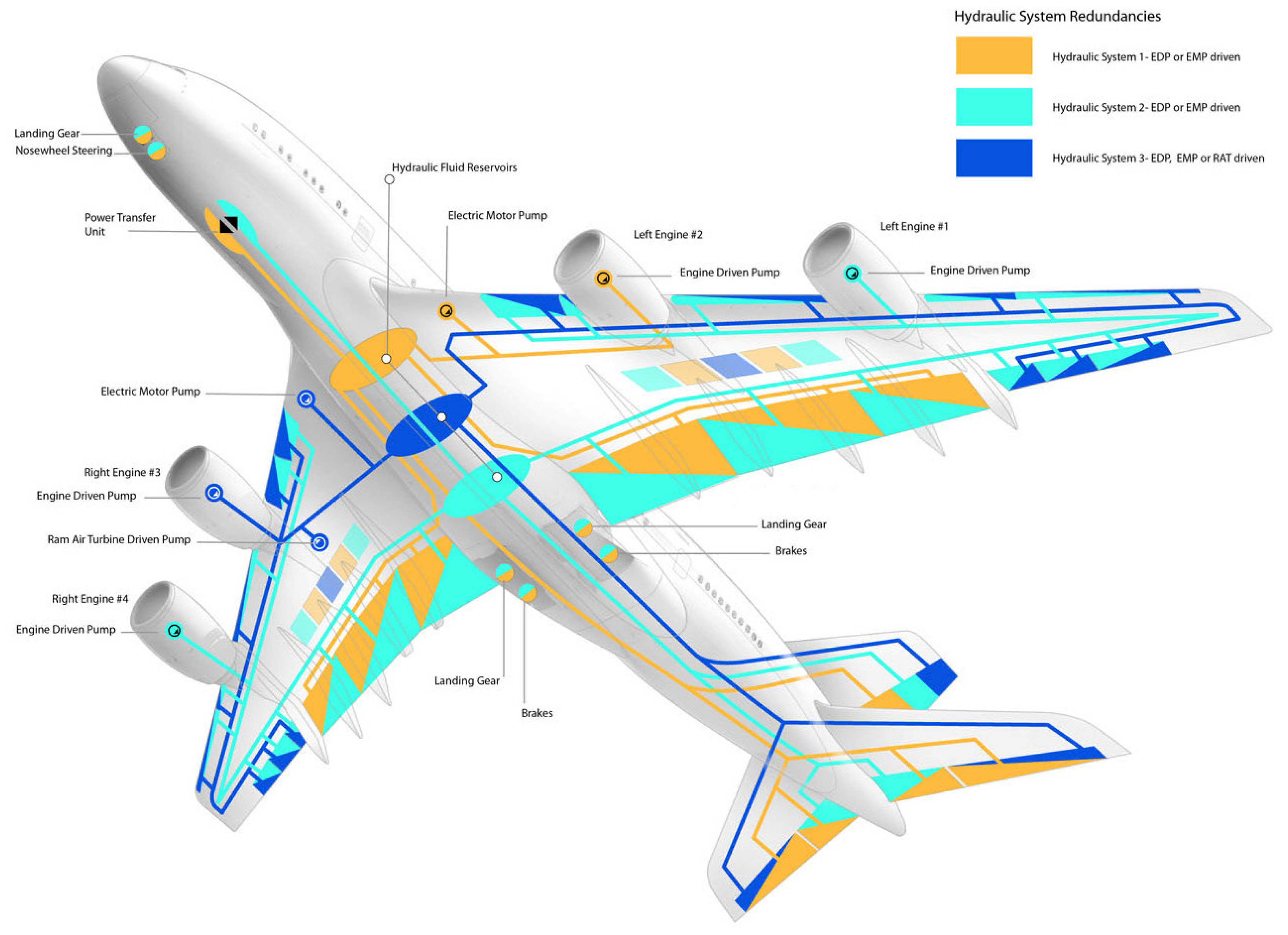
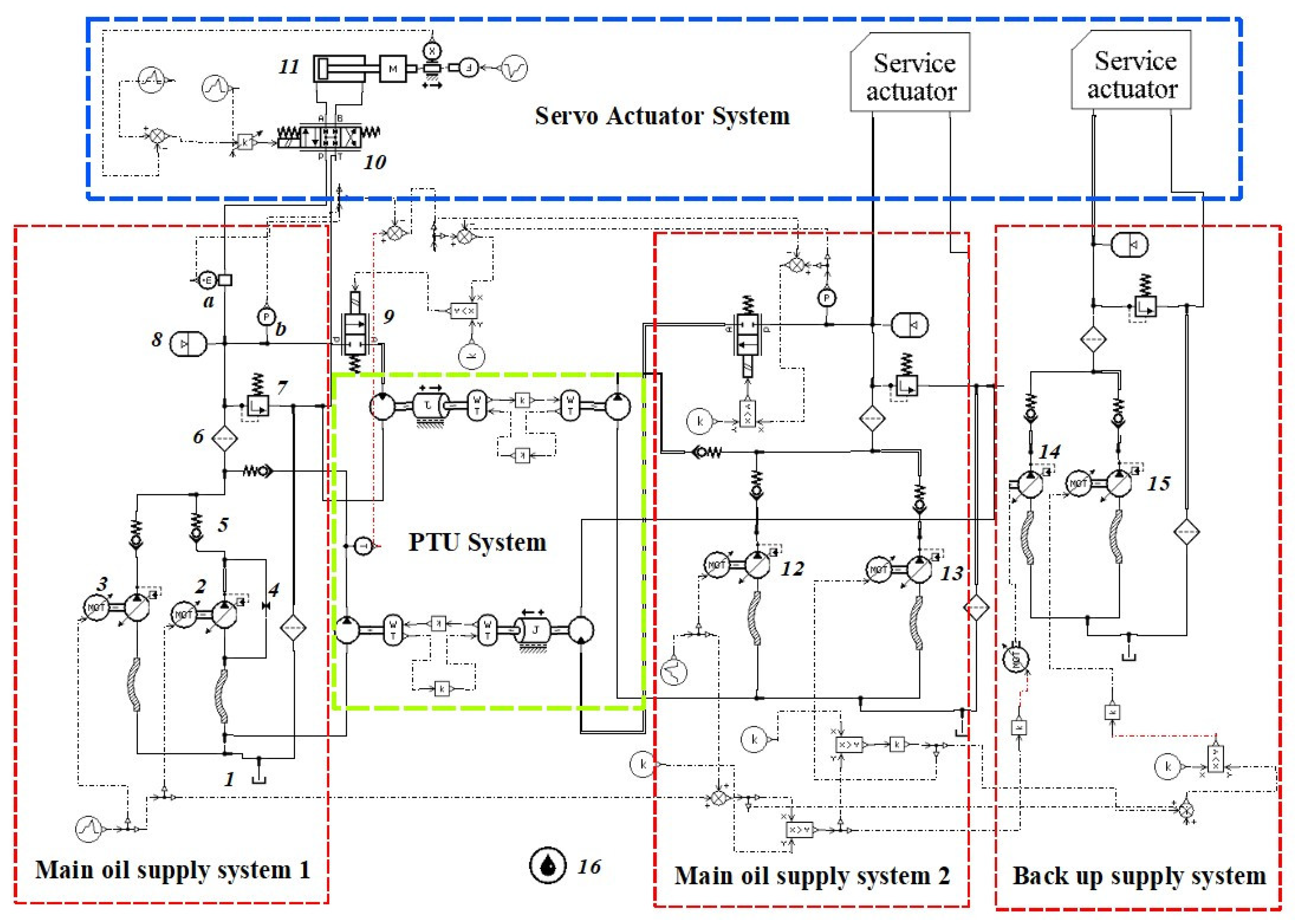





| Number | AME-Element | Key Parameter | Value | Meaning |
|---|---|---|---|---|
| 1 | signal03 | Output | 5000 r·min−1 | The shaft speed is 5000 r/min, and the pressure of the pump is 3000 psi. |
| 3 | Accumulato2 | Gas pressure accumulator volume | 1885 psi 2.62 L | Accumulator reduces pressure, as an emergency source. |
| 4 | presscontol01 | Relief valve cracking pressure | 3436 psi | Pressure relief value, for system discharge. |
| 5 | tank01 | Tank pressure | 50 psi | Booster tank, for pre-boost to 50 psi. |
| 7 | pump13 | Nominal shaft speed | 5000 r·min−1 | Left engine drive pump (EDP). |
| 11~14 | pump13 | nominal shaft speed | 5000 r·min−1 4166 r·min−1 | Right EDP, Yellow system EMP, Blue system EMP, and RAT. Rated pressure of RAT is 2500 psi. |
| 10 | constant_3 | constant value | 34.4738 bar | PTU opens when the pressure difference between green and yellow systems is 34.4738 bar. |
| Num | Fault Category and Category Number | Key Parameter | Normal Value | Fault Value |
|---|---|---|---|---|
| 2 | pump leakage-1 | Equivalent orifice diameter (mm) | 0.1~0.3 | 1~2 |
| 6 | filter blockage-2 | Equivalent orifice diameter (mm) | 5~7 | 3~4 |
| 7 | relief valve spring failure-3 | Open pressure (psi) | 3400 | 2600–3300 |
| 11 | Actuator inner leakage-4 | Leakage coefficient (L·min−1·bar−1) | 0~0.01 | 0.03~0.05 |
| 16 | oil pollution-5 | Air content (%) | 0.1~0.3 | 5~15 |
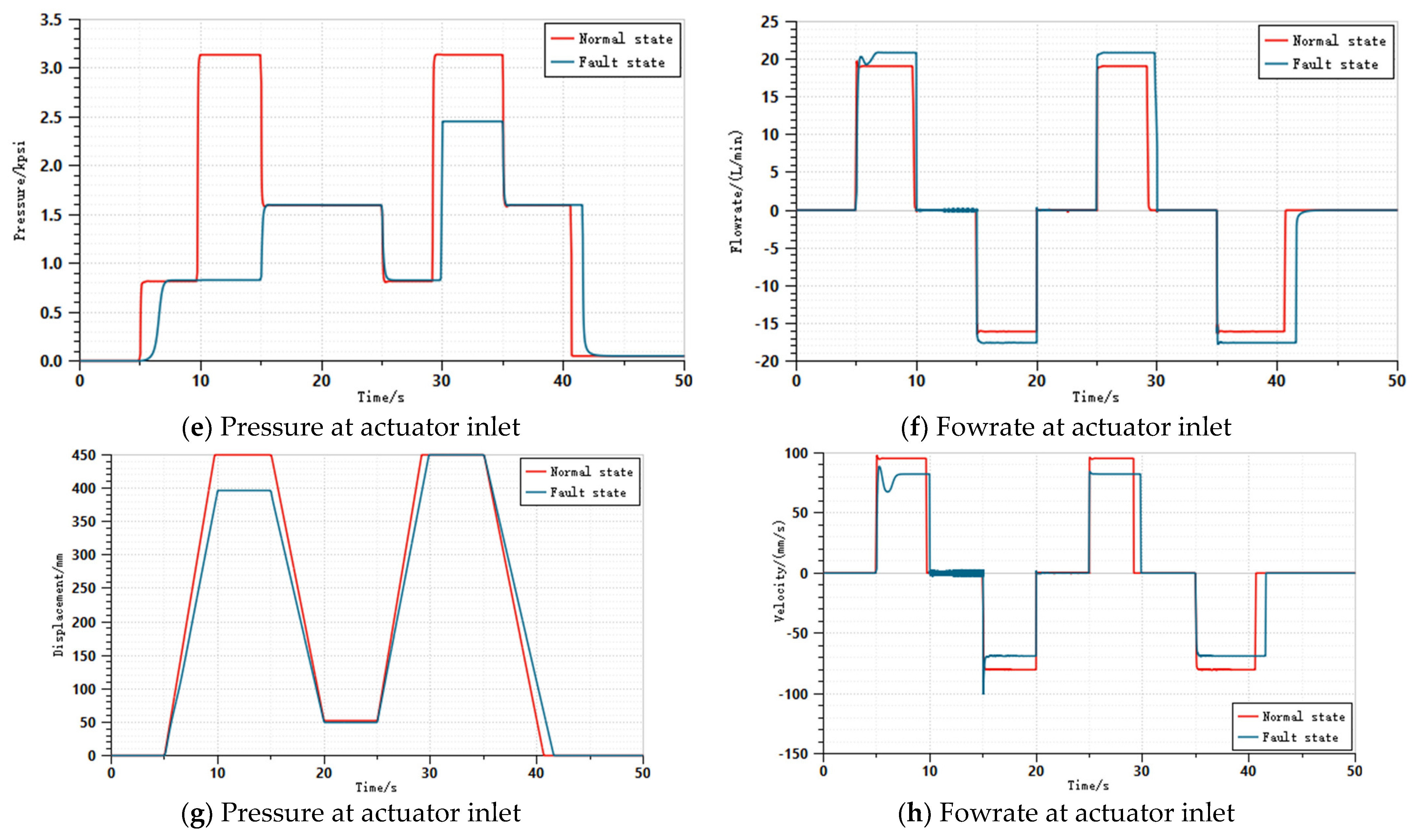
| Position | Signal | Mark | Position | Signal | Mark |
|---|---|---|---|---|---|
| Pump | Pressure | Pp | Actuator | Pressure | Pa |
| Flowrate | Qp | Flowrate | Qa | ||
| Oil filter | Pressure | Pf | Displacement | Da | |
| Flowrate | Qf | Velocity | Va |
| Parameter Name | Value |
|---|---|
| Lr | 0.001 |
| Lr decaying | lr = lr × 0.9/epoch |
| Batch size | 800 |
| Dropout rate | 0.4 |
| Training epochs | 200 |
| Activation function | ReLU |
| Optimizer | Adam |
| Class Number | States | Fault Value | Training Data | Testing Data | Sample Length | Feature |
|---|---|---|---|---|---|---|
| 0 | Normal state | - | 800 | 200 | 5000 | 40 |
| 1 | Pump leakage | 1~2 | 800 | 200 | 5000 | 40 |
| 2 | Filter blockage | 3~4 | 800 | 200 | 5000 | 40 |
| 3 | Relief valve spring failure | 2600–3300 | 800 | 200 | 5000 | 40 |
| 4 | Oil pollution | 5~15 | 800 | 200 | 5000 | 40 |
| 5 | Actuator inner leakage | 0.03~0.05 | 800 | 200 | 5000 | 40 |
| Class | Algorithm | Accuracy/% | Test Time/s | Software/Mb |
|---|---|---|---|---|
| 1 | LSTM | 97.33 | 1.68 | 5.9 |
| 2 | LSTM with observation | 97.08 | 1.77 | 7.5 |
| 3 | GRU | 98.25 | 1.61 | 3.2 |
| Class | Fault Diagnostic Model Structure | Accuracy | Test Time | Mode Size |
|---|---|---|---|---|
| 1 | GRU without EMD | 93.16% | 1.31 s | 2.6 mb |
| 2 | GRU without PCA | 96.33% | 3.99 s | 7.3 mb |
| 3 | EMD-8-GRU | 95.71% | 1.43 s | 10.3 mb |
| 4 | EMD-GRU | 98.25% | 1.61 s | 3.2 mb |
| Learning rate | 0.1 | 0.01 | 0.001 | 0.0001 | 0.00001 | 0.000001 |
| Accuracy/% | 25.5 | 60.4 | 91.2 | 98.1 | 93.2 | 79.2 |
| Training time/s | 22 | 47 | 85 | 116 | 456 | 695 |
| Batch size | 100 | 200 | 400 | 800 | 1200 | 1600 |
| Accuracy/% | 63.5 | 85.2 | 96.8 | 98.4 | 94.5 | 88.2 |
| Training time/s | 283 | 209 | 135 | 105 | 99 | 92 |
| Algorithm | Accuracy/% | ||
|---|---|---|---|
| Without Noise | SNR = 70 dB | SNR = 40 dB | |
| BP | 73.88 | 59.53 | 35.91 |
| SVM | 65.26 | 55.25 | 36.53 |
| RF | 75.52 | 66.95 | 44.77 |
| CNN | 82.98 | 79.41 | 50.66 |
| LSTM | 92.56 | 90.44 | 54.47 |
| EMD-GRU (this article) | 98.25 | 95.29 | 89.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, K.; Zhao, D. An EMD-LSTM Deep Learning Method for Aircraft Hydraulic System Fault Diagnosis under Different Environmental Noises. Aerospace 2023, 10, 55. https://doi.org/10.3390/aerospace10010055
Shen K, Zhao D. An EMD-LSTM Deep Learning Method for Aircraft Hydraulic System Fault Diagnosis under Different Environmental Noises. Aerospace. 2023; 10(1):55. https://doi.org/10.3390/aerospace10010055
Chicago/Turabian StyleShen, Kenan, and Dongbiao Zhao. 2023. "An EMD-LSTM Deep Learning Method for Aircraft Hydraulic System Fault Diagnosis under Different Environmental Noises" Aerospace 10, no. 1: 55. https://doi.org/10.3390/aerospace10010055
APA StyleShen, K., & Zhao, D. (2023). An EMD-LSTM Deep Learning Method for Aircraft Hydraulic System Fault Diagnosis under Different Environmental Noises. Aerospace, 10(1), 55. https://doi.org/10.3390/aerospace10010055






