Development of a Parametric Regional Multivariate Statistical Weather Generator for Risk Assessment Studies in Areas with Limited Data Availability
Abstract
:1. Introduction
2. Literature Review
3. Model Description
3.1. Precipitation States
3.2. Precipitation Amount
3.3. Maximum and Minimum Air Temperature
3.4. Wind Speed Magnitude
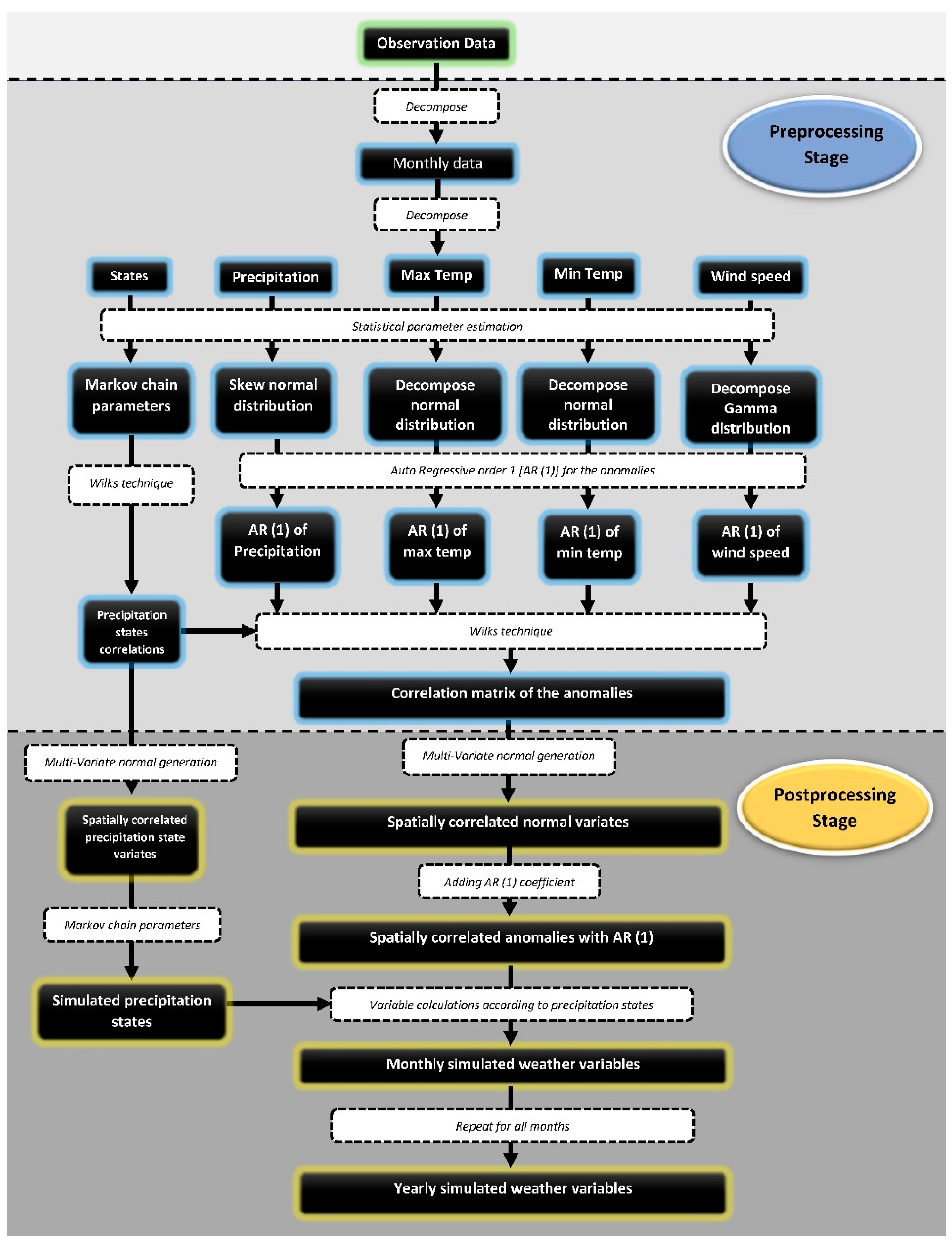
4. Model Implementation
4.1. Preprocessing: Parameter Estimation and Matrix Preparation
- 1)
- Assume , , and , in which ω is a non-positive-definite correlation matrix.
- 2)
- Let .
- 3)
- Find , and , such that .
- 4)
- Replace the negative eigenvalues of by a small positive value to construct .
- 5)
- Set and . Then, replace all diagonal elements with 1.
- 6)
- Test whether is a positive-defined matrix or not. If not, repeat the steps from two to six by making and .
- 1)
- Generate the standard normal random deviate set y; y ~ N (0,1).
- 2)
- Use y with Equations (1) and (2) to identify the dry and wet days.
- 3)
- Generate a standard normal random deviate set x; x ~ N (0,1).
- 4)
- Apply the AR(1) of arbitrary values between –1 and 1 (e.g., φ’z).
- 5)
- Obtain the anomalies z by standardizing x of Step 4.
- 6)
- Apply Equations (6) and (7) to obtain T’X.
- 7)
- Calculate the AR (1) of TX (e.g., φ’v) and plot versus the φ’z, then regress them.
- 8)
- Use the regression equation obtained in Step 7 with the observed value φv (e.g., 0.82) to determine φz. In this case, 0.88 (as shown in Figure 2b).
4.2. Postprocessing Stage: Variable Generation
- 1)
- Use Equation (13) with ωs to generate Y anomalies that denote S. The length of Y denotes the day number of the generated time series. In this case, the user can generate any length (independently of the historic observation length).
- 2)
- Use Equations (1) and (2) with the estimated FTMC parameters ( and ) to identify the dry and wet day occurrences.
- 3)
- Apply Equation (13) with ωv to generate Z anomalies that denote the variable values. Of course, the length of Z must be the same of Y.
- 4)
- Obtain P for the wet days using Equations (3) and (4) with the estimated parameters µp, σp, and ιp. This will make sure the generated P have similar observed statistics.
- 5)
- Apply the AR (1) with coefficients Фz for Tx, TN and the WS anomalies to consider the auto-correlation magnitude for the variables.
- 6)
- Re-standardize the anomalies for TX and TN, as follows:where Zstd represents the standardized anomalies Z of Step 5, and µ(Z) and σ(Z) are the mean and standard deviation of Z, respectively.
- 7)
- Apply Zstd in Equations (6)–(9) with the estimated parameters µX0, µX1, µN0, µN1, σX0, σX1, σN0, and σN1 to calculate Tx and TN.
- 8)
- Convert the anomalies Z of the WS to be uniformly distributed between 0 and 1 ZU, as follows:
- 9)
- Apply ZU in Equations (11) and (12) with the estimated parameters α0, α1, β0, and β1 to calculate the WS. Steps 3 to 9 enable us to preserve the observation statistics of Tx, TN and the WS and the spatial, temporal, and cross correlations with consideration of the precipitation states effects through decomposing their distribution functions.
- 10)
- Repeat Steps 1 to 9 for all months m.
5. Case Study and Data
6. Results and Discussion
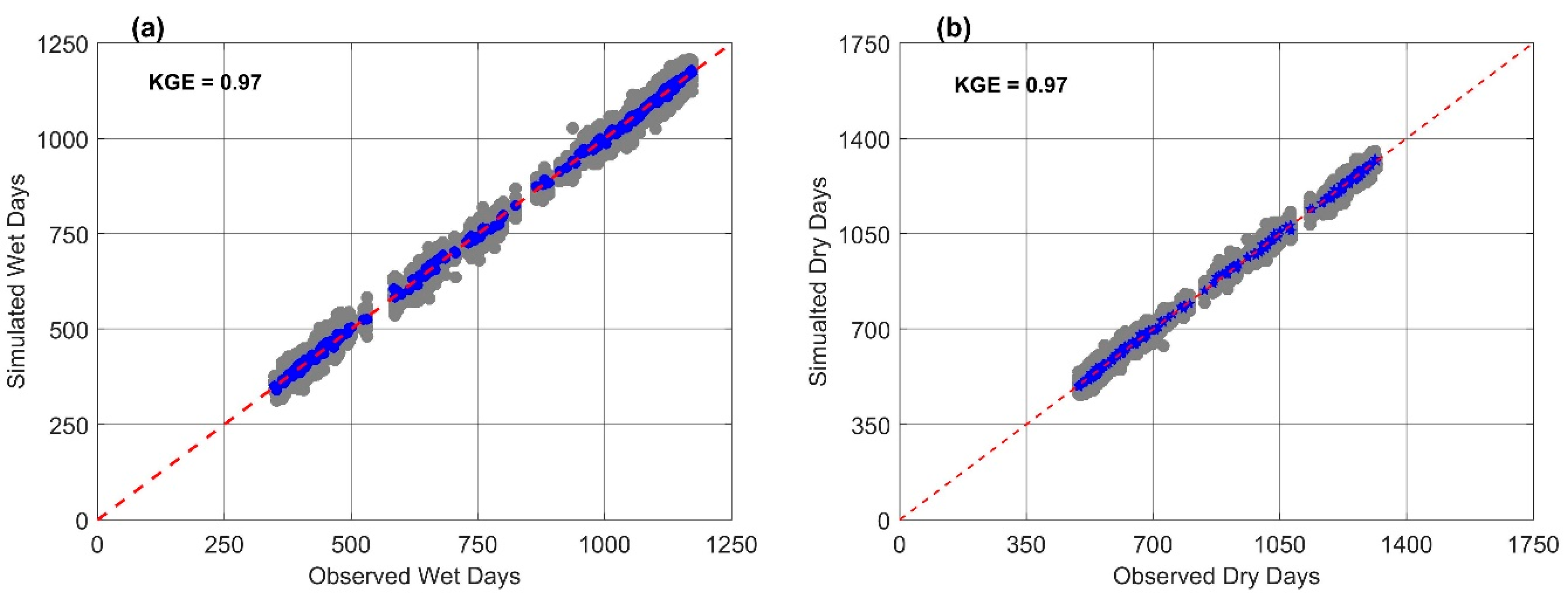
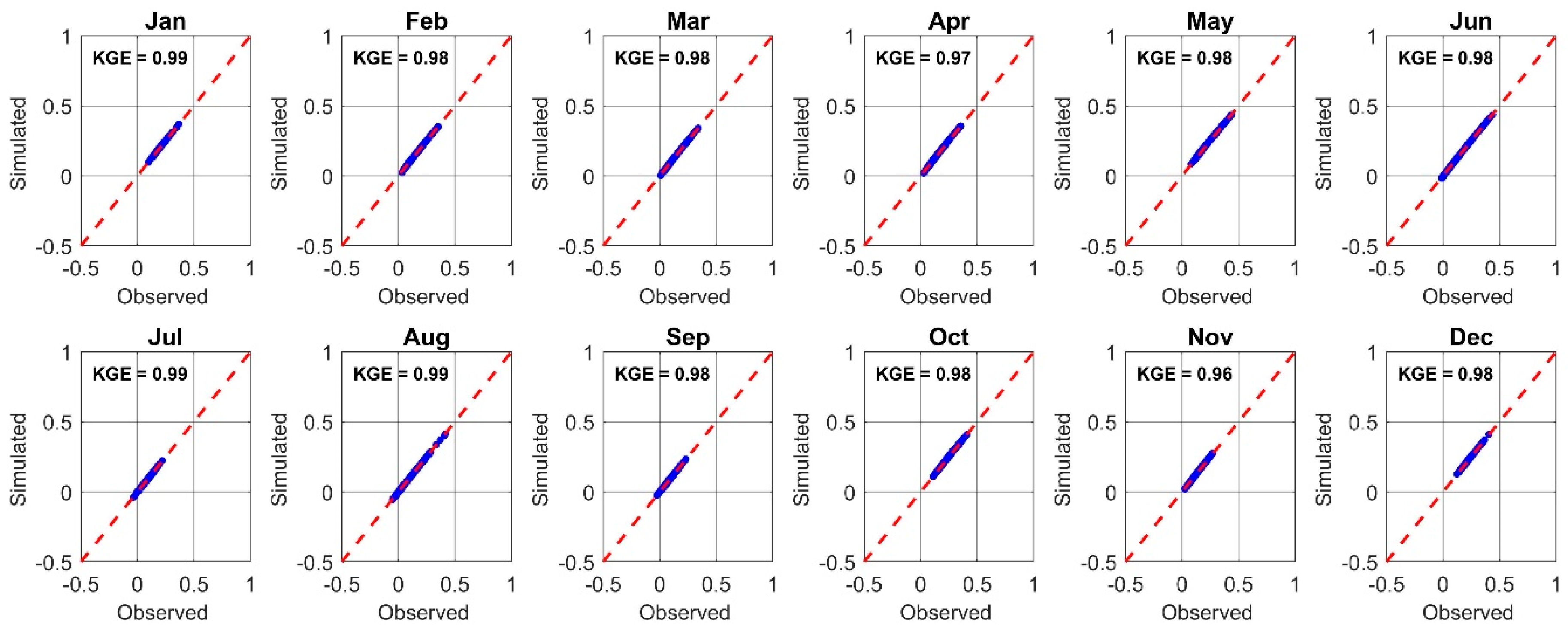
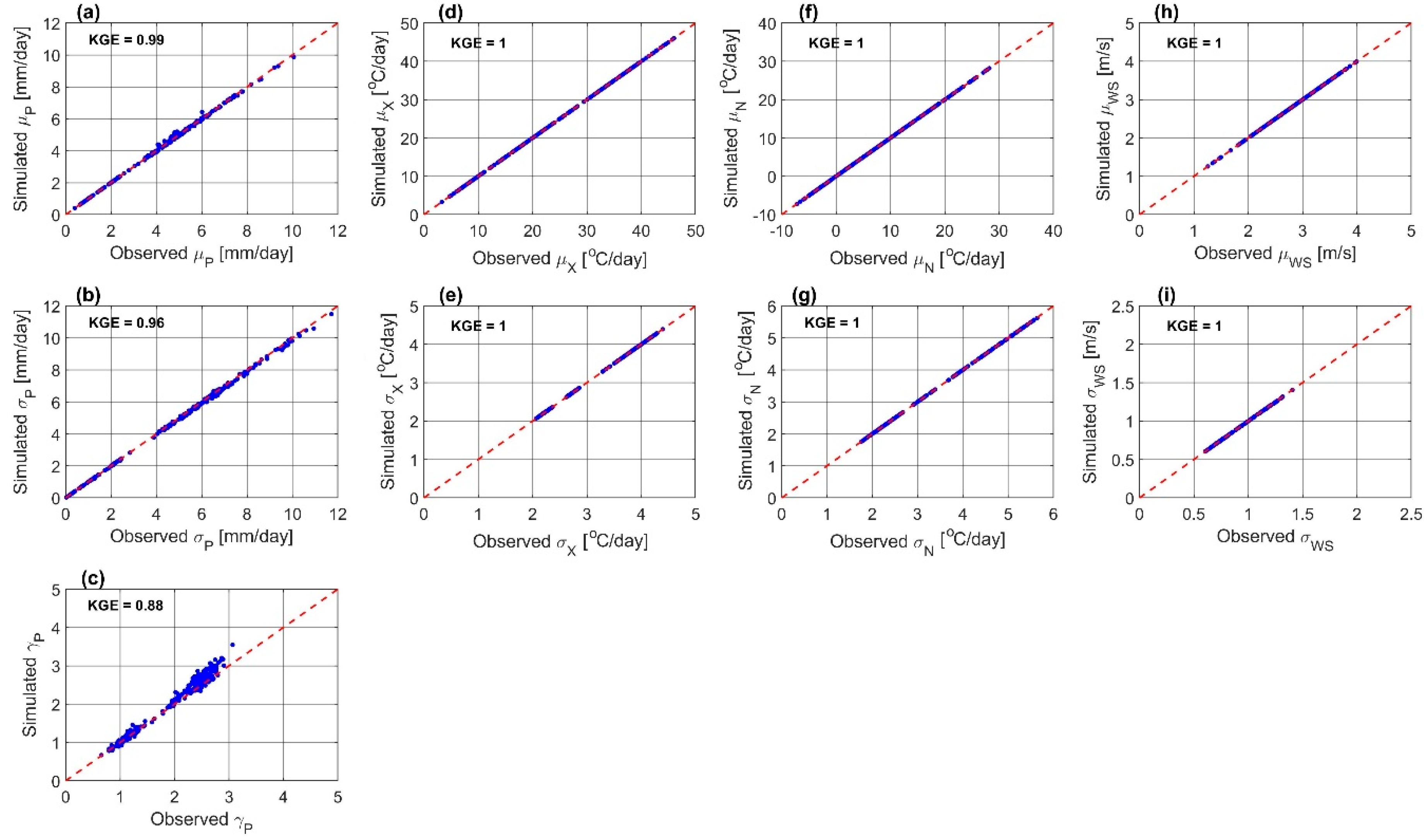
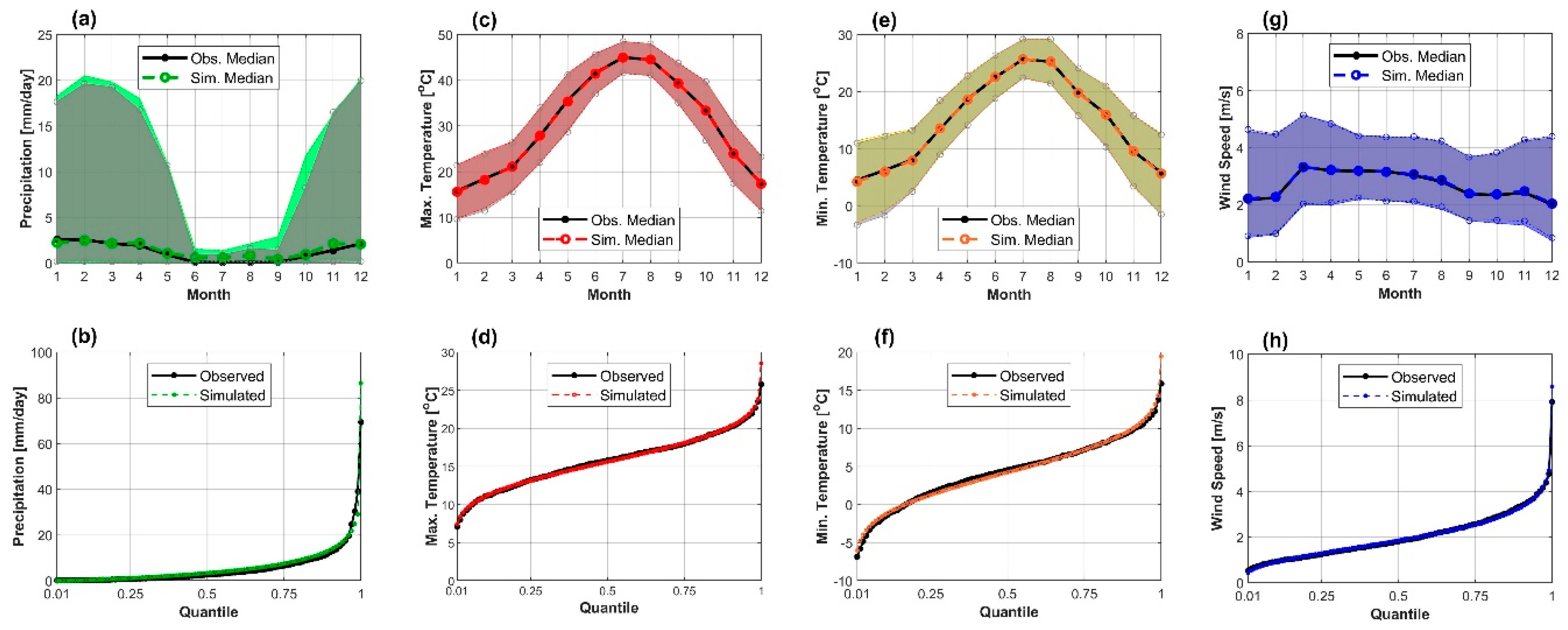
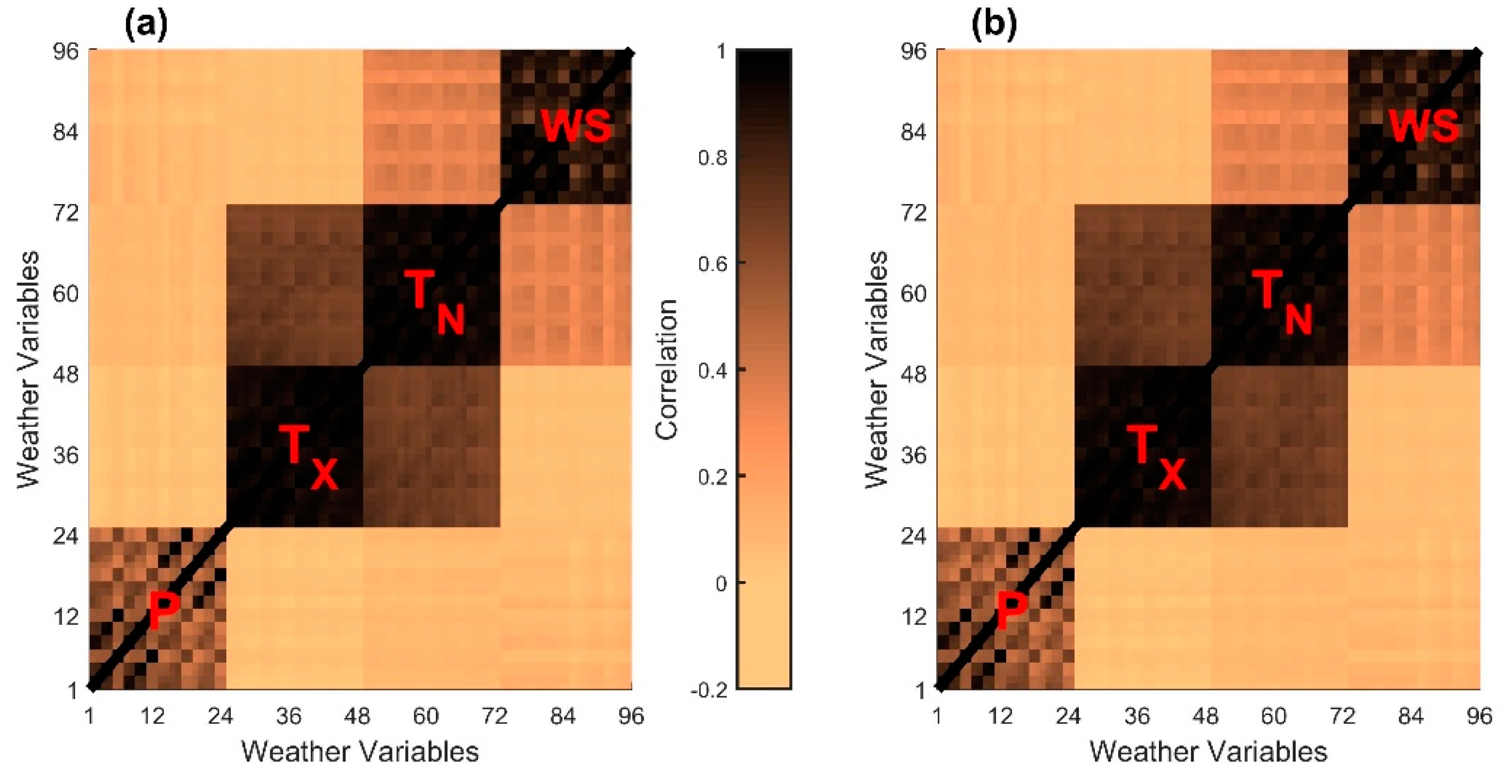
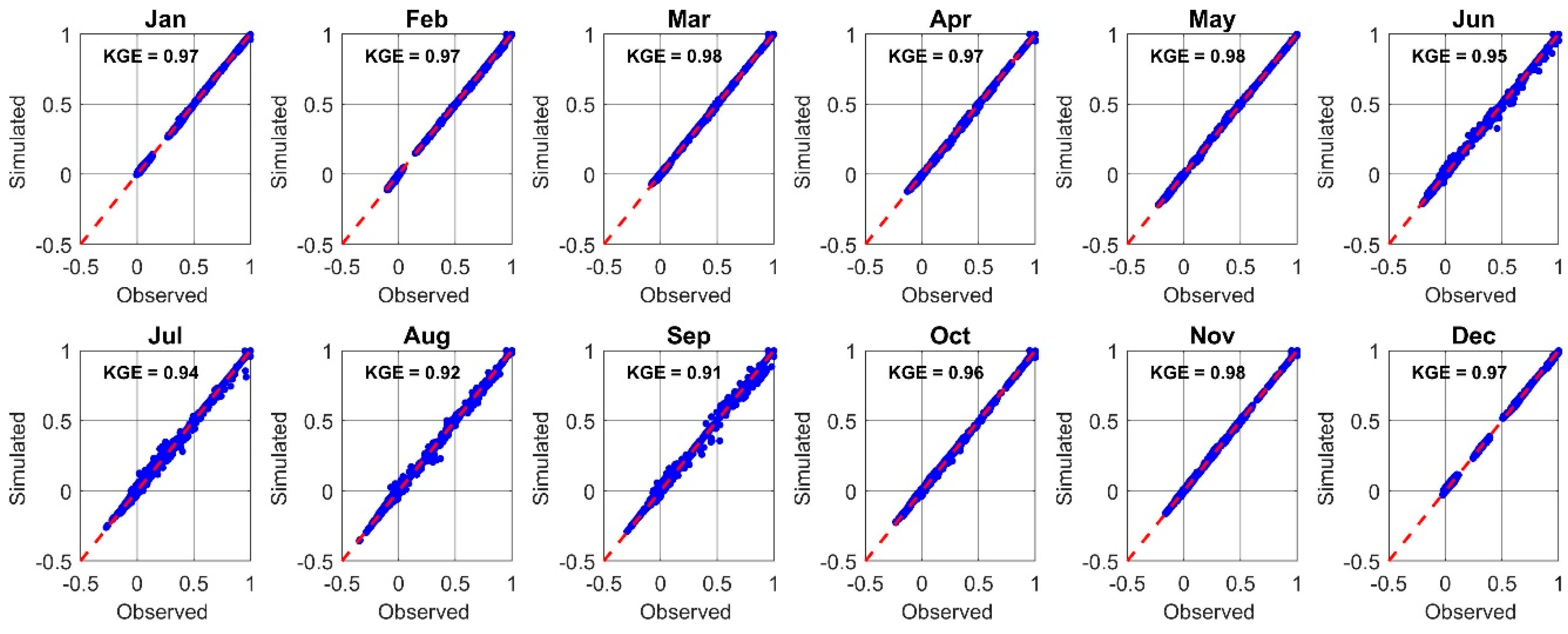
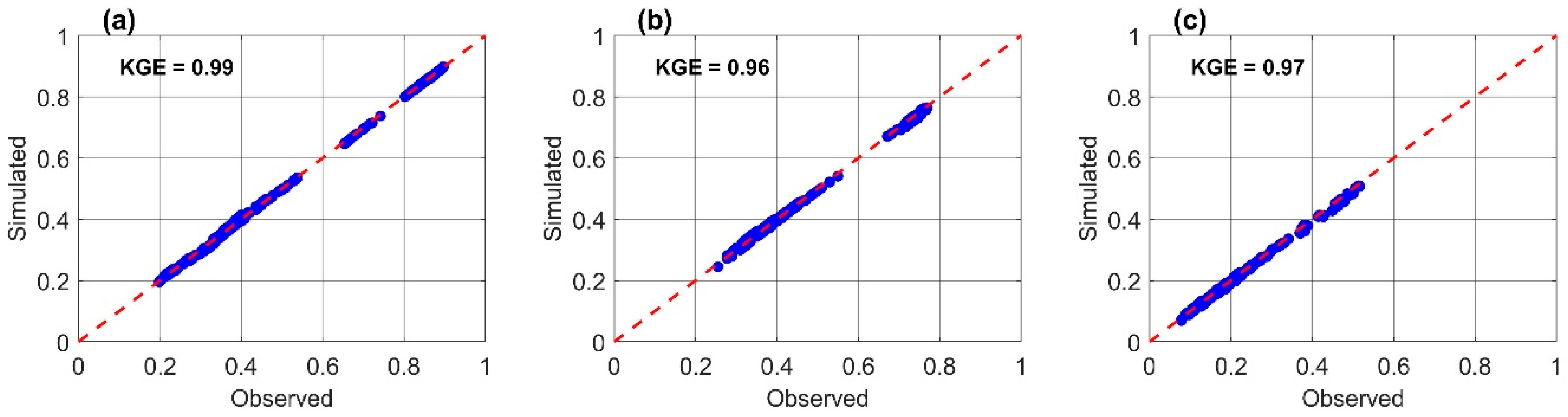
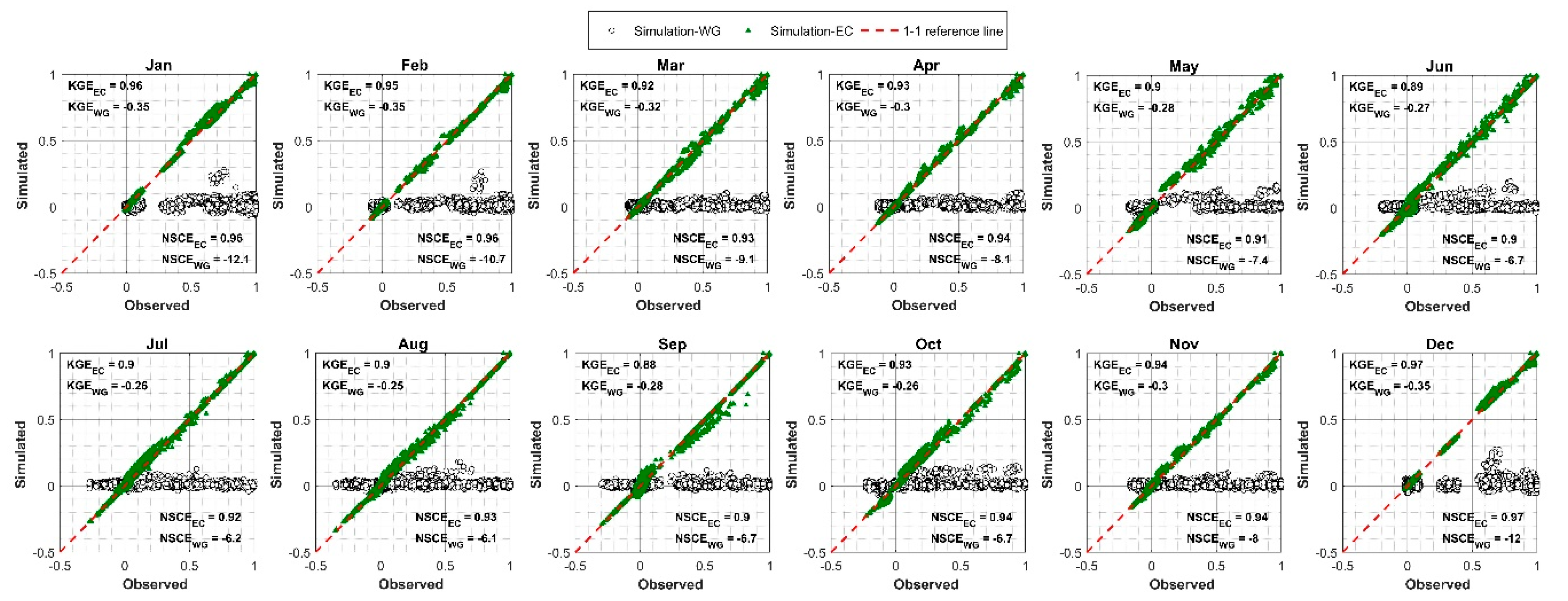
6.1. Model Performance Evaluation
6.2. Model Validation
6.3. Model Comparison
6.4. Simulation of the Future Forecasting Scenarios
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hallegatte, S.; Shah, A.; Lempert, R.; Brown, C.; Gill, S. Investment Decision Making under Deep Uncertainty-Application to Climate Change; The World Bank: Washington, DC, USA, 2012. [Google Scholar]
- Brown, C.; Wilby, R.L. An alternate approach to assessing climate risks. Eos, Trans. Am. Geophys. Union 2012, 93, 401–402. [Google Scholar] [CrossRef]
- Stephenson, D.; Collins, M.; Rougier, J.C.; Chandler, R.E. Statistical problems in the probabilistic prediction of climate change. Environmetrics 2012, 23, 364–372. [Google Scholar] [CrossRef]
- Steinschneider, S.; Brown, C. A semiparametric multivariate, multisite weather generator with low-frequency variability for use in climate risk assessments. Water Resour. Res. 2013, 49, 7205–7220. [Google Scholar] [CrossRef]
- Waheed, S.Q.; Grigg, N.S.; Ramirez, J.A. Variable Infiltration-Capacity Model Sensitivity, Parameter Uncertainty, and Data Augmentation for the Diyala River Basin in Iraq. J. Hydrol. Eng. 2020, 25, 04020040. [Google Scholar] [CrossRef]
- Culley, S.; Noble, S.; Yates, A.; Timbs, M.; Westra, S.; Maier, H.R.; Giuliani, M.; Castelletti, A. A bottom-up approach to identifying the maximum operational adaptive capacity of water resource systems to a changing climate. Water Resour. Res. 2016, 52, 6751–6768. [Google Scholar] [CrossRef] [Green Version]
- Weaver, C.P.; Lempert, R.J.; Brown, C.; Hall, J.A.; Revell, D.; Sarewitz, D. Improving the contribution of climate model information to decision making: The value and demands of robust decision frameworks. Wiley Interdiscip. Rev. Clim. Chang. 2012, 4, 39–60. [Google Scholar] [CrossRef]
- Turner, S.W.; Marlow, D.; Ekström, M.; Rhodes, B.G.; Kularathna, U.; Jeffrey, P. Linking climate projections to performance: A yield-based decision scaling assessment of a large urban water resources system. Water Resour. Res. 2014, 50, 3553–3567. [Google Scholar] [CrossRef]
- Steinschneider, S.; Wi, S.; Brown, C. The integrated effects of climate and hydrologic uncertainty on future flood risk assessments. Hydrol. Process. 2014, 29, 2823–2839. [Google Scholar] [CrossRef]
- Zhang, E.; Yin, X.; Xu, Z.; Yang, Z. Bottom-up quantification of inter-basin water transfer vulnerability to climate change. Ecol. Indic. 2018, 92, 195–206. [Google Scholar] [CrossRef]
- Whateley, S.; Steinschneider, S.; Brown, C. A climate change range-based method for estimating robustness for water resources supply. Water Resour. Res. 2014, 50, 8944–8961. [Google Scholar] [CrossRef]
- Moody, P.; Brown, C. Robustness indicators for evaluation under climate change: Application to the upper Great Lakes. Water Resour. Res. 2013, 49, 3576–3588. [Google Scholar] [CrossRef]
- Steinschneider, S.; McCrary, R.; Wi, S.; Mulligan, K.B.; Mearns, L.O.; Brown, C. Expanded Decision-Scaling Framework to Select Robust Long-Term Water-System Plans under Hydroclimatic Uncertainties. J. Water Resour. Plan. Manag. 2015, 141, 04015023. [Google Scholar] [CrossRef]
- Wilks, D. Multisite generalization of a daily stochastic precipitation generation model. J. Hydrol. 1998, 210, 178–191. [Google Scholar] [CrossRef]
- Verdin, A.P.; Rajagopalan, B.; Kleiber, W.; Podestá, G.; Bert, F. BayGEN: A Bayesian Space-Time Stochastic Weather Generator. Water Resour. Res. 2019, 55, 2900–2915. [Google Scholar] [CrossRef]
- Wilks, D.S. A gridded multisite weather generator and synchronization to observed weather data. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef] [Green Version]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Furrer, E.; Katz, R.W. Improving the simulation of extreme precipitation events by stochastic weather generators. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Jie, C.; Brissette, F.P.; Zhang, X.J. A multi-site stochastic weather generator for daily precipitation and temperature. Trans. ASABE 2014, 57, 1375–1391. [Google Scholar]
- Chen, J.; Brissette, F.P. Stochastic generation of daily precipitation amounts: Review and evaluation of different models. Clim. Res. 2014, 59, 189–206. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Brissette, F.P. Comparison of five stochastic weather generators in simulating daily precipitation and temperature for the Loess Plateau of China. Int. J. Climatol. 2014, 34, 3089–3105. [Google Scholar] [CrossRef]
- Acharya, N.; Frei, A.; Chen, J.; DeCristofaro, L.; Owens, E.M. Evaluating Stochastic Precipitation Generators for Climate Change Impact Studies of New York City’s Primary Water Supply. J. Hydrometeorol. 2017, 18, 879–896. [Google Scholar] [CrossRef]
- Mukundan, R.; Acharya, N.; Gelda, R.K.; Frei, A.; Owens, E.M. Modeling streamflow sensitivity to climate change in New York City water supply streams using a stochastic weather generator. J. Hydrol. Reg. Stud. 2019, 21, 147–158. [Google Scholar] [CrossRef]
- Mehrotra, R.; Westra, S.; Sharma, A.; Srikanthan, R. Continuous rainfall simulation: 2. A regionalized daily rainfall generation approach. Water Resour. Res. 2012, 48, 48. [Google Scholar] [CrossRef] [Green Version]
- Richardson, C.W. Stochastic simulation of daily precipitation, temperature, and solar radiation. Water Resour. Res. 1981, 17, 182–190. [Google Scholar] [CrossRef]
- Qian, B.; Xu, H. Multisite stochastic weather models for impact studies. Int. J. Clim. 2002, 22, 1377–1397. [Google Scholar] [CrossRef]
- Brissette, F.; Khalili, M.; Leconte, R. Efficient stochastic generation of multi-site synthetic precipitation data. J. Hydrol. 2007, 345, 121–133. [Google Scholar] [CrossRef]
- Srikanthan, R.; Pegram, G. A nested multisite daily rainfall stochastic generation model. J. Hydrol. 2009, 371, 142–153. [Google Scholar] [CrossRef]
- Baigorria, G.A.; Jones, J.W. GiST: A Stochastic Model for Generating Spatially and Temporally Correlated Daily Rainfall Data. J. Clim. 2010, 23, 5990–6008. [Google Scholar] [CrossRef]
- Leander, R.; Buishand, T.A. A daily weather generator based on a two-stage resampling algorithm. J. Hydrol. 2009, 374, 185–195. [Google Scholar] [CrossRef]
- King, L.M.; McLeod, A.I.; Simonovic, S.P. Improved Weather Generator Algorithm for Multisite Simulation of Precipitation and Temperature. JAWRA J. Am. Water Resour. Assoc. 2015, 51, 1305–1320. [Google Scholar] [CrossRef] [Green Version]
- Srivastav, R.K.; Simonovic, S.P. Multi-site, multivariate weather generator using maximum entropy bootstrap. Clim. Dyn. 2014, 44, 3431–3448. [Google Scholar] [CrossRef]
- Khalili, M.; Brissette, F.; Leconte, R. Effectiveness of Multi-Site Weather Generator for Hydrological Modeling1. JAWRA J. Am. Water Resour. Assoc. 2011, 47, 303–314. [Google Scholar] [CrossRef]
- Murray, V.; Ebi, K.L. IPCC Special Report on Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation (SREX). J. Epidemiol. Community Heal. 2012, 66, 759–760. [Google Scholar] [CrossRef] [PubMed]
- Mehrotra, R.; Li, J.; Westra, S.; Sharma, A. A programming tool to generate multi-site daily rainfall using a two-stage semi parametric model. Environ. Model. Softw. 2015, 63, 230–239. [Google Scholar] [CrossRef]
- Wang, W.; Flanagan, D.C.; Yin, S.; Yu, B. Assessment of CLIGEN precipitation and storm pattern generation in China. Catena 2018, 169, 96–106. [Google Scholar] [CrossRef]
- John, S.; Pailleux, J.; Thielen, J.; Arritt, R.; Hamill, T.; Luo, L.; Martin, E.; McCollor, D.; Pappenberger, F. Summary of recommendations of the first workshop on Postprocessing and Downscaling Atmospheric Forecasts for Hydrologic Applications held at Météo-France, Toulouse, France, 15–18 June 2009. Atmos. Sci. Lett. 2010, 11, 59–63. [Google Scholar]
- Li, Z. A new framework for multi-site weather generator: A two-stage model combining a parametric method with a distribution-free shuffle procedure. Clim. Dyn. 2013, 43, 657–669. [Google Scholar] [CrossRef]
- Li, C.; Sinha, E.; Horton, D.E.; Diffenbaugh, N.S.; Michalak, A.M. Joint bias correction of temperature and precipitation in climate model simulations. J. Geophys. Res. Atmos. 2014, 119, 13–153. [Google Scholar] [CrossRef]
- Chen, J.; Li, C.; Brissette, F.P.; Chen, H.; Wang, M.; Essou, G.R. Impacts of correcting the inter-variable correlation of climate model outputs on hydrological modeling. J. Hydrol. 2018, 560, 326–341. [Google Scholar] [CrossRef]
- Li, X.; Babovic, V. A new scheme for multivariate, multisite weather generator with inter-variable, inter-site dependence and inter-annual variability based on empirical copula approach. Clim. Dyn. 2018, 52, 2247–2267. [Google Scholar] [CrossRef]
- Guillermo, A.B.; Jones, J.W. GiST: A stochastic model for generating spatially and temporally correlated daily Investment Decision Making under Deep Uncertainty—Application to Climate Change rainfall data. What kind of data is needed to identify climate impacts? How can data be managed and organized through data catalogues? J. Clim. 2010, 23, 5990–6008. [Google Scholar]
- Haugen, A.; Bertolin, C.; Leijonhufvud, G.; Olstad, T.; Broström, T. A Methodology for Long-Term Monitoring of Climate Change Impacts on Historic Buildings. Geosciences 2018, 8, 370. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Brissette, F.; Chen, J. Assessing the applicability of six precipitation probability distribution models on the Loess Plateau of China. Int. J. Clim. 2013, 34, 462–471. [Google Scholar] [CrossRef]
- Mehan, S.; Guo, T.; Gitau, M.W.; Flanagan, D.C. Comparative Study of Different Stochastic Weather Generators for Long-Term Climate Data Simulation. Climate 2017, 5, 26. [Google Scholar] [CrossRef]
- Nicks, A.D.; Gander, G.A. CLIGEN: A Weather Generator for Climate Inputs to Water Resource and Other Models. In Proceedings of the Fifth International Conference on Computers in Agriculture, Orlando, FL, USA, 6–9 February 1994; Available online: https://www.worldcat.org/title/cligen-a-weather-generator-for-climate-inputs-to-water-resource-and-other-models/oclc/693437629 (accessed on 7 August 2020).
- Harmel, R.D.; Richardson, C.W.; Hanson, C.L.; Johnson, G.L. Evaluating the Adequacy of Simulating Maximum and Minimum Daily Air Temperature with the Normal Distribution. J. Appl. Meteorol. 2002, 41, 744–753. [Google Scholar] [CrossRef]
- Harmel, R.D.; Richardson, C.W.; Hanson, C.L.; Johnson, G.L. Simulating maximum and minimum daily temperature with the normal distribution. In Proceedings of the 2001 ASAE Annual Meeting. American Society of Agricultural and Biological Engineers, Sacramento, CA, USA, 29 July–1 August 2001. [Google Scholar]
- Pobočíková, I.; Sedliačková, Z.; Michalková, M. Application of Four Probability Distributions for Wind Speed Modeling. Procedia Eng. 2017, 192, 713–718. [Google Scholar] [CrossRef]
- Back, L.E.; Bretherton, C.S. The Relationship between Wind Speed and Precipitation in the Pacific ITCZ. J. Clim. 2005, 18, 4317–4328. [Google Scholar] [CrossRef]
- Saralees, N. A review of results on sums of random variables. Acta Appl. Math. 2008, 103, 131–140. [Google Scholar]
- Mehrotra, R.; Srikanthan, R.; Sharma, A. A comparison of three stochastic multi-site precipitation occurrence generators. J. Hydrol. 2006, 331, 280–292. [Google Scholar] [CrossRef]
- Khalili, M.; Leconte, R.; Brissette, F. Stochastic Multisite Generation of Daily Precipitation Data Using Spatial Autocorrelation. J. Hydrometeorol. 2007, 8, 396–412. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Zhang, X. Hydrological Modeling Using a Multisite Stochastic Weather Generator. J. Hydrol. Eng. 2016, 21, 04015060. [Google Scholar] [CrossRef]
- Maree, S.C. Correcting Non Positive Definite Correlation Matrices. Bachelor’s Thesis, Department of Applied Mathematics, Delft University of Technology, Delft, Australia, 2012. [Google Scholar]
- Eamonn, N.J.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar]
- Chen, J.; Brissette, F.P.; Leconte, R.; Caron, A. A Versatile Weather Generator for Daily Precipitation and Temperature. Trans. ASABE 2012, 55, 895–906. [Google Scholar] [CrossRef]
- Meyer, C. General Description of the CLIGEN Model and Its History; USDA-ARS National Soil Erosion Laboratory: West Lafayette, IN, USA, 2011. [Google Scholar]
- Rolda´n, J.; Woolhiser, D.A.; Roldán, J. Stochastic daily precipitation models: 1. A comparison of occurrence processes. Water Resour. Res. 1982, 18, 1451–1459. [Google Scholar] [CrossRef]
- Wilks, D.S. Simultaneous stochastic simulation of daily precipitation, temperature and solar radiation at multiple sites in complex terrain. Agric. For. Meteorol. 1999, 96, 85–101. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.; Leconte, R. A daily stochastic weather generator for preserving low-frequency of climate variability. J. Hydrol. 2010, 388, 480–490. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waheed, S.Q.; Grigg, N.S.; Ramirez, J.A. Development of a Parametric Regional Multivariate Statistical Weather Generator for Risk Assessment Studies in Areas with Limited Data Availability. Climate 2020, 8, 93. https://doi.org/10.3390/cli8080093
Waheed SQ, Grigg NS, Ramirez JA. Development of a Parametric Regional Multivariate Statistical Weather Generator for Risk Assessment Studies in Areas with Limited Data Availability. Climate. 2020; 8(8):93. https://doi.org/10.3390/cli8080093
Chicago/Turabian StyleWaheed, Saddam Q., Neil S. Grigg, and Jorge A. Ramirez. 2020. "Development of a Parametric Regional Multivariate Statistical Weather Generator for Risk Assessment Studies in Areas with Limited Data Availability" Climate 8, no. 8: 93. https://doi.org/10.3390/cli8080093
APA StyleWaheed, S. Q., Grigg, N. S., & Ramirez, J. A. (2020). Development of a Parametric Regional Multivariate Statistical Weather Generator for Risk Assessment Studies in Areas with Limited Data Availability. Climate, 8(8), 93. https://doi.org/10.3390/cli8080093





