Global-Scale Synchronization in the Meteorological Data: A Vectorial Analysis That Includes Higher-Order Differences
Abstract
1. Introduction
2. Methodology
2.1. Modified Vectorial Analysis
2.2. Statistical Analysis
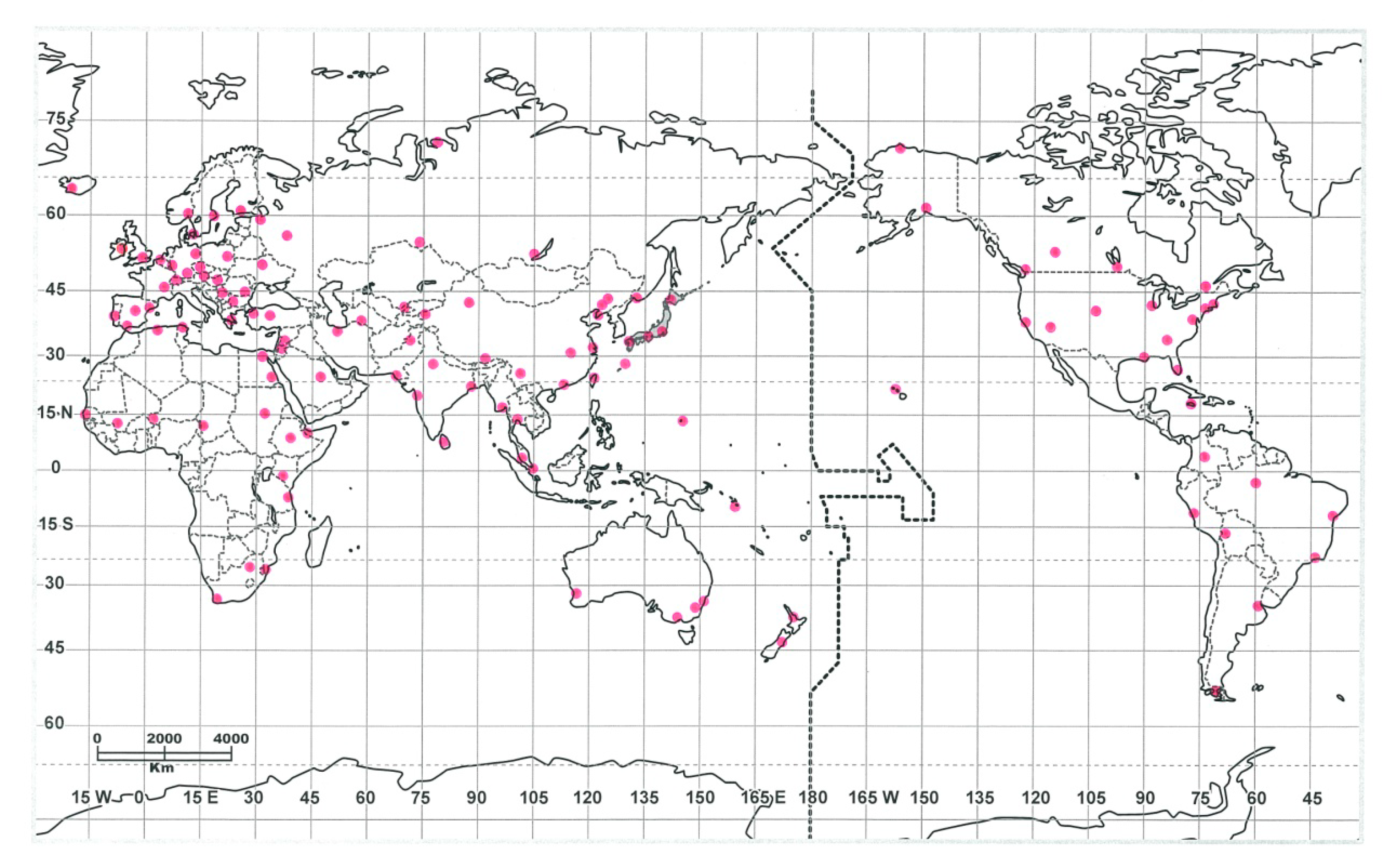
3. Data
4. Results
4.1. Global Analysis
- (1)
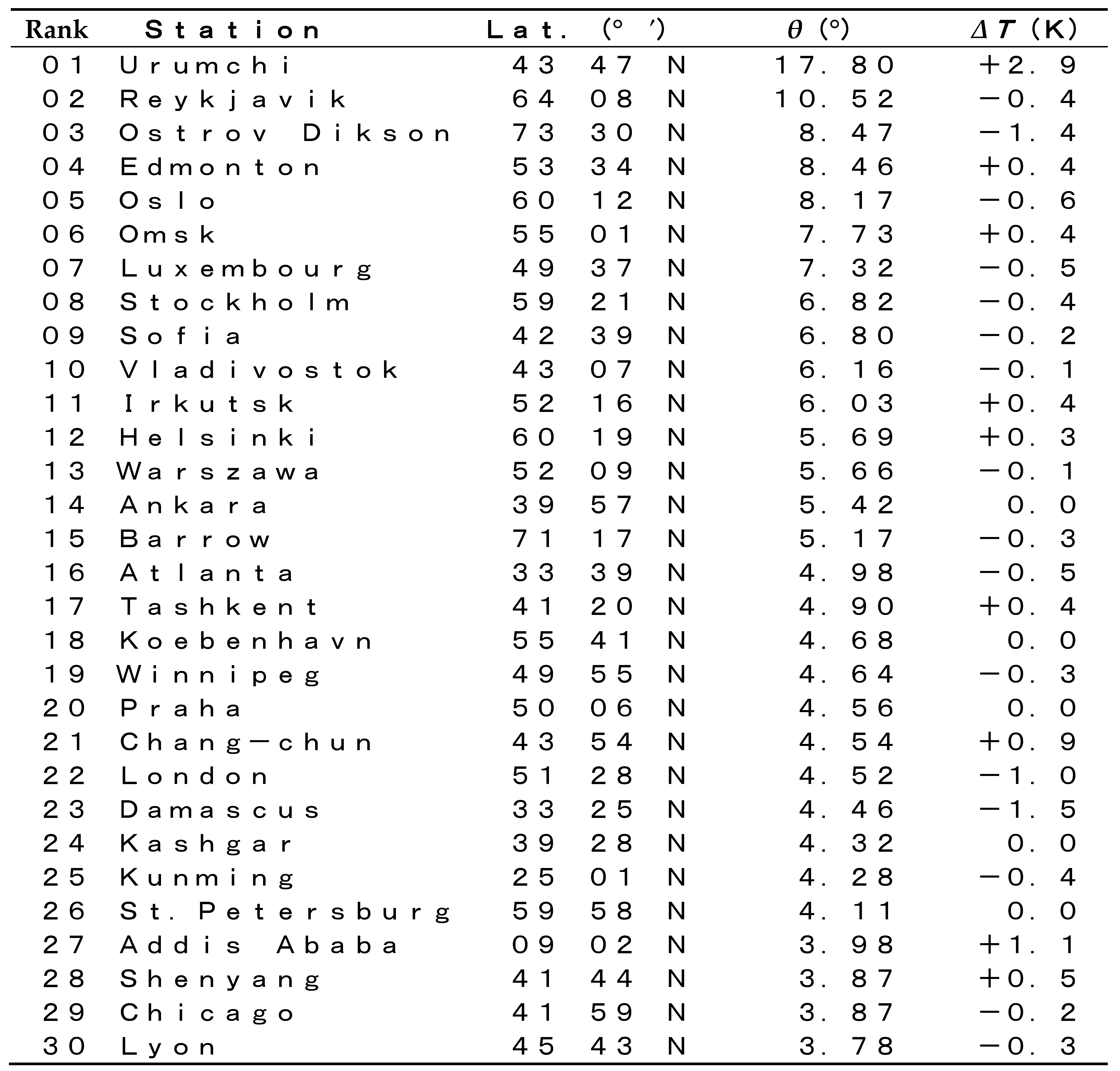
- In Figure 2a, which plots the rotation between Period I (1931–1960) and Period II (1951–1980), the best fit has been found to be exponential with r = 0.738 and d = 1.788 > dU = 1.55 (n = 97). (cf. for the linear regression of Equation (8), r = 0.589 with d = 1.815.) It is evident from Table 1 that the top-thirty ranking is occupied by the stations with relatively high latitudes. Exceptions are #16: Atlanta (33°39′ N; h = 312 m), #23: Damascus (33°25′ N; 608 m), #25: Kunming (25°01′ N; 1892 m), and #27: Addis Ababa (09°02′ N; 2354 m).
- (2)
- In Figure 2b, which plots the rotation between Period II (1951–1980) and Period III (1981–2010), the best regression has again been exponential with r = 0.843 but, in contrast to Figure 2a, d = 1.089 < dL = 1.51 (n = 97), indicating that the hypothesis H made in the Durbin-Watson testing (Section 2.2) cannot be rejected. A generalization of Equation (9) as lnθ= a + bχc has given the best fit (r, d) = (0.844, 1.159) for c = 0.9, preserving a slightly stretched exponentiality. (cf. for the linear regression, r = 0.801 with d = 1.265 < dL. A generalization of Equation (8) as θ= a + bχc has given the best fit (r, d) = (0.819, 1.406) for c = 1.7, exhibiting a power-law growth, though the magnitude of d remains smaller than dL.) The stations that have raised ranking substantially (bold-faced in Table 2) are #38→#2: Anchorage (61°09′ N), #26→#6: St. Petersburg (59°58′ N), #34→#8: Moskva (55°50′ N), #88→#17: Muenchen (48°21′ N), #65→#20: Vancouver (49°11′ N), #80→#21: Denver (39°46′ N), and #63→#30: Bucuresti (44°30′ N), most of which are sited on the relatively high latitude, implying the enhanced snow/ice-albedo feedback due to the global warming. Autocorrelation between the rotation for the latter (Period II–III) and that for the former (Period I–II) has been found to be r = 0.764 and d = 1.710 > dU = 1.55 (n = 97) with the best logarithmic fit.
- (3)
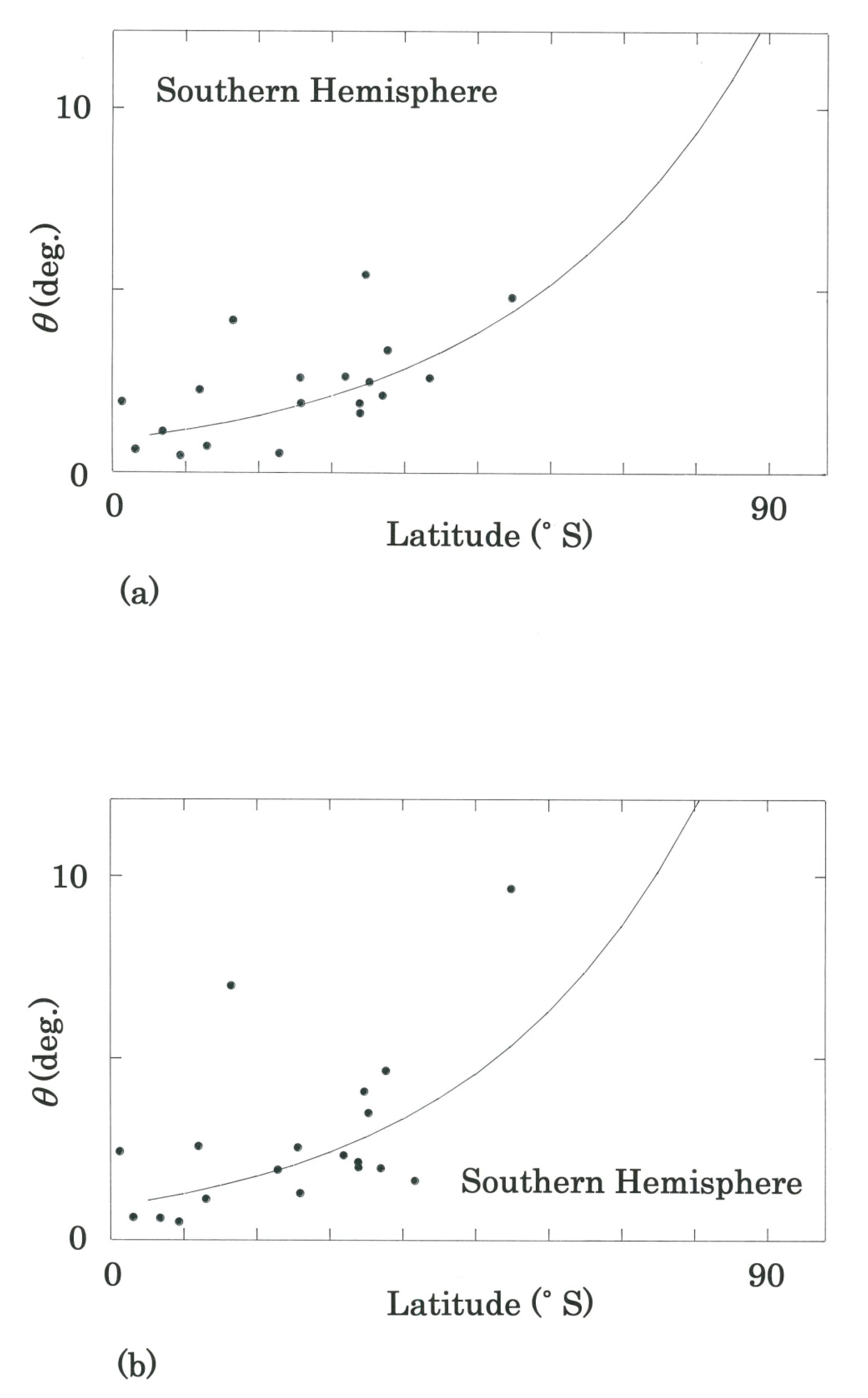
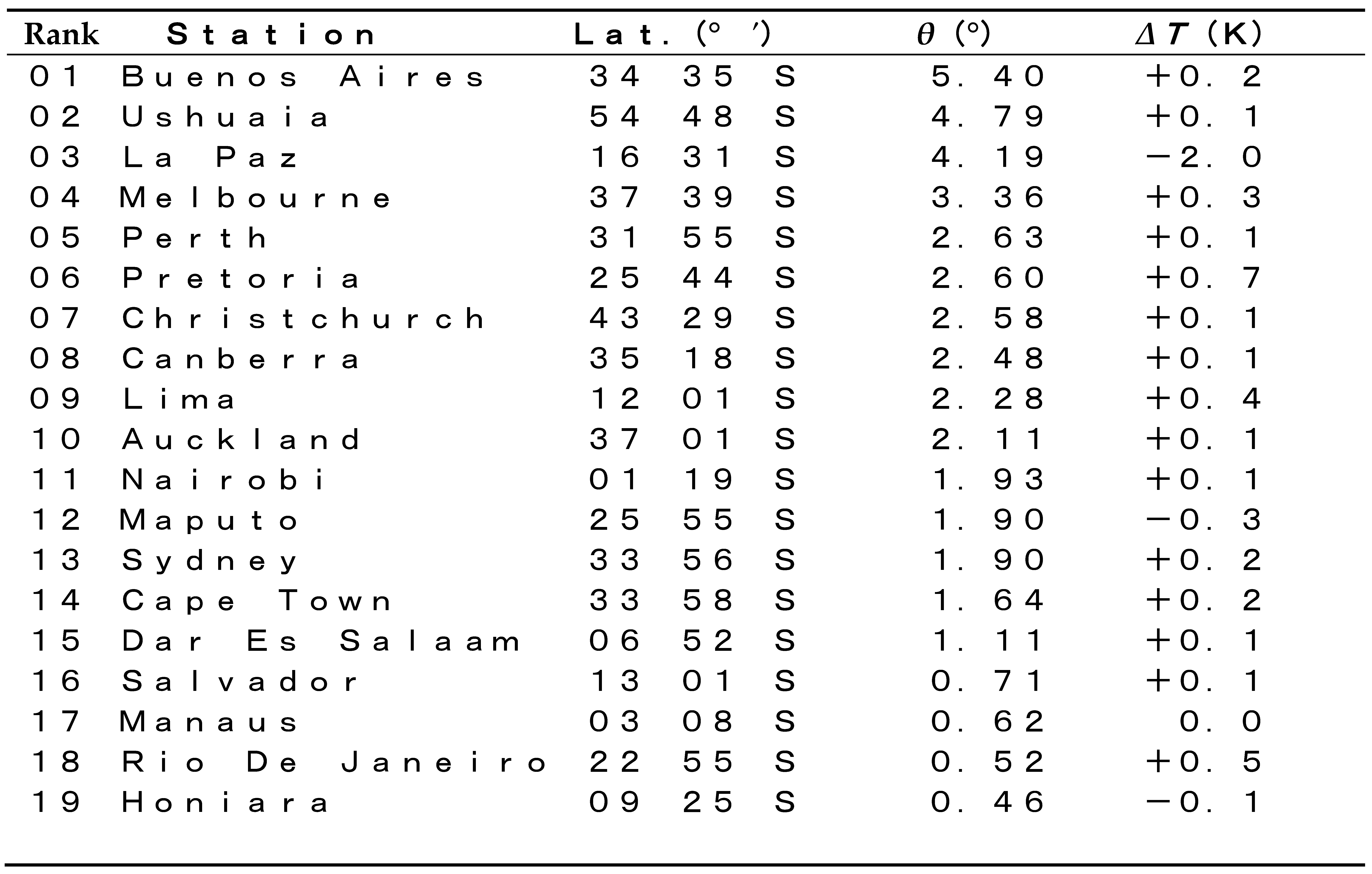
- From the results plotted on Figure 3 and from those listed in Table 3 and Table 4, it is found that although the effect due to the warming is not as strong as in the northern counterpart the conclusion for the Northern Hemisphere is also applicable to the Southern Hemisphere. Autocorrelation between the rotation for the latter (Period II–III) and that for the former (Period I–II) has been found to be r = 0.843 and d = 1.806 > dU = 1.13 (n = 19), but with the best exponential fit, showing contrast to the best logarithmic fit seen for the northern counterpart.
- (4)
- In contrast to the temperature, for the World precipitation, independently of the hemisphere as well as the period, no significant correlation has been seen in the latitudinal dependence. For the respective sequence the top-thirty rankings of the rotation angle are given in Tables S3 and S4 (Northern Hemisphere) and in Tables S5 and S6 (Southern Hemisphere) in Supplementary Material.
- (5)
- First, for the monthly precipitation on the Northern Hemisphere, irrespective of the period, the best fit on the rotation angle versus the latitude has been obtained for the linear regression. To be specific, (r, d) = (−0.107, 1.861) for Period I (1931–1960) to Period II (1951–1980), and (r, d) = (0.014, 2.210) for Period II (1951–1980) to Period III (1981–2010). In sharp contrast to this, autocorrelation between the rotation for the latter (Period II–III) and that for the former (Period I–II) has been found to be (r, d) = (0.666, 1.797) with the best logarithmic fit, showing moderate inertia throughout eighty years under consideration. The fact that Asswan (23°57′ N, 32°49′ E, h = 201 m) gains top score in both Tables S3 and S4 can be explained by noticing that the station which belongs with the Köppen’s climatic classification to BW [68] has little precipitation because of the extremely dry climate inherent in the Sahara Desert. Indeed, on Asswan the monthly precipitation data (mm) [66,67,68] are cited, from January to December (semicolon in the middle indicates the boundary between June and July), with (0.0, 0.0, 0.0, 0.0, 1.0, 0.0; 0.0, 0.0, 0.0, 0.0, 0.0, 0.0) for Period I (1931–1960), (0.1, 0.0, 0.1, 0.3, 0.0, 0.0; 0.0, 0.0, 0.0, 0.0, 0.0, 0.0) for Period II (1951–1980), (0.7, 0.0, 0.8, 0.4, 0.3, 0.0; 0.0, 0.0, 0.0, 0.6, 0.2, 0.1) for Period III (1981–2010). Here, one sees a series of nulls. The stations that have raised the ranking considerably (bold-faced in Table S4) are #47→#6: Kingston (17°56′ N), #76→#8: Karachi (24°54′ N), #56→#9: Athinai (37°44′ N), #78→#10: Lyon (45°43′ N), #68→#12: New Orleans (29°59′ N), #46→#13: Sofia (42°39′ N), #50→#14: Hong Kong (22°18′ N), #88→#18: Koebenhavn (55°41′ N), #52→#20: Anchorage (61°09′ N), #70→#21: Gibraltar (36°09′ N), # 58→#26: Madrid (40°24′ N), and #62→#28: Ankara (39°57′ N).
- (6)
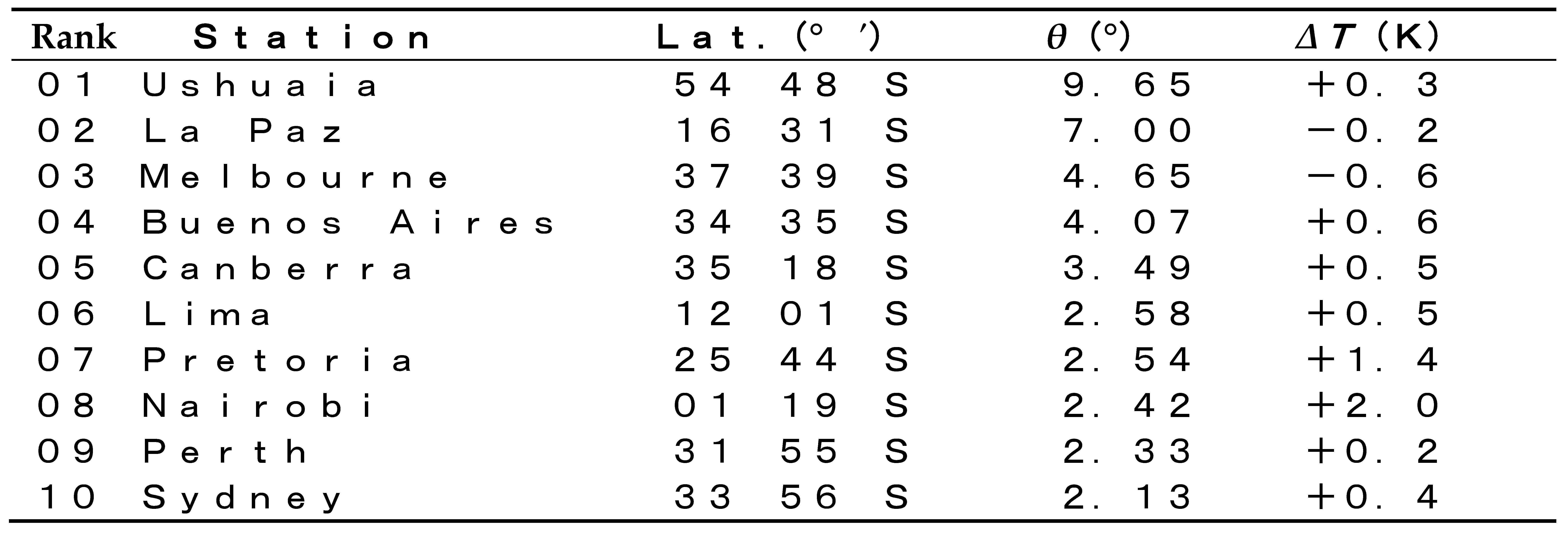
- Next, for the monthly precipitation in the Southern Hemisphere, independently of the period, the best fit on the rotation angle versus the latitude has been obtained for the exponential regression, namely, (r, d) = (0.440, 2.780) for Period I (1931–1960) to Period II (1951–1980), whereas (r, d) = (0.409, 2.422) for Period II (1951–1980) to Period III (1981–2010). Autocorrelation between the rotation for the latter (Period II–III) and that for the former (Period I–II) has been found to be (r, d) = (0.289, 2.148) with the best logarithmic fit, indicating weak inertia over the eighty years. The three stations that follow raise the ranking significantly (see Tables S5 and S6): #11→#3: Canberra (35°18′ S), #12→#4: Salvador (13°01′ S), and #13→#5: Rio De Janeiro (22°55′ S).
4.2. Regional Analysis
- (1)
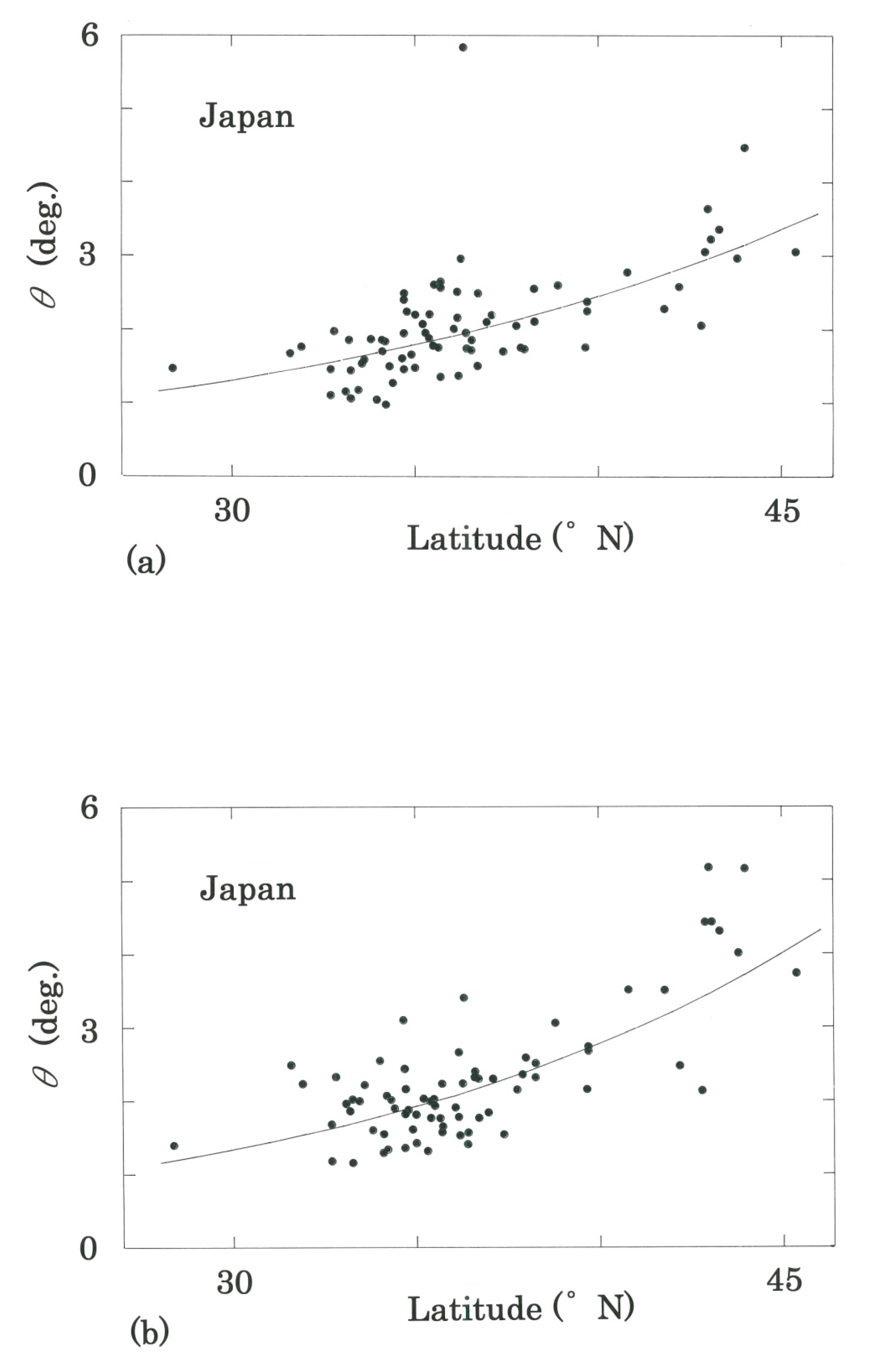
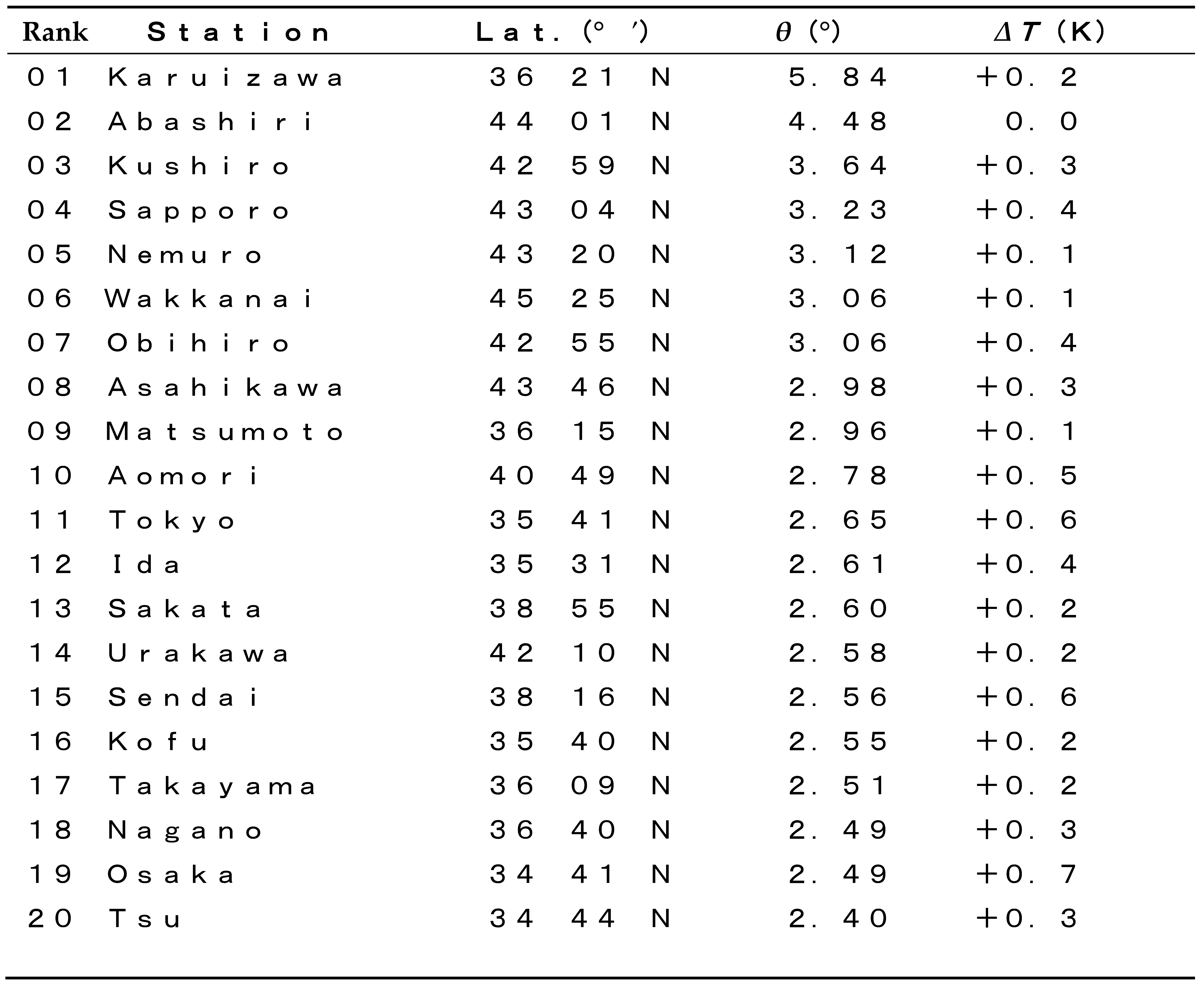
- In Figure 4a, which plots the rotation between Period I (1931–1960) and Period II (1951–1980), in the same way as its global counterparts (Figure 2a and Figure 3a) the best fit has been found to be exponential but with r = 0.642 and d = 1.867 > dU = 1.50 (n =75). (cf. for the linear regression of Equation (8), r = 0.597 with d = 1.876.) It can be seen from Table 5 that the top-twenty ranking is occupied by the stations of the northern areas being located on Hokkaido (#2 - #8, and #14) and the Tohoku Region (#10, #13, and #15), as well as the Nagano Prefecture (#1, #9, and #18). Moreover, it is interesting to note that besides #4: Sapporo and #15: Sendai there are two megacities, #11: Tokyo and #19: Osaka, on that ranking.
- (2)
- In Figure 4b, which plots the rotation between Period II (1951–1980) and Period III (1981–2010), the best regression has again been exponential but with r = 0.723 and d = 1.616 > dU = 1.50 (n = 75). (Note that, although, for the linear regression of Equation (8), we have obtained r = 0.752, the ratio d = 1.461 has been below dU.) The stations that have raised ranking substantially (see boldfaces in Table 6) are #22→#9: Hakodate (41′49′ N), #57→#11: Okayama (34°40′ N), #21→#13: Morioka (39°42′ N), #23→#14: Akita (39°43′ N), #51→#16: Aikawa (38°02′ N), #74→#17: Shimonoseki (33°57′ N), #29→#18: Yamagata (38°15′ N), and #55→#19: Kagoshima (31°33′ N). It should be noted in Table 6 that the occupation by the three cold districts remains high, namely, there are nine stations in Hokkaido (#1–#7, #9, and #20), five stations in the Tohoku Region (#8, #12 - #14, and #18), and one station in the Nagano Prefecture (#10). Autocorrelation between the rotation for the latter (Period II–III) and that for the former (Period I–II) has been found to be r = 0.687 and d = 1.322 < dL = 1.45 for n = 75 with the best linear fit.
- (3)
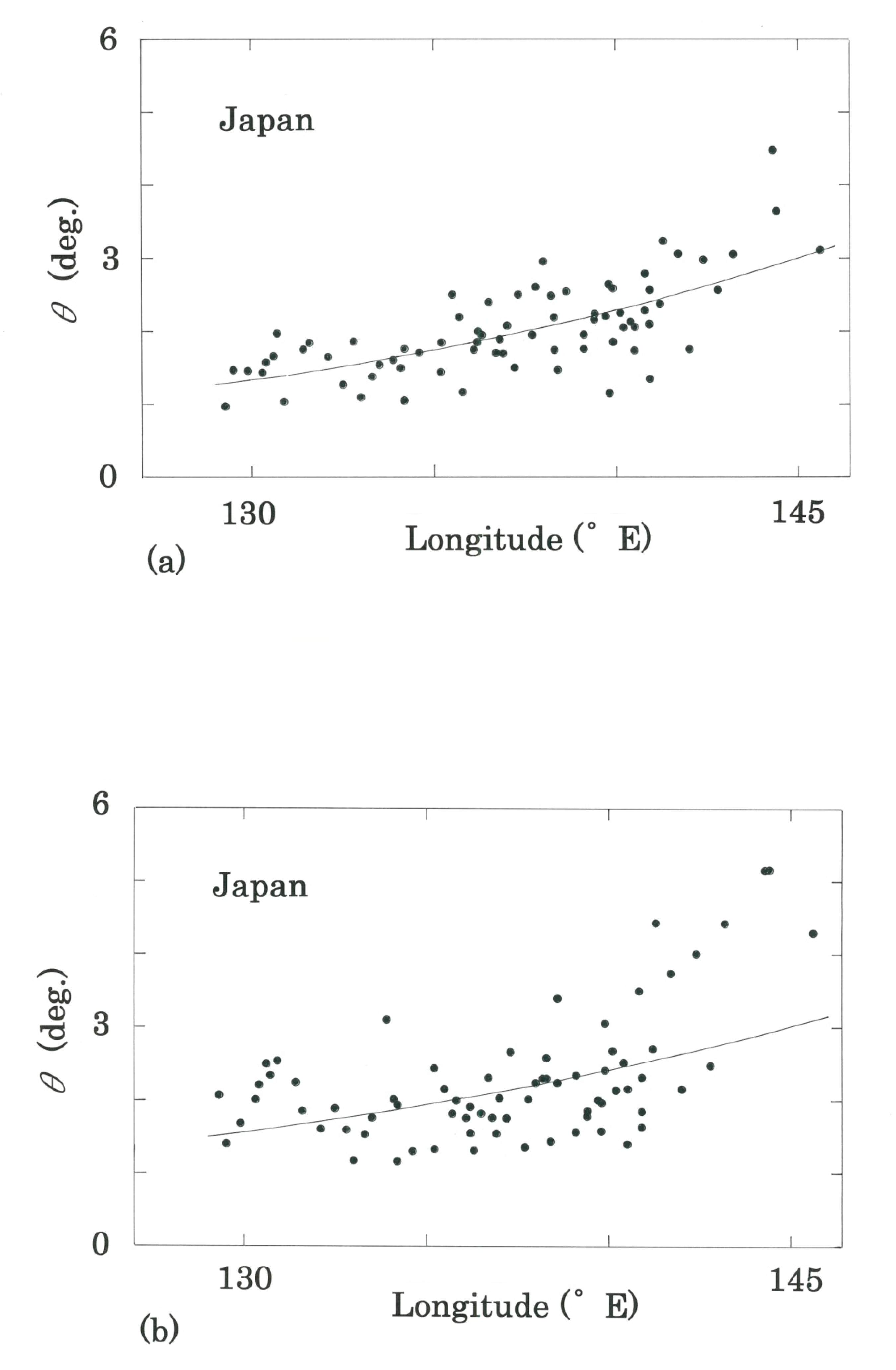
- To reinforce the conclusion above, the dependence of the rotation angle on the longitude is shown in Figure 5a for Period I (1931–1960) to Period II (1951–1980) and Figure 5b for Period II (1951–1980) to Period III (1981–2010). For both cases the best fit has been made for the exponential function: (r, d) = (0.648, 1.930) for Figure 5a, whereas (r, d) = (0.511, 1.120) for Figure 5b. The results are consistent with the fact that the latitudes of the Japanese stations depend exponentially on their longitudes, with (r, d) = (0.831, 1.402). In a comparison between Figure 5a, b, it should be noted that, unlike the observation on the comparison between Figure 4a, b, no increase of the gradient of the regressive curve is seen in the longitudinal dependence of the angle, concluding that from both plots, effects due to the snow/ice-albedo feedback are not detectable longitudinally.
- (4)
- Concerning the period of snow cover, higher correlation has been found on the latitude. Specifically, for Figure 6a, r = 0.890 (linear fit) with d = 1.634 > dU = 1.47 (n = 65), and for Figure 6b, r = 0.888 (linear fit) with d = 1.758 > dU = 1.47 (n = 65). A comparison between the result of Figure 6a and that of Figure 6b shows that in Japan the latitudinal dependence of snow cover decreases gradually. Note that the gradient of the regressive line on Figure 6b is 96% that on Figure 6a.
- (5)
- Irrespective of the period, for the precipitation data, the latitudinal dependence of the angle has been shown to obey the linear model: for the results between Period I (1931–1960) and Period II (1951–1980), r = 0.399 with d = 1.671 > dU = 1.50 (n = 75), while for those between Period II (1951–1980) and Period III (1981–2010), r = 0.120 with d = 1.920 > dU = 1.50 (n = 75). The top-twenty ranking is given, respectively, in Table S8 and Table S9 in Supplementary Material. In Table S9 the stations that have raised ranking remarkably are #23→#3: Nemuro (43°20′ N), #39→#6: Murotomisaki (33°15′ N), #31→#8: Matsumoto (36°15′ N), #67→#12: Ida (35°31′ N), #48→#14: Tsu (34°44′ N), #45→#15: Kobe (34°42′ N), #33→#16: Aomori (40° 49′ N), and #60→#19: Naze (28°23′ N). Autocorrelation between the sequence has also been found to obey the linear regression: r = 0.392 with 4 - d = 1.755 > dU = 1.50 (n = 75).
4.3. Toward Detecting Synchronization
- (1)
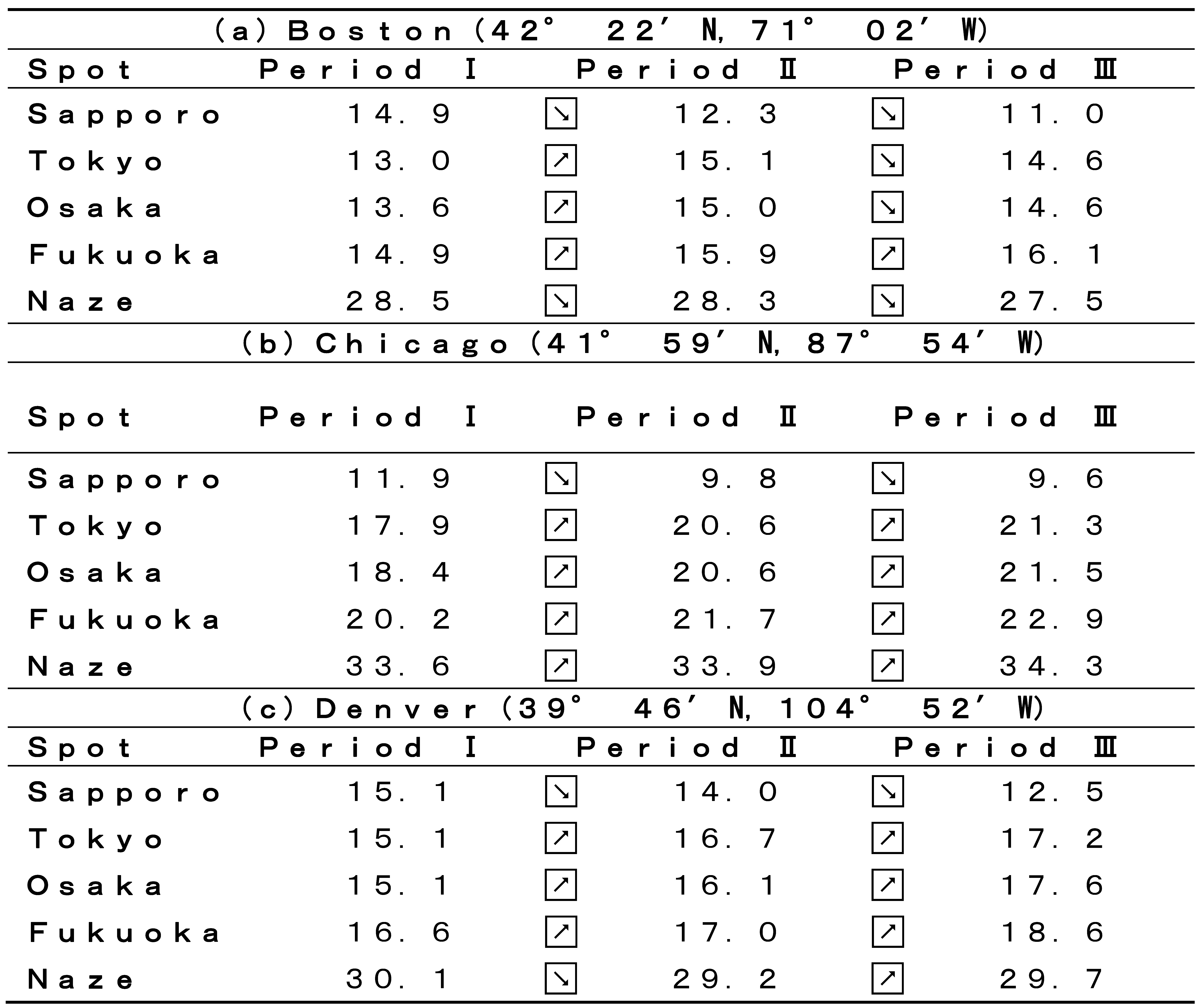
- First, the complete sequences of the cross angle of the monthly distributions of temperature between three North American stations (#37: Boston, #38: Chicago, and #46: Denver in Table S1) and the five Japanese stations are summarized in Table 7. It appears that synchronization arises solely at Sapporo, which shows striking contrast to the decreasing synchronization at the other three (Tokyo, Osaka, and Fukuoka).
- (2)
- (3)
- Other results that seem to be worth noticing are selected in what follows (I→II→III; numerals in degrees; boldfaces highlight the difference between the beginning and the last.):#58: Tehran (35°41′ N) - #62: Atlanta (33°39′ N): 7.4→6.2→4.0,#61: Peshawar (34°01′ N) - #69: New Orleans (29°59′ N): 5.8→5.0→4.1,#42: Istanbul (40°54′ N) - #59: Tokyo (35°41′ N): 6.6→6.5→5.5,#24: Muenchen (48°21′ N) - #37: Boston (42°22′ N): 7.8→7.2→6.7,#13: Dublin (53°26′ N) - #59: Tokyo (35°41′ N): 10.2→10.1→8.1,#55: Dar-El-Beida (36°41′ N) - #63: Fukuoka (33°35′ N): 11.2→10.7→8.3,#15: Irkutsk (52°16′ N) - #21: Winnipeg (49°55′ N): 14.5→13.9→9.4,#61: Peshawar (34°01′ N) - #72: Naze (28°23′ N): 10.3→10.1→9.6,#37: Boston (42°22′ N) - #40: Tashkent (41°20′ N): 11.2→10.0→9.8,#38: Chicago (41°59′ N) - #39: Shenyang (41°44′ N): 16.3→14.8→12.9,#35: Sapporo (43°04′ N) - #45: Ankara (39°57′ N): 17.3→15.9→13.7,#19: Kiev (50°24′ N) - #37: Boston (42°22′ N): 16.2→15.0→14.5.
- (4)
- Of the 19C2 (=171) combinations possible on the Southern Hemisphere, a synchronous trend has been detectable as follows (I→II→III; numerals in degrees):#07: Cape Town (33°58′ S) - #08: Sydney (33°56′ S): 3.5→2.4→2.0,#04: Auckland (37°01′ S) - #06: Buenos Aires (34°35′ S): 6.3→6.3→5.7,#02: Christchurch (43°29′ S) - #07: Cape Town (33°58′ S): 9.7→9.3→8.8,#05: Canberra (35°18′ S) - #07: Cape Town (33°58′ S): 12.8→12.8→11.9,#04: Auckland (37°01′ S) - #18: Manaus (03°08′ S): 14.3→14.2→13.9,#02: Christchurch (43°29′ S) - #18: Manaus (03°08′ S): 21.7→21.7→21.4.Although it appears that, at least in the six combinations, the two temperature distributions are no doubt in synchronization, the effect is found to be much weaker than that revealed in the northern counterpart.
- (5)
- In contrast to the ubiquitous examples of the synchronization, it is difficult to detect remarkable de-synchronization wherein two temperature patterns diverge constantly. Three rare examples are cited below (I→II→III; numerals in degrees):#10: Koebenhavn (55°41′ N) - #38: Chicago (41°59′ N): 10.4→12.0→13.7,#25: Wien (48°14′ N) - #38: Chicago (41°59′ N): 9.5→9.6→11.7,#21: Winnipeg (49°55′ N) - #32: Chang-chun (43°54′ N): 9.4→11.1→11.2
5. Discussion
5.1. Global Analysis
- (1)
- The emission of major greenhouse gases such as the carbon dioxide, methane, ozone, and chlorofluorocarbons (CFCs) is unevenly distributed toward the former hemisphere, particularly in the region over 30° N to 60° N where there are many industrialized countries. The emission from the latter hemisphere cannot bear comparison with this.
- (2)
- As is well-known the distribution of the Earth’s continents is unevenly distributed toward the Northern Hemisphere where the land area amounts to 1.0 × 1010 ha, whereas that of the Southern Hemisphere is 4.9 × 109 ha. Note that the land has a specific heat lower than the sea.
- (3)
- In striking contrast to the critical circumstance in the Arctic, the temperature growth on the Antarctica is not as steep as the northern counterpart. The reason is that the extremely thick ice (2.0 to 2.5 km) on the Antarctic Continent is free from the exposure of the ground, making ineffective the positive feedback due to the reduced albedo (i.e., the enhanced absorption) of the surface. Note again that the optical reflectivity for snow is at least 85% to 90%.
5.2. Regional Analysis
- (1)
- A recent report of numerical simulations by the Okhotsk Sea Ice Museum of Hokkaido [85] has predicted that in the near future there will be no sea ice drifting from a north region of the Sea of Okhotsk to the northern coast of Hokkaido, the northernmost island of Japan. The sea ice is produced in the sea of northeastern area of Sakhalin, and the south drift is caused either by the East Sakhalin Current or by an Okhotsk anticyclone that produces an air mass [86,87]. According to the report [84] the temperature around the northern area of the Sea has risen two degrees over the last fifty years, the increment of which amounts to the three times larger than the world average. Eventually, the rise in temperature has resulted in the 30% shrinkage of the ice area over the entire Sea. It should be noted here that the freezing temperature of the sea ice is −1.8 °C [88]. Because the flow in the vicinity of the southern border of the sea ice is much susceptive of the warming, one can regard the shrinkage as a high-sensitivity sensor for the global warming. Indeed, the moving average of the temperatures on Abashiri (see Rank #2 in Table 5 and Table 6), a spot on the coastland of the Sea, versus the sea-ice force off the coast of the spot has demonstrated the negative correlation over the last thirty years [89].
- (2)
- Comparison between the result of Figure 6a and that of Figure 6b reveals that in Japan both the period and the latitudinal dependence of snow cover decrease gradually. Specifically, the regression lines on the plots can be written aswhere x and y represent the latitude (° N) and the period of snow cover (days/year), respectively. Here it should be highlighted again that the coefficient of regression on the latter is 96% that on the former, demonstrating the influence due to the warming. Moreover, a comparison between the two plots shows that on the spot of 45° N the period of snow cover shortens for eight days in Figure 6b. Indeed, every year, ski resorts in Japan are hit by the snow shortage. Furthermore, the quality of their snow is degrading. To discuss this concern, we note that a pattern of atmospheric pressure in which the high-pressure area lies to the west and the low-pressure area to the east is characteristic of winter of the Japanese Islands. The physical mechanism of the pressure configuration can be explained as follows: First, because of the radiative cooling, temperatures in winter fall substantially on the inland areas of Siberia and China. Second, the enhanced density of the cooled air generates a descending air current, which is responsible for the emergence of the high pressure in the west of Hokkaido. Third, collision of two air masses coming from the North Pole and from the equator produces a large-scale stable vortex in the vicinity of the Kuriles and the southern area of the Kamchatka Peninsula; eventually the vortex is responsible for observing the low pressure in the east of Hokkaido. The warming as shown especially in the relatively high latitudes of the Northern Hemisphere (see Figure 2) is responsible for reducing the radiative cooling, i.e., reducing the strength of a seasonal wind from the Eurasian Continent to Hokkaido. In Table 2, one can confirm the reason, for instance, on Rank #13: Vladivostok (43°07′ N), #14: Irkutsk (52°16′ N), and #23: Chang-chun (43°54′ N). In response to the shrinkage of the Siberian cold mass moving southeast from the Maritime Territory (Primorsky Kray) of Russia to the Hidaka mountains, the world-renowned powdery snow on resorts in Hokkaido threatens to be in a critical condition.
5.3. Toward Detecting Synchronization
6. Conclusions
Supplementary Materials
Funding
Conflicts of Interest
References
- Weart, S.R. The Discovery of Global Warming; Harvard University Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Stocker, T.F.; Qin, D.; Plattner, G.-K.; Tignor, M.M.B.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. (Eds.) Climate Change 2013: The Physical Science Basis (Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change); Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- GOSAT Project, the National Institute for Environmental Studies, Japan. A Prompt Report on the Monthly Mean Carbon-Dioxide Concentration Averaged over the Entire Atmosphere. 2016. Available online: http://www.gosat.nies.go.jp/recent-global-co2.html (accessed on 19 July 2020).
- HadCRUT4 dataset produced by the Met Office and the Climatic Research Unit at the University of East Anglia. Global Climate in Context as the World Approaches 1 °C above Pre-Industrial for the First Time; 2015. Available online: https://www.metoffice.gov.uk/research/news/2015/global-average-temperature-2015 (accessed on 19 July 2020).
- An Opinion Offered by the Medical Association of Japan. 2018. Available online: https://www.asahi.com/articles/ASLBY5FX1LBY5X1LBYULZU00H.html (accessed on 12 August 2020).
- Yamamoto, R.; Hoshiai, M. Fluctuations of the Northern Hemisphere mean surface air temperature during recent 100 years estimated by optimum interpolation. J. Meteor. Soc. Jpn. 1980, 58, 187–193. [Google Scholar] [CrossRef][Green Version]
- Hansen, J.E.; Johnson, D.; Lacis, A.; Lebedeff, S.; Lee, P.; Rind, D.; Russell, G. Climatic impact of increasing atmospheric carbon dioxide. Science 1981, 213, 957–966. [Google Scholar] [CrossRef]
- Jones, P.D.; Wigley, T.M.L.; Kelly, P.M. Variations in surface air temperatures: Part 1. Northern Hemisphere, 1881–1980. Mon. Weather Rev. 1982, 110, 59–72. [Google Scholar] [CrossRef]
- Jones, P.D.; Kelly, P.M. The spatial and temporal characteristics of Northern Hemisphere surface air temperature variations. J. Climatol. 1983, 3, 243–252. [Google Scholar] [CrossRef]
- Jones, P.D.; Raper, S.C.B.; Bradley, R.S.; Diaz, H.F.; Kelly, P.M.; Wigley, T.M.L. Northern hemisphere surface air temperature variations: 1851–1984. J. Clim. Appl. Meteor. 1986, 25, 161–179. [Google Scholar] [CrossRef]
- Hansen, J.E.; Lebedeff, S. Global trends of measured surface air temperature. J. Geophys. Res. 1987, 92, 13345–13372. [Google Scholar] [CrossRef]
- Lacis, A.A.; Wuebbles, D.J.; Logan, J.A. Radiative forcing of climate by changes in the vertical distribution of ozone. J. Geophys. Res. 1990, 95, 9971–9981. [Google Scholar] [CrossRef]
- Bloomfield, P. Trends in global temperature. Clim. Chang. 1992, 21, 1–16. [Google Scholar] [CrossRef]
- Bloomfield, P.; Nychka, D.W. Climate spectra and detecting climate change. Clim. Chang. 1992, 21, 275–287. [Google Scholar] [CrossRef]
- Wallace, J.M.; Zhang, Y.; Renwick, J.A. Dynamic contribution to hemispheric mean temperature trends. Science 1995, 270, 780–783. [Google Scholar] [CrossRef]
- Hansen, J.; Sato, M.; Glascoe, J.; Ruedy, R. A common-sense climate index: Is climate changing noticeably? Proc. Natl. Acad. Sci. USA 1998, 95, 4113–4120. [Google Scholar] [CrossRef]
- Jones, P.D.; New, M.; Parker, D.E.; Martin, S.; Rigor, I.G. Surface air temperature and its changes over the past 150 years. Rev. Geophys. 1999, 37, 173–199. [Google Scholar] [CrossRef]
- Gaffen, D.J.; Ross, R.J. Climatology and trends of U.S. surface humidity and temperature. J. Clim. 1999, 12, 811–828. [Google Scholar] [CrossRef]
- New, M.; Hulme, M.; Jones, P. Representing twentieth-century space-time climate variability. Part I: Development of a 1961-90 mean monthly terrestrial climatology. J. Clim. 1999, 12, 829–856. [Google Scholar] [CrossRef]
- Berntsen, T.K.; Myhre, G.; Stordal, F.; Isaksen, I.S.A. Time evolution of tropospheric ozone and its radiative forcing. J. Geophys. Res. 2000, 105, 8915–8930. [Google Scholar] [CrossRef]
- Deser, C.; Walsh, J.E.; Timlin, M.S. Arctic sea ice variability in the context of recent atmospheric circulation trends. J. Clim. 2000, 13, 617–633. [Google Scholar] [CrossRef]
- Lelieveld, J.; Dentener, F.J. What controls tropospheric ozone? J. Geophys. Res. 2000, 105, 3531–3551. [Google Scholar] [CrossRef]
- New, M.; Hulme, M.; Jones, P. Representing twentieth-century space-time climate variability. Part II: Development of 1901-96 monthly grids of terrestrial surface climate. J. Clim. 2000, 13, 2217–2238. [Google Scholar] [CrossRef]
- Zhang, X.; Vincent, L.A.; Hogg, W.D.; Niitsoo, A. Temperature and precipitation trends in Canada during the 20th century. Atmos.-Ocean. 2000, 38, 395–429. [Google Scholar] [CrossRef]
- Hansen, J.E.; Ruedy, R.; Sato, M.; Imhoff, M.; Lawrence, W.; Easterling, D.; Peterson, T.; Karl, T. A closer look at United States and global surface temperature change. J. Geophys. Res. 2001, 106, 23947–23963. [Google Scholar] [CrossRef]
- Hansen, J.E.; Sato, M. Trends of measured climate forcing agents. Proc. Natl. Acad. Sci. USA 2001, 98, 14778–14783. [Google Scholar] [CrossRef]
- Wang, J.X.L.; Gaffen, D.J. Late-twentieth-century climatology and trends of surface humidity and temperature in China. J. Clim. 2001, 14, 2833–2845. [Google Scholar] [CrossRef]
- Thompson, D.; Solomon, S. Interpretation of recent Southern Hemisphere climate change. Science 2002, 296, 895–899. [Google Scholar] [CrossRef]
- Jones, P.D.; Moberg, A. Hemispheric and large-scale surface air temperature variations: An extensive revision and an update to 2001. J. Clim. 2003, 16, 206–223. [Google Scholar] [CrossRef]
- Philipona, R.; Duerr, B. Greenhouse forcing outweighs decreasing solar radiation driving rapid temperature rise over land. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Luterbacher, J.; Dietrich, D.; Xoplaki, E.; Grosjean, M.; Wanner, H. European seasonal and annual temperature variability, trends, and extremes since 1500. Science 2004, 303, 1499–1503. [Google Scholar] [CrossRef]
- Meehl, G.A.; Tebaldi, C. More intense, more frequent, and longer lasting heat waves in the 21st century. Science 2004, 305, 994–997. [Google Scholar] [CrossRef]
- Philipona, R.; Duerr, B.; Ohmura, A.; Ruckstuhl, C. Anthropogenic greenhouse forcing and strong water vapor feedback increase temperature in Europe. Geophys. Res. Lett. 2005, 32, L19809. [Google Scholar] [CrossRef]
- Tebaldi, C.; Hayhoe, K.; Arblaster, J.M.; Meehl, G.A. Going to the extremes: An intercomparison of model-simulated historical and future changes in extreme events. Clim. Chang. 2006, 79, 185–211. [Google Scholar] [CrossRef]
- Seidel, D.J.; Randel, W.J. Recent widening of the tropical belt: Evidence from tropopause observations. J. Geophys. Res. 2007, 112, D20113. [Google Scholar] [CrossRef]
- Vincent, L.A.; van Wijngaarden, W.A.; Hopkinson, R. Surface temperature and humidity trends in Canada for 1953–2005. J. Clim. 2007, 20, 5100–5113. [Google Scholar] [CrossRef]
- Thompson, D.W.J.; Kennedy, J.J.; Wallace, J.M.; Jones, P.D. A large discontinuity in the mid-twentieth century observed global-mean surface temperature. Nature 2008, 453, 646–649. [Google Scholar] [CrossRef] [PubMed]
- Portmann, R.W.; Solomon, S.; Hegerl, G.C. Spatial and seasonal patterns in climate change, temperatures, and precipitation across the United States. Proc. Natl. Acad. Sci. USA 2009, 106, 7324–7329. [Google Scholar] [CrossRef]
- Swanson, K.L.; Sugihara, G.; Tsonis, A.A. Long-term natural variability and 20th century climate change. Proc. Natl. Acad. Sci. USA 2009, 106, 16120–16130. [Google Scholar] [CrossRef]
- Morak, S.; Hegerl, G.C.; Kenyon, J. Detectable regional changes in the number of warm nights. Geophys. Res. Lett. 2011, 38, L17703. [Google Scholar] [CrossRef]
- Arblaste, J.M.; Meehl, G.A.; Karoly, D.J. Future climate change in the Southern Hemisphere: Competing effects of ozone and greenhouse gases. Geophys. Res. Lett. 2011, 38, L02701. [Google Scholar] [CrossRef]
- Francis, J.A.; Vavrus, S.J. Evidence linking Arctic amplification to extreme weather in mid-latitudes. Geophys. Res. Lett. 2012, 39, L06801. [Google Scholar] [CrossRef]
- Franzke, C. On the statistical significance of surface air temperature trends in the Eurasian Arctic region. Geophys. Res. Lett. 2012, 39, L23705. [Google Scholar] [CrossRef]
- Hansen, J.; Sato, M.; Ruedy, R. Perception of climate change. Proc. Natl. Acad. Sci. USA 2012, 109, E2415–E2423. [Google Scholar] [CrossRef]
- Jones, P.D.; Lister, D.H.; Osborn, T.J.; Harpham, C.; Salmon, M.; Morice, C.P. Hemispheric and large-scale land surface air temperature variations: An extensive revision and an update to 2010. J. Geophys. Res. 2012, 117, D05127. [Google Scholar] [CrossRef]
- Mika, J. Changes in weather and climate extremes: Phenomenology and empirical approaches. Clim. Chang. 2013, 121, 15–26. [Google Scholar] [CrossRef]
- Ji, F.; Wu, Z.; Huang, J.; Chassignet, E.P. Evolution of land surface air temperature trend. Nat. Clim. Chang. 2014, 4, 462–466. [Google Scholar] [CrossRef]
- Screen, J.A. Arctic amplification decreases temperature variance in northern mid- to high-latitudes. Nat. Clim. Chang. 2014, 4, 577–582. [Google Scholar] [CrossRef]
- Robeson, S.M.; Willmott, C.J.; Jones, P.D. Trends in hemispheric warm and cold anomalies. Geophys. Res. Lett. 2014, 41, 9065–9071. [Google Scholar] [CrossRef]
- Ganopolski, A.; Rahmstorf, S. Abrupt glacial climate changes due to stochastic resonance. Phys. Rev. Lett. 2002, 88, 038501. [Google Scholar] [CrossRef]
- Király, A.; Jánosi, I.M. Stochastic modeling of daily temperature fluctuations. Phys. Rev. E 2002, 65, 051102. [Google Scholar] [CrossRef] [PubMed]
- Lind, P.G.; Mora, A.; Gallas, J.A.C.; Haase, M. Reducing stochasticity in the North Atlantic Oscillation index with coupled Langevin equations. Phys. Rev. E 2005, 72, 056706. [Google Scholar] [CrossRef]
- Redner, S.; Petersen, M.R. Role of global warming on the statistics of record-breaking temperatures. Phys. Rev. E 2006, 74, 061114. [Google Scholar] [CrossRef]
- Verdes, P.F. Global warming is driven by anthropogenic emissions: A time series analysis approach. Phys. Rev. Lett. 2007, 99, 048501. [Google Scholar] [CrossRef]
- Adair, R.K. Stochastic contribution to global temperature changes. Phys. Rev. Lett. 2008, 100, 148501. [Google Scholar] [CrossRef]
- Newman, W.I.; Malamud, B.D.; Turcotte, D.L. Statistical properties of record-breaking temperatures. Phys. Rev. E 2010, 82, 066111. [Google Scholar] [CrossRef] [PubMed]
- Tamazian, A.; Ludescher, J.; Bunde, A. Significance of trends in long-term correlated records. Phys. Rev. E 2015, 91, 032806. [Google Scholar] [CrossRef] [PubMed]
- Drótos, G.; Bódai, T.; Tél, T. Quantifying nonergodicity in nonautonomous dissipative dynamical systems: An application to climate change. Phys. Rev. E 2016, 94, 022214. [Google Scholar] [CrossRef]
- Huang, X.; Hassani, H.; Ghodsi, M.; Mukherjee, Z.; Gupta, R. Do trend extraction approaches affect causality detection in climate change studies? Phys. A 2017, 469, 604–624. [Google Scholar] [CrossRef][Green Version]
- Zhang, F.; Yang, P.; Fraedrich, K.; Zhou, X.; Wang, G. Reconstruction of driving forces from nonstationary time series including stationary regions and application to climate change. Phys. A 2017, 473, 337–343. [Google Scholar] [CrossRef]
- Matcharashvili, T.; Zhukova, N.; Chelidze, T.; Founda, D.; Gerasopoulos, E. Analysis of long-term variation of the annual number of warmer and colder days using Mahalanobis distance metrics: A case study for Athens. Phys. A 2017, 487, 22–31. [Google Scholar] [CrossRef]
- Popović, P.; Cael, B.B.; Silber, M.; Abbot, D.S. Simple rules govern the patterns of Arctic sea ice melt ponds. Phys. Rev. Lett. 2018, 120, 148701. [Google Scholar] [CrossRef] [PubMed]
- Moon, W.; Agarwal, S.; Wettlaufer, J.S. Intrinsic pink-noise multidecadal global climate dynamics mode. Phys. Rev. Lett. 2018, 121, 108701. [Google Scholar] [CrossRef]
- Hassani, H.; Silva, E.S.; Gupta, R.; Das, S. Predicting global temperature anomaly: A definitive investigation using an ensemble of twelve competing forecasting models. Phys. A 2018, 509, 121–139. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Z.-H.; Sun, L. Early-warning signals for critical temperature transitions. Geophys. Res. Lett. 2020, 47, e2020GL088503. [Google Scholar] [CrossRef]
- The National Astronomical Observatory, Japan (Ed.) Chronological Scientific Tables; Maruzen: Tokyo, Japan, 1985; Volume 59. [Google Scholar]
- The National Astronomical Observatory, Japan (Ed.) Chronological Scientific Tables; Maruzen: Tokyo, Japan, 1992; Volume 66. [Google Scholar]
- The National Astronomical Observatory, Japan (Ed.) Chronological Scientific Tables; Maruzen: Tokyo, Japan, 2017; Volume 91. [Google Scholar]
- Wadhams, P. A Farewell to Ice: A Report from the Arctic; Penguin Books: London, UK, 2016. [Google Scholar]
- von Storch, H.; Zwiers, F.W. Statistical Analysis in Climate Research; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- von Storch, H.; Navarra, A. (Eds.) Analysis of Climate Variability: Applications of Statistical Techniques, 2nd ed.; Springer: Berlin, Germany, 2010. [Google Scholar]
- Chatterjee, S.; Hadi, A.S. Regression Analysis by Example, 5th ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Seber, G.A.F.; Wild, C.J. Nonlinear Regression; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Wang, C.; Wang, Z.-H.; Li, Q. Emergence of urban clustering among U.S. cities under environmental stressors. Sustain. Cities Soc. 2020, 63, 102481. [Google Scholar] [CrossRef]
- Duane, G.S. Synchronized chaos in extended systems and meteorological teleconnections. Phys. Rev. E 1997, 56, 6475. [Google Scholar] [CrossRef]
- Rybski, D.; Havlin, S.; Bunde, A. Phase synchronization in temperature and precipitation records. Phys. A 2003, 320, 601–610. [Google Scholar] [CrossRef]
- Castrejón-Pita, A.A.; Read, P.L. Synchronization in a pair of thermally coupled rotating baroclinic annuli: Understanding atmospheric teleconnections in the laboratory. Phys. Rev. Lett. 2010, 104, 204501. [Google Scholar] [CrossRef]
- Zhou, D.; Gozolchiani, A.; Ashkenazy, Y.; Havlin, S. Teleconnection paths via climate network direct link detection. Phys. Rev. Lett. 2015, 115, 268501. [Google Scholar] [CrossRef]
- Yizhaq, H.; Ashkenazy, Y. Why do active and stabilized dunes coexist under the same climatic conditions? Phys. Rev. Lett. 2007, 98, 188001. [Google Scholar] [CrossRef] [PubMed]
- Kutschan, B.; Morawetz, K.; Gemming, S. Modeling the morphogenesis of brine channels in sea ice. Phys. Rev. E 2010, 81, 036106. [Google Scholar] [CrossRef]
- Alberti, T.; Primavera, L.; Vecchio, A.; Lepreti, F.; Carbone, V. Spatial interactions in a modified daisyworld model: Heat diffusivity and greenhouse effects. Phys. Rev. E 2015, 92, 052717. [Google Scholar] [CrossRef]
- Lucarini, V.; Bódai, T. Transitions across melancholia states in a climate model: Reconciling the deterministic and stochastic points of view. Phys. Rev. Lett. 2019, 122, 158701. [Google Scholar] [CrossRef]
- Berger, J.J. Climate Peril; Northbrae: Berkeley, CA, USA, 2014. [Google Scholar]
- Welch, C.; Orlinsky, K. The threat below. Natl. Geogr. 2019, 9, 74–99. [Google Scholar]
- The Ministry of the Environment, Japan. Vanishing Floating Ice: A Symptom of Warming? 2016. Available online: https://www.youtube.com/watch?v=MuSgY5G-64I (accessed on 19 July 2020).
- Kimura, N.; Wakatsuchi, M. Processes controlling the advance and retreat of sea ice in the Sea of Okhotsk. J. Geophys. Res. 1999, 104, 11137–11150. [Google Scholar] [CrossRef]
- Kimura, N.; Wakatsuchi, M. Increase and decrease of ice area in the Sea of Okhotsk: Ice production in coastal polynyas and dynamic thickening in convergence zones. J. Geophys. Res. 2004, 109, C09S03. [Google Scholar] [CrossRef]
- The Okhotsk Sea Ice Museum of Hokkaido. Where Does the Sea Ice Come from? 2020. Available online: http://giza-ryuhyo.com/ (accessed on 11 September 2020).
- Aota, M. A Nightmare of the Disappearance of Sea Ice. 2006. Available online: https://www.cger.nies.go.jp/publications/news/series/watch/6-6.pdf (accessed on 11 September 2020).
- Watanabe, O. (Ed.) The Alaskan Glacier: A Book of Travels by Ukichiro Nakaya; Iwanami Shoten: Tokyo, Japan, 2002. [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayata, K. Global-Scale Synchronization in the Meteorological Data: A Vectorial Analysis That Includes Higher-Order Differences. Climate 2020, 8, 128. https://doi.org/10.3390/cli8110128
Hayata K. Global-Scale Synchronization in the Meteorological Data: A Vectorial Analysis That Includes Higher-Order Differences. Climate. 2020; 8(11):128. https://doi.org/10.3390/cli8110128
Chicago/Turabian StyleHayata, Kazuya. 2020. "Global-Scale Synchronization in the Meteorological Data: A Vectorial Analysis That Includes Higher-Order Differences" Climate 8, no. 11: 128. https://doi.org/10.3390/cli8110128
APA StyleHayata, K. (2020). Global-Scale Synchronization in the Meteorological Data: A Vectorial Analysis That Includes Higher-Order Differences. Climate, 8(11), 128. https://doi.org/10.3390/cli8110128





