Development of a Matrix Based Statistical Framework to Compute Weight for Composite Hazards, Vulnerability and Risk Assessments
Abstract
1. Introduction and Statement of Problem
Research Gap, Research Question, Objectives, and Significance
- (a)
- To form the correlation matrix between different sets of indicators.
- (b)
- To determine relative weight from the Eigenvector corresponding to the highest Eigenvalue.
- (c)
- To show applicability of this method for giving appropriate weights to the indicators.
- (d)
- To test the validity of this method by assessing vulnerability for the Bangladesh coast.
2. Overview of Other Weightage Methods and a Comparison with the New MSF Method
3. Advantages and Disadvantages of MSF
- MSF does not need to consider how many Eigenvalues are greater than 1; it considers just what is the largest Eigenvalue, which implies the Eigenvector is considered as the relative weights of the variables.
- MSF directly gives the ‘decision’ to select the Eigenvector as relative weights that corresponds to the largest Eigenvalue.
- In terms of application to assign weights to large number of indicators, MSF is comparatively easy and simple to apply compared to other methods. It does not need any ‘decision’ to be taken about the ‘components’.
- MSF has one component vector; in that case, the expected relative weights of indicators does not depend on the linear combination of component vectors with the variances (weights of component vectors), which is simple.
- MSF considers linear assumptions between the variables during the computation of Eigenvectors corresponding to Eigenvalues.
- In MSF, there are many statistical distributions where mean and covariance do not give relevant physical information of variables.
4. Methods
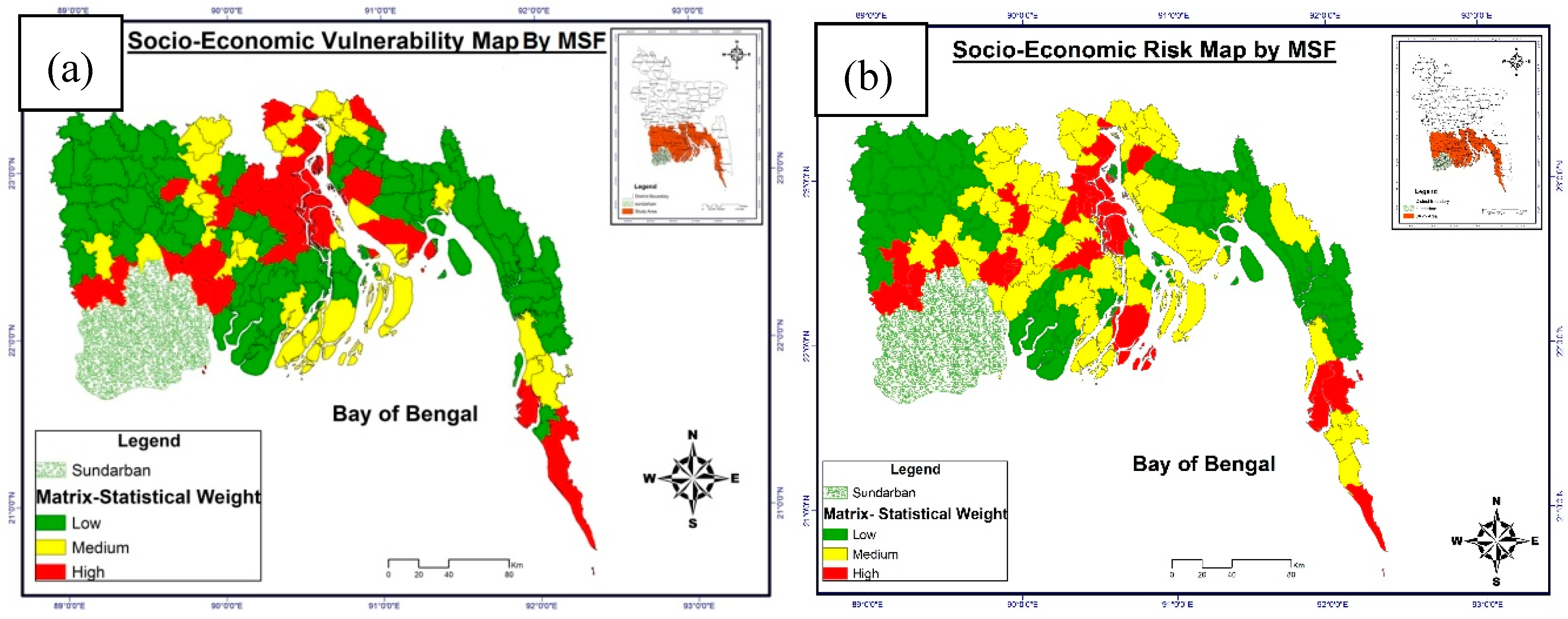
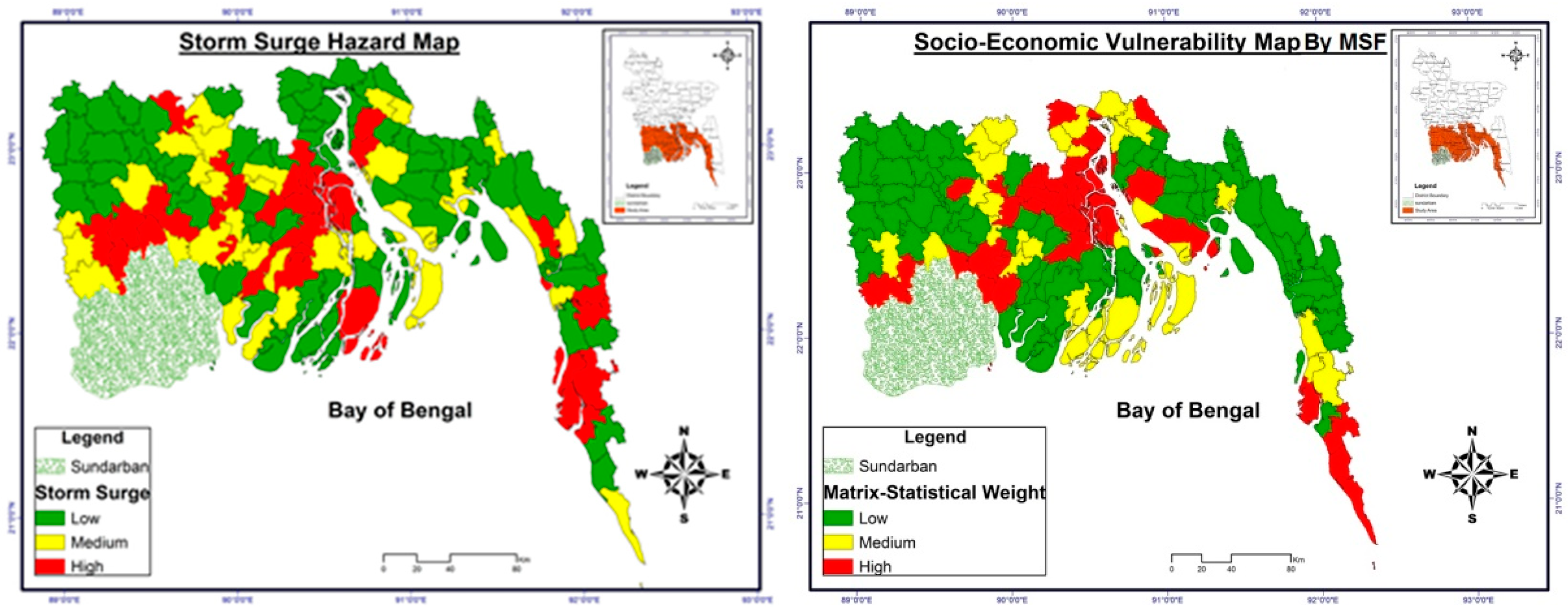
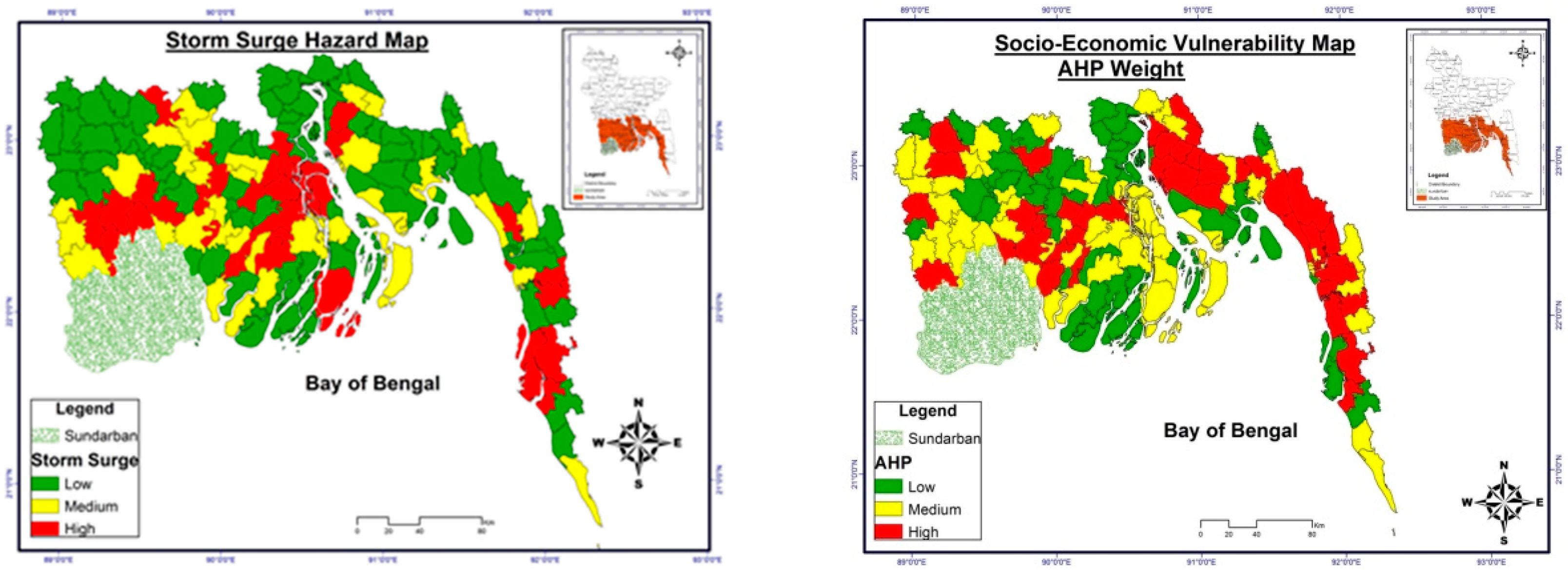
5. Application of MSF for Vulnerability and Risk Assessment of the Bangladesh Coast
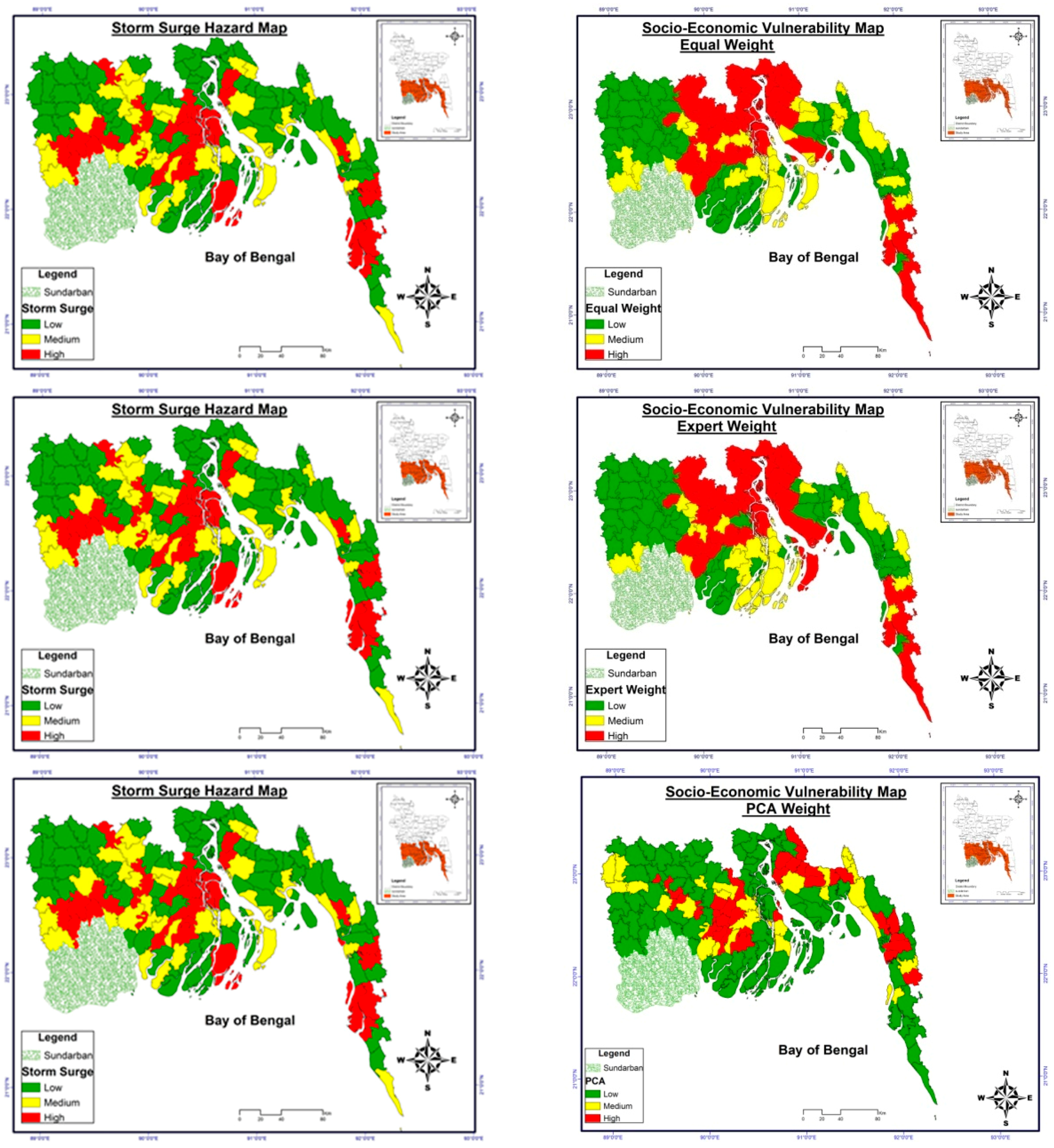
6. Comparison of Weights Computed by MSF with Other Methods
7. Accuracy of MSF Compared to Other Methods
8. Conclusions and Recommendations
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix
| Pseudocode |
| [Val, Ind] = max(eig(corr(data))); |
| [EgVc, EgVl] = eig(corr(data)); |
| Dim = size(data,2); |
| RowD = []; |
| for i = 1: Dim |
| ColD = []; |
| for j = 1: Dim |
| t1 = data(:,i)-mean(data(:,i)); |
| t2 = data(:,j)-mean(data(:,j)); |
| ColD = [ColD,sum(t1.*t2)]; |
| end |
| RowD = [RowD;ColD]; |
| end |
| fprintf(’SS = \n’); |
| disp(RowD); |
| fprintf(’Corr = \n’); |
| disp(corr(data)); |
| fprintf(’Eigen Value = %f\n\n’,Val); |
| fprintf(’Eigen Vactor =\n’); |
| disp(EgVc(:,Ind)) |
References
- UNFCCC. 1992. Available online: http://unfccc.int/essential_background/items/6031.php (accessed on 17 May 2017).
- World Bank. Turn Down the Heat: Why a 4 °C Warmer World Must Be Avoided; World Bank: Washington, DC, USA, 2012. [Google Scholar]
- IPCC. Summary for Policymakers. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Lázár, A.N.; Clarke, D.; Adams, H.; Razzaque, A.; Szabo, S.; Nicholls, R.J.; Matthews, Z.; Begum, D.; Saleh, A.F.M.; Abedin, M.A.; et al. Agricultural livelihoods in coastal Bangladesh under climate and environmental change—A model framework. Environ Sci. Process. Impacts 2015, 17, 1018–1031. [Google Scholar]
- Wolters, M.; Kuenzer, C. Vulnerability assessments of coastal river deltas—Categorization and review. J. Coast. Cons. 2015, 19, 345–368. [Google Scholar] [CrossRef]
- Sebesvari, Z.; Foufoula-Georgiou, E.; Harrison, I.; Brondizio, E.; Bucx, T.; Dearing, J.A.; Ganguly, D.; Ghosh, T.; Goodbred, S.L.; Hagenlocher, M.; et al. Imperatives for Sustainable Delta Futures. Brief for GSDR. Sustainable Development Knowledge Platform. 2016. Available online: https://sustainabledevelopment.un.org/content/documents/972032_Sebesvari_Imperatives%20for%20sustainable%20delta%20futures.pdf (accessed on 12 September 2017).
- Sebesvari, Z.; Renaud, F.G.; Haas, S.; Tessler, Z.; Hagenlocher, M.; Kloos, J.; Szabo, S.; Tejedor, A.; Kuenzer, C. A review of vulnerability indicators for deltaic social–ecological systems. Sustain. Sci. 2016, 11, 575–590. [Google Scholar] [CrossRef]
- Preston, B.L.; Yuen, E.J.; Westaway, R.M. Putting vulnerability to climate change on the map: A review of approaches, benefits, and risks. Sustain. Sci. 2011, 6, 177–202. [Google Scholar] [CrossRef]
- Fünfgeld, H.; McEvoy, D. Framing Climate Change Adaptation in Policy and Practice VCCCAR Working Paper 1, VCCCAR Project: Framing Adaptation in the Victorian Context; Victorian Centre for Climate Change Adaptation Research (VCCCAR): Melbourne, Australia, 2011; p. 65. [Google Scholar]
- Hahn, M.B.; Riederer, A.M.; Foster, S.O. The livelihood vulnerability index: Apragmatic approach to assessing risks from climate variability and change—A case study in mozambique. Glob. Environ. Chang. 2009, 19, 74–88. [Google Scholar] [CrossRef]
- Sullivan, C.; Meigh, J. Targeting attention on local vulnerabilities using an integrated index approach: The example of the climate vulnerability index. Water Sci. Technol. J. (Int. Assoc. Water Pollut. Res.) 2005, 51, 69–78. [Google Scholar] [CrossRef]
- Maggino, F.; Ruviglioni, E. Obtaining Weights: From Objective to Subjective Approaches in View of More Participative Methods in the Construction of Composite Indicators; New Techniques and Technologies for Statistics, Eurostat: Brussels, Belgium, 2011. [Google Scholar]
- Kalaba, R.E.; Spingarn, K. Numerical approaches to the eigenvalues of Saaty’s matrices for fuzzy sets. Comput. Math. Appl. 1978, 4, 369–375. [Google Scholar] [CrossRef][Green Version]
- Jeong, D.H.; Ziemkiewicz, C.; Ribarsky, W.; Chang, R.; Center, C.V. Understanding Principal Component Analysis Using a Visual Analytics Tool; Charlotte Visualization Center, UNC Charlotte: Charlotte, NC, USA, 2009. [Google Scholar]
- Weisstein, E.W. Eigenvalue (Power Point slides). 2002. Available online: http://mathworld.wolfram.com/Eigenvalue.html (accessed on 28 April 2016).
- Getahun, Y.S.; Gebre, S.L. Flood Hazard Assessment and Mapping of Flood Inundation Area of the Awash River Basin in Ethiopia using GIS and HEC-GeoRAS/HEC-RAS Model. J. Civ. Environ. Eng. 2015, 5, 179. [Google Scholar]
- Titman, S.; Wessels, R. The determinants of capital structure choice. J. Financ. 1988, 43, 1–19. [Google Scholar] [CrossRef]
- Kim, J.O.; Mueller, C.W. Factor Analysis: Statistical Methods and Practical Issues; Sage: Beverly Hills, CA, USA, 1978. [Google Scholar]
- Bellman, R. Introduction to Matrix Analysis; McGraw-Hill: New York, NY, USA, 1960. [Google Scholar]
- Bellman, R. An iterative method for finding the perron root of a matrix. Proc. Am. Math. Soc. 1955, 6, 719–725. [Google Scholar] [CrossRef]
- Roy, D.C.; Blaschke, T. Spatial vulnerability assessment of floods in the coastal regions of Bangladesh. Geomatics. Nat. Hazards Risk 2015, 6, 21–44. [Google Scholar] [CrossRef]
- Ahsan, M.N.; Warner, J. The socioeconomic vulnerability index: A pragmatic approach for assessing climate change led risks—A case study in the south-western coastal Bangladesh. Int. J. Disaster Risk Reduct. 2014, 8, 32–49. [Google Scholar] [CrossRef]
- Younus, M. An assessment of vulnerability and adaptation to cyclones through impact assessment guidelines: A bottom-up case study from Bangladesh coast. Nat. Hazards 2017, 89, 1437–1459. [Google Scholar] [CrossRef]
- Younus, M.A.F.; Harvey, N. Community-Based Flood Vulnerability and Adaptation Assessment: A Case Study from Bangladesh. J. Environ. Assess. Policy Manag. 2013, 15. [Google Scholar] [CrossRef]
- Toufique, K.A.; Yunus, M. Vulnerability of livelihoods in the coastal districts of Bangladesh. Bangladesh Dev. Stud. 2013, XXXVI, 95–120. [Google Scholar]
- Islam, M.A. Constructing an area-based climate and disaster vulnerability index (CDVI) for Bangladesh. UNDP. 2014. Available online: http://procurement-notices.undp.org/view_file.cfm?doc_id=35734 (accessed on 23 October 2018).
- Adger, W.N.; Kelly, P.M.; Nguyen, N.H. (Eds.) Living with Environmental Change: Social Vulnerability, Adaptation and Resilience in Vietnam, 1st ed.; Routledge: London, UK; New York, NY, USA, 2001. [Google Scholar]
- Ravindranath, N.H.; Rao, S.; Sharma, N.; Nair, M.; Gopalakrishnan, R.; Rao, A.S.; Malaviya, S.; Tiwari, R.; Sagadevan, A.; Munsi, M.; et al. Climate change vulnerability profiles for North East India. Curr. Sci. 2011, 101, 384–394. [Google Scholar]
- Bangladesh Bureau of Statistics (BBS). Community Series 2011, Planning Division, Ministry of Planning, Government of the People’s Republic of Bangladesh. 2011. Available online: http://www.bbs.gov.bd/ (accessed on 16 January 2016).
- ManiMurali, R.; Ankita, M.; Amrita, S.; Vethamony, P. Coastal vulnerability assessment of Puducherry coast, India, using the analytical hierarchical process. 2013; Unpublished. [Google Scholar]
- Armaş, I.; Gavriş, A. Census-based social vulnerability assessment for Bucharest. Procedia Environ. Sci. 2013, 32, 138–146. [Google Scholar] [CrossRef]
- Kabir, R. Determination of Critical Risk Due to Storm Surges in the Coastal Zone of Bangladesh. Master’s Thesis, Institute of Water and Flood Management, Bangladesh University of Engineering and Technology, Dhaka, Bangladesh, November 2017. [Google Scholar]
- Cutter, S.L.; Boruff, B.J.; Shirley, W.L. Social vulnerability to environmental hazards. Soc. Sci. Q. 2003, 84, 242–261. [Google Scholar] [CrossRef]
- Cutter, S.L.; Smith, M.M. Fleeing from the hurricane’s wrath: Evacuation and the two Americas. Environ. Sci. Policy Sustain. Dev. 2009, 51, 26–36. [Google Scholar] [CrossRef]
- Rygel, L.; O’sullivan, D.; Yarnal, B. A method for constructing a social vulnerability index: An application to hurricane storm surges in a developed country. Mitig. Adapt. Strateg. Glob. Chang. 2006, 11, 741–764. [Google Scholar] [CrossRef]
- Lundgren, L.; Jonsson, A.C. Assessment of Social Vulnerability: A Literature Review of Vulnerability Related to Climate Change and Natural Hazards; Centre for Climate Science and Policy Research, Linköping University Electronic Press: Norrköpping, Sweden, 2012. [Google Scholar]
- Blaikie, P.; Cannon, T.; Davis, I.; Wisner, B. At Risk: Natural Hazards, People’s Vulnerability and Disasters; Routledge: New York, NY, USA, 2014. [Google Scholar]
- MR, I.S.; Hamid, H.; Hwa, L.T.; Farhan, A. Identification of hazardous road sections: Crash data versus composite index method. Int. J. Eng. Technol. 2014, 6, 481. [Google Scholar]
- Flanagan, B.E.; Gregory, E.W.; Hallisey, E.J.; Heitgerd, J.L.; Lewis, B. A social vulnerability index for disaster management. J. Homel. Secur. Emerg. Manag. 2011, 8. [Google Scholar] [CrossRef]
- Zanetti, V.B.; Junior, W.; Freitas, D. A Climate Change Vulnerability Index and Case Study in a Brazilian Coastal City. Sustainability 2016, 8, 881. [Google Scholar] [CrossRef]
- Bruijn, K. Resilience indicators for flood risk management systems of lowland rivers. Int. J. River Basin Manag. 2004, 2, 199–210. [Google Scholar] [CrossRef]
- Satterthwaite, D. Climate change and urbanization: Effects and implications for urban governance. In United Nations Expert Group Meeting on Population Distribution, Urbanization, Internal Migration and Development; DESA: New York, NY, USA, January 2008; pp. 21–23. [Google Scholar]
- Sakib, M.; Nihal, F.; Haque, A.; Rahman, M.; Ali, M. Sundarban as a Buffer against Storm Surge Flooding. World J. Eng. Technol. 2015, 3, 59–64. [Google Scholar] [CrossRef]
- Hargrove, W.W.; Hoffman, F.M.; Hessburg, P.F. Mapcurves: A quantitative method for comparing categorical maps. J. Geogr. Syst. 2006, 8, 187–208. [Google Scholar] [CrossRef]
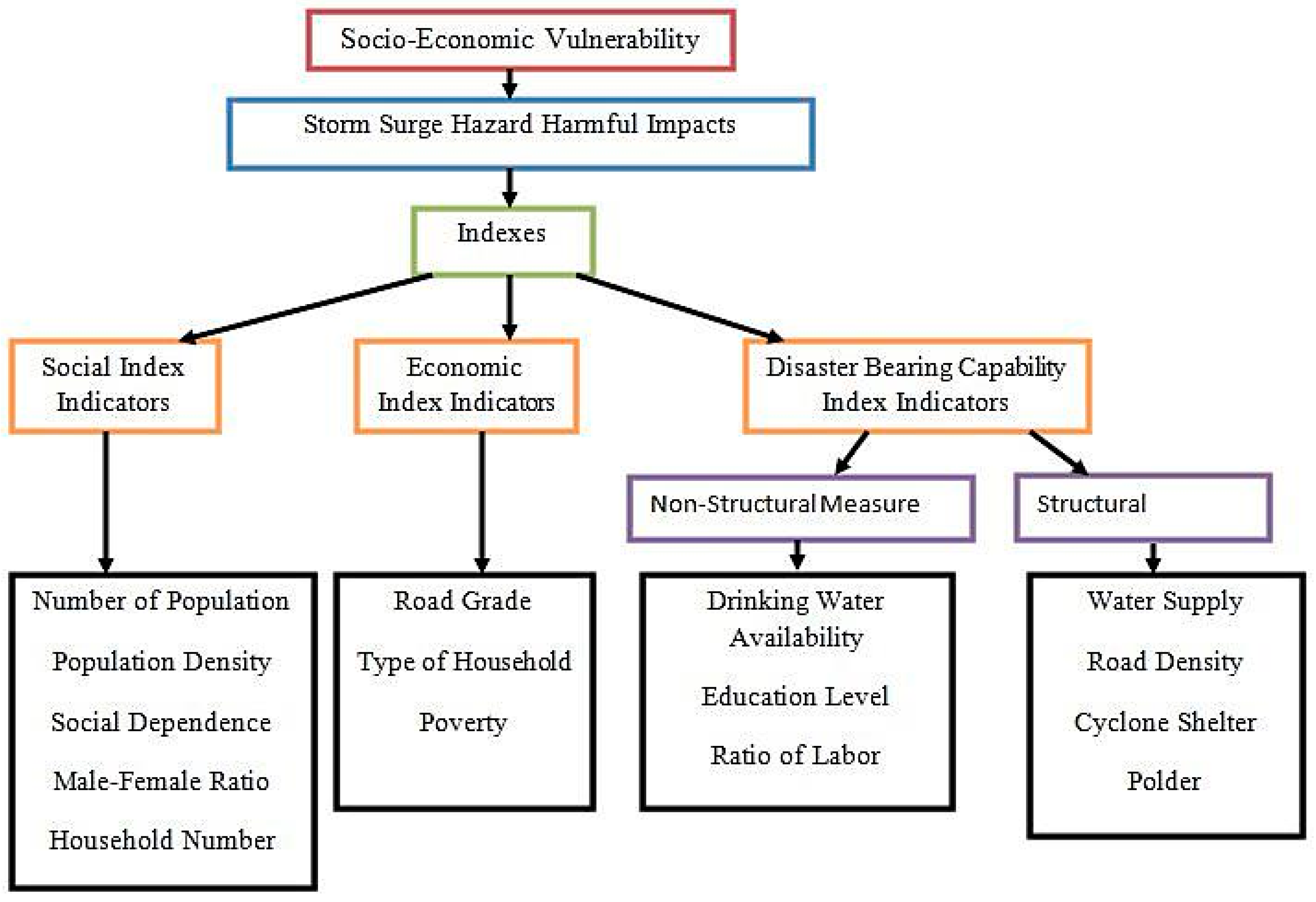
| Domain | Socio-Economic Indicators | Indicator Description | Data Description |
|---|---|---|---|
| Social Index Indicators | Number of population | Populations is susceptible to hazard impacts [30]. | Data source: BBS, 2011. Data unit: Total number of population in each upazila. |
| Number of households | Increased number of households leads to increased risk [31,32] | Data source: BBS, 2011. Data unit: Percentage of number of households per unit upazila area (square kilometer). | |
| Population density | Denser population increases risk due to lack of quality housing and social services network, which may not have had time to adjust with the population demand [32,33] | Data source: BBS, 2011. Data unit: Number of population per unit upazila area (square kilometer). | |
| Female to male ratio | Female to male ratio has impact on vulnerability; hence it increases risk as female population are more vulnerable than male population. | Data source: BBS, 2011. Data unit: ratio of female to male population | |
| Social dependence | Children and elders are the most vulnerable groups in hazards [34] Children, especially in the youngest age groups, cannot protect themselves during disasters like storm surges [35] because they lack the necessary resources, knowledge, or life experiences to effectively cope with the situation [36]. | Data source: BBS, 2011. Data unit: Percentage of summation of women, children under the age of 18, and elderly people to the total upazila population. | |
| Economic Index Indicators | Poverty rate | Poverty rate has serious impact on vulnerability. Higher poverty rate results in higher vulnerability. Poverty level generally indicates the social status, standard, and dignity [37]. | Data source: World bank report, 2010. Data unit: Percentage of extreme poor lying below poverty line. |
| Type of household | A stronger house, like a packa and semi packa house, reduces risk, whereas a weak and unoccupied house, like a kutcha and jhupri house, amplify risk [25,32]. | Data source: BBS, 2011. Data unit: Percentage of Kutcha and Jhupri house per upazila. Here Kutcha and Jhupri means houses made with timber, log, and tree leaf. | |
| Road grade | Road grade indicates the various types and classes of roads. It symbolizes the economic condition in such a way, where there are various types and classes of roads, regions are very much capable of handling all types of facilities because of having transportability [38]. | Data source: BBS, 2011. Data unit: Percentage of metaled and semi-metaled road length to total length of road per upazila. | |
| Disaster Bearing Capability Index Indicators (structural measures) | Water supply | Where there is a suitable water supply, higher road density, large number of cyclone shelter and embankments, the resilience will increase [39]. | Data source: BBS, 2011. Data unit: Percentage of tap water and other pond type surface water per upazila area |
| Cyclone shelter | Cyclone shelter is a structural measure that increases resiliency of a community to cope up with the adverse consequences of storm surge hazard [32,40]. Shelters and households have direct impacts on storm surge hazard [34]. | Data source: CEGIS, 2009. Data unit: Number of cyclone shelters per upazila population. | |
| Polder embankment | Polder is a flood control embankment, which is considered as a structural adaptation to reduce flood risk [32,41]. | Data source: BWDB, 2012. Data unit: Percentage of total poldered area (km2) per upazila area. | |
| Road density | Significant amount of road density ensures improved mobility/accessibility to services. It increases coping capacity of a community in case of any hazard occurrence. | Data source: BBS. Data unit: Road length per upazila area. | |
| Disaster Bearing Capability Index Indicators (non-structural measures) | Education level | Illiterate people are more vulnerable than literate people [25,31,32,33]. | Data source: BBS, 2011. Data unit: Percentage of number of literate people per upazila population. |
| Drinking water availability | When higher percentage of households drink unsafe water (tap, pond, and other open water), risk is increased [25,31,32,33]. | Data Source: BBS, 2011. Data Unit: Percentage of safe drinking water source to total population per upazila population. | |
| Labor ratio | Employed populations are less vulnerable to climatic hazards as they have high capability to cope with the vulnerable situation [42]. | Data source: BBS, 2011. Data unit: Percentage of employed people to total population. |
| Indexes | Largest Eigenvalue | |
|---|---|---|
| Social Index Indicators | 2.955 | |
| Economic Index Indicators | 1.355 | |
| Disaster Bearing Capability Index Indicators | Non-Structural Measure | Structural Measure |
| 1.930 | 1.599 | |
| Socio-Economic Indicators | MSF | Explicit Weighting | Statistical Weighting | ||
|---|---|---|---|---|---|
| Equal Weighting | Expert Weighting | PCA | AHP | ||
| Social Index | |||||
| No. of Population | 16.42 | 20 | 15 | 13.65 | 9.84 |
| Population Density | 25.07 | 20 | 25 | 24.32 | 19.15 |
| Male–Female Ratio | 24.65 | 20 | 10 | 19.60 | 25.95 |
| Social Dependence | 8.47 | 20 | 20 | 15.16 | 25.87 |
| Household Number | 25.39 | 20 | 30 | 27.27 | 19.19 |
| Economic Index | |||||
| Type of Household | 48.34 | 33.33 | 50 | 33.33 | 70.40 |
| Road Grade | 3.85 | 33.33 | 20 | 29.34 | 0.32 |
| Poverty | 47.81 | 33.33 | 30 | 37.33 | 29.28 |
| Disaster Bearing Capability Index | |||||
| Structural Measure | |||||
| Water Supply | 39.84 | 25 | 10 | 37.33 | 14.25 |
| Road Density | 37.78 | 25 | 25 | 8.12 | 3.26 |
| Cyclone shelter | 11.80 | 25 | 30 | 12.57 | 7.76 |
| Polder | 10.58 | 25 | 35 | 41.98 | 74.73 |
| Non-Structural Measure | |||||
| Drinking Water Availability | 14.36 | 33.33 | 30 | 18.76 | 42.58 |
| Education Level | 42.16 | 33.33 | 50 | 40.21 | 33.53 |
| Labor Ratio | 43.48 | 33.33 | 20 | 41.03 | 23.89 |
| Weighting Method | Similarity in Percentage with Hazard Map | ||
|---|---|---|---|
| Exactly-Similar | Partly-Similar | Not-Similar | |
| MSF | 49 | 27 | 24 |
| Equal Weighting | 41 | 31 | 28 |
| Expert Opinion | 42 | 29 | 29 |
| PCA | 47 | 25 | 28 |
| AHP | 35 | 41 | 24 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kabir, R.; Akter, M.; Karim, D.S.; Haque, A.; Rahman, M.; Sakib, M. Development of a Matrix Based Statistical Framework to Compute Weight for Composite Hazards, Vulnerability and Risk Assessments. Climate 2019, 7, 56. https://doi.org/10.3390/cli7040056
Kabir R, Akter M, Karim DS, Haque A, Rahman M, Sakib M. Development of a Matrix Based Statistical Framework to Compute Weight for Composite Hazards, Vulnerability and Risk Assessments. Climate. 2019; 7(4):56. https://doi.org/10.3390/cli7040056
Chicago/Turabian StyleKabir, Rubaiya, Marin Akter, Dewan Sadia Karim, Anisul Haque, Munsur Rahman, and Mohiuddin Sakib. 2019. "Development of a Matrix Based Statistical Framework to Compute Weight for Composite Hazards, Vulnerability and Risk Assessments" Climate 7, no. 4: 56. https://doi.org/10.3390/cli7040056
APA StyleKabir, R., Akter, M., Karim, D. S., Haque, A., Rahman, M., & Sakib, M. (2019). Development of a Matrix Based Statistical Framework to Compute Weight for Composite Hazards, Vulnerability and Risk Assessments. Climate, 7(4), 56. https://doi.org/10.3390/cli7040056





