Modeling Hydrological Response to Climate Change in a Data-Scarce Glacierized High Mountain Astore Basin Using a Fully Distributed TOPKAPI Model
Abstract
1. Introduction
2. Materials and Methods
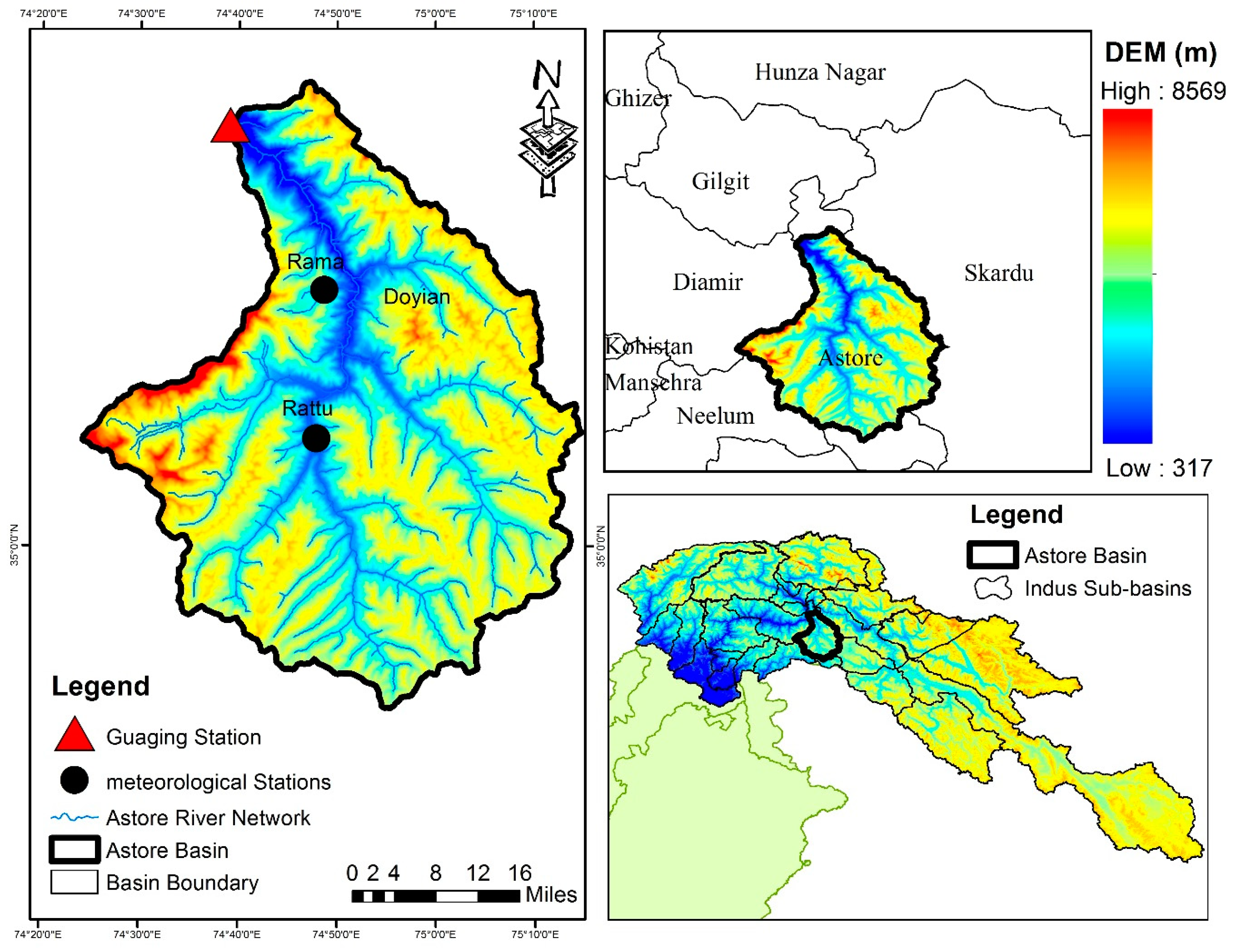
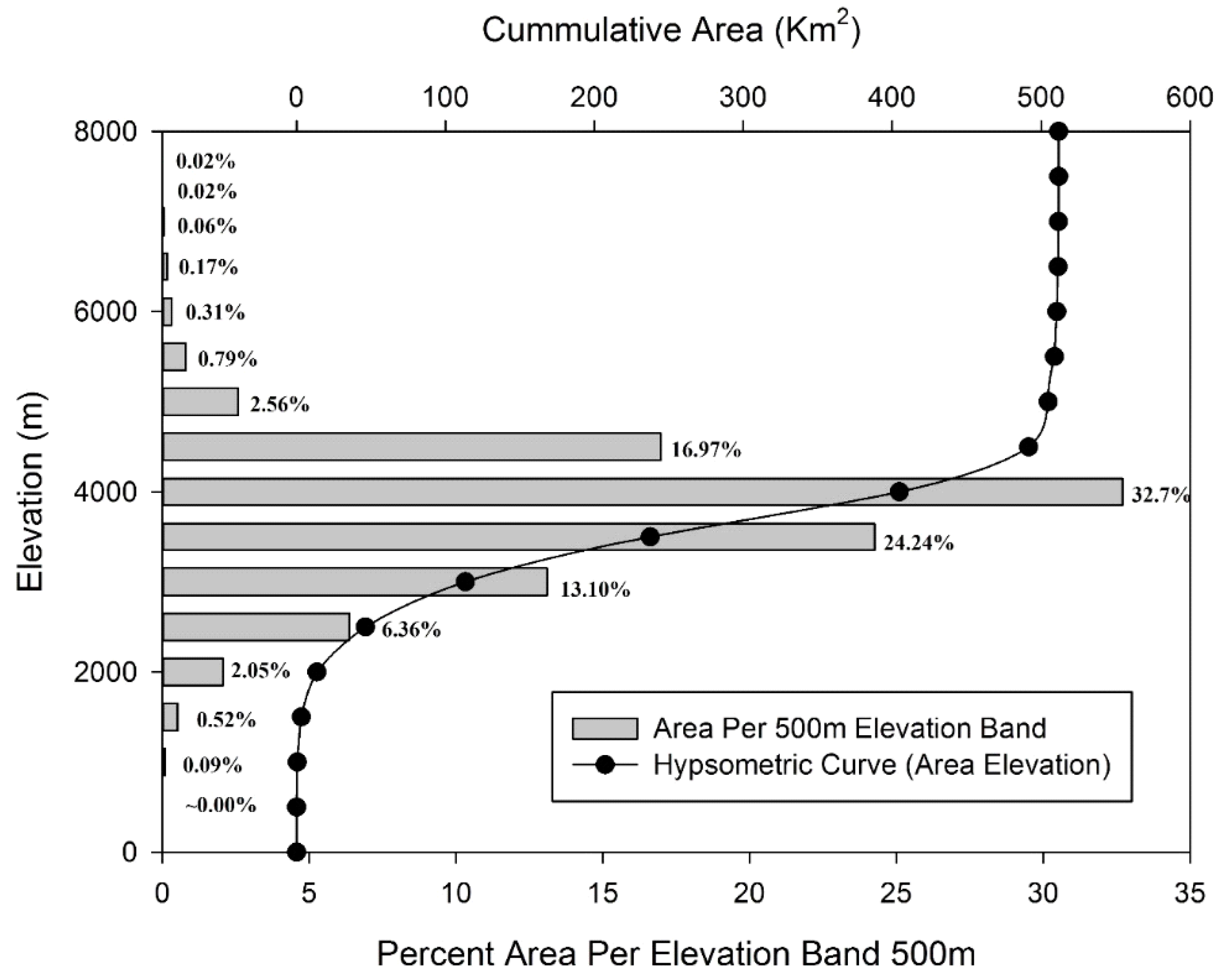
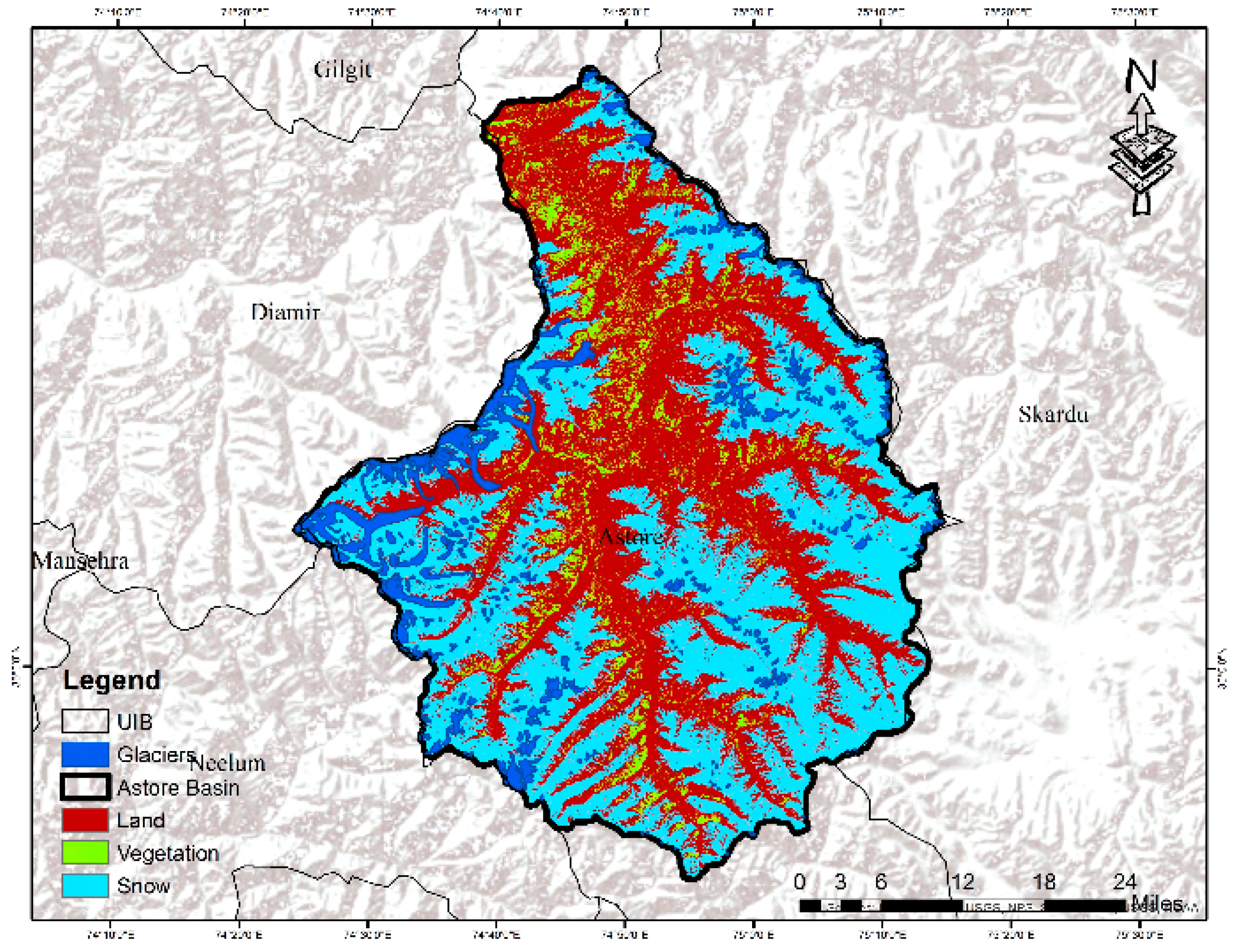
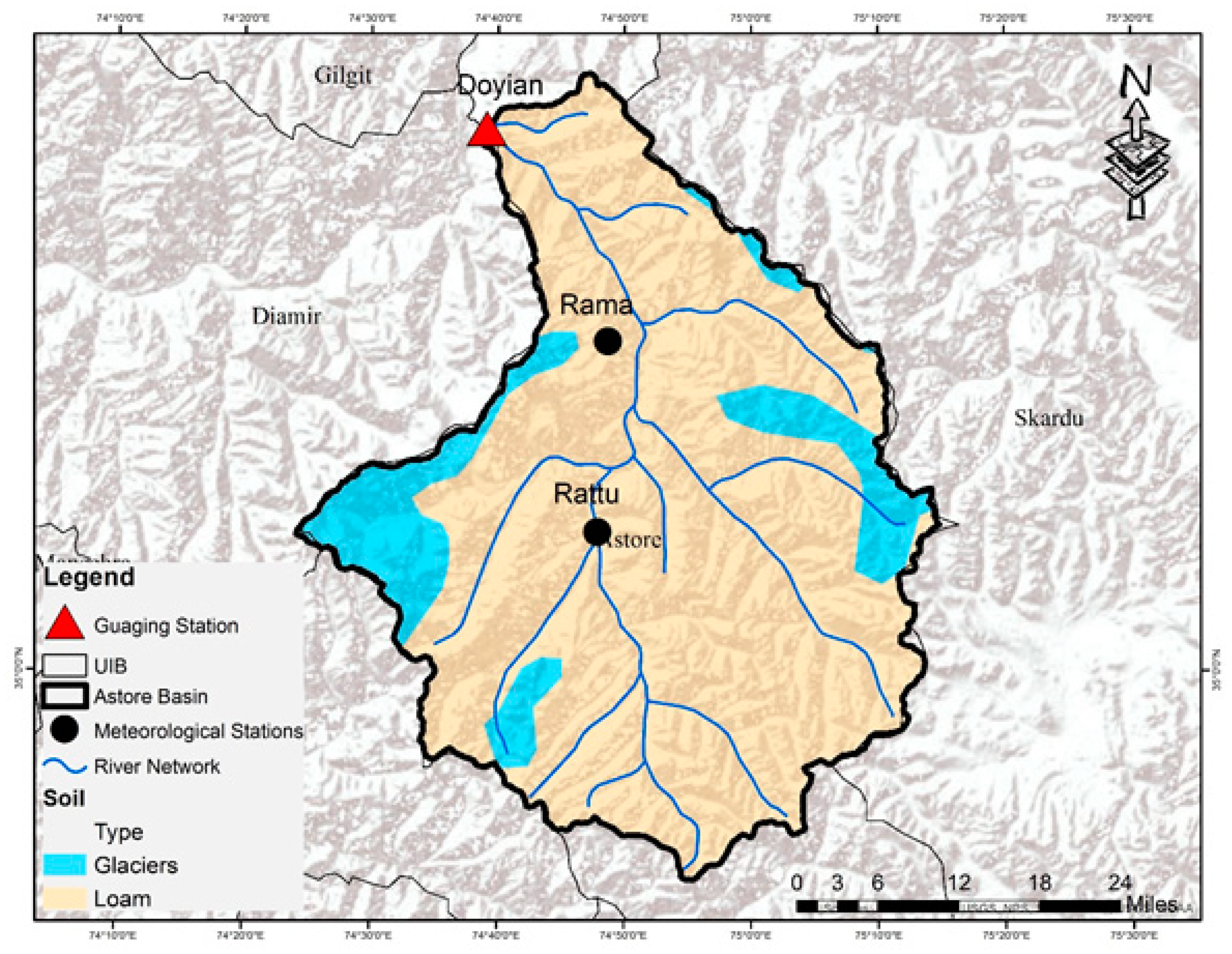
2.1. Study Area
2.2. TOPKAPI Model
2.3. Data Input to Model
Future Climate Projection Data
2.4. Sensitivity Analysis of the Model Parameters
Model Calibration and Validation
3. Results and Discussion
3.1. Model Calibration
3.2. Model Validation
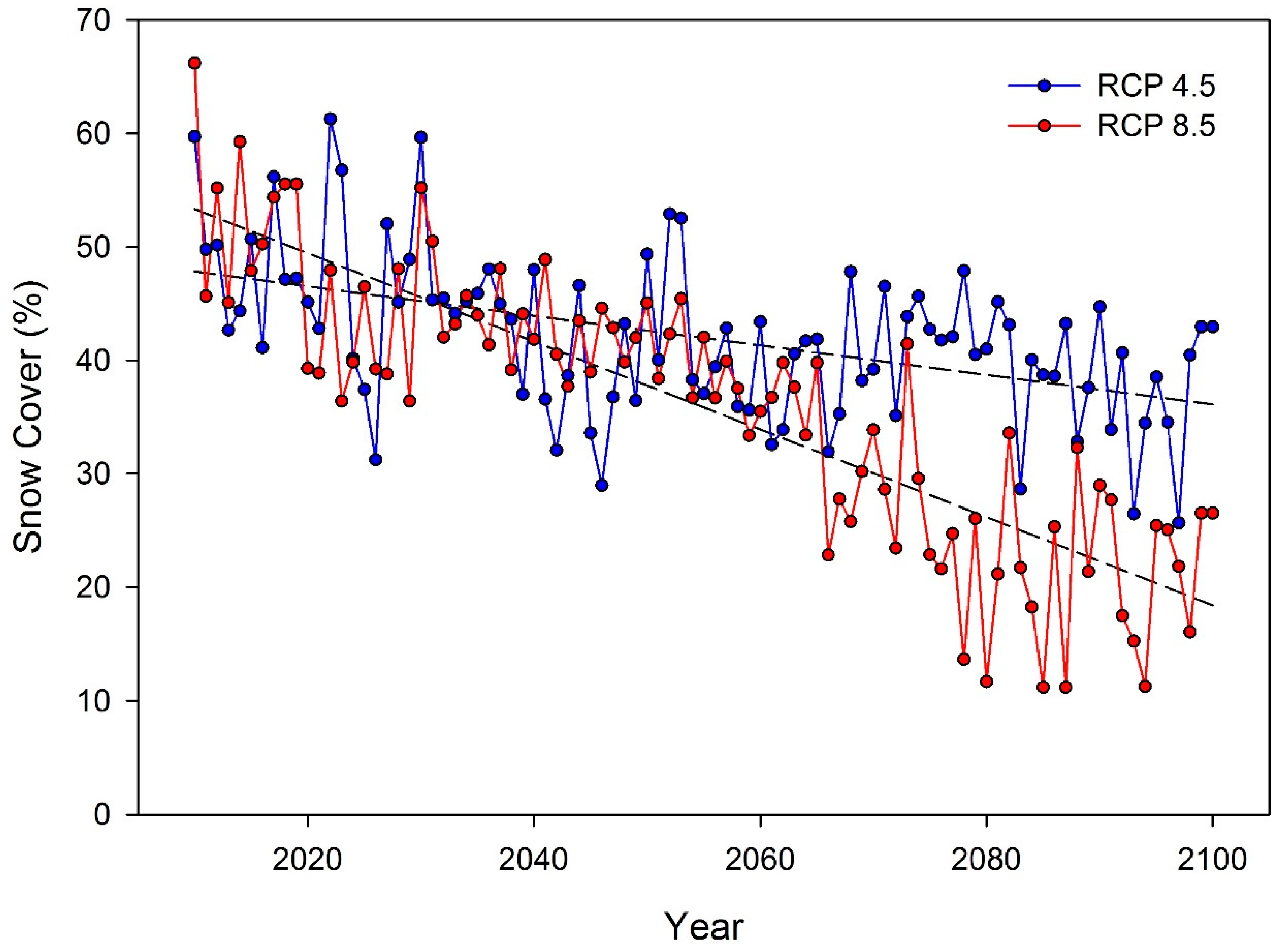
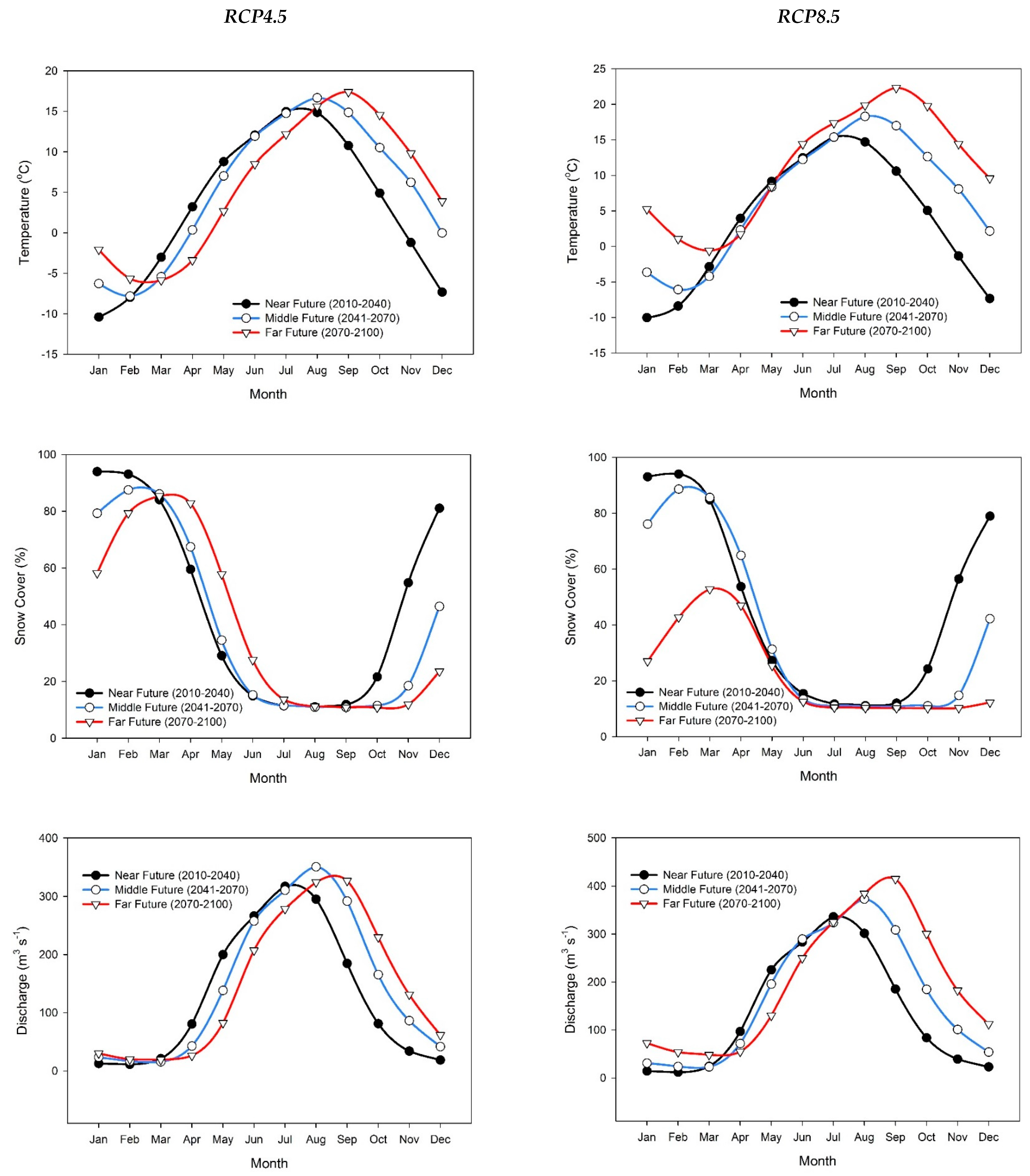
3.3. Future Climate Projections (2010–2100)
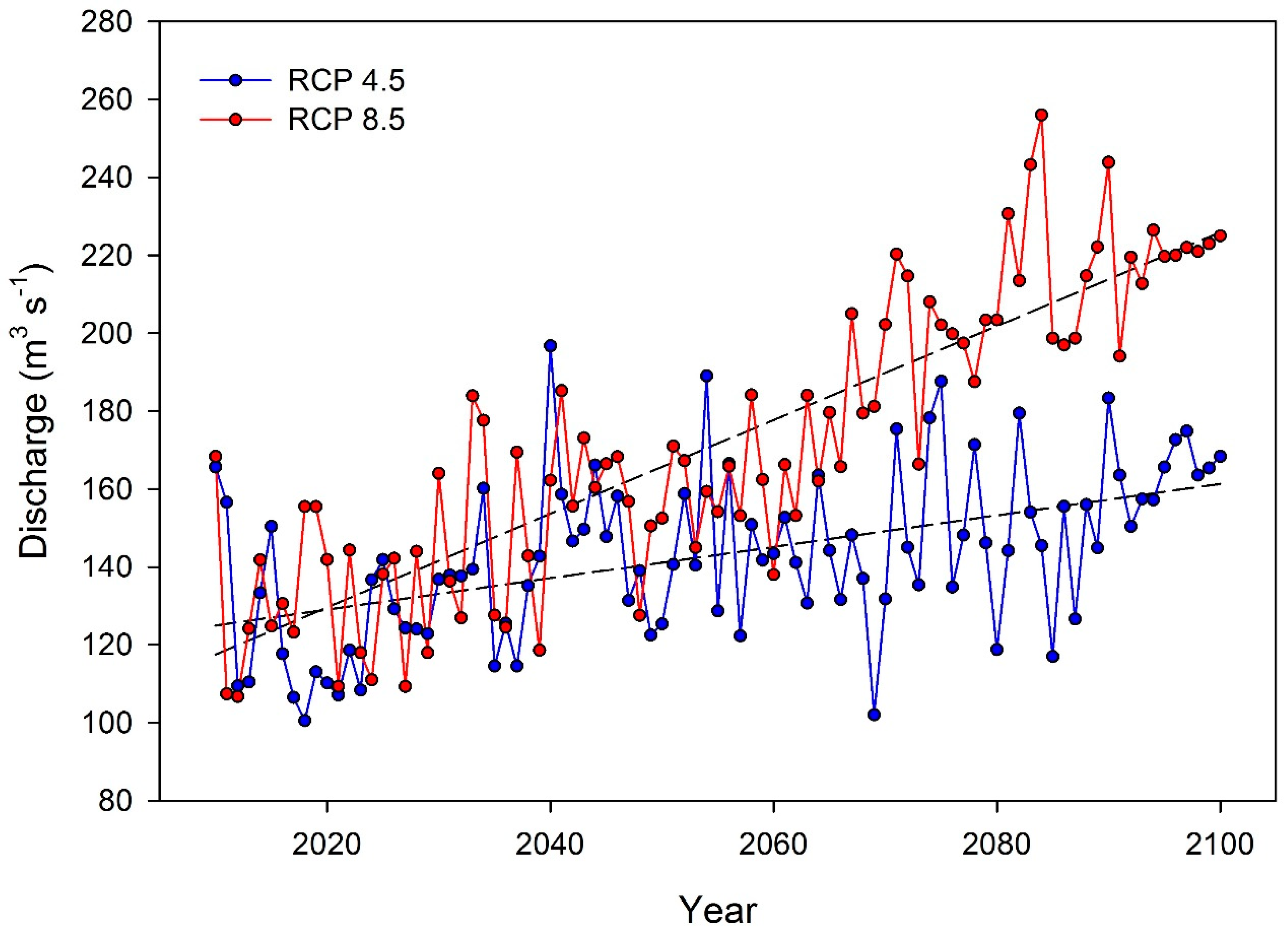
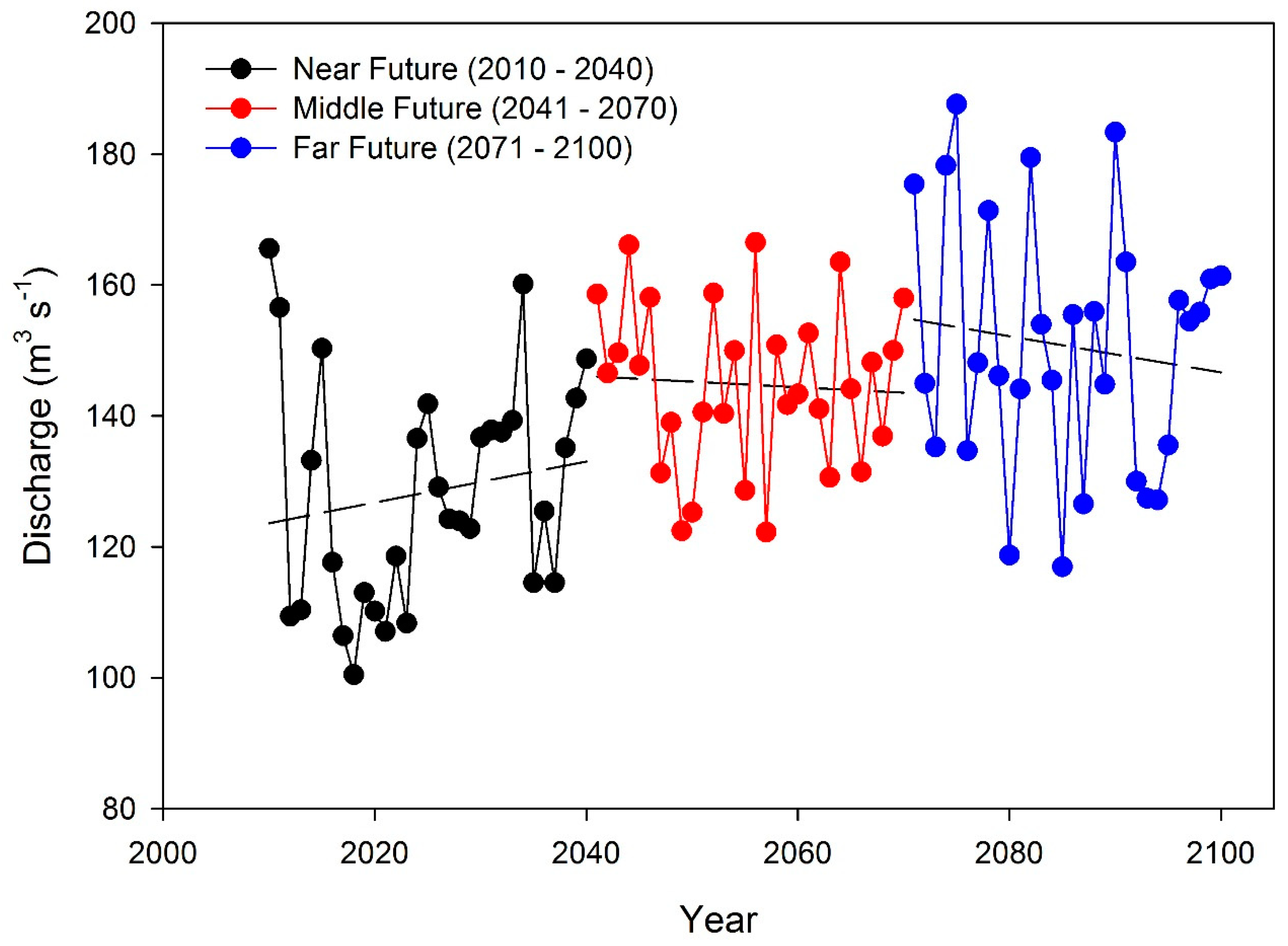
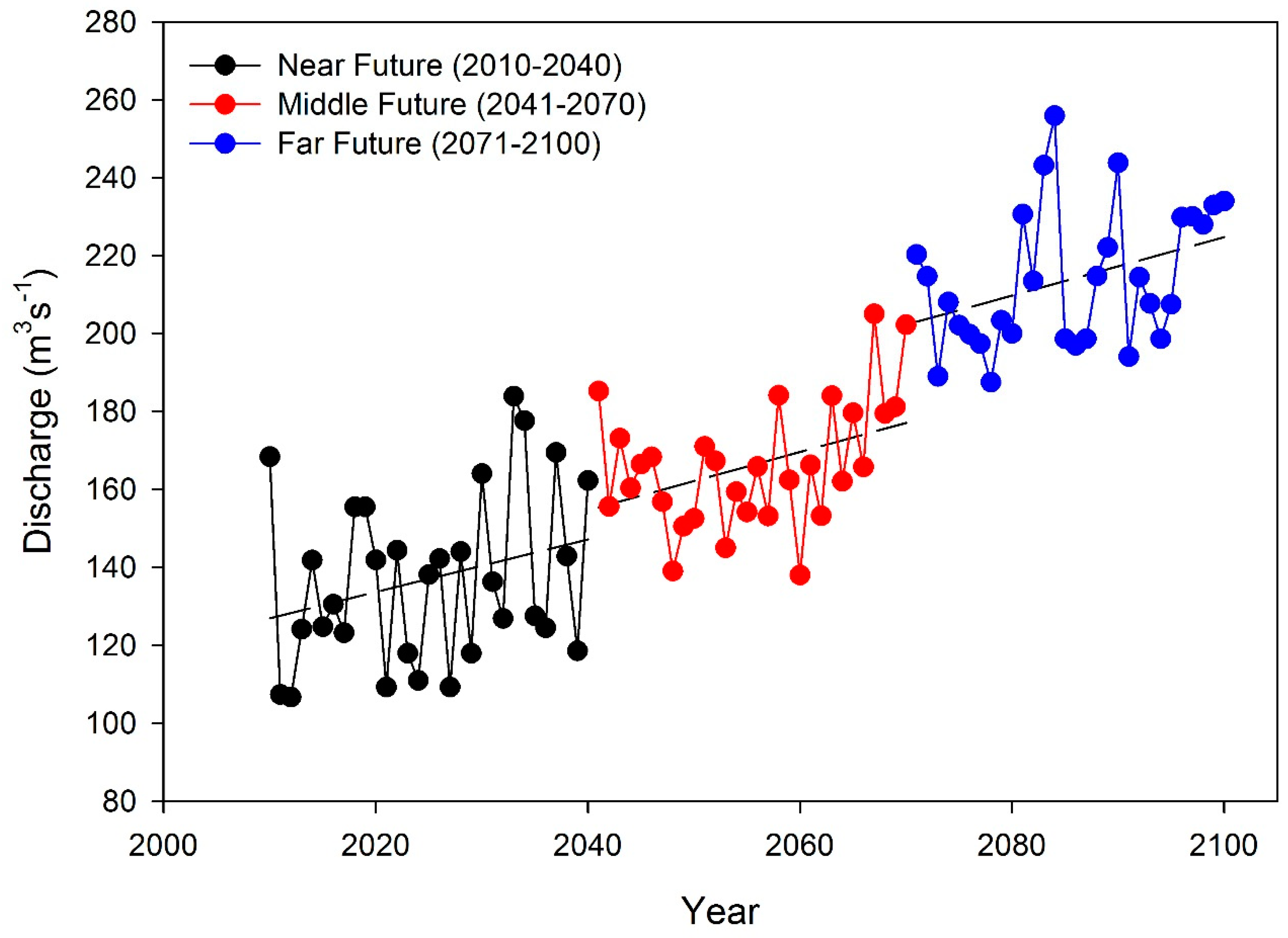
3.4. Future (2010–2100) Hydrological Flows Trend
3.5. Pattern of Hydroclimatic Shift in Astore Basin
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bolch, T.; Kulkarni, A.; Kääb, A.; Huggel, C.; Paul, F.; Cogley, J.; Frey, H.; Kargel, J.S.; Fujita, K.; Scheel, M. The state and fate of Himalayan glaciers. Science 2012, 336, 310–314. [Google Scholar] [CrossRef] [PubMed]
- Kapnick, S.B.; Delworth, T.L.; Ashfaq, M.; Malyshev, S.; Milly, P.C. Snowfall less sensitive to warming in Karakoram than in Himalayas due to a unique seasonal cycle. Nat. Geosci. 2014, 7, 834. [Google Scholar] [CrossRef]
- Cannon, F.; Carvalho, L.M.; Jones, C.; Bookhagen, B. Multi-annual variations in winter westerly disturbance activity affecting the Himalaya. Clim. Dyn. 2015, 44, 441–455. [Google Scholar] [CrossRef]
- Berghuijs, W.; Woods, R.; Hrachowitz, M. A precipitation shift from snow towards rain leads to a decrease in streamflow. Nat. Clim. Chang. 2014, 4, 583. [Google Scholar] [CrossRef]
- Adnan, M.; Nabi, G.; Poomee, M.S.; Ashraf, A. Snowmelt runoff prediction under changing climate in the Himalayan cryosphere: A case of Gilgit River Basin. Geosci. Front. 2017, 8, 941–949. [Google Scholar] [CrossRef]
- Ahmed, M. Democracy and Corruption. 2018. Available online: https://dailytimes.com.pk/246272/democracy-and-corruption/ (accessed on 11 July 2018).
- Tahir, A.A.; Chevallier, P.; Arnaud, Y.; Neppel, L.; Ahmad, B. Modeling snowmelt-runoff under climate scenarios in the Hunza River basin, Karakoram Range, Northern Pakistan. J. Hydrol. 2011, 409, 104–117. [Google Scholar] [CrossRef]
- Akhtar, M.; Ahmad, N.; Booij, M.J. The impact of climate change on the water resources of Hindukush–Karakorum–Himalaya region under different glacier coverage scenarios. J. Hydrol. 2008, 355, 148–163. [Google Scholar] [CrossRef]
- Bookhagen, B.; Burbank, D.W. Toward a complete Himalayan hydrological budget: Spatiotemporal distribution of snowmelt and rainfall and their impact on river discharge. J. Geophys. Res. Earth Surf. 2010, 115, F3. [Google Scholar] [CrossRef]
- Mahmood, R.; Jia, S.; Babel, M.S. Potential impacts of climate change on water resources in the Kunhar River Basin, Pakistan. Water 2016, 8, 23. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Wagener, T.; Tallaksen, L.; Engeland, K. Evaluation of nine large-scale hydrological models with respect to the seasonal runoff climatology in Europe. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Rees, H.G.; Collins, D.N. Regional differences in response of flow in glacier-fed Himalayan rivers to climatic warming. Hydrol. Process. Int. J. 2006, 20, 2157–2169. [Google Scholar] [CrossRef]
- Beven, K.J. Uniqueness of place and process representations in hydrological modelling. Hydrol. Earth Syst. Sci. Discuss. 2000, 4, 203–213. [Google Scholar] [CrossRef]
- Liu, Z.; Martina, M.L.; Todini, E. Flood forecasting using a fully distributed model: Application of the TOPKAPI model to the Upper Xixian Catchment. Hydrol. Earth Syst. Sci. Discuss. 2005, 9, 347–364. [Google Scholar] [CrossRef]
- Liu, Z.; Todini, E. Towards a comprehensive physically-based rainfall-runoff model. Hydrol. Earth Syst. Sci. Discuss. 2002, 6, 859–881. [Google Scholar] [CrossRef]
- Kampf, S.K.; Burges, S.J. A framework for classifying and comparing distributed hillslope and catchment hydrologic models. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Cruz, R.; Harasawa, H.; Lal, M.; Wu, S.; Anokhin, Y.; Punsalmaa, B.; Honda, Y.; Jafari, M.; Li, C.; Huu Ninh, N. Asia. In Climate Change 2007: Impacts, Adaptation and Vulnerability—Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Parry, M.L., Canziani, O.F., Palutikof, J.P., van der Linden, P.J., Hanson, C.E., Eds.; Cambridge University Press: Cambridge, UK, 2007; pp. 469–506. [Google Scholar]
- Immerzeel, W.W.; Droogers, P.; De Jong, S.; Bierkens, M. Large-scale monitoring of snow cover and runoff simulation in Himalayan river basins using remote sensing. Remote Sens. Environ. 2009, 113, 40–49. [Google Scholar] [CrossRef]
- Beniston, M. Climatic change in mountain regions: A review of possible impacts. In Climate Variability and Change in High Elevation Regions: Past, Present & Future; Springer: Berlin, Germany, 2003; pp. 5–31. [Google Scholar]
- Zhang, L.; Su, F.; Yang, D.; Hao, Z.; Tong, K. Discharge regime and simulation for the upstream of major rivers over Tibetan Plateau. J. Geophys. Res. Atmos. 2013, 118, 8500–8518. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhang, S.; Ding, Y.J.; Wang, J.; Han, H.; Xu, J.; Zhao, C.; Guo, W.; Shangguan, D. Modeling hydrologic response to climate change and shrinking glaciers in the highly glacierized Kunma Like River Catchment, Central Tian Shan. J. Hydrometeorol. 2015, 16, 2383–2402. [Google Scholar] [CrossRef]
- Ren, Z.; Su, F.; Xu, B.; Xie, Y.; Kan, B. A Coupled Glacier-Hydrology Model and Its Application in Eastern Pamir. J. Geophys. Res. Atmos. 2018, 123, 13692–13713. [Google Scholar] [CrossRef]
- Archer, D. Contrasting hydrological regimes in the upper Indus Basin. J. Hydrol. 2003, 274, 198–210. [Google Scholar] [CrossRef]
- Fowler, H.; Archer, D. Conflicting signals of climatic change in the Upper Indus Basin. J. Clim. 2006, 19, 4276–4293. [Google Scholar] [CrossRef]
- Singh, P.; Bengtsson, L. Hydrological sensitivity of a large Himalayan basin to climate change. Hydrol. Process. 2004, 18, 2363–2385. [Google Scholar] [CrossRef]
- Arnold, N.; Richards, K.; Willis, I.; Sharp, M. Initial results from a distributed, physically based model of glacier hydrology. Hydrol. Process. 1998, 12, 191–219. [Google Scholar] [CrossRef]
- Hock, R. Glacier melt: A review of processes and their modelling. Prog. Phys. Geogr. 2005, 29, 362–391. [Google Scholar] [CrossRef]
- Devia, G.K.; Ganasri, B.; Dwarakish, G. A review on hydrological models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Freeze, R.A.; Harlan, R. Blueprint for a physically-based, digitally-simulated hydrologic response model. J. Hydrol. 1969, 9, 237–258. [Google Scholar] [CrossRef]
- Paparrizos, S.; Maris, F. Hydrological simulation of Sperchios River basin in Central Greece using the MIKE SHE model and geographic information systems. Appl. Water Sci. 2017, 7, 591–599. [Google Scholar] [CrossRef]
- Bao, H.; Wang, L.; Zhang, K.; Li, Z. Application of a developed distributed hydrological model based on the mixed runoff generation model and 2D kinematic wave flow routing model for better flood forecasting. Atmos. Sci. Lett. 2017, 18, 284–293. [Google Scholar] [CrossRef]
- Kan, G.; Tang, G.; Yang, Y.; Hong, Y.; Li, J.; Ding, L.; He, X.; Liang, K.; He, L.; Li, Z. An improved coupled routing and excess storage (crest) distributed hydrological model and its verification in Ganjiang River Basin, China. Water 2017, 9, 904. [Google Scholar] [CrossRef]
- Ciarapica, L.; Todini, E. TOPKAPI: A model for the representation of the rainfall-runoff process at different scales. Hydrol. Process. 2002, 16, 207–229. [Google Scholar] [CrossRef]
- Ragettli, S.; Pellicciotti, F.; Immerzeel, W.W.; Miles, E.S.; Petersen, L.; Heynen, M.; Shea, J.M.; Stumm, D.; Joshi, S.; Shrestha, A. Unraveling the hydrology of a Himalayan catchment through integration of high resolution in situ data and remote sensing with an advanced simulation model. Adv. Water Resour. 2015, 78, 94–111. [Google Scholar] [CrossRef]
- Ortiz, E.; Guna, V. Distributed hydrological models: Comparison between TOPKAPI, a physically based model and TETIS, a conceptually based model. In Proceedings of the EGU General Assembly 2009, Vienna, Austria, 19–24 April 2009. [Google Scholar]
- Shrestha, M.; Koike, T.; Hirabayashi, Y.; Xue, Y.; Wang, L.; Rasul, G.; Ahmad, G.R.A. Integrated simulation of snow and glacier melt in water and energy balance-based, distributed hydrological modeling framework at Hunza River Basin of Pakistan Karakoram region. JGR 2015, 120, 4889–4919. [Google Scholar] [CrossRef]
- Pellicciotti, F.; Brock, B.; Strasser, U.; Burlando, P.; Funk, M.; Corripio, J. An enhanced temperature-index glacier melt model including the shortwave radiation balance: Development and testing for Haut Glacier d’Arolla, Switzerland. J. Glaciol. 2005, 51, 573–587. [Google Scholar] [CrossRef]
- Pellicciotti, F.; Buergi, C.; Immerzeel, W.W.; Konz, M.; Shrestha, A.B. Challenges and uncertainties in hydrological modeling of remote Hindu Kush–Karakoram–Himalayan (HKH) basins: Suggestions for calibration strategies. Mt. Res. Dev. 2012, 32, 39–50. [Google Scholar] [CrossRef]
- Cogley, J.; Hock, R.; Rasmussen, L.; Arendt, A.; Bauder, A.; Braithwaite, R.; Jansson, P.; Kaser, G.; Möller, M.; Nicholson, L. Glossary of glacier mass balance and related terms. IHP-VII Tech. Doc. Hydrol. 2011, 86, 965. [Google Scholar]
- Kargel, J.S.; Cogley, J.G.; Leonard, G.J.; Haritashya, U.; Byers, A. Himalayan glaciers: The big picture is a montage. Proc. Natl. Acad. Sci. USA 2011, 108, 14709–14710. [Google Scholar] [CrossRef]
- Rango, A. Application of remote sensing methods to hydrology and water resources. Hydrol. Sci. J. 1994, 39, 309–320. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.; Yan, G.; Zhang, X. A review of current methodologies for regional evapotranspiration estimation from remotely sensed data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef]
- Tang, Q.; Gao, H.; Lu, H.; Lettenmaier, D.P. Remote sensing: Hydrology. Prog. Phys. Geogr. 2009, 33, 490–509. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J. Satellite remote sensing applications for surface soil moisture monitoring: A review. Front. Earth Sci. China 2009, 3, 237–247. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M. Retrieving leaf area index (LAI) using remote sensing: Theories, methods and sensors. Sensors 2009, 9, 2719–2745. [Google Scholar] [CrossRef] [PubMed]
- Dietz, A.J.; Kuenzer, C.; Gessner, U.; Dech, S. Remote sensing of snow—A review of available methods. Int. J. Remote Sens. 2012, 33, 4094–4134. [Google Scholar] [CrossRef]
- Skoulikaris, C.; Filali-Meknassi, Y.; Aureli, A.; Amani, A.; Jiménez-Cisneros, B.E. Information-Communication Technologies as an Integrated Water Resources Management (IWRM) Tool for Sustainable Development. Achiev. Chall. Integr. River Basin Manag. 2018, 179–181. [Google Scholar]
- Afshan, N.; Khalid, A.; Iqbal, S.; Niazi, A.; Sultan, A. Puccinia subepidermalis sp. nov. and new records of rust fungi from Fairy Meadows, Northern Pakistan. Mycotaxon 2009, 110, 173–182. [Google Scholar] [CrossRef]
- Finger, D.; Pellicciotti, F.; Konz, M.; Rimkus, S.; Burlando, P. The value of glacier mass balance, satellite snow cover images, and hourly discharge for improving the performance of a physically based distributed hydrological model. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Todini, E. The ARNO rainfall—Runoff model. J. Hydrol. 1996, 175, 339–382. [Google Scholar] [CrossRef]
- Atif, I.; Mahboob, M.A.; Iqbal, J. Snow cover area change assessment in 2003 and 2013 using MODIS data of the Upper Indus Basin, Pakistan. J. Himal. Earth Sci. 2015, 48. [Google Scholar]
- Atif, I.; Iqbal, J.; Mahboob, M.A. Modelling semi-automated delineation of supra-glacial debris and clean ice glacial changes of shigar basin. Geosciences 2016, 9, 259. [Google Scholar]
- Farjad, B.; Gupta, A.; Sartipizadeh, H.; Cannon, A. A novel approach for selecting extreme climate change scenarios for climate change impact studies. Sci. Total Environ. 2019, 678, 476–485. [Google Scholar] [CrossRef]
- Lazoglou, G.; Anagnostopoulou, C.; Skoulikaris, C.; Tolika, K. Bias Correction of Climate Model’s Precipitation Using the Copula Method and Its Application in River Basin Simulation. Water 2019, 11, 600. [Google Scholar] [CrossRef]
- Wood, A.W.; Leung, L.R.; Sridhar, V.; Lettenmaier, D. Hydrologic implications of dynamical and statistical approaches to downscaling climate model outputs. Clim. Chang. 2004, 62, 189–216. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Van Beek, L.; Konz, M.; Shrestha, A.; Bierkens, M. Hydrological response to climate change in a glacierized catchment in the Himalayas. Clim. Chang. 2012, 110, 721–736. [Google Scholar] [CrossRef] [PubMed]
- Ross, P.J. SWIM: A Simulation Model for Soil Water Infiltration and Movement: Reference Manual; CSIRO: Canberra, Australia, 1990. [Google Scholar]
- Coccia, G.; Mazzetti, C.; Ortiz, E.A.; Todini, E. Application of the topkapi model within the dmip 2 project. In Proceedings of the 23rd Conference on Hydrology, San Antonio, TX, USA, 10–12 January 2009. [Google Scholar]
- Veith, T.; Ghebremichael, L. How to: Applying and interpreting the SWAT auto-calibration tools. In Proceedings of the 2009 International SWAT Conference, Boulder, CO, USA, 5–7 August 2009. [Google Scholar]
- Silvestro, F.; Gabellani, S.; Rudari, R.; Delogu, F.; Laiolo, P.; Boni, G. Uncertainty reduction and parameter estimation of a distributed hydrological model with ground and remote-sensing data. Hydrol. Earth Syst. Sci. 2015, 19, 1727–1751. [Google Scholar] [CrossRef]
- Vieux, B.E.; Cui, Z.; Gaur, A. Evaluation of a physics-based distributed hydrologic model for flood forecasting. J. Hydrol. 2004, 298, 155–177. [Google Scholar] [CrossRef]
- Vieux, B.E.; Moreda, F.G. Ordered Physics-Based Parameter Adjustment of a Distributed. Calibration Watershed Models 2003, 267. [Google Scholar] [CrossRef]
- Looper, J.P.; Vieux, B.E. An assessment of distributed flash flood forecasting accuracy using radar and rain gauge input for a physics-based distributed hydrologic model. J. Hydrol. 2012, 412, 114–132. [Google Scholar] [CrossRef]
- Tolson, B.A.; Shoemaker, C.A. Dynamically dimensioned search algorithm for computationally efficient watershed model calibration. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.; Van Griensven, A.; Van Liew, M.W. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Sadegh, M.; Majd, M.S.; Hernandez, J.; Haghighi, A.T. The Quest for Hydrological Signatures: Effects of Data Transformation on Bayesian Inference of Watershed Models. Water Resour. Manag. 2018, 32, 1867–1881. [Google Scholar] [CrossRef]
- Kim, J.; Ryu, J.H. Quantifying the performances of the semi-distributed hydrologic model in parallel computing—A case study. Water 2019, 11, 823. [Google Scholar] [CrossRef]
- Ritter, A.; Muñoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Coffey, M.E.; Workman, S.R.; Taraba, J.L.; Fogle, A.W. Statistical procedures for evaluating daily and monthly hydrologic model predictions. Trans. ASAE 2004, 47, 59. [Google Scholar] [CrossRef]
- Doorenbos, J. Guidelines for Predicting Crop Water Requirements; FAO: Rome, Italy, 1975. [Google Scholar]
- Chow, V.; Maidment, D.; Mays, L. Applied Hydrology—Series in Water Resources and Environmental Engineering; McGraw-Hill Inc.: New York, NY, USA, 1988. [Google Scholar]
- Wechsler, S.P.; Kroll, C.N. Quantifying DEM uncertainty and its effect on topographic parameters. Photogramm. Eng. Remote Sens. 2006, 72, 1081–1090. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Lutz, A.F.; Immerzeel, W.; Kraaijenbrink, P.; Shrestha, A.B.; Bierkens, M.F. Climate change impacts on the upper Indus hydrology: Sources, shifts and extremes. PLoS ONE 2016, 11, e0165630. [Google Scholar] [CrossRef]
- Atif, I.; Iqbal, J.; Mahboob, M.A. Investigating Snow Cover and Hydrometeorological Trends in Contrasting Hydrological Regimes of the Upper Indus Basin. Atmosphere 2018, 9, 162. [Google Scholar] [CrossRef]
- Latif, Y.; Yaoming, M.; Yaseen, M. Spatial analysis of precipitation time series over the Upper Indus Basin. Theor. Appl. Climatol. 2018, 131, 761–775. [Google Scholar] [CrossRef]
- Baig, S.U.; Khan, H.; Din, A. Spatio-temporal analysis of glacial ice area distribution of Hunza River Basin, Karakoram region of Pakistan. Hydrol. Process. 2018, 32, 1491–1501. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Bair, E.H.; Rittger, K.; Davis, R.E.; Painter, T.H.; Dozier, J. Validating reconstruction of snow water equivalent in California’s Sierra Nevada using measurements from the NASA Airborne Snow Observatory. Water Resour. Res. 2016, 52, 8437–8460. [Google Scholar] [CrossRef]
- Derksen, C.; Walker, A.; Goodison, B. A comparison of 18 winter seasons of in situ and passive microwave-derived snow water equivalent estimates in Western Canada. Remote Sens. Environ. 2003, 88, 271–282. [Google Scholar] [CrossRef]
- Rajbhandari, R.; Shrestha, A.; Kulkarni, A.; Patwardhan, S.; Bajracharya, S. Projected changes in climate over the Indus river basin using a high resolution regional climate model (PRECIS). Clim. Dyn. 2015, 44, 339–357. [Google Scholar] [CrossRef]
- Ul Islam, S.; Rehman, N.; Sheikh, M.M. Future change in the frequency of warm and cold spells over Pakistan simulated by the PRECIS regional climate model. Clim. Chang. 2009, 94, 35–45. [Google Scholar] [CrossRef]
- Forsythe, N.; Kilsby, C.G.; Fowler, H.J.; Archer, D.R. Assessment of runoff sensitivity in the Upper Indus Basin to interannual climate variability and potential change using MODIS satellite data products. Mt. Res. Dev. 2012, 32, 16–29. [Google Scholar] [CrossRef]
- Romshoo, S.A.; Dar, R.A.; Rashid, I.; Marazi, A.; Ali, N.; Zaz, S.N. Implications of shrinking cryosphere under changing climate on the streamflows in the Lidder catchment in the Upper Indus Basin, India. Arct. Antarct. Alp. Res. 2015, 47, 627–644. [Google Scholar] [CrossRef]
- Boyce, B. Investigation of Hydrometeorological Relationships, Pasu Glacier Basin, Northern Pakistan. Ph.D. Thesis, Wilfrid Laurier University, Waterloo, ON, Canada, 1992. [Google Scholar]
- Soncini, A.; Bocchiola, D.; Confortola, G.; Bianchi, A.; Rosso, R.; Mayer, C.; Lambrecht, A.; Palazzi, E.; Smiraglia, C.; Diolaiuti, G. Future hydrological regimes in the upper indus basin: A case study from a high-altitude glacierized catchment. J. Hydrometeorol. 2015, 16, 306–326. [Google Scholar] [CrossRef]
- Rasul, G.; Dahe, Q.; Chaudhry, Q. Global warming and melting glaciers along southern slopes of HKH ranges. Pak. J. Meteorol. 2008, 5, 9. [Google Scholar]
- Prudhomme, C.; Giuntoli, I.; Robinson, E.L.; Clark, D.B.; Arnell, N.W.; Dankers, R.; Fekete, B.M.; Franssen, W.; Gerten, D.; Gosling, S.N. Hydrological droughts in the 21st century, hotspots and uncertainties from a global multimodel ensemble experiment. Proc. Natl. Acad. Sci. USA 2014, 111, 3262–3267. [Google Scholar] [CrossRef] [PubMed]
- Zweifel, A.; Sevruk, B. Comparative accuracy of solid precipitation measurement using heated recording gauges in the Alps. In Proceedings of the WCRP Workshop on Determination of Solid Precipitation in Cold Climate Regions, Fairbanks, AK, USA, 9–12 June 2002. [Google Scholar]
- Hewitt, K. Glacier change, concentration, and elevation effects in the Karakoram Himalaya, Upper Indus Basin. Mt. Res. Dev. 2011, 31, 188–201. [Google Scholar] [CrossRef]
- Burhan, A.; Waheed, I.; Syed, A.; Rasul, G.; Shreshtha, A.; Shea, J.; Change, C. Generation of high-resolution gridded climate fields for the upper Indus River Basin by downscaling CMIP5 outputs. J. Earth Sci. Clim. Chang. 2015, 6, 1. [Google Scholar]
- Hawkins, E.; Osborne, T.M.; Ho, C.K.; Challinor, A.; Meteorology, F. Calibration and bias correction of climate projections for crop modelling: An idealised case study over Europe. Agric. For. Meteorol. 2013, 170, 19–31. [Google Scholar] [CrossRef]

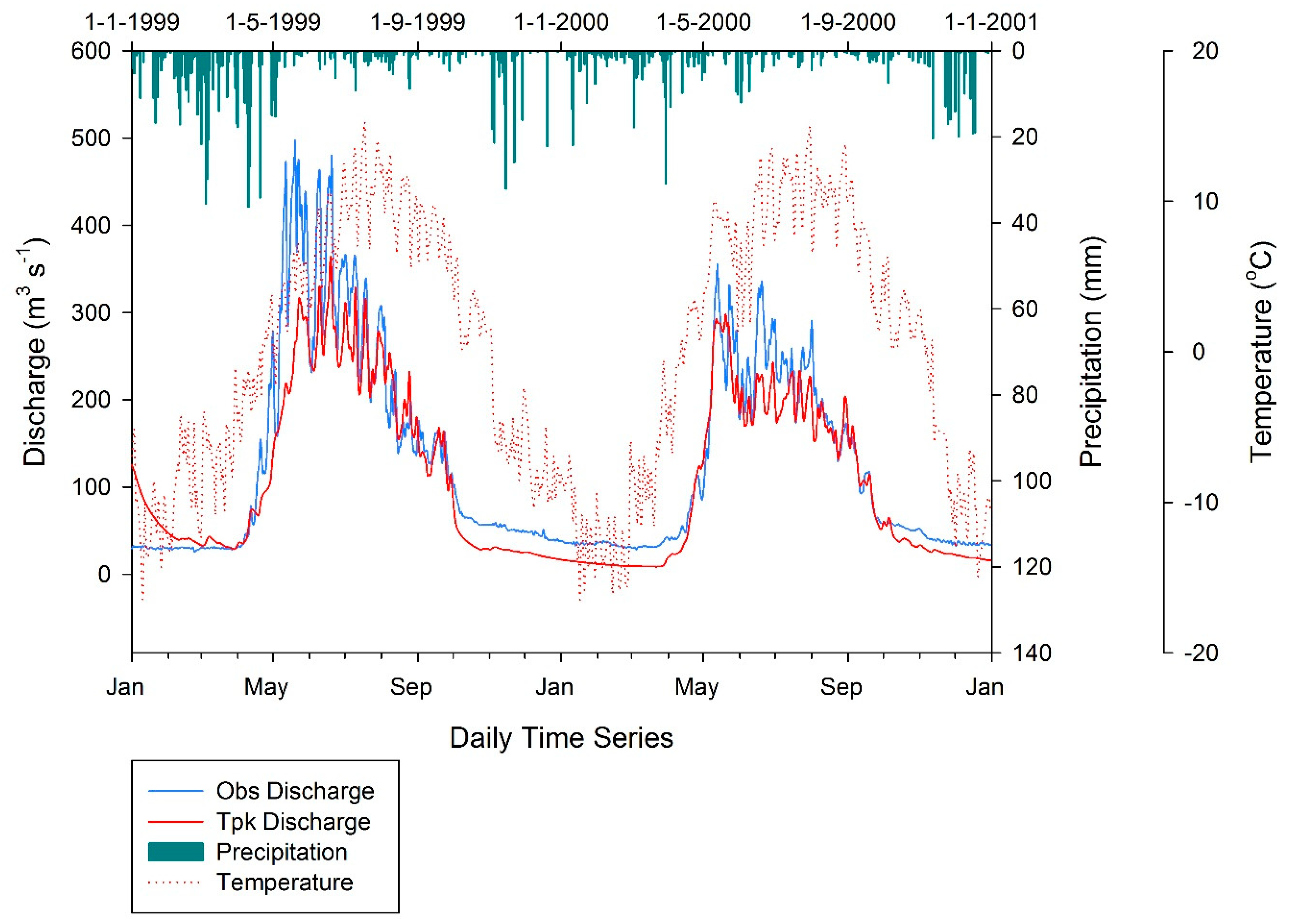
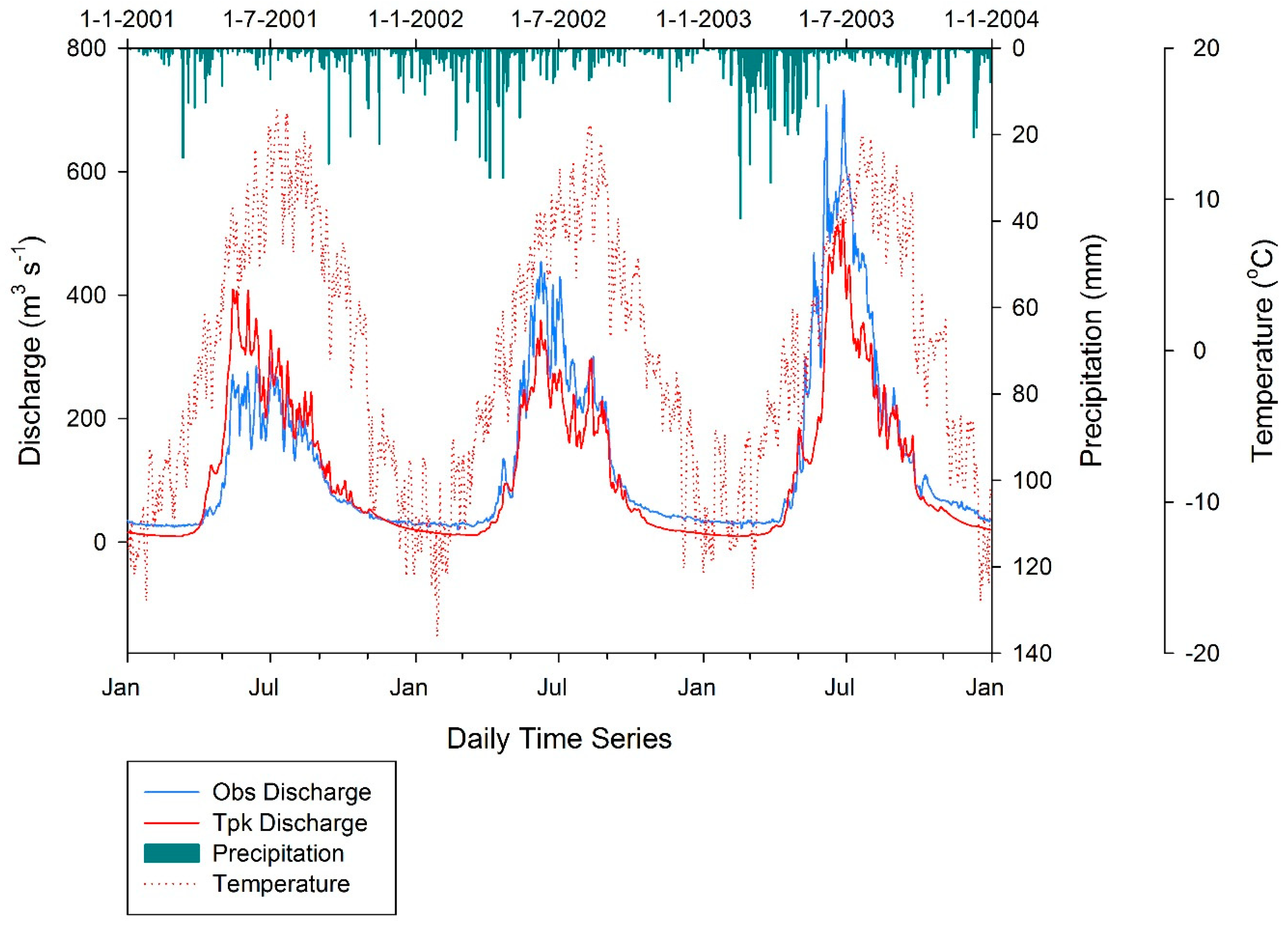
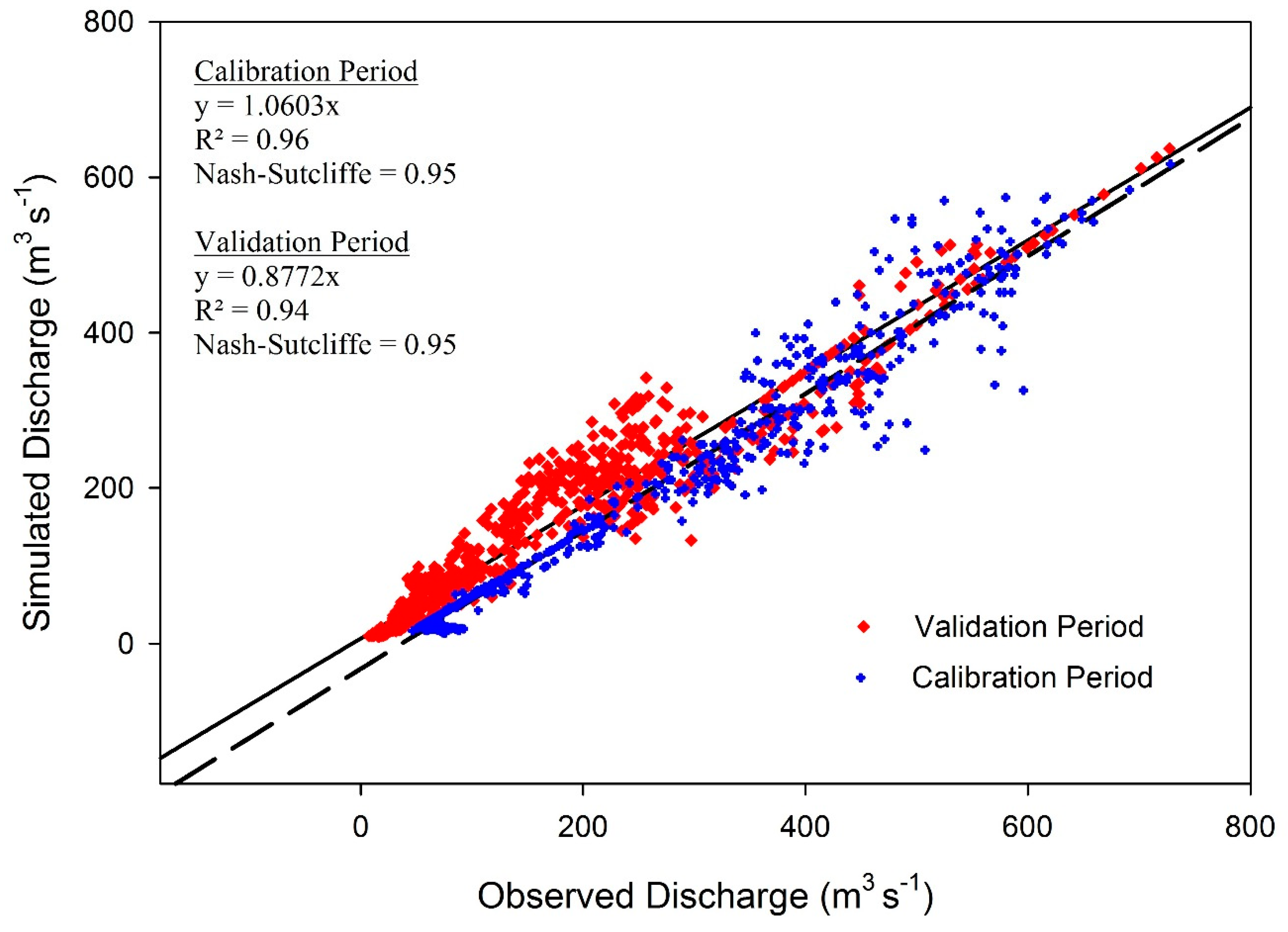
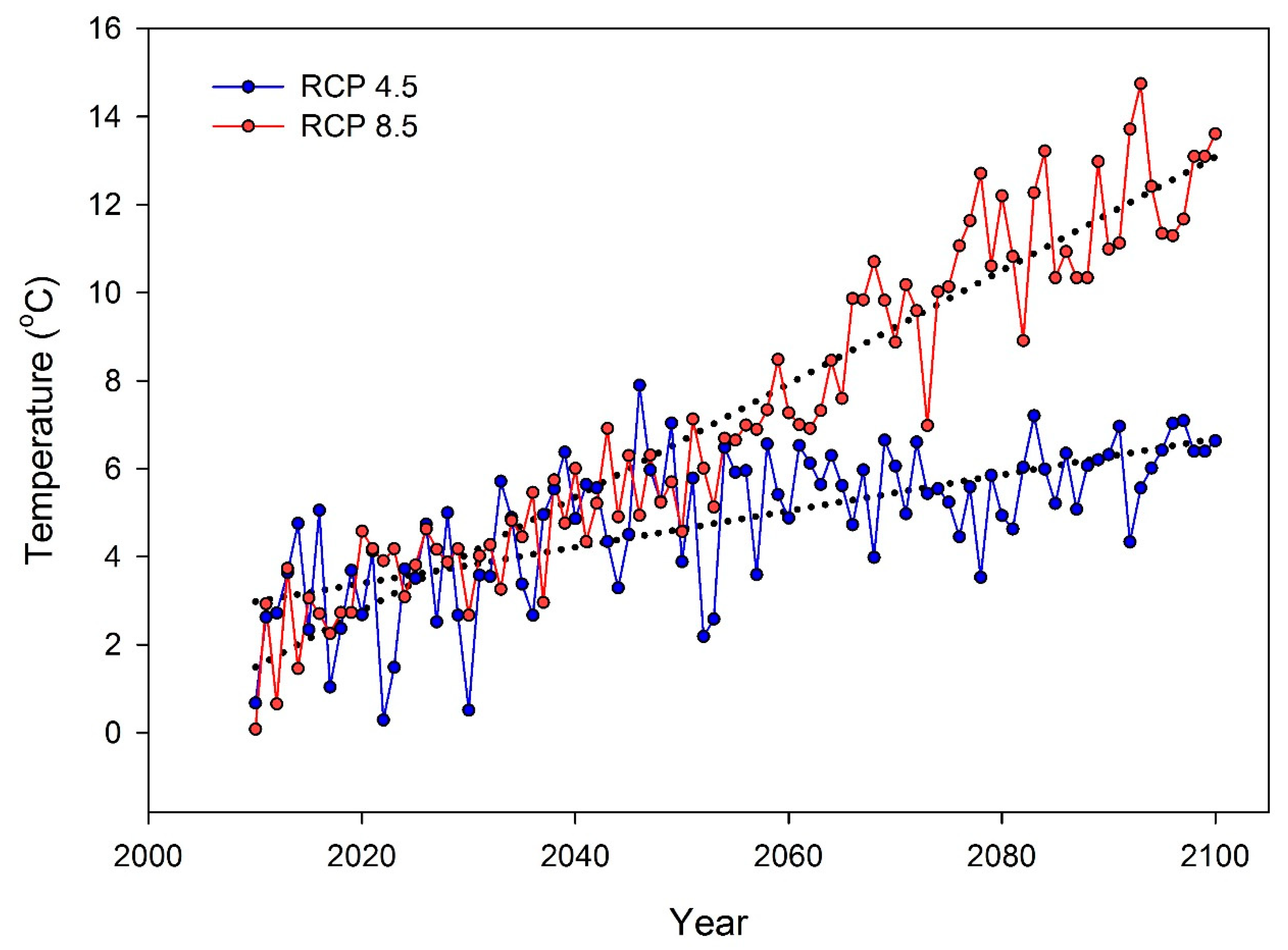
| Parameter | Pre-Calibration Value | Origin and References | Post-Calibration Value |
|---|---|---|---|
| Cell specific | |||
| Ground Slope tan, β | 1.7E-4–1.81E-1 | [62] | |
| Channel Slope tan, βc | 1.7E-4–1.81E-1 | [62] | |
| Depth of surface soil layer (m), L | 0.1–0.81 | [67] | 0.1–4.5 |
| Saturated hydraulic conductivity (m.s−1) Ks | 1.09E-8–1.09E-6 | [72] | 1E-12–1E-002 |
| Residual soil moisture content (cm3/cm3) θr | 0.01–0.047 | [14] | |
| Saturated soil moisture content (cm3/cm3) θs | 0.1–0.46 | [14] | |
| Manning’s surface roughness coeff. (m−1/3.s−1) no | 0.03–0.1 | [61,73] | 0.001–0.25 |
| Manning’s channel roughness coeff. (m−1/3s−1) nc | 0.02–0.07 | [15] | 0.11–0.43 |
| Non-linear soil exponent αs | 2.5 | [15] | |
| Crop factor kc | 1.0 | [62] | 0.01–1 |
| Horizontal dimension of cell (m) X | 1 000 | [74] | |
| Max. channel width at outlet (m) Wmax | 10 | [62] | |
| Min. channel width (m) Wmin | 1 | - | |
| Area required to initiate channel (m2) Athreshold | 25,000,000 | [51] | |
| Event | R2 | NSE | d1 |
|---|---|---|---|
| 1999 | 0.97 * | 0.95 * | 0.93 * |
| 2000 | 0.93 * | 0.94 * | 0.97 * |
| 1999 to 2001 | 0.96 * | 0.95 * | 0.95 * |
| Event | R2 | NSE | D |
|---|---|---|---|
| 2001 2002 2003 | 0.98 * | 0.95 * | 0.94 * |
| 0.97 * | 0.92 * | 0.94 * | |
| 0.97 * | 0.93 * | 0.96 * | |
| 2001 to 2003 | 0.96 * | 0.93 * | 0.95 * |
| Month | Temperature (ºC) | Precipitation (mm) | Soil Moisture (%) | Snow Cover (%) | SWE (mm) | ETP (mm) | ETA (mm) | Percolation (mm) |
|---|---|---|---|---|---|---|---|---|
| Jan | −11.33 | 1.57 | 17.02 | 91.35 | 229.84 | 0.00 | 0.00 | 0.00 |
| Feb | −10.31 | 3.09 | 16.09 | 91.76 | 290.47 | 0.00 | 0.00 | 0.00 |
| Mar | −6.77 | 4.56 | 15.82 | 89.33 | 404.26 | 0.00 | 0.01 | 0.00 |
| Apr | −1.00 | 4.70 | 18.55 | 89.76 | 453.86 | 0.00 | 0.11 | 0.04 |
| May | 4.29 | 2.27 | 27.46 | 61.41 | 315.41 | 0.52 | 0.33 | 0.35 |
| Jun | 8.16 | 1.09 | 31.18 | 31.00 | 88.21 | 1.08 | 0.46 | 0.27 |
| Jul | 11.00 | 0.86 | 27.63 | 10.62 | 18.16 | 1.46 | 0.47 | 0.03 |
| Aug | 10.71 | 1.00 | 25.05 | 8.17 | 12.02 | 1.39 | 0.44 | 0.02 |
| Sep | 6.39 | 1.32 | 22.99 | 11.40 | 11.98 | 0.81 | 0.31 | 0.02 |
| Oct | 0.17 | 1.09 | 20.45 | 41.39 | 18.63 | 0.06 | 0.08 | 0.02 |
| Nov | −4.95 | 4.09 | 19.00 | 72.19 | 71.83 | 0.00 | 0.01 | 0.01 |
| Dec | −9.46 | 3.13 | 17.82 | 86.99 | 187.91 | 0.00 | 0.00 | 0.00 |
| Period | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Annual |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RCP4.5 | |||||||||||||
| 2010–2040 | −10.4 | −8 | −3.0 | 3.2 | 8.8 | 12.1 | 15 | 14.9 | 10.8 | 4.9 | −1.2 | −7.3 | 3.4 |
| 2041–2070 | −6.3 | −7.8 | −5.4 | 0.4 | 7.0 | 11.9 | 14.8 | 16.7 | 14.9 | 10.5 | 6.2 | 0.0 | 5.3 |
| 2070–2100 | −2.1 | −5.7 | −5.9 | −3.4 | 2.7 | 8.5 | 12.2 | 15.6 | 17.4 | 14.6 | 9.8 | 3.9 | 5.7 |
| 2010–2100 | −6.2 | −7.1 | −4.8 | 0.0 | 6.1 | 10.8 | 14 | 15.7 | 14.4 | 10 | 5.0 | −1.1 | 4.8 |
| RCP8.5 | |||||||||||||
| 2010–2040 | −10 | −8.4 | −2.8 | 4.0 | 9.1 | 12.5 | 15.4 | 14.7 | 10.6 | 5.1 | −1.3 | −7.3 | 3.5 |
| 2041–2070 | −3.6 | −6.1 | −4.2 | 2.3 | 8.4 | 12.2 | 15.4 | 18.3 | 17.0 | 12.6 | 8.1 | 2.2 | 6.9 |
| 2070–2100 | 5.3 | 1.0 | −0.6 | 1.7 | 8.4 | 14.4 | 17.4 | 19.9 | 22.3 | 19.8 | 14.4 | 9.6 | 11.2 |
| 2010–2100 | −2.8 | −4.5 | −2.6 | 2.7 | 8.6 | 13 | 16.0 | 17.6 | 16.6 | 12.5 | 7.1 | 1.5 | 7.2 |
| Period | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Annual |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RCP4.5 | |||||||||||||
| 2010–2040 | 1.3 | 1.8 | 2.0 | 2.0 | 2.0 | 1.9 | 1.6 | 1.7 | 1.4 | 0.9 | 0.9 | 1.1 | 1.6 |
| 2041–2070 | 1.3 | 1.5 | 1.4 | 1.6 | 1.9 | 1.6 | 1.8 | 2.2 | 1.8 | 1.0 | 1.0 | 1.2 | 1.5 |
| 2070–2100 | 0.9 | 1.9 | 2.6 | 2.2 | 2.2 | 2.6 | 2 | 1.5 | 1.6 | 1.1 | 0.9 | 0.7 | 1.7 |
| 2010–2100 | 1.3 | 1.8 | 2.0 | 2.0 | 2.0 | 1.9 | 1.6 | 1.7 | 1.4 | 0.9 | 0.9 | 1.1 | 1.6 |
| RCP8.5 | |||||||||||||
| 2010–2040 | 1.8 | 2.1 | 2.1 | 2.6 | 2.3 | 1.3 | 1.2 | 1.5 | 0.9 | 0.8 | 1.4 | 1.4 | 1.6 |
| 2041–2070 | 2.7 | 2.5 | 1.9 | 1.7 | 2.6 | 2.4 | 1.5 | 1.5 | 1 | 0.6 | 0.9 | 1.8 | 1.8 |
| 2070–2100 | 1.3 | 2.3 | 2.3 | 1.6 | 1.2 | 1.5 | 1.5 | 1.5 | 1.8 | 0.9 | 0.9 | 1.1 | 1.5 |
| 2010–2100 | 1.9 | 2.3 | 2.1 | 2.0 | 2.0 | 1.8 | 1.4 | 1.5 | 1.2 | 0.8 | 1.1 | 1.4 | 1.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atif, I.; Iqbal, J.; Su, L.-j. Modeling Hydrological Response to Climate Change in a Data-Scarce Glacierized High Mountain Astore Basin Using a Fully Distributed TOPKAPI Model. Climate 2019, 7, 127. https://doi.org/10.3390/cli7110127
Atif I, Iqbal J, Su L-j. Modeling Hydrological Response to Climate Change in a Data-Scarce Glacierized High Mountain Astore Basin Using a Fully Distributed TOPKAPI Model. Climate. 2019; 7(11):127. https://doi.org/10.3390/cli7110127
Chicago/Turabian StyleAtif, Iqra, Javed Iqbal, and Li-jun Su. 2019. "Modeling Hydrological Response to Climate Change in a Data-Scarce Glacierized High Mountain Astore Basin Using a Fully Distributed TOPKAPI Model" Climate 7, no. 11: 127. https://doi.org/10.3390/cli7110127
APA StyleAtif, I., Iqbal, J., & Su, L.-j. (2019). Modeling Hydrological Response to Climate Change in a Data-Scarce Glacierized High Mountain Astore Basin Using a Fully Distributed TOPKAPI Model. Climate, 7(11), 127. https://doi.org/10.3390/cli7110127




