Multi-Model Forecasts of Very-Large Fire Occurences during the End of the 21st Century
Abstract
1. Introduction
2. Methods
2.1. Fire Occurrence Data
2.2. Meteorological Covariates
2.3. Probability Estimation Trees
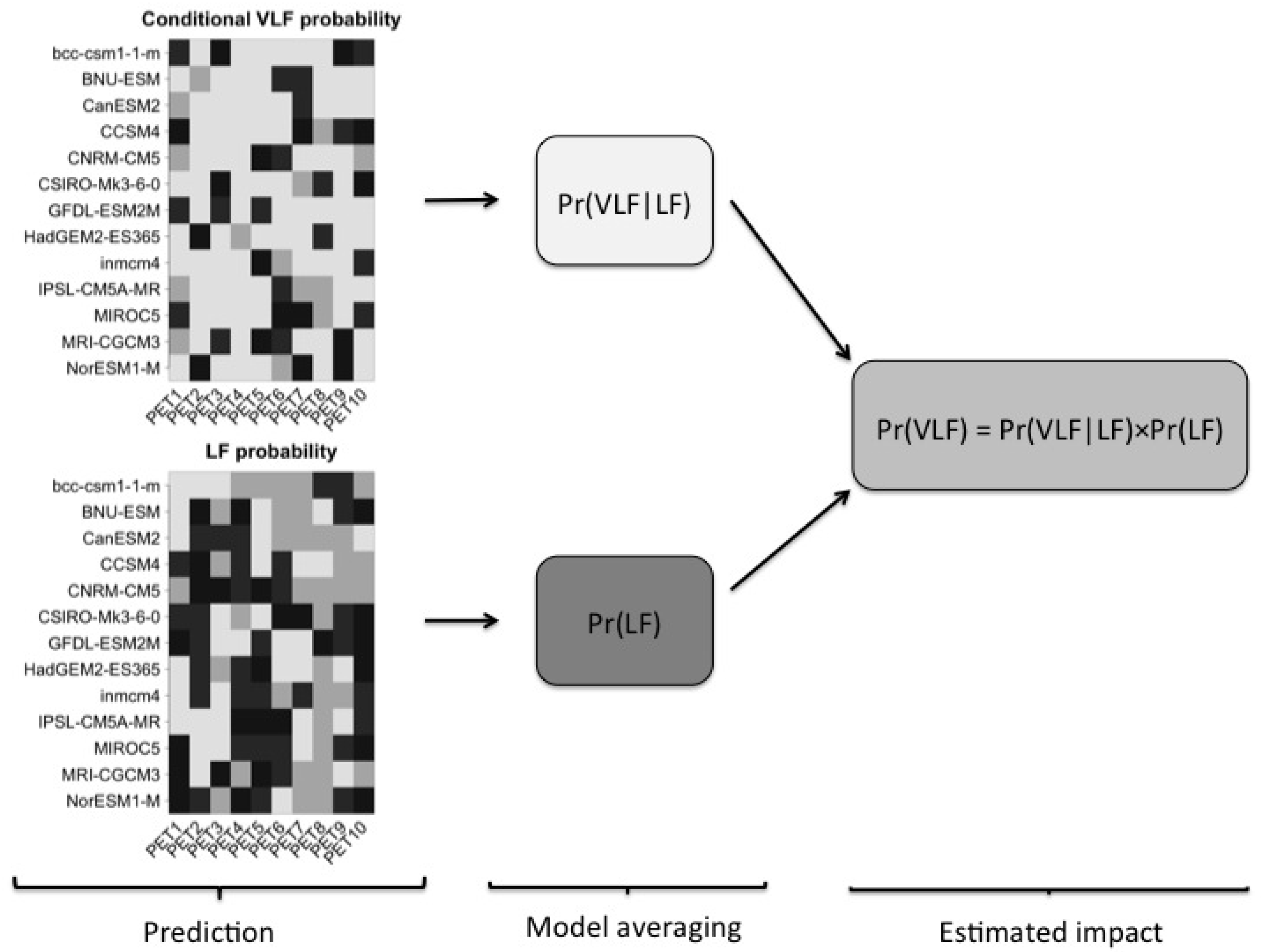
2.4. Multi-Model Very-Large Fire Predictions
2.5. Ensemble Assessment
3. Results
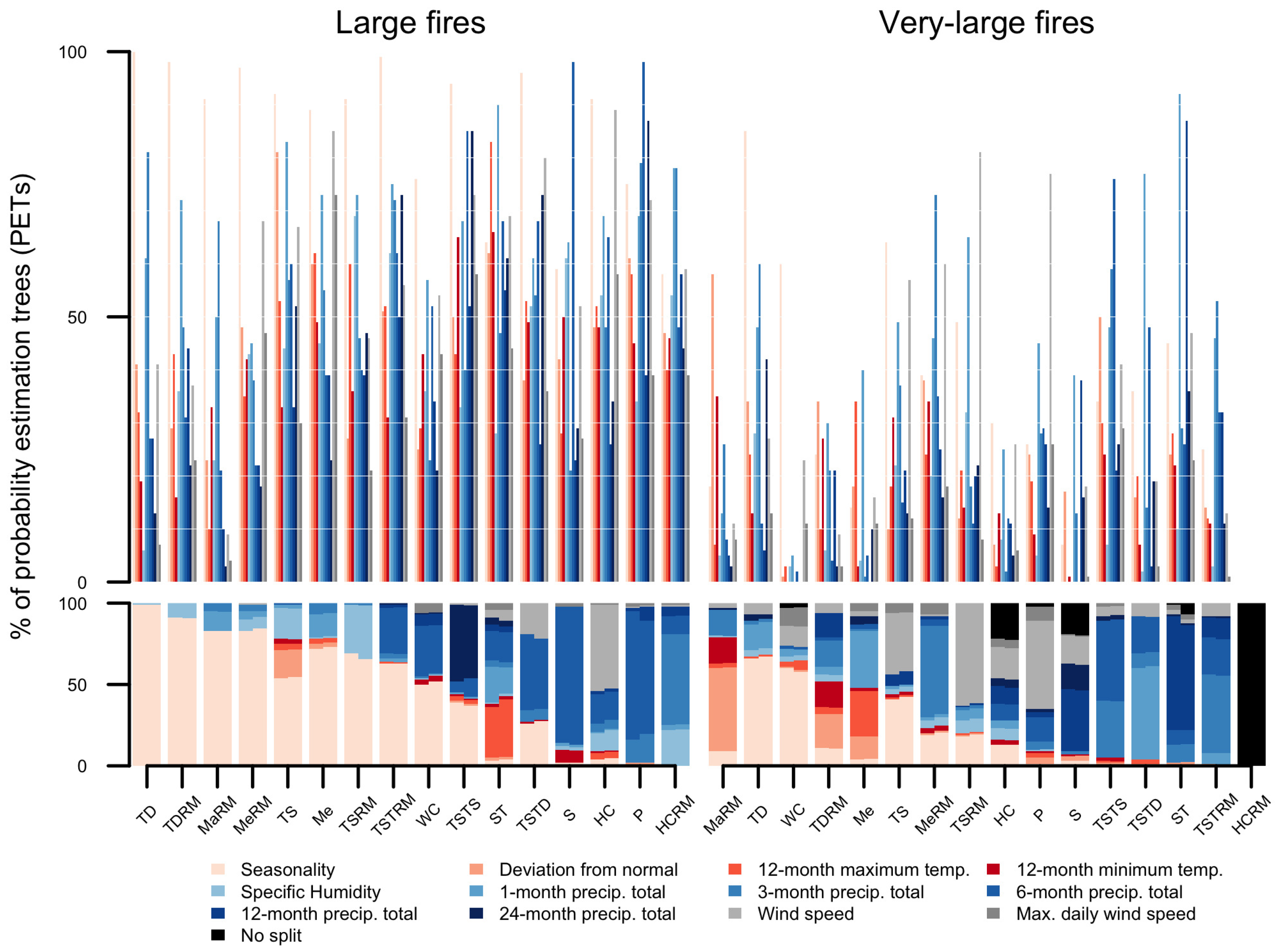
3.1. Important Predictors of Very-Large Fires
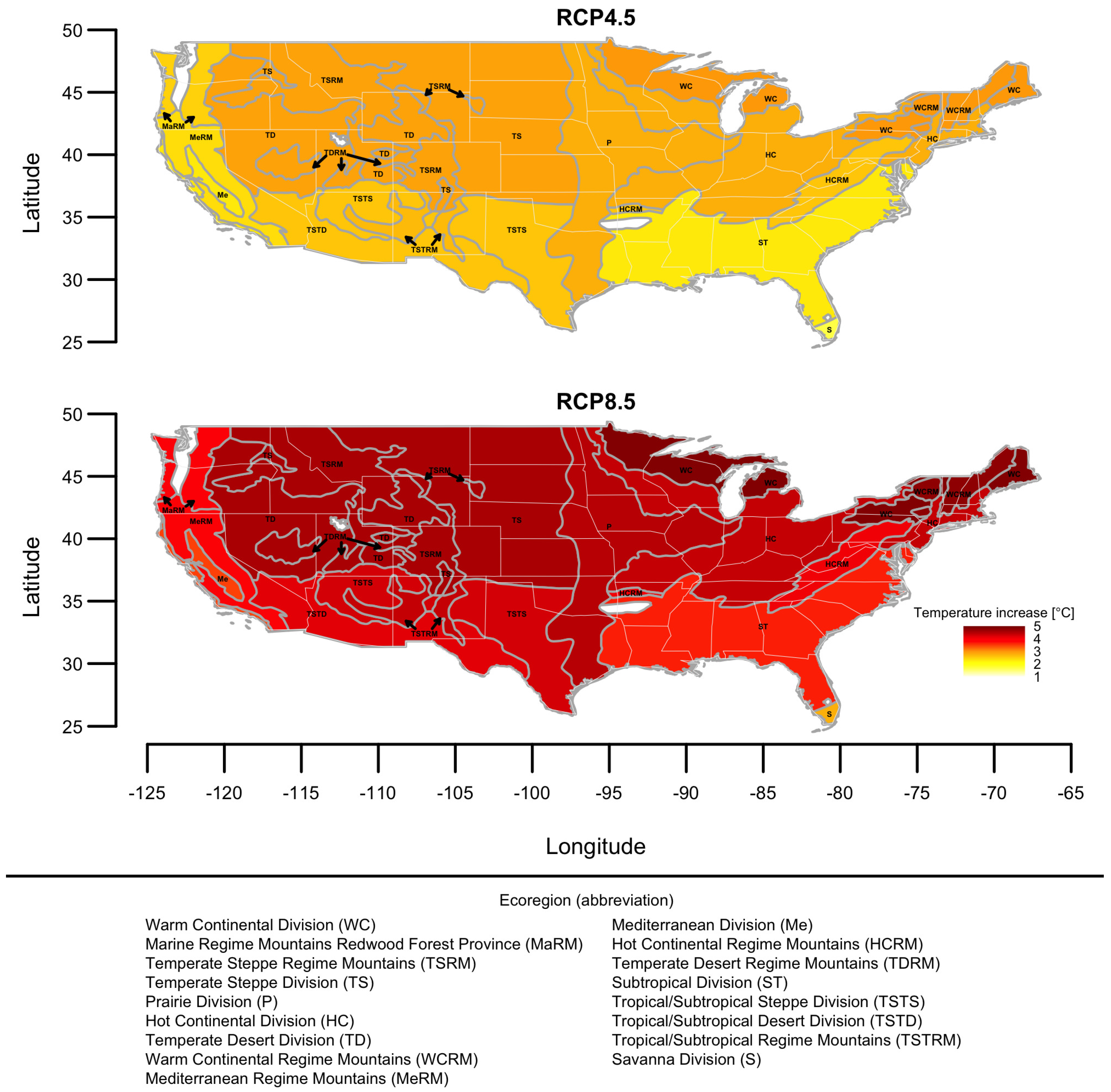
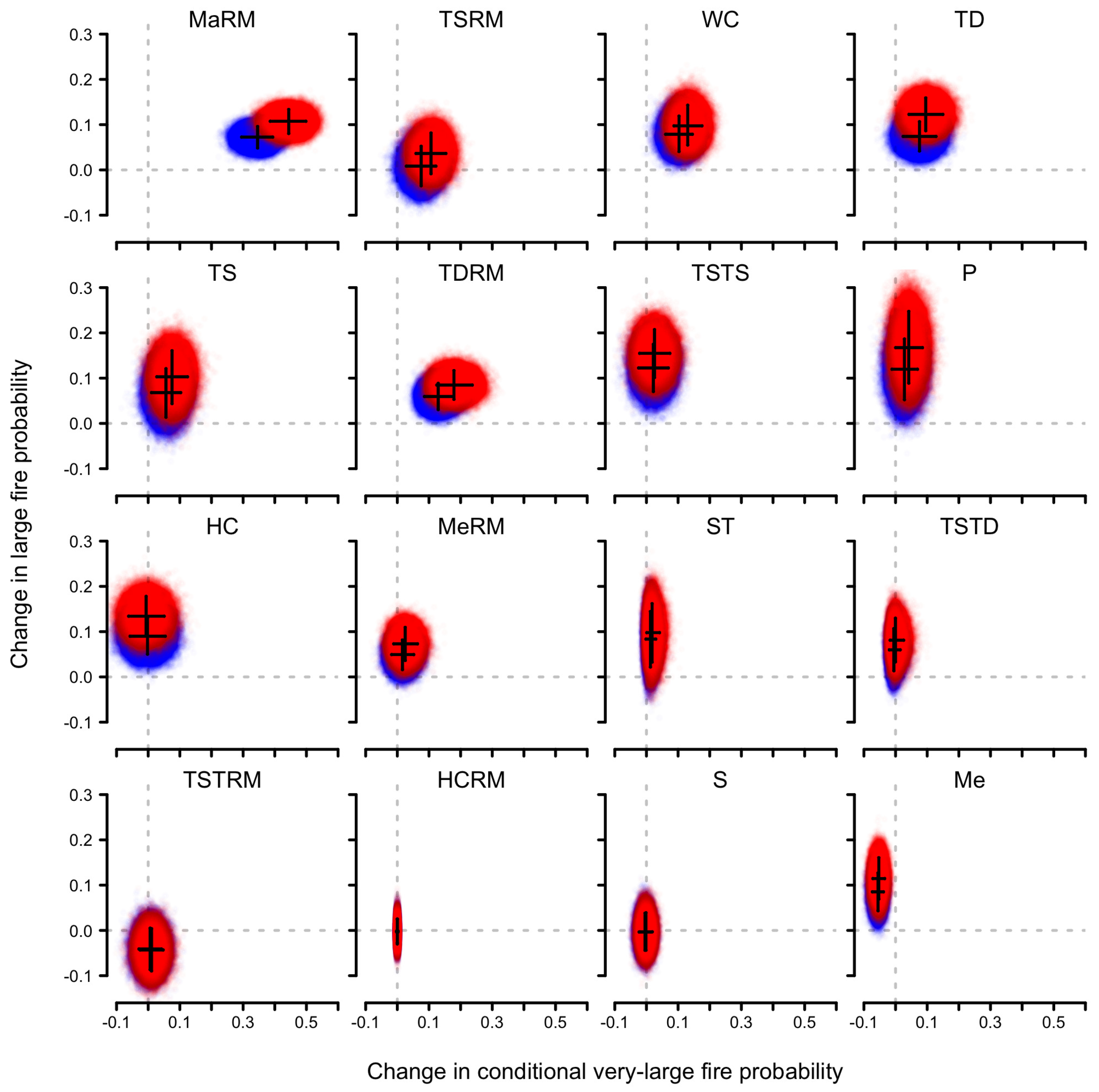
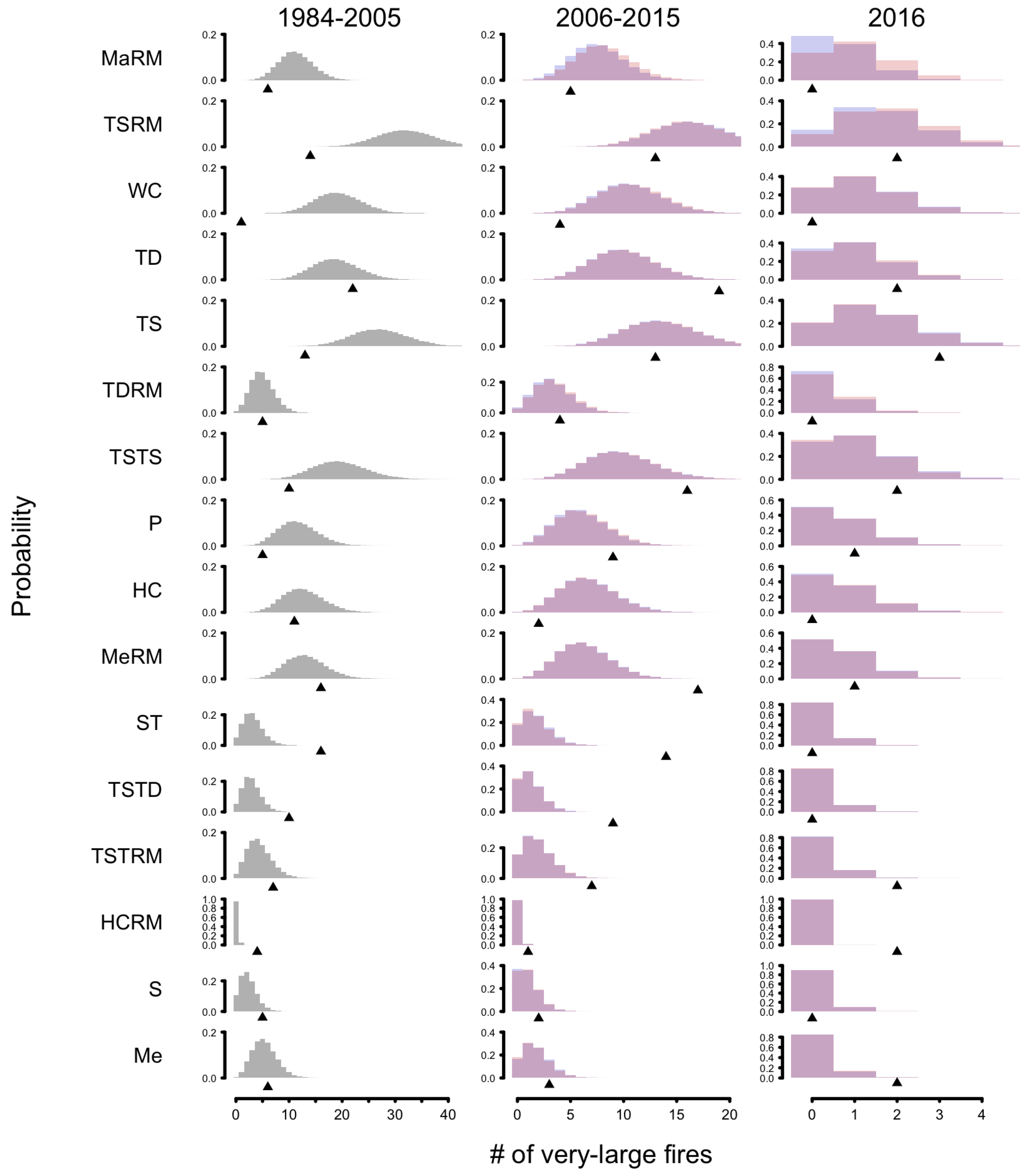
3.2. Climate Change and Very-Large Fire Occurrence
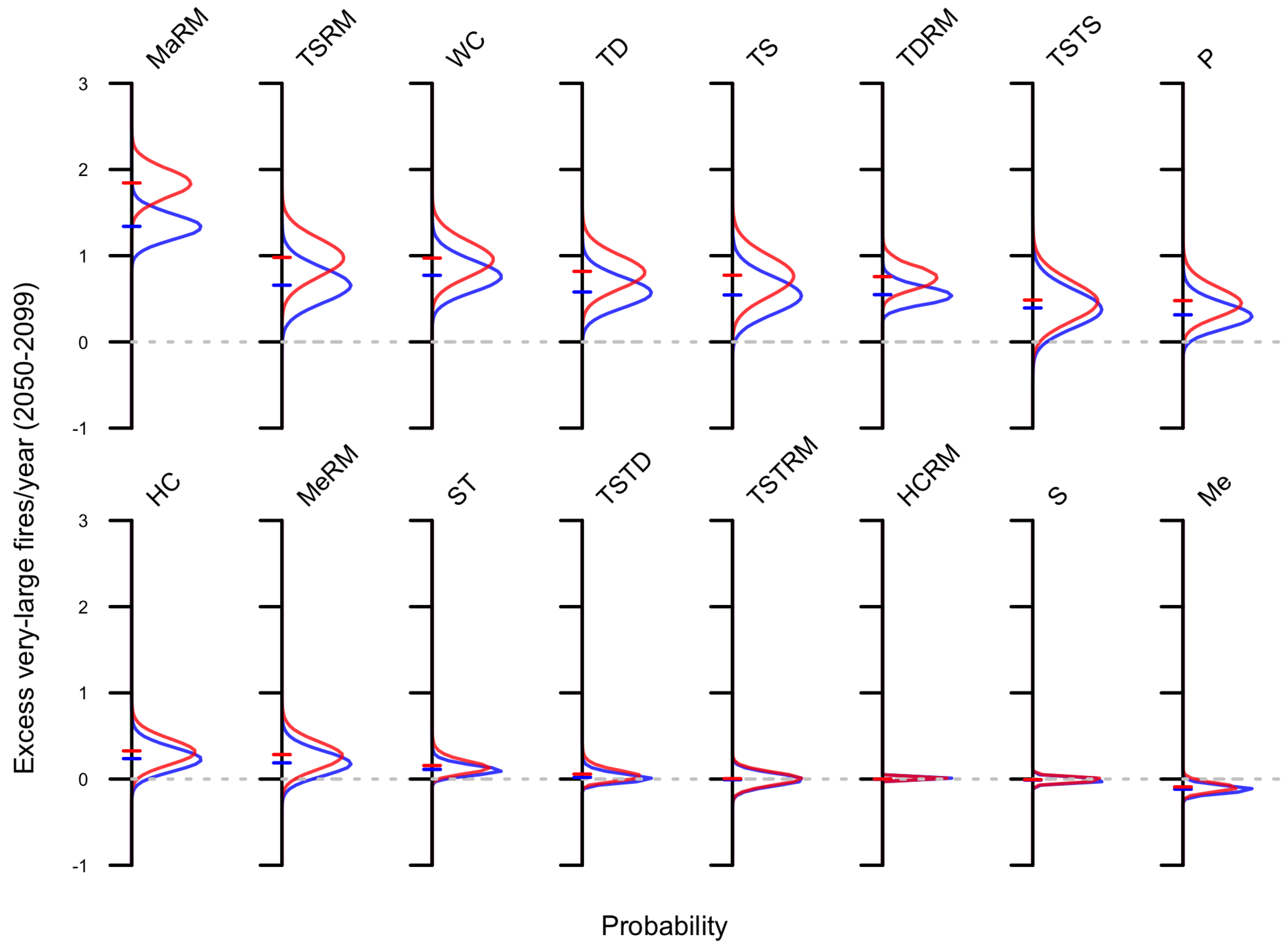
3.3. Ensemble Assessment
4. Discussion
4.1. Important Predictors of Very-Large Fires
4.2. Climate Change and Very-Large Fire Occurrence
4.3. Caveats and Future Work
5. Conclusions
Supplementary Materials
Supplementary File 1Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barrett, K. The Full Community Costs of Wildfire. Headwaters Economics. Available online: https:// headwaterseconomics.org/wp-content/uploads/full-wildfire-costs-report.pdf (accessed on 14 December 2018).
- González-Cabán, A. Economic Cost of Initial Attack and Large-Fire Suppression; USDA Forest Service General Technical Report PSW-068; U.S. Department of Agriculture, Forest Service, Pacific Southwest Forest and Range Experiment Station: Berkeley, CA, USA, 1983; 7p.
- Stephens, S.L.; Burrows, N.; Buyantuyev, A.; Gray, R.W.; Keane, R.E.; Kubian, R.; Liu, S.; Seijo, F.; Shu, L.; Tolhurst, K.G.; et al. Temperate and boreal forest mega-fires: Characteristics and challenges. Front. Ecol. Environ. 2014, 12, 115–122. [Google Scholar] [CrossRef]
- Dale, L. The True Cost of Wildfire in The Western US; Western Forestry Leadership Coalition: Denver, CO, USA, 2009. [Google Scholar]
- Neary, D.G.; Gottfried, G.J.; Ffolliott, P.F. Post-wildfire watershed flood responses. In Proceedings of the 2nd International Fire Ecology Conference, American Meteorological Society, Orlando, FL, USA, 28 November–2 December 2003; Volume 65982. [Google Scholar]
- Peppin, D.L.; Fulé, P.Z.; Sieg, C.H.; Beyers, J.L.; Hunter, M.E.; Robichaud, P.R. Recent trends in post-wildfire seeding in western US forests: Costs and seed mixes. Int. J. Wildl. Fire 2011, 20, 702–708. [Google Scholar] [CrossRef]
- Beverly, J.L.; Bothwell, P. Wildfire evacuations in Canada 1980–2007. Nat. Hazards 2011, 59, 571–596. [Google Scholar] [CrossRef]
- Beverly, J.L.; Flannigan, M.D.; Stocks, B.J.; Bothwell, P. The association between Northern Hemisphere climate patterns and interannual variability in Canadian wildfire activity. Can. J. For. Res. 2011, 41, 2193–2201. [Google Scholar] [CrossRef]
- Forster, C.; Wandinger, U.; Wotawa, G.; James, P.; Mattis, I.; Althausen, D.; Simmonds, P.; O’Doherty, S.; Jennings, S.G.; Kleefeld, C.; et al. Transport of boreal forest fire emissions from Canada to Europe. J. Geophys. Res. Atmos. 2001, 106, 22887–22906. [Google Scholar] [CrossRef]
- Val Martin, M.; Heald, C.L.; Ford, B.; Prenni, A.J.; Wiedinmyer, C. A decadal satellite analysis of the origins and impacts of smoke in Colorado. Atmos. Chem. Phys. 2013, 13, 7429–7439. [Google Scholar] [CrossRef]
- Reid, C.E.; Brauer, M.; Johnston, F.H.; Jerrett, M.; Balmes, J.R.; Elliott, C.T. Critical review of health impacts of wildfire smoke exposure. Environ. Health Perspect. 2016, 124, 1334. [Google Scholar] [CrossRef] [PubMed]
- Achtemeier, G.L. On the formation and persistence of superfog in woodland smoke. Meteorol. Appl. 2009, 16, 215–225. [Google Scholar] [CrossRef]
- Moeltner, K.; Kim, M.K.; Zhu, E.; Yang, W. Wildfire smoke and health impacts: A closer look at fire attributes and their marginal effects. J. Environ. Econ. Manag. 2013, 66, 476–496. [Google Scholar] [CrossRef]
- Crawford, J.A.; Wahren, C.H.; Kyle, S.; Moir, W.H. Responses of exotic plant species to fires in Pinus ponderosa forests in northern Arizona. J. Veg. Sci. 2001, 12, 261–268. [Google Scholar] [CrossRef]
- Rocca, M.E.; Miniat, C.F.; Mitchell, R.J. Introduction to the regional assessments: Climate change, wildfire, and forest ecosystem services in the USA. For. Ecol. Manag. 2014, 327, 8. [Google Scholar] [CrossRef]
- Haffey, C.; Sisk, T.D.; Allen, C.D.; Thode, A.E.; Margolis, E.Q. Limits to Ponderosa Pine Regeneration following Large High-Severity Forest Fires in the United States Southwest. Fire Ecol. 2018, 14, 143–163. [Google Scholar]
- Williams, J. Exploring the onset of high-impact mega-fires through a forest land management prism. For. Ecol. Manag. 2013, 294, 4–10. [Google Scholar] [CrossRef]
- Dennison, P.E.; Brewer, S.C.; Arnold, J.D.; Moritz, M.A. Large wildfire trends in the western United States. Geophys. Res. Lett. 2014, 41, 2928–2933. [Google Scholar] [CrossRef]
- Barbero, R.; Abatzoglou, J.T.; Steel, E.A.; Larkin, N.K. Modeling very large-fire occurrences over the continental United States from weather and climate forcing. Environ. Res. Lett. 2014, 9, 124009. [Google Scholar] [CrossRef]
- Stavros, E.N.; Abatzoglou, J.T.; McKenzie, D.; Larkin, N.K. Regional projections of the likelihood of very large wildland fires under a changing climate in the contiguous Western United States. Clim. Chang. 2014, 126, 455–468. [Google Scholar] [CrossRef]
- Barbero, R.; Abatzoglou, J.T.; Larkin, N.K.; Kolden, C.A.; Stocks, B. Climate change presents increased potential for very large fires in the contiguous United States. Int. J. Wildl. Fire 2015, 24, 892–899. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Poulin, A.; Leconte, R. Overall uncertainty study of the hydrological impacts of climate change for a Canadian watershed. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Morgan, M.G.; Henrion, M.; Small, M. Uncertainty: A Guide to Dealing With Uncertainty in Quantitative Risk and Policy Analysis; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Syphard, A.D.; Sheehan, T.; Rustigian-Romsos, H.; Ferschweiler, K. Mapping future fire probability under climate change: Does vegetation matter? PLoS ONE 2018, 13, e0201680. [Google Scholar] [CrossRef] [PubMed]
- Sitch, S.; Huntingford, C.; Gedney, N.; Levy, P.E.; Lomas, M.; Piao, S.L.; Betts, R.; Cias, P.; Cox, P.; Friedlingstein, P.; et al. Evaluation of the terrestrial carbon cycle, future plant geography and climate-carbon cycle feedbacks using five Dynamic Global Vegetation Models (DGVMs). Glob. Chang. Biol. 2008, 14, 2015–2039. [Google Scholar] [CrossRef]
- Westerling, A.L.; Bryant, B.P.; Preisler, H.K.; Holmes, T.P.; Hidalgo, H.G.; Das, T.; Shrestha, S.R. Climate change and growth scenarios for California wildfire. Clim. Chang. 2011, 109, 445–463. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Flannigan, M.D.; Krawchuk, M.A.; de Groot, W.J.; Wotton, B.M.; Gowman, L.M. Implications of changing climate for global wildland fire. Int. J. Wildl. Fire 2009, 18, 483–507. [Google Scholar] [CrossRef]
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Kitzberger, T.; Rigling, A.; Breshears, D.D.; Hogg, E.H.; et al. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef]
- Bentz, B.J.; Régnière, J.; Fettig, C.J.; Hansen, E.M.; Hayes, J.L.; Hicke, J.A.; Kelsey, R.G.; Negrón, J.F.; Seybold, S.J. Climate change and bark beetles of the western United States and Canada: Direct and indirect effects. BioScience 2010, 60, 602–613. [Google Scholar] [CrossRef]
- Westerling, A.L. Increasing western US forest wildfire activity: Sensitivity to changes in the timing of spring. Philos. Trans. R. Soc. B 2016, 371, 20150178. [Google Scholar] [CrossRef] [PubMed]
- Meyn, A.; White, P.S.; Buhk, C.; Jentsch, A. Environmental drivers of large, infrequent wildfires: The emerging conceptual model. Prog. Phys. Geogr. 2007, 31, 287–312. [Google Scholar] [CrossRef]
- De Groot, W.J.; Johnston, J.; Jurko, N.; Cantin, A.S. Fuel moisture sensitivity to temperature and precipitation: Climate change implications. Clim. Chang. 2016, 134, 59–71. [Google Scholar]
- Bradley, B.A.; Curtis, C.A.; Chambers, J.C. Bromus response to climate and projected changes with climate change. In Exotic Brome-Grasses in Arid and Semiarid Ecosystems of the Western US; Springer International Publishing: New York, NY, USA, 2016; pp. 257–274. [Google Scholar]
- Zargar, A.; Sadiq, R.; Naser, B.; Khan, F.I. A review of drought indices. Environ. Rev. 2011, 19, 333–349. [Google Scholar] [CrossRef]
- Holsinger, L.; Parks, S.A.; Miller, C. Weather, fuels, and topography impede wildland fire spread in western US landscapes. For. Ecol. Manag. 2016, 380, 59–69. [Google Scholar] [CrossRef]
- Mallick, B.K.; Gelfand, A.E. Generalized linear models with unknown link functions. Biometrika 1994, 81, 237–245. [Google Scholar] [CrossRef]
- Littell, J.S.; McKenzie, D.; Kerns, B.K.; Cushman, S.; Shaw, C.G. Managing uncertainty in climate-driven ecological models to inform adaptation to climate change. Ecosphere 2011, 2, 1–19. [Google Scholar] [CrossRef]
- Raftery, A.E.; Zheng, Y. Discussion: Performance of Bayesian model averaging. J. Am. Stat. Assoc. 2003, 98, 931–938. [Google Scholar] [CrossRef]
- Fragoso, T.M.; Bertoli, W.; Louzada, F. Bayesian model averaging: A systematic review and conceptual classification. Int. Stat. Rev. 2018, 86, 1–28. [Google Scholar] [CrossRef]
- Plummer, M. JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling. In Proceedings of the 3rd International Workshop on Distributed Statistical Computing, Vienna, Austria, 20–22 March 2003. [Google Scholar]
- Carpenter, B.; Gelman, A.; Hoffman, M.D.; Lee, D.; Goodrich, B.; Brubaker, M.; Guo, J.; Betancourt, M.; Li, P.; Riddell, A. Stan: A probabilistic programming language. J. Stat. Softw. 2017, 76. [Google Scholar] [CrossRef]
- Rue, H.; Martino, S.; Chopin, N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Soc. 2009, 71, 319–392. [Google Scholar] [CrossRef]
- Monnahan, C.C.; Thorson, J.T.; Branch, T.A. Faster estimation of Bayesian models in ecology using Hamiltonian Monte Carlo. Methods Ecol. Evol. 2017, 8, 339–348. [Google Scholar] [CrossRef]
- Monitoring Trends in Burn Severity. Available online: http://www.mtbs.gov (accessed on 21 November 2017).
- Bailey, R.G. Bailey’s ecoregions and subregions of the United States, Puerto Rico, and the U.S. Virgin Islands; Forest Service Research Data Archive: Fort Collins, CO, USA, 2016. Available online: https://doi.org/10.2737/RDS-2016-0003 (accessed on 14 December 2018).
- Climatology Lab. Available online: http://www.climatologylab.org (accessed on 29 January 2018).
- Weiss, A.; Hays, C.J. Calculating daily mean air temperatures by different methods: Implications from a non-linear algorithm. Agric. For. Meteorol. 2005, 128, 57–65. [Google Scholar] [CrossRef]
- Provost, F.; Domingos, P. Well-Trained PETs: Improving Probability Estimation Trees, CeDER Working Paper #IS-00-04, Stern School of Business; New York University: New York, NY, USA, 2000. [Google Scholar]
- Wang, H.; Yang, F.; Leu, Z. An experimental study of the intrinsic stability of random forest variable importance measures. BMC Bioinf. 2016, 17, 60. [Google Scholar] [CrossRef] [PubMed]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Hido, S.; Kashima, H.; Takahashi, Y. Roughly balanced bagging for imbalanced data. Statistical Analysis and Data Mining: ASA Data Sci. J. 2009, 2, 412–426. [Google Scholar] [CrossRef]
- Development Core Team R. A Language and Environment for Statistical Computing. 2008. Available online: http://www.R-project.org (accessed on 14 December 2018).
- Brooks, S.P.; Gelman, A. General methods for monitoring convergence of iterative simulations. J. Comput. Gr. Stat. 1998, 7, 434–455. [Google Scholar]
- Gelman, A.; Shirley, K. Inference from simulations and monitoring convergence. In Handbook of Markov chain Monte Carlo; CRC Press: Boca Raton, FL, USA, 2011; pp. 163–174. [Google Scholar]
- Stavros, E.N.; Abatzoglou, J.; Larkin, N.K.; McKenzie, D.; Steel, E.A. Climate and very large wildland fires in the contiguous western USA. Int. J. Wildl. Fire 2014, 23, 899–914. [Google Scholar] [CrossRef]
- Barbero, R.; Abatzoglou, J.T.; Kolden, C.A.; Hegewisch, K.C.; Larkin, N.K.; Podschwit, H. Multi-scalar influence of weather and climate on very large-fires in the Eastern United States. Int. J. Climatol. 2015, 35, 2180–2186. [Google Scholar] [CrossRef]
- Arpaci, A.; Eastaugh, C.S.; Vacik, H. Selecting the best performing fire weather indices for Austrian ecoregions. Theor. Appl. Climatol. 2013, 114, 393–406. [Google Scholar] [CrossRef] [PubMed]
- Flannigan Mike, D. Forest fires and climate change in the 21 st century. Mitig. Adapt. Strateg. Global Chang. 2006, 11, 847–859. [Google Scholar] [CrossRef]
- Slocum, M.G.; Beckage, B.; Platt, W.J.; Orzell, S.L.; Taylor, W. Effect of climate on wildfire size: A cross-scale analysis. Ecosystems 2010, 13, 828–840. [Google Scholar] [CrossRef]
- Krueger, E.S.; Ochsner, T.E.; Engle, D.M.; Carlson, J.D.; Twidwell, D.L. Soil Moisture Affects Growing-Season Wildfire Size in the Southern Great Plains. Soil Sci. Soc. Am. J. 2015, 79, 1567–1576. [Google Scholar] [CrossRef]
- Syphard, A.D.; Radeloff, V.C.; Keeley, J.E.; Hawbaker, T.J.; Clayton, M.K.; Stewart, S.I.; Hammer, R.B. Human influence on California fire regimes. Ecol. Appl. 2007, 17, 1388–1402. [Google Scholar] [CrossRef] [PubMed]
- Syphard, A.D.; Keeley, J.E.; Pfaff, A.H.; Ferschweiler, K. Human presence diminishes the importance of climate in driving fire activity across the United States. Proc. Natl. Acad. Sci. USA 2017, 201713885. [Google Scholar] [CrossRef] [PubMed]
- Taylor, S.W.; Woolford, D.G.; Dean, C.B.; Martell, D.L. Wildfire prediction to inform fire management: Statistical science challenges. Stat. Sci. 2013, 28, 586–615. [Google Scholar] [CrossRef]
- Arguez, A.; Vose, R.S. The definition of the standard WMO climate normal: The key to deriving alternative climate normals. Bull. Am. Meteorol. Soc. 2011, 92, 699–704. [Google Scholar] [CrossRef]
- Westerling, A.L.; Swetnam, T.W. Interannual to decadal drought and wildfire in the western United States. EOS 2003, 84, 545–555. [Google Scholar] [CrossRef]
- Marlon, J.R.; Bartlein, P.J.; Gavin, D.G.; Long, C.J.; Anderson, R.S.; Briles, C.E.; Brown, K.J.; Colombaroli, D.; Hallett, D.J.; Power, M.J.; et al. Long-term perspective on wildfires in the western USA. Proc. Natl. Acad. Sci. USA 2012, 109, E535–E543. [Google Scholar] [CrossRef] [PubMed]
- Clyde, M. Model averaging. Subject. Object. Bayesian Stat. 2003, 25, 320–326. [Google Scholar]
- Tedim, F.; Leone, V.; Amraoui, M.; Bouillon, C.; Coughlan, M.R.; Delogu, G.M.; Fernandes, P.M.; Ferreira, C.; McCaffrey, S.; McGee, T.K.; et al. Defining extreme wildfire events: Difficulties, challenges, and impacts. Fire 2018, 1, 9. [Google Scholar] [CrossRef]
- Weber, E.U.; Johnson, E.J. Decisions under uncertainty: Psychological, economic, and neuroeconomic explanations of risk preference. Neuroeconomics 2009, 2009, 127–144. [Google Scholar]

| Domain | Division | 95th Size Percentile (ha) | Total # of Fires | # of Large Fire Months | # of Very-Large Fire Months | |||
|---|---|---|---|---|---|---|---|---|
| ’84-’05 | ’06-’15 | ’84-’05 | ’06-’15 | ’84-’05 | ’06-’15 | |||
| Dry | Temperate Desert (TD) | 16,007 | 1623 | 833 | 119 | 55 | 22 | 19 |
| Temperate Desert Regime Mountains (TDRM) | 11,765 | 121 | 78 | 52 | 31 | 5 | 4 | |
| Temperate Steppe (TS) | 11,664 | 464 | 347 | 119 | 70 | 13 | 13 | |
| Temperate Steppe Regime Mountains (TSRM) | 19,853 | 798 | 541 | 101 | 56 | 14 | 13 | |
| Tropical/Subtropical Desert (TSTD) | 11,616 | 365 | 254 | 94 | 57 | 10 | 9 | |
| Tropical/Subtropical Regime Mountains (TSTRM) | 13,169 | 168 | 143 | 71 | 45 | 7 | 7 | |
| Tropical/Subtropical Steppe (TSTS) | 10,243 | 388 | 546 | 126 | 79 | 10 | 16 | |
| Temperate | Hot Continental (HC) | 6180 | 267 | 75 | 67 | 41 | 11 | 2 |
| Hot Continental Regime Mountains (HCRM) | 4586 | 169 | 45 | 30 | 27 | 4 | 1 | |
| Marine Regime Mountains Redwood Forest Province (MaRM) | 21,776 | 136 | 130 | 48 | 33 | 6 | 5 | |
| Mediterranean (Me) | 10,980 | 149 | 64 | 82 | 35 | 6 | 3 | |
| Mediterranean Regime Mountains (MeRM) | 17,772 | 799 | 374 | 143 | 60 | 16 | 17 | |
| Prairie (P) | 6707 | 155 | 275 | 47 | 56 | 5 | 9 | |
| Subtropical (ST) | 5908 | 431 | 312 | 149 | 82 | 16 | 14 | |
| Subtropical Regime Mountains (SRM) | 3927 | 4 | 16 | 3 | 12 | 0 | 1 | |
| Warm Continental (WC) | 6466 | 73 | 20 | 40 | 12 | 1 | 4 | |
| Humid | Savanna (S) | 20,623 | 89 | 45 | 44 | 24 | 5 | 2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Podschwit, H.R.; Larkin, N.K.; Steel, E.A.; Cullen, A.; Alvarado, E. Multi-Model Forecasts of Very-Large Fire Occurences during the End of the 21st Century. Climate 2018, 6, 100. https://doi.org/10.3390/cli6040100
Podschwit HR, Larkin NK, Steel EA, Cullen A, Alvarado E. Multi-Model Forecasts of Very-Large Fire Occurences during the End of the 21st Century. Climate. 2018; 6(4):100. https://doi.org/10.3390/cli6040100
Chicago/Turabian StylePodschwit, Harry R., Narasimhan K. Larkin, E. Ashley Steel, Alison Cullen, and Ernesto Alvarado. 2018. "Multi-Model Forecasts of Very-Large Fire Occurences during the End of the 21st Century" Climate 6, no. 4: 100. https://doi.org/10.3390/cli6040100
APA StylePodschwit, H. R., Larkin, N. K., Steel, E. A., Cullen, A., & Alvarado, E. (2018). Multi-Model Forecasts of Very-Large Fire Occurences during the End of the 21st Century. Climate, 6(4), 100. https://doi.org/10.3390/cli6040100






