Assessing Climate Driven Malaria Variability in Ghana Using a Regional Scale Dynamical Model
Abstract
:1. Introduction
2. Method and Data
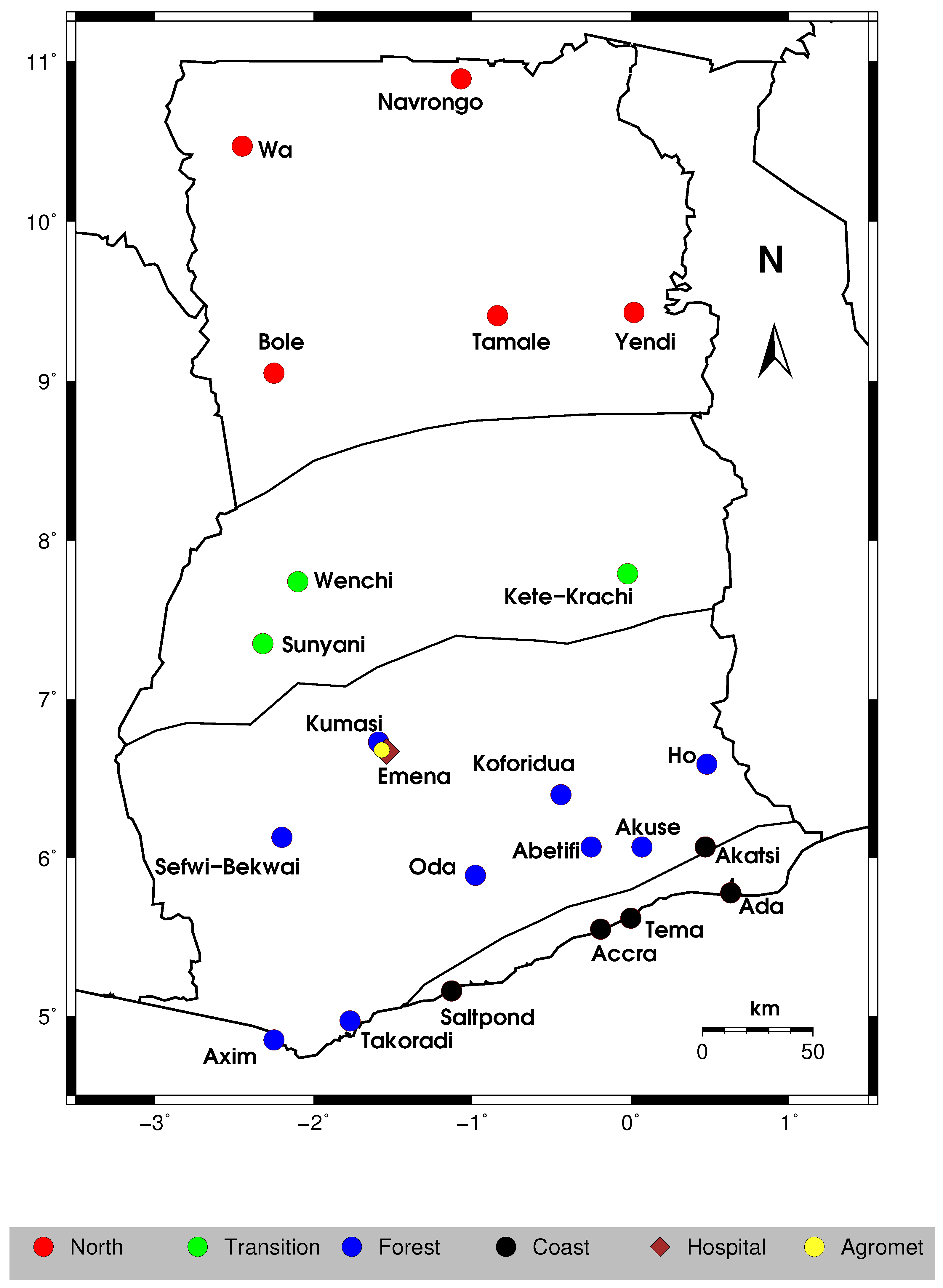
2.1. Study Area and Data
2.2. Malaria Morbidity Data
2.3. VECTRI Model
3. Results and Discussion
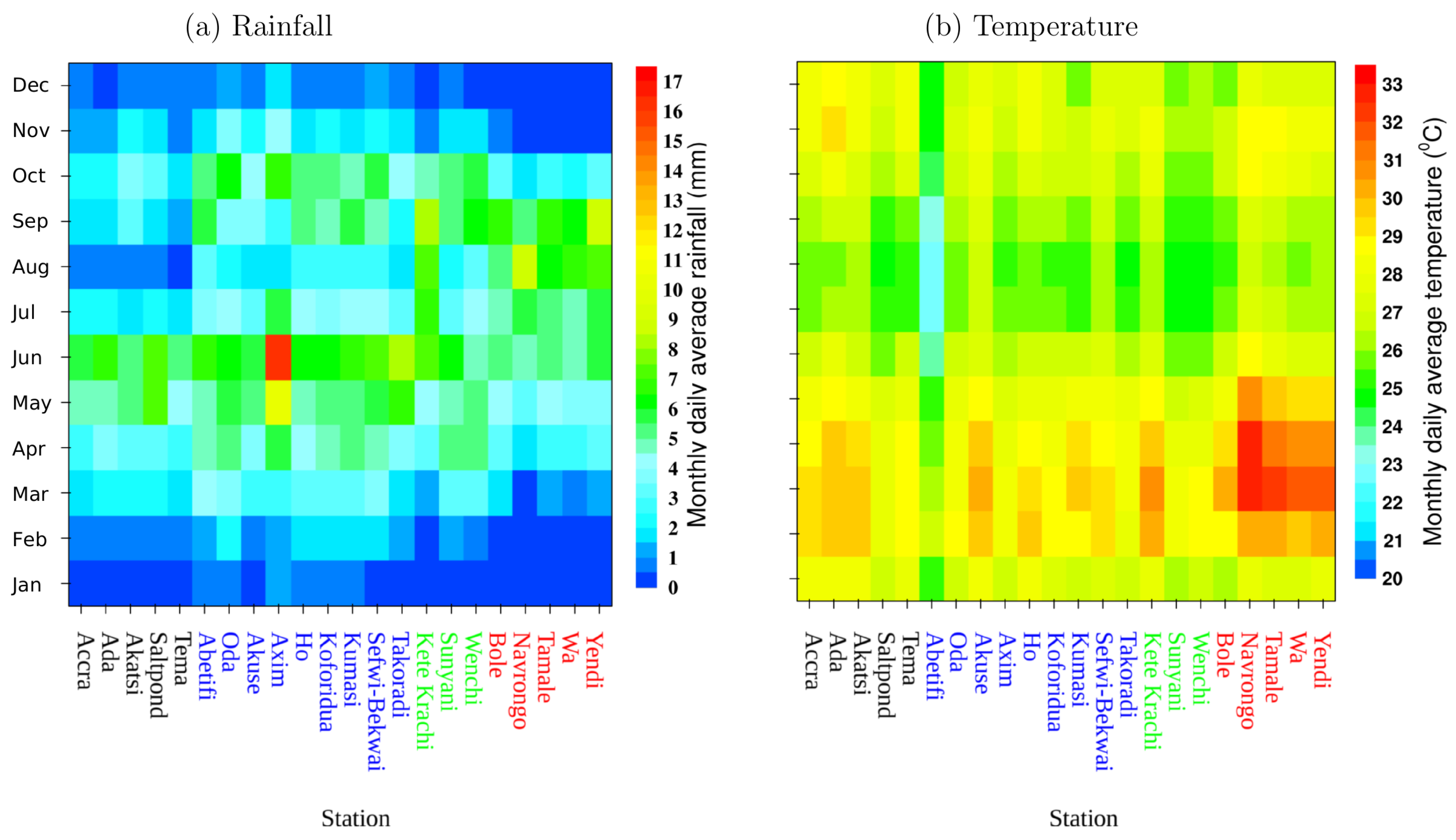
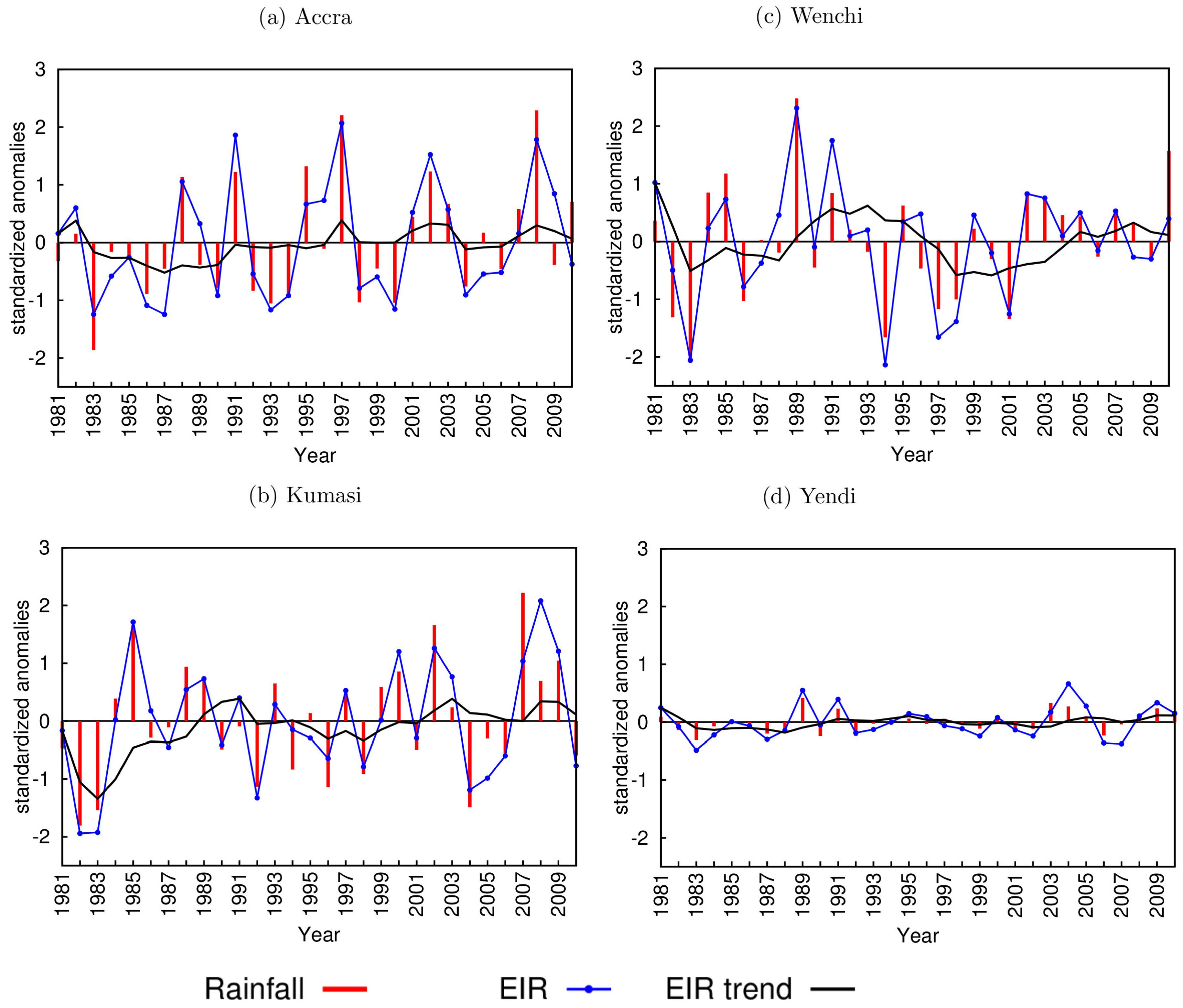
3.1. Rainfall and Temperature Variability
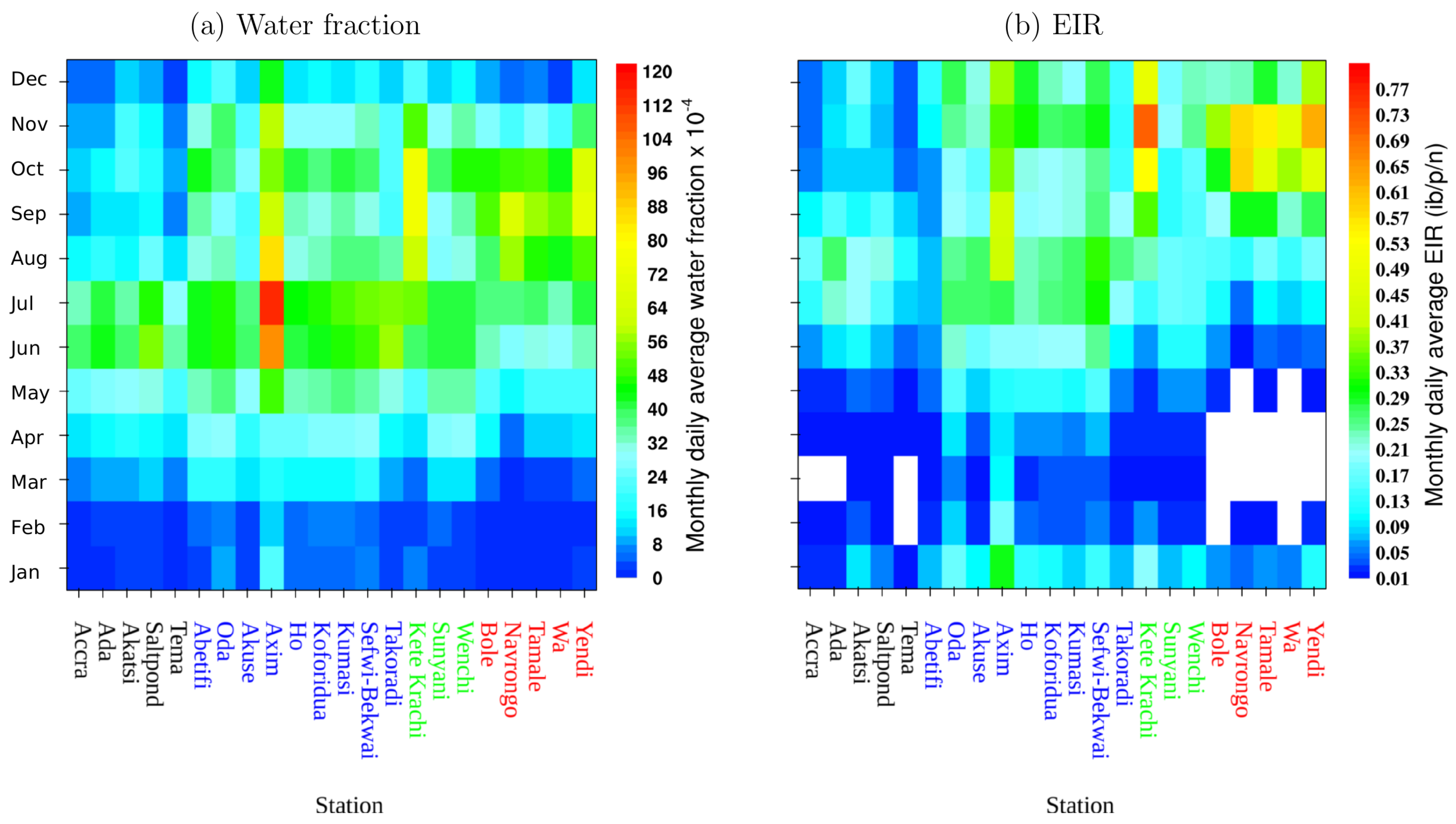
3.2. Model Results
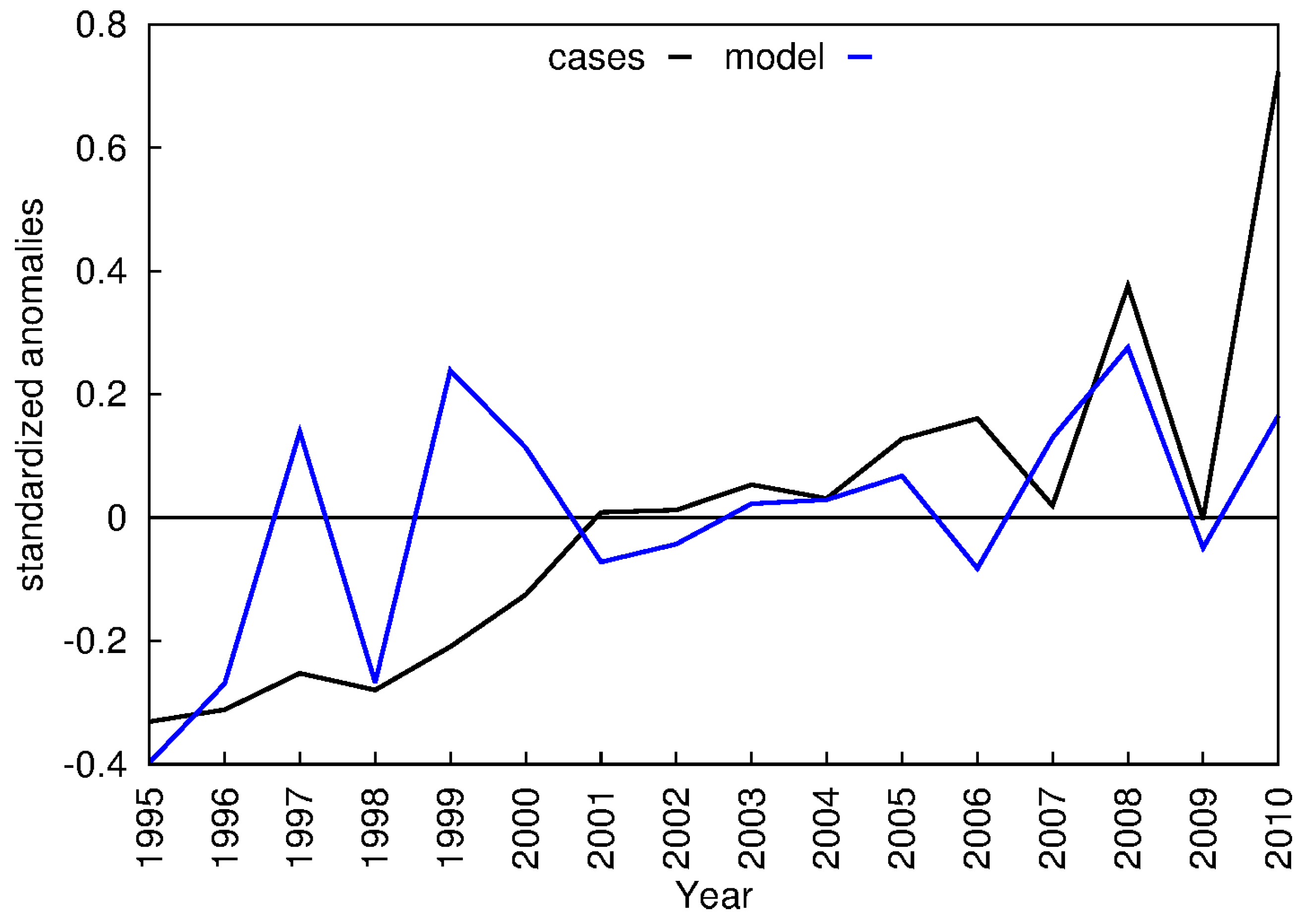
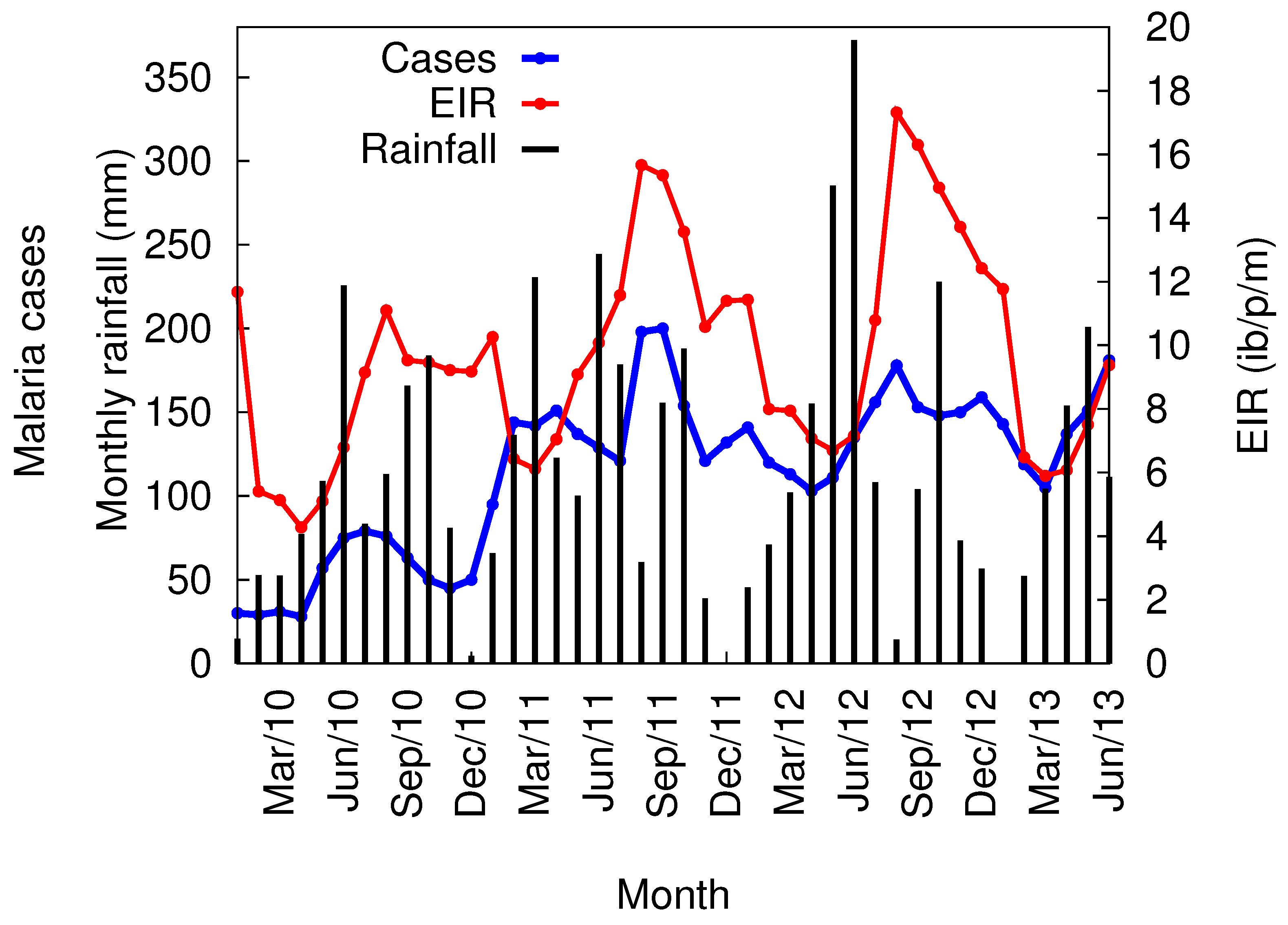
3.3. VECTRI Simulated EIR and Annual Malaria Cases
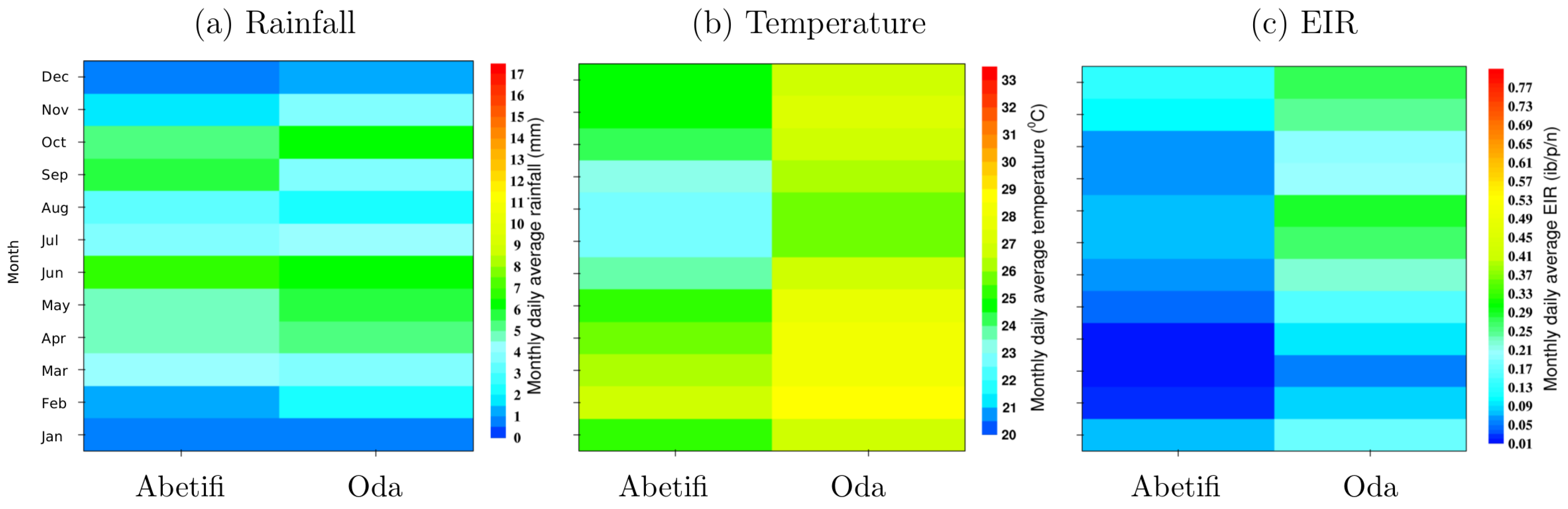
3.4. Local Scale Malaria Transmission
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| VECTRI | vector-borne disease community model of the International Centre for Theoretical Physics, Trieste |
| GMet | Ghana Meteorological Agency |
| EIR | entomological inoculation rate |
| HYDREMATS | hydrology, entomology, and malaria transmission simulator model |
| ib/p/y | infective bites/person/year |
| ib/p/n | infective bites/person/night |
References
- Adams, I.; Darko, D.; Accorsi, S. Malaria: A burden explored. Bull. Health Inf. 2004, 1, 28–34. [Google Scholar]
- National Malaria Control Programme (NMCP). Annual Report; National Malaria Control Programme (NMCP), Ministry of Health: Accra, Ghana, 2008.
- Ghana Health Service (GHS). Annual Report; National Malaria Control Programme (NMCP), Ministry of Health: Accra, Ghana, 2011.
- Asante, F.A.; Asenso-Okyere, K. Economic Burden of Malaria in Ghana; World Health Organ (WHO): Geneva, Switzerland, 2003; pp. 1–83. [Google Scholar]
- Sicuri, E.; Vieta, A.; Lindner, L.; Constenla, D.; Sauboin, C. The economic costs of malaria in children in three sub-Saharan countries: Ghana, Tanzania and Kenya. Malar. J. 2013, 12, 307. [Google Scholar] [CrossRef] [PubMed]
- Ghana Health Service (GHS). Strategic Plan for Malaria Control in Ghana 2008–2015; National Malaria Control Programme (NMCP), Ministry of Health: Accra, Ghana, 2009.
- Dontwi, I.; Dedu, V.; Aboagye, N. Ascertaining the Financial Cost of Malaria and Mitigating against It Using Actuarial Models for Financial Cost. Int. J. Financ. Res. 2013, 4, 94. [Google Scholar] [CrossRef]
- Akazili, J.; Aikins, M.; Binka, F.N. Malaria treatment in Northern Ghana: What is the treatment cost per case to households? Afr. J. Health Sci. 2008, 14, 70–79. [Google Scholar] [CrossRef]
- Appawu, M.; Baffoe-Wilmot, A.; Afari, E.; Nkrumah, F.; Petrarca, V. Species composition and inversion polymorphism of the Anopheles gambiae complex in some sites of Ghana, west Africa. Acta Trop. 1994, 56, 15–23. [Google Scholar] [CrossRef]
- Appawu, M.; Owusu-Agyei, S.; Dadzie, S.; Asoala, V.; Anto, F.; Koram, K.; Rogers, W.; Nkrumah, F.; Hoffman, S.L.; Fryauff, D.J. Malaria transmission dynamics at a site in northern Ghana proposed for testing malaria vaccines. Trop. Med. Int. Health 2004, 9, 164–170. [Google Scholar] [CrossRef] [PubMed]
- Yawson, A.; McCall, P.; Wilson, M.; Donnelly, M. Species abundance and insecticide resistance of Anopheles gambiae in selected areas of Ghana and Burkina Faso. Med. Vet. Entomol. 2004, 18, 372–377. [Google Scholar] [CrossRef] [PubMed]
- De Souza, D.; Kelly-Hope, L.; Lawson, B.; Wilson, M.; Boakye, D. Environmental factors associated with the distribution of Anopheles gambiae ss in Ghana; an important vector of lymphatic filariasis and malaria. PLoS ONE 2010, 5, e9927. [Google Scholar] [CrossRef] [PubMed]
- Kasasa, S.; Asoala, V.; Gosoniu, L.; Anto, F.; Adjuik, M.; Tindana, C.; Smith, T.; Owusu-Agyei, S.; Vounatsou, P. Spatio-temporal malaria transmission patterns in Navrongo demographic surveillance site, northern Ghana. Malar. J. 2013, 12, 63. [Google Scholar] [CrossRef] [PubMed]
- Dadzie, S.K.; Brenyah, R.; Appawu, M.A. Role of species composition in malaria transmission by the Anopheles funestus group (Diptera: Culicidae) in Ghana. J. Vector Ecol. 2013, 38, 105–110. [Google Scholar] [CrossRef] [PubMed]
- Afari, E.; Appawu, M.; Dunyo, S.; Baffoe-Wilmot, A.; Nkrumah, F. Malaria infection, morbidity and transmission in two ecological zones Southern Ghana. Afr. J. Health Sci. 1995, 2, 312–315. [Google Scholar] [PubMed]
- Klinkenberg, E.; McCall, P.; Hastings, I.; Wilson, M.; Amerasinghe, F.; Donnelly, M. Malaria and irrigated crops, Accra, Ghana. Emerg. Infect. Dis. 2005, 11, 1290. [Google Scholar] [CrossRef] [PubMed]
- Koram, K.; Owusu-Agyei, S.; Fryauff, D.; Anto, F.; Atuguba, F.; Hodgson, A.; Hoffman, S.; Nkrumah, F. Seasonal profiles of malaria infection, anaemia, and bednet use among age groups and communities in northern Ghana. Trop. Med. Int. Health 2003, 8, 793–802. [Google Scholar] [CrossRef] [PubMed]
- Dinko, B.; Oguike, M.C.; Larbi, J.A.; Bousema, T.; Sutherland, C.J. Persistent detection of Plasmodium falciparum, P. malariae, P. ovale curtisi and P. ovale wallikeri after ACT treatment of asymptomatic Ghanaian school-children. Int. J. Parasitol. Drugs Drug Resist. 2013, 3, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Afari, E.; Akanmori, B.; Nakano, T.; Ofori-Adjei, D. Plasmodium falciparum: Sensitivity to chloroquine in vivo in three ecological zones in Ghana. Trans. R. Soc. Trop. Med. Hyg. 1992, 86, 231–232. [Google Scholar] [CrossRef]
- Dery, D.B.; Brown, C.; Asante, K.P.; Adams, M.; Dosoo, D.; Amenga-Etego, S.; Wilson, M.; Chandramohan, D.; Greenwood, B.; Owusu-Agyei, S. Patterns and seasonality of malaria transmission in the forest-savannah transitional zones of Ghana. Malar. J. 2010, 9, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Donovan, C.; Siadat, B.; Frimpong, J. Seasonal and socio-economic variations in clinical and self-reported malaria in Accra, Ghana: Evidence from facility data and a community survey. Ghana Med. J. 2012, 46, 85–94. [Google Scholar] [PubMed]
- Klinkenberg, E.; McCall, P.; Wilson, M.; Amerasinghe, F.; Donnelly, M. Impact of urban agriculture on malaria vectors in Accra, Ghana. Malar. J. 2008, 7, 151. [Google Scholar] [CrossRef] [PubMed]
- Okoye, P.; Wilson, M.; Boakye, D.; Brown, C. Impact of the Okyereko irrigation project in Ghana on the risk of human malaria infection by Anopheles species (Diptera: Culicidae). Afr. Entomol. 2005, 13, 249. [Google Scholar]
- Akpalu, W.; Codjoe, S.N.A. Economic analysis of climate variability impact on malaria prevalence: The case of Ghana. Sustainability 2013, 5, 4362–4378. [Google Scholar] [CrossRef]
- Owusu-Agyei, S.; Asante, K.; Adjuik, M.; Adjei, G.; Awini, E.; Adams, M.; Newton, S.; Dosoo, D.; Dery, D.; Agyeman-Budu, A.; et al. Epidemiology of malaria in the forest-savanna transitional zone of Ghana. Malar. J. 2009, 8, 220. [Google Scholar] [CrossRef] [PubMed]
- Baird, J.K.; Agyei, S.O.; Utz, G.C.; Koram, K.; Barcus, M.J.; Jones, T.R.; Fryauff, D.J.; Binka, F.N.; Hoffman, S.L.; Nkrumah, F.N. Seasonal malaria attack rates in infants and young children in northern Ghana. Am. J. Trop. Med. Hyg. 2002, 66, 280–286. [Google Scholar] [PubMed]
- Tay, S.; Danuor, S.; Mensah, D.; Acheampong, G.; Abruquah, H.; Morse, A.; Caminade, C.; Badu, K.; Tompkins, A.; Hassan, H. Climate Variability and Malaria Incidence in Peri-urban, Urban and Rural Communities Around Kumasi, Ghana: A Case Study at Three Health Facilities; Emena, Atonsu and Akropong. Int. J. Parasitol. Res. 2012, 4, 83. [Google Scholar]
- Klutse, N.A.B.; Aboagye-Antwi, F.; Owusu, K.; Ntiamoa-Baidu, Y. Assessment of Patterns of Climate Variables and Malaria Cases in Two Ecological Zones of Ghana. Open J. Ecol. 2014, 4, 764. [Google Scholar] [CrossRef]
- Danuor, S.; Tay, S.; Annor, T.; Forkuo, E.; Bosompem, K.; Antwi, V. The impact of climate variability on malaria incidence and prevalence in the forest zone of Ghana–A case study at two (2) hospitals located within the Kumasi Metropolitan area of the Ashanti Region of Ghana. In Proceedings of the 2nd International Conference: Climate, Sustainability and Development in Semi-Arid Regions, Fortaleza, Brazil, 16–20 August 2010; pp. 16–20.
- Krefis, A.; Schwarz, N.; Krüger, A.; Fobil, J.; Nkrumah, B.; Acquah, S.; Loag, W.; Sarpong, N.; Adu-Sarkodie, Y.; Ranft, U.; et al. Modeling the Relationship between Precipitation and Malaria Incidence in Children from a Holoendemic Area in Ghana. Am. J. Trop. Med. Hyg. 2011, 84, 285–291. [Google Scholar] [CrossRef] [PubMed]
- Kelly-Hope, L.; Hemingway, J.; McKenzie, F. Environmental factors associated with the malaria vectors Anopheles gambiae and Anopheles funestus in Kenya. Malar. J. 2009, 8, 268. [Google Scholar] [CrossRef] [PubMed]
- Lowe, R.; Chirombo, J.; Tompkins, A.M. Relative importance of climatic, geographic and socio-economic determinants of malaria in Malawi. Malar. J. 2013, 12, 416. [Google Scholar] [CrossRef] [PubMed]
- Tompkins, A.M.; Ermert, V. A regional-scale, high resolution dynamical malaria model that accounts for population density, climate and surface hydrology. Malar. J. 2013, 12, 65. [Google Scholar] [CrossRef] [PubMed]
- Smith, M.; Macklin, M.G.; Thomas, C.J. Hydrological and geomorphological controls of malaria transmission. Earth-Sci. Rev. 2013, 116, 109–127. [Google Scholar] [CrossRef]
- Asare, E.O.; Tompkins, A.M.; Amekudzi, L.K.; Ermert, V. A breeding site model for regional, dynamical malaria simulations evaluated using in situ temporary ponds observations. Geospat. Health 2016, 11, 390. [Google Scholar] [CrossRef] [PubMed]
- Tompkins, A.M.; Di Giuseppe, F. Potential predictability of malaria in Africa using ECMWF monthly and seasonal climate forecasts. J. Appl. Meteorol. Climatol. 2015, 54, 521–540. [Google Scholar] [CrossRef]
- Owusu, K.; Waylen, P.R. The changing rainy season climatology of mid-Ghana. Theor. Appl. Climatol. 2013, 112, 419–430. [Google Scholar] [CrossRef]
- Manzanas, R.; Amekudzi, L.; Preko, K.; Herrera, S.; Gutiérrez, J.M. Precipitation variability and trends in Ghana: An intercomparison of observational and reanalysis products. Clim. Chang. 2014, 124, 805–819. [Google Scholar] [CrossRef]
- Amekudzi, L.K.; Yamba, E.I.; Preko, K.; Asare, E.O.; Aryee, J.; Baidu, M.; Codjoe, S.N. Variabilities in Rainfall Onset, Cessation and Length of Rainy Season for the Various Agro-Ecological Zones of Ghana. Climate 2015, 3, 416–434. [Google Scholar] [CrossRef]
- Ghana Ministry of Health. Facts and Figures. 2015. Available online: https://en.wikipedia.org/wiki/Main_Page (accessed on 3 December 2015).
- Robert, V.; Macintyre, K.; Keating, J.; Trape, J.; Duchemin, J.; Warren, M.; Beier, J. Malaria transmission in urban sub-Saharan Africa. Am. J. Trop. Med. Hyg. 2003, 68, 169–176. [Google Scholar] [PubMed]
- Paaijmans, K.; Wandago, M.; Githeko, A.; Takken, W. Unexpected high losses of Anopheles gambiae larvae due to rainfall. PLoS ONE 2007, 2, e1146. [Google Scholar] [CrossRef] [PubMed]
- United States Department of Agriculture (USDA). National Engineering Handbook, Section 4: Hydrology; United States Department of Agriculture: Washington, DC, USA, 1972.
- Asare, E.O.; Tompkins, A.M.; Bomblies, A. A Regional Model for Malaria Vector Developmental Habitats Evaluated Using Explicit, Pond-Resolving Surface Hydrology Simulations. PLoS ONE 2016, 11, e0150626. [Google Scholar] [CrossRef] [PubMed]
- Bomblies, A.; Duchemin, J.; Eltahir, E. Hydrology of malaria: Model development and application to a Sahelian village. Water Resour. Res. 2008, 44, W12445. [Google Scholar] [CrossRef]
- Ghana Statistical Service (GSS). Ghana Multiple Indicator Cluster Survey with an Enhanced Malaria Module and Biomarker; Final Report; Ghana Statistical Service: Accra, Ghana, 2011.
- Koram, K.A.; Owusu-Agyei, S.; Utz, G.; Binka, F.N.; Baird, J.K.; Hoffman, S.L.; Nkrumah, F.K. Severe anemia in young children after high and low malaria transmission seasons in the Kassena-Nankana district of northern Ghana. Am. J. Trop. Med. Hyg. 2000, 62, 670–674. [Google Scholar] [PubMed]
- Dieng, H.; Rahman, G.S.; Hassan, A.A.; Salmah, M.C.; Satho, T.; Miake, F.; Boots, M.; Sazaly, A. The effects of simulated rainfall on immature population dynamics of Aedes albopictus and female oviposition. Int. J. Biometeorol. 2012, 56, 113–120. [Google Scholar] [CrossRef] [PubMed]
- Paaijmans, K.; Read, A.; Thomas, M. Understanding the link between malaria risk and climate. Proc. Natl. Acad. Sci. USA 2009, 106, 13844–13849. [Google Scholar] [CrossRef] [PubMed]
- Craig, M.; Snow, R.; Le Sueur, D. A climate-based distribution model of malaria transmission in sub-Saharan Africa. Parasitol. Today 1999, 15, 105–111. [Google Scholar] [CrossRef]
- Owusu, E.D.; Buabeng, V.; Dadzie, S.; Brown, C.A.; Grobusch, M.P.; Mens, P. Characteristics of asymptomatic Plasmodium spp. parasitaemia in Kwahu-Mpraeso, a malaria endemic mountainous district in Ghana, West Africa. Malar. J. 2016, 15, 1. [Google Scholar] [CrossRef] [PubMed]
- Wihibeturo, B.A. Effect of Seasonal Variability on the Incidence and Transmission Patterns of Malaria in Urban, Peri-Urban and Rural Communities around Kumasi, Ghana. Master’s Thesis, Kwame Nkrumah University of Science and Technology, Kumasi, Ghana, 2014. [Google Scholar]
| Symbol | Value | Units |
|---|---|---|
| 0.1 | ||
| 0.005 | ||
| 250 | mm | |
| p | 1.5 | |
| 250 | mm | |
| E | 5 | mm |
| 90 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asare, E.O.; Amekudzi, L.K. Assessing Climate Driven Malaria Variability in Ghana Using a Regional Scale Dynamical Model. Climate 2017, 5, 20. https://doi.org/10.3390/cli5010020
Asare EO, Amekudzi LK. Assessing Climate Driven Malaria Variability in Ghana Using a Regional Scale Dynamical Model. Climate. 2017; 5(1):20. https://doi.org/10.3390/cli5010020
Chicago/Turabian StyleAsare, Ernest O., and Leonard K. Amekudzi. 2017. "Assessing Climate Driven Malaria Variability in Ghana Using a Regional Scale Dynamical Model" Climate 5, no. 1: 20. https://doi.org/10.3390/cli5010020
APA StyleAsare, E. O., & Amekudzi, L. K. (2017). Assessing Climate Driven Malaria Variability in Ghana Using a Regional Scale Dynamical Model. Climate, 5(1), 20. https://doi.org/10.3390/cli5010020





