Reliability and Robustness Analysis of the Masinga Dam under Uncertainty
Abstract
:1. Introduction and Background
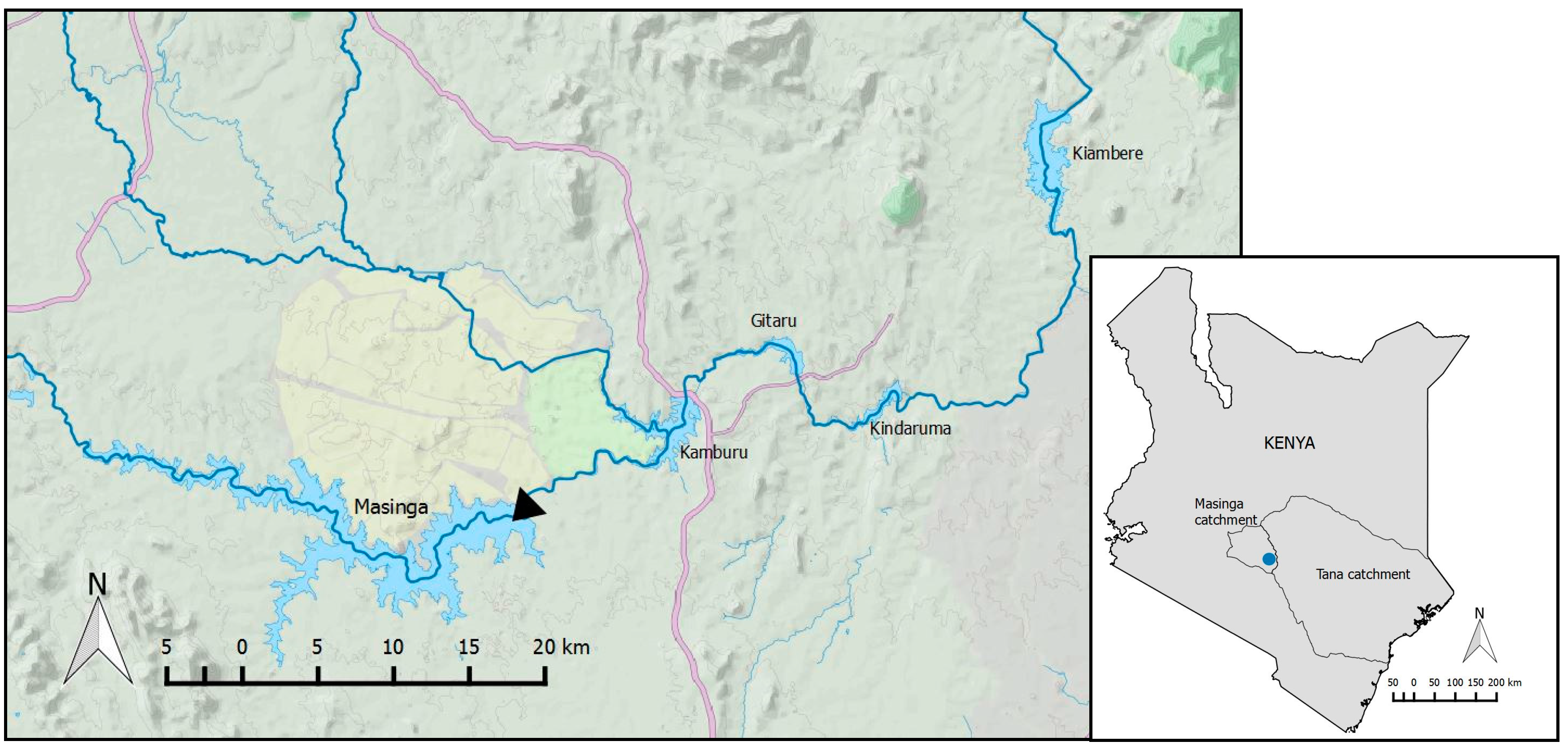
Case Study: Kenya’s Masinga Dam
2. Masinga Dam Model Building
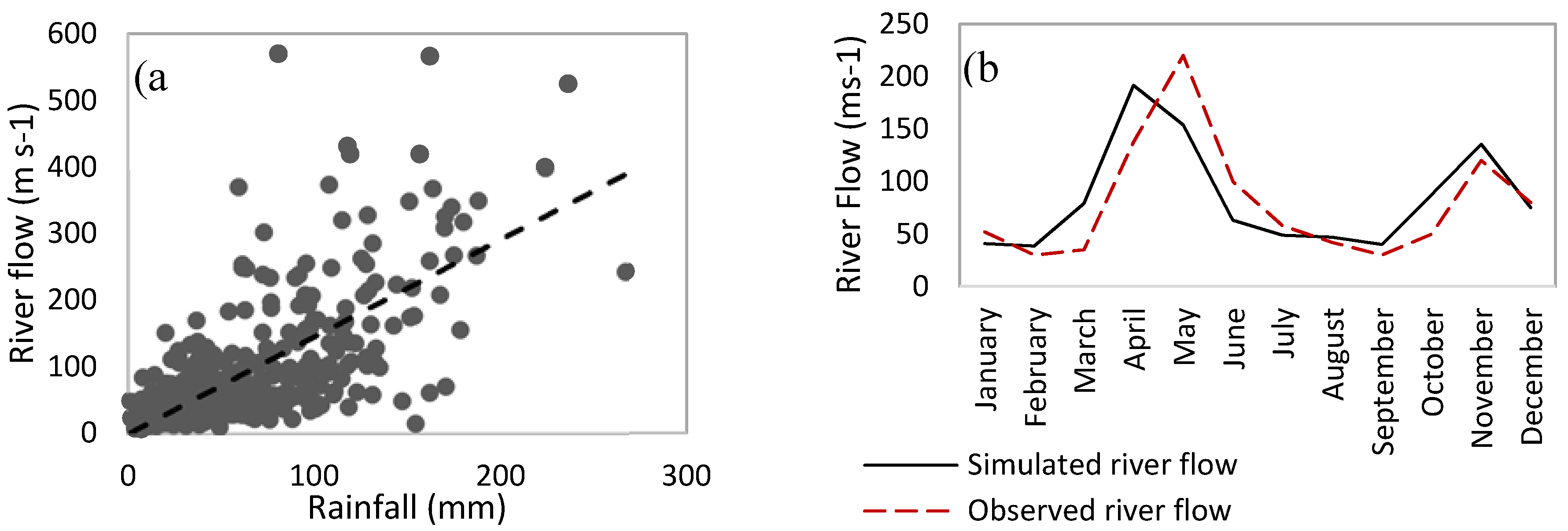
2.1. Data Collection
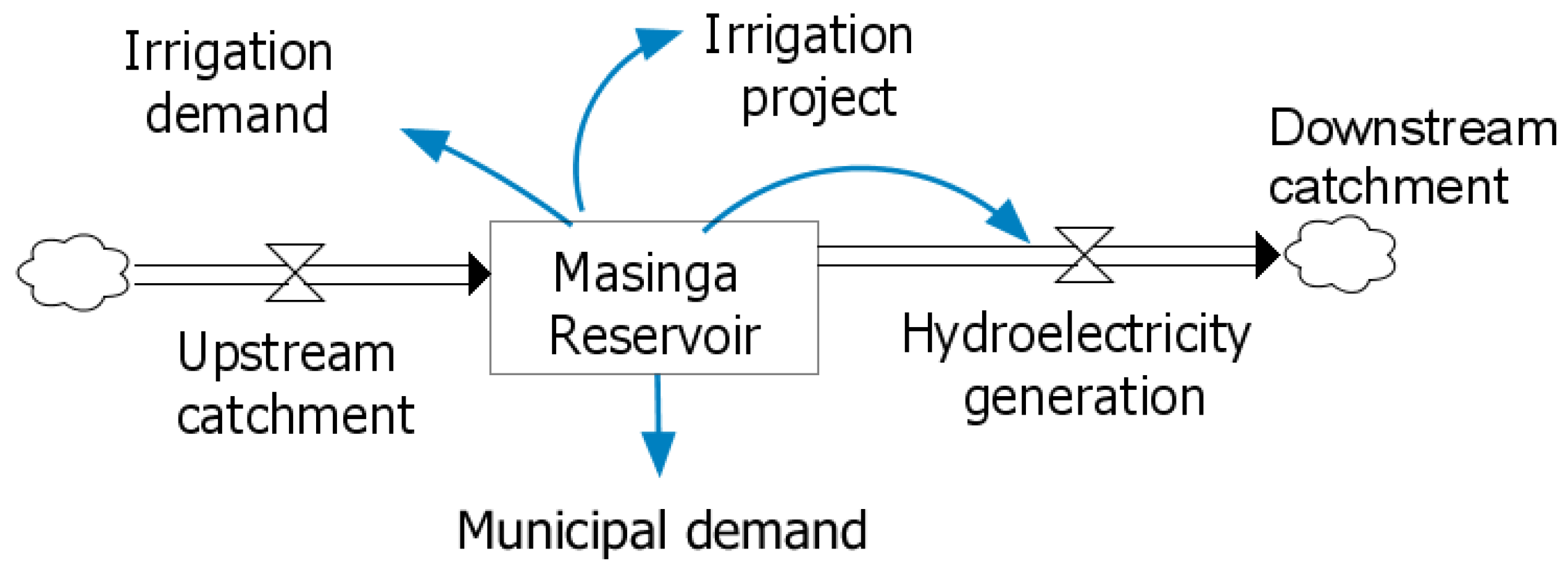
2.2. Model Construction
2.3. Model Setting and Scenario Building
3. Results
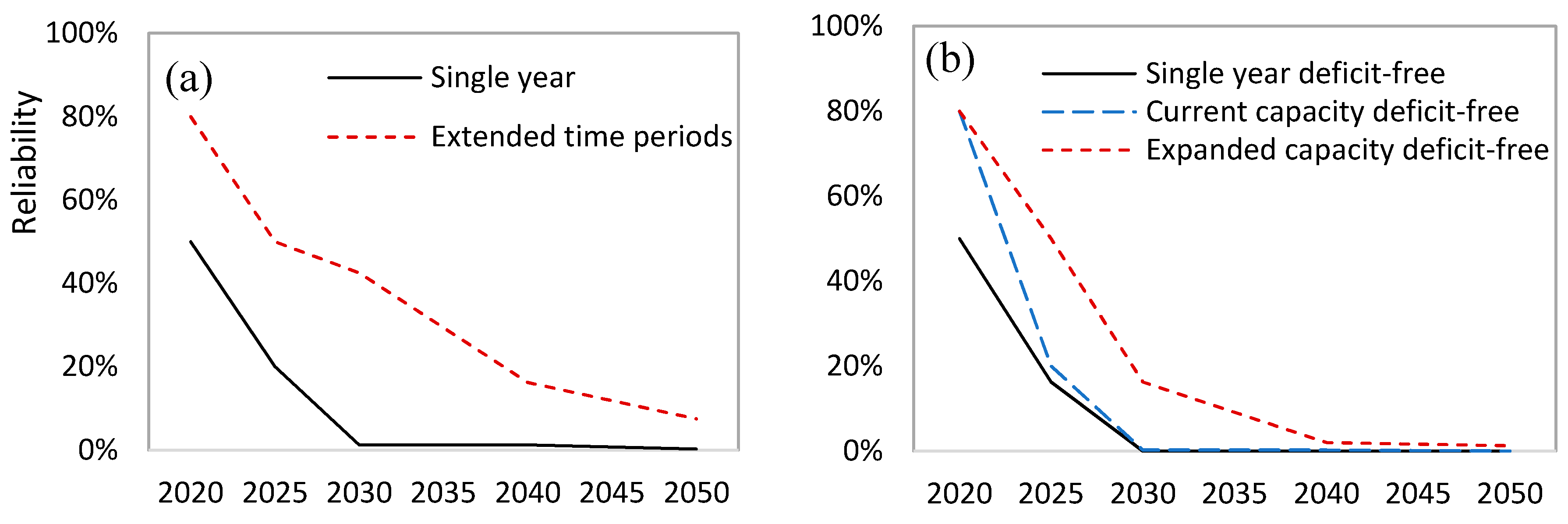
3.1. Single Year Models—Short-Term Planning
3.2. Multiple Years Models—Long Term Planning
3.3. Increased Capacity Model—Long Term Planning
3.4. Reliability
4. Discussion
5. Conclusions and Future Work
Author Contributions
Conflicts of Interest
References
- United Nations Educational, Scientific and Cultural Organization (UNESCO). Managing Water under Uncertainty and Risk. The United Nations World Water Development Report 4; UNESCO: Paris, France, 2012; Volume 1. [Google Scholar]
- Ding, N.; Erfani, R.; Mokhtar, H.; Erfani, T. Agent based modelling for water resource allocation in the transboundary Nile River. Water 2016, 8, 139. [Google Scholar] [CrossRef]
- Tan, C.; Erfani, T.; Erfani, R. Water for Energy and Food: A System Modelling Approach for Blue Nile River Basin. Environments 2017, 4, 15. [Google Scholar] [CrossRef]
- Erfani, T.; Erfani, R. An evolutionary approach to solve a system of multiple interrelated agent problems. Appl. Soft Comput. 2015, 37, 40–47. [Google Scholar] [CrossRef]
- Erfani, T.; Erfani, R. Fair resource allocation using multi-population evolutionary algorithm. In Applications of Evolutionary Computation, Proceedings of the European Conference, EvoApplications, Copenhagen, Denmark, 8–10 April 2015; Springer: Copenhagen, Denmark, 2015. [Google Scholar]
- Erfani, T.; Binions, O.; Harou, J.J. Protecting environmental flows through enhanced water licensing and water markets. Hydrol. Earth Syst. Sci. 2015, 19, 675–689. [Google Scholar] [CrossRef]
- Erfani, T.; Binions, O.; Harou, J.J. Simulating water markets with transaction costs. Water Resour. Res. 2014, 50, 4726–4745. [Google Scholar] [CrossRef] [PubMed]
- Wilby, R.L. A review of climate change impacts on the built environment. Built Environ. 2007, 33, 31–45. [Google Scholar] [CrossRef]
- Vörösmarty, C.J.; Green, P.; Salisbury, J.; Lammers, R.B. Global water resources: Vulnerability from climate change and population growth. Science 2000, 289, 284–288. [Google Scholar] [CrossRef] [PubMed]
- Arnell, N.W. Climate change and global water resources: SRES emissions and socio-economic scenarios. Glob. Environ. Chang. 2004, 14, 31–52. [Google Scholar] [CrossRef]
- Alcamo, J.; Flörke, M.; Märker, M. Future long-term changes in global water resources driven by socio-economic and climatic changes. Hydrol. Sci. J. 2007, 52, 247–275. [Google Scholar] [CrossRef]
- Herman, J.D.; Reed, P.M.; Zeff, H.B.; Characklis, G.W. How should robustness be defined for water systems planning under change? J. Water Resour. Plan. Manag. 2015, 141, 04015012. [Google Scholar] [CrossRef]
- Turner, S.W.; Blackwell, R.J.; Smith, M.A.; Jeffrey, P.J. Risk-based water resources planning in England and Wales: Challenges in execution and implementation. Urban Water J. 2016, 13, 182–197. [Google Scholar] [CrossRef]
- Hall, J.; Borgomeo, E. Risk-based principles for defining and managing water security. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2013, 371, 20120407. [Google Scholar] [CrossRef] [PubMed]
- Borgomeo, E.; Hall, J.W.; Fung, F.; Watts, G.; Colquhoun, K.; Lambert, C. Risk-based water resources planning: Incorporating probabilistic nonstationary climate uncertainties. Water Resour. Res. 2014, 50, 6850–6873. [Google Scholar] [CrossRef]
- Giuliani, M.; Castelletti, A. Is robustness really robust? How different definitions of robustness impact decision-making under climate change. Clim. Chang. 2016, 135, 409–424. [Google Scholar]
- Parkinson, S.C.; Djilali, N. Robust response to hydro-climatic change in electricity generation planning. Clim. Chang. 2015, 130, 475–489. [Google Scholar] [CrossRef]
- Wilby, R.L.; Dessai, S. Robust adaptation to climate change. Weather 2010, 65, 180–185. [Google Scholar] [CrossRef]
- Hashimoto, T.; Stedinger, J.R.; Loucks, D.P. Reliability, resiliency, and vulnerability criteria for water resource system performance evaluation. Water Resour. Res. 1982, 18, 14–20. [Google Scholar] [CrossRef]
- Howell, L. Global Risks 2013, Eighth Edition: An Initiative of the Risk Response Network; World Economic Forum: Geneva, Switzerland, 2013. [Google Scholar]
- UNEP. Tapping the Tana. Available online: http://www.unep.org/stories/Ecosystems/Tapping-the-Tana.asp (accessed on 26 January 2017).
- UN Water. World Water Assessment Programme: Case Study Kenya; WWAP Kenya National Water Development Report, UN-Water; UNESCO World Water Assessment Programme Secretariat: Colombella, Italy, 2006. [Google Scholar]
- Energy Regulatory Commission (ERC). Scaling-Up Renewable Energy Program (SREP): Investment Plan for Kenya; Draft; Republic of Kenya: Nairobi, Kenya, 2011. [Google Scholar]
- Piesold, D.D.A.; Tattersfield, J.; Hodgson, C.W. Masinga dam in Kenya. In Institution of Civil Engineers Proceedings; Thomas Telford: London, UK, 1984; Volume 76, pp. 999–1025. [Google Scholar]
- Hurford, A.P.; Harou, J.J. Balancing ecosystem services with energy and food security–Assessing trade-offs from reservoir operation and irrigation investments in Kenya’s Tana Basin. Hydrol. Earth Syst. Sci. 2014, 18, 3259–3277. [Google Scholar] [CrossRef]
- Lebrun, D.; Hamerlynck, O.; Duvail, S.; Nyunja, J. The importance of flexibility: An analysis of the largescale Tana delta irrigation project in Kenya, implemented under an estate system. In Shared Waters, Shared Opportunities; French Institute for Research in Africa (IFRA): Nairobi, Kenya, 2010; pp. 261–282. [Google Scholar]
- International Atomic Energy Agency (IEAE). Brief of the Kenyan energy sector and current status of nuclear power program. In Proceedings of the IAEA Meeting on Topical Issues in the Development of Nuclear Power Infrastructure, Nairobi, Kenya, 3–6 February 2015.
- Government of Kenya. Kenya Vision 2030—A Globally Competitive and Prosperous Kenya. Available online: https://www.opendata.go.ke/api/file_data/IyRGPwVuC0MJhKZnMa1YA3s0vXBJkCVeDWgy_AS5d_0?filename=VISION_2030.pdf (accessed on 19 August 2015).
- Mireri, C.; Onjala, J.; Oguge, N. The Economic Valuation of the Proposed Tana Integrated Sugar Project (TISP), Kenya; Prepared for Nature Kenya; Royal Society for the Protection of Birds: London, UK, 2008. [Google Scholar]
- Nippon Koei. The Project on the Development of the National Water Master Plan 2030; Final Report, Volume III Part F—Tana Catchment Area; The Republic of Kenya, Water Resources Management Authority: Nairobi, Kenya, 2013. [Google Scholar]
- Vörösmarty, C.J.; Fekete, B.M.; Tucker, B.A. Global River Discharge, 1807–1991, Version 1.1 (RivDIS Data Set); Oak Ridge National Laboratory Distributed Active Archive Center: Oak Ridge, TN, USA, 1998. [Google Scholar]
- Oludhe, C.; Sankarasubramanian, A.; Sinha, T.; Devineni, N.; Lall, U. The role of multimodel climate forecasts in improving water and energy management over the Tana River Basin, Kenya. J. Appl. Meteorol. Climatol. 2013, 52, 2460–2475. [Google Scholar] [CrossRef]
- Hoff, H.; Noel, S.; Droogers, P. Water Use and Demand in the Tana Basin: Analysis Using the Water Evaluation and Planning Tool (WEAP); Green Water Credits Report 4; ISRIC—World Soil Information: Wageningen, The Netherlands, 2007. [Google Scholar]
- Jillo, R. KenGen Closes Masinga Dam; Business & Tech, CAPITALFM. CO.KE.: Nairobi, Kenya, 2009. [Google Scholar]
- The American Society of Mechanical Engineers (ASME). The Guide to Hydropower Mechanical Design; HCI Publications: Kansas City, MO, USA, 1996. [Google Scholar]
- Mitchell, T.D.; Carter, T.R.; Jones, P.D.; Hulme, M.; New, M. A Comprehensive Set of High-Resolution Grids of Monthly Climate for Europe and the Globe: The Observed Record (1901–2000) and 16 Scenarios (2001–2100); Working Paper 55; Tyndall Centre for Climate Change Research: Norwich, UK, 2004. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2001: The Scientific Basis. Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Houghton, J.T., Ding, Y., Griggs, D.J., Noguer, M., van der Linden, P.J., Dai, X., Maskell, K., Johnson, C.A., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2001. [Google Scholar]
- United Nations. Probabilistic Population Projections based on the World Population Prospects: The 2012 Revision. Population Division, DESA. ST/ESA/SER.A/353. 2014. Available online: http://esa.un.org.unpd/ppp/ (accessed on 1 August 2015).
- Nippon Koei. The Project on the Development of the National Water Master Plan 2030—Progress Report (4). 2012. Available online: http://www.wrma.or.ke/images/presspdf/ProgressReport_4_%20NWMP%202030.pdf (accessed on 2 August 2015).
- Kiptala, J.K. Intersectoral Allocation in the Tana River Basin (Kenya). Master Thesis, Institute for Water Education, UNESCO-IHE, Delft, The Netherlands, 2008. [Google Scholar]
- South African Government. Statistics South Africa on Municipal Electricity and Water Purchases and Sales. Available online: http://www.gov.za/speeches/statistics-south-africa-municipal-electricity-and-water-purchases-31-mar-2015-0000 (accessed on 26 January 2017).
- Low, K.G.; Grant, S.B.; Hamilton, A.J.; Gan, K.; Saphores, J.; Arora, M.; Feldman, D.L. Fighting drought with innovation: Melbourne’s response to the Millennium Drought in Southeast Australia. Wiley Interdiscip. Rev. Water 2015, 2, 315–328. [Google Scholar] [CrossRef]
- Faisal, I.M.; Parveen, S. Food security in the face of climate change, population growth, and resource constraints: Implications for Bangladesh. Environ. Manag. 2004, 34, 487–498. [Google Scholar] [CrossRef] [PubMed]
- Droogers, P.; Kauffman, J.H.; Immerzeel, W.W.; Dijkshoorn, J.A.; Huting, J.R.M. Green and Blue Water Services in Tana River Basin, Kenya. Exploring Options Using an Integrated Modeling Framework; ISRIC-World Soil Information: Wageningen, The Netherlands, 2006. [Google Scholar]
- Hongling, L.; Chuanwen, J.; Yan, Z. A review on risk-constrained hydropower scheduling in deregulated power market. Renew. Sustain. Energy Rev. 2008, 12, 1465–1475. [Google Scholar] [CrossRef]
- Lund, J.R. Developing Seasonal and Long-Term Reservoir System Operation Plans Using HEC-PRM; (No. Hec-RD-40); Hydrologic Engineering Center: Davis, CA, USA, 1996. [Google Scholar]
- Pritchard, G.; Philpott, A.B.; Neame, P.J. Hydroelectric reservoir optimization in a pool market. Math. Program. 2005, 103, 445–461. [Google Scholar] [CrossRef]
- Chen, L. Real Coded Genetic Algorithm Optimization of Long Term Reservoir Operation. J. Am. Water Resour. Assoc. 2003, 39, 1157–1165. [Google Scholar] [CrossRef]
- Bessler, F.T.; Savic, D.A.; Walters, G.A. Water reservoir control with data mining. J. Water Resour. Plan. Manag. 2003, 129, 26–34. [Google Scholar] [CrossRef]
- Waithaka, J. KenGen Now Plans Expansion of Dam to Boost Power Output. 2010. Available online: http://www.businessdailyafrica.com/Corporate-News/KenGen-now-plans-expansion-of-dam-to-boost-power-output/-/539550/917226/-/item/1/-/9twdl1z/-/index.html (accessed on 31 December 2016).
- Knoop, L.; Sambalino, F.; van Steenbergen, F. Securing Water and Land in the Tana Basin: A Resource Book for Water Managers and Practitioners; UNEP/WRMA/3R Water Secretaria: Wageningen, The Netherlands, 2012. [Google Scholar]
- Rockström, J.; Karlberg, L.; Wani, S.P.; Barron, J.; Hatibu, N.; Oweis, T.; Bruggeman, A.; Farahani, J.; Qiang, Z. Managing water in rainfed agriculture—The need for a paradigm shift. Agric. Water Manag. 2010, 97, 543–550. [Google Scholar] [CrossRef]
- Jensen, J.P.; Jeppesen, E.; Olrik, K.; Kristensen, P. Impact of nutrients and physical factors on the shift from yanobacterial to chlorophyte dominance in shallow Danish lakes. Can. J. Fish. Aquat. Sci. 1994, 51, 1692–1699. [Google Scholar] [CrossRef]
- Mooij, W.M.; Hülsmann, S.; de Senerpont Domis, L.N.; Nolet, B.A.; Bodelier, P.L.E.; Boers, P.C.M.; Miguel Dionisio Pires, L.; Gons, H.J.; Ibelings, B.W.; Lammens, E.H.; et al. The impact of climate change on lakes in the Netherlands: A review. Aquat. Ecol. 2005, 39, 381–400. [Google Scholar] [CrossRef]
- Jumbe, J.J. The Effect of Changing Water Level, the Fishes and Fisheries of Masinga and Kamburu Dams, Tana River, Kenya. Ph.D. Thesis, Kenyatta University, Nairobi, Kenya, 2012. [Google Scholar]
- Abila, R.; Muthangya, M.; Mutuku, E.; Mutati, K.; Munguti, M.; Musyoka, C.M. Physico-chemical and bacteriological quality assessment of shallow wells in Kitui town, Kenya. J. Environ. Sci. Water Resour. 2012, 1, 27–33. [Google Scholar]
- De Wit, M.; Stankiewicz, J. Changes in surface water supply across Africa with predicted climate change. Science 2006, 311, 1917–1921. [Google Scholar] [CrossRef] [PubMed]
- Challinor, A.; Wheeler, T.; Garforth, C.; Craufurd, P.; Kassam, A. Assessing the vulnerability of food crop systems in Africa to climate change. Clim. Chang. 2007, 83, 381–399. [Google Scholar] [CrossRef]
- Ragab, R.; Prudhomme, C. Sw—Soil and Water: Climate change and water resources management in arid and semi-arid regions: Prospective and challenges for the 21st century. Biosyst. Eng. 2002, 81, 3–34. [Google Scholar] [CrossRef]
- Bou-Zeid, E.; El-Fadel, M. Climate change and water resources in Lebanon and the Middle East. J. Water Resour. Plan. Manag. 2002, 128, 343–355. [Google Scholar] [CrossRef]
- Nelson, G.C.; Rosegrant, M.W.; Koo, J.; Robertson, R.; Sulser, T.; Zhu, T.; Ringler, C.; Msangi, S.; Palazzo, A.; Batka, M.; et al. Climate Change: Impact on Agriculture and Costs of Adaptation; International Food Policy Research Institute: Washington, DC, USA, 2009. [Google Scholar]
- Nippon Koei. The Project on the Development of the National Water Master Plan 2030; Final Report; Volume V Sectoral Report (E)—Agriculture and Irrigation; The Republic of Kenya, Water Resources Management Authority: Nairobi, Kenya, 2013.
- Jager, H.I.; Smith, B.T. Sustainable reservoir operation: can we generate hydropower and preserve ecosystem values? River Res. Appl. 2008, 24, 340–352. [Google Scholar] [CrossRef]
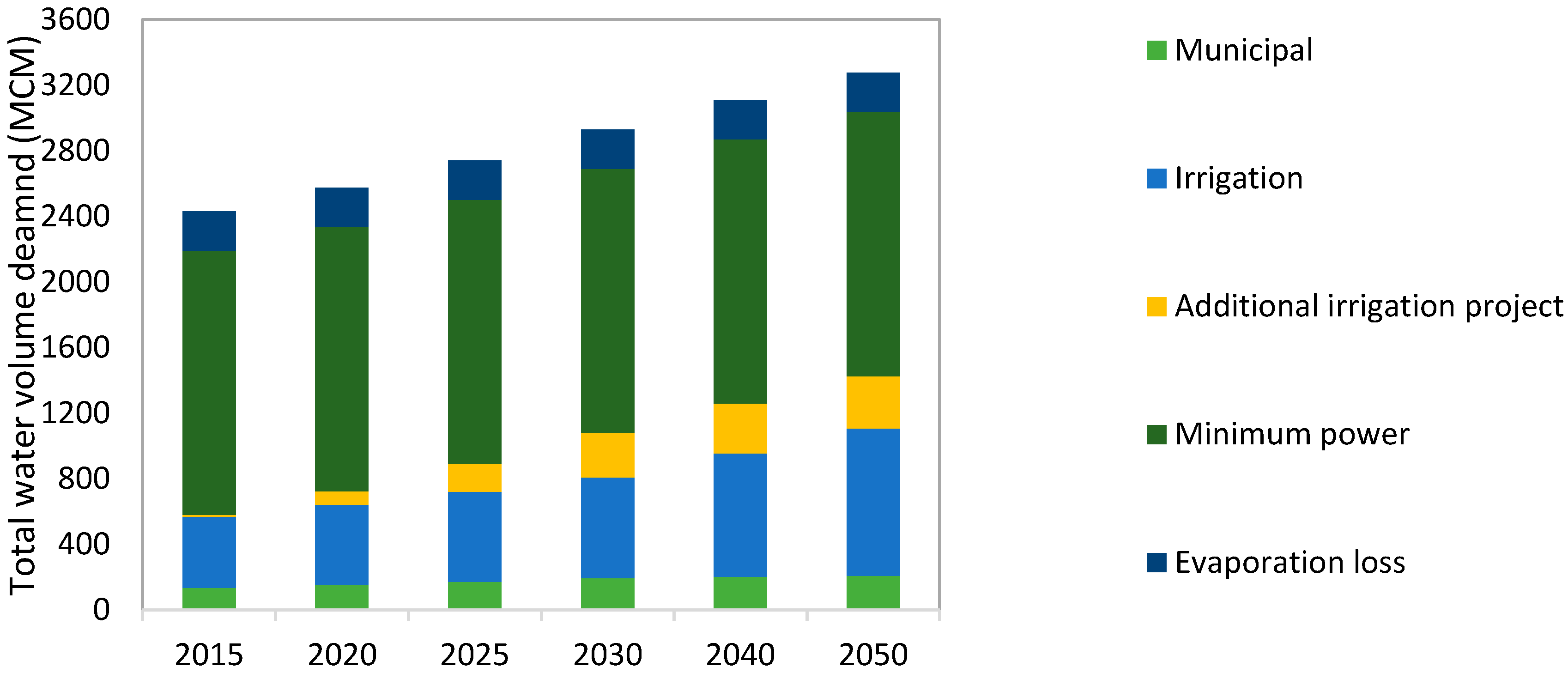
| 2020 | ||||||||||
| Flow rate projection percentile | Population projection percentile | |||||||||
| 5% | 20% | 50% | 80% | 95% | ||||||
| D | S | D | S | D | S | D | S | D | S | |
| 5% | −2.57% | −4.20% | −2.90% | −4.76% | −3.56% | −5.87% | −4.18% | −6.94% | −4.54% | −7.58% |
| 20% | −0.34% | −0.55% | −0.68% | −1.11% | −1.34% | −2.22% | −2.44% | −3.51% | −2.77% | −3.93% |
| 50% | 4.99% | 8.16% | 4.63% | 7.59% | 3.93% | 6.49% | 3.26% | 5.42% | 2.86% | 4.78% |
| 80% | 9.11% | 14.9% | 8.73% | 14.3% | 8.01% | 13.2% | 7.31% | 12.1% | 6.90% | 11.5% |
| 95% | 11.3% | 18.5% | 10.9% | 17.9% | 10.2% | 16.8% | 9.45% | 15.7% | 9.04% | 15.1% |
| 2025 | ||||||||||
| Flow rate projection percentile | Population projection percentile | |||||||||
| 5% | 20% | 50% | 80% | 95% | ||||||
| D | S | D | S | D | S | D | S | D | S | |
| 5% | −8.36% | −14.4% | −9.08% | −15.8% | −10.2% | −17.9% | −11.4% | −20.3% | −11.8% | −21.2% |
| 20% | −5.94% | −10.3% | −6.55% | −11.4% | −13.5% | −23.8% | −9.07% | −16.2% | −9.51% | −17.0% |
| 50% | −0.24% | −0.42% | −0.88% | −1.53% | −2.07% | −3.63% | −3.42% | −6.09% | −3.89% | −6.97% |
| 80% | 4.17% | 7.19% | 3.50% | 6.08% | 2.27% | 3.98% | 3.75% | 6.68% | 6.43% | 11.5% |
| 95% | 6.51% | 11.2% | 5.83% | 10.1% | 4.57% | 8.02% | 3.12% | 5.56% | 2.62% | 4.69% |
| 2030 | ||||||||||
| Flow rate projection percentile | Population projection percentile | |||||||||
| 5% | 20% | 50% | 80% | 95% | ||||||
| D | S | D | S | D | S | D | S | D | S | |
| 5% | −14.1% | −25.7% | −14.9% | −27.4% | −16.5% | −31.1% | −18.4% | −35.3% | −19.0% | −36.9% |
| 20% | −11.3% | −20.6% | −12.3% | −22.6% | −14.0% | −26.3% | −15.9% | −30.5% | −16.6% | −32.1% |
| 50% | −5.31% | −9.68% | −6.32% | −11.6% | −8.14% | −15.3% | −10.2% | −19.6% | −10.9% | −21.1% |
| 80% | −0.60% | −1.09% | −1.66% | −3.05% | −3.57% | −6.71% | −5.71% | −11.0% | −6.48% | −12.6% |
| 95% | 1.87% | 3.41% | 0.78% | 1.44% | −1.18% | −2.22% | −3.37% | −6.49% | −4.16% | −8.07% |
| 2040 | ||||||||||
| Flow rate projection percentile | Population projection percentile | |||||||||
| 5% | 20% | 50% | 80% | 95% | ||||||
| D | S | D | S | D | S | D | S | D | S | |
| 5% | −17.0% | −31.5% | −18.6% | −35.2% | −21.5% | −42.2% | −24.5% | −49.8% | −25.9% | −53.7% |
| 20% | −13.4% | −24.8% | −15.1% | −28.5% | −18.1% | −35.5% | −21.2% | −43.2% | −22.7% | −47.0% |
| 50% | −6.21% | −11.5% | −8.04% | −15.2% | −11.3% | −22.2% | −14.7% | −29.8% | −16.2% | −33.7% |
| 80% | −0.21% | −0.39% | −2.16% | −4.07% | −5.63% | −11.0% | −9.19% | −18.7% | −10.9% | −22.5% |
| 95% | 2.84% | 5.27% | 0.84% | 1.58% | −2.75% | −5.38% | −6.41% | −13.1% | −8.14% | −16.9% |
| 2050 | ||||||||||
| Flow rate projection percentile | Population projection percentile | |||||||||
| 5% | 20% | 50% | 80% | 95% | ||||||
| D | S | D | S | D | S | D | S | D | S | |
| 5% | −22.1% | −42.5% | −24.5% | −48.7% | −28.8% | −60.7% | −33.0% | −74.0% | −35.3% | −81.8% |
| 20% | −17.3% | −33.4% | −19.9% | −39.5% | −24.5% | −51.6% | −28.9% | −64.9% | −31.3% | −72.7% |
| 50% | −8.97% | −17.3% | −11.8% | −23.4% | −16.8% | −35.5% | −21.8% | −48.8% | −24.4% | −56.6% |
| 80% | −1.80% | −3.46% | −4.84% | −9.62% | −10.3% | −21.7% | −15.6% | −35.0% | −18.4% | −42.8% |
| 95% | 1.96% | 3.78% | −1.19% | −2.37% | −6.84% | −14.4% | −12.4% | −27.7% | −15.3% | −35.5% |
| 2016–2020 | ||||||||||
| Flow rate projection percentile | Population projection percentile | |||||||||
| 5% | 20% | 50% | 80% | 95% | ||||||
| D | S | D | S | D | S | D | S | D | S | |
| 5% | −0.49% | −3.92% | −0.76% | −6.10% | −1.29% | −10.4% | −1.66% | −13.5% | −2.07% | −16.8% |
| 20% | 1.78% | 14.3% | 1.50% | 12.1% | 0.96% | 7.75% | 0.58% | 4.71% | 0.17% | 1.36% |
| 50% | 7.34% | 58.7% | 7.05% | 56.6% | 3.27% | 26.4% | 2.88% | 23.4% | 2.46% | 20.0% |
| 80% | 11.3% | 90.6% | 11.0% | 88.4% | 7.22% | 58.3% | 6.82% | 55.2% | 6.38% | 51.9% |
| 95% | 13.4% | 108% | 13.2% | 105% | 9.34% | 75.3% | 8.93% | 72.3% | 8.48% | 69.0% |
| 2016–2025 | ||||||||||
| Flow rate projection percentile | Population projection percentile | |||||||||
| 5% | 20% | 50% | 80% | 95% | ||||||
| D | S | D | S | D | S | D | S | D | S | |
| 5% | −3.36% | −55.2% | −3.74% | −61.8% | −4.47% | −74.4% | −5.18% | −86.8% | −5.58% | −93.9% |
| 20% | −1.05% | −17.3% | −1.44% | −23.8% | −2.19% | −36.5% | −2.92% | −48.9% | −3.33% | −56.0% |
| 50% | 4.51% | 74.1% | 4.09% | 67.6% | 3.30% | 54.9% | 2.54% | 42.5% | 2.11% | 35.4% |
| 80% | 8.65% | 142% | 8.22% | 136% | 7.40% | 123% | 6.60% | 111% | 6.15% | 104% |
| 95% | 10.9% | 179% | 10.4% | 172% | 9.58% | 159% | 8.77% | 147% | 8.31% | 140% |
| 2016–2030 | ||||||||||
| Flow rate projection percentile | Population projection percentile | |||||||||
| 5% | 20% | 50% | 80% | 95% | ||||||
| D | S | D | S | D | S | D | S | D | S | |
| 5% | −6.31% | −160% | −6.85% | −175% | −7.84% | −202% | −8.90% | −232% | −9.37% | −245% |
| 20% | −3.92% | −100% | −4.47% | −114% | −5.49% | −142% | −6.58% | −172% | −7.05% | −185% |
| 50% | 1.75% | 44.5% | 1.18% | 30.0% | 0.09% | 2.40% | −1.06% | −27.6% | −1.56% | −40.9% |
| 80% | 6.05% | 154% | 5.45% | 139% | 4.32% | 111% | 3.12% | 81.5% | 2.60% | 68.1% |
| 95% | 8.34% | 211% | 7.72% | 197% | 6.57% | 169% | 5.35% | 139% | 4.81% | 126% |
| 2016–2040 | ||||||||||
| Flow rate projection percentile | Population projection percentile | |||||||||
| 5% | 20% | 50% | 80% | 95% | ||||||
| D | S | D | S | D | S | D | S | D | S | |
| 5% | −9.72% | −800% | −10.6% | −465% | −12.2% | −545% | −13.9% | −633% | −14.6% | −673% |
| 20% | −7.00% | −601% | −7.89% | −347% | −9.53% | −426% | −11.3% | −515% | −12.0% | −554% |
| 50% | −0.87% | −186% | −1.82% | −80.0% | −3.57% | −160% | −5.44% | −248% | −6.25% | −288% |
| 80% | 3.92% | 148% | 2.92% | 128% | 1.09% | 48.6% | −0.87% | −39.8% | −1.72% | −79.3% |
| 95% | 6.43% | 322% | 5.40% | 237% | 3.53% | 158% | 1.52% | 69.3% | 0.65% | 29.8% |
| 2016–2050 | ||||||||||
| Flow rate projection percentile | Population projection percentile | |||||||||
| 5% | 20% | 50% | 80% | 95% | ||||||
| D | S | D | S | D | S | D | S | D | S | |
| 5% | −12.8% | −800% | −14.1% | −892% | −16.4% | −1070% | −18.8% | −1260% | −20.0% | −1360% |
| 20% | −9.62% | −601% | −10.9% | −693% | −13.3% | −869% | −15.0% | −1060% | −17.1% | −1160% |
| 50% | −2.98% | −186% | −4.39% | −278% | −6.98% | −455% | −9.67% | −649% | −11.0% | −747% |
| 80% | 2.38% | 148% | 0.89% | 56.2% | −1.84% | −120% | −4.68% | −314% | −6.06% | −413% |
| 95% | 5.16% | 322% | 3.63% | 230% | 0.83% | 53.8% | −2.09% | −140% | −3.51% | −239% |
| 2016–2020 | ||||||||||
| Flow rate projection percentile | Population projection percentile | |||||||||
| 5% | 20% | 50% | 80% | 95% | ||||||
| D | S | D | S | D | S | D | S | D | S | |
| 5% | −0.49% | −3.06% | −0.76% | −4.76% | −1.29% | −8.1% | −1.66% | −10.5% | −2.07% | −13.1% |
| 20% | 1.78% | 11.1% | 1.50% | 9.4% | 0.96% | 6.05% | 0.58% | 3.67% | 0.17% | 1.06% |
| 50% | 7.34% | 45.8% | 7.05% | 44.1% | 3.27% | 20.6% | 2.88% | 18.2% | 2.46% | 15.6% |
| 80% | 11.32% | 70.7% | 11.02% | 69.0% | 7.22% | 45.5% | 6.82% | 43.1% | 6.38% | 40.5% |
| 95% | 13.45% | 84.0% | 13.15% | 82.3% | 9.34% | 58.80% | 8.93% | 56.4% | 8.48% | 53.8% |
| 2016–2025 | ||||||||||
| Flow rate projection percentile | Population projection percentile | |||||||||
| 5% | 20% | 50% | 80% | 95% | ||||||
| D | S | D | S | D | S | D | S | D | S | |
| 5% | −3.36% | −43.1% | −3.74% | −48.2% | −4.47% | −58.0% | −5.18% | −67.7% | −5.58% | −73.2% |
| 20% | −1.05% | −13.5% | −1.44% | −18.6% | −2.19% | −28.4% | −2.92% | −38.2% | −3.33% | −43.7% |
| 50% | 4.51% | 57.8% | 4.09% | 52.7% | 3.30% | 42.9% | 2.54% | 33.2% | 2.11% | 27.6% |
| 80% | 8.65% | 111% | 8.22% | 106% | 7.40% | 96.0% | 6.60% | 86.3% | 6.15% | 80.8% |
| 95% | 10.86% | 139% | 10.42% | 134% | 9.58% | 124% | 8.77% | 115% | 8.31% | 109% |
| 2016–2030 | ||||||||||
| Flow rate projection percentile | Population projection percentile | |||||||||
| 5% | 20% | 50% | 80% | 95% | ||||||
| D | S | D | S | D | S | D | S | D | S | |
| 5% | −6.31% | −125% | −6.85% | −136% | −7.84% | −158% | −8.90% | −181% | −9.37% | −191% |
| 20% | −3.92% | −77.6% | −4.47% | −88.9% | −5.49% | −110% | −6.58% | −134% | −7.05% | −144% |
| 50% | 1.75% | 34.7% | 1.18% | 23.4% | 0.09% | 1.87% | −1.06% | −21.5% | −1.56% | −31.9% |
| 80% | 6.05% | 120% | 5.45% | 108% | 4.32% | 86.9% | 3.12% | 63.6% | 2.60% | 53.1% |
| 95% | 8.34% | 165% | 7.72% | 154% | 6.57% | 132% | 5.35% | 109% | 4.81% | 98.3% |
| 2016–2040 | ||||||||||
| Flow rate projection percentile | Population projection percentile | |||||||||
| 5% | 20% | 50% | 80% | 95% | ||||||
| D | S | D | S | D | S | D | S | D | S | |
| 5% | −9.72% | −330% | −10.6% | −363% | −12.2% | −425% | −13.9% | −494% | −14.6% | −525% |
| 20% | −7.00% | −237% | −7.89% | −270% | −9.53% | −333% | −11.3% | −402% | −12.0% | −432% |
| 50% | −0.87% | −29.4% | −1.82% | −62.4% | −3.57% | −125% | −5.44% | −194% | −6.25% | −224% |
| 80% | 3.92% | 133% | 2.92% | 100% | 1.09% | 37.9% | −0.87% | −31.1% | −1.72% | −61.9% |
| 95% | 6.43% | 218% | 5.40% | 185% | 3.53% | 123% | 1.52% | 54.0% | 0.65% | 23.2% |
| 2016–2050 | ||||||||||
| Flow rate projection percentile | Population projection percentile | |||||||||
| 5% | 20% | 50% | 80% | 95% | ||||||
| D | S | D | S | D | S | D | S | D | S | |
| 5% | −12.8% | −624% | −14.1% | −696% | −16.4% | −833% | −18.8% | −985% | −20.0% | −1060% |
| 20% | −9.62% | −469% | −10.9% | −541% | −13.3% | −678% | −15.0% | −830% | −17.1% | −906% |
| 50% | −2.98% | −145% | −4.39% | −217% | −6.98% | −355% | −9.67% | −506% | −11.0% | −583% |
| 80% | 2.38% | 116% | 0.89% | 43.8% | −1.84% | −93.5% | −4.68% | −245% | −6.06% | −322% |
| 95% | 5.16% | 251% | 3.63% | 179% | 0.83% | 42.0% | −2.09% | −110% | −3.51% | −186% |
| Variable | Value |
|---|---|
| Reservoir maximum storage | 1560 MCM |
| Reservoir minimum storage 1 | 1000 MCM |
| Initial storage volume | 1300 MCM |
| Evaporation 2 | 20 MCM·month−1 |
| Max turbine flow | 227.0 MCM·month−1 |
| Min turbine flow | 134.3 MCM·month−1 |
| Max Power output | 40 MW |
| Min operating power output 3 | 14 MW |
| Dam head | 29–49 m |
| Dam efficiency 4 | 95% |
| Municipal demand per unit population | 122.0 m3·month−1 |
| Irrigation demand per unit population | 238.42–1208.7 m3 (month-dependent) |
| Project demand for 1000 ha in 2030 (inter-year variability) | 271 MCM·year−1 |
| Month | Rice | Cotton | Sugar Cane |
|---|---|---|---|
| January | 20.2 | 3.3 | 112.0 |
| February | 21.8 | 0.0 | 83.5 |
| March | 22.7 | 0.0 | 29.9 |
| April | 0.0 | 0.0 | 44.8 |
| May | 0.0 | 0.0 | 121.7 |
| June | 0.0 | 0.0 | 159.7 |
| July | 16.0 | 3.6 | 156.8 |
| August | 15.5 | 6.3 | 160.5 |
| September | 22.5 | 10.5 | 167.4 |
| October | 21.5 | 8.9 | 143.4 |
| November | 0.0 | 8.4 | 116.5 |
| December | 19.3 | 8.3 | 99.3 |
| Projected Flow Probability Interval | Projected Population Probability Interval | ||||
|---|---|---|---|---|---|
| 5% | 20% | 50% | 80% | 95% | |
| 5% | 0.25% | 1.0% | 2.5% | 1.0% | 0.25% (w) |
| 20% | 1.0% | 4.0% | 10.% | 4.0% | 1.0% |
| 50% | 2.5% | 10% | 25% (m) | 10% | 2.5% |
| 80% | 1.0% | 4.0% | 10% | 4.0% | 1.0% |
| 95% | 0.25% (b) | 1.0% | 2.5% | 1.0% | 0.25% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Postle-Floyd, H.; Erfani, T. Reliability and Robustness Analysis of the Masinga Dam under Uncertainty. Climate 2017, 5, 12. https://doi.org/10.3390/cli5010012
Postle-Floyd H, Erfani T. Reliability and Robustness Analysis of the Masinga Dam under Uncertainty. Climate. 2017; 5(1):12. https://doi.org/10.3390/cli5010012
Chicago/Turabian StylePostle-Floyd, Hayden, and Tohid Erfani. 2017. "Reliability and Robustness Analysis of the Masinga Dam under Uncertainty" Climate 5, no. 1: 12. https://doi.org/10.3390/cli5010012
APA StylePostle-Floyd, H., & Erfani, T. (2017). Reliability and Robustness Analysis of the Masinga Dam under Uncertainty. Climate, 5(1), 12. https://doi.org/10.3390/cli5010012





