Precipitation Intensity Trend Detection using Hourly and Daily Observations in Portland, Oregon
Abstract
:1. Introduction
- Is the daily or hourly scale better for trend detection in precipitation intensity?
- How is precipitation intensity related to volume?
- How does precipitation intensity magnitude differ at the daily or hourly scales?
- What is the relation among precipitation intensity, volume, and frequency of wet days/hours at a representative station?
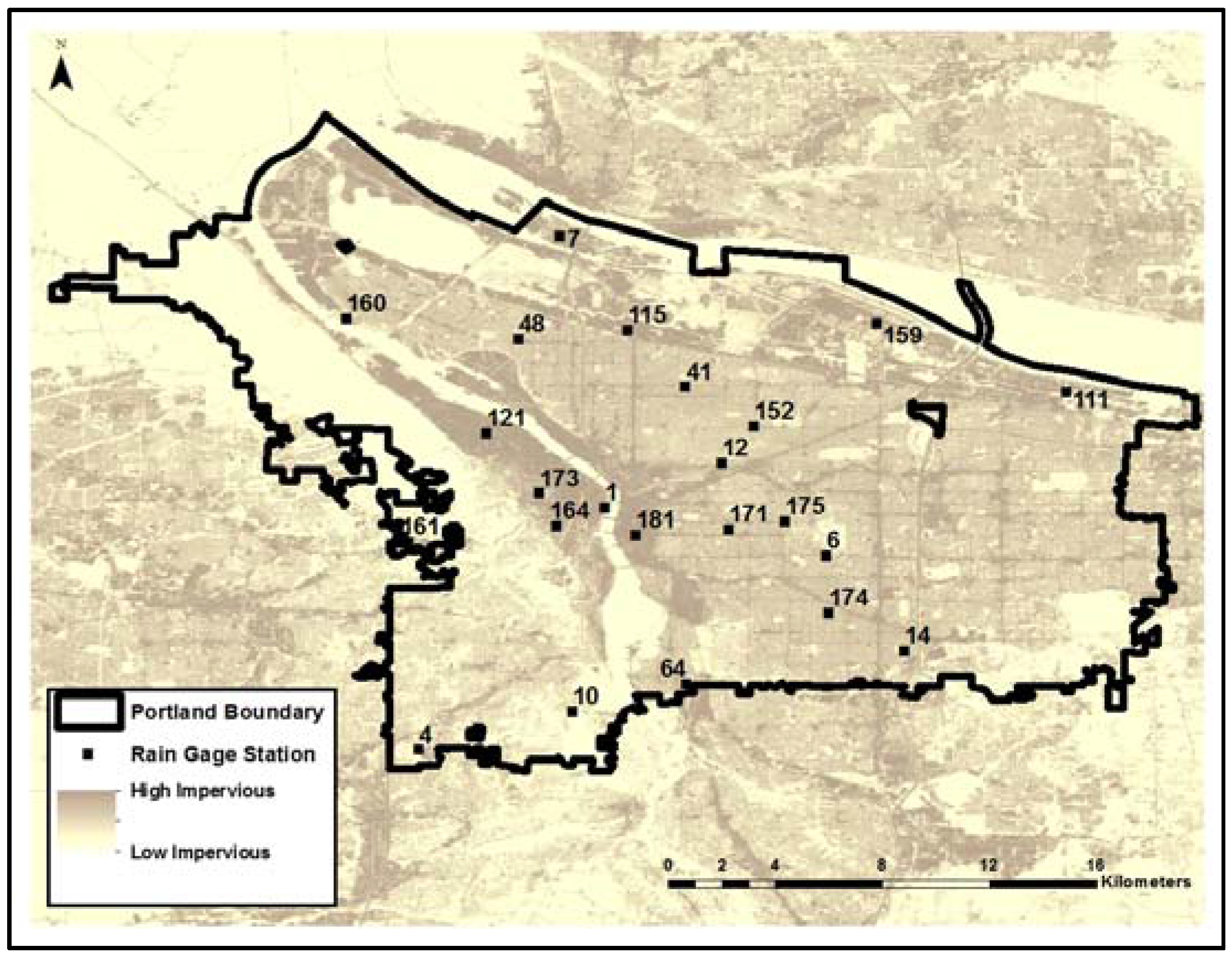
2. Materials and Methods
3. Results
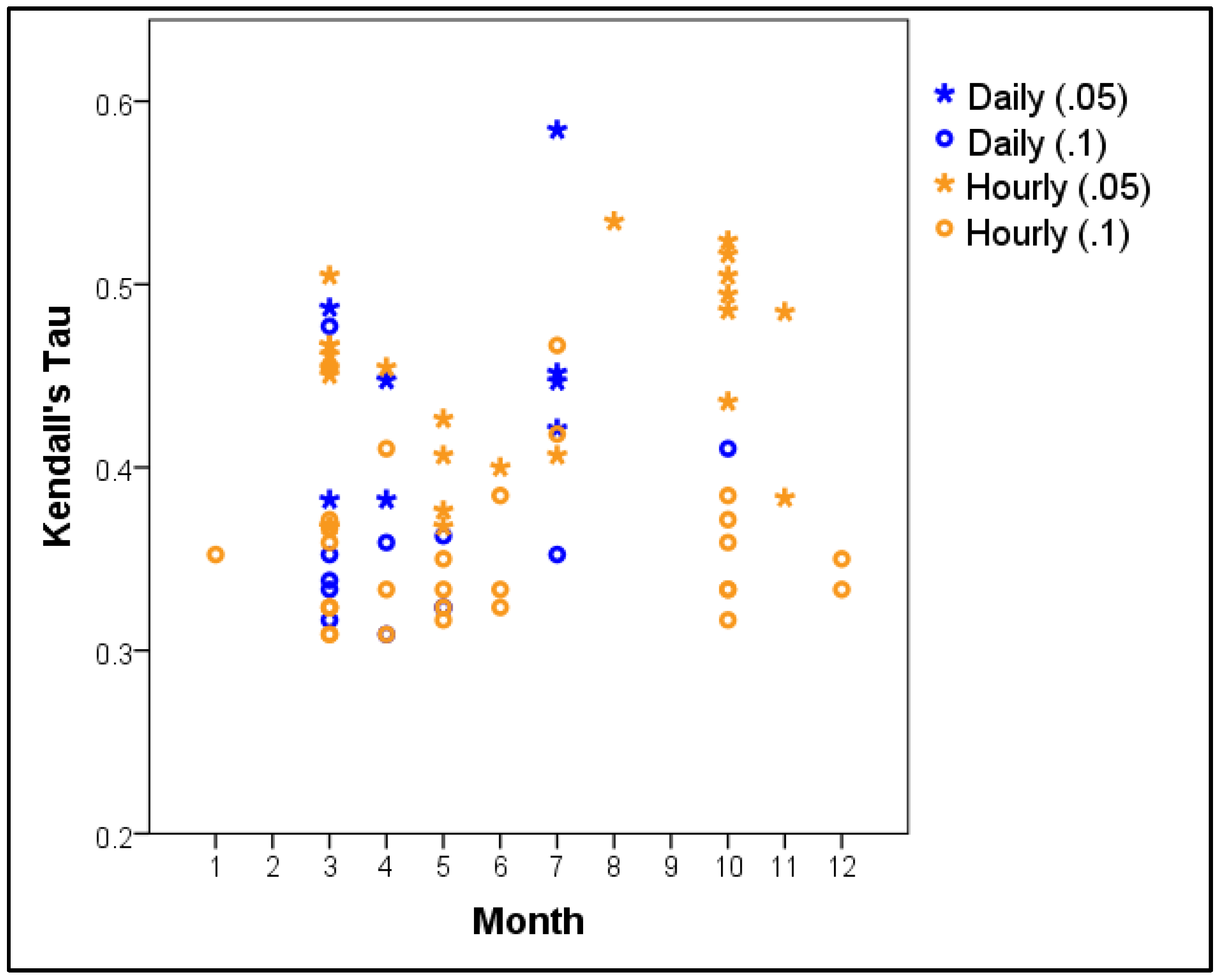
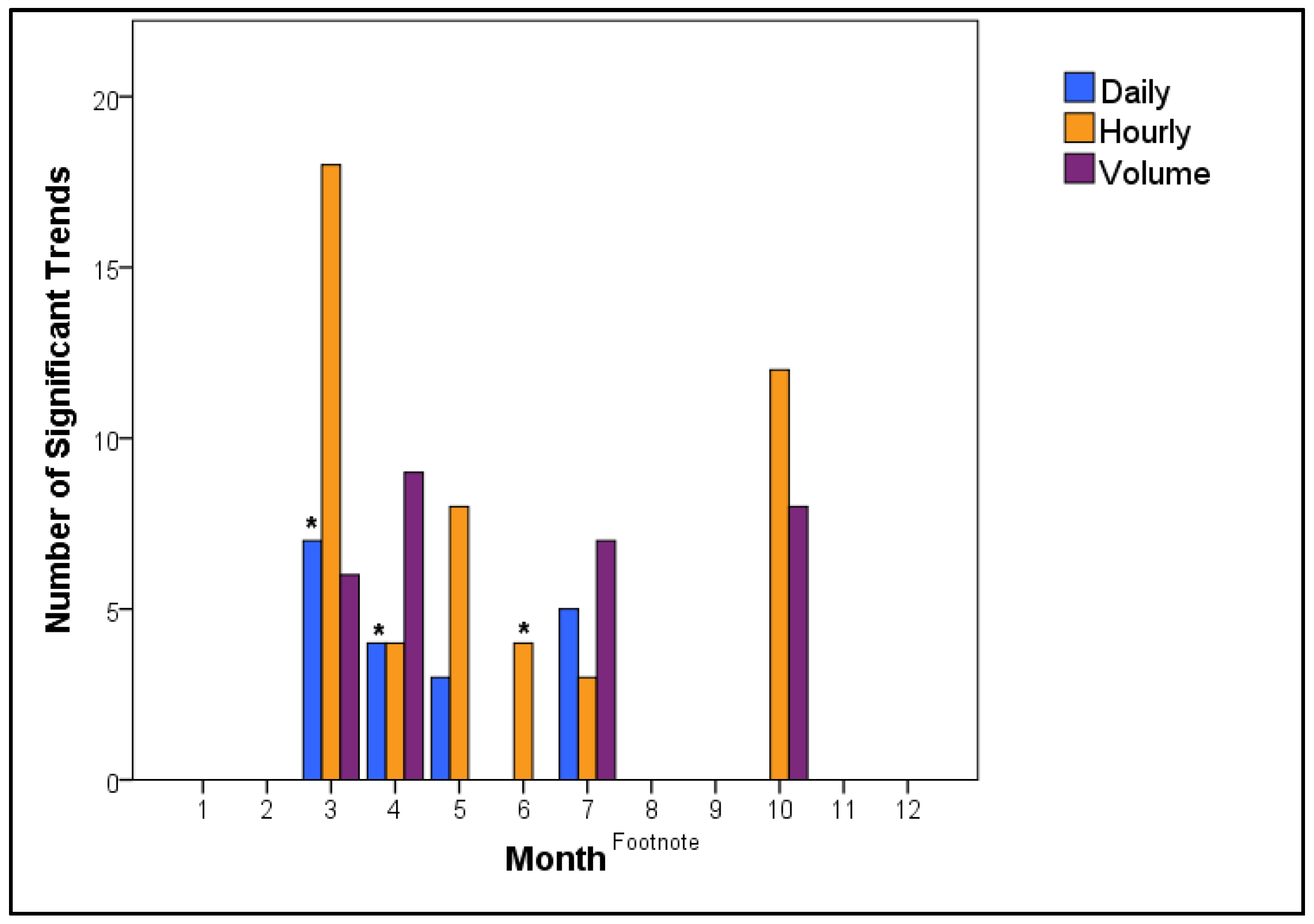
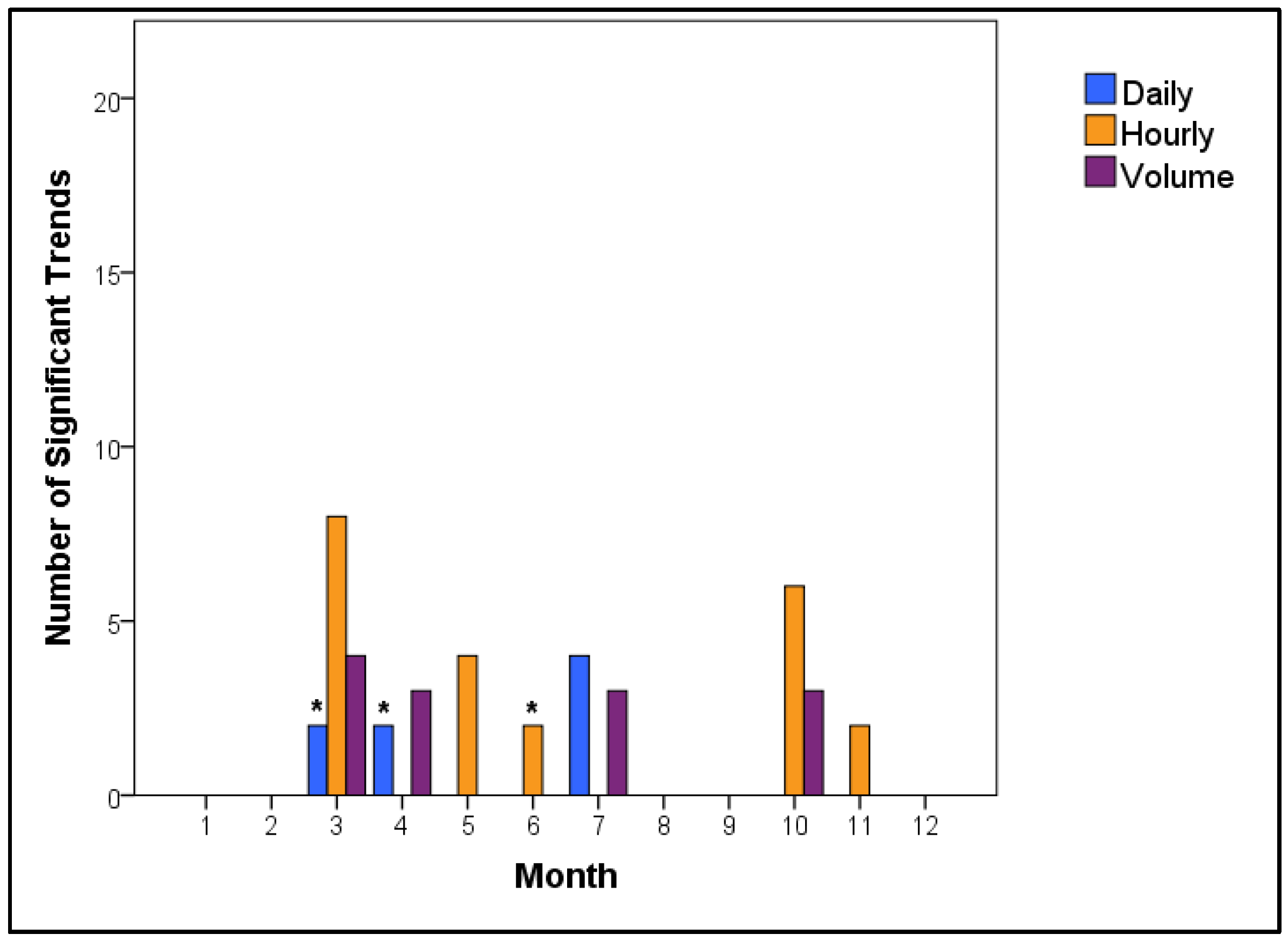
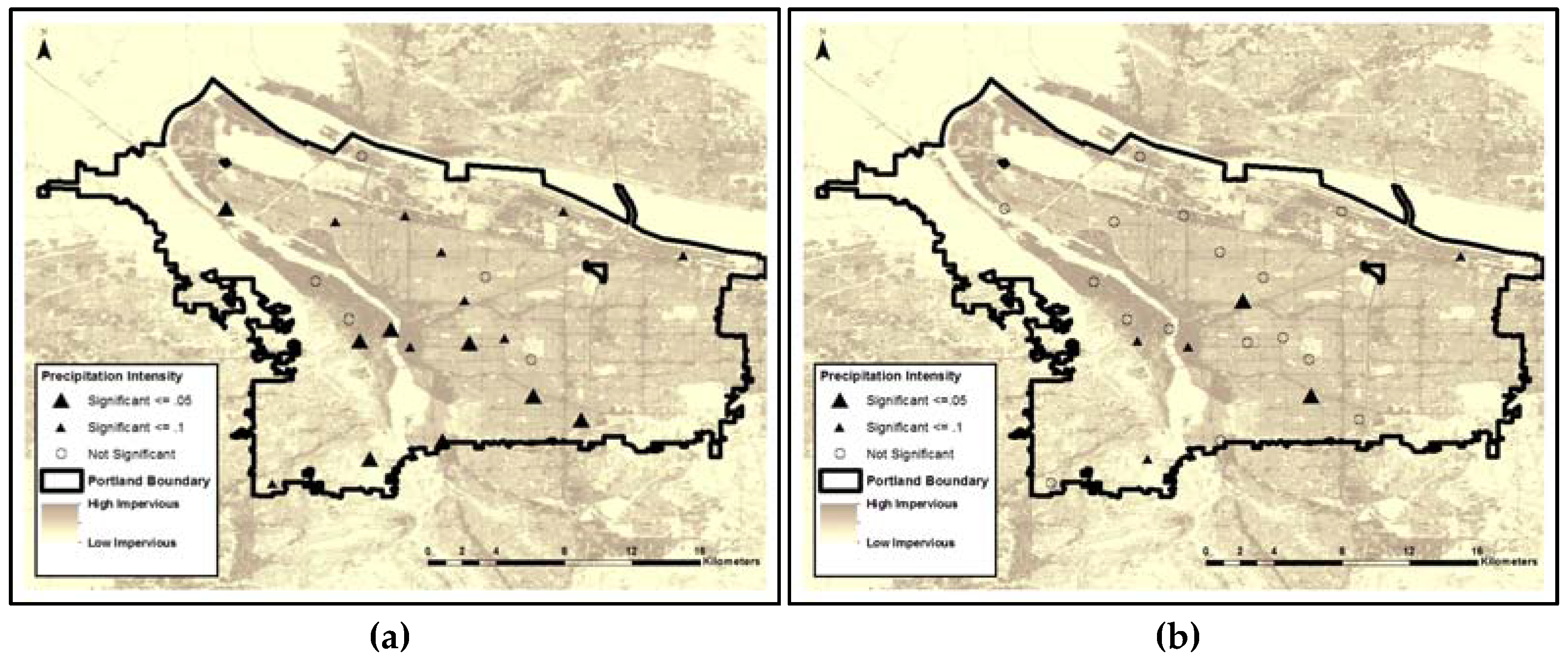
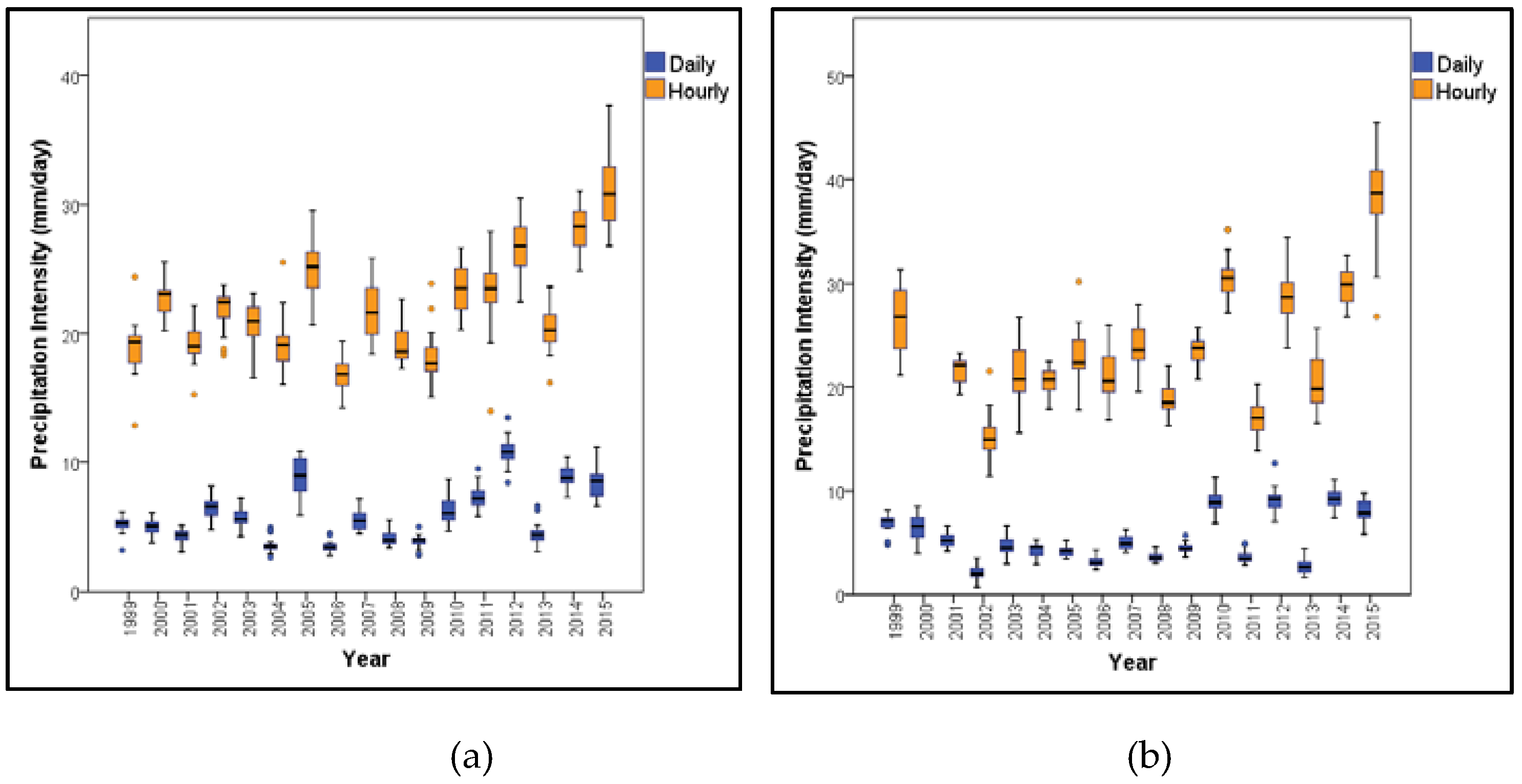
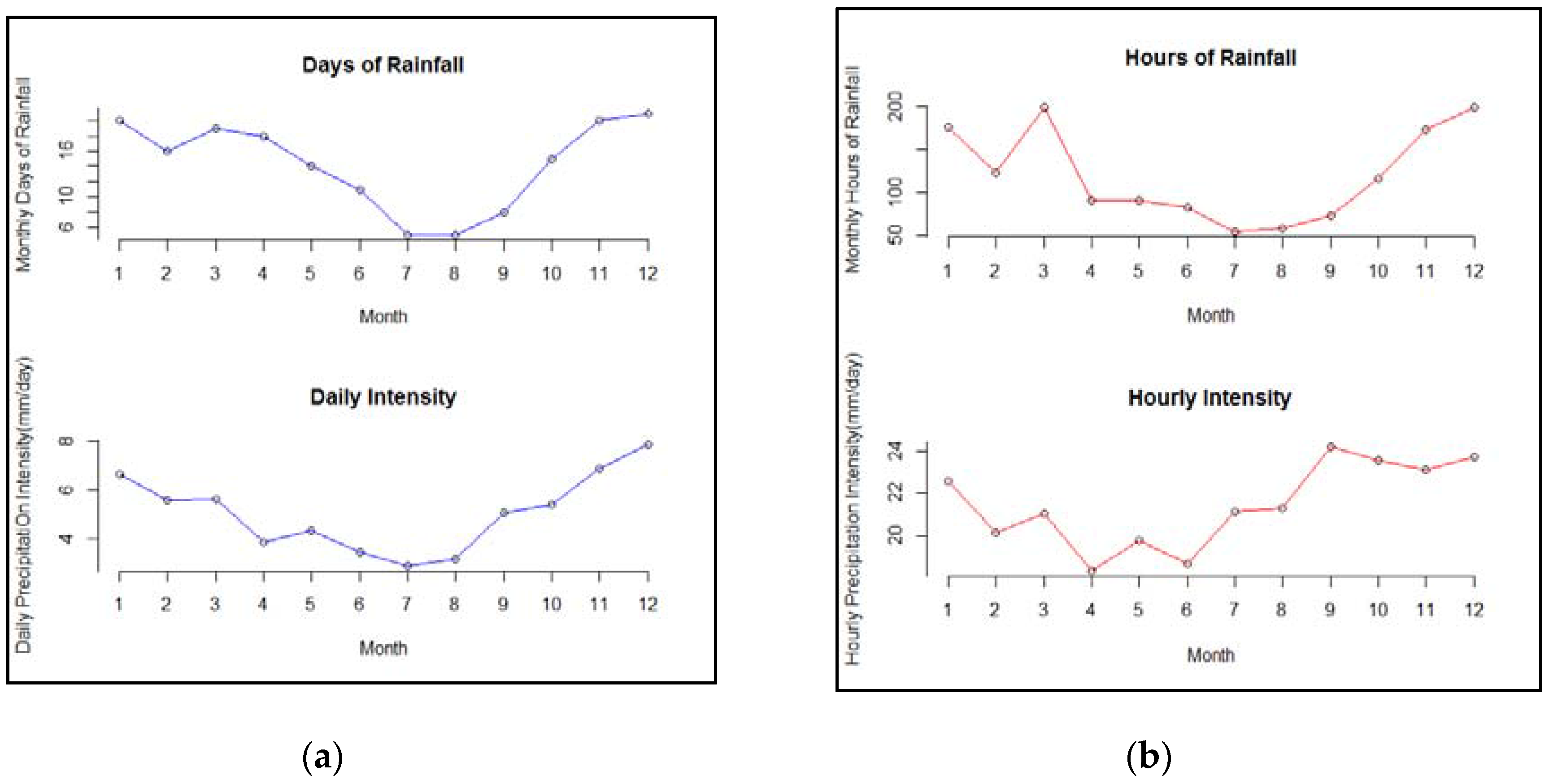
3.1. Daily vs. Hourly Trend Detection
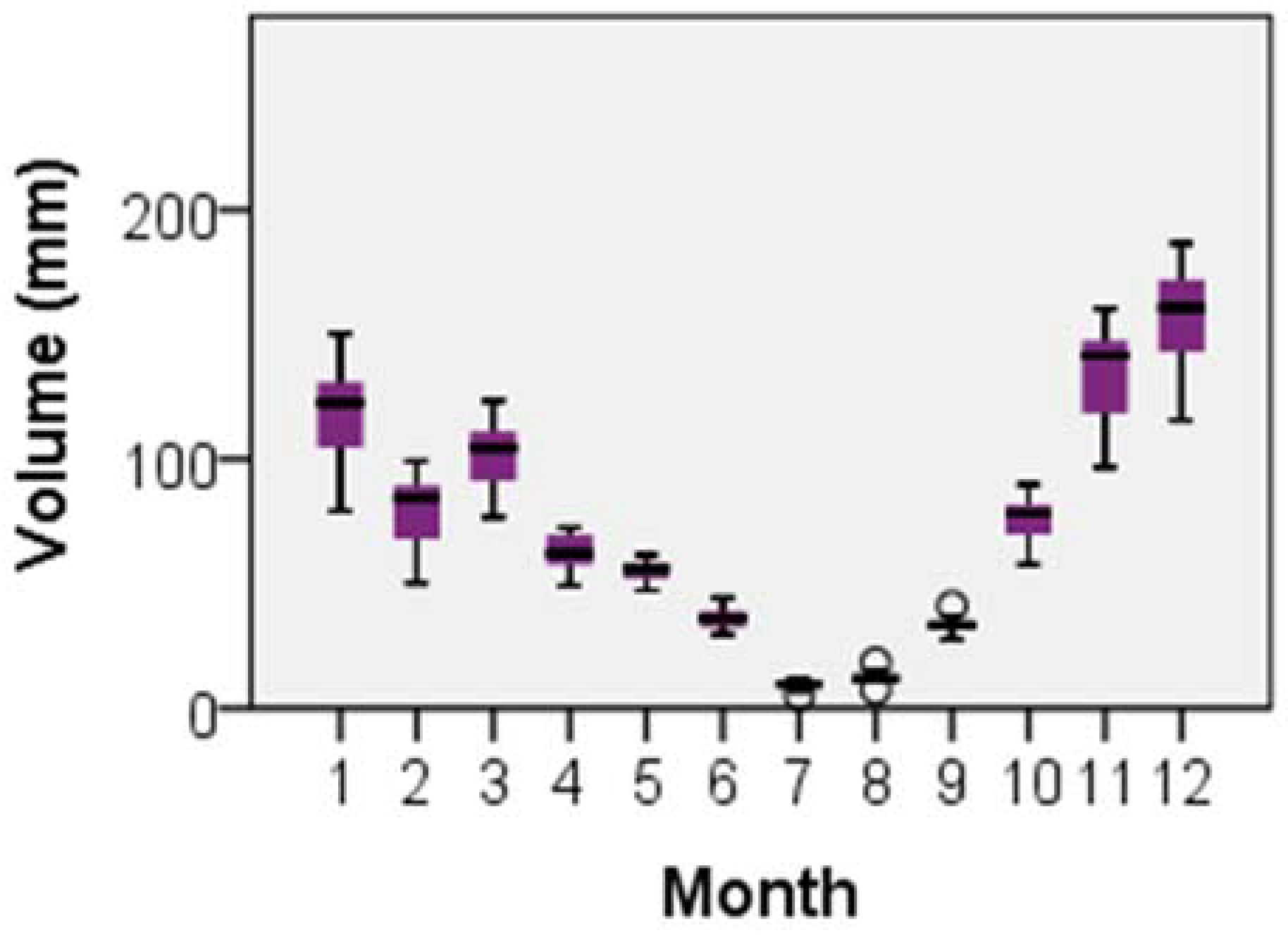
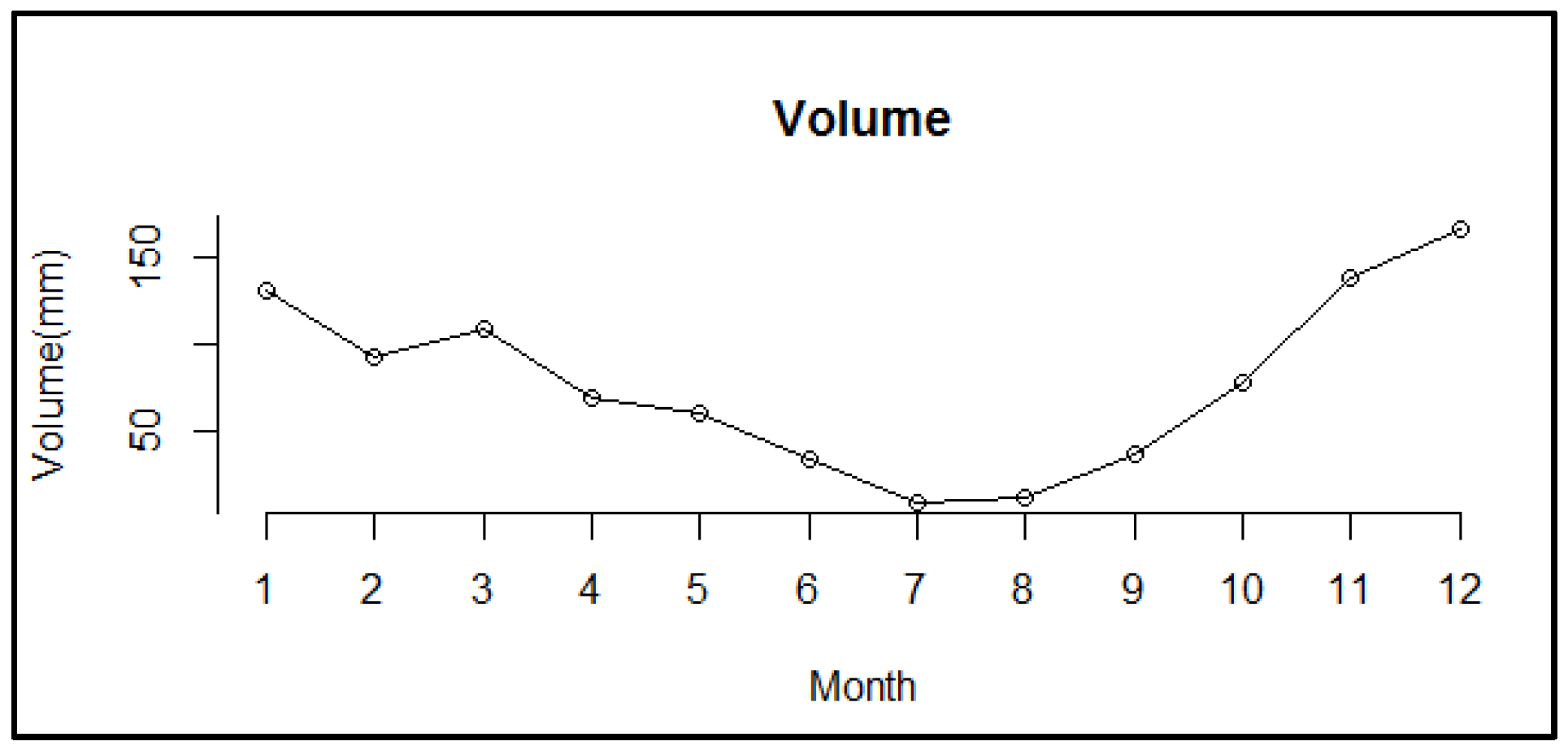
3.2. Volume Trend Detection
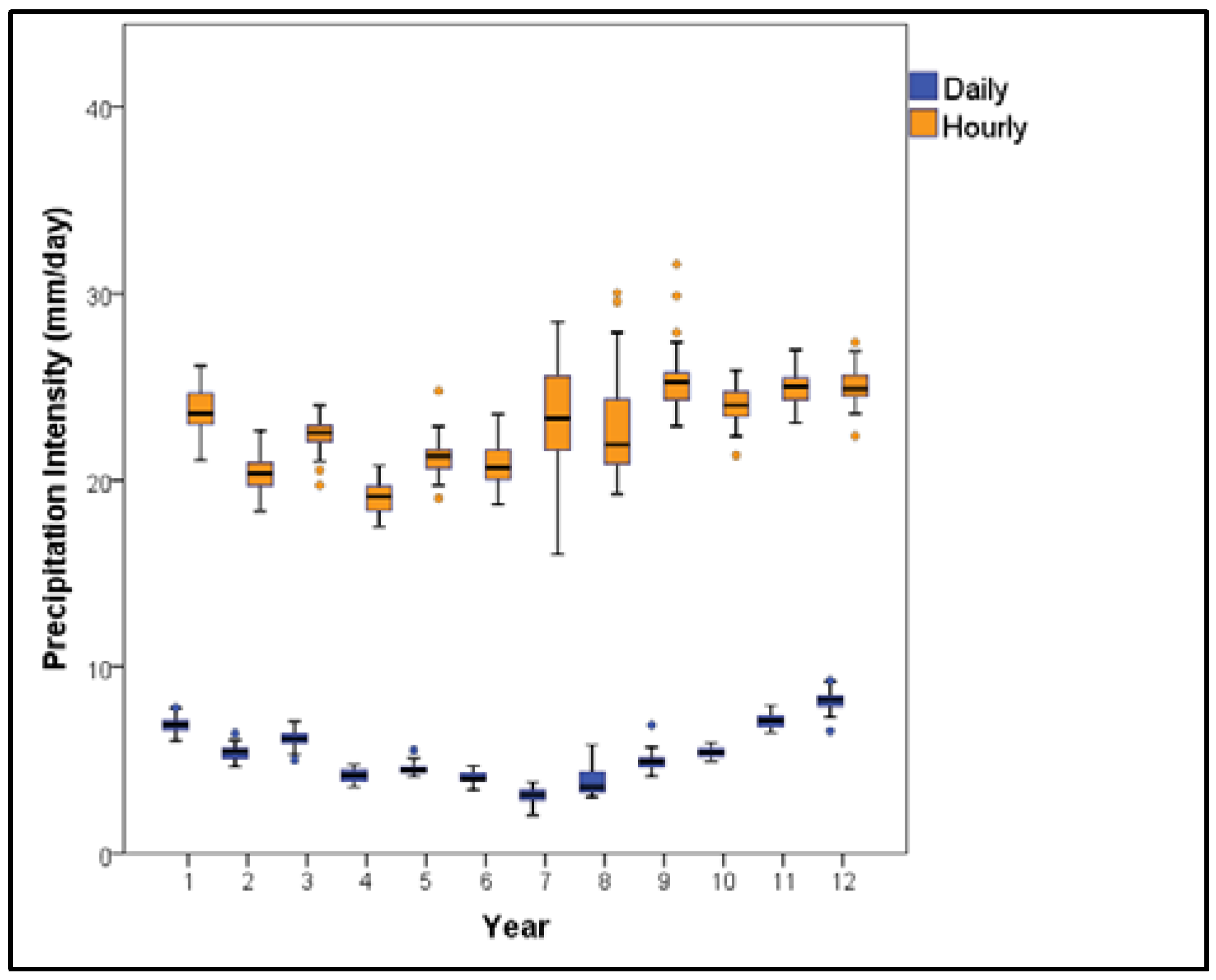
3.3. Effect of Temporal Scale on Precipitation Intensity Magnitude
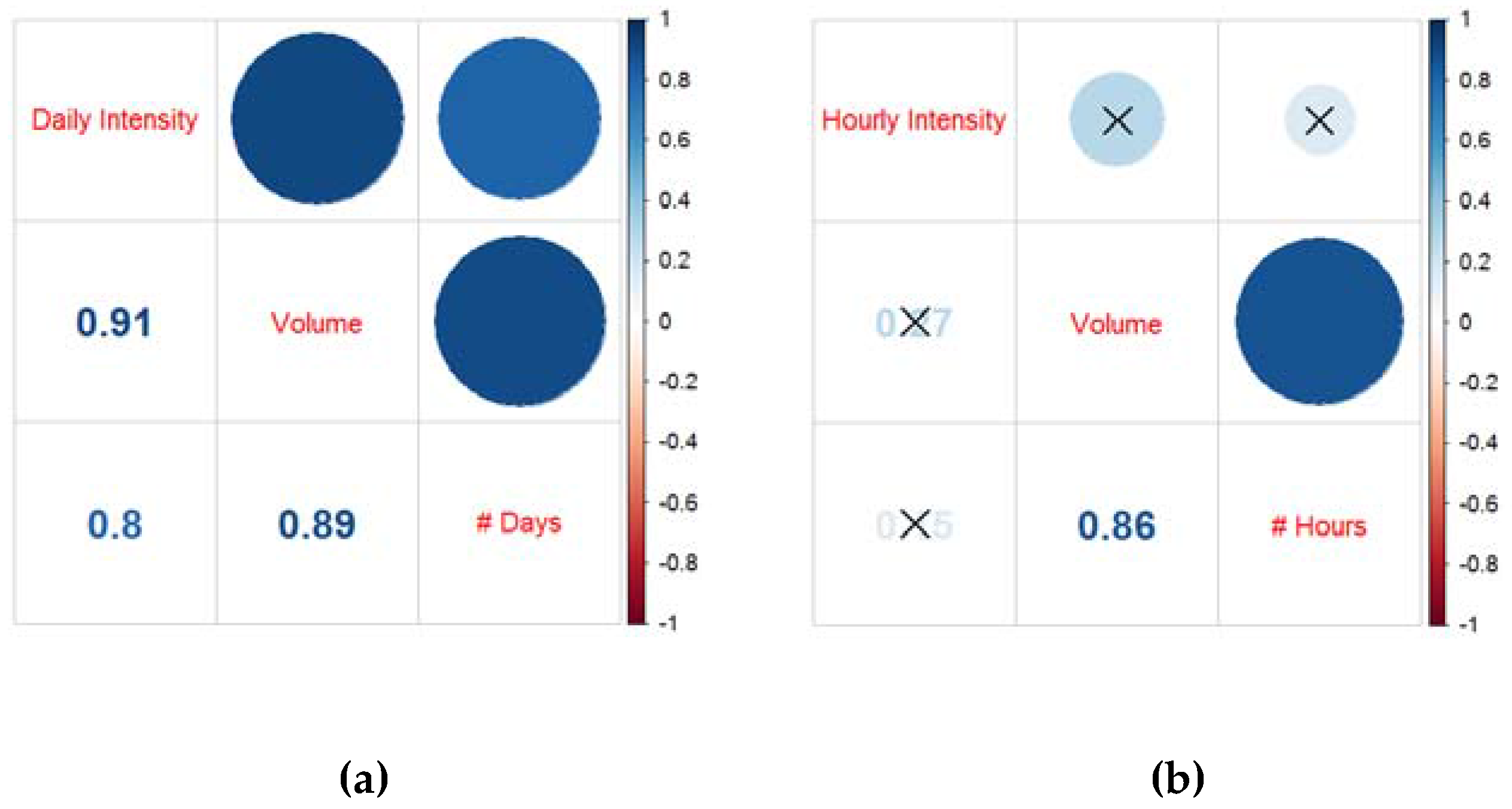
3.4. Relationship between Precipitation Intensity, Volume, and Frequency of Wet Days/Hours
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Precipitation Intensity Trends (Hourly Scale) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Station ID | Jan. | Feb. | Mar. | Apr. | May. | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | Dec. |
| 1 | - | - | 0.45 ** | - | 0.33 * | - | - | - | - | 0.52 ** | - | - |
| 4 | - | - | 0.31 * | 0.31 * | - | 0.33 * | - | - | - | 0.37 * | - | - |
| 6 | - | - | - | - | 0.38 ** | - | - | - | - | 0.33 * | - | - |
| 7 | - | - | - | - | - | 0.32 * | - | - | - | - | - | - |
| 10 | - | - | 0.47 ** | 0.33 * | - | - | - | - | - | 0.36 * | - | - |
| 12 | - | - | 0.32 * | - | 0.37 ** | - | - | - | - | 0.49 ** | - | 0.33 * |
| 14 | - | - | 0.37 ** | - | - | - | - | - | - | - | - | - |
| 41 | - | - | 0.32 * | - | - | - | - | - | - | - | - | - |
| 48 | - | - | 0.32 * | - | - | - | - | - | - | - | - | - |
| 58 | - | - | - | 0.32 * | - | 0.41 ** | - | - | - | - | - | |
| 64 | - | - | 0.37 ** | - | 0.32 * | - | - | - | - | 0.32 * | 0.38 ** | - |
| 111 | - | - | 0.37 * | - | 0.35 * | 0.40 ** | - | - | - | 0.50 ** | - | - |
| 115 | - | - | 0.31 * | - | - | - | - | - | - | 0.33 * | - | - |
| 121 | - | - | - | - | - | - | - | - | - | - | - | - |
| 152 | - | - | - | 0.43 ** | - | - | - | - | - | - | 0.35 * | |
| 159 | - | - | 0.45 * | - | - | - | 0.47 * | - | - | - | - | - |
| 160 | - | - | 0.47 ** | - | - | 0.38 * | - | - | - | - | - | - |
| 161 | - | - | 0.37 * | - | - | - | - | - | - | 0.49 ** | - | - |
| 164 | 0.35 * | - | 0.50 ** | - | 0.41 ** | - | - | - | - | 0.52 ** | - | - |
| 171 | - | - | 0.45 ** | - | - | - | 0.42 * | - | - | - | - | - |
| 173 | - | - | 0.41 * | - | - | - | 0.53 ** | - | - | 0.48 ** | - | |
| 174 | - | - | 0.46 ** | 0.45 ** | - | - | - | - | - | 0.44 ** | - | - |
| 175 | - | - | 0.36 * | - | - | - | - | - | - | 0.38 * | - | - |
| 181 | - | - | 0.45 * | - | - | - | - | - | - | - | - | - |
| Moran’s Index | - | - | - | - | - | 0.26 ** | - | - | - | - | - | - |
| Precipitation Intensity Trends (Daily Scale) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Station ID | Jan. | Feb. | Mar. | Apr. | May. | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | Dec. |
| 1 | - | - | - | - | - | - | - | - | - | - | - | - |
| 4 | - | - | - | - | - | - | - | - | - | - | - | - |
| 6 | - | - | - | - | - | - | - | - | - | - | - | - |
| 7 | - | - | - | - | 0.32 * | - | - | - | - | - | - | - |
| 10 | - | - | 0.35 * | 0.45 ** | - | - | - | - | - | - | - | - |
| 12 | - | - | 0.38 ** | - | - | - | - | - | - | - | - | - |
| 14 | - | - | - | - | - | - | 0.45 ** | - | - | - | - | - |
| 41 | - | - | - | - | - | - | 0.35 * | - | - | - | - | - |
| 48 | - | - | - | - | - | - | - | - | - | - | - | |
| 58 | - | - | - | - | - | - | 0.42 ** | - | - | - | - | - |
| 64 | - | - | 0.34 * | 0.38 ** | - | - | - | - | - | - | - | - |
| 111 | - | - | - | 0.31 * | 0.32 * | - | - | - | - | - | - | - |
| 115 | - | - | - | - | - | - | - | - | - | - | - | - |
| 121 | - | - | - | - | - | - | - | - | - | - | - | - |
| 152 | - | - | - | - | - | - | - | - | - | - | - | - |
| 159 | - | - | - | - | - | - | - | - | - | - | - | - |
| 160 | - | - | - | - | - | - | - | - | - | - | - | - |
| 161 | - | - | 0.32 * | - | - | - | - | - | - | - | - | - |
| 164 | - | - | 0.33 * | - | - | - | - | - | - | - | - | - |
| 171 | - | - | - | - | - | - | - | - | - | - | - | - |
| 173 | - | - | - | - | - | - | 0.45 ** | - | - | 0.41 * | - | - |
| 174 | - | - | 0.49 ** | 0.36 * | 0.36 * | - | - | - | - | - | - | |
| 175 | - | - | - | - | - | - | 0.58 ** | - | - | - | - | - |
| 181 | - | - | 0.48 * | - | - | - | - | - | - | - | - | |
| Moran’s Index | - | - | 0.29 ** | 0.26 ** | - | - | - | 0.14 * | - | 0.42 ** | - | - |
| Volume Trends | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Station ID | Jan. | Feb. | Mar. | Apr. | May. | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | Dec. |
| 1 | - | - | - | - | - | - | - | - | - | 0.33 * | - | - |
| 4 | - | - | - | 0.45 ** | - | - | - | - | - | - | - | - |
| 6 | - | - | - | - | - | - | - | - | - | - | - | - |
| 7 | - | - | - | - | - | - | - | - | - | - | - | - |
| 10 | - | - | 0.39 ** | 0.42 ** | - | - | - | - | - | - | - | - |
| 12 | - | - | - | 0.35 * | - | - | - | - | - | 0.43 ** | - | - |
| 14 | - | - | - | - | - | - | 0.34 * | - | - | - | - | - |
| 41 | - | - | - | - | - | - | 0.35 * | - | - | - | - | - |
| 48 | - | - | - | 0.37 * | - | - | - | - | - | - | - | - |
| 58 | −0.33 * | - | - | 0.42 ** | - | - | - | - | - | - | - | - |
| 64 | - | - | 0.37 ** | 0.31 * | - | - | - | - | - | 0.35 ** | - | - |
| 111 | - | - | 0.37 ** | 0.34 * | - | - | - | - | - | 0.43 ** | - | - |
| 115 | - | - | - | 0.33 * | - | - | - | - | - | - | - | - |
| 121 | - | - | - | - | - | - | - | - | - | - | - | - |
| 152 | - | - | - | - | - | - | - | - | - | 0.35 * | - | - |
| 159 | - | - | - | - | - | - | - | - | - | - | - | - |
| 160 | - | - | 0.40 ** | - | - | - | - | - | - | - | - | - |
| 161 | - | 0.37 * | 0.37 * | 0.39 * | - | - | 0.39 * | - | - | - | - | - |
| 164 | - | - | 0.35 * | - | - | - | - | - | - | - | - | - |
| 171 | - | - | - | - | - | - | 0.41 * | - | - | - | - | - |
| 173 | - | - | - | - | - | - | 0.49 ** | - | - | 0.41 * | - | - |
| 174 | - | - | - | - | - | - | - | - | - | - | - | - |
| 175 | - | - | - | - | - | - | 0.51 ** | - | - | 0.38 * | - | - |
| 181 | - | - | - | - | - | - | 0.51 ** | - | - | 0.38 * | - | - |
| Moran’s Index | - | - | - | - | - | - | - | - | - | - | - | - |
References
- Preston, B.L.; Mustelin, J.; Maloney, M.C. Climate adaptation heuristics and the science/policy divide. Mitig. Adapt. Strateg. Glob. Chang. 2015, 20, 467–497. [Google Scholar] [CrossRef]
- Kwasinski, A. Effects of hurricanes Isaac and sandy on data and communications power infrastructure. In Proceedings of the 35th International Telecommunications Energy Conference ’Smart Power and Efficiency’ (INTELEC), Hamburg, Germany, 13–17 October 2013.
- Redman, C.L.; Miller, T.R. The technosphere and earth stewardship. In Earth Stewardship; Springer: Berlin, Germany, 2015; pp. 269–279. [Google Scholar]
- Mailhot, A.; Duchesne, S.; Caya, D.; Talbot, G. Assessment of future change in intensity duration frequency (IDF) curves for Southern Quebec using the Canadian Regional Climate Model (CRCM). J. Hydrol. 2007, 347, 197–210. [Google Scholar] [CrossRef]
- Trenberth, K.E. Conceptual framework for changes of extremes of the hydrological cycle with climate change. In Weather and Climate Extremes; Karl, T.R., Nicholls, N., Ghazi, A., Eds.; Springer: Berlin, Germany, 1999; pp. 327–339. [Google Scholar]
- Meehl, G.A.; Arblaster, J.M.; Tebaldi, C. Understanding future patterns of increased precipitation intensity in climate model simulations. Geophys. Res. Lett. 2005. [Google Scholar] [CrossRef]
- Doswell, C.A., III; Brooks, H.E.; Maddox, R.A. Flash flood forecasting: An ingredients-based methodology. Weather Forecast. 1996, 11, 560–581. [Google Scholar] [CrossRef]
- Semadeni-Davies, A.; Hernebring, C.; Svensson, G.; Gustafsson, L.-G. The impacts of climate change and urbanisation on drainage in Helsingborg, Sweden: Suburban stormwater. J. Hydrol. 2008, 350, 114–125. [Google Scholar] [CrossRef]
- Rosenberg, E.A.; Keys, P.W.; Booth, D.B.; Hartley, D.; Burkey, J.; Steinemann, A.C.; Lettenmaier, D.P. Precipitation extremes and the impacts of climate change on stormwater infrastructure in Washington State. Clim. Chang. 2010, 102, 319–349. [Google Scholar] [CrossRef]
- Chou, C.; Chen, C.-A.; Tan, P.-H.; Chen, K.T. Mechanisms for global warming impacts on precipitation frequency and intensity. J. Clim. 2012, 25, 3291–3306. [Google Scholar] [CrossRef]
- Osborn, T.J.; Hulme, M.; Jones, P.D.; Basnett, T.A. Observed trends in the daily intensity of United Kingdom precipitation. Int. J. Climatol. 2000, 20, 347–364. [Google Scholar] [CrossRef]
- Groisman, P.Y.; Knight, R.W.; Easterling, D.R.; Karl, T.R.; Hegerl, G.C.; Razuvaev, V.N. Trends in intense precipitation in the climate record. J. Clim. 2005, 18, 1326–1350. [Google Scholar] [CrossRef]
- He, S.; Raghavan, S.V.; Nguyen, N.S.; Liong, S.-Y. Ensemble rainfall forecasting with numerical weather prediction and radar-based nowcasting models. Hydrol. Process. 2013, 27, 1560–1571. [Google Scholar] [CrossRef]
- Di Paola, F.; Ricciardelli, E.; Cimini, D.; Romano, F.; Viggiano, M.; Cuomo, V. Analysis of Catania flash flood case study by using combined microwave and infrared technique. J. Hydrometeorol. 2014, 15, 1989–1998. [Google Scholar] [CrossRef]
- Di Paola, F.; Casella, D.; Dietrich, S.; Mugnai, A.; Ricciardelli, E.; Romano, F.; Sanò, P. Combined MW-IR Precipitation Evolving Technique (PET) of convective rain fields. Nat. Hazards Earth Syst. Sci. 2012, 12, 3557–3570. [Google Scholar] [CrossRef]
- Casella, D.; Dietrich, S.; Paola, F.D.; Formenton, M.; Mugnai, A.; Porcu, F.; Sano, P. PM-GCD–a combined IR–MW satellite technique for frequent retrieval of heavy precipitation. Nat. Hazards Earth Syst. Sci. 2012, 12, 231–240. [Google Scholar] [CrossRef]
- Munoz, E.A.; Di Paola, F.; Lanfri, M.; Arteaga, F.J. Observing the troposphere through the Advanced Technology Microwave Sensor (ATMS) to retrieve rain rate. IEEE Lat. Am. Trans. 2016, 14, 586–594. [Google Scholar] [CrossRef]
- Munoz, E.A.; Di Paola, F.; Lanfri, M. Advances on rain rate retrieval from satellite platforms using artificial neural networks. IEEE Lat. Am. Trans. 2015, 13, 3179–3186. [Google Scholar] [CrossRef]
- Sanò, P.; Panegrossi, G.; Casella, D.; Di Paola, F.; Milani, L.; Mugnai, A.; Petracca, M.; Dietrich, S. The Passive microwave Neural network Precipitation Retrieval (PNPR) algorithm for AMSU/MHS observations: Description and application to European case studies. Atmos. Meas. Tech. 2015, 8, 837–857. [Google Scholar] [CrossRef]
- Karl, T.R.; Knight, R.W. Secular trends of precipitation amount, frequency, and intensity in the United States. Bull. Am. Meteorol. Soc. 1998, 79, 231–241. [Google Scholar] [CrossRef]
- Hense, A.; Krahe, P.; Flohn, H. Recent fluctuations of tropospheric temperature and water vapour content in the tropics. Meteorol. Atmos. Phys. 1988, 38, 215–227. [Google Scholar] [CrossRef]
- Trenberth, K.E. Atmospheric moisture residence times and cycling: Implications for rainfall rates and climate change. Clim. Chang. 1998, 39, 667–694. [Google Scholar] [CrossRef]
- Krishnamurthy, C.K.B.; Lall, U.; Kwon, H.-H. Changing frequency and intensity of rainfall extremes over India from 1951 to 2003. J. Clim. 2009, 22, 4737–4746. [Google Scholar] [CrossRef]
- Ma, S.; Zhou, T.; Dai, A.; Han, Z. Observed changes in the distributions of daily precipitation frequency and amount over China from 1960 to 2013. J. Clim. 2015, 28, 6960–6978. [Google Scholar] [CrossRef]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Gutowski, W.J., Jr.; Decker, S.G.; Donavon, R.A.; Pan, Z.; Arritt, R.W.; Takle, E.S. Temporal-spatial scales of observed and simulated precipitation in central US climate. J. Clim. 2003, 16, 3841–3847. [Google Scholar] [CrossRef]
- Praskievicz, S.; Chang, H. Winter precipitation intensity and ENSO/PDO variability in the Willamette Valley of Oregon. Int. J. Climatol. 2009, 29, 2033–2039. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Rupp, D.E.; Mote, P.W. Seasonal climate variability and change in the Pacific Northwest of the United States. J. Clim. 2014, 27, 2125–2142. [Google Scholar] [CrossRef]
- Mote, P.W. Trends in temperature and precipitation in the Pacific Northwest during the twentieth century. 2003, 77, 271–282. [Google Scholar]
- Mote, P.W.; Salathé, E.P., Jr. Future climate in the Pacific Northwest. Clim. Chang. 2010, 102, 29–50. [Google Scholar] [CrossRef]
- Jakob, M.; McKendry, I.; Lee, R. Long-term changes in rainfall intensities in Vancouver, British Columbia. Can. Water Resour. J. Rev. Can. Ressour. Hydr. 2003, 28, 587–604. [Google Scholar] [CrossRef]
- Burn, D.H.; Mansour, R.; Zhang, K.; Whitfield, P.H. Trends and variability in extreme rainfall events in British Columbia. Can. Water Resour. J. 2011, 36, 67–82. [Google Scholar] [CrossRef]
- Dart, J.O.; Johnson, D.M. Oregon, Wet, High and Dry; Hapi Press: Portland, OR, USA, 1981. [Google Scholar]
- Salathé, E.P. Comparison of various precipitation downscaling methods for the simulation of streamflow in a rainshadow river basin. Int. J. Climatol. 2003, 23, 887–901. [Google Scholar] [CrossRef]
- Chang, H. Comparative streamflow characteristics in urbanizing basins in the Portland Metropolitan Area, Oregon, USA. Hydrol. Process. 2007, 21, 211–222. [Google Scholar] [CrossRef]
- Jones, D.M.; Sims, A.L. Climatology of instantaneous rainfall rates. J. Appl. Meteorol. 1978, 17, 1135–1140. [Google Scholar] [CrossRef]
- Salathé, E.P., Jr.; Hamlet, A.F.; Mass, C.F.; Lee, S.-Y.; Stumbaugh, M.; Steed, R. Estimates of twenty-first-century flood risk in the Pacific Northwest based on regional climate model simulations. J. Hydrometeorol. 2014, 15, 1881–1899. [Google Scholar] [CrossRef]
- Ahilan, S.; Guan, M.; Sleigh, A.; Wright, N.; Chang, H. The influence of floodplain restoration on flow and sediment dynamics in an urban river. J. Flood Risk Manag. 2016. [Google Scholar] [CrossRef]
- Mearns, L.O.; Giorgi, F.; McDaniel, L.; Shields, C. Analysis of daily variability of precipitation in a nested regional climate model: Comparison with observations and doubled CO2 results. Glob. Planet. Chang. 1995, 10, 55–78. [Google Scholar] [CrossRef]
- Frich, P.; Alexander, L.; Della-marta, P.; Gleason, B.; Haylock, M.; Klein, T.A.; Tc, P. Observed coherent changes in climatic extremes during 2nd half of the 20th century. Clim. Res. 2002, 19, 193–212. [Google Scholar] [CrossRef]
- Helsel, D.R.; Hirsch, R.M. Statistical Methods in Water Resources Techniques of Water Resources Investigations. U.S. Geological Survey, 2002; Book 4, Chapter A3. Available online: https://www.epa.gov/quality/statistical-methods-water-resources-techniques-water-resources-investigations-united-states (accessed on 12 February 2017).
- Kendall, M.G. Rank Correlation Measures; Charles Griffin: London, UK, 1975. [Google Scholar]
- Chang, H.; Jung, I.-W.; Steele, M.; Gannett, M. Spatial patterns of March and September streamflow trends in Pacific Northwest Streams, 1958–2008. Geogr. Anal. 2012, 22, 2644–2656. [Google Scholar] [CrossRef]
- McLeod, A.I. Kendall: Kendall Rank Correlation and Mann-Kendall Trend Test. R Package Version 22. Available online: https://cran.r-project.org/web/packages/Kendall/index.html (accessed on 12 February 2017).
- Livezey, R.E.; Chen, W.Y. Statistical field significance and its determination by Monte Carlo techniques. Mon. Weather Rev. 1983, 111, 46–59. [Google Scholar] [CrossRef]
- Rogerson, P.A. Statistical Methods for Geography: A Student’s Guide; SAGE: San Mateo, CA, USA, 2014. [Google Scholar]
- Douglas, E.M.; Vogel, R.M.; Kroll, C.N. Trends in floods and low flows in the United States: Impact of spatial correlation. J. Hydrol. 2000, 240, 90–105. [Google Scholar] [CrossRef]
- Limjirakan, S.; Limsakul, A.; Sriburi, T. Trends in temperature and rainfall extreme changes in Bangkok Metropolitan area. Appl. Environ. Res. 2010, 32, 31–48. [Google Scholar]
- Wang, W.; Shao, Q.; Yang, T.; Peng, S.; Yu, Z.; Taylor, J.; Xing, W.; Zhao, C.; Sun, F. Changes in daily temperature and precipitation extremes in the Yellow River Basin, China. Stoch. Environ. Res. Risk Assess. 2013, 27, 401–421. [Google Scholar] [CrossRef]
- National Weather Service Portland, OR Record Report. Available online: http://w2.weather.gov/climate/getclimate.php?date=&wfo=pqr&sid=PQR&pil=RER&recent=yes&specdate=2016-10-31+11%3A55%3A10 (accessed on 2 February 2017).
- Pathirana, A.; Herath, S. Multifractal modelling and simulation of rain fields exhibiting spatial heterogeneity. Hydrol. Earth Syst. Sci. 2002, 6, 695–708. [Google Scholar] [CrossRef]
- Daily Weather Records|Data Tools|Climate Data Online (CDO)|National Climatic Data Center (NCDC). Available online: https://www.ncdc.noaa.gov/cdo-web/datatools/records (accessed on 25 August 2016).
- Hamlet, A.F.; Lettenmaier, D.P. Columbia River streamflow forecasting based on ENSO and PDO climate signals. J. Water Resour. Plan. Manag. 1999, 125, 333–341. [Google Scholar] [CrossRef]
- Salathé, E.P. Influences of a shift in North Pacific storm tracks on western North American precipitation under global warming. Geophys. Res. Lett. 2006. [Google Scholar] [CrossRef]
| Moran’s Index | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Jan. | Feb. | Mar. | Apr. | May. | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | Dec. | |
| Hourly Precipitation Intensity | - | - | - | - | - | 0.26 ** | - | - | - | - | - | - |
| Daily Precipitation Intensity | - | - | 0.29 ** | 0.26 ** | - | - | - | 0.14 * | - | 0.42 ** | - | - |
| Volume | - | - | - | - | - | - | - | - | - | - | - | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cooley, A.; Chang, H. Precipitation Intensity Trend Detection using Hourly and Daily Observations in Portland, Oregon. Climate 2017, 5, 10. https://doi.org/10.3390/cli5010010
Cooley A, Chang H. Precipitation Intensity Trend Detection using Hourly and Daily Observations in Portland, Oregon. Climate. 2017; 5(1):10. https://doi.org/10.3390/cli5010010
Chicago/Turabian StyleCooley, Alexis, and Heejun Chang. 2017. "Precipitation Intensity Trend Detection using Hourly and Daily Observations in Portland, Oregon" Climate 5, no. 1: 10. https://doi.org/10.3390/cli5010010
APA StyleCooley, A., & Chang, H. (2017). Precipitation Intensity Trend Detection using Hourly and Daily Observations in Portland, Oregon. Climate, 5(1), 10. https://doi.org/10.3390/cli5010010






