Daytime Variation of Urban Heat Islands: The Case Study of Doha, Qatar
Abstract
:1. Introduction
2. Materials and Methods
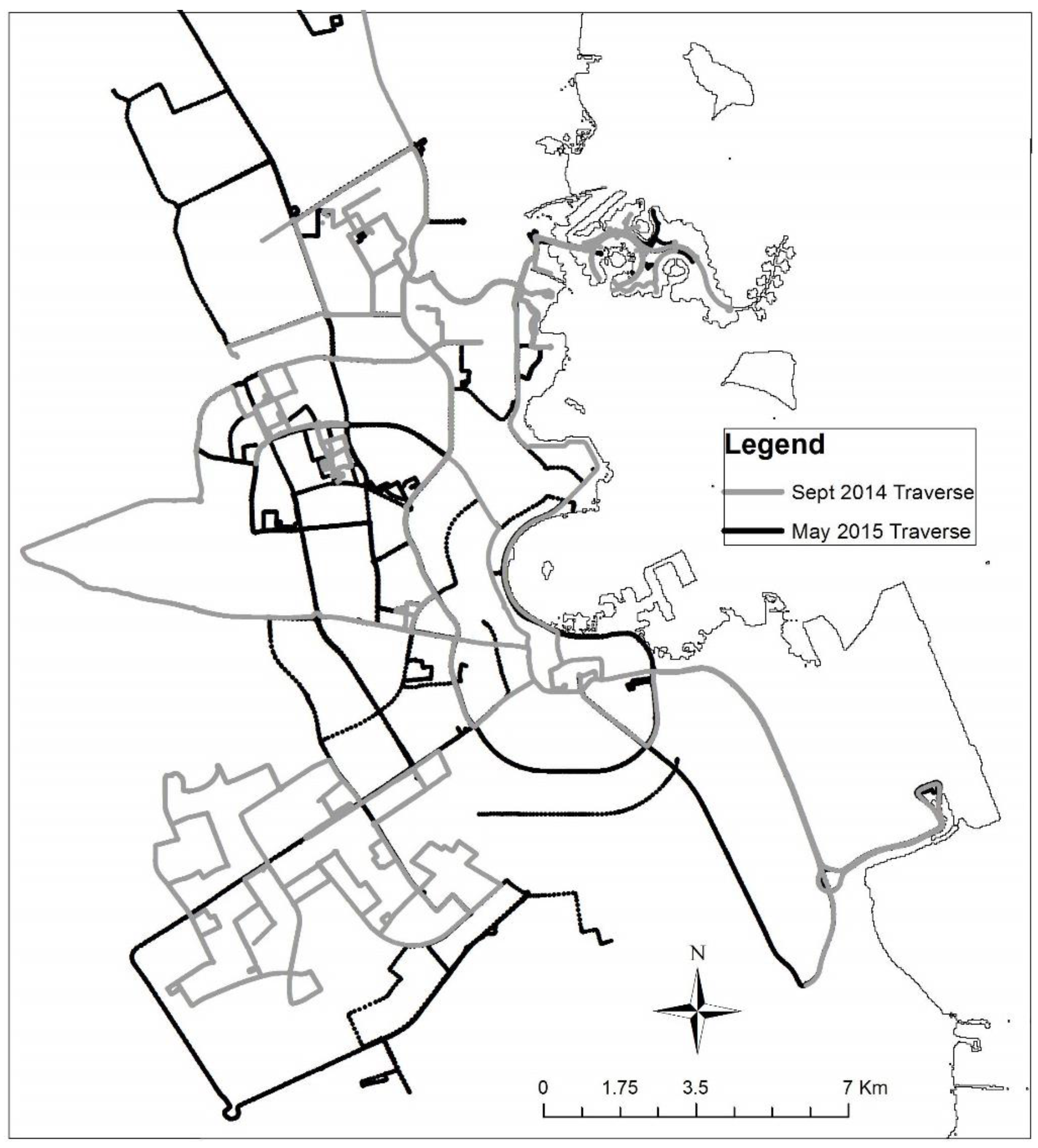
2.1. Vehicle Temperature Traverses
2.2. Land Use and Land Cover Variables
2.2.1. Classification and Albedo
2.2.2. Accuracy Assessment
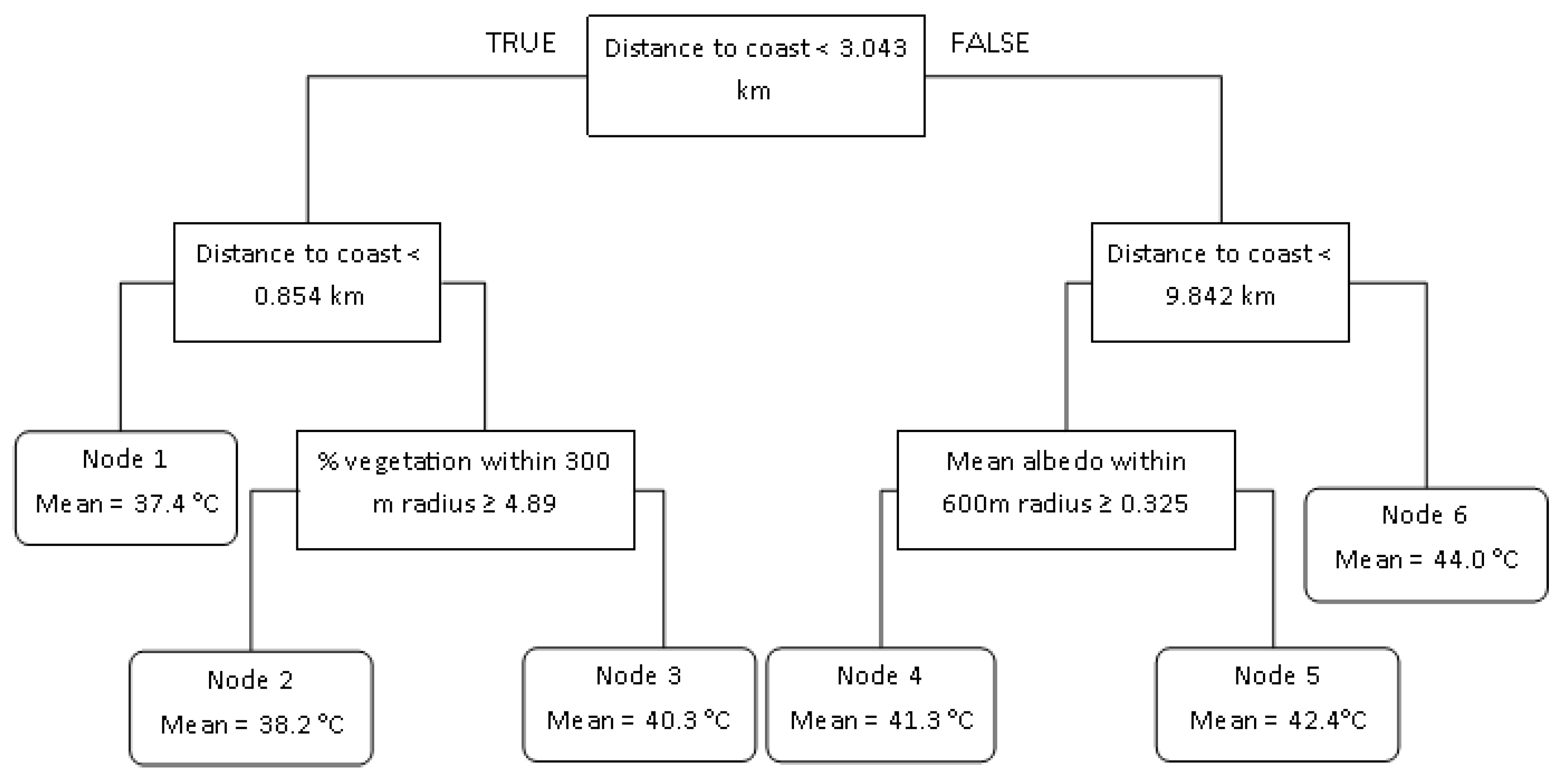
2.3. Analysis
- -
- Mean albedo within a certain radius (a#)
- -
- Percentage of urban area within a certain radius (u#)
- -
- Percentage of vegetation cover within a certain radius (v#)
- -
- Distance to the coast (w_dist)
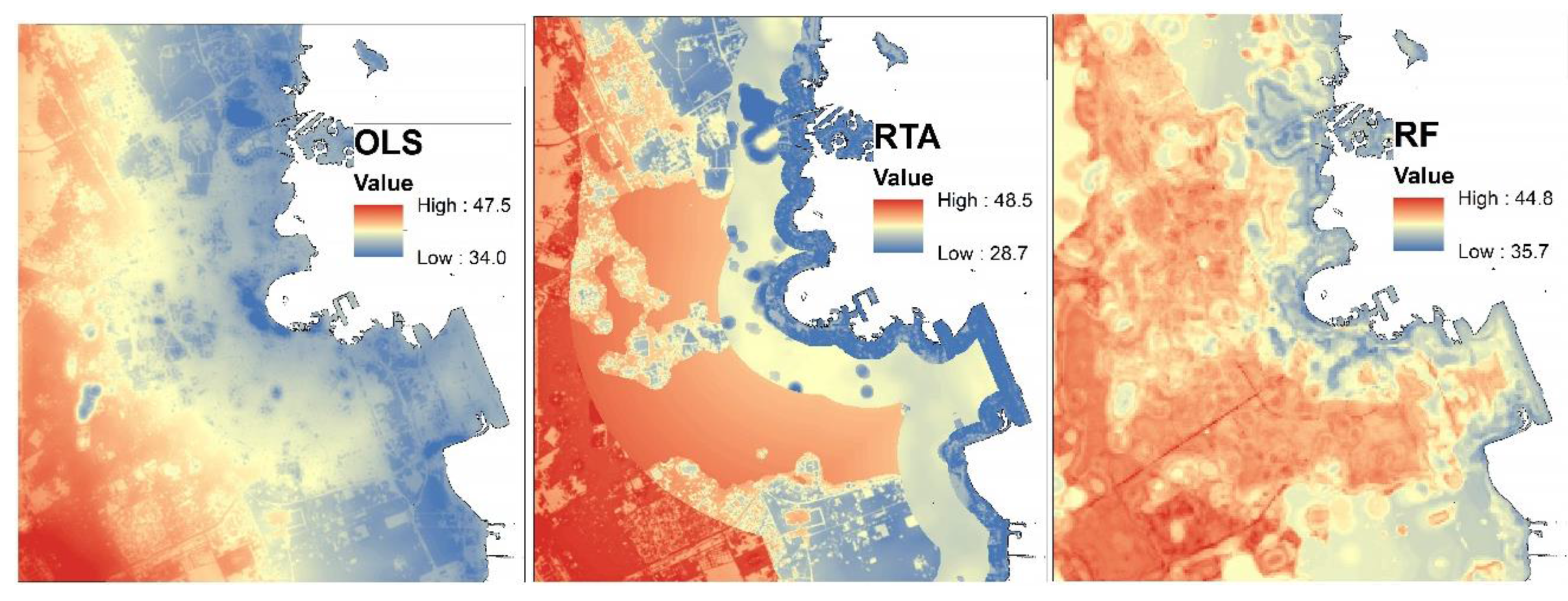
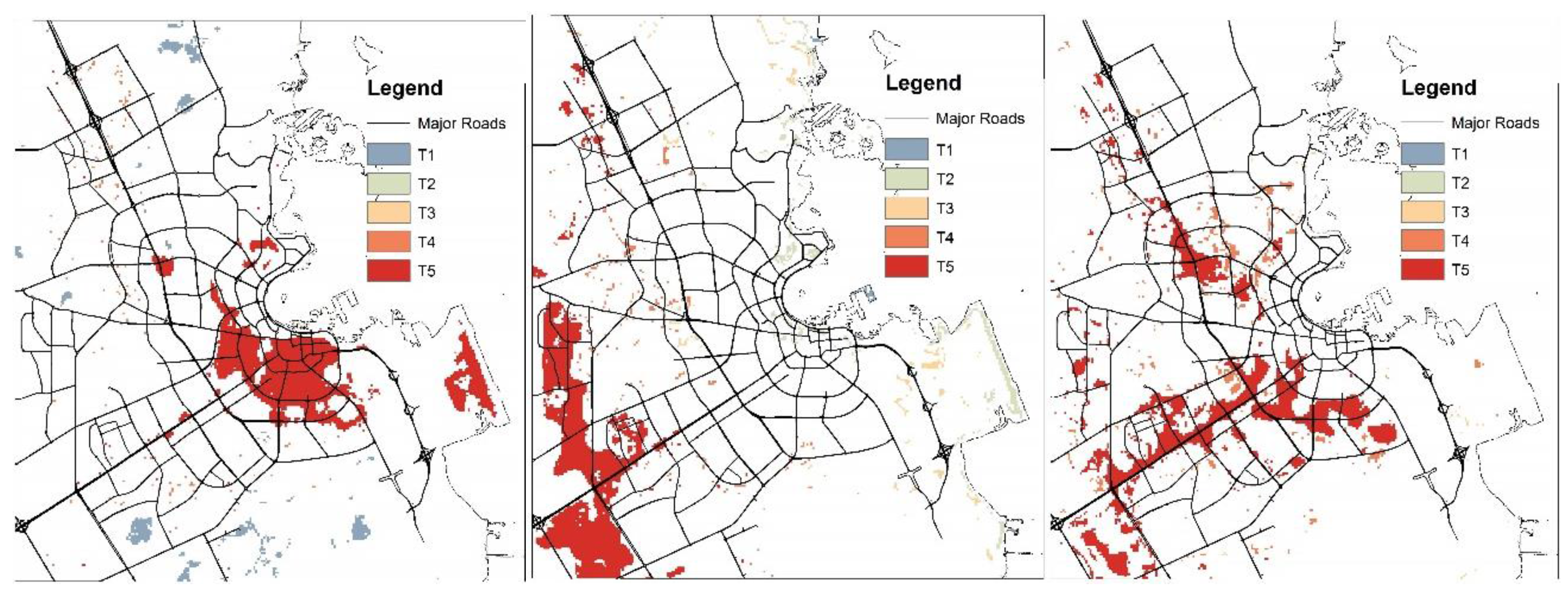
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Luber, G.; McGeehin, M. Climate change and extreme heat events. Am. J. Public Health 2008, 35, 429–435. [Google Scholar] [CrossRef] [PubMed]
- Reid, C.E.; O’Neill, M.S.; Gronlund, C.J.; Brines, S.J.; Brown, D.G.; Diez-Roux, A.V.; Schwartz, J. Mapping community determinants of heat vulnerability. Environ. Health Perspect. 2009, 117, 1730. [Google Scholar] [CrossRef] [PubMed]
- Knowlton, K. Projecting heat-related mortality impacts under a changing climate in the New York City region. Am. J. Public Health 2007, 97, 2028–2034. [Google Scholar] [CrossRef] [PubMed]
- Balbus, J.M.; Malina, C. Identifying vulnerable subpopulations for climate change health effects in the United States. J. Occup. Environ. Med. 2009, 51, 33–37. [Google Scholar] [CrossRef] [PubMed]
- Oke, T.R. The heat island of the urban boundary layer: Characteristics, causes and effects. In Wind Climate in Cities; Springer: Dordrecht, The Netherlands, 1995; pp. 81–107. [Google Scholar]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Lazzarini, M.; Marpu, P.R.; Ghedira, H. Temperature-land cover interactions: The inversion of urban heat island phenomenon in desert city areas. Remote Sens. Environ. 2013, 130, 136–152. [Google Scholar] [CrossRef]
- Rasul, A.; Balzter, H.; Smith, C. Spatial variation of the daytime surface urban cool island during the dry season in Erbil, Iraqi Kurdistan, from Landsat 8. Urban Clim. 2015, 14, 176–186. [Google Scholar] [CrossRef]
- Brazel, A.P.; Gober, S.-J.; Lee, S.; Grossman-Clarke, J.; Hedquist, Z.B.; Comparri, E. Determinants of changes in the regional urban heat island in metropolitan Phoenix (Arizona, USA) between 1990 and 2004. Clim. Res. 2007, 33, 171–182. [Google Scholar] [CrossRef]
- Nassar, A.K.; Blackburn, G.A.; Whyatt, J.D. Developing the desert: The pace and process of urban growth in Dubai. Comput. Environ. Urban Syst. 2014, 45, 50–62. [Google Scholar] [CrossRef]
- Rao, P.K. Remote sensing of urban heat islands from an environmental satellite. Bull. Am. Meteorol. Soc. 1972, 53, 647. [Google Scholar]
- Yuan, F.; Bauer, M.E. Comparison of impervious surface area and normalized difference vegetation index as indicators of surface urban heat island effects in Landsat imagery. Remote Sens. Environ. 2007, 106, 375–386. [Google Scholar] [CrossRef]
- Li, J.; Song, C.; Cao, L.; Zhu, F.; Meng, X.; Wu, J. Impacts of landscape structure on surface urban heat islands: A case study of Shanghai, China. Remote Sens. Environ. 2011, 115, 3249–3263. [Google Scholar] [CrossRef]
- Frey, C.M.; Rigo, G.; Parlow, E. Urban radiation balance of two coastal cities in a hot and dry environment. Int. J. Remote Sens. 2007, 28, 2695–2712. [Google Scholar] [CrossRef]
- Su, Y.F.; Foody, G.M.; Cheng, K.S. Spatial non-stationarity in the relationships between land cover and surface temperature in an urban heat island and its impacts on thermally sensitive populations. Landsc. Urban Plan. 2012, 107, 172–180. [Google Scholar] [CrossRef]
- Zhou, W.; Qian, Y.; Li, X.; Li, W.; Han, L. Relationships between land cover and the surface urban heat island: Seasonal variability and effects of spatial and thematic resolution of land cover data on predicting land surface temperatures. Landsc. Ecol. 2014, 29, 153–167. [Google Scholar] [CrossRef]
- Oke, T.R. The distinction between canopy and boundary-layer urban heat islands. Atmosphere 1976, 14, 268–277. [Google Scholar]
- Hart, M.A.; Sailor, D.J. Quantifying the influence of land-use and surface characteristics on spatial variability in the urban heat island. Theor. Appl. Climatol. 2009, 95, 397–406. [Google Scholar] [CrossRef]
- Heusinkveld, B.G.; Steeneveld, G.J.; Hove, L.V.; Jacobs, C.M.J.; Holtslag, A.A.M. Spatial variability of the Rotterdam urban heat island as influenced by urban land use. J. Geophys. Res. Atmos. 2014, 119, 677–692. [Google Scholar] [CrossRef]
- Yan, H.; Fan, S.; Guo, C.; Wu, F.; Zhang, N.; Dong, L. Assessing the effects of landscape design parameters on intra-urban air temperature variability: The case of Beijing, China. Build. Environ. 2014, 76, 44–53. [Google Scholar] [CrossRef]
- Ho, H.C.; Knudby, A.; Sirovyak, P.; Xu, Y.; Hodul, M.; Henderson, S.B. Mapping maximum urban air temperature on hot summer days. Remote Sens. Environ. 2014, 154, 38–45. [Google Scholar] [CrossRef]
- Yokobori, T.; Ohta, S. Effect of land cover on air temperatures involved in the development of an intra-urban heat island. Clim. Res. 2016, 39, 61. [Google Scholar] [CrossRef]
- Adham, K. Petro urbanism: The geo-politics of urban development in Doha, Qatar. Int. J. Hous. Sci. 2009, 33, 77–87. [Google Scholar]
- Jensen, J.R. Introductory Digital Image Processing; Prentice-Hall: Englewood Cliffs, NJ, USA, 1986. [Google Scholar]
- Zha, Y.; Gao, J.; Ni, S. Use of normalized difference built-up index in automatically mapping urban areas from TM imagery. Int. J. Remote Sens. 2003, 24, 583–594. [Google Scholar] [CrossRef]
- Shandas, V.; Makido, Y.; Hong, C.; Ferwati, S.; Sailor, D. Rapid urban growth and development patterns in the Middle East: The Case of Doha, Qatar. Unpublished work. 2016. [Google Scholar]
- Lo, C.P.; Choi, J. A hybrid approach to urban land use/cover mapping using Landsat 7 Enhanced Thematic Mapper Plus (ETM+) images. Int. J. Remote Sens. 2004, 25, 2687–2700. [Google Scholar] [CrossRef]
- Lillesand, T.; Kiefer, R.W.; Chipman, J. Remote Sensing and Image Interpretation; John Wiley & Sons: New York, NY, USA, 2014. [Google Scholar]
- YCEO. Yale Center for Earth Observation, How to Convert Landsat DNs to Albedo. Available online: http://yceo.yale.edu/how-convert-landsat-dns-albedo (accessed on 20 April 2016).
- Liang, S. Narrowband to broadband conversions of land surface albedo I: Algorithms. Remote Sens. Environ. 2001, 76, 213–238. [Google Scholar] [CrossRef]
- Smith, R.B. The Heat Budget of the Earth s Surface Deduced from Space. Available online: http://yceo.yale.edu/sites/default/files/files/Surface_Heat_Budget_From_Space.pdf (accessed on 20 April 2016).
- Yale University. Land Surface Properties, Regioanl Climate Feedbacks and Urban Adaptations. Available online: http://surfaceheat.sites.yale.edu/sites/default/files/Albedo.pdf (accessed on 20 April 2016).
- Schowengerdt, R.A. Remote Sensing: Models and Methods for Image Processing, (No. 621.367 S476 1997); Academic Press: Boston, MA, USA, 1997. [Google Scholar]
- Brower, B.V.; Laben, C.A. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pansharpening. U.S. Patent 6,011,875, 4 January 2000. [Google Scholar]
- Anderson, J.R.; Hardy, E.E.; Roach, J.T.; Witmer, R.E. A Land Use and Land Cover Classification System for Use with Remote Sensor Data; U.S. Government Printing Office (GPO): Washington, DC, USA, 1976.
- Krüger, E.; Givoni, B. Outdoor measurements and temperature comparisons of seven monitoring stations: Preliminary studies in Curitiba, Brazil. Build. Environ. 2007, 42, 1685–1698. [Google Scholar] [CrossRef]
- Ho, H.C.; Knudby, A.; Xu, Y.; Hodul, M.; Aminipouri, M. A comparison of urban heat islands mapped using skin temperature, air temperature, and apparent temperature (Humidex), for the greater Vancouver area. Sci. Total Environ. 2016, 544, 929–938. [Google Scholar] [CrossRef] [PubMed]
- Yuan, F.; Wu, C.; Bauer, M.E. Comparison of spectral analysis techniques for impervious surface estimation using Landsat imagery. Photogramm. Eng. Remote Sens. 2008, 74, 1045–1055. [Google Scholar] [CrossRef]
- Hansen, M.C.; DeFries, R.S.; Townshend, J.R.G.; Sohlberg, R.; Dimiceli, C.; Carroll, M. Towards an operational MODIS continuous field of percent tree cover algorithm: Examples using AVHRR and MODIS data. Remote Sens. Environ. 2002, 83, 303–319. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Prasad, A.M.; Iverson, L.R.; Liaw, A. Newer classification and regression tree techniques: Bagging and random forests for ecological prediction. Ecosystems 2006, 9, 181–199. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing. The R Foundation for Statistical Computing: Vienna, Austria. Available online: http://www.R-project.org/ (accessed on 20 April 2016).
- Therneau, T.; Atkinson, B.; Ripley, B.; Ripley, M.B. Package “rpart”. Available online: cran.ma.ic.ac.uk/web/packages/rpart/rpart.pdf (accessed on 20 April 2016).
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. IJCAI 1995, 14, 1137–1145. [Google Scholar]
- Breiman, L. RandomForest: Breiman and Cutler’s Random Forests for Classification and Regression. Available online: https://www.stat.berkeley.edu/~breiman/RandomForests/ (accessed on 20 April 2016).
- World sea temperature. Doha average August sea temperature. Available online: http://www.seatemperature.org/middle-east/qatar/doha-august.htm (accessed on 20 April 2016).
- Wong, M.S.; Nichol, J.; Ng, E. A study of the “wall effect” caused by proliferation of high-rise buildings using GIS techniques. Landsc. Urban Plan. 2011, 102, 245–253. [Google Scholar] [CrossRef]
- Nichol, J. Remote sensing of urban heat islands by day and night. Photogramm. Eng. Remote Sens. 2005, 71, 613–621. [Google Scholar] [CrossRef]


| Classes | Definition |
|---|---|
| Urban | All built-up surfaces, including roads, commercial, industrial pavements, and construction sites. |
| Vegetation | All areas of vegetation, including farms, parks golf courses, and lawns. |
| Soil | Bare and exposed rock, coastal sands, and sand dunes. |
| Water | All areas of open water, including lakes and the ocean. |
| Reference Data | User’s Accuracy (%) | ||||||
|---|---|---|---|---|---|---|---|
| Urban | Vegetation | Soil | Water | Total | |||
| Classified Data | Urban | 63 | 1 | 4 | 0 | 68 | 92.7 |
| Vegetation | 8 | 47 | 4 | 0 | 59 | 79.7 | |
| Soil | 7 | 1 | 52 | 0 | 60 | 86.7 | |
| Water | 7 | 1 | 1 | 40 | 49 | 81.6 | |
| Total | 85 | 50 | 61 | 40 | 236 | ||
| Producer’s accuracy (%) | 74.1 | 94.0 | 85.3 | 100.0 | |||
| 8 September 2014 | 9 September 2014 | ||||||||
| 6 am | 1 pm | 7 pm | 6 am | 1 pm | 7 pm | ||||
| Albedo | 50 | 400 | 150 | 50 | 400 | 50 | |||
| Urban | 500 | 600 | 600 | 600 | 600 | 600 | |||
| Vegetation | 100 | 400 | 150 | 50 | 350 | 150 | |||
| 12 May 2015 | 14 May 2015 | 15 May 2015 | |||||||
| 6 am | 1 pm | 7 pm | 6 am | 1 pm | 7 pm | 6 am | 1 pm | 7 pm | |
| Albedo | 150 | 600 | 600 | 50 | 400 | 600 | 50 | 600 | 200 |
| Urban | 600 | 50 | 50 | 100 | 600 | 300 | 50 | 600 | 600 |
| Vegetation | 50 | 300 | 600 | 600 | 100 | 200 | 50 | 600 | 600 |
| 8 September 2014 | 9 September 2014 | ||||||||
| 6 am | 1 pm | 7 pm | 6 am | 1 pm | 7 pm | ||||
| OLS | 1.28 | 1.21 | 0.62 | 0.96 | 1.22 | 0.63 | |||
| RTA | 1.05 | 1.09 | 0.53 | 0.80 | 1.06 | 0.57 | |||
| RF | 0.43 | 0.75 | 0.34 | 0.35 | 0.79 | 0.39 | |||
| 12 May 2014 | 14 May 2014 | 15 May 2014 | |||||||
| 6 am | 1 pm | 7 pm | 6 am | 1 pm | 7 pm | 6 am | 1 pm | 7 pm | |
| OLS | 1.19 | 1.81 | 1.72 | 1.44 | 2.71 | 0.96 | 0.79 | 1.15 | 1.00 |
| RTA | 0.93 | 1.44 | 0.82 | 1.34 | 1.33 | 0.76 | 0.72 | 1.05 | 0.93 |
| RF | 0.63 | 1.05 | 0.54 | 0.82 | 0.99 | 0.47 | 0.46 | 0.97 | 0.79 |
| 8 September 2014 | 9 September 2014 | 12 May 2015 | 14 May 2015 | 15 May 2015 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 6 am | w_dist | 91.9 | w_dist | 104.6 | w_dist | 75.7 | w_dist | 61.0 | w_dist | 67.0 |
| a50 | 47.5 | v600 | 52.1 | u600 | 32.0 | a50 | 35.4 | v600 | 31.8 | |
| v600 | 41.1 | v550 | 38.3 | v600 | 28.5 | a600 | 31.0 | a600 | 25.7 | |
| 1 pm | w_dist | 133.8 | w_dist | 134.0 | w_dist | 151.8 | w_dist | 63.4 | w_dist | 113.7 |
| v600 | 36.8 | u200 | 34.9 | a50 | 37.6 | v550 | 19.6 | a50 | 26.5 | |
| a150 | 31.0 | u350 | 34.6 | a600 | 29.8 | a600 | 19.3 | v600 | 21.7 | |
| 7 pm | w_dist | 105.8 | w_dist | 129.2 | w_dist | 59.4 | w_dist | 105.9 | w_dist | 73.5 |
| v600 | 37.3 | v600 | 37.5 | v600 | 24.8 | v550 | 23.6 | v600 | 24.1 | |
| a50 | 37.1 | a50 | 35.6 | v550 | 20.2 | v600 | 19.4 | v550 | 23.9 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makido, Y.; Shandas, V.; Ferwati, S.; Sailor, D. Daytime Variation of Urban Heat Islands: The Case Study of Doha, Qatar. Climate 2016, 4, 32. https://doi.org/10.3390/cli4020032
Makido Y, Shandas V, Ferwati S, Sailor D. Daytime Variation of Urban Heat Islands: The Case Study of Doha, Qatar. Climate. 2016; 4(2):32. https://doi.org/10.3390/cli4020032
Chicago/Turabian StyleMakido, Yasuyo, Vivek Shandas, Salim Ferwati, and David Sailor. 2016. "Daytime Variation of Urban Heat Islands: The Case Study of Doha, Qatar" Climate 4, no. 2: 32. https://doi.org/10.3390/cli4020032
APA StyleMakido, Y., Shandas, V., Ferwati, S., & Sailor, D. (2016). Daytime Variation of Urban Heat Islands: The Case Study of Doha, Qatar. Climate, 4(2), 32. https://doi.org/10.3390/cli4020032







