Changes in Average Annual Precipitation in Argentina’s Pampa Region and Their Possible Causes
Abstract
:1. Introduction
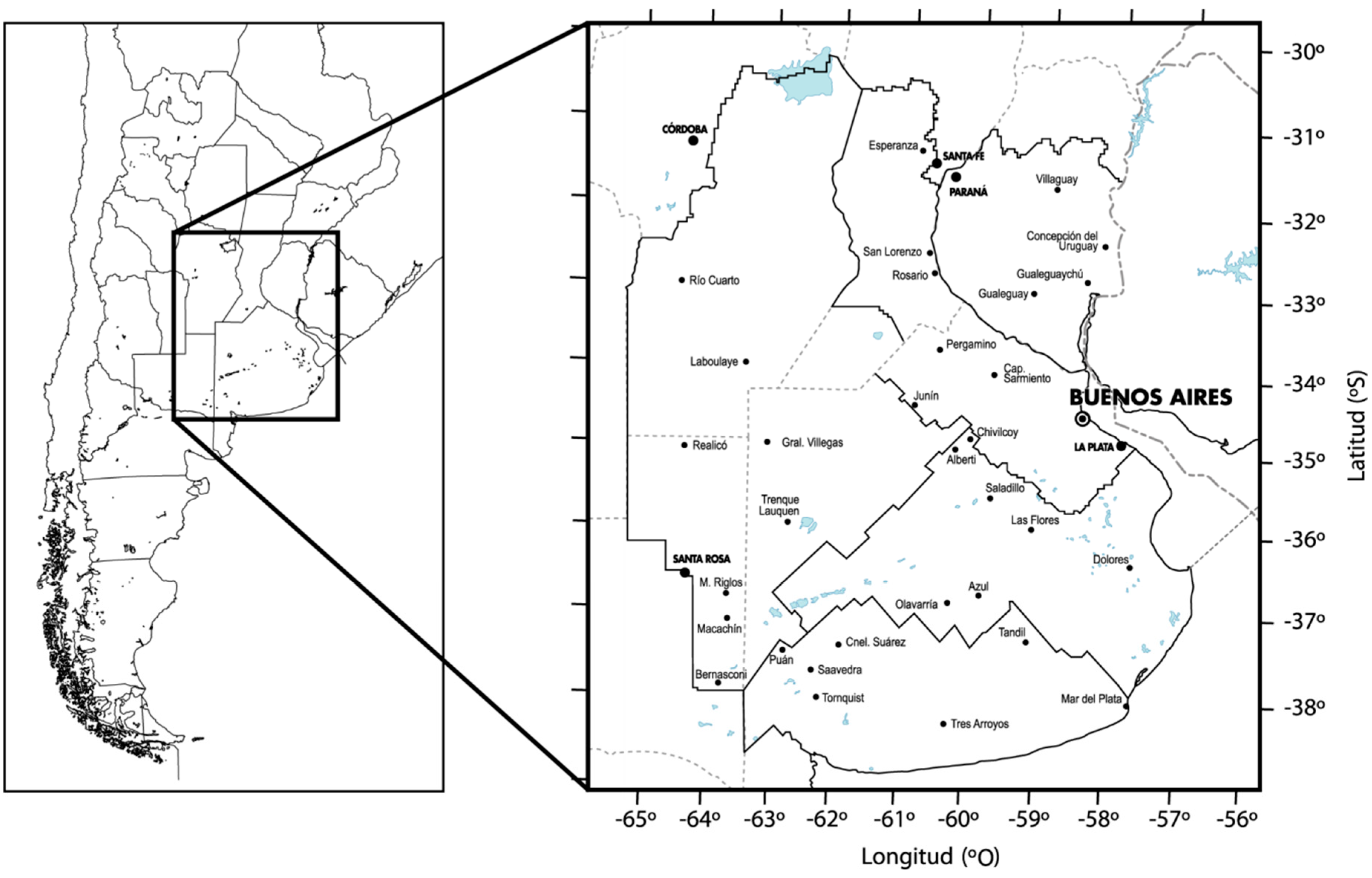
2. Materials and Methods
| Location | Latitude (S) | Longitude (W) | Altitude (msl) | Pampa Sub-Region |
|---|---|---|---|---|
| Esperanza | 31°27′ | 60° 55′ | 38 | Rolling |
| San Lorenzo | 32°44′ | 60° 44′ | 40 | Rolling |
| Rosario | 32°57′ | 60° 39′ | 25 | Rolling |
| Pergamino | 33°44′ | 60° 36′ | 56 | Rolling |
| Cap. Sarmiento | 34°10′ | 59° 48′ | 54 | Rolling |
| Junin | 34°35′ | 60° 56′ | 81 | Rolling |
| La Plata | 34°55′ | 57° 57′ | 26 | Rolling |
| Paraná | 31°43′ | 60° 31′ | 77 | Mesopotamian |
| Villaguay | 31°52′ | 59° 00′ | 40 | Mesopotamian |
| C del Uruguay | 32°29′ | 58° 14′ | 50 | Mesopotamian |
| Gualeguaychú | 33°00′ | 58° 30′ | 15 | Mesopotamian |
| Gualeguay | 33°08′ | 59° 19′ | 12 | Mesopotamian |
| Río Cuarto | 33°07′ | 64° 20′ | 452 | Central |
| Laboulaye | 34°07′ | 63° 23′ | 131 | Central |
| Gral. Villegas | 35°01′ | 63° 00′ | 105 | Central |
| Realicó | 35°01′ | 64° 15′ | 146 | Central |
| Trenque Lauquen | 35°58′ | 62° 43′ | 80 | Central |
| Riglos | 36°51′ | 63° 42′ | 126 | Central |
| Macachín | 37°09′ | 63° 39′ | 130 | Central |
| Bernasconi | 37°54′ | 63° 43′ | 162 | Central |
| Chivilcoy | 34°53′ | 60° 01′ | 53 | Flooding |
| Alberti | 35°01′ | 60° 16′ | 38 | Flooding |
| Saladillo | 35°38′ | 59° 46′ | 43 | Flooding |
| Las Flores | 36°03′ | 59° 06′ | 36 | Flooding |
| Dolores | 36°18′ | 57° 40′ | 7 | Flooding |
| Azul | 36°46′ | 59° 51′ | 137 | Flooding |
| Olavarría | 36°53′ | 60° 19′ | 150 | Flooding |
| Tandil | 37°19′ | 59° 08′ | 188 | Southern |
| Cnel.Suárez | 37°28′ | 61° 56′ | 298 | Southern |
| Puán | 37°32′ | 62° 46′ | 222 | Southern |
| Saavedra | 37°45′ | 62° 21′ | 334 | Southern |
| Mar del Plata | 38°00′ | 57° 33′ | 38 | Southern |
| Tornquist | 38°06′ | 62° 14′ | 276 | Southern |
| Tres Arroyos | 38°22′ | 60° 16′ | 98 | Southern |
2.1. Homogeneity Test
2.2. Detecting Shifts in the Mean
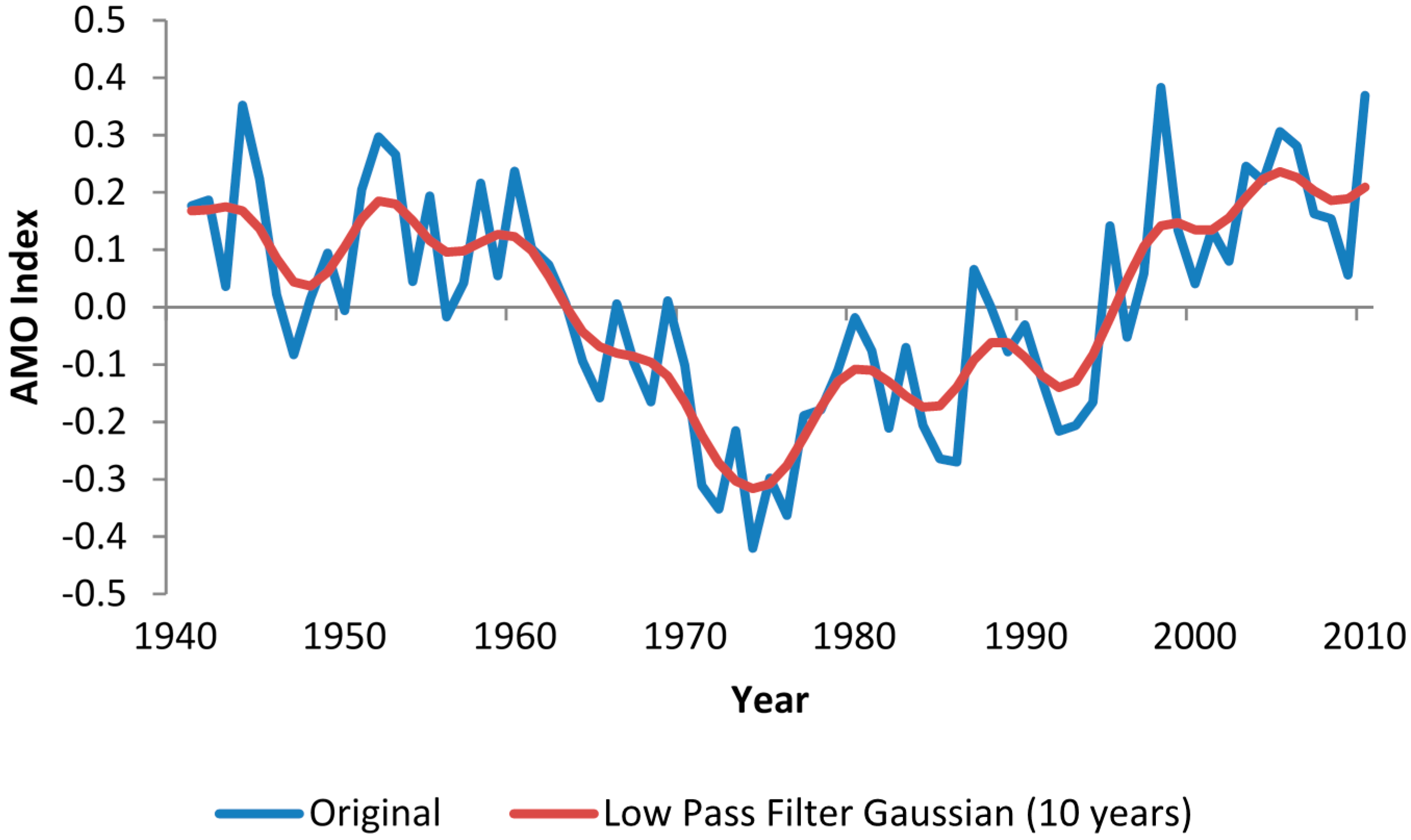
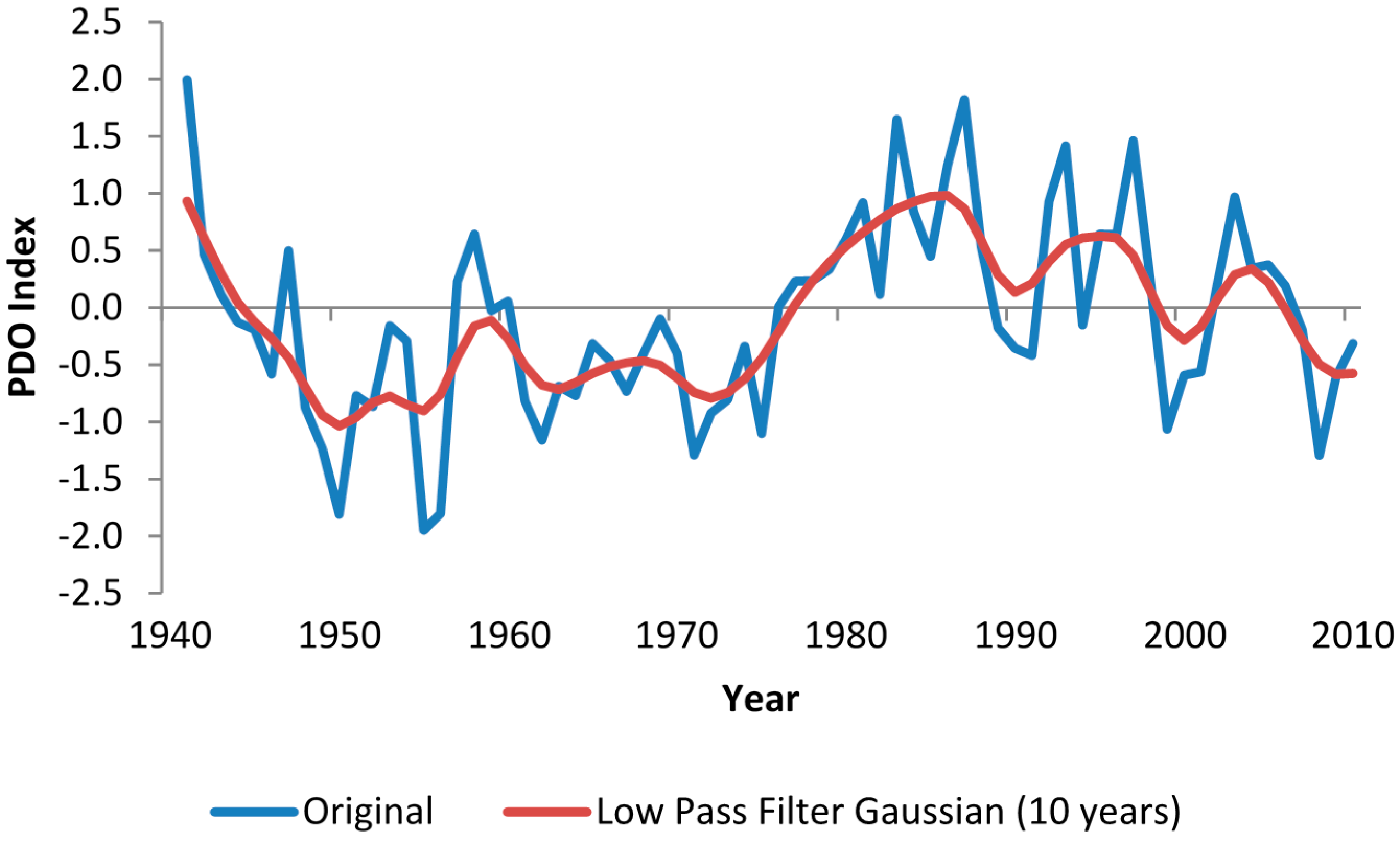
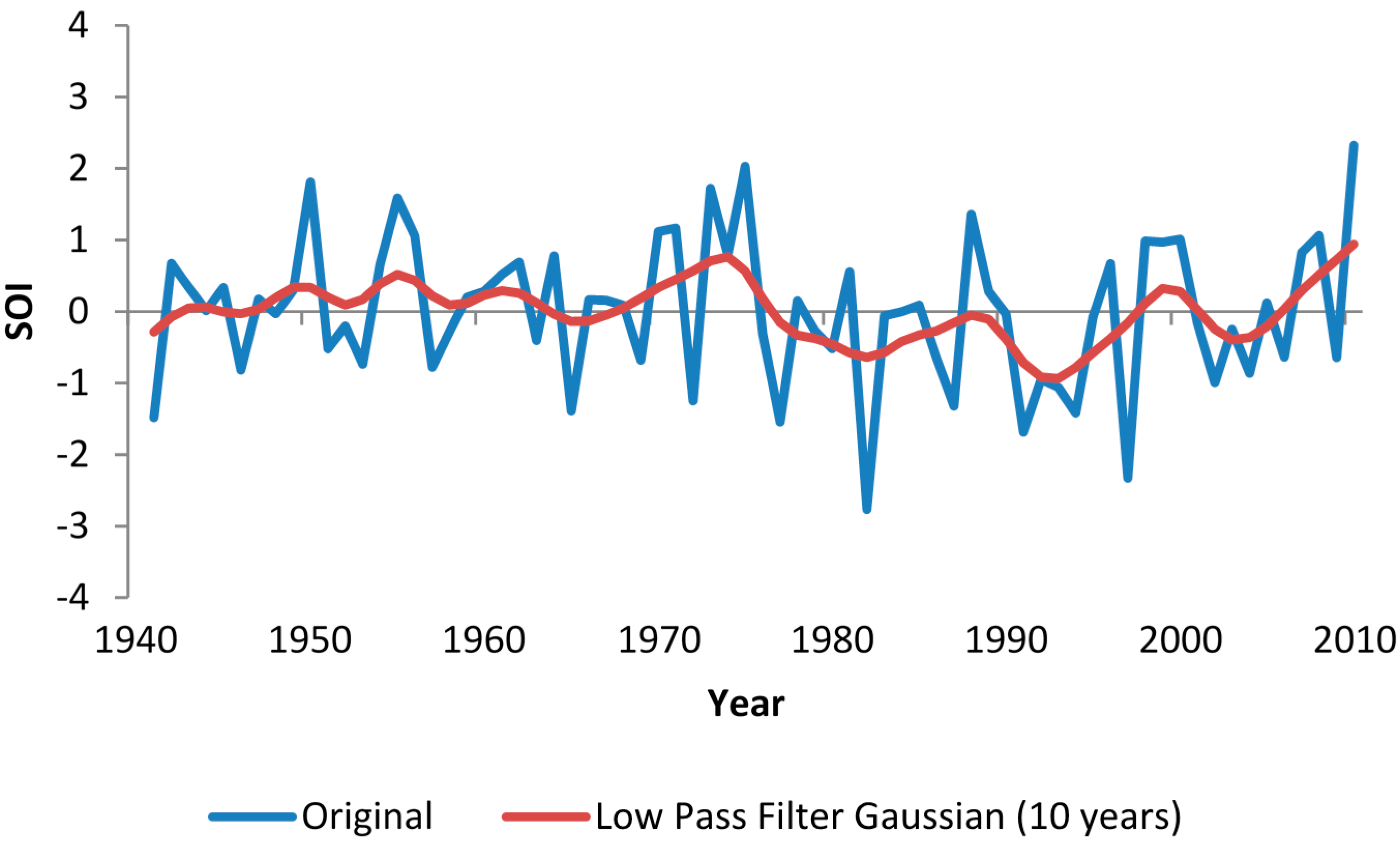
2.3.The AMO-PDO-SOI-precipitation relationship
3. Results and Discussion
3.1. Homogeneity Test
| Location | Shift Year | T Value | Shift Year Adjusted | T Value Adjusted | |
|---|---|---|---|---|---|
| Esperanza | 1944 | 4.315 | |||
| San Lorenzo | 2003 | 3.356 | |||
| Rosario | 1973 | 13.954 | * | 1996 | 7.493 |
| Pergamino | 2005 | 6.993 | |||
| Cap. Sarmiento | 1952 | 24.639 | * | 1996 | 5.321 |
| Junin | 2001 | 3.305 | |||
| La Plata | 2008 | 7.669 | |||
| Paraná | 1948 | 5.299 | |||
| Villaguay | 1943 | 6.498 | |||
| C del Uruguay | 1995 | 5.444 | |||
| Gualeguaychú | 1979 | 3.302 | |||
| Gualeguay | 1975 | 8.022 | |||
| Río Cuarto | 1968 | 22.476 | * | 1985 | 3.796 |
| Laboulaye | 1976 | 5.436 | |||
| Gral. Villegas | 2003 | 5.370 | |||
| Realicó | 2010 | 6.746 | |||
| Trenque Lauquen | 1956 | 7.366 | |||
| Riglos | 1977 | 10.936 | * | 1946 | 3.084 |
| Macachín | 2009 | 3.678 | |||
| Bernasconi | 2005 | 5.645 | |||
| Chivilcoy | 1990 | 15.885 | * | 1999 | 6.327 |
| Alberti | 2000 | 2.906 | |||
| Saladillo | 1977 | 3.186 | |||
| Las Flores | 1990 | 2.312 | |||
| Dolores | 2001 | 5.103 | |||
| Azul | 1991 | 6.187 | |||
| Olavarría | 1944 | 4.596 | |||
| Tandil | 1982 | 5.874 | |||
| Cnel. Suárez | 2005 | 9.750 | * | 2009 | 2.843 |
| Puán | 1976 | 2.431 | |||
| Saavedra | 1958 | 9.530 | * | 2009 | 4.720 |
| Mar del Plata | 2000 | 3.226 | |||
| Tornquist | 1964 | 3.887 | |||
| Tres Arroyos | 2010 | 10.071 | * | 1963 | 2.905 |
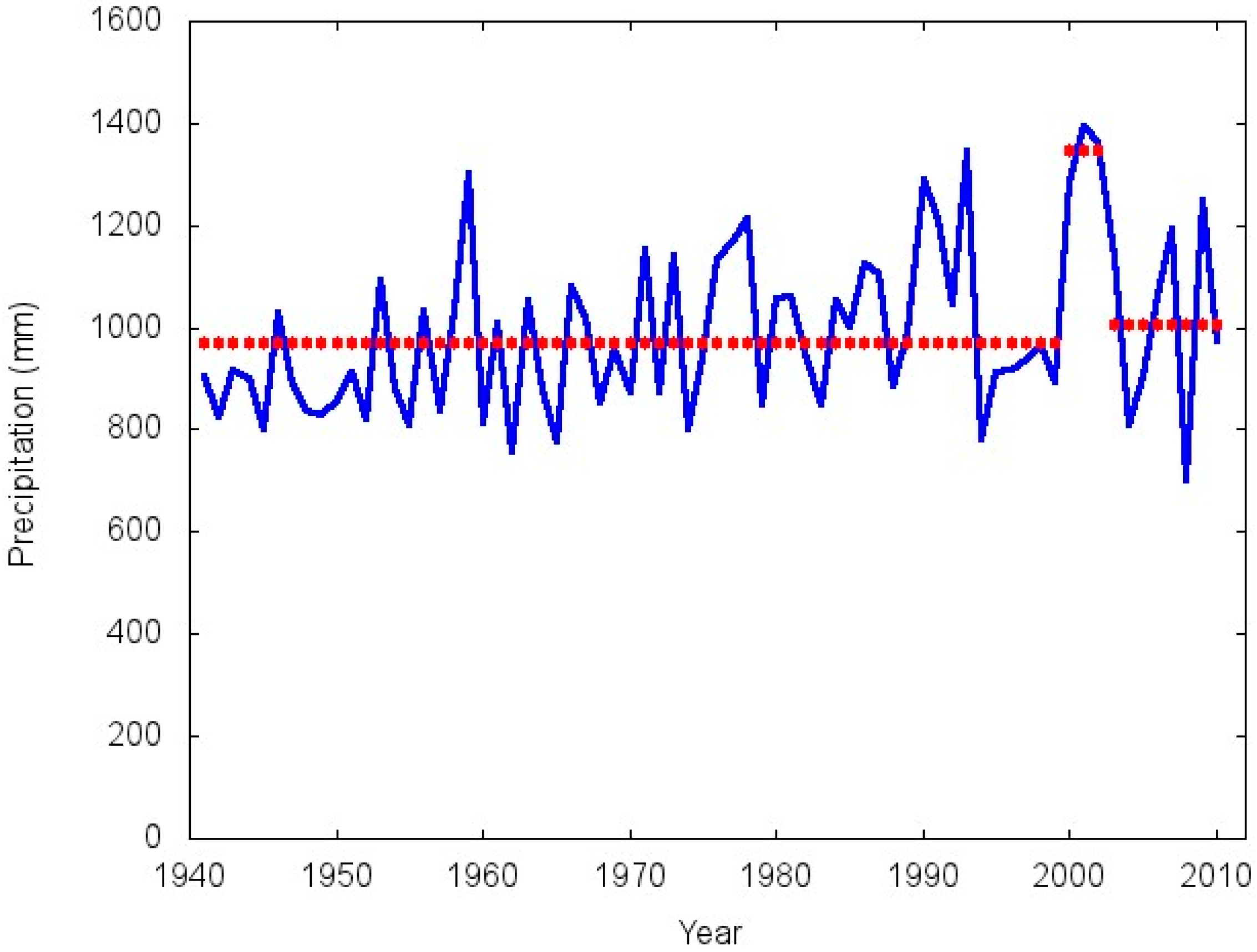
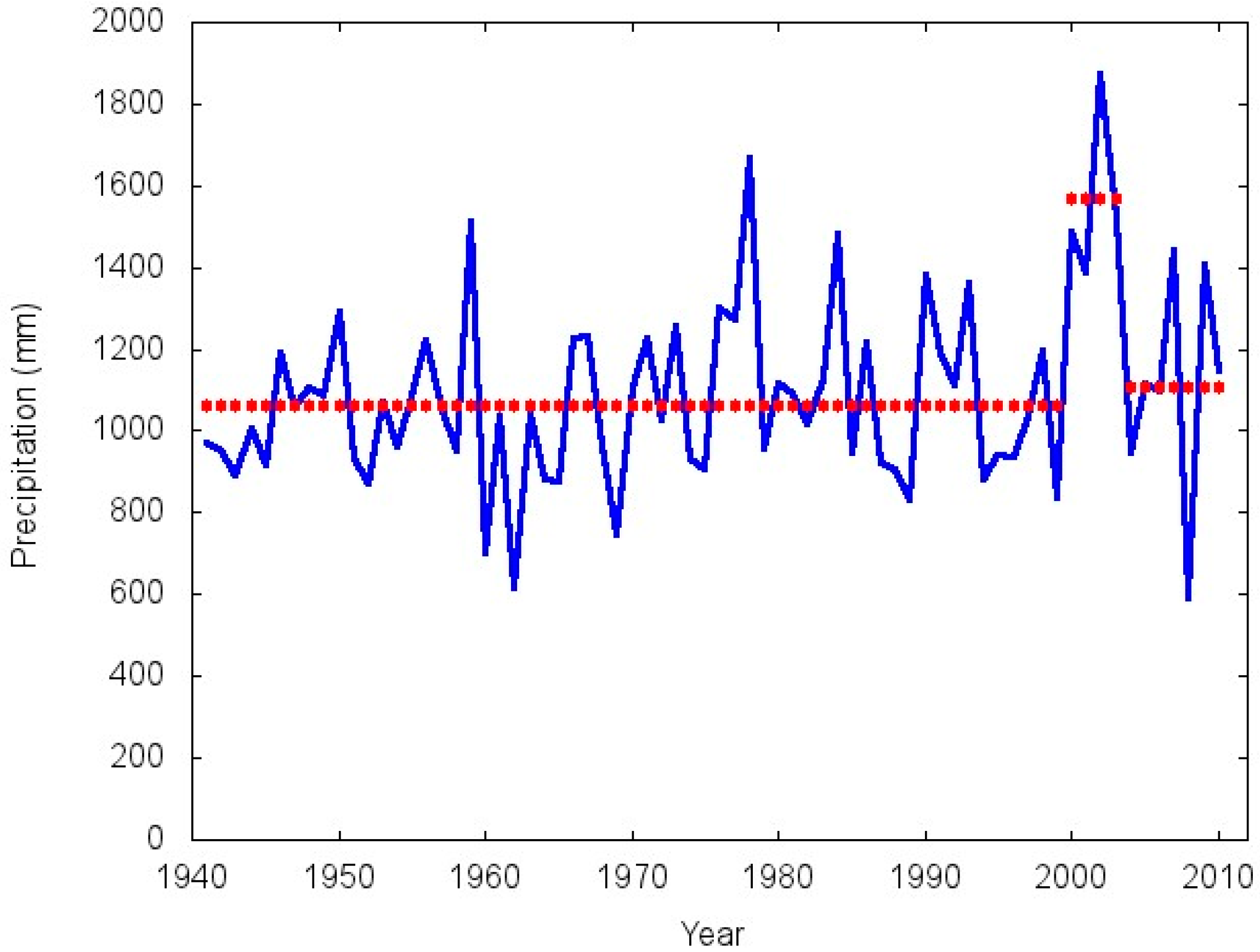
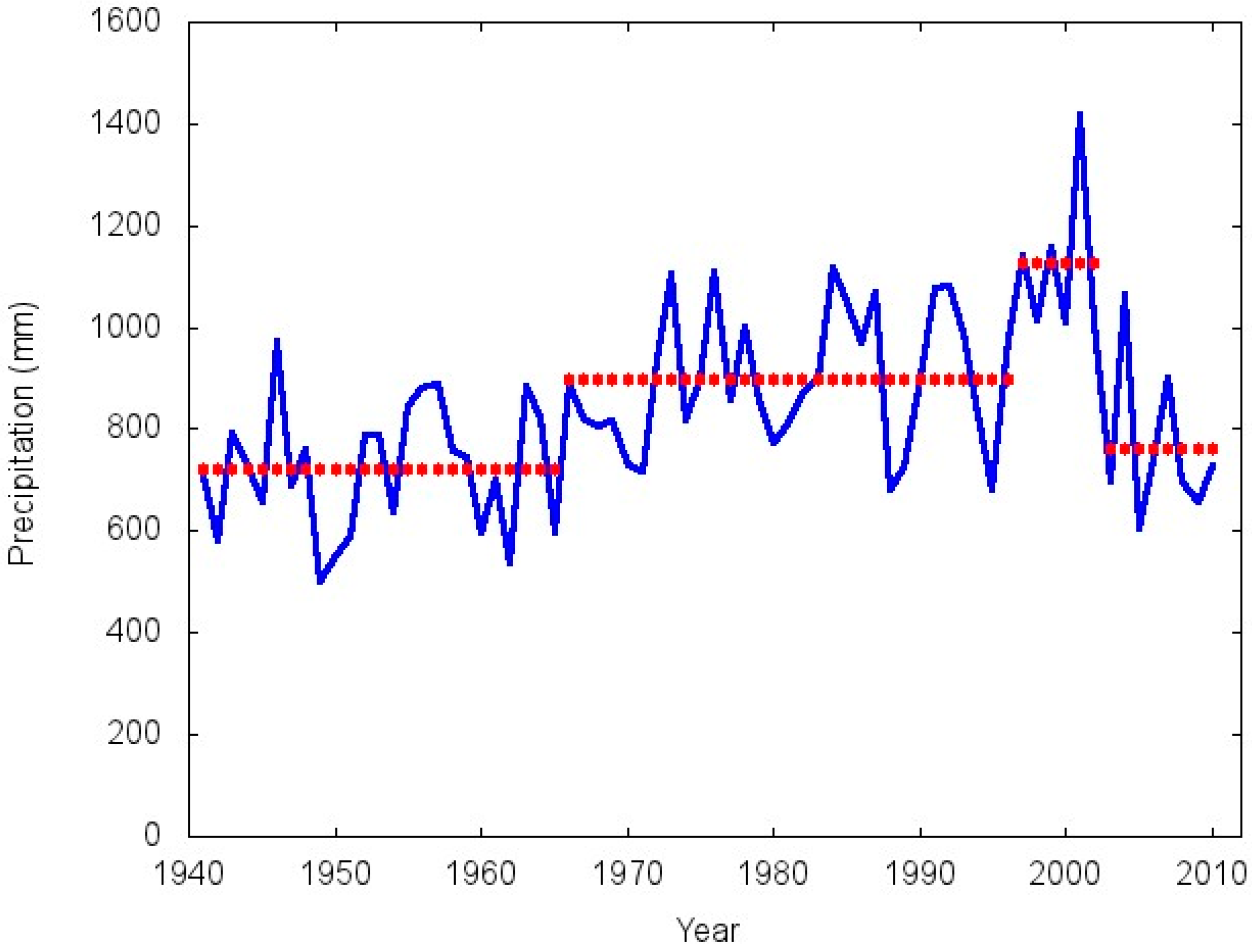
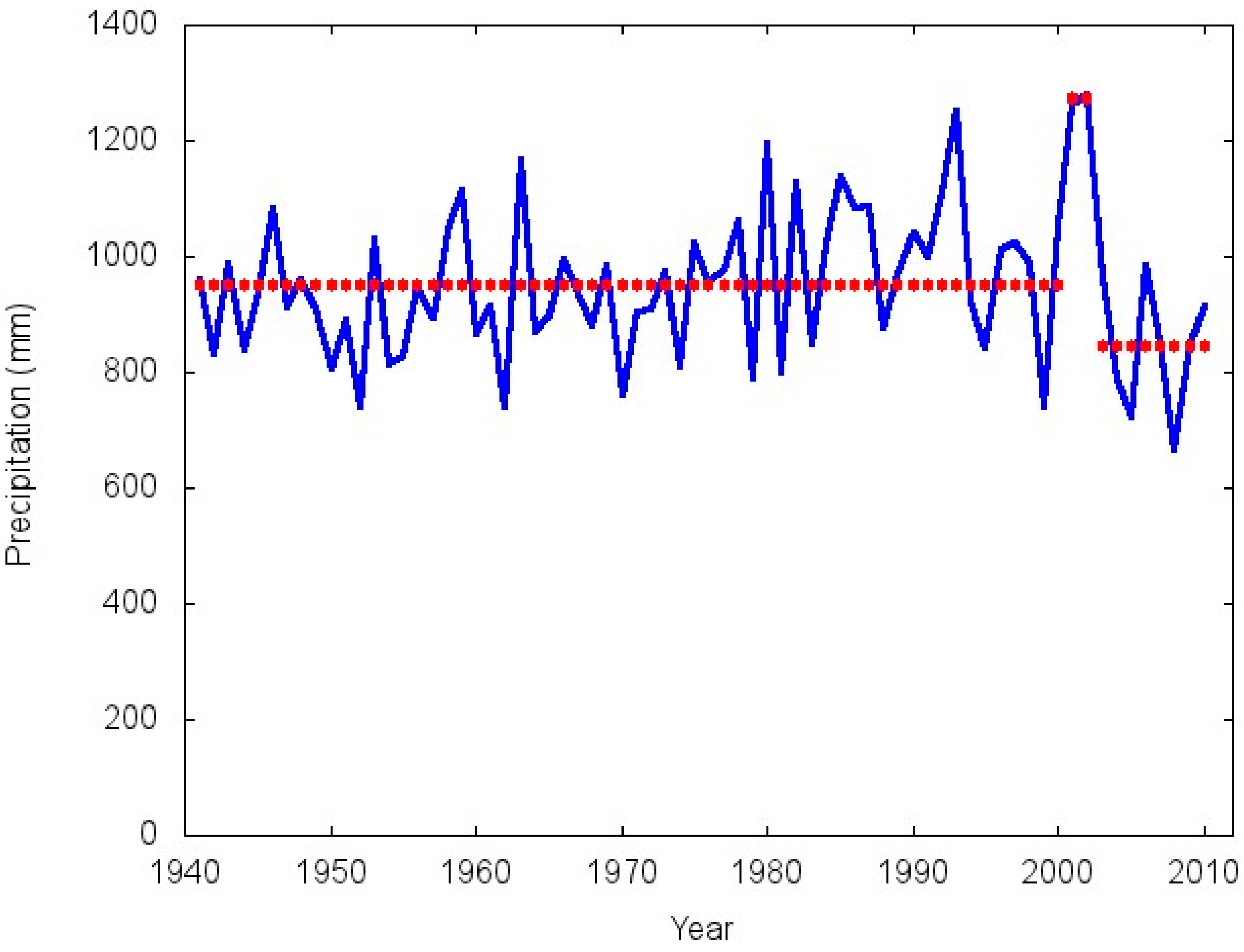
3.2. Detecting Changes in the Mean
| Sub-Regions | Sub-Period | Mean (mm) | Standard Deviation | Variation Coefficient |
|---|---|---|---|---|
| Rolling Pampa | 1941–1999 | 971.9 | 142.8 | 14.7 |
| 2000–2002 | 1349.3 | 56.7 | 4.2 | |
| 2003–2010 | 1005.2 | 191.8 | 19.0 | |
| Mesopotamian Pampa | 1941–1999 | 1062.9 | 197.9 | 18.6 |
| 2000–2003 | 1568.9 | 211.1 | 13.4 | |
| 2004–2010 | 1108.0 | 289.5 | 26.1 | |
| Central Pampa | 1941–1965 | 721.3 | 126.2 | 17.5 |
| 1966–1996 | 900.0 | 132.8 | 14.7 | |
| 1997–2002 | 1126.0 | 158.8 | 14.1 | |
| 2003–2010 | 762.2 | 149.9 | 19.7 | |
| Flooding Pampa | 1941–2000 | 952.7 | 118.9 | 12.5 |
| 2001–2002 | 1272.2 | 10.9 | 0.9 | |
| 2003–2010 | 844.5 | 112.9 | 13.4 | |
| Southern Pampa | 1941–2000 | 819.3 | 137.1 | 16.7 |
| 2001–2002 | 1155.2 | 85.9 | 7.4 | |
| 2003–2010 | 745.3 | 103.5 | 13.9 |
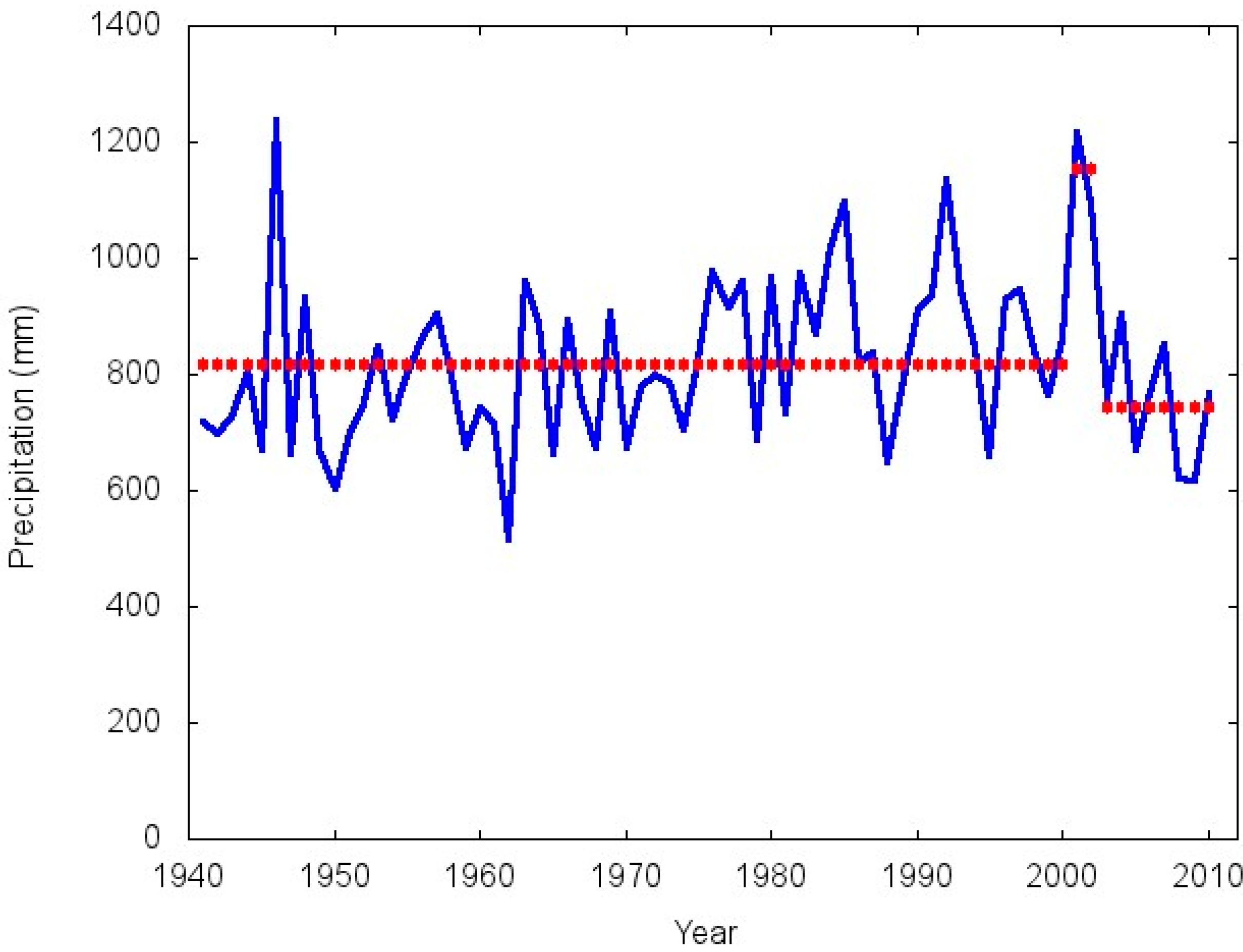
3.3. Associations from Rainfall to the AMO, PDO and SOI
| Lag | RP | MP | CP | FP | SP |
|---|---|---|---|---|---|
| −20 | −0.0234 | −0.0295 | −0.1298 | −0.0865 | −0.0985 |
| −19 | −0.1980 | −0.1183 | −0.2139 | −0.1938 | −0.1513 |
| −18 | −0.1817 | −0.0829 | −0.2486 | −0.2476 | −0.2433 |
| −17 | −0.3121 | −0.1666 | −0.3049 | −0.2739 | −0.2880 |
| −16 | −0.3537 | −0.2378 | −0.3474 | −0.2631 | −0.2292 |
| −15 | −0.2213 | 0.0011 | −0.3032 | −0.1528 | −0.1696 |
| −14 | −0.1662 | −0.0323 | −0.2564 | −0.0857 | −0.1255 |
| −13 | −0.2599 | −0.0959 | −0.3388 | −0.2031 | −0.2153 |
| −12 | −0.1894 | −0.0677 | −0.3549 | −0.2341 | −0.2339 |
| −11 | −0.1803 | −0.1188 | −0.4051 | −0.2725 | −0.2863 |
| −10 | −0.3154 | −0.2784 | −0.4779 | −0.3924 | −0.4367 |
| −9 | −0.2784 | −0.2620 | −0.4186 | −0.3249 | −0.3048 |
| −8 | −0.2263 | −0.1892 | −0.5283 | −0.3139 | −0.4121 |
| −7 | −0.2617 | −0.1803 | −0.5054 | −0.2564 | −0.3619 |
| −6 | −0.1967 | −0.1124 | −0.3399 | −0.2136 | −0.2970 |
| −5 | −0.1884 | −0.0405 | −0.4449 | −0.1158 | −0.2295 |
| −4 | −0.1047 | 0.0457 | −0.2532 | −0.1703 | −0.1450 |
| −3 | −0.0188 | 0.0391 | −0.1540 | −0.0716 | −0.0566 |
| −2 | −0.0887 | −0.0878 | −0.2529 | −0.1607 | −0.0947 |
| −1 | −0.0956 | −0.0383 | −0.2681 | −0.2482 | −0.2158 |
| 0 | −0.1376 | −0.1107 | −0.3000 | −0.2237 | −0.2291 |
| Lag | RP | MP | CP | FP | SP |
|---|---|---|---|---|---|
| −20 | −0.0543 | 0.0568 | −0.1610 | −0.0764 | −0.0577 |
| −19 | 0.0604 | 0.2292 | −0.1320 | −0.0274 | −0.0830 |
| −18 | 0.0036 | 0.0694 | −0.0706 | −0.0665 | −0.0220 |
| −17 | −0.0109 | −0.0062 | −0.0415 | 0.0065 | 0.0634 |
| −16 | −0.0577 | 0.0683 | 0.0108 | −0.0543 | 0.0128 |
| −15 | −0.0162 | 0.1001 | 0.0764 | 0.0620 | 0.0741 |
| −14 | 0.0008 | 0.1935 | 0.0422 | −0.0051 | −0.0054 |
| −13 | 0.0029 | 0.0735 | −0.0938 | −0.1100 | −0.0600 |
| −12 | −0.0055 | 0.0036 | −0.0171 | −0.0738 | 0.0647 |
| −11 | −0.2090 | −0.1962 | −0.0649 | −0.1414 | −0.0270 |
| −10 | 0.0132 | 0.1259 | 0.0272 | 0.0514 | 0.0792 |
| −9 | 0.0106 | 0.0590 | 0.0504 | 0.1032 | 0.0867 |
| −8 | 0.0225 | 0.0808 | −0.0227 | −0.0027 | 0.0134 |
| −7 | 0.0333 | 0.0667 | 0.0253 | 0.0142 | 0.0136 |
| −6 | 0.1821 | 0.1085 | 0.1702 | 0.3433 | 0.3007 |
| −5 | 0.1672 | 0.1228 | 0.1776 | 0.3301 | 0.2436 |
| −4 | 0.1207 | −0.0415 | 0.3078 | 0.2349 | 0.2802 |
| −3 | 0.0286 | −0.0770 | 0.1123 | 0.0310 | 0.0494 |
| −2 | −0.1187 | −0.1685 | −0.0357 | −0.0684 | −0.1233 |
| −1 | −0.0206 | −0.0640 | 0.0991 | 0.1014 | 0.0436 |
| 0 | 0.1565 | 0.0601 | 0.2094 | 0.2731 | 0.1721 |
| Lag | RP | MP | CP | FP | SP |
|---|---|---|---|---|---|
| −20 | −0.1412 | −0.1968 | −0.1222 | −0.1595 | −0.1755 |
| −19 | −0.1681 | −0.1501 | −0.0653 | −0.0865 | −0.0105 |
| −18 | −0.0929 | −0.1157 | 0.0724 | 0.0818 | 0.1036 |
| −17 | 0.1892 | 0.2180 | 0.0089 | 0.1039 | 0.0454 |
| −16 | 0.0157 | −0.0846 | 0.0048 | 0.0524 | 0.0439 |
| −15 | −0.0841 | −0.1398 | −0.2318 | −0.0977 | −0.1329 |
| −14 | −0.0134 | −0.0185 | −0.0278 | 0.1175 | 0.0237 |
| −13 | −0.0938 | −0.1056 | 0.0423 | 0.1033 | 0.0166 |
| −12 | −0.0162 | 0.0007 | 0.0804 | 0.1292 | 0.0089 |
| −11 | 0.0608 | 0.0579 | 0.0197 | 0.0456 | 0.0087 |
| −10 | −0.2102 | −0.1870 | −0.2033 | −0.1881 | −0.1416 |
| −9 | −0.1095 | −0.0979 | −0.0246 | −0.0499 | −0.0109 |
| −8 | −0.2023 | −0.2033 | −0.0182 | −0.1213 | −0.0179 |
| −7 | −0.0267 | −0.0123 | −0.2904 | −0.0061 | −0.1194 |
| −6 | −0.1305 | −0.1348 | −0.1356 | −0.1974 | −0.1360 |
| −5 | −0.0313 | 0.0223 | −0.1598 | −0.0586 | −0.1237 |
| −4 | −0.0491 | 0.0403 | −0.1913 | −0.0097 | −0.0418 |
| −3 | 0.1789 | 0.2257 | 0.0934 | 0.0505 | 0.0424 |
| −2 | 0.2139 | 0.1670 | 0.0626 | 0.1313 | 0.1420 |
| −1 | −0.0056 | −0.1194 | 0.0347 | −0.0336 | 0.0004 |
| 0 | −0.1580 | −0.0407 | −0.2212 | −0.3848 | −0.3741 |
4. Conclusions
- (1)
- Stable behavior during the middle and final portions of the XX Century.
- (2)
- A very short lived abrupt positive shift at the beginning of the XXI Century.
- (3)
- An abrupt negative shift in the mid 2000s which returned the rainfall average to approximately its previous level.
Author Contributions
Conflicts of Interest
References
- Roberto, Z.E.; Casagrande, G.; Viglizzo, E. Lluvias en la Pampa Central: Tendencia y variaciones del siglo. Bol. INTA Centro Reg. La Pampa-San Luis 1994, 2, 1–27. [Google Scholar]
- Viglizzo, E.F.; Roberto, Z.E.; Filippin, M.C.; Pordomingo, A.J. Climate variability and agroecological change in the Central Pampas of Argentina. Agric. Ecosyst. Environ. 1995, 55, 7–16. [Google Scholar] [CrossRef]
- Podestá, G.P.; Messina, C.D.; Grondona, M.O.; Magrin, G.O. Associations between grain crop yields in Central-Eastern Argentina and El Niño–Southern Oscillation. J. Appl. Meteor. 1999, 38, 1488–1498. [Google Scholar] [CrossRef]
- Sierra, E.M.; Pérez, S.P. Tendencia del régimen de precipitación y el manejo sustentable de los agroecosistemas: Estudio de un caso en el noroeste de la provincia de Buenos Aires, Argentina. Rev. de Climatolog. 2006, 6, 1–12. [Google Scholar]
- Viglizzo, E.F.; Frank, F.C. Land use options for Del Plata Basin in South America: Tradeoffs analysis based on ecosystem service provision. Ecol. Econ. 2006, 57, 140–151. [Google Scholar] [CrossRef]
- Manuel-Navarrete, D.; Gallopín, G.G.; Blanco, M.; Díaz-Zorita, M.; Ferraro, D.O.; Herzer, H.; Laterra, P.; Murmis, M.R.; Podestá, G.P.; Rabinovich, J.; et al. Multicausal and integrated assessment of sustainability: The case of agriculturization in the Argentine Pampas. Environ. Dev. Sustain. 2009, 11, 621–638. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Castañeda, M.E.; Barros, V. Las tendencias de la precipitación en el Cono Sur de América al este de los Andes. Meteorológica 1994, 19, 23–32. [Google Scholar]
- Sierra, E.M.; Hurtado, R.; Spescha, L. Corrimiento de las isoyetas anuales medias decenales en la Región Pampeana 1941–1990. Rev. Fac. Agron. 1994, 14, 139–144. [Google Scholar]
- Satorre, E.H. Cambios tecnológicos en la agricultura argentina actual. Cienc. Hoy 2005, 15, 24–31. [Google Scholar]
- Trigo, E. Consecuencias económicas de la transformación agrícola. Cienc. Hoy 2005, 15, 46–51. [Google Scholar]
- Carril, A.F.; Menéndez, C.G.; Nuñez, M.M. Climate change scenarios over the South American region: An intercomparison of coupled general atmosphere-ocean circulation models. J. Climatol. 1997, 17, 1613–1633. [Google Scholar] [CrossRef]
- Minetti, J.L.; Vargas, W.M.; Poblete, A.G.; Acuña, L.G.; Casagrande, G. Non-linear trends and low frequency oscillations in annual precipitation over Argentina and Chile, 1931–1999. Atmósfera 2003, 16, 119–135. [Google Scholar]
- Barros, V. El Cambio Climático Global, 2nd ed.; Libros del Zorzal: Buenos Aires, Argentina, 2005; p. 176. [Google Scholar]
- Suriano, J.M.; Ferpozzi, L.H. Los cambios climáticos en la Pampa también son historia. Todo es Historia 1993, 306, 8–25. [Google Scholar]
- Pérez, S.; Sierra, E.M.; Casagrande, G.; Vergara, G.; Bernal, F. Comportamiento de las precipitaciones (1918/2000) en el centro oeste de la provincia de Buenos Aires (Argentina). Rev. de la Facultad de Agronomía de la Universidad Nacional de La Pampa 2003, 14, 39–46. [Google Scholar]
- Pérez, S.; Sierra, E.; López, E.; Nizzero, G.; Momo, F.; Massobrio, M. Abrupt changes in rainfall in the Eastern area of La Pampa Province, Argentina. Theor. Appl. Climatol. 2011, 103, 159–165. [Google Scholar] [CrossRef]
- Pérez, S.; Sierra, E. Changes in rainfall patterns in the eastern area of La Pampa province, Argentina. Rev. Ambiente Agua Interdiscip. J. Appl. Sci. 2012, 7, 24–35. [Google Scholar] [CrossRef]
- Giddings, L.; Soto, M. Teleconexiones y precipitación en América del Sur. Rev. Climatol. 2006, 6, 13–20. [Google Scholar]
- Méndez González, J.; Ramírez Leyva, A.; Cornejo Oviedo, E.; Zárate Lupercio, A.; Cavazos Pérez, T. Teleconexiones de la Oscilación Decadal del Pacífico (PDO) a la precipitación y temperatura en México. Investig. Geogr. 2010, 73, 57–70. [Google Scholar]
- Dieppois, B. Etude par Analyses Spectrales de l’ Instabilité Spatio-Temporelle des Téléconnexions Basse-Fréquences Entre les Fluctuations Globales du Secteur Atlantique et les Climats de l’ Europe du NW (1700–2010) et du Sahel Ouest Africain (1900–2010). Ph.D. Thesis, Université de Rouen, Rouen, France, May 2013. [Google Scholar]
- Scafetta, N. Multi-scale dynamical analysis (MSDA) of sea level records vs PDO, AMO, and NAO indexes. Clim. Dyn. 2014, 43, 175–192. [Google Scholar] [CrossRef]
- McPhaden, M.J.; Zebiak, S.E.; Glantz, M.H. ENSO as an integrating concept in earth science. Science 2006, 314, 1740–1745. [Google Scholar] [CrossRef] [PubMed]
- Conrad, V.; Pollack, L.W. Methods in Climatology, 2nd ed.; Harvard University Press: Cambridge, MA, USA, 1950; p. 459. [Google Scholar]
- Wijngaard, J.B.; Klein Tank, A.M.G.; Können, G.P. Homogeneity of 20th century European daily temperature and precipitation series. Int. J. Climatol. 2003, 23, 679–692. [Google Scholar] [CrossRef]
- Hoffmann, J.A. Características de las series de precipitación en la República Argentina. Meteorológ 1970, 1, 166–191. [Google Scholar]
- Alexandersson, H.; Moberg, A. Homogenization of Swedish temperature data. Part I: Homogeneity test for linear trends. Int. J. Climatol. 1997, 17, 25–34. [Google Scholar] [CrossRef]
- Štĕpánek, P. AnClim Software for Time Series Analysis; Department of Geography, Faculty of Sciences, Masaryk University: Brno, Czech Republic, 2006. [Google Scholar]
- Khaliq, M.N.; Quarda, T.B.M.J. On the critical values on the standard normal homogeneity test (SNHT). Int. J. Climatol. 2007, 27, 681–687. [Google Scholar] [CrossRef]
- Alexandersson, H. A homogeneity test applied to precipitation data. Int. J. Climatol. 1986, 6, 661–675. [Google Scholar] [CrossRef]
- Hubert, P.; Carbonnel, P.; Chaouche, A. Segmentation des séries hydrométriques. Application à des séries de précipitations et de débits de l’Afrique de l’ouest. J. Hydrol. 1989, 110, 349–367. [Google Scholar] [CrossRef]
- Dagnélie, P. Théorie et méthodes statistiques: Applications agronomiques. Les Méthodes de l’Inférence Statistique, 2nd ed.; Les Presses Agronomiques de Gembloux: Gembloux, Belgique, 1975; p. 462. [Google Scholar]
- Mantua, N.J.; Hare, S.; Zhang, Y.; Wallace, J.M.; Francis, R.C. A Pacific interdecadal climate oscillation with impacts on salmon production. Bull. Am. Meteorol. Soc. 1997, 78, 1069–1079. [Google Scholar] [CrossRef]
- Enfield, D.B.; Mestas-Nuñez, A.M. Interannual to multidecadal climate variability and its relationship to global sea surface temperature. In Interhemispheric Climate Linkages; Markgraf, V., Ed.; Academic Press: Boulder, CO, USA, 2001; pp. 17–29. [Google Scholar]
- Mantua, N.J.; Hare, S.R. The pacific decadal oscillation. J. Oceanogr. 2002, 58, 35–44. [Google Scholar] [CrossRef]
- Gray, S.T.; Graumlich, L.J.; Betancourt, J.L.; Pederson, G.T. A tree-ring based reconstruction of the Atlantic Multidecadal Oscillation since 1567. Geophys. Res. Lett. 2004, 31, 1–4. [Google Scholar] [CrossRef]
- Knight, G.R.; Folland, C.K.; Scaife, A.A. Climate impacts of the Atlantic Multidecadal Oscillation. Geophys. Res. Lett. 2006, 33, 1–4. [Google Scholar] [CrossRef]
- McBride, J.L.; Nicholls, N. Seasonal Relationships between Australian Rainfall and the Southern Oscillation. Mon. Weather Rev. 1983, 111, 1998–2004. [Google Scholar] [CrossRef]
- Almeira, G.J.; Scian, B. Some atmospheric and oceanic indices as predictor of seasonal rainfall in the Del Plata Basin of Argentina. J. Hydrol. 2006, 329, 350–359. [Google Scholar] [CrossRef]
- Frank, F.C.; Viglizzo, E.F. Water use in rain-fed farming at different scales in the Pampas of Argentina. Agric. Syst. 2012, 109, 35–42. [Google Scholar] [CrossRef]
- Viglizzo, E.F.; Ricard, F.M.; Jobbágy, E.G.; Frank, F.C.; Carreño, L.V. Assessing the cross-scale impact of 50 years of agricultural transformation in Argentina. Field Crops Res. 2011, 124, 186–194. [Google Scholar] [CrossRef]
- Viglizzo, E.F.; Jobbágy, E.G.; Carreño, L.V.; Frank, F.C.; Aragón, R.; de Oro, L.; Salvador, V.S. The dynamics of cultivation and floods in arable lands of Central Argentina. Hydrol. Earth Syst. Sci. 2009, 13, 1–12. [Google Scholar] [CrossRef]
- Drinkwater, K.F.; Miles, M.; Medhaug, I.; Ottera, O.H.; Kristiansen, T.; Sundby, S.; Gao, Y. The Atlantic Multidecadal Oscillation: Its manifestations and impacts with special emphasis on the Atlantic region north of 60°N. J. Mar. Syst. 2014, 133, 117–130. [Google Scholar] [CrossRef]
- Sydeman, W.J.; Thompson, S.A.; García-Reyes, M.; Kahru, M.; Peterson, W.T.; Largier, J.L. Multivariate ocean-climate indicators (MOCI) for the central California Current: Environmental change, 1990–2010. Progress Oceanogr. 2014, 120, 352–369. [Google Scholar] [CrossRef]
- Travasso, M.I.; Magrin, G.O.; Rodriguez, G.R. Relations between sea-surface temperature and crop yields in Argentina. Int. J. Climatol. 2003, 23, 1655–1662. [Google Scholar] [CrossRef]
- Carreño, L.V.; Pereyra, H.; Viglizzo, E.F. Los servicios ecosistémicos en áreas de transformación agropecuaria intensiva. In El Chaco sin Bosques: La Pampa o el Desierto del Futuro; Morello, J.H., Rodríguez, A.F., Eds.; UNESCO, MAB, GEPAMA. Orientación Gráfica Editora SRL: Buenos Aires, Argentina, 2009; pp. 229–246. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez, S.; Sierra, E.; Momo, F.; Massobrio, M. Changes in Average Annual Precipitation in Argentina’s Pampa Region and Their Possible Causes. Climate 2015, 3, 150-167. https://doi.org/10.3390/cli3010150
Pérez S, Sierra E, Momo F, Massobrio M. Changes in Average Annual Precipitation in Argentina’s Pampa Region and Their Possible Causes. Climate. 2015; 3(1):150-167. https://doi.org/10.3390/cli3010150
Chicago/Turabian StylePérez, Silvia, Eduardo Sierra, Fernando Momo, and Marcelo Massobrio. 2015. "Changes in Average Annual Precipitation in Argentina’s Pampa Region and Their Possible Causes" Climate 3, no. 1: 150-167. https://doi.org/10.3390/cli3010150
APA StylePérez, S., Sierra, E., Momo, F., & Massobrio, M. (2015). Changes in Average Annual Precipitation in Argentina’s Pampa Region and Their Possible Causes. Climate, 3(1), 150-167. https://doi.org/10.3390/cli3010150





