1. Introduction
The evolving climate system has increased extreme weather events, such as droughts, heatwaves, floods, and storms. The impacts of climate change vary across regions, with some experiencing reduced rainfall and droughts, while others face increased storms and flooding. These contrasting impacts highlight the varying vulnerabilities of different areas to climate-related changes [
1,
2,
3]. Understanding these dynamics is essential for mitigating the impacts of extreme weather events, so comprehensive modelling approaches are required.
Climate classification systems offer a framework for understanding diverse and complex climates using environmental indicators, life zone classification, and weather patterns. The most common system, the weather pattern, divides climates into the following five categories: tropical (mega-thermal), dry (arid and semiarid), temperate (mesothermal), continental (microthermal), and polar and alpine (montane). For example, tropical climates found near the equator experience high temperatures, humidity, and significant rainfall, with two main seasons driven by the movement of the Intertropical Convergence Zone (ITCZ) [
4]. Temperate climates located beyond the tropics experience distinct seasonal changes, with warm summers, cold winters, and more evenly distributed precipitation. In contrast, polar climates at higher latitudes are cold and have extreme weather.
Rainfall is a complex hydrological element that varies spatially and temporally. It plays a vital role in shaping climate differences between climatic regions, primarily tropical and temperate regions. Predicting rainfall depends on accurate meteorological data, as it is influenced by factors like temperature, pressure, wind, and humidity, just like climate and weather.
Comprehensive rainfall studies are necessary for effective water resource management and climate adaptation. Various studies have examined long-term rainfall trends, such as research on century-long patterns in Sri Lanka [
5], 81 years of analysis in Jordan [
6], and 30 years of rainfall data in Nigeria [
7]. These studies emphasise the necessity of comprehensive rainfall studies for effective water resource management and adaptation to climate variability; understanding the spatial and temporal variability of rainfall is vital, as rainfall can be linked to specific atmospheric/synoptic regimes [
8]. Rainfall can trigger natural disasters, such as floods and landslides, especially when compounded by extreme weather events [
9,
10,
11]. These occurrences highlight the need for advanced weather prediction systems, particularly as climate change alters global rainfall patterns [
11]. Effective forecasting can mitigate these risks and support sustainable development.
Tropical climates are marked by intense, localised rainfall, primarily in rainforest and monsoon regions, while temperate climates have more predictable, broader rainfall patterns. Most climate models are based on temperate regions, leading to poor predictions in tropical areas due to their distinctive convective dynamics. Climate change exacerbates these challenges, as tropical regions are particularly vulnerable to climate change [
12], particularly with shifts in the Intertropical Convergence Zone (ITCZ) expected to disrupt rainfall patterns [
4], hence affecting global water resources and food production.
This study evaluates the accuracy of next-day rainfall predictions in temperate and tropical climate regions by analysing atmospheric parameters, while ensuring comparably similar geographic (oceanic and topographic) conditions across the selected locations. The following contributions are achieved in this work:
Examination of climatic differences between temperate and tropical climate regions influence on rainfall prediction modelling, emphasising the considerable variations in rainfall behaviour across these climates. The analysis specifically investigates the impact of these climatic dynamics on predictive accuracy and model performance within comparable geographic contexts.
Identification of key atmospheric variables critical for improving rainfall prediction accuracy, thereby providing insights into the underlying physical processes governing rainfall. The study emphasises the latitudinal impact/influence on model reliability (accuracy) and underscores the limitations of relying exclusively on standard weather parameters, particularly in tropical regions where rainfall prediction is inherently more complex.
Evaluation of the effectiveness and adaptability of machine learning models across diverse climatic conditions. Its findings directly enhance rainfall forecasting methodologies by addressing climate-specific variability and refining model calibration strategies.
Weather forecasting, particularly for rain, is inherently complex due to the nonlinear and chaotic behaviour of the atmosphere. Minor uncertainties in initial conditions grow over time, making predictions less reliable as the forecast horizon extends [
13]. The work published in [
14] highlights that while some atmospheric states exhibit significant predictability, others change abruptly and unpredictably. The complex atmospheric dynamics and limited knowledge of atmospheric processes lead to reduced forecast accuracy as the time interval between the current and forecasted period increases. These dynamics have driven the shift toward probabilistic forecasting, quantifying uncertainty and enhancing confidence in predicting precipitation patterns. This approach is essential for extending forecast time ranges beyond the deterministic limits. The forecast time range in rain forecasting is categorised as short-range (1 h to 3 days), medium-range (3 to 10 days), extended-range (10 to 30 days), and long-range (one month or more). The seasonal (1 to 3 months) and sub-seasonal (3 to 6 weeks) are sub-ranges within the extended to long range. Forecasts are crucial for all sectors, as they provide timely and accurate predictions for decision making.
Rainfall forecasting methods are primarily divided into empirical and dynamical approaches. The dynamical approach uses physical models such as General Circulation Models (GCM) [
15] and Weather Research and Forecasting (WRF) [
16] models that are based on equations to predict climate evolution. The effectiveness of a model is determined by its ability to accurately represent the relevant meteorological scale (microscale to large-scale) processes specific to a particular region. While general circulation models (GCMs) are commonly used to evaluate climate change, they are not suitable for projecting local or regional climates due to their coarse spatial resolution, which limits their ability to capture the finer details and variations that occur at smaller scales [
11,
17,
18]. However, the WRF models overcome this limitation. Despite their relative effectiveness, computational costs and spatial and temporal resolutions remain a challenge, driving interest in data mining (empirical) alternatives. The empirical approach, including machine learning (ML) and statistical techniques like fuzzy logic (FL), rely on historical data and the relationships within and between atmospheric variables.
Several studies have demonstrated that machine learning algorithms outperform statistical techniques, showcasing their greater predictive accuracy [
19,
20]. Overall, studies [
21,
22,
23] have proven the effectiveness of machine learning algorithms in modelling complex weather patterns. They have demonstrated significant potential in enhancing rainfall prediction, offering improved predictive accuracy and reduced correlations. By utilising extensive datasets and integrating key meteorological factors, these models provide deeper insights for rain forecasting. Their versatility enables applications across diverse regions and temporal scales, making them valuable tools for informed decision making in climate-sensitive areas.
To aid in comprehension ease of analysis,
Table 1 explains the meaning of each column heading, while
Table 2 provides a summary of the contributions reviewed, offering a snapshot of the current state of the art. Key features have been identified and compared to highlight this study’s unique contributions.
Research has been conducted on predicting rainfall and rainfall states in different parts of the world. In the temperate climate regions, the authors of [
24] used 50 years of data to predict daily rainfall states in Shih-Men Reservoir, located in the Danshui River basin in northern Taiwan. The performance of three classification methods, namely linear discriminant analysis (LDA), random forest (RF), and support vector classification (SVC), was compared. The results showed that RF outperforms LDA and SVC for rainfall state classification. This means that the outputs of RF classification models were selected as inputs for the Least Square Support Vector Regression (LS-SVR) models to simulate rainfall amounts. Using RF for rainfall state classification and LS-SVR for rainfall amount prediction improved the extreme rainfall prediction. This proposed modified statistical downscaling approach was inspired by the weakness of support vector machines (SVM) in downscaling extreme rainfall based on the methods used by [
32,
33] for improving the extreme rainfall prediction using downscaling. Also, the authors of [
25] carried out the state prediction of rainfall using binary logistic regression and a dataset from Canberra, Australia. The significant (based on
p-value) and important (based on Wald/z statistics) weather parameters needed for the accurate prediction of rain the next day were identified.
The characteristics of rainfall differ considerably across all climatic regions [
34]. While most models provide reasonable rain prediction accuracies for higher latitudes like temperate regions, they mostly underestimate in tropical zones [
35]. Additionally, models developed based on temperate data struggle with the variability introduced by tropical terrain, mostly yielding significant errors [
36]. This is because the unique characteristics of rain in tropical regions—frequent, high-intensity rainfall with smaller rain cells and larger raindrop sizes—pose challenges for accurately modelling and predicting rain. These challenges are further compounded by the lack of region-specific rain measurement data [
37]. This highlights the need for tailored approaches to rainfall modelling to improve the accuracy of rain predictions to mitigate the impact of climate change and disasters.
Several studies have been carried out on rainfall state prediction in the tropical climatic region. In Southeast Asia, the authors of [
26] conducted a study in Selangor, Malaysia, with 4 years of data from 2010 to identify the most effective techniques for rainfall state prediction. They conducted a comparative analysis of various supervised learning methods, namely support vector machine (SVM), naïve Bayes (NB), decision tree (DT), neural network (NN), and random forest (RF). The experimental results showed the RF algorithm as the leading technique among those evaluated, as it performed exceptionally well due to its ability to achieve high F-measure scores, while effectively training on limited data. Thus, the study highlights the potential of these models for forecasting in new geographical areas like Malaysia.
Still within the same geographic region, the authors of [
27] applied the SVM technique to analyse the various parameters influencing atmospheric precipitation in Singapore within five years and identified the following five important weather features: temperature (T), relative humidity (RH), solar radiation (SR), dew point temperature (DPT), and precipitable water vapor (PWV). The study showed that PWV contributed the most to achieving a high detection rate. By considering both seasonal and diurnal variables, which are in most cases not included, the study revealed that alongside the SR variable, day-of-year and hour-of-day contribute to reducing false alarm rates. Thus, the findings underscore the importance of these often-overlooked parameters in enhancing predictive models for atmospheric precipitation events.
In West Africa, the authors of [
28] explored five classification algorithms DT, multilayer perceptron (MLP), RF, extreme gradient boosting (XGB), and K-nearest neighbour (KNN) to identify the most effective techniques for predicting rainfall state in Ghana using data spanning 39 years. The study addressed the importance of selecting appropriate rainfall prediction models for classifying rainfall across tropical climatic regions. Overall, random forest, extreme gradient boosting, and multilayer perceptron achieved strong performance, suggesting that ensemble and deep learning models effectively predict rainfall across Ghana’s ecological zones.
Studies have been carried out on rain prediction using locations with different climatic zones. In a country with contrasting climates like Brazil, the authors of [
29] applied artificial neural networks (ANNs) to develop a methodology for predicting rainfall occurrence. They employed 65 years of historical data from 10 locations that are either tropical or temperate in climate. The ANN model was designed to predict rainfall events exceeding 5 mm across different climatic seasons for cumulative periods ranging from 3 to 7 days. This approach is to reduce model variance, enhance data bias, and filter out zero rainfall occurrences, which can distort results; the results demonstrate that the ANNs can forecast rainfall events with an average accuracy of 78% in summer, 71% in winter, 62% in spring, and 56% in autumn.
Data from 26 geographically diverse locations across Australia exhibiting tropical, dry, temperate, or continental climate characteristics were used in [
30]. A comparative analysis was conducted on an optimised neural network (deep learning) and eight (8) machine learning algorithms (logistic regression, linear discriminant analysis, quadratic discriminant analysis, K-nearest neighbour, decision tree, gradient boosting, random forest, Bernoulli naïve Bayes) with data spanning 10 years and evaluated the performance of these models in the prediction of rainfall. The results show that the deep learning model outperformed all models, achieving an F1-score of 88.61% and precision of 98.26%, which underscores the potential of optimised neural networks for accurate rainfall prediction. While the logistic regression model achieved the highest F1-score (86.87%) and precision (97.14%) among the statistical models. Hence, the framework demonstrates the effectiveness of ANN in short-term, season-specific rainfall event forecasting.
The study further buttresses this result from [
31] in Australia using rainfall data from 49 cities situated in the various climate zones (tropical, dry, temperate, and continental) covering 10 years to analyse the use of machine learning algorithms (K-nearest neighbour decision tree, random forest, neural network) for modelling rainfall, with the neural networks excelling once again. The study highlighted the importance of regional data, as algorithms perform better when trained on location-specific information, allowing more accurate and efficient predictions for individual cities.
Although previous studies have examined rainfall prediction across various climatic zones, they did not focus on comparing the influence of climate itself on prediction accuracy. Specifically, no existing literature has been found that conducts a comparative analysis of rainfall prediction models under similar oceanic and topographic conditions to isolate the effects of climatic differences. Furthermore, a gap remains in identifying and evaluating the critical atmospheric variables that influence prediction accuracy across latitudes. This study addresses that gap by comparing rainfall prediction performance in both tropical and temperate climates, with an emphasis on understanding the latitudinal impact and the key variables that drive predictive accuracy. This motivation forms the basis for the present manuscript.
The rest of the paper is organized as follows.
Section 2 describes the materials and methods, by introducing the study area, analysing the datasets used, and comparing the linear and nonlinear machine learning models’ designs. The performance and comparative results of the models are shown in
Section 3 and discussed in
Section 4. Finally,
Section 5 concludes the paper and outlines directions for future research.
3. Results
The binary logistics regression with stepwise AIC and random forest approaches were applied to data from various locations to create the four models for predicting next-day rainfall. They are the Alor Setar model for the tropical climate and the Vercelli, Williams, and Ashburton models for the temperate climate. The predictor variables are pressure, temperature, dewpoint, humidity, wind direction, and wind speed.
3.1. Logistic Regression Model Analysis
The odds ratio (OR) is used to demonstrate the strength of the relationship between predictors and the outcomes. For the OR > 1, the odds are increased, and for OR < 1, the odds are decreased for the said outcome. The sign (+ or −) of the coefficient determines the effect of the variable on the outcome, where a positive sign (+) is indicative of a positive impact on rain falling the next day, while the negative sign (−) implies the variable has a negative effect on rain falling the next day. The Wald or z statistics are used to determine the importance of a variable in a model. Using the cut-off value of 2, variables with absolute z values above the cut-off are seen to be important variables in the forecast model. The variable importance in a model is further corroborated using the p-value. Using a significance level of alpha equal to 0.05 when the p-value of the predictor variable is less than the alpha value, this implies that the independent variables have a statistically significant relationship with the dependent variable in the model. Covariates that are not significant do not mean that these covariates have no relationship with the dependent variable; it means that the relationship is not strong enough to be detected at a given confidence level (95% level).
Table 4 is the summary analysis of the tropical climate model, Alor Setar. Dewpoint has a negative effect, while humidity and windspeed positively affect next-day rainfall. The dewpoint and windspeed variables are seen not to be important, as their z-values are below 2, and not significant, as their
p-values are both above the alpha value of 0.05. Hence, humidity is the only important and significant variable in the model. For the odd ratio, for every one-unit increase in humidity, the odds of rainfall rises by about 16.1%.
From the coefficient column in
Table 5, pressure, temperature, and wind direction all have a negative effect on next-day rainfall. All variables in the model are both important and significant. The dewpoint and windspeed variables have odd ratios greater than one, hence rain falling the next day is increased by a factor of 36.6 and 5.5, respectively, with a unit increase in either variable. Also, the odds of rain falling the next day decreases by a factor of 6.4, 22.2, and 0.2 for a unit increase in pressure, dewpoint, and wind direction, respectively.
The summary analysis of the Williams model is represented in
Table 6. The effect on next-day rainfall is positive for the dew and windspeed covariates and negative for the pressure, temp, and humidity covariates. Although all covariates in the Williams model are important, the most important predictor variable is temperature. The odds of rain falling the next day decrease with a unit increase in either pressure, temperature, or humidity, and a unit increase in the value of the dew covariate is associated with the odds of rain falling the next day by a double factor.
Table 7 is a summary of the Ashburton model. The pressure and dew variables have a negative effect on next-day rainfall, while temperature and humidity positively affect next-day rainfall. All covariates are important and significant in the model, as their z-value is above the cut-off, and their
p-value is less than the significant level. For a one-unit increase in pressure or dewpoint measurements, the odds of rain falling the next day decrease by a factor of approximately 7 and 31.9, respectively. For a unit increase in temperature or humidity, there is an approximately 49.2- and 12.7-factor increase, respectively, in the odds of rain falling the next day.
3.2. Random Forest Model Analysis
Random forest features importance metrics that fall into two groups. Permutation-based measures—reported as overall mean decrease accuracy (MDA) and class-specific NO and YES scores—estimate how much out of bag accuracy drops when a predictor is replaced by noise. Large positive values signal that the model relies heavily on the variable; negative class-specific values indicate that the variable may be misleading for that class. The split-based measure, captured by the mean decrease Gini (MDG), record the total reduction in Gini impurity contributed by all splits using the predictor. Higher Gini scores show that the variable is frequently chosen and consistently produces purer partitions. Because the Gini scale is model-specific, comparisons are meaningful only within the same forest. Together, these metrics reveal both the performance impact of each variable and their structural role in the model.
Table 8 summarises the feature importance of the Alor Setar model. Humidity is seen to be the principal driver for both MDA classes (11.98 and 14.52) and overall MDA (21.65), with dewpoint (19.67) in second place and temperature (11.6) a distant third. Wind direction and pressure help classify NO cases but reduce accuracy for YES cases, while wind speed is seen to have negligible influence. Hence, humidity is the most relied upon feature, alongside being the most frequent splitter (102.46).
The summary analysis of the Vercelli random forest model is represented in
Table 9. From the permutation-based measures, the YES outcomes rely on humidity, pressure, and wind direction, while the NO cases depend on humidity, dew point, temperature, and windspeed. Based on MDG, dewpoint, pressure, and wind direction are seen to have moderate to high scores. With comparable impact, each supply structure the model finds useful, as the split nodes effectively. So, humidity is once again seen to be the most dominant feature in the model, hence an indispensable predictor, with the highest overall MDA and MDG of 33.97 and 91.84, respectively.
From the MDA NO and YES columns in
Table 10, the NO outcomes relay on temperature, humidity, dew point, pressure, and wind direction, the YES outcomes depend on humidity and wind direction, and the negative YES score of −5.04 in dewpoint is unreliable for YES predictions. With a MDG score of 44.98, the forest model is seen to structurally depend on the humidity predictor.
Table 11 is the feature importance summary of the temperate climate model, Ashburton. Pressure feature dominates the model, as it is a key driver for both MDA classes. Humidity is the second most balanced contributor to the model, as it is the only other predictor that helps in the identification of rain events (YES class), with a score of 3.09, and non-rain events (NO class), with a score of 9.08. Wind direction, windspeed, dewpoint, and temperature are valuable for predicting the NO class, but their negative values for the YES class implies that they harm/limit the recognition of Yes cases. The MDG mirrors the MDA ranking, as pressure is also structurally central to the forest.
3.3. Comparative Analysis
The evaluation process is carried out by recognising class imbalance in each dataset, which helps inform and contextualise the assessment metric. Class imbalance is a common classification problem in machine learning that has an adverse effect on model accuracy. It is common in most naturally occurring domains like weather, as with the next-day rainfall occurrence. In imbalanced datasets, models tend to perform well by predicting the majority class but struggle with the minority class, which is most times the focal class of the prediction. In all four datasets examined, the majority class is “No” (no rain), while the minority class is “Yes” (rain). Since the goal is to predict whether it will rain (the minority class), the traditional accuracy measure can be misleading. F1-score another important classification evaluation metric is also not applied, as it is influenced by the class distribution, hence not suitable for comparing models based on datasets with varying imbalance ratios.
To address this, the balanced accuracy metric offers a more accurate assessment of the model’s performance, as it accounts for the imbalance in class distribution. It is the average of the proportion of actual positive cases correctly identified as positive (True Positive Rate (TPR) or Sensitivity/Recall) and the proportion of actual negative cases correctly identified as negative (True Negative Rate (TNR) or Specificity/Selectivity).
Hence, this metric overcomes the bias that exists in the model due to the dichotomous imbalance in the dataset. It reduces the emphasis placed on the majority class by giving the minority class equal importance/weight, as the accuracies of both classes are evaluated. Thus, giving a full overview of how well the model can generalise to both majority and minority classes. This evaluation metric is important in this study, as predicting when it will not rain, accurately, is also useful to telecoms operators, farms, and event planners to mention but a few.
A review of
Figure 6 reveals that using the logistic regression algorithm, all three temperate climate models outperformed the tropical climate model, Alor Setar, with the Williams logistic regression model having the highest balanced accuracy value at 78.9%.
The plot in
Figure 7 also supports the prediction models accuracies in
Figure 6; thus, that random forest prediction models from Williams, Vercelli, and Ashburton, with respective accuracies of 77.7%, 72.4%, and 66%, all achieved better results than the tropical climate model, Alor Setar, with a balanced accuracy of 64.7%.
Area under the curve (AUC) [
50] also referred to as the concordance (c) statistic, it measures the total area below a probability curve, ranging from 0 to 1 on both the x-axis and y-axis. It is a rank-based measure of the predictive power of a model, reflecting the probability that a model ranks a randomly chosen positive instance (Yes or 1) higher than a randomly chosen negative instance (No or 0). This can be mathematically expressed as follows:
where A refers to the score distribution for positive class instances, and B refers to the score distribution for negative class instances. The AUC is a critical metric for assessing model fit and comparing the performance of classification models independent of the decision threshold applied. It provides insight into the model’s ability to differentiate between outcomes, where a perfect AUC of 1 signifies flawless prediction, and an AUC of 0.5 indicates predictions no better than a random chance. At the same time, an AUC of 0 implies all predictions are incorrect. Most models yield an AUC between 0.5 and 1, with higher values reflecting better class discrimination. Thus, when comparing classification models, the one with the higher AUC is considered superior in performance.
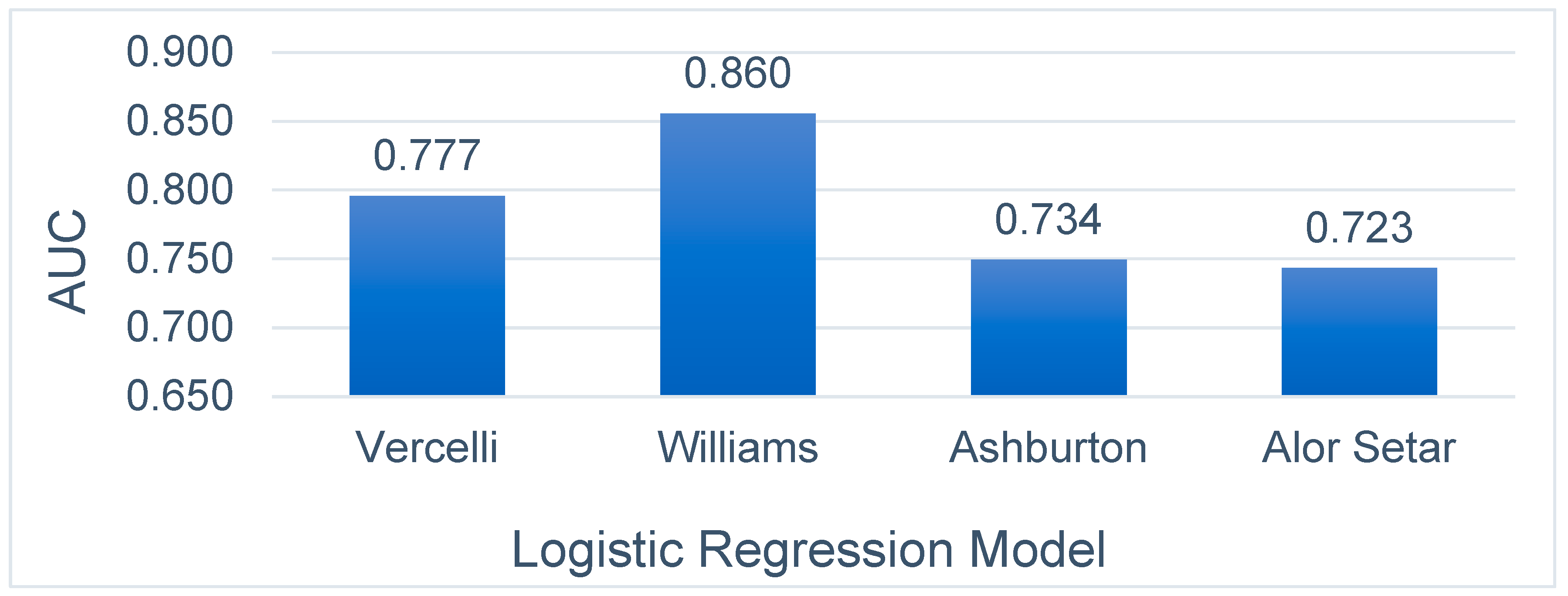
Figure 8 illustrates the calculated AUROC curve for the four logistic regression next-day rainfall prediction models. It shows the AUC of all three temperate climate models to be higher than the AUC of the tropical climate model. As also seen, the Williams model has the highest AUC of 86%, followed by the Vercelli model at 77.7%, and the Ashburton model the lowest for the temperate models with an AUC value of 73.4%.
Figure 9 demonstrates the AUROC metric for the four random forest next-day rainfall prediction models. Again, all three temperate climate models outperform the tropical climate model in terms of AUC, with values of 85.2%, 78.3%, and 68.8%, for the Williams, Vercelli, and Ashburton models, respectively, compared to 68.6% for the tropical climate model.
Comparative evaluation of models’ performance based on ML algorithms shows that the logistic regression models outperform the random forest models on both balanced accuracy and AUC for all locations, except the Vercelli location, where the random forest model outperforms the logistic regression model. This could be due to the inclusion and the high importance of humidity in the random forest model, which was not captured by logistic regression. The identification of the humidity variable as the key predictor of both rain and non-rain outcomes by the random forest model is due to the algorithm’s ability in capturing interactions and nonlinearities amongst predictors. The nonlinear and/or interactions of humidity with others, which appeared to be crucial in the tree-based splits, were captured.
4. Discussion
Rain happens when several conditions interact in the right way to allow precipitation to form and fall. This means that rainfall is not determined by a single variable/atmospheric parameter but instead depends on the combined influence of multiple atmospheric (and topographic) factors acting together. Thus, rainfall prediction is said to be multifactorial in nature, hence models must integrate many variables (not just one) to accurately predict rain. Understanding which variables and variable combinations matter most improves forecast skill, especially across different climates, as forecast errors often happen when one key factor/variable is missing/omitted or misjudged. Therefore, the multifactorial nature of rainfall prediction reflects the fact that rainfall results from the interplay of several meteorological variables, such as pressure, temperature, humidity, and wind, which must combine properly for precipitation/rain to occur.
Next, regarding the models’ importance analysis, a strong model concordance is observed on the main drivers in each climate, as both logistic and RF models identify the same broad patterns. Overall, the top-ranked predictors by both methods usually agree qualitatively, where it is humidity in Am, pressure in Cfb, and a combination of both in Csa and Cfa climates. Where they differ tends to involve nuances in class-specific importance or the identification of nonlinear interactions. For example, humidity was not significant/included in logistic model for Cfa but featured as the most importance predictor in the RF model, suggesting a nonlinear effect that the logistic model could not capture with a linear term. Also, conflicts, like humidity’s low importance in RF for Cfb despite significance in logistic, can be explained by the interplay between predictors rather than fundamentally different conclusions. This means the models are consistent that moisture matters in a humid climate and pressure matters in a cyclone-prone climate, but they partition the explanatory power slightly differently. Importantly, both models together give a fuller/comprehensive picture, where logistic highlights the independent contribution of each variable and their directional effect, while RF accounts for interactions, nonlinear impacts, and even class-specific contributions, which in some cases exposed subtleties, like dew point being mostly a “no-rain” indicator in some/all climates’ reviews/discussed.
Across all four climates, tropical-monsoon (Am), marine/oceanic (Cfb), hot-summer Mediterranean (Csa), and humid-subtropical (Cfa), humidity has an impact on the next day rain prediction outcomes in these climates, thus becoming the common criterion. Nevertheless, rain falls mainly when two key ingredients meet, which is ample moisture (universal prerequisite) and a mechanism that lifts or concentrates it. Alor Setar’s tropical monsoon climate (Köppen Am) is marked by consistently elevated temperatures above 23 °C year-round and distinct seasonal patterns dictated by southwest (onshore) and northeast (offshore) monsoon winds. The climate’s persistent boundary-layer humidity exceeding 80%, and high dew-point temperatures above 24 °C create conditions consistently near saturation. Rainfall predominantly occurs during the southwest monsoon, as moist maritime air from the Indian Ocean promotes convective storms. Conversely, the northeast monsoon from the South China Sea delivers dry continental air, inhibiting precipitation. Relative humidity stands out as the critical indicator, triggering rainfall once it surpasses a threshold that allows convection without requiring large-scale atmospheric disturbances. Hence, rather than dewpoint, which is an indicator of the moisture content in the atmosphere, or temperature, which is directly related to the formation of clouds, humidity is identified as the dominant predictor of rainfall, confirmed by both logistic regression and random forest models’ analyses. For effective forecasting in Alor Setar, focus should be primarily on the real-time monitoring of humidity, supplemented by temperature and dew point profiles to gauge storm intensity, while recognizing that detailed wind or pressure measurements offer minimal predictive advantage for tropical rain. This reflects the low variability in atmospheric pressure typical of the tropical climates. Also, the rainfall is mainly caused by localised convection rather than large-scale frontal systems driven by pressure changes. Therefore, pressure becomes less useful as a short-term predictive tool for tropical rain.
The three temperate climates rely on humidity and pressure to varying degrees, their unique Köppen classifications dictate distinct hierarchies. In temperate regions, pressure (lift mechanism) patterns can indicate atmospheric instability. A falling barometric reading (decreasing pressure) often indicates increasing instability and an approaching low-pressure system, suggesting a higher chance of rain or storms. Hence, it is a critical variable for predicting rainfall, as it plays a prominent role in driving large-scale weather systems like high- and low-pressure systems, weather fronts, and cyclones, significantly influencing weather patterns, including precipitation. For high- and low-pressure systems, the low-pressure system tends to pull in moist air, which enhances the likelihood of rain, while the high-pressure systems generally cause sinking air, which warms and dries out, leading to clear, dry conditions. Understanding which pressure system is dominant is a key mechanism for predicting rainfall in temperate climates. In temperate climates, weather fronts are significant rain sources, as the cold front brings colder, denser air that forces warm, moist air to rise, forming clouds and causing precipitation. The low-pressure systems (cyclones) often develop and deepen, leading to more organised and widespread rainfall, such as with mid-latitude cyclones.
The temperate oceanic climate (Cfb) is used to design the Ashburton model. Rainfall results primarily from synoptic-scale weather dynamics involving mid-latitude cyclones and associated frontal systems. These systems, guided by easterly and northeasterly winds, bring moisture-rich maritime air from the Pacific Ocean, leading to widespread and sustained rainfall events. Conversely, stable, high-pressure conditions introduce drier northwesterly to westerly wind flows, suppressing precipitation. Hence, barometric pressure emerges as the most reliable rainfall predictor, because it drives the weather systems that produce precipitation, where falling pressure signals incoming storms, and rising pressure indicates dry periods. Moisture variables, such as relative humidity and dew point, help refine predictions but function as secondary indicators, clarifying timing and intensity rather than initiating rain. Wind direction and speed further indicate storm characteristics, with easterly/northeasterly winds commonly associated with incoming moisture and active frontal passages. Forecasting practices in Ashburton emphasize monitoring pressure changes to anticipate rainfall, supported by humidity and wind observations, underscoring the dominance of synoptic dynamics in rainfall prediction for Cfb climates.
In the Williams model, drawn on the Mediterranean (Csa) climate, rainfall primarily occurs during cooler months when mid-latitude cyclones disrupt the typically dominant subtropical high-pressure systems, which otherwise create prolonged, dry summers. Winter precipitation depends on the simultaneous presence of dynamic triggers, such as migrating low-pressure systems and suitable thermodynamic conditions, including elevated humidity levels, and lower temperatures promote condensation essential for winter rain formation. Conversely, summer’s persistent high-pressure patterns suppress convection and precipitation despite occasional humidity spikes, and wind patterns significantly influence rainfall events; westerlies and southerlies transport moist oceanic air essential for winter rains, while calm or northeasterly winds reinforce dry conditions during summer. In general, rainfall in Mediterranean climates is typically associated with the passage of cold fronts linked to low-pressure systems from the polar jet stream that moved in, while in warmer seasons, rainfall is rare due to the dominance of high-pressure systems and dry conditions. Effective rainfall forecasting in Williams requires recognizing the intersection of dynamic (pressure changes, wind shifts) and thermodynamic thresholds (humidity, temperature), emphasizing the seasonal specificity of Mediterranean precipitation and the nuanced interplay between cyclonic systems and suitable atmospheric conditions.
The humid subtropical (Cfa) climate of Vercelli features rainfall governed by a combination of abundant moisture and dynamic atmospheric triggers, influenced both by tropical moisture influx and mid-latitude weather systems. Rain events commonly occur when humid, unstable air interacts dynamically with frontal systems or low-pressure disturbances, often resulting in thunderstorms and severe weather. High humidity followed by elevated dew points critically enhance convective potential, making moisture indispensable for significant precipitation events. Barometric pressure and wind direction provide dynamic context, where specific wind patterns signal either incoming moist tropical air favourable for rainfall or dry continental flows suppressing it. Temperature acts in a supportive capacity, with excessively hot conditions often corresponding with stable, dry air masses. Rainfall prediction models emphasize relative humidity as the leading predictive factor, asserting that adequate moisture combined with dynamic lifting mechanisms (pressure and wind shift) reliably forecasts rain events. Accurate rainfall predictions in Vercelli thus rely on simultaneously assessing moisture conditions, pressure trends, and wind patterns to capture the complex interplay between thermodynamic fuel and dynamic triggers inherent to humid subtropical climates.
The results show that despite relative similarities in topography, predicting rainfall in tropical climates is generally more complex than in temperate climates, especially regarding short-range rain forecasts. This is due to several key factors, namely convective rainfall, which dominates this climatic region. This more sporadic and less predictable rainfall type can develop quickly with less warning than the frontal systems standard in temperate climates. Another factor is the lack of well-defined weather systems, as tropical climate regions experience more distinct and smaller-scale weather patterns, making it harder to track and predict precipitation. In contrast, temperate climates are regions where rain is mainly associated with large, well-defined weather systems, like cold fronts or low-pressure systems, which move predictably over time. As a factor, the Intertropical Convergence Zone (ITCZ) is a large-scale phenomenon that strongly influences tropical climates. Despite the significant impact on weather patterns in the tropics, ITCZ is complex and challenging to model accurately, leading to more significant uncertainty in rain forecasts. Together, these factors make rainfall in tropical climate regions more chaotic and less predictable than temperate climate zones’ more structured frontal weather systems. Hence, there are factors beyond weather parameters that are unique to tropical climates that are instrumental in the occurrence of rainfall. Therefore, the non-capture of these factors in the prediction of rainfall or/and the use of prediction models based on a temperate climate that capture a different set of weather parameters as significant will always lead to a poor rainfall model prediction in the tropics.
For next-day rainfall forecasting across the four studied climates, begin with the variable that the models show is most often in short supply and, therefore, most predictive when it spikes or plunges. For the Alor Setar (Am) climate, attention shifts to synoptic flow, as humidity is nearly always saturated, so rainfall hinges on dynamic triggers, such as a reversal to moist onshore monsoon flow, which mostly guarantees widespread showers, while a return to easterlies signals a dry interlude. In moisture-rich Ashburton (Cfb), the barometer and wind sector provide the earliest warning, because moisture is seldom scarce; hence, once pressure tendency charts show a falling trend and the wind veers onshore, rain is likely even if temperatures stay mild. In Williams (Csa), the limiting factor is almost always moisture, so real-time humidity (or dew point) is the critical threshold variable, with pressure and wind used to fine-tune timing for the arriving fronts. Finally, the Vercelli (Cfa) region demands a trio (dew, humidity, pressure) of checks, led unequivocally by humidity. So, when surface trough or frontal zone (providing lift) aligns with ample moisture, boosting instability, the stage is set for explosive convection and potentially intense rains.
5. Conclusions
Rainfall forecasting is imperative for many sectors, including agriculture, telecommunications, and environmental agencies. It is essential for food production, flood prediction and mitigation, water resources management, and all activities in nature, especially to achieve the sustainable development goals (SDGs).
This study examined the relative ease of predicting rainfall events between tropical and temperate climates, highlighting the key atmospheric parameters influencing these predictions. To focus specifically on climatic effects, locations with similar topographies were carefully selected. Alor Setar in Malaysia represents the tropical climate, while Vercelli in Italy, Williams in the USA, and Ashburton in New Zealand were chosen to represent different subtypes of temperate climates. Predictor variables included daily measurements of atmospheric pressure, temperature, dewpoint, relative humidity, wind speed, and wind direction, with the outcome variable being the binary occurrence of rainfall the following day. Uniform modelling approaches and algorithms were consistently applied across all datasets to minimize geographical and methodological biases. Both linear (logistic regression) and nonlinear (random forest) algorithms were utilized to ensure that findings regarding prediction accuracy remained robust regardless of the chosen modelling technique.
Both binary logistic regression and random forest models were designed using four years of data (from 1 January 2012 to 31 December 2015) from each site. The two methodologies differ significantly in terms of interpretability and computational demands/complexity. Logistic regression affords complete transparency, its coefficient estimates directly quantify the influence of each predictor, the probability outputs are typically well calibrated, and both model training and inference incur minimal computational overhead. While random forest is adept at uncovering nonlinear feature interactions, its less transparent operations entail longer training and prediction times and complicate the elucidation/explanation of individual forecasts. Results showed that both algorithms can be modelled to predict next-day rainfall occurrence. In the next-day rainfall classification prediction, the models for the different climatic locations can identify important weather parameters for the prediction of next-day rainfall. Humidity appears to be a model favourite for all four climate zones, and pressure is seen as important for only temperate models. For Am, sustained humidity is the predominant predictor, with secondary support from the dewpoint. Cfb prioritizes pressure, but pressure gradients, wind direction, and humidity are key, reflecting maritime storm tracks. Humidity is crucial in Csa climates, which are centred on seasonal temperature, alongside seasonal pressure shifts, wind-driven moisture transport, and dewpoint that define wet/dry phases. Cfa emphasizes humidity thresholds and thermal instability with pressure, as dewpoint spreads and moisture-laden winds drive convective rainfall. While all parameters contribute, their relative importance shifts with climatic context. Thus, predictive models must prioritize these zone-specific dynamics to distinguish events from non-events.
Several evaluation metrics were applied to evaluate the models, and all models have balanced accuracy and AUC ROC scores above 60%. This indicates the occurrence of high recall and precision in the models. Also, the temperate climate models outperformed the tropical climate model on all evaluation metrics. Across the four meteorological stations evaluated, logistic regression demonstrated superior average performance in rain forecasting relative to the random forest classifier. When evaluated by balanced accuracy, which compensates for the inherent class imbalance between rain and non-rain observations, logistic regression attains an average score of approximately 0.716, whereas random forest achieves 0.702. Similarly, the area under the receiver operating characteristic curve (AUC) favours logistic regression (0.775) over random forest (0.752). However, station-specific analysis reveals notable heterogeneity. At Alor (Am) and Ashburton (Cfb) locations, characterised by tropical or maritime/oceanic climatic influences, the linear decision boundary imposed by logistic regression provides better generalisation to new data, indicating that random forest’s flexibility in modelling complex interactions does not yield additional predictive benefit in these environments. At Williams (Csa), by contrast, the predominant drivers of rainfall appear sufficiently strong and linear that logistic regression effectively captures nearly the entire predictive signal, leaving minimal incremental value for the ensemble-based model. Conversely, for Vercelli (Cfa), where complex/nonlinear interdependencies among meteorological covariates (such as humidity, atmospheric pressure, and temperature) govern/significantly influence precipitation processes, the random forest classifier yields/attains marginally higher discrimination (an uplift of 1.1 percentage points in balanced accuracy and 0.6 points in AUC). In this report, logistic regression served as the baseline rain-prediction model, owing to its robustness, efficiency, and ease of deployment. Nevertheless, for sites that consistently exhibit nonlinear meteorological dynamic (for example Vercelli), it is advisable to monitor random forest performance.
A key limitation of this paper’s findings is the use of a short data collection period (four years), which restricts the ability to compare trends or variations across multiple years. Furthermore, the identification of similar geographical topographical locations with varying climates was challenging.
Further research will focus on expanding the scope of rainfall forecasting from next-day predictions to short-range and medium-range forecasts across the four selected locations. This extension aims to analyse how prediction accuracy varies over different forecast horizons (short to medium range). The study will also involve a comparative evaluation of the predictive models used for each location, examining the stability and significance of their key input variables over time. By identifying the most influential atmospheric parameters at varying forecast intervals, the research will provide deeper insight into the temporal dynamics of rainfall prediction and guide the selection of robust models for different climatic contexts.