Abstract
Reliable rainfall prediction is essential for effective climate adaptation yet remains challenging due to complex atmospheric interactions that vary across regions. This study investigates next-day rainfall predictability in tropical and temperate climates using daily atmospheric data—including pressure, temperature, dew point, relative humidity, wind speed, and wind direction—collected from topographically similar sites in Alor Setar (tropical) and Vercelli, Williams, and Ashburton (temperate) between 2012 and 2015. Logistic regression and random forest models were used to predict rainfall occurrence as a binary outcome. Key variables were identified using Wald’s statistics and p-values in the logistic regression models, while the random forest models relied on mean decrease accuracy for ranking variable importance. The results reveal that rainfall in temperate climates is significantly more predictable than in tropical regions, with the Williams model demonstrating the highest accuracy. Atmospheric pressure consistently emerged as the dominant predictor in temperate regions but was not significant in the tropical model, reflecting the greater atmospheric variability and complexity in tropical rainfall mechanisms. Crucially, the study highlights that as global warming continues to alter temperate climate patterns—bringing increased variability and more convective rainfall—these regions may experience the same predictive uncertainties currently observed in tropical climates. These findings underscore the urgency of developing robust, climate-specific rainfall prediction models that account for changing atmospheric dynamics, with critical implications for weather forecasting, disaster preparedness, and climate resilience planning.
1. Introduction
The evolving climate system has increased extreme weather events, such as droughts, heatwaves, floods, and storms. The impacts of climate change vary across regions, with some experiencing reduced rainfall and droughts, while others face increased storms and flooding. These contrasting impacts highlight the varying vulnerabilities of different areas to climate-related changes [1,2,3]. Understanding these dynamics is essential for mitigating the impacts of extreme weather events, so comprehensive modelling approaches are required.
Climate classification systems offer a framework for understanding diverse and complex climates using environmental indicators, life zone classification, and weather patterns. The most common system, the weather pattern, divides climates into the following five categories: tropical (mega-thermal), dry (arid and semiarid), temperate (mesothermal), continental (microthermal), and polar and alpine (montane). For example, tropical climates found near the equator experience high temperatures, humidity, and significant rainfall, with two main seasons driven by the movement of the Intertropical Convergence Zone (ITCZ) [4]. Temperate climates located beyond the tropics experience distinct seasonal changes, with warm summers, cold winters, and more evenly distributed precipitation. In contrast, polar climates at higher latitudes are cold and have extreme weather.
Rainfall is a complex hydrological element that varies spatially and temporally. It plays a vital role in shaping climate differences between climatic regions, primarily tropical and temperate regions. Predicting rainfall depends on accurate meteorological data, as it is influenced by factors like temperature, pressure, wind, and humidity, just like climate and weather.
Comprehensive rainfall studies are necessary for effective water resource management and climate adaptation. Various studies have examined long-term rainfall trends, such as research on century-long patterns in Sri Lanka [5], 81 years of analysis in Jordan [6], and 30 years of rainfall data in Nigeria [7]. These studies emphasise the necessity of comprehensive rainfall studies for effective water resource management and adaptation to climate variability; understanding the spatial and temporal variability of rainfall is vital, as rainfall can be linked to specific atmospheric/synoptic regimes [8]. Rainfall can trigger natural disasters, such as floods and landslides, especially when compounded by extreme weather events [9,10,11]. These occurrences highlight the need for advanced weather prediction systems, particularly as climate change alters global rainfall patterns [11]. Effective forecasting can mitigate these risks and support sustainable development.
Tropical climates are marked by intense, localised rainfall, primarily in rainforest and monsoon regions, while temperate climates have more predictable, broader rainfall patterns. Most climate models are based on temperate regions, leading to poor predictions in tropical areas due to their distinctive convective dynamics. Climate change exacerbates these challenges, as tropical regions are particularly vulnerable to climate change [12], particularly with shifts in the Intertropical Convergence Zone (ITCZ) expected to disrupt rainfall patterns [4], hence affecting global water resources and food production.
This study evaluates the accuracy of next-day rainfall predictions in temperate and tropical climate regions by analysing atmospheric parameters, while ensuring comparably similar geographic (oceanic and topographic) conditions across the selected locations. The following contributions are achieved in this work:
- Examination of climatic differences between temperate and tropical climate regions influence on rainfall prediction modelling, emphasising the considerable variations in rainfall behaviour across these climates. The analysis specifically investigates the impact of these climatic dynamics on predictive accuracy and model performance within comparable geographic contexts.
- Identification of key atmospheric variables critical for improving rainfall prediction accuracy, thereby providing insights into the underlying physical processes governing rainfall. The study emphasises the latitudinal impact/influence on model reliability (accuracy) and underscores the limitations of relying exclusively on standard weather parameters, particularly in tropical regions where rainfall prediction is inherently more complex.
- Evaluation of the effectiveness and adaptability of machine learning models across diverse climatic conditions. Its findings directly enhance rainfall forecasting methodologies by addressing climate-specific variability and refining model calibration strategies.
Weather forecasting, particularly for rain, is inherently complex due to the nonlinear and chaotic behaviour of the atmosphere. Minor uncertainties in initial conditions grow over time, making predictions less reliable as the forecast horizon extends [13]. The work published in [14] highlights that while some atmospheric states exhibit significant predictability, others change abruptly and unpredictably. The complex atmospheric dynamics and limited knowledge of atmospheric processes lead to reduced forecast accuracy as the time interval between the current and forecasted period increases. These dynamics have driven the shift toward probabilistic forecasting, quantifying uncertainty and enhancing confidence in predicting precipitation patterns. This approach is essential for extending forecast time ranges beyond the deterministic limits. The forecast time range in rain forecasting is categorised as short-range (1 h to 3 days), medium-range (3 to 10 days), extended-range (10 to 30 days), and long-range (one month or more). The seasonal (1 to 3 months) and sub-seasonal (3 to 6 weeks) are sub-ranges within the extended to long range. Forecasts are crucial for all sectors, as they provide timely and accurate predictions for decision making.
Rainfall forecasting methods are primarily divided into empirical and dynamical approaches. The dynamical approach uses physical models such as General Circulation Models (GCM) [15] and Weather Research and Forecasting (WRF) [16] models that are based on equations to predict climate evolution. The effectiveness of a model is determined by its ability to accurately represent the relevant meteorological scale (microscale to large-scale) processes specific to a particular region. While general circulation models (GCMs) are commonly used to evaluate climate change, they are not suitable for projecting local or regional climates due to their coarse spatial resolution, which limits their ability to capture the finer details and variations that occur at smaller scales [11,17,18]. However, the WRF models overcome this limitation. Despite their relative effectiveness, computational costs and spatial and temporal resolutions remain a challenge, driving interest in data mining (empirical) alternatives. The empirical approach, including machine learning (ML) and statistical techniques like fuzzy logic (FL), rely on historical data and the relationships within and between atmospheric variables.
Several studies have demonstrated that machine learning algorithms outperform statistical techniques, showcasing their greater predictive accuracy [19,20]. Overall, studies [21,22,23] have proven the effectiveness of machine learning algorithms in modelling complex weather patterns. They have demonstrated significant potential in enhancing rainfall prediction, offering improved predictive accuracy and reduced correlations. By utilising extensive datasets and integrating key meteorological factors, these models provide deeper insights for rain forecasting. Their versatility enables applications across diverse regions and temporal scales, making them valuable tools for informed decision making in climate-sensitive areas.
To aid in comprehension ease of analysis, Table 1 explains the meaning of each column heading, while Table 2 provides a summary of the contributions reviewed, offering a snapshot of the current state of the art. Key features have been identified and compared to highlight this study’s unique contributions.

Table 1.
Key to the summarised analysis of the related works.

Table 2.
Summarised analysis of related works highlighting literature gaps in climate-based rainfall prediction modelling relative to our contribution.
Research has been conducted on predicting rainfall and rainfall states in different parts of the world. In the temperate climate regions, the authors of [24] used 50 years of data to predict daily rainfall states in Shih-Men Reservoir, located in the Danshui River basin in northern Taiwan. The performance of three classification methods, namely linear discriminant analysis (LDA), random forest (RF), and support vector classification (SVC), was compared. The results showed that RF outperforms LDA and SVC for rainfall state classification. This means that the outputs of RF classification models were selected as inputs for the Least Square Support Vector Regression (LS-SVR) models to simulate rainfall amounts. Using RF for rainfall state classification and LS-SVR for rainfall amount prediction improved the extreme rainfall prediction. This proposed modified statistical downscaling approach was inspired by the weakness of support vector machines (SVM) in downscaling extreme rainfall based on the methods used by [32,33] for improving the extreme rainfall prediction using downscaling. Also, the authors of [25] carried out the state prediction of rainfall using binary logistic regression and a dataset from Canberra, Australia. The significant (based on p-value) and important (based on Wald/z statistics) weather parameters needed for the accurate prediction of rain the next day were identified.
The characteristics of rainfall differ considerably across all climatic regions [34]. While most models provide reasonable rain prediction accuracies for higher latitudes like temperate regions, they mostly underestimate in tropical zones [35]. Additionally, models developed based on temperate data struggle with the variability introduced by tropical terrain, mostly yielding significant errors [36]. This is because the unique characteristics of rain in tropical regions—frequent, high-intensity rainfall with smaller rain cells and larger raindrop sizes—pose challenges for accurately modelling and predicting rain. These challenges are further compounded by the lack of region-specific rain measurement data [37]. This highlights the need for tailored approaches to rainfall modelling to improve the accuracy of rain predictions to mitigate the impact of climate change and disasters.
Several studies have been carried out on rainfall state prediction in the tropical climatic region. In Southeast Asia, the authors of [26] conducted a study in Selangor, Malaysia, with 4 years of data from 2010 to identify the most effective techniques for rainfall state prediction. They conducted a comparative analysis of various supervised learning methods, namely support vector machine (SVM), naïve Bayes (NB), decision tree (DT), neural network (NN), and random forest (RF). The experimental results showed the RF algorithm as the leading technique among those evaluated, as it performed exceptionally well due to its ability to achieve high F-measure scores, while effectively training on limited data. Thus, the study highlights the potential of these models for forecasting in new geographical areas like Malaysia.
Still within the same geographic region, the authors of [27] applied the SVM technique to analyse the various parameters influencing atmospheric precipitation in Singapore within five years and identified the following five important weather features: temperature (T), relative humidity (RH), solar radiation (SR), dew point temperature (DPT), and precipitable water vapor (PWV). The study showed that PWV contributed the most to achieving a high detection rate. By considering both seasonal and diurnal variables, which are in most cases not included, the study revealed that alongside the SR variable, day-of-year and hour-of-day contribute to reducing false alarm rates. Thus, the findings underscore the importance of these often-overlooked parameters in enhancing predictive models for atmospheric precipitation events.
In West Africa, the authors of [28] explored five classification algorithms DT, multilayer perceptron (MLP), RF, extreme gradient boosting (XGB), and K-nearest neighbour (KNN) to identify the most effective techniques for predicting rainfall state in Ghana using data spanning 39 years. The study addressed the importance of selecting appropriate rainfall prediction models for classifying rainfall across tropical climatic regions. Overall, random forest, extreme gradient boosting, and multilayer perceptron achieved strong performance, suggesting that ensemble and deep learning models effectively predict rainfall across Ghana’s ecological zones.
Studies have been carried out on rain prediction using locations with different climatic zones. In a country with contrasting climates like Brazil, the authors of [29] applied artificial neural networks (ANNs) to develop a methodology for predicting rainfall occurrence. They employed 65 years of historical data from 10 locations that are either tropical or temperate in climate. The ANN model was designed to predict rainfall events exceeding 5 mm across different climatic seasons for cumulative periods ranging from 3 to 7 days. This approach is to reduce model variance, enhance data bias, and filter out zero rainfall occurrences, which can distort results; the results demonstrate that the ANNs can forecast rainfall events with an average accuracy of 78% in summer, 71% in winter, 62% in spring, and 56% in autumn.
Data from 26 geographically diverse locations across Australia exhibiting tropical, dry, temperate, or continental climate characteristics were used in [30]. A comparative analysis was conducted on an optimised neural network (deep learning) and eight (8) machine learning algorithms (logistic regression, linear discriminant analysis, quadratic discriminant analysis, K-nearest neighbour, decision tree, gradient boosting, random forest, Bernoulli naïve Bayes) with data spanning 10 years and evaluated the performance of these models in the prediction of rainfall. The results show that the deep learning model outperformed all models, achieving an F1-score of 88.61% and precision of 98.26%, which underscores the potential of optimised neural networks for accurate rainfall prediction. While the logistic regression model achieved the highest F1-score (86.87%) and precision (97.14%) among the statistical models. Hence, the framework demonstrates the effectiveness of ANN in short-term, season-specific rainfall event forecasting.
The study further buttresses this result from [31] in Australia using rainfall data from 49 cities situated in the various climate zones (tropical, dry, temperate, and continental) covering 10 years to analyse the use of machine learning algorithms (K-nearest neighbour decision tree, random forest, neural network) for modelling rainfall, with the neural networks excelling once again. The study highlighted the importance of regional data, as algorithms perform better when trained on location-specific information, allowing more accurate and efficient predictions for individual cities.
Although previous studies have examined rainfall prediction across various climatic zones, they did not focus on comparing the influence of climate itself on prediction accuracy. Specifically, no existing literature has been found that conducts a comparative analysis of rainfall prediction models under similar oceanic and topographic conditions to isolate the effects of climatic differences. Furthermore, a gap remains in identifying and evaluating the critical atmospheric variables that influence prediction accuracy across latitudes. This study addresses that gap by comparing rainfall prediction performance in both tropical and temperate climates, with an emphasis on understanding the latitudinal impact and the key variables that drive predictive accuracy. This motivation forms the basis for the present manuscript.
The rest of the paper is organized as follows. Section 2 describes the materials and methods, by introducing the study area, analysing the datasets used, and comparing the linear and nonlinear machine learning models’ designs. The performance and comparative results of the models are shown in Section 3 and discussed in Section 4. Finally, Section 5 concludes the paper and outlines directions for future research.
2. Materials and Methods
2.1. Study Area
Weather forecasting is influenced both by the local geography and by the time horizon.
2.1.1. Tropical Climate
The study used data from Malaysia, see Figure 1, to understand the climatic zone dependency on rainfall. Malaysia has a tropical climate based on the Koppen–Geiger climate classification [38]. It also has regions that are influenced by monsoon winds, which bring about seasonal variations in rainfall.
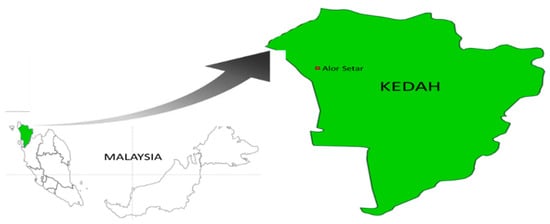
Figure 1.
Map of Malaysia and Kedah with the location of the Alor Setar weather station.
Alor Setar is situated along the western coast of Peninsular Malaysia at approximately 6.12° N latitude and 100.37° E longitude [39]. It has a tropical monsoon climate (Köppen Am), characterised by distinct wet and dry seasons, with substantial rainfall during the monsoon months. Although Alor Setar does have characteristics of a tropical rainforest climate due to high temperatures and humidity, influenced by its proximity to the Equator, its distinct wet and dry seasons and overall rainfall patterns align more closely with a tropical monsoon climate. The region receives significant rainfall, with the Northeast Monsoon bringing cooler, drier air. At the same time, warmer and wetter conditions characterise the Southwest Monsoon.
The low-lying geography of Alor Setar makes it susceptible to natural disasters, particularly flooding during the rainy season due to heavy rainfall. Droughts can also occur during prolonged dry spells. As climate change presents challenges, the region faces increased rainfall variability, rising temperatures, and potential sea-level rise, which could adversely affect agriculture and local communities.
2.1.2. Temperate Climate
To identify locations with analogous geographic features but non-tropical in climate, the focus will be on areas with comparable geographic features—flat terrain, proximity to water bodies and highlands/elevations, and significant agricultural activity. Areas with these features include the Po Valley in Italy, which benefits from a subtropical climate; the Central Valley in California, where a Mediterranean climate supports large-scale agriculture; and New Zealand’s Canterbury Plains, a vast lowland in a temperate climate. Although these regions differ significantly in weather patterns, they share similar physical geography and agricultural potential, making them analogous to Alor Setar in topography and land use.
Vercelli, located in northwestern Italy’s Piedmont region, lies within the fertile Po Valley at 45.32° N latitude and 8.42° E longitude [40], see Figure 2. The area experiences a humid subtropical climate (Köppen Cfa), influenced by the Alps to the north and the Apennines to the south. This climate is marked by four distinct seasons, where high humidity is common in both summer and winter, often resulting in muggy conditions and dense fog, particularly in winter.
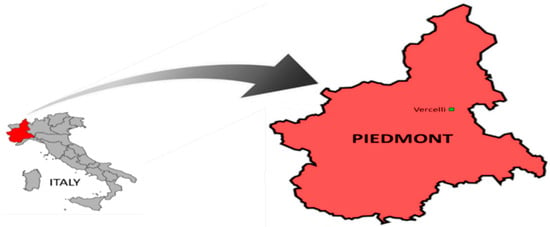
Figure 2.
Map of Italy and Piedmont with the location of the Vercelli weather station.
Williams is in Colusa County, northern California, in the Sacramento Valley, part of the Central Valley [41], as shown in Figure 3. It experiences a Mediterranean climate (Köppen Csa) characterised by hot, dry summers and mild, wet winters, typical of the California Central Valley. The landscape is predominantly flat, with the Coastal Range to the west and the Sierra Nevada Mountains to the east. Climate change presents increasing challenges for Williams, with frequent droughts, severe heat waves, and unpredictable rainfall patterns.
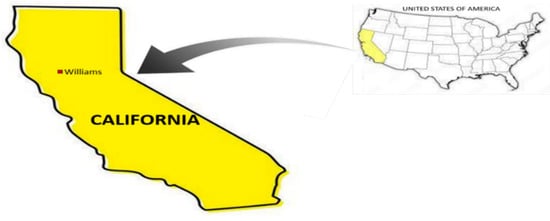
Figure 3.
Map of the United States of America and California with the location of the Williams weather station.
Ashburton, also known by its Māori name, Hakatere, is in the Canterbury region of New Zealand [42]. Nestled on the fertile Canterbury Plains, see Figure 4, which stretches between the Pacific Ocean to the east and the Southern Alps to the west, Ashburton benefits from a temperate oceanic climate (Köppen Cfb). This climate is characterised by mild summers, cool winters, and relatively consistent rainfall throughout the year, influenced by occasional cold fronts from the south. The temperature in Ashburton varies significantly, and it experiences moderate rainfall.
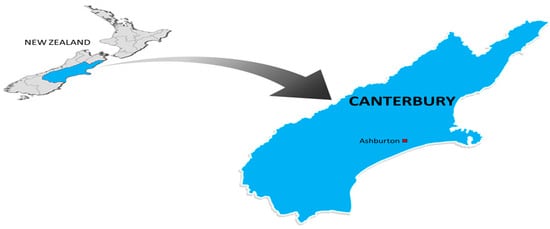
Figure 4.
Map of New Zealand and Canterbury with the location of the Ashburton weather station.
2.2. Data Analysis
The datasets [43] from Alor Setar, Ashburton, Williams, and Vercelli each comprised 365 daily observations from January to December 2014, and 7 variables, namely Pressure (hPa), Temperature (°C), DewPoint (°C), Humidity (%), WindSpeed (m/s), WindDirection (degrees), Rain_Nextday Yes or No). Humidity and WindDirection are integer variables, Rain_Nextday is a categorical variable, whilst Pressure, Temperature, DewPoint, and WindSpeed are numeric variables.
The bar plot in Figure 5 displays the percentage frequency of rainfall occurrence with the year at the selected tropical and temperate locations. Williams has the lowest number of days that rain fell, while Alor Setar has the highest, synonymous with the tropical climate. This rainfall plot further supports the frequency of rainfall synonymous with their region. Alor Setar has between 2000 mm and 3000 mm of rainfall annually, Vercelli receives 850–950 mm, Ashburton experiences annual rainfall ranging from 600 mm to 700 mm, and the yearly rainfall amount on average in Williams is 400 mm to 600 mm.
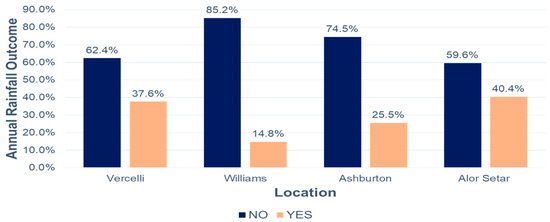
Figure 5.
Plot of percentage annual rainfall outcomes for the four climate locations.
Analysis of the variables in each study area using moments to enable descriptive understanding and comparison of the distribution characteristics for each variable in the different locations. The first four moments in use are mean (μ), variance (σ2), skewness (γ), and kurtosis (κ). This analysis uses the standard deviation (σ) as the second moment instead of the variance. This is for ease of interpretation as the unit of the standard deviation and the variable are the same.
From Table 3, the Williams data has the highest mean pressure value, and the Alor Setar data has the lowest value. Alor Setar has a small σ, which indicates that the mean pressure variable is a good representation of the dataset. For Vercelli, Williams and Ashburton, the σ appears larger, indicative of high variability in the pressure values for each dataset, with Ashburton showing the highest variability in pressure values. In the third moment, the pressure data in Vercelli, Ashburton, and Alor Setar are negative, hence being left-skewed, which means a longer left tail in their distribution. In contrast, the Williams pressure data has a longer right tail, as it is a positively skewed distribution. The kurtosis in all four pressure variable data is seen to be a platykurtic distribution as all four values are less than 3. Hence, their pressure distributions are short tailed.

Table 3.
The first four moments of the pressure, temperature, dew point, and humidity variables at the four climate locations.
The mean temperature values reflect the characteristics of their different climates, as Alor Setar is a clear representation of a tropical climate location with a high mean temperature. The distribution of the temperature variable in Alor Setar is seen to be left-skewed and platykurtic with low variability. In contrast, Vercelli, also left-skewed, is platykurtic in distribution and has more variability. Ashburton and Williams both have platykurtic and right-skewed distributions, with standard deviation values suggesting that on average, their temperature values deviate from the mean temperature by a large magnitude of 4.30 °C and 6.93 °C, respectively.
The dewpoint, which measures the air’s moisture content and indicates the point at which dew, fog, or precipitation may form, is expected to replicate the same distributional characteristics as the temperature variable. This is the case for Vercelli, Ashburton, and Alor Setar data. The William dewpoint data presents a different distributional characteristic, as it has the lowest mean dewpoint value, although it has the second highest mean temperature value. Even with the same platykurtic distribution as in the temperature variable, it has a left-tailed distribution, unlike the temperature variable. The magnitude of deviation from the mean dewpoint is 4.95 °C, which is approximately 2 °C lower in deviation than the temperature variable. Hence, the dewpoint variable has a lower variability than the temperature variable in the Williams dataset.
Williams has the lowest mean humidity value at 54.45%, and Alor Setar has the highest value at 89.98%. Alor Setar has a lower variability of 7.94% compared to Vercelli, Williams, and Ashburton, at 15.38%, 15.46%, and 12.37%, respectively. The humidity variable distribution is platykurtic for all datasets, with a right-tailed distribution in the Williams data and a left-tailed in the other three datasets.
2.3. Binary Logistic Regression with Backward Akaike Information Criterion
Precise rainfall forecasting remains a global challenge in meteorology. While several weather prediction techniques exist, selecting suitable methods for predicting rainfall in a region is crucial. Equally important is identifying significant input variables for effective prediction, a factor often overlooked by current approaches [44].
Logistic regression is commonly applied due to its suitability for classification problems, such as predicting the occurrence or non-occurrence of an event. It is a simple yet informative classification algorithm that is useful in discovering relationships in the data. Logistic regression is easy to implement and interpret, highly efficient to train, and quick to update with new data. Additionally, it is less prone to overfitting in low-dimensional datasets. It performs best with under-sampled data but struggles with oversampled data, highlighting the importance of input data quality. As a probabilistic classifier, it solves classification problems by determining the most effective variables for classification and calculating probabilities to categorise new data. It calculates the probability of a categorical dependent variable with values between 0 and 1, making it well-suited for predicting binary outcomes, such as whether it will rain the next day.
Over the past decade, logistic regression has been extensively used for prediction and forecasting in various fields, including meteorology. Previous studies [45,46] have successfully used this method in medium-range precipitation and temperature forecasts; the authors of [47] demonstrated how to use logistic regression and generalised linear models (GLM) to predict future rainfall volumes under different climate scenarios, with Hong Kong as a case study.
The study in [25] applied logistic regression to predict whether it will rain the next day in Canberra, while identifying important/significant weather variables. Three model/variable selection approaches namely, Backward AIC, Stepwise BIC, and Lasso, were applied and compared to the full model. The result showed the backward selection AIC logistic regression model outperformed all the other models. This is because the focus of the BIC approach is to yield a parsimonious model, hence it strongly penalises extra predictors, and Lasso shrinks coefficients towards zero, which introduces bias even for important variables.
2.3.1. Binary Logistic Regression
From the dataset, the key predictive task is to determine the likelihood of rainfall occurrence on the next day based on the observed atmospheric variables. Since the answer to this question is binary, the variable is measured on a binary scale, yes or no. A binomial distribution is proposed for the response data, as it is used to determine the odds of an event’s occurrence or to predict its success or failure.
Assuming Y to be a binary random variable
here are the probabilities in the Bernoulli distribution.
Logistic regression [25], an extension of linear regression, is a classifier used when outcomes fall into categories. Therefore, binary logistic regression is a binary probabilistic classifier from the binomial family of generalised linear models (GLMs) that is commonly used in cases where outcomes are dichotomous (e.g., rain or no rain).
It is applied to determine the relationship between the probability of a positive outcome of next-day rainfall, p (Yes), which is binomially distributed with the independent variables. So, for independent observations , where the observation is a realisation of the random variable , where if ith next-day rainfall outcome is Yes, and otherwise. Then, the independent variable is said to be binomially distribution , if the probability of success = and probability of failure = . Thus, to determine the odds of an event occurring is given as
As linear regression combines multiple input variables linearly. Logistic regression transforms these linear combinations into probabilities using the logit (log-odds) function, enabling modelling of binary outcomes such as predicting next-day rainfall. Given the range of the odds is from zero to ∞ (infinity), to set it to the same range as the linear regression, a log transformation is applied. This transformation is called the logarithm of odds, which is the ratio of the probability that rain will fall the next day () over the probability that rain will not fall the next day . This is written as
As binary logistic regression models the relationship between the independent variables and the log-odds (logarithm of the odds) of the dependent variable, the odds that it will rain the next day is written as
where the β coefficients represent the weights assigned to each predictor variable determining their impact on the outcome. The function used is the logistic function, transforming the linear combination of predictors into a probability between 0 and 1.
2.3.2. Akaike Information Criterion (AIC)
Akaike Information Criterion (AIC) [48] is used to assess the adequacy of a model in fitting the data by quantifying the amount of information lost. While it does not provide much insight on its own, its value lies in comparing multiple models derived from the same dataset to determine the best balance between goodness of fit and simplicity.
AIC backward selection is applied as the model selection criterion for the binary logistic regression, as it penalises models with more parameters, favouring simpler ones that still perform well. This method allows for the comparison of non-nested models, where candidate models are ranked based on their AIC values, with the model having the smallest AIC score chosen as the best fit, which is the model that does not overfit or underfit the data. Identifying the best model is carried out by generating subsets of input variables using , where n represents the total number of input variables, and x is the number of variables included in each model. By penalising overly complex models, AIC ensures that only the most relevant predictors are included, as it holds model performance as an essential criterion. AIC is calculated as:
where k is the number of parameters, and is the maximum log-likelihood estimate of the model. As the number of parameters increases, the term 2k increases, introducing a penalty for complexity. Simultaneously, as decreases, the model improves in fitting the data because is negative. A full model may have a low AIC but may include unnecessary variables. Hence, AIC helps find a more parsimonious model with fewer predictors, reducing redundancy, while maintaining good explanatory power.
2.4. Random Forest
Random forest [49] is a nonlinear ensemble learning algorithm that automatically discovers complex interactions among predictor variables, while addressing the limitations of individual decision trees, such as overfitting and high variance. By building a collection of K decision trees, with each grown on a bootstrap sample of the training data. At every split, a tree considers only a random subset of features, so the two layers of randomness—row bagging and feature bagging—produce trees that are mutually decorrelated. Approximately one-third of the training observations are left out of each bootstrap sample; these out-of-bag (OOB) cases supply an internal, unbiased estimate of generalisation error, removing the need for a separate validation set.
Combining their predictions to produce robust results sharply reduces the variance of any single tree and guards against overfitting, while still capturing complex interactions among predictors. For classification tasks, the final prediction is determined by majority voting among all trees, while regression tasks use averaging, as follows:
here, K represents the number of trees in the forest, k each tree, and denotes the prediction of the k-th tree for input x.
While traditionally motivated by bootstrapping and variance reduction, its probabilistic foundation can also be linked to the Bernoulli distribution for binary classification tasks. From Equation (1), each tree’s vote is, therefore, a Bernoulli (p) trial; where . To build a forest of K trees, each trained on an independent bootstrap sample and making an independent prediction, hence the total number of correct votes can be defined as follows:
Now, inside each tree a different optimisation is taking place; at each node, the algorithm greedily chooses a split that most reduces impurity—measured by Gini or entropy. These node-level metrics come from the same Bernoulli equation, only applied locally. For any node with n binary targets and empirical class proportion ,
which is also the sample variance estimator for a Bernoulli variable. So, for a node containing a binary label Y ϵ {0,1} with class proportion Pr (Y = 1), the Gini impurity G, which is twice the Bernoulli variance, is as follows:
A candidate split into left and right child nodes (with and samples, respectively) is evaluated/scored using the Gini gain, as follows:
where , , and are the Gini impurities of the parent and child nodes, and n is the total number of samples at the parent node. The random forest algorithm chooses the split that maximises , i.e., the largest drop in the within-node/child Bernoulli variance (or log-loss of the Bernoulli outcomes), thus by reducing lowers the local probability of misclassification.
Feature Importance
Random forest also offers a permutation test based on the out-of-bag (OOB) samples called mean decrease accuracy (MDA). It corrects the bias of by checking how the predicted success probability p changes when the link between and Y is broken. Thus, for each tree k the OOB samples play the same role, as they provide an unbiased estimate of the tree’s true accuracy; this is known as the baseline OOB accuracy. By randomly permutating/shuffling feature among/within the OOB samples/data, leaving other features unchanged or at a constant, and recomputing the accuracy, the average of the accuracy drop over all trees is as follows:
where is the baseline OOB accuracy, and is the accuracy after permuting feature . So, if permuting leaves accuracy unchanged, contributes little beyond what the other features already captured. A large drop means it is essential for many trees to make correct (majority vote) predictions. Thus, a large accuracy loss means the permutation has lowered each tree’s individual success rate and even a small average drop in p after permutation can translate into a noticeable rise in forest error—hence a high MDA score. A large MDA means that permuting destroys information the model needs, so feature is highly important. Generally, the advantages of MDA are that it adjusts for feature scale and cardinality, and it reflects the global impact of the feature on predictive performance, not just its use in splits.
Random forest is a robust and flexible algorithm known for reducing overfitting and handling nonlinearities, missing data, and mixed feature types. It provides useful insights through feature importance (e.g., MDA) and out-of-bag error estimates. However, it has limitations, including bias toward dominant classes, inability to extrapolate beyond training targets, reduced effectiveness with correlated features, and step-like decision boundaries. The model can be memory-intensive, slow to train, and difficult to optimize due to many hyperparameters. Additionally, it struggles with sparse, high-dimensional data, time-dependent patterns, and highly imbalanced classes without special handling.
3. Results
The binary logistics regression with stepwise AIC and random forest approaches were applied to data from various locations to create the four models for predicting next-day rainfall. They are the Alor Setar model for the tropical climate and the Vercelli, Williams, and Ashburton models for the temperate climate. The predictor variables are pressure, temperature, dewpoint, humidity, wind direction, and wind speed.
3.1. Logistic Regression Model Analysis
The odds ratio (OR) is used to demonstrate the strength of the relationship between predictors and the outcomes. For the OR > 1, the odds are increased, and for OR < 1, the odds are decreased for the said outcome. The sign (+ or −) of the coefficient determines the effect of the variable on the outcome, where a positive sign (+) is indicative of a positive impact on rain falling the next day, while the negative sign (−) implies the variable has a negative effect on rain falling the next day. The Wald or z statistics are used to determine the importance of a variable in a model. Using the cut-off value of 2, variables with absolute z values above the cut-off are seen to be important variables in the forecast model. The variable importance in a model is further corroborated using the p-value. Using a significance level of alpha equal to 0.05 when the p-value of the predictor variable is less than the alpha value, this implies that the independent variables have a statistically significant relationship with the dependent variable in the model. Covariates that are not significant do not mean that these covariates have no relationship with the dependent variable; it means that the relationship is not strong enough to be detected at a given confidence level (95% level).
Table 4 is the summary analysis of the tropical climate model, Alor Setar. Dewpoint has a negative effect, while humidity and windspeed positively affect next-day rainfall. The dewpoint and windspeed variables are seen not to be important, as their z-values are below 2, and not significant, as their p-values are both above the alpha value of 0.05. Hence, humidity is the only important and significant variable in the model. For the odd ratio, for every one-unit increase in humidity, the odds of rainfall rises by about 16.1%.

Table 4.
Coefficient, z statistics, p-value, and odds ratio of the Alor Setar model.
From the coefficient column in Table 5, pressure, temperature, and wind direction all have a negative effect on next-day rainfall. All variables in the model are both important and significant. The dewpoint and windspeed variables have odd ratios greater than one, hence rain falling the next day is increased by a factor of 36.6 and 5.5, respectively, with a unit increase in either variable. Also, the odds of rain falling the next day decreases by a factor of 6.4, 22.2, and 0.2 for a unit increase in pressure, dewpoint, and wind direction, respectively.

Table 5.
Coefficient, z statistics, p-value, and odds ratio of the Vercelli model.
The summary analysis of the Williams model is represented in Table 6. The effect on next-day rainfall is positive for the dew and windspeed covariates and negative for the pressure, temp, and humidity covariates. Although all covariates in the Williams model are important, the most important predictor variable is temperature. The odds of rain falling the next day decrease with a unit increase in either pressure, temperature, or humidity, and a unit increase in the value of the dew covariate is associated with the odds of rain falling the next day by a double factor.

Table 6.
Coefficient, z statistics, p-value, and odds ratio of the Williams model.
Table 7 is a summary of the Ashburton model. The pressure and dew variables have a negative effect on next-day rainfall, while temperature and humidity positively affect next-day rainfall. All covariates are important and significant in the model, as their z-value is above the cut-off, and their p-value is less than the significant level. For a one-unit increase in pressure or dewpoint measurements, the odds of rain falling the next day decrease by a factor of approximately 7 and 31.9, respectively. For a unit increase in temperature or humidity, there is an approximately 49.2- and 12.7-factor increase, respectively, in the odds of rain falling the next day.

Table 7.
Coefficient, z statistics, p-value, and odds ratio of the Ashburton model.
3.2. Random Forest Model Analysis
Random forest features importance metrics that fall into two groups. Permutation-based measures—reported as overall mean decrease accuracy (MDA) and class-specific NO and YES scores—estimate how much out of bag accuracy drops when a predictor is replaced by noise. Large positive values signal that the model relies heavily on the variable; negative class-specific values indicate that the variable may be misleading for that class. The split-based measure, captured by the mean decrease Gini (MDG), record the total reduction in Gini impurity contributed by all splits using the predictor. Higher Gini scores show that the variable is frequently chosen and consistently produces purer partitions. Because the Gini scale is model-specific, comparisons are meaningful only within the same forest. Together, these metrics reveal both the performance impact of each variable and their structural role in the model.
Table 8 summarises the feature importance of the Alor Setar model. Humidity is seen to be the principal driver for both MDA classes (11.98 and 14.52) and overall MDA (21.65), with dewpoint (19.67) in second place and temperature (11.6) a distant third. Wind direction and pressure help classify NO cases but reduce accuracy for YES cases, while wind speed is seen to have negligible influence. Hence, humidity is the most relied upon feature, alongside being the most frequent splitter (102.46).

Table 8.
Permutation-based measures and split-based measure of the Alor Setar model.
The summary analysis of the Vercelli random forest model is represented in Table 9. From the permutation-based measures, the YES outcomes rely on humidity, pressure, and wind direction, while the NO cases depend on humidity, dew point, temperature, and windspeed. Based on MDG, dewpoint, pressure, and wind direction are seen to have moderate to high scores. With comparable impact, each supply structure the model finds useful, as the split nodes effectively. So, humidity is once again seen to be the most dominant feature in the model, hence an indispensable predictor, with the highest overall MDA and MDG of 33.97 and 91.84, respectively.

Table 9.
Permutation-based measures and split-based measure of the Vercelli model.
From the MDA NO and YES columns in Table 10, the NO outcomes relay on temperature, humidity, dew point, pressure, and wind direction, the YES outcomes depend on humidity and wind direction, and the negative YES score of −5.04 in dewpoint is unreliable for YES predictions. With a MDG score of 44.98, the forest model is seen to structurally depend on the humidity predictor.

Table 10.
Permutation-based measures and split-based measure of the Williams model.
Table 11 is the feature importance summary of the temperate climate model, Ashburton. Pressure feature dominates the model, as it is a key driver for both MDA classes. Humidity is the second most balanced contributor to the model, as it is the only other predictor that helps in the identification of rain events (YES class), with a score of 3.09, and non-rain events (NO class), with a score of 9.08. Wind direction, windspeed, dewpoint, and temperature are valuable for predicting the NO class, but their negative values for the YES class implies that they harm/limit the recognition of Yes cases. The MDG mirrors the MDA ranking, as pressure is also structurally central to the forest.

Table 11.
Permutation-based measures and split-based measure of the Ashburton model.
3.3. Comparative Analysis
The evaluation process is carried out by recognising class imbalance in each dataset, which helps inform and contextualise the assessment metric. Class imbalance is a common classification problem in machine learning that has an adverse effect on model accuracy. It is common in most naturally occurring domains like weather, as with the next-day rainfall occurrence. In imbalanced datasets, models tend to perform well by predicting the majority class but struggle with the minority class, which is most times the focal class of the prediction. In all four datasets examined, the majority class is “No” (no rain), while the minority class is “Yes” (rain). Since the goal is to predict whether it will rain (the minority class), the traditional accuracy measure can be misleading. F1-score another important classification evaluation metric is also not applied, as it is influenced by the class distribution, hence not suitable for comparing models based on datasets with varying imbalance ratios.
To address this, the balanced accuracy metric offers a more accurate assessment of the model’s performance, as it accounts for the imbalance in class distribution. It is the average of the proportion of actual positive cases correctly identified as positive (True Positive Rate (TPR) or Sensitivity/Recall) and the proportion of actual negative cases correctly identified as negative (True Negative Rate (TNR) or Specificity/Selectivity).
Hence, this metric overcomes the bias that exists in the model due to the dichotomous imbalance in the dataset. It reduces the emphasis placed on the majority class by giving the minority class equal importance/weight, as the accuracies of both classes are evaluated. Thus, giving a full overview of how well the model can generalise to both majority and minority classes. This evaluation metric is important in this study, as predicting when it will not rain, accurately, is also useful to telecoms operators, farms, and event planners to mention but a few.
A review of Figure 6 reveals that using the logistic regression algorithm, all three temperate climate models outperformed the tropical climate model, Alor Setar, with the Williams logistic regression model having the highest balanced accuracy value at 78.9%.
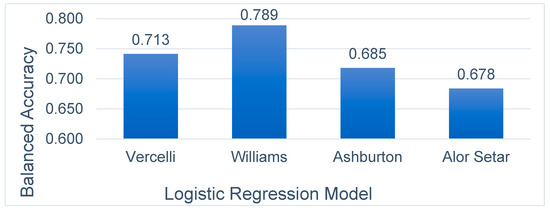
Figure 6.
Balanced accuracy metric of the 4 logistic regression prediction models for the next day rain forecast.
The plot in Figure 7 also supports the prediction models accuracies in Figure 6; thus, that random forest prediction models from Williams, Vercelli, and Ashburton, with respective accuracies of 77.7%, 72.4%, and 66%, all achieved better results than the tropical climate model, Alor Setar, with a balanced accuracy of 64.7%.
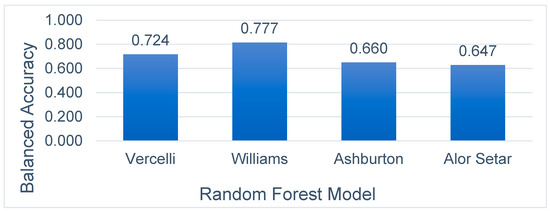
Figure 7.
Balanced accuracy metric of the 4 random forest prediction models for the next day rain forecast.
Area under the curve (AUC) [50] also referred to as the concordance (c) statistic, it measures the total area below a probability curve, ranging from 0 to 1 on both the x-axis and y-axis. It is a rank-based measure of the predictive power of a model, reflecting the probability that a model ranks a randomly chosen positive instance (Yes or 1) higher than a randomly chosen negative instance (No or 0). This can be mathematically expressed as follows:
where A refers to the score distribution for positive class instances, and B refers to the score distribution for negative class instances. The AUC is a critical metric for assessing model fit and comparing the performance of classification models independent of the decision threshold applied. It provides insight into the model’s ability to differentiate between outcomes, where a perfect AUC of 1 signifies flawless prediction, and an AUC of 0.5 indicates predictions no better than a random chance. At the same time, an AUC of 0 implies all predictions are incorrect. Most models yield an AUC between 0.5 and 1, with higher values reflecting better class discrimination. Thus, when comparing classification models, the one with the higher AUC is considered superior in performance.
Figure 8 illustrates the calculated AUROC curve for the four logistic regression next-day rainfall prediction models. It shows the AUC of all three temperate climate models to be higher than the AUC of the tropical climate model. As also seen, the Williams model has the highest AUC of 86%, followed by the Vercelli model at 77.7%, and the Ashburton model the lowest for the temperate models with an AUC value of 73.4%.
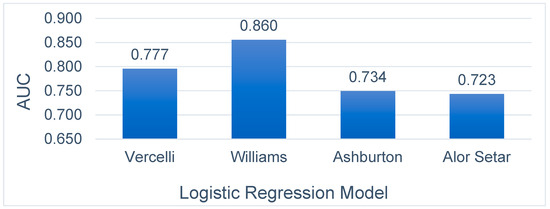
Figure 8.
Area under the ROC curve of the 4 logistic regression prediction models for the next-day rain forecast.
Figure 9 demonstrates the AUROC metric for the four random forest next-day rainfall prediction models. Again, all three temperate climate models outperform the tropical climate model in terms of AUC, with values of 85.2%, 78.3%, and 68.8%, for the Williams, Vercelli, and Ashburton models, respectively, compared to 68.6% for the tropical climate model.
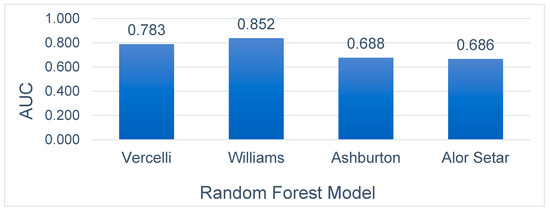
Figure 9.
Area under the ROC curve of the 4 random forest prediction models for the next-day rain forecast.
Comparative evaluation of models’ performance based on ML algorithms shows that the logistic regression models outperform the random forest models on both balanced accuracy and AUC for all locations, except the Vercelli location, where the random forest model outperforms the logistic regression model. This could be due to the inclusion and the high importance of humidity in the random forest model, which was not captured by logistic regression. The identification of the humidity variable as the key predictor of both rain and non-rain outcomes by the random forest model is due to the algorithm’s ability in capturing interactions and nonlinearities amongst predictors. The nonlinear and/or interactions of humidity with others, which appeared to be crucial in the tree-based splits, were captured.
4. Discussion
Rain happens when several conditions interact in the right way to allow precipitation to form and fall. This means that rainfall is not determined by a single variable/atmospheric parameter but instead depends on the combined influence of multiple atmospheric (and topographic) factors acting together. Thus, rainfall prediction is said to be multifactorial in nature, hence models must integrate many variables (not just one) to accurately predict rain. Understanding which variables and variable combinations matter most improves forecast skill, especially across different climates, as forecast errors often happen when one key factor/variable is missing/omitted or misjudged. Therefore, the multifactorial nature of rainfall prediction reflects the fact that rainfall results from the interplay of several meteorological variables, such as pressure, temperature, humidity, and wind, which must combine properly for precipitation/rain to occur.
Next, regarding the models’ importance analysis, a strong model concordance is observed on the main drivers in each climate, as both logistic and RF models identify the same broad patterns. Overall, the top-ranked predictors by both methods usually agree qualitatively, where it is humidity in Am, pressure in Cfb, and a combination of both in Csa and Cfa climates. Where they differ tends to involve nuances in class-specific importance or the identification of nonlinear interactions. For example, humidity was not significant/included in logistic model for Cfa but featured as the most importance predictor in the RF model, suggesting a nonlinear effect that the logistic model could not capture with a linear term. Also, conflicts, like humidity’s low importance in RF for Cfb despite significance in logistic, can be explained by the interplay between predictors rather than fundamentally different conclusions. This means the models are consistent that moisture matters in a humid climate and pressure matters in a cyclone-prone climate, but they partition the explanatory power slightly differently. Importantly, both models together give a fuller/comprehensive picture, where logistic highlights the independent contribution of each variable and their directional effect, while RF accounts for interactions, nonlinear impacts, and even class-specific contributions, which in some cases exposed subtleties, like dew point being mostly a “no-rain” indicator in some/all climates’ reviews/discussed.
Across all four climates, tropical-monsoon (Am), marine/oceanic (Cfb), hot-summer Mediterranean (Csa), and humid-subtropical (Cfa), humidity has an impact on the next day rain prediction outcomes in these climates, thus becoming the common criterion. Nevertheless, rain falls mainly when two key ingredients meet, which is ample moisture (universal prerequisite) and a mechanism that lifts or concentrates it. Alor Setar’s tropical monsoon climate (Köppen Am) is marked by consistently elevated temperatures above 23 °C year-round and distinct seasonal patterns dictated by southwest (onshore) and northeast (offshore) monsoon winds. The climate’s persistent boundary-layer humidity exceeding 80%, and high dew-point temperatures above 24 °C create conditions consistently near saturation. Rainfall predominantly occurs during the southwest monsoon, as moist maritime air from the Indian Ocean promotes convective storms. Conversely, the northeast monsoon from the South China Sea delivers dry continental air, inhibiting precipitation. Relative humidity stands out as the critical indicator, triggering rainfall once it surpasses a threshold that allows convection without requiring large-scale atmospheric disturbances. Hence, rather than dewpoint, which is an indicator of the moisture content in the atmosphere, or temperature, which is directly related to the formation of clouds, humidity is identified as the dominant predictor of rainfall, confirmed by both logistic regression and random forest models’ analyses. For effective forecasting in Alor Setar, focus should be primarily on the real-time monitoring of humidity, supplemented by temperature and dew point profiles to gauge storm intensity, while recognizing that detailed wind or pressure measurements offer minimal predictive advantage for tropical rain. This reflects the low variability in atmospheric pressure typical of the tropical climates. Also, the rainfall is mainly caused by localised convection rather than large-scale frontal systems driven by pressure changes. Therefore, pressure becomes less useful as a short-term predictive tool for tropical rain.
The three temperate climates rely on humidity and pressure to varying degrees, their unique Köppen classifications dictate distinct hierarchies. In temperate regions, pressure (lift mechanism) patterns can indicate atmospheric instability. A falling barometric reading (decreasing pressure) often indicates increasing instability and an approaching low-pressure system, suggesting a higher chance of rain or storms. Hence, it is a critical variable for predicting rainfall, as it plays a prominent role in driving large-scale weather systems like high- and low-pressure systems, weather fronts, and cyclones, significantly influencing weather patterns, including precipitation. For high- and low-pressure systems, the low-pressure system tends to pull in moist air, which enhances the likelihood of rain, while the high-pressure systems generally cause sinking air, which warms and dries out, leading to clear, dry conditions. Understanding which pressure system is dominant is a key mechanism for predicting rainfall in temperate climates. In temperate climates, weather fronts are significant rain sources, as the cold front brings colder, denser air that forces warm, moist air to rise, forming clouds and causing precipitation. The low-pressure systems (cyclones) often develop and deepen, leading to more organised and widespread rainfall, such as with mid-latitude cyclones.
The temperate oceanic climate (Cfb) is used to design the Ashburton model. Rainfall results primarily from synoptic-scale weather dynamics involving mid-latitude cyclones and associated frontal systems. These systems, guided by easterly and northeasterly winds, bring moisture-rich maritime air from the Pacific Ocean, leading to widespread and sustained rainfall events. Conversely, stable, high-pressure conditions introduce drier northwesterly to westerly wind flows, suppressing precipitation. Hence, barometric pressure emerges as the most reliable rainfall predictor, because it drives the weather systems that produce precipitation, where falling pressure signals incoming storms, and rising pressure indicates dry periods. Moisture variables, such as relative humidity and dew point, help refine predictions but function as secondary indicators, clarifying timing and intensity rather than initiating rain. Wind direction and speed further indicate storm characteristics, with easterly/northeasterly winds commonly associated with incoming moisture and active frontal passages. Forecasting practices in Ashburton emphasize monitoring pressure changes to anticipate rainfall, supported by humidity and wind observations, underscoring the dominance of synoptic dynamics in rainfall prediction for Cfb climates.
In the Williams model, drawn on the Mediterranean (Csa) climate, rainfall primarily occurs during cooler months when mid-latitude cyclones disrupt the typically dominant subtropical high-pressure systems, which otherwise create prolonged, dry summers. Winter precipitation depends on the simultaneous presence of dynamic triggers, such as migrating low-pressure systems and suitable thermodynamic conditions, including elevated humidity levels, and lower temperatures promote condensation essential for winter rain formation. Conversely, summer’s persistent high-pressure patterns suppress convection and precipitation despite occasional humidity spikes, and wind patterns significantly influence rainfall events; westerlies and southerlies transport moist oceanic air essential for winter rains, while calm or northeasterly winds reinforce dry conditions during summer. In general, rainfall in Mediterranean climates is typically associated with the passage of cold fronts linked to low-pressure systems from the polar jet stream that moved in, while in warmer seasons, rainfall is rare due to the dominance of high-pressure systems and dry conditions. Effective rainfall forecasting in Williams requires recognizing the intersection of dynamic (pressure changes, wind shifts) and thermodynamic thresholds (humidity, temperature), emphasizing the seasonal specificity of Mediterranean precipitation and the nuanced interplay between cyclonic systems and suitable atmospheric conditions.
The humid subtropical (Cfa) climate of Vercelli features rainfall governed by a combination of abundant moisture and dynamic atmospheric triggers, influenced both by tropical moisture influx and mid-latitude weather systems. Rain events commonly occur when humid, unstable air interacts dynamically with frontal systems or low-pressure disturbances, often resulting in thunderstorms and severe weather. High humidity followed by elevated dew points critically enhance convective potential, making moisture indispensable for significant precipitation events. Barometric pressure and wind direction provide dynamic context, where specific wind patterns signal either incoming moist tropical air favourable for rainfall or dry continental flows suppressing it. Temperature acts in a supportive capacity, with excessively hot conditions often corresponding with stable, dry air masses. Rainfall prediction models emphasize relative humidity as the leading predictive factor, asserting that adequate moisture combined with dynamic lifting mechanisms (pressure and wind shift) reliably forecasts rain events. Accurate rainfall predictions in Vercelli thus rely on simultaneously assessing moisture conditions, pressure trends, and wind patterns to capture the complex interplay between thermodynamic fuel and dynamic triggers inherent to humid subtropical climates.
The results show that despite relative similarities in topography, predicting rainfall in tropical climates is generally more complex than in temperate climates, especially regarding short-range rain forecasts. This is due to several key factors, namely convective rainfall, which dominates this climatic region. This more sporadic and less predictable rainfall type can develop quickly with less warning than the frontal systems standard in temperate climates. Another factor is the lack of well-defined weather systems, as tropical climate regions experience more distinct and smaller-scale weather patterns, making it harder to track and predict precipitation. In contrast, temperate climates are regions where rain is mainly associated with large, well-defined weather systems, like cold fronts or low-pressure systems, which move predictably over time. As a factor, the Intertropical Convergence Zone (ITCZ) is a large-scale phenomenon that strongly influences tropical climates. Despite the significant impact on weather patterns in the tropics, ITCZ is complex and challenging to model accurately, leading to more significant uncertainty in rain forecasts. Together, these factors make rainfall in tropical climate regions more chaotic and less predictable than temperate climate zones’ more structured frontal weather systems. Hence, there are factors beyond weather parameters that are unique to tropical climates that are instrumental in the occurrence of rainfall. Therefore, the non-capture of these factors in the prediction of rainfall or/and the use of prediction models based on a temperate climate that capture a different set of weather parameters as significant will always lead to a poor rainfall model prediction in the tropics.
For next-day rainfall forecasting across the four studied climates, begin with the variable that the models show is most often in short supply and, therefore, most predictive when it spikes or plunges. For the Alor Setar (Am) climate, attention shifts to synoptic flow, as humidity is nearly always saturated, so rainfall hinges on dynamic triggers, such as a reversal to moist onshore monsoon flow, which mostly guarantees widespread showers, while a return to easterlies signals a dry interlude. In moisture-rich Ashburton (Cfb), the barometer and wind sector provide the earliest warning, because moisture is seldom scarce; hence, once pressure tendency charts show a falling trend and the wind veers onshore, rain is likely even if temperatures stay mild. In Williams (Csa), the limiting factor is almost always moisture, so real-time humidity (or dew point) is the critical threshold variable, with pressure and wind used to fine-tune timing for the arriving fronts. Finally, the Vercelli (Cfa) region demands a trio (dew, humidity, pressure) of checks, led unequivocally by humidity. So, when surface trough or frontal zone (providing lift) aligns with ample moisture, boosting instability, the stage is set for explosive convection and potentially intense rains.
5. Conclusions
Rainfall forecasting is imperative for many sectors, including agriculture, telecommunications, and environmental agencies. It is essential for food production, flood prediction and mitigation, water resources management, and all activities in nature, especially to achieve the sustainable development goals (SDGs).
This study examined the relative ease of predicting rainfall events between tropical and temperate climates, highlighting the key atmospheric parameters influencing these predictions. To focus specifically on climatic effects, locations with similar topographies were carefully selected. Alor Setar in Malaysia represents the tropical climate, while Vercelli in Italy, Williams in the USA, and Ashburton in New Zealand were chosen to represent different subtypes of temperate climates. Predictor variables included daily measurements of atmospheric pressure, temperature, dewpoint, relative humidity, wind speed, and wind direction, with the outcome variable being the binary occurrence of rainfall the following day. Uniform modelling approaches and algorithms were consistently applied across all datasets to minimize geographical and methodological biases. Both linear (logistic regression) and nonlinear (random forest) algorithms were utilized to ensure that findings regarding prediction accuracy remained robust regardless of the chosen modelling technique.
Both binary logistic regression and random forest models were designed using four years of data (from 1 January 2012 to 31 December 2015) from each site. The two methodologies differ significantly in terms of interpretability and computational demands/complexity. Logistic regression affords complete transparency, its coefficient estimates directly quantify the influence of each predictor, the probability outputs are typically well calibrated, and both model training and inference incur minimal computational overhead. While random forest is adept at uncovering nonlinear feature interactions, its less transparent operations entail longer training and prediction times and complicate the elucidation/explanation of individual forecasts. Results showed that both algorithms can be modelled to predict next-day rainfall occurrence. In the next-day rainfall classification prediction, the models for the different climatic locations can identify important weather parameters for the prediction of next-day rainfall. Humidity appears to be a model favourite for all four climate zones, and pressure is seen as important for only temperate models. For Am, sustained humidity is the predominant predictor, with secondary support from the dewpoint. Cfb prioritizes pressure, but pressure gradients, wind direction, and humidity are key, reflecting maritime storm tracks. Humidity is crucial in Csa climates, which are centred on seasonal temperature, alongside seasonal pressure shifts, wind-driven moisture transport, and dewpoint that define wet/dry phases. Cfa emphasizes humidity thresholds and thermal instability with pressure, as dewpoint spreads and moisture-laden winds drive convective rainfall. While all parameters contribute, their relative importance shifts with climatic context. Thus, predictive models must prioritize these zone-specific dynamics to distinguish events from non-events.
Several evaluation metrics were applied to evaluate the models, and all models have balanced accuracy and AUC ROC scores above 60%. This indicates the occurrence of high recall and precision in the models. Also, the temperate climate models outperformed the tropical climate model on all evaluation metrics. Across the four meteorological stations evaluated, logistic regression demonstrated superior average performance in rain forecasting relative to the random forest classifier. When evaluated by balanced accuracy, which compensates for the inherent class imbalance between rain and non-rain observations, logistic regression attains an average score of approximately 0.716, whereas random forest achieves 0.702. Similarly, the area under the receiver operating characteristic curve (AUC) favours logistic regression (0.775) over random forest (0.752). However, station-specific analysis reveals notable heterogeneity. At Alor (Am) and Ashburton (Cfb) locations, characterised by tropical or maritime/oceanic climatic influences, the linear decision boundary imposed by logistic regression provides better generalisation to new data, indicating that random forest’s flexibility in modelling complex interactions does not yield additional predictive benefit in these environments. At Williams (Csa), by contrast, the predominant drivers of rainfall appear sufficiently strong and linear that logistic regression effectively captures nearly the entire predictive signal, leaving minimal incremental value for the ensemble-based model. Conversely, for Vercelli (Cfa), where complex/nonlinear interdependencies among meteorological covariates (such as humidity, atmospheric pressure, and temperature) govern/significantly influence precipitation processes, the random forest classifier yields/attains marginally higher discrimination (an uplift of 1.1 percentage points in balanced accuracy and 0.6 points in AUC). In this report, logistic regression served as the baseline rain-prediction model, owing to its robustness, efficiency, and ease of deployment. Nevertheless, for sites that consistently exhibit nonlinear meteorological dynamic (for example Vercelli), it is advisable to monitor random forest performance.
A key limitation of this paper’s findings is the use of a short data collection period (four years), which restricts the ability to compare trends or variations across multiple years. Furthermore, the identification of similar geographical topographical locations with varying climates was challenging.
Further research will focus on expanding the scope of rainfall forecasting from next-day predictions to short-range and medium-range forecasts across the four selected locations. This extension aims to analyse how prediction accuracy varies over different forecast horizons (short to medium range). The study will also involve a comparative evaluation of the predictive models used for each location, examining the stability and significance of their key input variables over time. By identifying the most influential atmospheric parameters at varying forecast intervals, the research will provide deeper insight into the temporal dynamics of rainfall prediction and guide the selection of robust models for different climatic contexts.
Author Contributions
O.E.: conceptualization, methodology, software, formal analysis, resources, data curation, writing—original draft preparation, visualization, investigation, validation, writing—reviewing and editing. D.N. and M.Z.S.: writing—reviewing and editing, supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Ethical review and approval were waived for this study due to L. maculatus not being classified as an endangered or protected species in China, and there is no requirement for permission to undertake experiments in China.
Data Availability Statement
Data generated or analysed during this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- IPCC. Global Warming of 1.5 °C: An IPCC Special Report; IPCC-Sr15: Geneva, Switzerland, 2018; Volume 2. [Google Scholar] [CrossRef]
- Arnell, N.W.; Lowe, J.A.; Challinor, A.J.; Osborn, T.J. Global and regional impacts of climate change at different levels of global temperature increase. Clim. Chang. 2019, 155, 377–391. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). IPCC: Climate Change 2021: The Physical Science Basis; Cambridge University Press (CUP): Cambridge, UK, 2021. [Google Scholar] [CrossRef]
- Mamalakis, A.; Randerson, J.T.; Yu, J.-Y.; Pritchard, M.S.; Magnusdottir, G.; Smyth, P.; Levine, P.A.; Yu, S.; Foufoula-Georgiou, E. Zonally contrasting shifts of the tropical rain belt in response to climate change. Nat. Clim. Change 2021, 11, 143–151. [Google Scholar] [CrossRef]
- Jayawardene, H.; Sonnadara, D.; Jayewardene, D. Trends of Rainfall in Sri Lanka over the Last Century. Sri Lankan J. Phys. 2005, 6, 7–17. [Google Scholar] [CrossRef]
- Smadi, M.M.; Zghoul, A. A Sudden Change In Rainfall Characteristics In Amman, Jordan During The Mid 1950s. Am. J. Environ. Sci. 2006, 2, 84–91. [Google Scholar] [CrossRef]
- Olatayo, T.O.; Taiwo, A.I. Statistical Modelling and Prediction of Rainfall Time Series Data. Glob. J. Comut. Sci. Technol. 2014, 14, 1–9. [Google Scholar]
- Wilson, L.; Manton, M.J.; Siems, S.T. Relationship between rainfall and weather regimes in south-eastern Queensland, Australia. Int. J. Climatol. 2013, 33, 979–991. [Google Scholar] [CrossRef]
- Shahid, S. Trends in extreme rainfall events of Bangladesh. Theor. Appl. Clim. 2011, 104, 489–499. [Google Scholar] [CrossRef]
- Su, B.D.; Jiang, T.; Jin, W.B. Recent trends in observed temperature and precipitation extremes in the Yangtze River basin, China. Theor. Appl. Clim. 2006, 83, 139–151. [Google Scholar] [CrossRef]
- Pour, S.H.; Harun, S.B.; Shahid, S. Genetic programming for the downscaling of extreme rainfall events on the east coast of peninsular Malaysia. Atmosphere 2014, 5, 914–936. [Google Scholar] [CrossRef]
- UCAR Center for Science Education. Climate Change: Regional Impacts; UCAR: Boulder, CO, USA, 2021. [Google Scholar]
- Slingo, J.; Palmer, T. Uncertainty in weather and climate prediction. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369. [Google Scholar] [CrossRef]
- Rotunno, R.; Snyder, C. A generalization of Lorenz’s model for the predictability of flows with many scales of motion. J. Atmos. Sci. 2008, 65, 1063–1076. [Google Scholar] [CrossRef]
- Stocker, T.F.; Qin, D.; Plattner, G.-K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. Climate Change 2013 the Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 9781107057999. [Google Scholar] [CrossRef]
- Powers, J.G.; Klemp, J.B.; Skamarock, W.C.; Davis, C.A.; Dudhia, J.; Gill, D.O.; Coen, J.L.; Gochis, D.J.; Ahmadov, R.; Peckham, S.E.; et al. The weather research and forecasting model: Overview, system efforts, and future directions. Bull. Am. Meteorol. Soc. 2017, 98, 1717–1737. [Google Scholar] [CrossRef]
- Solman, S.A. Regional climate modeling over south america: A review. Adv. Meteorol. 2013, 2013, 504357. [Google Scholar] [CrossRef]
- Mejía, S.N.; Villegas-Lituma, C.; Crespo, P.; Córdova, M.; Gualán, R.; Ochoa, J.; Guzmán, P.; Ballari, D.; Chávez, A.; Paz, S.M.; et al. Downscaling precipitation and temperature in the Andes: Applied methods and performance—A systematic review protocol. Environ. Évid. 2023, 12, 29. [Google Scholar] [CrossRef]
- Balamurugan, M.S.; Manojkumar, R. Study of short term rain forecasting using machine learning based approach. Wirel. Netw. 2021, 27, 5429–5434. [Google Scholar] [CrossRef]
- Helen, A.; Helen, A.A.; Bolanle, O.A.; Samuel, F.O. Comparative Analysis of Rainfall Prediction Models Using Neural Network and Fuzzy Logic. Int. J. Soft Comput. Eng. (IJSCE) 2016, 5, 4–7. [Google Scholar]
- Liyew, C.M.; Melese, H.A. Machine learning techniques to predict daily rainfall amount. J. Big Data 2021, 8, 153. [Google Scholar] [CrossRef]
- Pham, B.T.; Le, L.M.; Le, T.-T.; Bui, K.-T.T.; Le, V.M.; Ly, H.-B.; Prakash, I. Development of advanced artificial intelligence models for daily rainfall prediction. Atmos. Res. 2020, 237, 104845. [Google Scholar] [CrossRef]
- Kumarasiri, A.D.; Sonnadara, U.J. Performance of an artificial neural network on forecasting the daily occurrence and annual depth of rainfall at a tropical site. Hydrol. Process 2008, 22, 3535–3542. [Google Scholar] [CrossRef]
- Pham, Q.B.; Yang, T.C.; Kuo, C.M.; Tseng, H.W.; Yu, P.S. Combing random forest and least square support vector regression for improving extreme rainfall downscaling. Water 2019, 11, 451. [Google Scholar] [CrossRef]
- Ejike, O.; Ndzi, D.L.; Al-Hassani, A.H. Logistic Regression Based Next-Day Rain Prediction Model. In Proceedings of the International Conference on Communication and Information Technology, ICICT 2021, Basrah, Iraq, 5–6 June 2021; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2021; pp. 262–267. [Google Scholar] [CrossRef]
- Zainudin, S.; Jasim, D.S.; Bakar, A.A. Comparative analysis of data mining techniques for malaysian rainfall prediction. Int. J. Adv. Sci. Eng. Inf. Technol. 2016, 6, 1148–1153. [Google Scholar] [CrossRef]
- Manandhar, S.; Dev, S.; Lee, Y.H.; Meng, Y.S.; Winkler, S. A Data-Driven Approach for Accurate Rainfall Prediction. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9323–9330. [Google Scholar] [CrossRef]
- Appiah-Badu, N.K.A.; Missah, Y.M.; Amekudzi, L.K.; Ussiph, N.; Frimpong, T.; Ahene, E. Rainfall Prediction Using Machine Learning Algorithms for the Various Ecological Zones of Ghana. IEEE Access 2022, 10, 5069–5082. [Google Scholar] [CrossRef]
- Esteves, J.T.; de Souza Rolim, G.; Ferraudo, A.S. Rainfall prediction methodology with binary multilayer perceptron neural networks. Clim. Dyn. 2019, 52, 2319–2331. [Google Scholar] [CrossRef]
- Raval, M.; Sivashanmugam, P.; Pham, V.; Gohel, H.; Kaushik, A.; Wan, Y. Automated predictive analytics tool for rainfall forecasting. Sci. Rep. 2021, 11, 17704. [Google Scholar] [CrossRef]
- Sarasa-Cabezuelo, A. Prediction of Rainfall in Australia Using Machine Learning. Information 2022, 13, 163. [Google Scholar] [CrossRef]
- Chen, S.T.; Yu, P.S.; Tang, Y.H. Statistical downscaling of daily precipitation using support vector machines and multivariate analysis. J. Hydrol. 2010, 385, 13–22. [Google Scholar] [CrossRef]
- Yang, T.C.; Yu, P.S.; Wei, C.M.; Chen, S.T. Projection of climate change for daily precipitation: A case study in Shih-Men reservoir catchment in Taiwan. Hydrol. Process 2011, 25, 1342–1354. [Google Scholar] [CrossRef]
- Lwas, A.K.; Islam, M.R.; Habaebi, M.H.; Mandeep, S.J.; Ismail, A.F.; Zyoud, A. Effects of wind velocity on slant path rain-attenuation for satellite application in Malaysia. Acta Astronaut. 2015, 117, 402–407. [Google Scholar] [CrossRef]
- Ulaganathen, K.; Rahman, T.A.; Rahim, S.K.A.; Islam, R.M. Review of rain attenuation studies in tropical and equatorial regions in Malaysia: An overview. IEEE Antennas Propag. Mag. 2013, 55, 103–113. [Google Scholar] [CrossRef]
- Semire, F.A.; Mohd-Mokhtar, R.; Ismail, W.; Mohamad, N.; Mandeep, J.S. Modeling of rain attenuation and site diversity predictions for tropical regions. Ann. Geophys. 2015, 33, 321–331. [Google Scholar] [CrossRef]
- Olurotimi, E.O.; Ojo, J.S. Testing rainfall rate models for rain attenuation prediction purposes in tropical climate. In Proceedings of the 2014 31th URSI General Assembly and Scientific Symposium, URSI GASS, Bejing, China, 14–17 August 2014. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Keya, T.A.; Sreeramanan, S.; Siventhiran, S.; Maheswaran, S.; Selvan, S.; Fernandez, K.; An, L.J.; Leela, A.; Prahankumar, R.; Lokeshmaran, A.; et al. Flood Susceptibility Mapping for Kedah State, Malaysia: Geographics Information System-Based Machine Learning Approach. Med. J. Dr. D. Y. Patil. Vidyapeeth 2024, 17, 990–1003. [Google Scholar] [CrossRef]
- De Luca, D.A.; Lasagna, M.; Debernardi, L. Hydrogeology of the western Po plain (Piedmont, NW Italy). J. Maps 2020, 16. [Google Scholar] [CrossRef]
- Conservation Biology Institute. Maps|Data Basin: Custom Map 90 m DEM for California, USA. Available online: https://databasin.org/maps/new/#datasets=78ac54fabd594db5a39f6629514752c0 (accessed on 31 July 2025).
- Land Information New Zealand. Canterbury, New Zealand 2018–2019 Digital Elevation Model. Available online: https://data.linz.govt.nz/layer/104931-canterbury-lidar-1m-dem-2018-2019/ (accessed on 31 July 2025).
- Visual Crossing Corporation. Visual Crossing Weather. Available online: https://www.visualcrossing.com/ (accessed on 31 July 2025).
- Sudha, M.; Balasubramanian, V. Identifying effective features and classifiers for short term rainfall forecast using rough sets maximum frequency weighted feature reduction technique. J. Comput. Inf. Technol. 2016, 24, 181–194. [Google Scholar] [CrossRef]
- Hamill, T.M.; Whitaker, J.S.; Wei, X. Ensemble reforecasting: Improving medium-range forecast skill using retrospective forecasts. Mon. Weather. Rev. 2004, 132, 1434–1447. [Google Scholar] [CrossRef]
- Wilks, D.S.; Hamill, T.M. Comparison of ensemble-MOS methods using GFS reforecasts. Mon. Weather. Rev. 2007, 135, 2379–2390. [Google Scholar] [CrossRef]
- Cheung, C.C.; Hart, A.M.; Peart, M.R. Projection of future rainfall in Hong Kong using logistic regression and generalized linear model. In Proceedings of the 5th International Workshop on Climate Informatics, Boulder, CO, USA, 24–25 September 2015; pp. 24–25. [Google Scholar]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Automat Contr. 1974. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).