Resolving the Faint Young Sun Paradox and Climate Extremes: A Unified Thermodynamic Closure Theory
Abstract
1. Introduction
2. Methodology
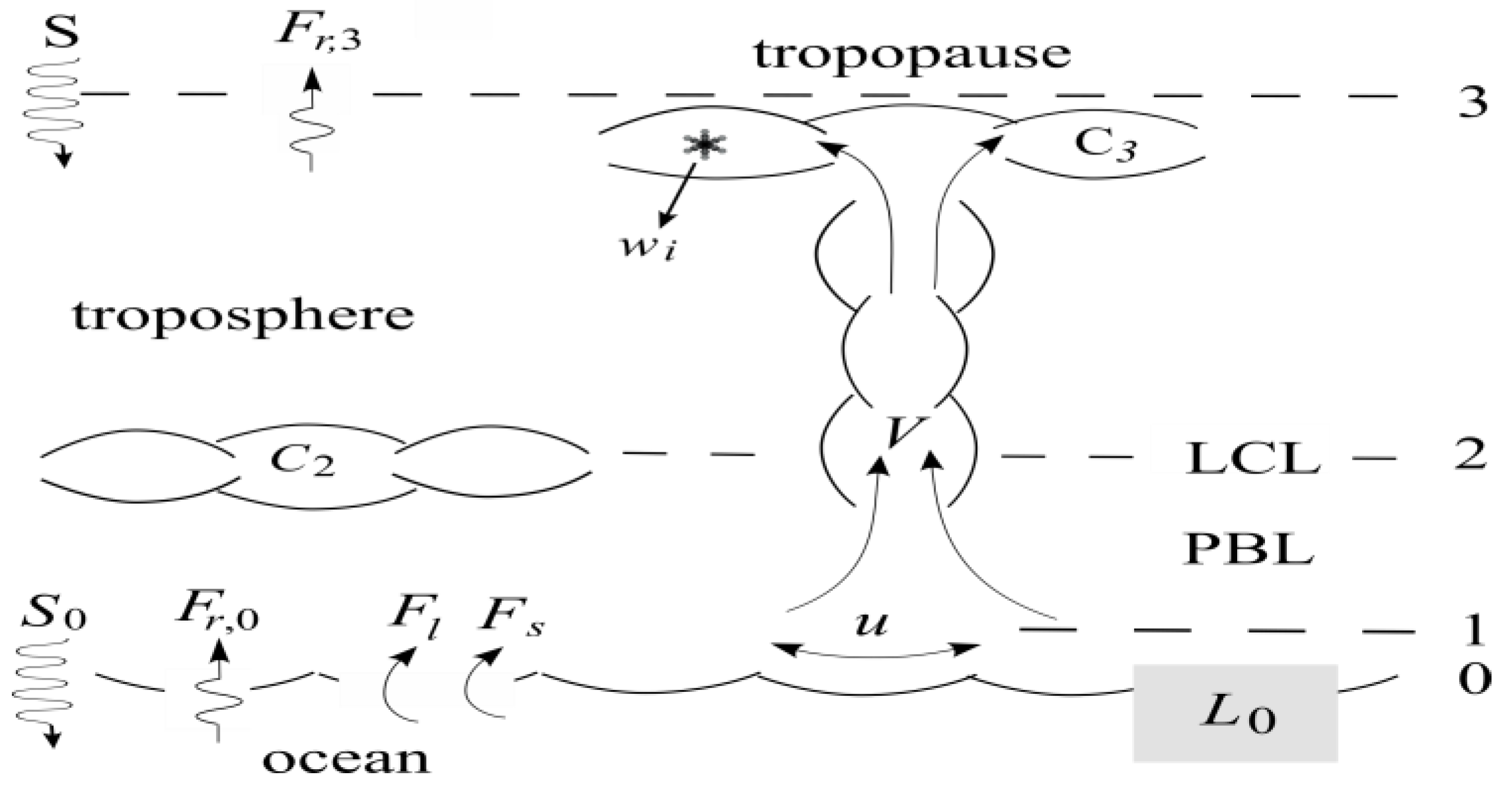
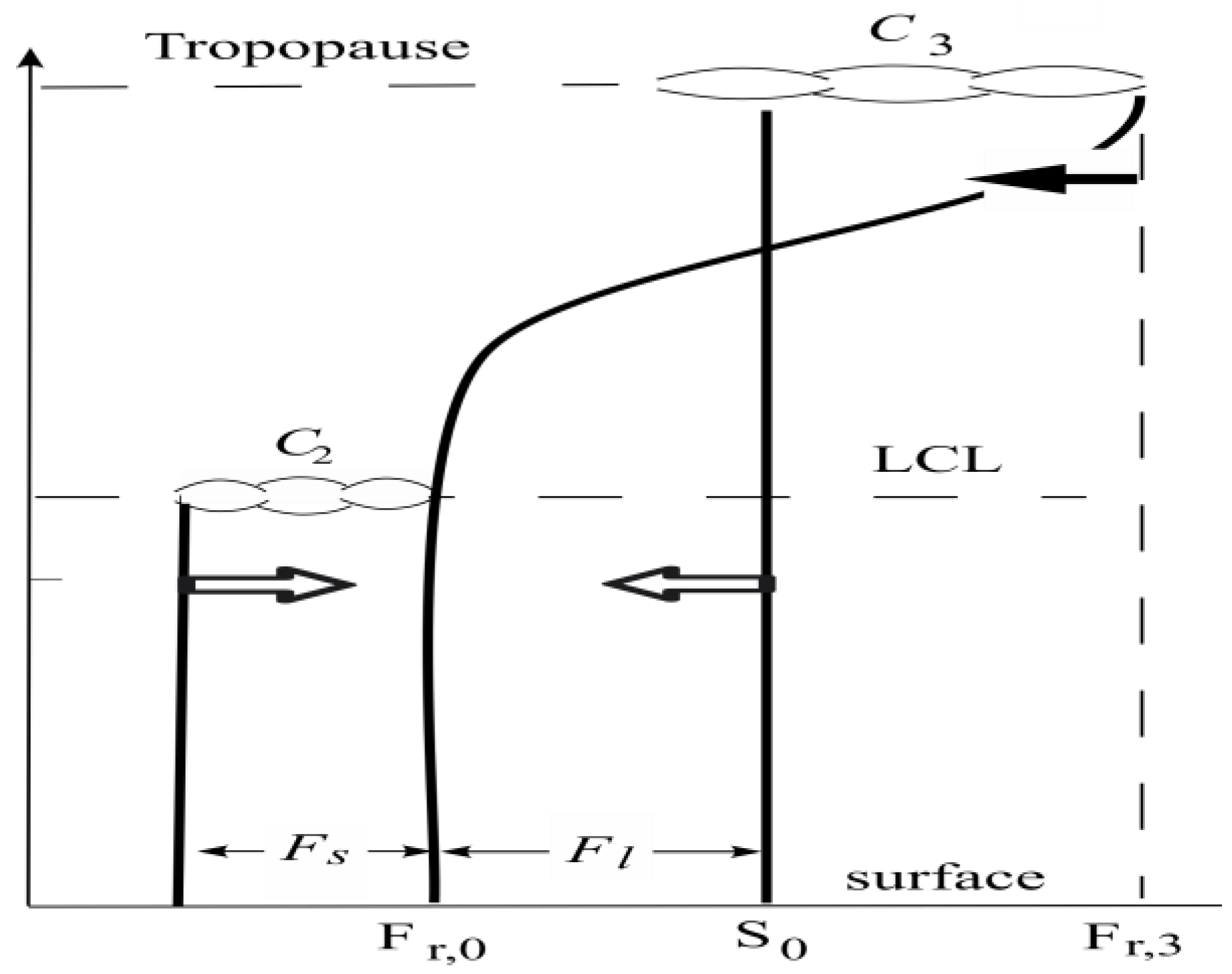
2.1. Physical Configuration
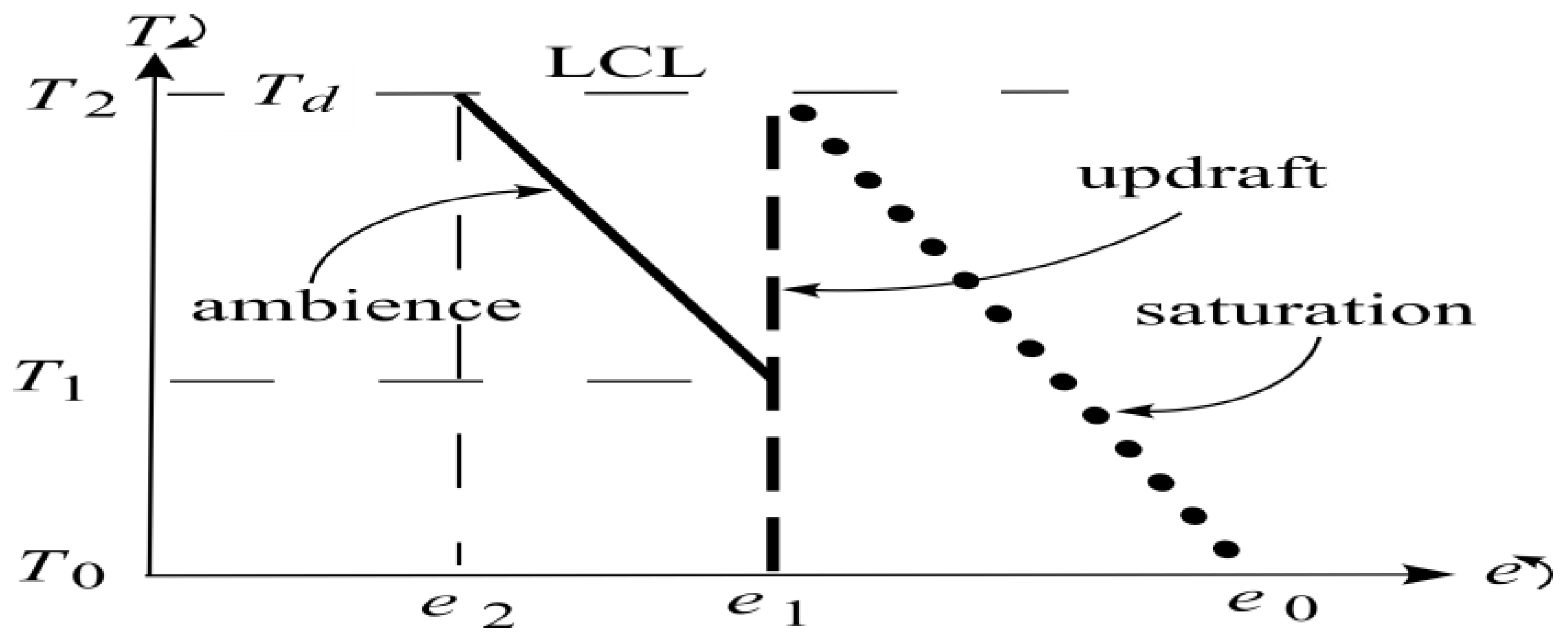
2.2. Thermal Template
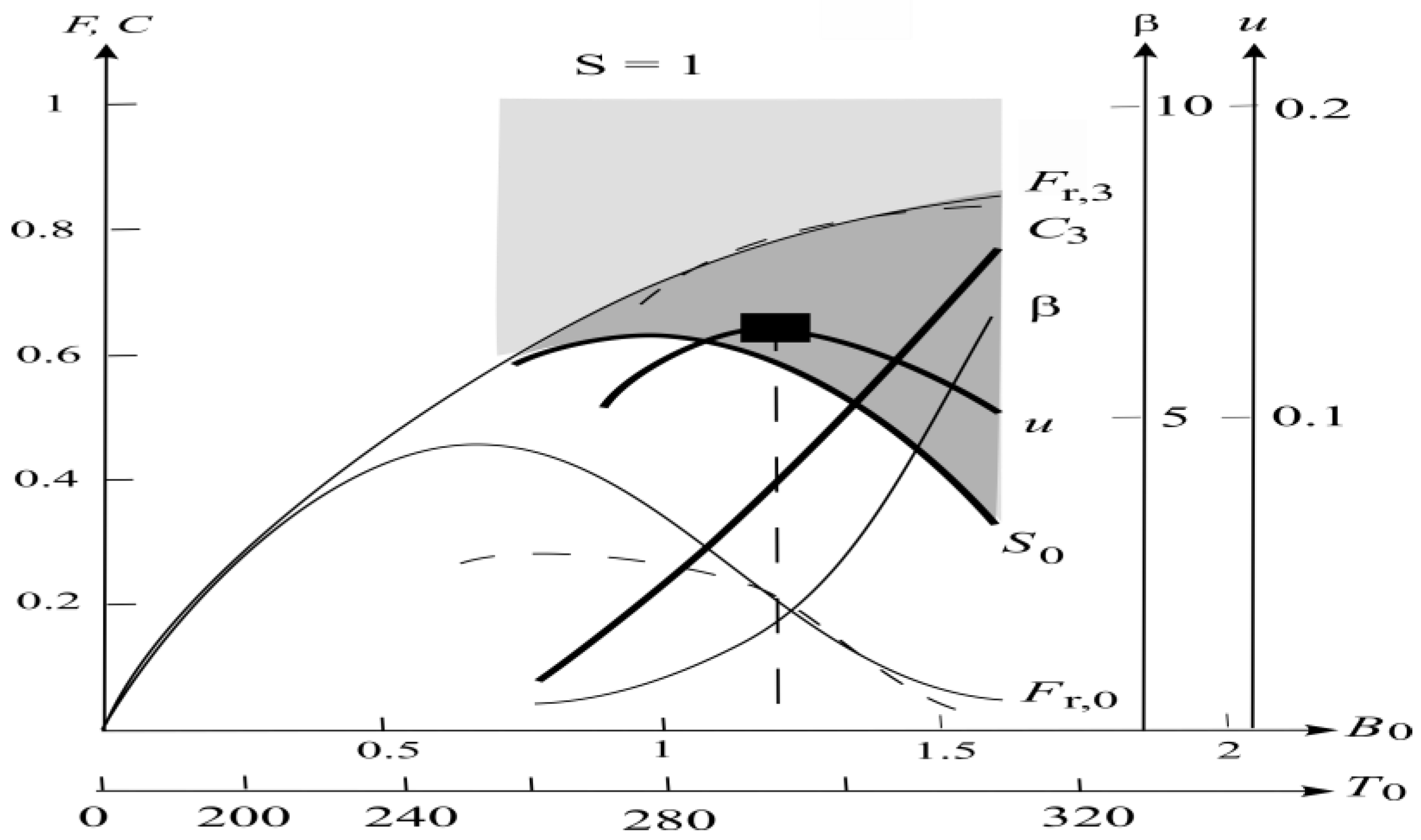
2.3. Heat Balances
2.4. Turbulent Wind
3. Results
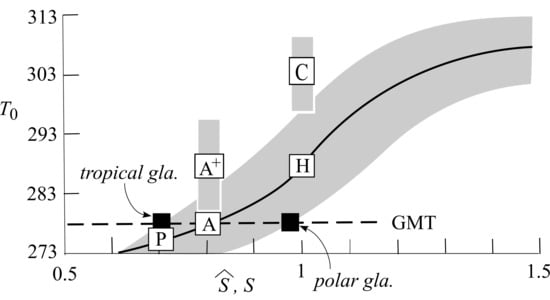
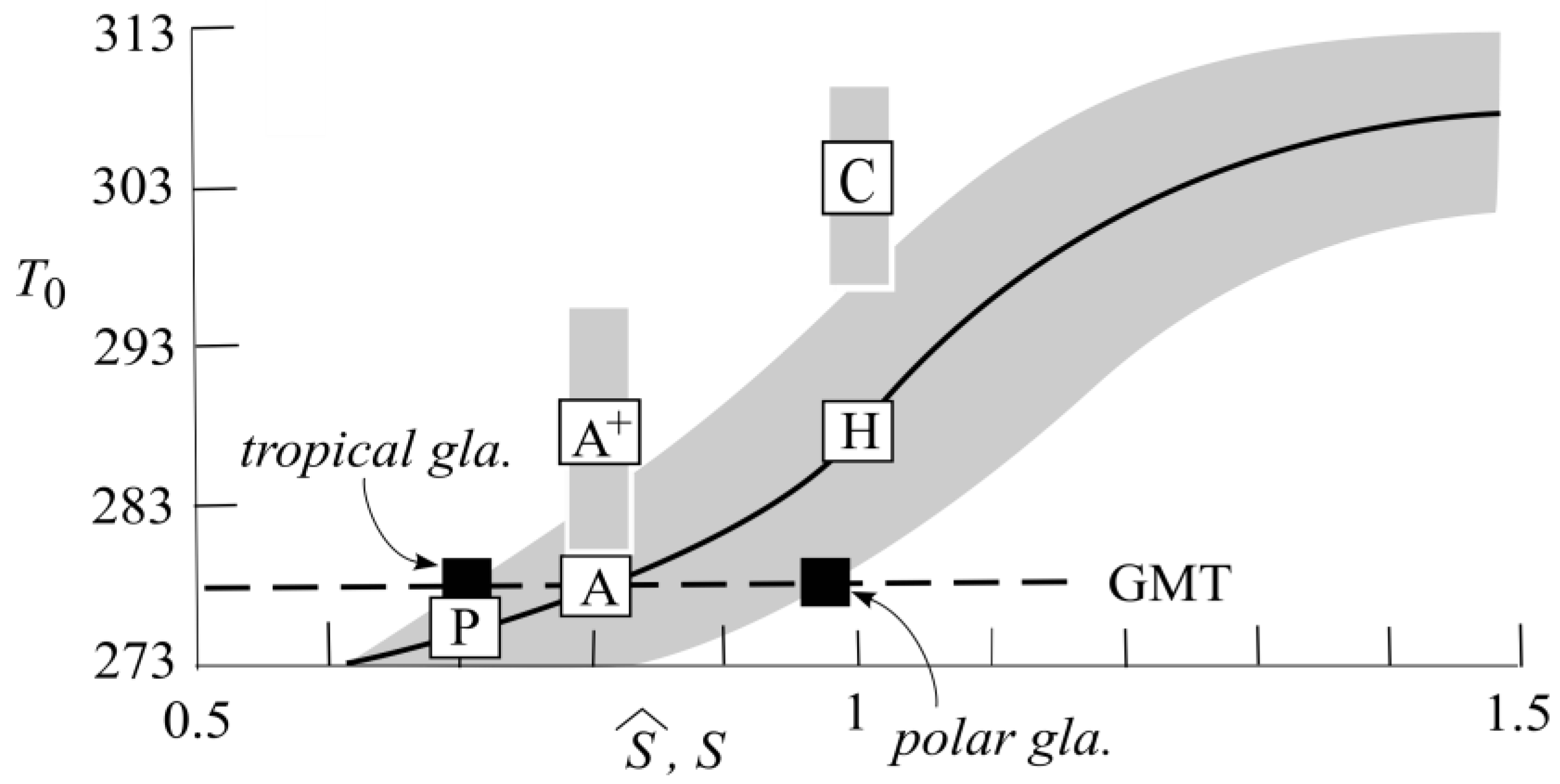
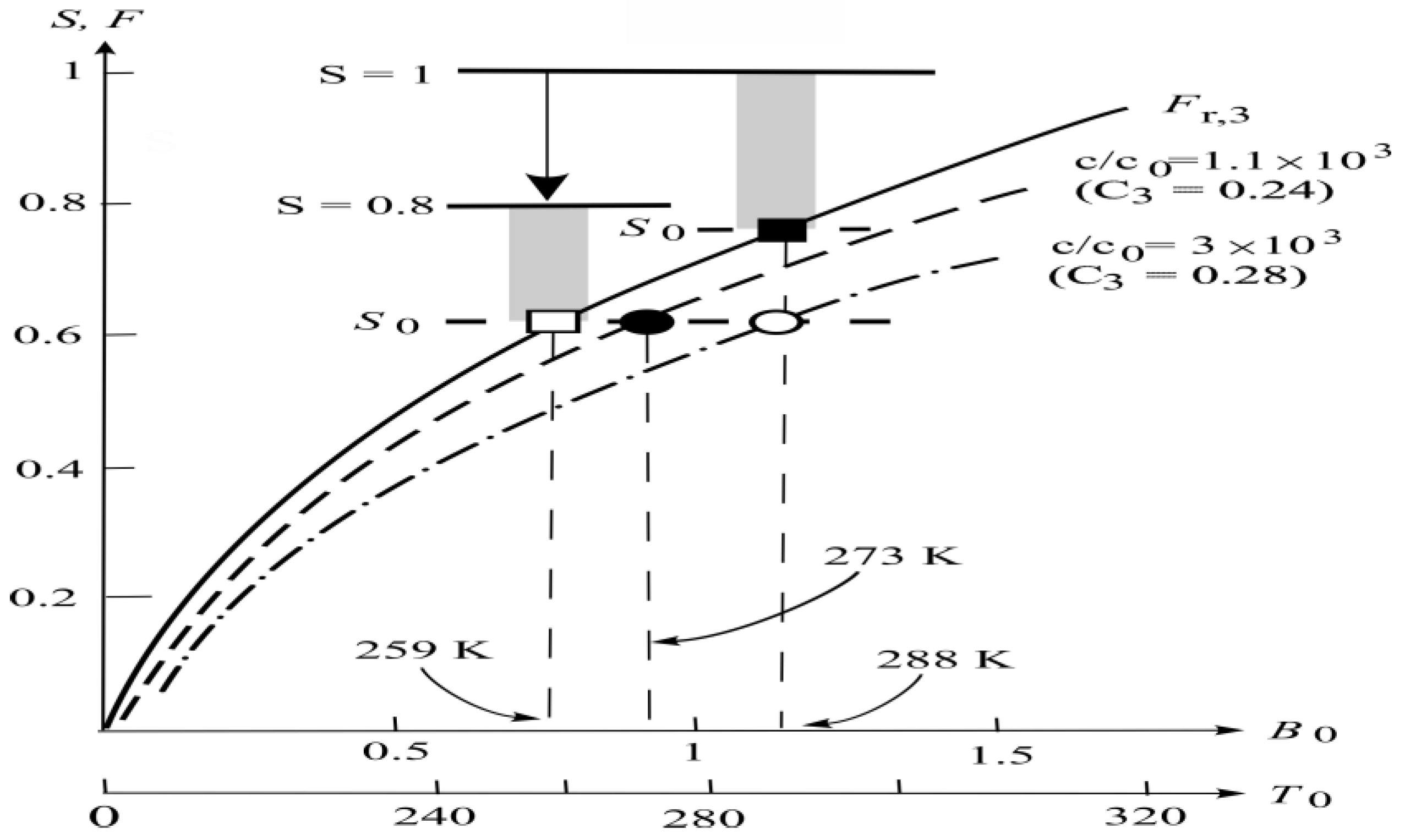
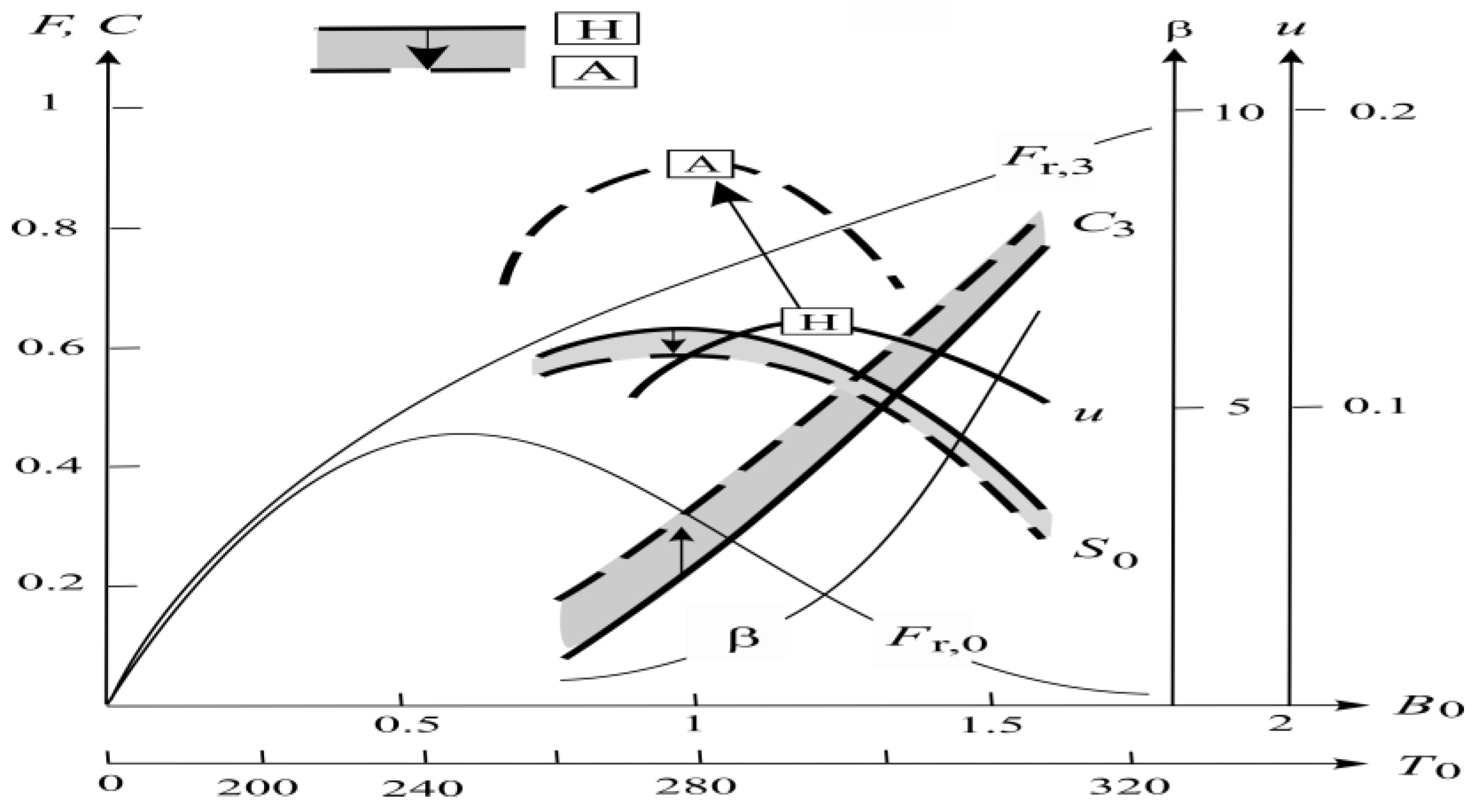
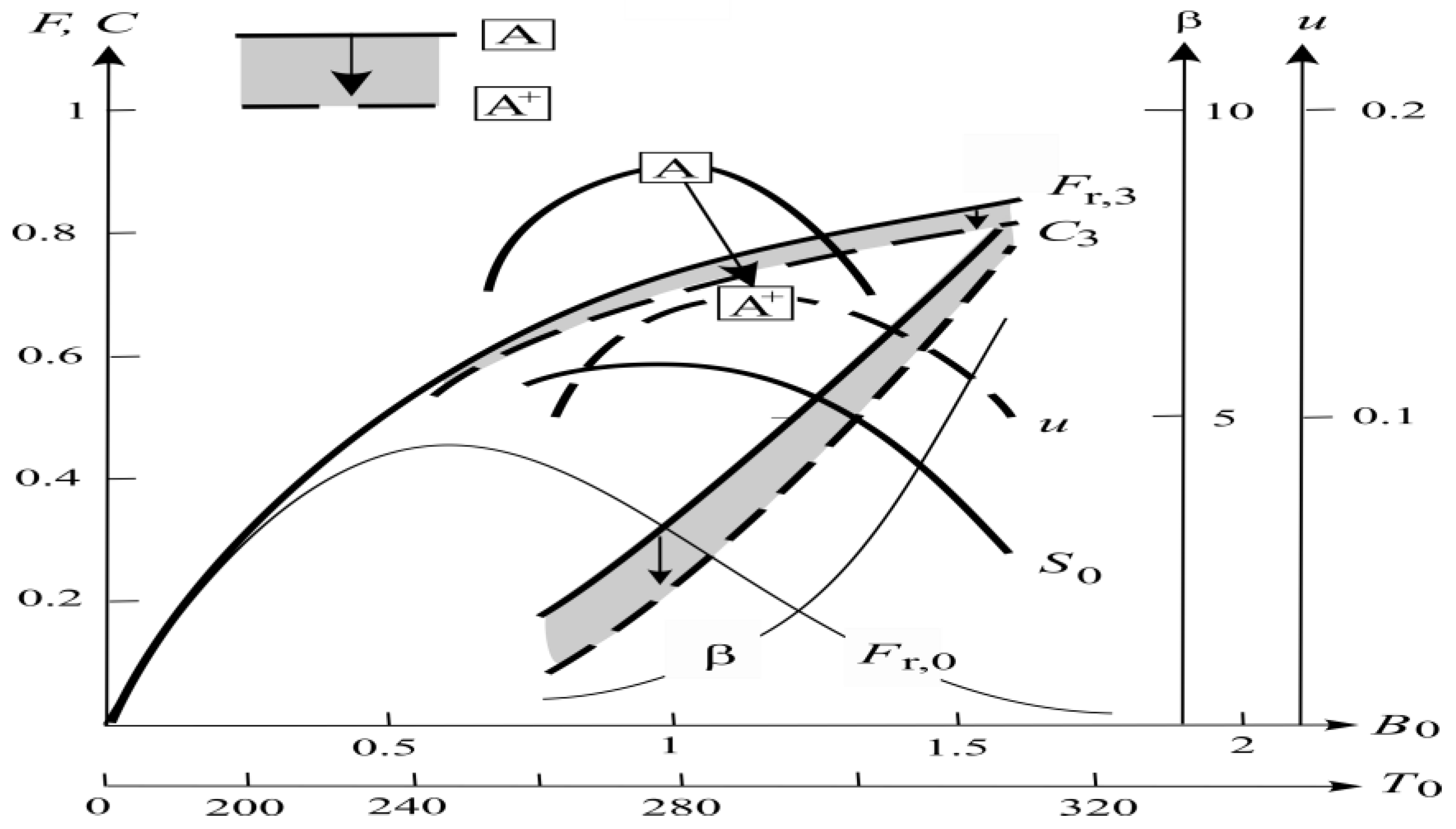
3.1. FYSP
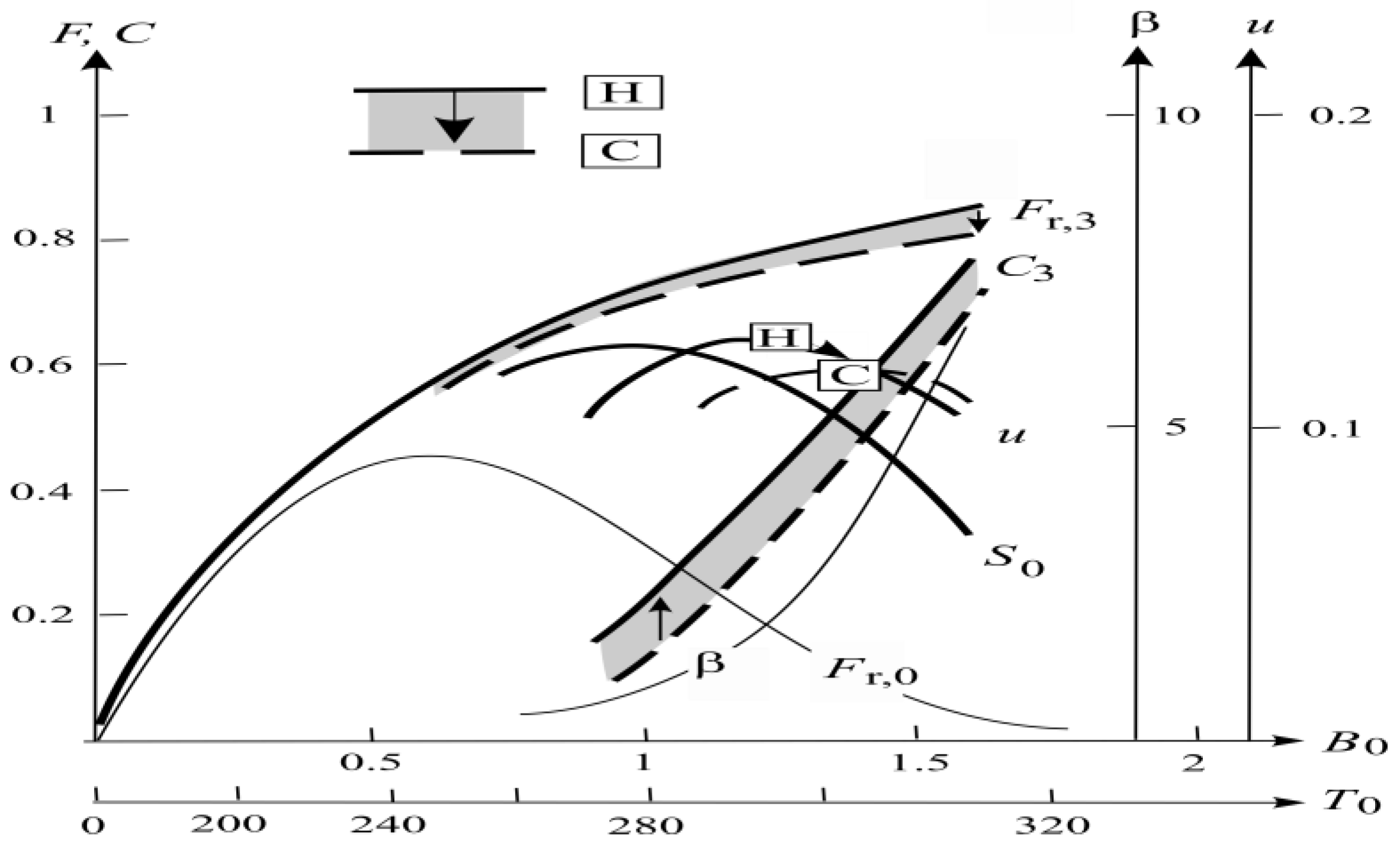
3.2. Warm Extreme
3.3. Cold Extreme
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Symbols
| A | Archean climate |
| A+ | Archean climate with high pCO2 |
| b | SW absorption |
| B0 | Surface blackbody radiance |
| c | pCO2 |
| Present pCO2 | |
| Specific heat of surface air (=103 J kg−1K−1) | |
| Cambrian/Cretaceous climate | |
| Drag coefficient (=10−3) | |
| Low-cloud cover | |
| High-cloud cover | |
| e | Water vapor pressure |
| Saturated vapor pressure | |
| Saturated vapor pressure at freezing point (=6.11 mb) | |
| Saturated moist static energy | |
| Sensible heat flux | |
| Latent heat flux | |
| Surface LW flux | |
| Tropopause LW flux | |
| H | Holocene climate |
| Latent heat of evaporation (=2.26 × 106 J kg−1) | |
| Tropical land area | |
| Precambrian climate with tropical supercontinent | |
| pCO2 | Partial pressure of atmospheric CO2 |
| Saturated specific humidity | |
| Cloud reflectance (=0.5) | |
| Land reflectance | |
| Gas constant of water vapor () | |
| Present solar constant ( | |
| Differential solar irradiance () | |
| S | Solar constant |
| Solar forcing | |
| Absorbed SW flux | |
| Temperature | |
| Dew point | |
| Freezing point | |
| Differential SST | |
| Scale of () | |
| Surface relative humidity () | |
| Surface turbulent wind | |
| [ | Scale of ( |
| Updraft volume flux | |
| Settling velocity of ice crystals () | |
| Air-sea exchange coefficient | |
| Scale of () | |
| Saturated inverse Bowen ratio | |
| Bowen constant ( | |
| Dry–adiabatic lapse rate ( | |
| Moist–adiabatic lapse rate | |
| Surface air density ( | |
| Ice density |
References
- Blake, R.E.; Chang, S.J.; Lapland, A. Phosphate oxygen isotopic evidence for a temperate and biologically active Archaean ocean. Nature 2010, 464, 1029–1032. [Google Scholar] [CrossRef] [PubMed]
- Kasting, J.F. Faint young Sun redux. Nature 2010, 464, 687–689. [Google Scholar] [CrossRef]
- Goldblatt, C.; Zahnle, K.J. Clouds and the faint young Sun paradox. Clim. Past 2011, 7, 203–220. [Google Scholar] [CrossRef]
- Ozawa, H.; Ohmura, A.; Lorenz, R.D.; Pujol, T. The second law of thermodynamics and the global climate system: A review of the maximum entropy production principle. Rev. Geophys. 2003, 41, 10182003. [Google Scholar] [CrossRef]
- Kleidon, A. Non-equilibrium thermodynamics and maximum entropy production in the Earth system: Applications and implications. Naturwissenschaften 2009, 96, 653–677. [Google Scholar] [CrossRef] [PubMed]
- Paltridge, G. Global dynamics and climate-a system of minimum entropy exchange. Q. J. R. Meteorol. Soc. 1975, 101, 475–484. [Google Scholar] [CrossRef]
- Dewar, R.C. Maximum entropy production and the fluctuation theorem. J. Phys. A Math. Gen. 2005, 38, L371–L381. [Google Scholar] [CrossRef]
- Ou, H.W. Thermohaline circulation: A missing equation and its climate change implica-tions. Clim. Dyn. 2018, 50, 641–653. [Google Scholar] [CrossRef]
- Evans, D.J.; Searle, D.J. The fluctuation theorem. Adv. Phys. 2002, 51, 1529. [Google Scholar] [CrossRef]
- Wang, G.M.; Sevick, E.M.; Mittag, E.; Searles, D.J.; Evans, D.J. Experimental demonstration of violations of the Second Law of Thermodynamics for small systems and short time scales. Phys. Rev. Lett. 2002, 89, 050601/1–050601/4. [Google Scholar] [CrossRef]
- Hogg, A.M.; Gayen, B. Ocean gyres driven by surface buoyancy forcing. Geophys. Res. Lett. 2020, 47, e2020GL088539. [Google Scholar] [CrossRef]
- Liu, T.; Ou, H.W.; Liu, X.; Chen, D. On the role of eddy mixing in the subtropical ocean circulation. Front. Mar. Sci. 2022, 9, 832992. [Google Scholar] [CrossRef]
- Ou, H.W. Meridional thermal field of a coupled ocean-atmosphere system: A conceptual model. Tellus 2006, 58A, 404–415. [Google Scholar] [CrossRef]
- Colin de Verdière, A. Buoyancy driven planetary flows. J. Mar. Res. 1988, 46, 215–265. [Google Scholar] [CrossRef]
- Ou, H.W. Possible bounds on the earth’s surface temperature: From the perspective of a conceptual global-mean model. J. Clim. 2001, 14, 2976–2988. [Google Scholar] [CrossRef]
- Lorenz, E.N. Generation of available potential energy and the intensity of the general circulation. In Climate Dynamics; Pfeffer, R.C., Ed.; Pergamon Press: Oxford, UK, 1960; pp. 86–92. [Google Scholar] [CrossRef]
- Kleidon, A. Working at the limit: A review of thermodynamics and optimality of the Earth system. Earth Syst. Dyn. 2023, 14, 861–896. [Google Scholar] [CrossRef]
- Feulner, G. The faint young Sun problem. Rev. Geophys. 2012, 50, RG2006. [Google Scholar] [CrossRef]
- Webster, P.J. The role of hydrological processes in ocean-atmosphere interactions. Rev. Geophys. 1994, 32, 427–476. [Google Scholar] [CrossRef]
- Ou, H.W. Hemispheric symmetry of planetary albedo: A corollary of nonequilibrium thermodynamics. Atmos 2023, 14, 1243. [Google Scholar] [CrossRef]
- Hartmann, D.L. Global Physical Climatology; Academic Press: New York, NY, USA, 1994; p. 411. [Google Scholar]
- Barron, E.J.; Sloan, J.L., II; Harrison, C.G. Potential significance of land-sea distribution and surface albedo variations as a climatic forcing factor: 180 m.y. to the present. Palaeogeogr. Palaeoclimatol. Palaeoecol. 1980, 30, 17–40. [Google Scholar] [CrossRef]
- Manabe, S.; Strickler, R.F. Thermal equilibrium of the atmosphere with a convective adjustment. J. Atm. Sci. 1964, 21, 361–385. [Google Scholar] [CrossRef]
- Ou, H.W. Hydrological cycle and ocean stratification in a coupled climate system: A theoretical study. Tellus A Dyn. Meteorol. Oceanogr. 2007, 59, 683–694. [Google Scholar] [CrossRef][Green Version]
- Pierrehumbert, R.T. Thermostats, radiator fins, and the local runaway greenhouse. J. Atmos. Sci. 1995, 52, 1784–1806. [Google Scholar] [CrossRef]
- Hartmann, D.L.; Michelsen, M.L. Large-scale effects on the regulation of tropical sea surface temperature. J. Clim. 1993, 6, 2049–2062. [Google Scholar] [CrossRef]
- Ramanathan, V. The role of earth radiation budget studies in climate and general circulation research. J. Geophys. Res. Atmos 1987, 92, 4075–4095. [Google Scholar] [CrossRef]
- Hartmann, D.L.; Doelling, D. On the net radiative effectiveness of clouds. J. Geophys. Res. Atmos 1991, 96, 869–891. [Google Scholar] [CrossRef]
- Borovikov, A.M.; Gaivoronskii, I.I.; Zak, E.G.; Kostarev, V.V.; Mazin, I.P.; Minervin, V.E.; Khrgian AK, S.M. Cloud Physics (Translated from Russian); Israel Program for Scientific Translations Ltd.: Jerusalem, Israel, 1963; p. 392. [Google Scholar]
- Donohoe, A.; Battisti, D.S. Atmospheric and surface contributions to planetary albedo. J. Clim. 2011, 24, 4402–4418. [Google Scholar] [CrossRef]
- Rosing, M.T.; Bird, D.K.; Sleep, N.H.; Bjerrum, C.J. No climate paradox under the faint early Sun. Nature 2010, 464, 744–747. [Google Scholar] [CrossRef] [PubMed]
- Myhre, G.; Highwood, E.J.; Shine, K.P.; Stordal, F. New estimates of radiative forcing due to well mixed greenhouse gases. Geophys. Res. Lett. 1998, 25, 2715–2718. [Google Scholar] [CrossRef]
- Sheldon, N.D. Precambrian paleosols and atmospheric CO2 levels. Precambrian Res. 2006, 147, 148–155. [Google Scholar] [CrossRef]
- NASA (n.d.) Planetary Fact Sheet—Metric. NASA Goddard Space Flight Center, Solar System Exploration Data Services. Available online: https://nssdc.gsfc.nasa.gov/planetary/factsheet/ (accessed on 18 April 2025).
- Sackmann, I.; Boothroyd, A.I.; Kraemer, K.E. Our sun III, Present and future. Astrophys. J. 1993, 418, 457. [Google Scholar] [CrossRef]
- Berner, R.A.; Kothavala, Z. GEOCARB III: A revised model of atmospheric CO2 over Phanerozoic time. Am. J. Sci. 2001, 301, 182–204. [Google Scholar] [CrossRef]
- Mills, B.J.; Krause, A.J.; Scotese, C.R.; Hill, D.J.; Shields, G.A.; Lenton, T.M. Modelling the long-term carbon cycle, atmospheric CO2, and Earth surface temperature from late Neoproterozoic to present day. Gondwana Res. 2019, 67, 172–186. [Google Scholar] [CrossRef]
- Hansen, J.E. A slippery slope: How much global warming constitutes “dangerous anthropogenic interference”? Clim. Chang. 2005, 68, 269–279. [Google Scholar] [CrossRef]
- Meehl, G.A.; Senior, C.A.; Eyring, V.; Flato, G.; Lamarque, J.F.; Stouffer, R.J.; Taylor, K.E.; Schlund, M. Context for interpreting equilibrium climate sensitivity and transient climate response from the CMIP6 Earth system models. Sci. Adv. 2020, 6, eaba1981. [Google Scholar] [CrossRef] [PubMed]
- Barron, E.J. A warm, equable Cretaceous: The nature of the problem. Earth-Sci. Rev. 1983, 19, 305–338. [Google Scholar] [CrossRef]
- Laskar, J.; Robutel, P. The chaotic obliquity of the planets. Nature 1993, 361, 608–612. [Google Scholar] [CrossRef]
- Ou, H.W. Tropical Glaciation and Glacio-Epochs: Their Tectonic Origin in Paleogeography. Climate 2025, 13, 9. [Google Scholar] [CrossRef]
- Hearing, T.W.; Harvey, T.H.; Williams, M.; Leng, M.J.; Lamb, A.L.; Wilby, P.R.; Gabbott, S.E.; Pohl, A.; Donnadieu, Y. An early Cambrian greenhouse climate. Sci. Adv. 2018, 5, eaar5690. [Google Scholar] [CrossRef]
- Barron, E.J.; Peterson, W.H.; Pollard, D.; Thompson, S. Past climate and the role of ocean heat transport: Model simulations for the Cretaceous. Paleoceanography 1993, 8, 785–798. [Google Scholar] [CrossRef]
- Eyles, N. Glacio-epochs and the supercontinent cycle after∼ 3.0 Ga: Tectonic boundary conditions for glaciation. Palaeogeogr. Palaeoclim. Palaeoecol. 2008, 258, 89–129. [Google Scholar] [CrossRef]
- Bahcall, J.N.; Pinsonneault, M.H.; Basu, S. Solar models: Current epoch and time dependences, neutrinos, and helioseismological properties. Astrophys. J. 2001, 10, 990. [Google Scholar] [CrossRef]
- Haberle, R.M.; McKay, C.P.; Schaeffer, J.; Cabrol, N.A.; Grin, E.A.; Zent, A.P.; Quinn, R. On the possibility of liquid water on present-day Mars. J. Geophys. Res. Planets 2001, 106, 23317–23326. [Google Scholar] [CrossRef]
- Hansen, J.; Ruedy, R.; Lacis, A.; Russell, G.; Sato, M.; Lerner, J.; Rind, D.; Stone, P. Wonderland climate model. J. Geophys. Res. Atmos. 1997, 102, 6823–6830. [Google Scholar] [CrossRef]
- Schmidt, G.A.; Kelley, M.; Nazarenko, L.; Ruedy, R.; Russell, G.L.; Aleinov, I.; Bauer, M.; Bauer, S.E.; Bhat, M.K.; Bleck, R.; et al. Configuration and assessment of the GISS ModelE2 contributions to the CMIP5 archive. JAMES 2014, 6, 141–184. [Google Scholar] [CrossRef]
- Webb, M.J.; Andrews, T.; Bodas-Salcedo, A.; Bony, S.; Bretherton, C.S.; Chadwick, R.; Chepfer, H.; Douville, H.; Good, P.; Kay, J.E.; et al. The cloud feedback model intercomparison project (CFMIP) contribution to CMIP6. Geosci. Model Dev. 2017, 10, 359–384. [Google Scholar] [CrossRef]
- Charnay, B.; Wolf, E.T.; Marty, B.; Forget, F. Is the faint young Sun problem for Earth solved? Space Sci. Rev. 2020, 216, 90. [Google Scholar] [CrossRef]
- Lindzen, R.S.; Chou, M.-D.; Hou, A.Y. Does the Earth have an adaptive infrared iris? Bull. Am. Meteorol. Soc. 2001, 82, 417–432. [Google Scholar] [CrossRef]
- Ito, M.; Masunaga, H. Process-level assessment of the Iris effect over tropical oceans. Geophys. Res. Lett. 2022, 49, e2022GL097997. [Google Scholar] [CrossRef]
- Berner, R.A.; Caldeira, K. The need for mass balance and feedback in the geochemical carbon cycle. GeoScienceWorld 1997, 25, 955–956. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, H.-W. Resolving the Faint Young Sun Paradox and Climate Extremes: A Unified Thermodynamic Closure Theory. Climate 2025, 13, 116. https://doi.org/10.3390/cli13060116
Ou H-W. Resolving the Faint Young Sun Paradox and Climate Extremes: A Unified Thermodynamic Closure Theory. Climate. 2025; 13(6):116. https://doi.org/10.3390/cli13060116
Chicago/Turabian StyleOu, Hsien-Wang. 2025. "Resolving the Faint Young Sun Paradox and Climate Extremes: A Unified Thermodynamic Closure Theory" Climate 13, no. 6: 116. https://doi.org/10.3390/cli13060116
APA StyleOu, H.-W. (2025). Resolving the Faint Young Sun Paradox and Climate Extremes: A Unified Thermodynamic Closure Theory. Climate, 13(6), 116. https://doi.org/10.3390/cli13060116