1. Introduction
The climate is a complex system, and its dynamical behaviour is one of the most challenging to determine. The standard method to approach the study of climate dynamics involves the development and application of so-called Global Climate Models (GCMs) which are complex models that take into consideration individual climate subsystems and their interactions through fundamental equations and parameterizations for processes occurring below the grid scale [
1,
2,
3].
Their application enables a quite accurate reconstruction of the climate of the recent past. Moreover, with the support of attribution studies, it is possible to understand the causes of its changes and to derive scenarios for the coming decades under the influence of external forcings. However, GCMs still have a limited resolution and show serious limitations [
4] when it comes to reconstructing and predicting small-scale climate trends in the future, in particular for meteorological parameters with pronounced variability such as precipitation. Thus, Regional Climate Models (RCMs) have been developed, nested within GCMs and with higher resolution, allowing for a more accurate ‘view’ at a smaller scale [
4,
5,
6]. However, even these models cannot allow for climate reconstruction and prediction at a local scale [
7] and are quite computationally expensive to run [
8]. In addition, if we want to predict a complex variable such as precipitation, which is often characterized by high spatial variability, then the issue becomes even more challenging [
9].
In this framework, neural network (NN) modelling may help. It is a machine learning technique designed to mimic the behaviour of the human nervous system’s cells, a network of neurons, in order to simulate the learning mechanisms observed in biological organisms. Here, however, our NNs are not considered as realistic models of the human brain but only for their capacity to catch nonlinear behaviours in the system studied.
As a matter of fact, NNs provide the opportunity to comprehensively consider the nonlinear nature of the climate system by a data-driven method that is completely independent from GCMs and RCMs so that we can obtain information on the robustness of the results by comparing relative outcomes on the same problem (e.g., attribution of recent climate change) [
10,
11,
12,
13].
But NNs should not be viewed simply as an alternative to dynamical modelling, as this mindset would overlook their potential to serve as a complementary approach [
14]. Recent research has indeed shown how machine learning (ML) techniques can be applied directly to precipitation model output [
9]. Combining the strengths of physical modelling and machine learning, it is possible to enhance the accuracy of precipitation modelling, improving parameterizations [
15,
16], or correcting the model bias of dynamic variables [
14].
In the recent past, NNs and other ML techniques have gained significant popularity in climate science [
17]. They have been used to detect extreme climate events through pattern recognition [
18,
19], to explore the possibility of outperforming Numerical Weather Prediction (NWP) [
20,
21,
22], for statistical modelling and forecasting and many other applications in extreme events [
17,
23,
24,
25], and, in general, for the hybridization of ML methods with Traditional Numerical Modelling [
26]. For a comprehensive review of neural network applications in climate studies, see [
27] or [
28], and for an overview of deep learning applications in Earth system science, refer to [
14].
A concrete example of “synergy” between the two methods is the case of downscaling GCMs through NNs. Specific examples of downscaling using neural networks can be found in [
8,
29].
In this framework, this work was conducted. By considering a 30-year climate simulation on the Greater Alpine Region (GAR) and observational precipitation provided by Meteotrentino, the official Civil Protection Weather Forecasting Agency of the Province of Trento (Italy), it was possible to perform downscaling and to analyse seasonal precipitation and extremes at two stations located in Trentino: Trento (Laste) and Passo Tonale. Then, once an NN “transfer function” to scale down from the regional to local scale in the past was obtained, it was possible to apply it to future regional scenarios, thus providing local precipitation projections.
The scientific community agrees on the relevance of studying the climate in mountain areas. These regions are considered climate hotspots and are believed to be more responsive and sensitive to climate change [
30,
31]. Moreover, several studies [
32,
33,
34] have identified the entire Mediterranean basin as a climate change-induced drought hotspot.
Global climate projections show a decrease in summer precipitation over the European Alps; however, precipitation change signals can be locally modulated by topography [
35]. Consequently, a high-resolution description of regional climate phenomena is necessary to characterize future climate evolutions at regional to local scales over Europe [
36].
Mountainous regions exhibit a distinctive climate due to their complex orography, and the GAR (4–19° E, 43–49° N, 0–3500 m asl) is characterized by extensive climate variability [
37]. In a strong climate-warming scenario (RCP 8.5), the mean seasonal summer precipitations are projected to decrease in this area [
7,
36], probably being linked to stronger summer warming. However, climate summer extremes, both drought and heavy precipitation, are likely to be more intense [
7,
38].
The distinctive feature of the climate simulations we use is their high temporal and spatial resolution, which resolves convection and enables the analysis of summer extremes. Additionally, future projection is conducted under the global warming scenario RCP 8.5, allowing us to compare it with previous findings [
7,
36,
37,
39]. However, due to the lack of direct correspondence between historical days from the model and observational data, we are limited in performing a seasonal analysis.
At first glance, this might seem like a significant issue, considering the shorter time series we obtain and the limited data available for the training of the network [
40]. However, we can overcome this barrier by adopting an NN tool—recently developed by one of us (A.P.)—which is particularly useful for the analysis of small datasets [
41]. This tool has been applied to the analysis of several climatic topics in the recent past, employing innovative methods, such as attributing recent temperature changes to anthropogenic forcing [
10], human migration flows [
42], climate change impacts on food security in Sahel [
43], changes in the Atlantic Multidecadal Oscillation (AMO) due to anthropogenic sulphates [
44], and meteo-climatic drivers affecting vectors of infectious diseases [
45]. Additionally, for a deeper discussion of these methods, see [
46].
2. Materials and Methods
2.1. Observational Data
We considered the observational daily precipitation recorded in Trento (Laste) and Passo Tonale from hydrological annals as the target of the neural network (NN). These data are open access and are freely provided by Meteotrentino.it at
https://www.meteotrentino.it/ (accessed on 4 October 2023).
We specifically selected data from these two stations due to their differing altitudes (Trento Laste is situated in the valley at 312 m, whereas Passo Tonale is positioned in the mountains at 1875 m; see
Figure 1) and the high quality of their time series. The data, which are available in CSV format, were validated and provide information on the quality of each measurement.
We considered the time span of 1979–2008, since our historical simulation output was conducted over this 30-year period. However, Passo Tonale’s station was dismissed on 20 January 2005, and therefore, we considered a shorter time series for this station.
We accumulated the precipitation for each station, and
Figure 2 shows the seasonal precipitation for Trento (Laste) (in panel a) and Passo Tonale (in panel b). Both daily time series contain some NaN values, which are highlighted with a blue line in the seasonal time series. To exclude seasons with excessive NaN values while avoiding an unnecessary reduction in our time series, we considered only the seasonal precipitation of those seasons with a maximum of 7% NaN values in our analysis.
We analyse the trend in our seasonal time series using a Mann–Kendall test, and both time series show no significant trend. We also assess stationarity using the Dickey–Fuller test: Trento (Laste) exhibits stationarity with high confidence (p-value < 0.05), while Passo Tonale shows weaker evidence of stationarity (p-value = 0.10).
In this study, we perform a seasonal analysis, and we refer to the different seasons using the standard climatological divisions: DJF (December, January, February), MAM (March, April, May), JJA (June, July, August), and SON (September, October, November) [
7].
2.2. Climate Model
We use model runs for the training of the NN. In particular, we consider the dynamical downscaling presented in Napoli et al. [
37]. The Weather Research and Forecasting (WRF) model is used to dynamically downscale the EC-Earth global model (25 km grid resolution) for two different periods: the historical run from 1979 to 2008 and the future projection, run under the global warming scenario RCP 8.5, from 2039 to 2068. The spatial domain includes the Greater Alpine Region (GAR), and the simulations are run at a convection-permitting resolution (4 km) to accurately model air mass interactions with the complex orography of the selected area. For further information also regarding the validation of the runs, refer to Napoli et al. [
37].
The historical run is used here as the training of the NN, while future projections to obtain local precipitation projections are used in order to analyse the anomalies of the mean seasonal precipitation and extremes. Since the climate model runs are conducted in “scenario-mode”, they do not provide a daily update of weather conditions, and there is no direct correspondence between historical days in the model runs and observational data in the same days. Therefore, for each station, we use the averaged seasonal precipitation data from the four closest grid points instead of daily precipitation as the variable to be fed into the neural network.
The altitudes of the four grid points, compared to the elevation of each station, are shown in
Table 1. The differences in altitude between the stations and the grid points are likely due to the presence of higher mountains near the stations and the averaging process performed by the model.
2.3. Neural Network Model
In this paper, we explore a possible application of Neural Networks (NNs) in climate studies: Feedforward Neural Networks with backpropagation training. They rely on a structure called “multilayer perceptron”, and being one of the simplest NN architectures, they can still provide realistic nonlinear multiple regressions and return accurate results. For the basics, refer to [
46,
47,
48], and for environmental applications, see, for instance, [
27,
49].
The ultimate goal is to find a transfer function that adequately captures the relationship between input and target variables, leading to an accurate prediction of the target variable when faced with independent data. In general, a neural network procedure returns reliable results if large amounts of data are provided. However, with the right strategy, it is possible to obtain accurate outcomes from small datasets.
In this paper, we want to present a possible application of a method called the generalized leave-one-out cross-validation procedure, which allows us to maximize the extension of the training set and provides accurate predictions even when large amounts of data are not available. This procedure was previously used in a tool developed by one of us (A.P.) [
41], and a schematic representation is illustrated in
Figure 3.
All input data are divided into three subsets: a training set, validation set, and test set. Referring to
Figure 3, the white squares represent the training set, while the black squares stand for the validation test, and lastly, the grey square represents the test pair. The reason why this method is unique lies in the iteration of the test pair as a “hole” through the dataset. Moreover, during the process, the training set and validation set are picked randomly. At the end of the procedure, all output values are estimated, and the training stops when an increase in the mean square error (MSE) appears in the validation set.
It follows that the results of this generalized leave-one-out procedure depend heavily on the random choices of the elements for the validation test. Additionally, the changes in the values in the initial weights are also critical for the outcomes and allow the model to widely explore every cost function. Therefore, to obtain more robust results, it is possible to perform ensemble runs of the NNs by repeating each estimation a fixed number of times (generally 20 or 30). After computing the average on the runs of the model, reliable results, which do not depend on the variability in random choices, are obtained. For more technical details on this NN tool, refer to [
41].
In this particular application, this process occurs twice: first in the reconstruction of the past and then in the projection of the future, with minor variations.
The input data for the reconstruction consist of the seasonal average of daily precipitation measured at each station (target) and the seasonal average of daily precipitation of the climate model (predictors). When the process outlined above is complete, the neural network reconstruction is obtained.
Now, the weights are fixed, and we can pass on the projections. This is a forward step, when the only data we fed to the NN are the seasonal average of daily precipitation of the climate model’s projection for every network, and we iterate the previous process for each corresponding season. Finally, we compute the ensemble mean, which is considered the local projected precipitation.
To assess the performance of the NNs, standard multilinear regressions are performed using the same training approach, and the resulting performance coefficients are reported. Moreover, the performance of the NNs in reconstructing past seasonal time series is evaluated by comparing their results with those obtained from the precipitation mean of the grid points.
2.4. Data Preprocessing
For each season, we considered the target to be the seasonal average of daily precipitation observed in each station. As a matter of fact, we noticed the presence of some NaN values in both daily time series, so we considered the seasonal precipitation of only those seasons that present a maximum of 7% NaN values (see
Figure 2). Then, to obtain normalized seasonal daily precipitation, we divided the total precipitation for each season by the number of “non-NaN” days.
Accordingly, we calculated the seasonal average of daily precipitation for the four grid points as well. It is important to underline that this procedure did not affect the seasonal analysis as the neural network still performed normalization.
Finally, due to the “scenario mode”, a synchronization procedure between the observational data and grid point data was needed. It consisted of the following steps.
The data were divided by season. For each season, target and grid point precipitation values were sorted in ascending order.
Subsequently, starting from the sorted data, every target season (e.g., DJF 2000) was linked with the corresponding season of the first grid point (e.g., DJF 2002). The remaining grid point values were then synchronized based on such association. Thus, each station’s seasonal precipitation value was connected to four grid point values per season.
Finally, the four subsets were merged into a single dataset; then, the observational data time series was reconstructed with temporal sorting, thus building a dataset to be fed to the NNs containing the normalized daily seasonal precipitation of all data (target and grid points).
We performed trend and stationarity analyses on the time series fed to the neural network. Similarly to what we found for the observation data, in general, we found no trend in each time series and stationary time series with high confidence (p-value < 0.5) for Trento (Laste) and less confidence (p-value < 0.10) for Passo Tonale.
3. Results
The compiled datasets described in the preceding paragraph were fed into our feedforward neural network, returning the following results.
3.1. Neural Network Reconstruction
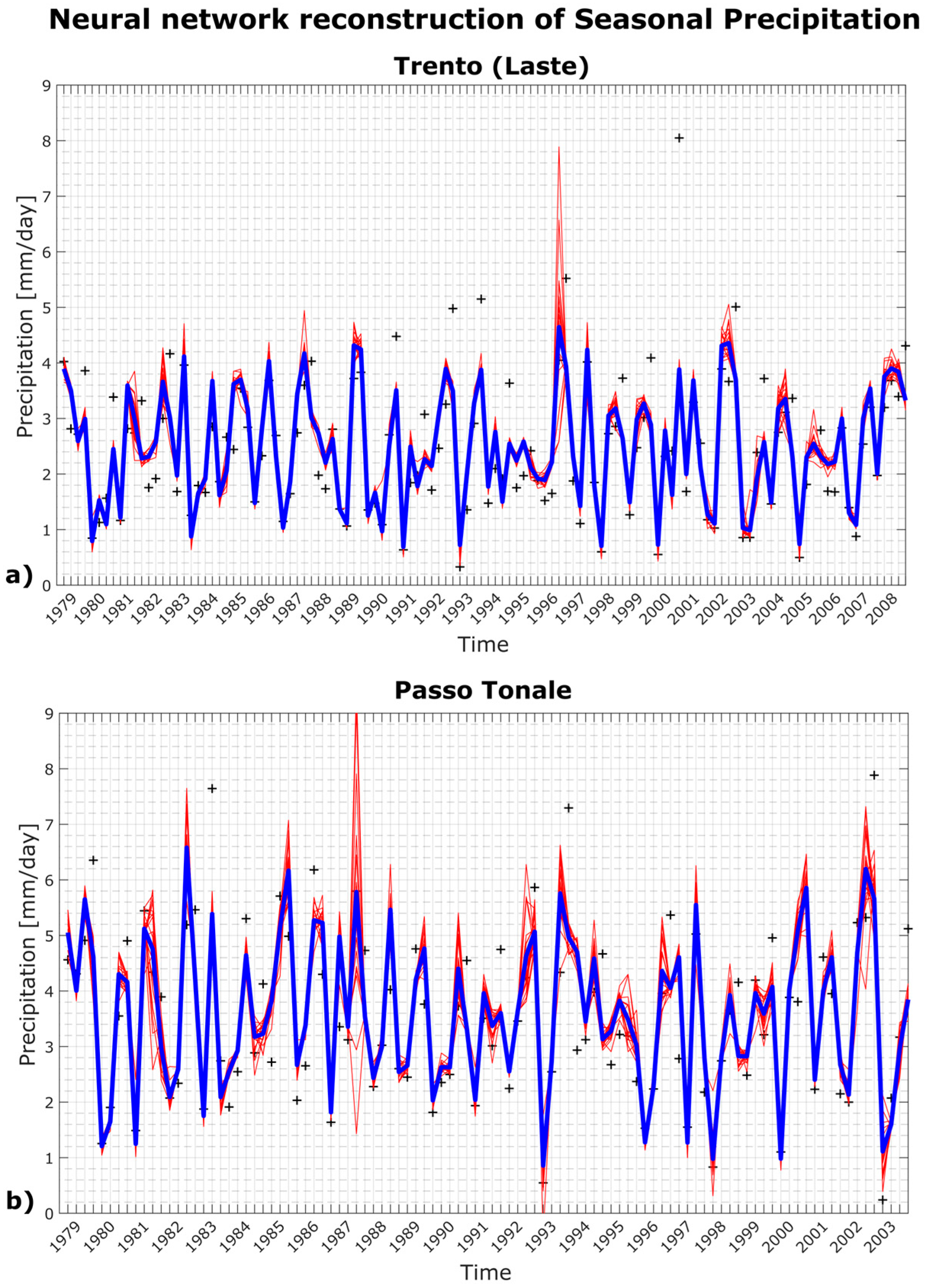
We reconstruct through the NN the historical seasonal time series for both stations using the precipitation data from the surrounding four grid points of the RCM as the input of the 4-4-1 networks: Trento (Laste) reconstruction is shown in
Figure 4a, while Passo Tonale’s is shown in
Figure 4b. It can be noticed that we are able to only reconstruct the period 1979–2003 for Passo Tonale since we have a shorter observational time series, and additionally, we have to exclude some seasons with too many NaNs.
Table 2 shows the coefficients of determination for the neural network (NN) and the linear regression (LR) reconstructions, and it also includes the coefficients of determination obtained from the precipitation mean of the grid points.
Table 2 shows that in both cases, NN reconstructions were characterized by good coefficients of determination, which outperformed the corresponding linear regression coefficients. The NN also performed better compared to the grid points, with a significant difference observed at Passo Tonale.
3.2. Does the Neural Network Perform Better than the Model?
In this section, we compare the neural network reconstructions with the seasonal precipitation observed at the stations and the mean precipitation of the closest grid points.
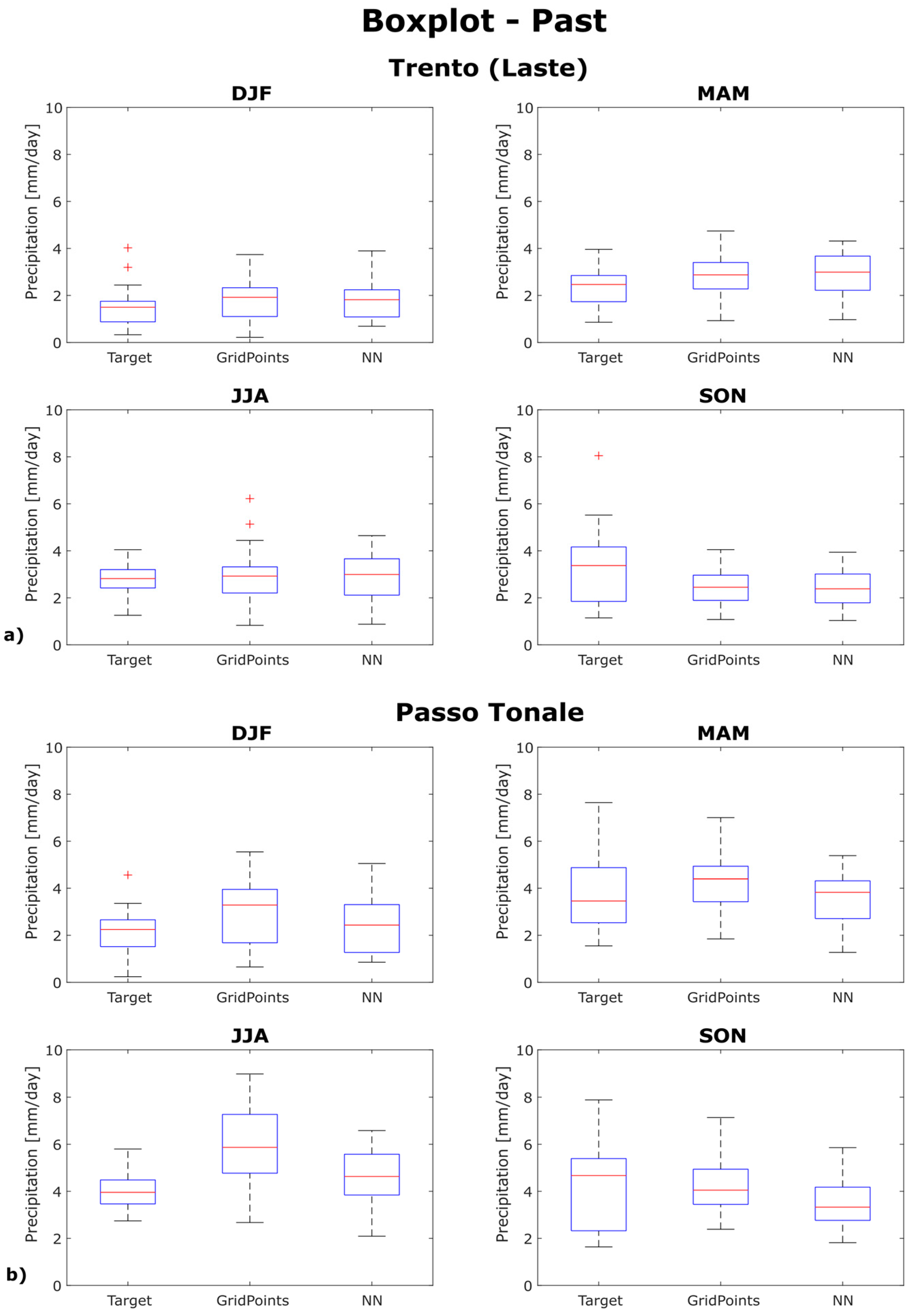
Figure 5 displays the averaged seasonal precipitation distribution for station observations (target), the model (grid points), and the neural network (NN) reconstructions.
The NN significantly outperforms the model in Passo Tonale, located at 1875 m, at least in three seasons (DJF, MAM, JJA in
Figure 5, panel b). This improvement is especially predominant in summer (JJA), where the 25th percentile of the model’s precipitation distribution exceeds the 75th percentile of the observed target values. In Trento (
Figure 5, panel a), the NN performs slightly better in spring (MAM) and corrects some outliers in JJA compared to the model, while in autumn (SON), when the target’s precipitation is characterized by great variability, the NN does not perform better than the model in either station.
When focusing on the top three precipitation extremes for each season, the results show a clear and distinct improvement in the NN in JJA (see
Table 3). For these extremes, we compare the values reconstructed by the NN and linear regression with station observations and the mean precipitation of the nearest grid points.
It is important to point out that the model overestimates JJA extremes in past simulations in both stations, with a particularly strong overestimation in Passo Tonale, where the model’s values are nearly double the observed ones, as shown in
Table 3b.
Concerning the other seasons, not pictured in the tables, the NN performs slightly better than the model in DJF in Passo Tonale and in MAM in Trento, while in SON, both the model and the NN underestimate the extremes.
Therefore, the neural network corrects the model’s bias in Passo Tonale and especially in summer precipitation, providing values that are closer to the observed data. This result is crucial since it allows us to be more confident in obtaining more realistic results in future local projections.
3.3. Neural Network Projection
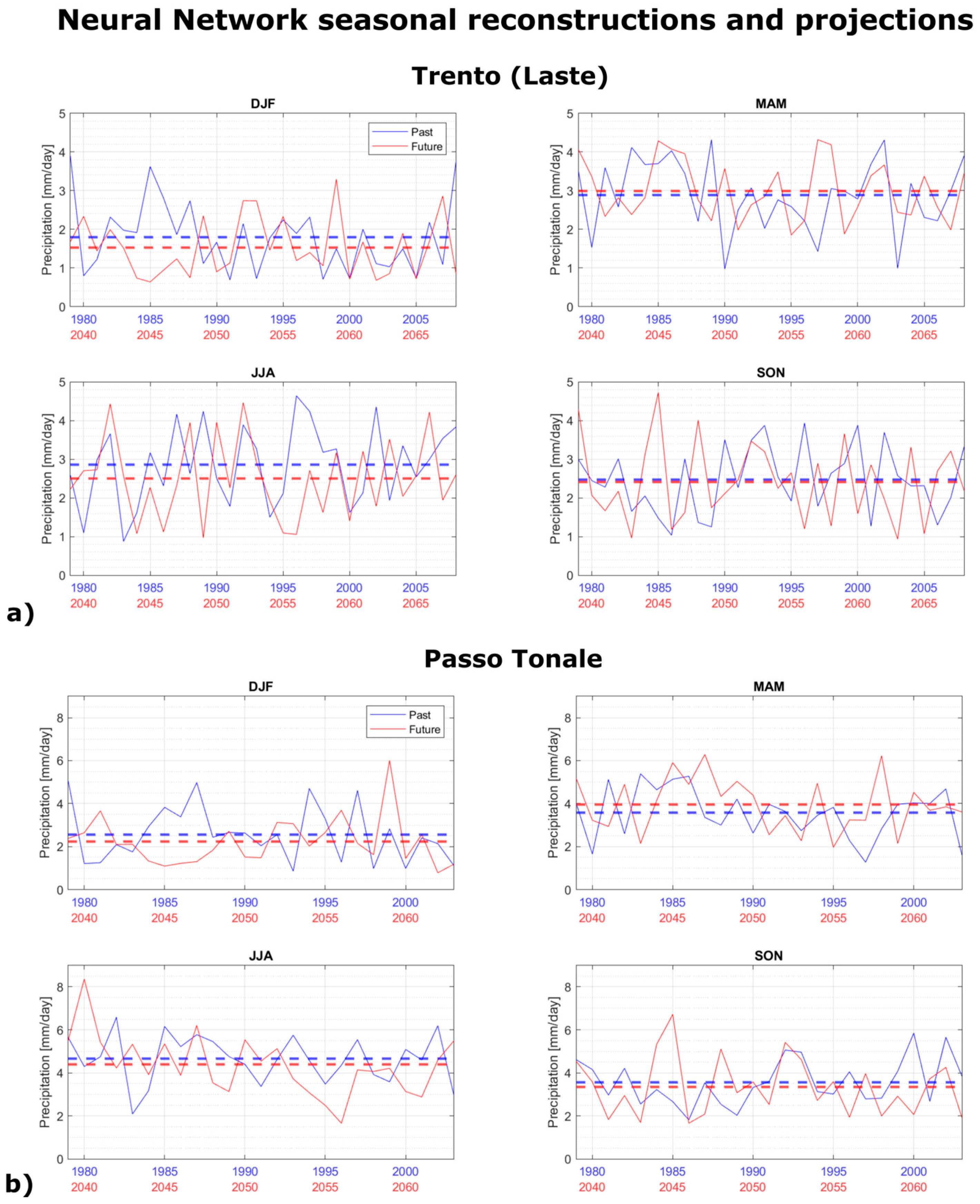
After the neural network reconstruction, the weights are fixed. In order to obtain the local NN predictions of precipitations, values for the four grid points in the projection dataset and for each season are provided as input. As output, the network returns the local projected precipitations. The resulting projections are shown in
Figure 6.
Passo Tonale shows a greater variability in seasonal precipitation compared to Trento (Laste) in both the past reconstructions and future projections. In the future projections, the maximum average daily precipitation value reaches 8.3 mm/day in Passo Tonale, corresponding to more than 760 mm in a single season, while Trento (Laste) shows precipitation never exceeding 5 mm/day.
We then focus our analysis on seasonal extremes and considering each season apart.
3.4. Mean Seasonal Precipitation and Extremes
Our goal in this section is to analyse the anomalies of the mean seasonal precipitation and extremes for each season. In order to achieve this, we accumulate the total seasonal precipitation for each season in both the past reconstructions and the future projections. By calculating the mean seasonal precipitations for both time series and computing the difference, we obtain the relative anomalies.
In order to assess the significance of our results, we perform Student’s t-test for independent samples for both analyses. It is important to note that this involves an approximation, as the forecast is considered independent from the neural reconstruction.
We observed a negative variation in the seasonal precipitation mean for all seasons except spring (MAM) in both stations. This effect is particularly pronounced in Passo Tonale, which shows a greater positive seasonal anomaly. Despite variations exceeding 10% for DJF in both stations, JJA in Trento, and MAM in Passo Tonale, none of these values have a p-value less than 0.05.
Next, we proceed to analyse the season extremes. We focus on the top three extreme values for each season by cumulating the top three values for both the future projections and past reconstructions. The average is then calculated for each set of values. Finally, we compute the difference between these two averages and the percentage variation. These results are presented in
Table 5. Statistically significant results (
p < 0.05) are shown in bold in the tables.
Focusing on the precipitation values of the top three seasonal extremes, we observe a general decrease in extreme precipitation during DJF in both stations, which is statistically significant in Trento (p-value = 0.03). In Passo Tonale, there is a general increase in extreme precipitation in the other seasons, with a significant rise during MAM (p-value = 0.01). In Trento, there is a positive 11% extreme precipitation increase in SON, although this change is not statistically significant since the p-value is larger than 0.05.
By comparing the results from both analysis tables, we are inclined to think that stations relatively close to each other at different altitudes can exhibit distinct results. It is important to emphasize that the statistically significant findings we report have consistently appeared, with slight variations, across all the neural network trials we conducted with different parameters. In addition, we observe similar absolute and relative anomalies in mean seasonal precipitation, though none with sufficiently small p-values. This could be influenced, at least for Passo Tonale, by the presence of outliers in the future NN projections.
Considering the results of other runs, we find that JJA extreme anomalies show great variability for both stations. In some cases, we observe a positive variation even in Trento. However, as one might suspect, none of these variations show significant p-values.
3.5. Grid Point Analysis
In order to compare the neural network results with the model, we perform the same seasonal analysis on the precipitation mean and extremes on the mean values of the four grid points. Trento Laste’s results are shown in
Table 6 and
Table 7 panel (a), while Passo Tonale’s are shown in panel (b).
By comparing
Table 6 with
Table 4, we observe a similar trend in the mean seasonal anomalies. There is a general decrease in seasonal precipitation during DJF, JJA, and SON in both stations, while MAM shows an increase, which is more pronounced in Passo Tonale.
The differences between the NN and the model’s relative anomalies of seasonal precipitation are stronger in Passo Tonale, with the decreases in DJF and JJA nearly doubling those observed in the model. Unfortunately, no statistically significant results are obtained.
When analysing extremes (
Table 5 and
Table 7), more differences are evident. The grid point analysis shows a negative JJA variation of 22% in Trento and 10% in Passo Tonale which is not observed in the NN analysis. The model indicates a clear, though not statistically significant, reduction in JJA extremes in both stations, whereas the NN shows a 6% increase in Passo Tonale and no variation in Trento.
Finally, the only statistically significant result (p-value < 0.05) found in this analysis is a decrease in DJF extremes in Trento, which is consistent with the NN result.
4. Discussion
In this paper, we perform downscaling through neural networks considering seasonal precipitation observed in Trento (Laste) and Passo Tonale and convection-permitting high-resolution climate outputs. Despite the short seasonal time series, we adopt a generalized leave-one-out cross-validation procedure and reconstruct the period from 1979 to 2008 for Trento and 1979 to 2003 for Passo Tonale. This approach allows us to achieve good coefficients of determination, 0.69 and 0.68, respectively, which outperformed those obtained through linear regression and the mean of the four closest grid points.
A key outcome of this work is the correction of the model’s bias in summer precipitation performed by the NN, particularly pronounced in Passo Tonale. The overestimation of precipitation over mountainous areas in very high-resolution models has been previously found in other papers (see, for instance, [
39]). A possible explanation is the overestimation of low-intensity events, particularly in summer [
50], or model deficiencies [
39].
Our result represents one of the many potential synergies between models and data-driven algorithms depicted in Reichstein et al. [
14]. It shows how machine learning techniques can be integrated into a hybrid modelling approach to, allegedly, enhance the predictive accuracy of seasonal forecasting.
Later, we performed a seasonal projection from 2039 to 2068 (2063) for the Trento (Passo Tonale) station. The simulations carried out for Passo Tonale show greater variability, and the mean seasonal precipitations are generally greater than the ones obtained in Trento (Laste). This is consistent with the orographic enhancement in precipitation, as Passo Tonale is located at a higher altitude.
Following this, we analysed the anomalies in the mean seasonal precipitation and top three extremes. Considering the neural network analysis performed in
Section 3.4 and the model analysis in
Section 3.5, we could perform a comparison of the results.
We observe similar mean seasonal anomalies between the two analyses. DJF, JJA, and SON show a general decrease, while MAM shows an increase, which is more pronounced in Passo Tonale. Despite the fact that none of these results proved to be statistically significant, the observed decrease in seasonal JJA precipitation in this area is consistent with previous studies [
7,
36,
37,
39]. Among these, the decrease in seasonal DJF precipitation in both stations is only documented in Napoli et al. [
37], as illustrated in
Figure 1 of that paper, where the data from the grid points are sourced. However, Ban et al. [
39], which compared the results between a very high-resolution and a coarser model, exhibit a decrease over the Po Valley and Swiss Alps and an increase in the surrounding area in the 10-year-long simulations CRM2 (2.2 km resolution) and CPM12 (12.5 km res.) and a stronger increase in the Alps and a smaller decrease in the valley considering the latter for a 30-year-long simulation. Therefore, even if they suggest that their results could be influenced by decadal variability, it shows that non-homogeneous patterns can arise when considering a finer-resolution model, unlike [
7], where a general decrease is found.
Considering large-scale circulation patterns, the decrease in summer precipitation is consistent with an increase in the anticyclonic circulation over the Mediterranean basin and Central Europe (see Reale et al. [
51] for an in-depth discussion on the future regime of cyclones in the Mediterranean area). Such a circulation pattern enhances downward motions and deflects storms northward [
35]. On the other hand, the dipolar DJF pattern is still not fully understood, but it is probably related to the long-term variability pattern of the North Atlantic Oscillation, whose storm track shifts are known [
37].
However, while the mean summer precipitation is projected to decrease, JJA extremes are expected to increase [
7,
36]. But also, from the point of view of basic physics, a change in extreme precipitation is expected in response to a warmer climate and its impact on saturation vapor pression through the Clausius–Clapeyron relation. From this equation, it is possible to obtain that a relative change in specific humidity is linked to the relative change in temperature. A 1% change in temperature (3 °C) corresponds to a 20% change in specific saturation humidity, or, alternatively, a 1 K change is associated with a 7% variation [
52,
53,
54]. This implies that the capacity of the atmosphere to hold water increases by approximately 6–7% per degree of warming, and if relative humidity stays constant, it follows that extreme precipitation can also change at the same rate [
39].
In the analysis of extremes, we find two statistically significant and robust results: a 21% decrease in Trento (Laste) DJF extremes and a 17% increase in Passo Tonale MAM extremes. We then find an increase in SON of 11% and 5% in Trento and Passo Tonale, respectively, and an increase in JJA of 6% in Passo Tonale. However, even though we did not obtain statistical results for JJA extremes, we want to highlight that in other neural network trials with different parameters, an increase in Trento in this season was obtained in many cases. Therefore, JJA extreme anomalies show great variability from a neutral to a positive increase, unlike the model that shows a decrease of 22% in Trento and 10% in Passo Tonale.
5. Conclusions
The prediction of precipitation patterns over the European Alps at the local scale possesses many challenges. This area is characterized by a complex orography which modulates climate signals, and therefore, in order to analyse and predict extreme precipitation accurately, high-resolution climate models are needed. Accounting for convection is essential, but on the other hand, considering convection-permitting resolution (4 km or less) conducted for long simulations could be computational expensive. Moreover, even at this resolution, some parametrizations are still made, and it is difficult to obtain reliable climate reconstruction and prediction at the local scale due to the underlying possibility of biases in the dynamic model such as, for instance, the overestimation of precipitation over mountainous areas [
39].
Here, we perform neural network downscaling considering high-resolution climate models’ seasonal precipitation and the one observed at the Trento (Laste) and Passo Tonale stations. In order to account for the limited time series, we adopt an ensemble and generalized leave-one-out cross-validation procedure, already tested in previous works [
10,
42,
43,
44,
45].
Our NN model manages to correct, in most cases, the model’s bias, which is predominant in the station at higher altitudes and even more when considering summer precipitation. This correction is even more pronounced when taking into account summer extremes, where the model even doubles the observed ones. Correcting this bias is fundamental for increasing confidence in obtaining more realistic results in future local projections.
When looking at future projections, we find a decrease in seasonal precipitation in winter and summer in both stations. This result is consistent with the model (as one can see in Napoli et al. [
37]) and with the concept that non-homogeneous patterns can arise in the Great Alpine Region (known also as GAR) when considering a finer-resolution model, as shown in [
37,
39], even with some differences. These non-homogeneous patterns are likely due to the complex topography of the area, which cannot be accurately captured by lower-resolution models.
Considering the extremes, we find two statistically significant results: a 21% decrease in Trento (Laste) for winter extremes and a 17% increase in Passo Tonale in spring. Unfortunately, no other statistically significant results were found, likely due to the presence of too many seasons with excessive NaN values in the initial time series, which forced us to exclude them and significantly shorten the series for Passo Tonale. On the other hand, it is important to highlight that summer extreme anomalies, when considering all the different runs of this analysis, showed considerable variability. In general, we observed a neutral to positive increase, in contrast to the model, which indicated a clear decrease in both stations.
Overall, our results are in agreement with the thermodynamics and dynamics (circulation) in the Mediterranean under global warming conditions, which indicate an increase in the anticyclonic circulation over the Mediterranean basin and Central Europe and a general increase in extreme precipitations.
Finally, it would be interesting to repeat the same analysis using more complete time series from different stations to determine whether the results we obtain for stations at different altitudes are the result of local effects or can also be observed in other locations. However, at present and to our knowledge, there are no known 30-year time series from stations in the Greater Alpine Region that are both available and of sufficient quality for use. Moreover, future work will focus on extending our approach by incorporating exogenous variables as inputs.