The Signature of Climate in Annual Burned Area in Portugal
Abstract
1. Introduction
2. Data and Methods
3. Results
3.1. BA and CDSR
3.2. Statistical Model of BA
3.3. Interannual Variability of BA
3.4. Trend in and Return Periods of BA
4. Discussion
5. Concluding Remarks
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- San-Miguel-Ayanz, J.; Durrant, T.; Boca, R.; Maianti, P.; Libertà, G.; Jacome Felix Oom, D.; Branco, A.; De Rigo, D.; Suarez-Moreno, M.; Ferrari, D.; et al. Forest Fires in Europe, Middle East and North Africa 2022; Publications Office of the European Union: Luxembourg, 2023; p. 189. [Google Scholar] [CrossRef]
- Pereira, J.M.C.; DaCamara, C.C.; Lisboa, M.L. Large-scale circulation patterns associated with monthly area burned by wildfires in continental Portugal. In Proceedings of the 2nd International Conference on Forest Fire Research, Coimbra, Portugal, 21–24 November 1994; Volume II, pp. 601–610. [Google Scholar]
- Pereira, M.G.; Trigo, R.M.; DaCamara, C.C.; Pereira, J.M.C.; Leite, S.M. Synoptic patterns associated with large summer forest fires in Portugal. Agric. For. Meteorol. 2005, 129, 11–25. [Google Scholar] [CrossRef]
- DaCamara, C.C.; Trigo, R.M.; Nascimento, M.L. Characterizing the secondary peak of Iberian fires in March. In Advances in Forest Fire Research; Viegas, D.X., Ed.; Imprensa da Universidade de Coimbra: Coimbra, Portugal, 2014; pp. 1671–1682. [Google Scholar] [CrossRef][Green Version]
- Amraoui, M.; Pereira, M.G.; DaCamara, C.C.; Calado, T.J. Atmospheric conditions associated with extreme fire activity in the Western Mediterranean region. Sci. Total Environ. 2015, 524, 32–39. [Google Scholar] [CrossRef] [PubMed]
- DaCamara, C.C.; Lajas, D.; Gouveia, C.; Pereira, J.M.C. A statistical model for prediction of burned areas by wildfires based on circulation types affecting Portugal. In Proceedings of the III Third International Conference on Forest FireResearch and 14th Conference on Fire and Forest Meteorology, Luso, Portugal, 16–20 November 1998; Volume I, pp. 1199–1206, ISBN 972-97973-0-7. [Google Scholar]
- DaCamara, C.C.; Trigo, R.M. Circulation weather types and their influence on the fire regime in Portugal. In Advances in Forest Fire Research 2018; Viegas, D.X., Ed.; Imprensa da Universidade de Coimbra: Coimbra, Portugal, 2018; pp. 372–380. [Google Scholar] [CrossRef]
- Sá, A.; Benali, A.; Pinto, R.; Fernandes, P.; Russo, A.; Santos, F.; Trigo, R.; Pereira, J.; DaCamara, C.C. Improving wildfire spread simulations using MODIS active fires: The FIRE-MODSAT project. In Advances in Forest Fire Research; Viegas, D.X., Ed.; Imprensa da Universidade de Coimbra: Coimbra, Portugal, 2014; pp. 811–822. [Google Scholar] [CrossRef][Green Version]
- Freire, J.G.; DaCamara, C.C. Using cellular automata to simulate wildfire propagation and to assist in fire management. Nat. Hazards Earth Syst. Sci. 2019, 19, 169–179. [Google Scholar] [CrossRef]
- Mota, B.; Freire, J.G.; Oliveira, M.; Nunes, S.A.; Dilão, R.; DaCamara, C.C. Using cellular automata to assess the role played by wind direction in two large fire episodes in Portugal. In Advances in Forest Fire Research 2022; Viegas, D.X., Viegas, L.M., Eds.; Imprensa da Universidade de Coimbra: Coimbra, Portugal, 2022; pp. 431–435. [Google Scholar] [CrossRef]
- Gouveia, C.; Bastos, A.; DaCamara, C.C.; Trigo, R.M. Drought impacts on vegetation in the pre and post-fire events over Iberian Peninsula. Nat. Hazards Earth Syst. Sci. 2012, 12, 3123–3137. [Google Scholar] [CrossRef]
- Russo, A.; Gouveia, C.M.; Páscoa, P.; DaCamara, C.C.; Sousa, P.M.; Trigo, R.M. Assessing the role of drought events on wildfires in the Iberian Peninsula. Agric. For. Meteorol. 2017, 237, 50–59. [Google Scholar] [CrossRef]
- Bento, V.A.; Russo, A.; Gouveia, C.M.; DaCamara, C.C. Recent change of burned area associated with summer heat extremes over Iberia. Int. J. Wildland Fire 2022, 31, 658–669. [Google Scholar] [CrossRef]
- Gouveia, C.; Trigo, R.M.; DaCamara, C.C. Drought and vegetation stress monitoring in Portugal using satellite data. Nat. Hazards Earth Syst. Sci. 2009, 9, 185–195. [Google Scholar] [CrossRef]
- DaCamara, C.C.; Calado, T.J.; Amraoui, M.; Pereira, J.M.C. The SAF for Land Surface Analysis: Wildfire applications. In Proceedings of the Joint 2007 EUMETSAT Meteorological Satellite Conference and the 15th Satellite Meteorology & Oceanography Conference of the American Meteorological Society, Amsterdam, The Netherlands, 24–28 September 2007; Available online: https://www.eumetsat.int/media/5433 (accessed on 25 March 2024).
- Trigo, R.M.; Pereira, J.M.C.; Pereira, M.G.; Mota, B.; Calado, M.T.; DaCamara, C.C.; Santo, F.E. Atmospheric conditions associated with the exceptional fire season of 2003 in Portugal. Int. J. Climatol. 2006, 26, 1741–1757. [Google Scholar] [CrossRef]
- Libonati, R.; Geirinhas, J.L.; Silva, P.S.; Russo, A.; Rodrigues, J.A.; Belém, L.B.C.; Nogueira, J.; Roque, F.O.; DaCamara, C.C.; Nunes, A.M.B.; et al. Assessing the role of compound drought and heatwave events on unprecedented 2020 wildfires in the Pantanal. Environ. Res. Lett. 2022, 17, 015005. [Google Scholar] [CrossRef]
- Libonati, R.; Geirinhas, J.L.; Silva, P.S.; Monteiro dos Santos, D.; Rodrigues, J.A.; Russo, A.; Peres, L.F.; Narcizo, L.; Gomes, M.E.R.; Rodrigues, A.P.; et al. Drought–heatwave nexus in Brazil and related impacts on health and fires: A comprehensive review. Ann. N. Y. Acad. Sci. 2022, 1517, 44–62. [Google Scholar] [CrossRef]
- Pinto, M.M.; Hurduc, A.; Trigo, R.M.; Trigo, I.F.; DaCamara, C.C. The extreme weather conditions behind the destructive fires of June and October 2017 in Portugal. In Advances in Forest Fire Research 2018; Viegas, D.X., Ed.; Imprensa da Universidade de Coimbra: Coimbra, Portugal, 2018; pp. 138–145. [Google Scholar] [CrossRef]
- Ramos, A.M.; Russo, A.; DaCamara, C.C.; Nunes, S.A.; Sousa, P.; Soares, P.M.M.; Lima, M.M.; Hurduc, A.; Trigo, R.M. The compound event that triggered the destructive fires of October 2017 in Portugal. iScience 2023, 26, 106141. [Google Scholar] [CrossRef] [PubMed]
- Trigo, R.M.; DaCamara, C.C. Circulation weather types and their Influence on the precipitation regime in Portugal. Int. J. Climatol. 2000, 20, 1559–1581. [Google Scholar] [CrossRef]
- Russo, A.C.; Gouveia, C.M.; Trigo, R.M.; Liberato, M.L.R.; DaCamara, C.C. The influence of circulation weather patterns at different spatial scales on drought variability in the Iberian Peninsula. Front. Environ. Sci. 2015, 3, 1. [Google Scholar] [CrossRef]
- Gouveia, C.; Trigo, R.; DaCamara, C.C.; Libonati, R.; Pereira, J.M.C. The North Atlantic Oscillation and European vegetation dynamics. Int. J. Climatol. 2008, 28, 1835–1847. [Google Scholar] [CrossRef]
- Amraoui, M.; Liberato, M.L.R.; Calado, T.J.; DaCamara, C.C.; Pinto-Coelho, L.; Trigo, R.M.; Gouveia, C.M. Fire activity over Mediterranean Europe based on information from Meteosat-8. For. Ecol. Manag. 2013, 294, 62–75. [Google Scholar] [CrossRef]
- Panisset, J.; DaCamara, C.C.; Libonati, R.; Peres, L.F.; Calado, T.J.; Barros, A. Assigning dates and identifying areas affected by fires in Portugal based on MODIS data. An. Acad. Bras. Ciênc. 2017, 89, 1487–1501. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Barroso, C.; Trigo, I.F.; Olesen, F.; DaCamara, C.C.; Queluz, M.P. Intercalibration of NOAA and Meteosat window channel brightness temperatures. Int. J. Remote Sens. 2005, 26, 3717–3733. [Google Scholar] [CrossRef]
- Peres, L.F.; DaCamara, C.C.; Trigo, I.F.; Freitas, S.C. Synergistic use of the two-temperature and split-window methods for land-surface temperature retrieval. Int. J. Remote Sens. 2010, 31, 4387–4409. [Google Scholar] [CrossRef]
- Ermida, S.L.; Trigo, I.F.; DaCamara, C.C.; Gottsche, F.M.; Olesen, F.S.; Hulley, G. Validation of remotely sensed surface temperature over an oak woodland landscape—The problem of viewing and illumination geometries. Remote Sens. Environ. 2014, 148, 16–27. [Google Scholar] [CrossRef]
- Bento, V.A.; DaCamara, C.C.; Trigo, I.F.; Martins, J.P.A.; Duguay-Tetzlaff, A. Improving Land Surface Temperature Retrievals over Mountainous Regions. Remote Sens. 2017, 9, 38. [Google Scholar] [CrossRef]
- Ermida, S.L.; Trigo, I.F.; DaCamara, C.C.; Jiménez, C.; Prigent, C. Quantifying the clear-sky bias of satellite land surface temperature using microwave-based estimates. J. Geophys. Res.-Atmos. 2019, 124, 844–857. [Google Scholar] [CrossRef]
- Trigo, I.F.; Peres, L.F.; DaCamara, C.C.; Freitas, S.C. Thermal land surface emissivity retrieved from SEVIRI/Meteosat. IEEE Trans. Geosci. Remote Sens. 2008, 46, 307–315. [Google Scholar] [CrossRef]
- Peres, L.F.; Libonati, R.; DaCamara, C.C. Land-Surface Emissivity Retrieval in MSG-SEVIRI TIR Channels Using MODIS Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5587–5600. [Google Scholar] [CrossRef]
- Madeira, C.; DaCamara, C.C. Comparison of downwelling surface longwave radiation fluxes derived from meteosat-8 with in situ measurements. In Proceedings of the 2005 EUMETSAT Meteorological Satellite Conference, Dubrovnik, Croatia, 19–23 September 2005; Available online: https://www.eumetsat.int/media/4273 (accessed on 25 March 2024).
- Amraoui, M.; DaCamara, C.C.; Pereira, J.M.C. Detection and monitoring of African vegetation fires using MSG-SEVIRI imagery. Remote Sens. Environ. 2010, 114, 1038–1052. [Google Scholar] [CrossRef]
- Calado, T.J.; DaCamara, C.C. Dating fire events on end of season maps of burnt scars. In geoENV VI—Geostatistics for Environmental Applications; Soares, A., Pereira, M.J., Dimitrakopoulos, R., Eds.; Springer: Dordrecht, The Netherlands, 2008; Volume 15, pp. 154–196. [Google Scholar] [CrossRef]
- Libonati, R.; DaCamara, C.C.; Pereira, J.M.C.; Peres, L.F. On a new coordinate system for improved discrimination of vegetation and burned areas using MIR/NIR information. Remote Sens. Environ. 2011, 115, 1464–1477. [Google Scholar] [CrossRef]
- Pinto, M.M.; Libonati, R.; Trigo, R.M.; Trigo, I.F.; DaCamara, C.C. A deep learning approach for mapping and dating burned areas using temporal sequences of satellite images. ISPRS J. Photogramm. Remote Sens. 2020, 160, 260–274. [Google Scholar] [CrossRef]
- Pinto, M.M.; Trigo, R.M.; Trigo, I.F.; DaCamara, C.C. A Practical Method for High-Resolution Burned Area Monitoring Using Sentinel-2 and VIIRS. Remote Sens. 2021, 13, 1608. [Google Scholar] [CrossRef]
- DaCamara, C.C.; Libonati, R.; Pinto, M.M.; Hurduc, A. Near- and Middle-Infrared Monitoring of Burned Areas from Space. In Satellite Information Classification and Interpretation; Rustamov, R.B., Ed.; IntechOpen: London, UK, 2019; pp. 1–18. [Google Scholar] [CrossRef]
- Gouveia, C.; DaCamara, C.C.; Trigo, R.M. Post-fire vegetation recovery in Portugal based on spot/vegetation data. Nat. Hazards Earth Syst. Sci. 2010, 10, 673–684. [Google Scholar] [CrossRef]
- Bastos, A.; Gouveia, C.M.; DaCamara, C.C.; Trigo, R.M. Modelling post-fire vegetation recovery in Portugal. Biogeosciences 2011, 8, 3359–3607. [Google Scholar] [CrossRef]
- Gouveia, C.; Páscoa, P.; DaCamara, C.C. Post-Fire Vegetation Recovery in Iberia Based on Remote-Sensing Information. In Forest Fire; Szmyt, J., Ed.; IntechOpen: London, UK, 2018; pp. 113–130. [Google Scholar] [CrossRef]
- DaCamara, C.C.; Trigo, R.M.; Pinto, M.M.; Nunes, S.A.; Trigo, I.F.; Gouveia, C.M.; Rainha, M. CeaseFire: A website to assist fire managers in Portugal. In Advances in Forest Fire Research 2018; Viegas, D.X., Ed.; Imprensa da Universidade de Coimbra: Coimbra, Portugal, 2018; pp. 941–949. [Google Scholar] [CrossRef]
- Trigo, I.F.; DaCamara, C.C.; Viterbo, P.; Roujean, J.-L.; Olesen, F.; Barroso, C.; Camacho-de Coca, F.; Freitas, S.C.; García-Haro, J.; Geiger, B.; et al. The Satellite Application Facility for Land Surface Analysis. Int. J. Remote Sens. 2011, 32, 2725–2744. [Google Scholar] [CrossRef]
- DaCamara, C.C.; Calado, T.J.; Ermida, S.L.; Trigo, I.F.; Amraoui, M.; Turkman, K.F. Calibration of the Fire Weather Index over Mediterranean Europe based on fire activity retrieved from MSG satellite imagery. Int. J. Wildland Fire 2014, 23, 945–958. [Google Scholar] [CrossRef]
- Pinto, M.M.; DaCamara, C.C.; Trigo, I.F.; Trigo, R.M.; Turkman, K.F. Fire danger rating over Mediterranean Europe based on fire radiative power derived from Meteosat. Nat. Hazards Earth Syst. Sci. 2018, 18, 515–529. [Google Scholar] [CrossRef]
- Pinto, M.M.; DaCamara, C.C.; Hurduc, A.; Trigo, R.M.; Trigo, I.F. Enhancing the fire weather index with atmospheric instability information. Environ. Res. Lett. 2020, 15, 0940b7. [Google Scholar] [CrossRef]
- Nunes, S.A.; DaCamara, C.C.; Turkman, K.F.; Calado, T.J.; Trigo, R.M.; Turkman, M.A.A. Wildland fire potential outlooks for Portugal using meteorological indices of fire danger. Nat. Hazards Earth Syst. Sci. 2019, 19, 1459–1470. [Google Scholar] [CrossRef]
- Bergonse, R.; Oliveira, S.; Gonçalves, A.; Nunes, S.; DaCamara, C.C.; Zêzere, J.L. A combined structural and seasonal approach to assess wildfire susceptibility and hazard in summertime. Nat. Hazards 2021, 106, 2545–2573. [Google Scholar] [CrossRef]
- Bergonse, R.; Oliveira, S.; Gonçalves, A.; Nunes, S.; DaCamara, C.C.; Zêzere, J.L. Predicting burnt areas during the summer season in Portugal by combining wildfire susceptibility and spring meteorological conditions. Geomat. Nat. Hazards Risk 2021, 12, 1039–1057. [Google Scholar] [CrossRef]
- LSA SAF: Wildfires. Available online: https://landsaf.ipma.pt/en/data/products/fire-products/ (accessed on 25 March 2024).
- Ceasefire: Customized Weather Information for Forest Fire Prevention, Planning and Fighting. Available online: https://www.ceasefire.pt/index.php?&l=eng (accessed on 25 March 2024).
- Santos, L.C.; Lima, M.M.; Bento, V.A.; Nunes, S.A.; DaCamara, C.C.; Russo, A.; Soares, P.M.M.; Trigo, R.M. An evaluation of the atmospheric instability effect on wildfire danger using ERA5 over the Iberian Peninsula. Fire 2023, 6, 120. [Google Scholar] [CrossRef]
- Libonati, R.; Trigo, I.F.; DaCamara, C.C. Assessment of fire weather index forecasts in continental Portugal. In Proceedings of the European Geosciences Union General Assembly 2005, Vienna, Austria, 24–29 April 2005; Available online: https://meetings.copernicus.org/www.cosis.net/abstracts/EGU05/04186/EGU05-J-04186.pdf (accessed on 25 March 2024).
- Liberato, M.L.R.; Paoletti, E.; DaCamara, C.C. Climate changes and forests. For. Ecol. Manag. 2011, 262, VII–IX. [Google Scholar] [CrossRef]
- Bento, V.A.; Gouveia, C.M.; DaCamara, C.C.; Trigo, I.F. A climatological assessment of drought impact on vegetation health index. Agric. For. Meteorol. 2018, 259, 286–295. [Google Scholar] [CrossRef]
- Nunes, S.A.; DaCamara, C.C.; Pereira, J.M.C.; Trigo, R.M. Assessing the role played by meteorological conditions on the interannual variability of fire activity in four subregions of Iberia. Int. J. Wildland Fire 2022, 32, 1529–1541. [Google Scholar] [CrossRef]
- Pereira, M.G.; Calado, T.J.; DaCamara, C.C.; Calheiros, T. Effects of regional climate change on rural fires in Portugal. Clim. Res. 2013, 57, 187–200. [Google Scholar] [CrossRef]
- Bento, V.A.; Lima, D.C.A.; Santos, L.C.; Lima, M.M.; Russo, A.; Nunes, S.A.; DaCamara, C.C.; Trigo, R.M.; Soares, P.M.M. The future of extreme meteorological fire danger under climate change scenarios for Iberia. Weather Clim. Extrem. 2023, 42, 100623. [Google Scholar] [CrossRef]
- Informação Estatística de Incêndios Rurais: Informação Oficial do SGIF (Statisical Information on Rural Fires: Oficial Information from SGIF). Available online: https://www.icnf.pt/florestas/gfr/gfrgestaoinformacao/estatisticas (accessed on 25 March 2024).
- Pereira, M.G.; Malamud, B.D.; Trigo, R.M.; Alves, P.I. The history and characteristics of the 1980–2005 Portuguese rural fire database. Nat. Hazards Earth Syst. Sci. 2011, 11, 3343–3358. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service, Climate Data Store. Fire Danger Indices Historical Data from the Copernicus Emergency Management Service. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2019. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/10.24381/cds.0e89c522?tab=overview (accessed on 25 March 2024).
- Fletcher, S.J. Data Assimilation for the Geosciences: From Theory to Application; Elsevier: Amsterdam, The Netherlands, 2017; pp. 101–107. [Google Scholar]
- Libonati, R.; Pereira, J.M.C.; DaCamara, C.C.; Peres, L.F.; Oom, D.; Rodrigues, J.A.; Santos, F.L.M.; Trigo, R.M.; Gouveia, C.M.; Machado-Silva, F.; et al. Twenty-first century droughts have not increasingly exacerbated fire season severity in the Brazilian Amazon. Sci. Rep. 2021, 11, 4400. [Google Scholar] [CrossRef]
- Bowman, D.M.J.S.; Balch, J.K.; Artaxo, P.; Bond, W.J.; Carlson, J.M.; Cochrane, M.A.; D’Antonio, C.M.; Defries, R.S.J.; Doyle, C.; Harrison, S.P.; et al. Fire in the Earth system. Science 2009, 324, 481–484. [Google Scholar] [CrossRef]
- Bowman, D.M.; Kolden, C.A.; Abatzoglou, J.T.; Johnston, F.H.; van der Werf, G.R.; Flannigan, M. Vegetation Fires in the Anthropocene. Nat. Rev. Earth Environ. 2020, 1, 500–515. [Google Scholar] [CrossRef]
- Moreno, J.M. (Ed.) Large Forest Fires; Backhuys Publishers: Leiden, The Netherlands, 1998; 239p, ISBN 978-9-073-34880-6. [Google Scholar]
- Scott, A.C.; Bowman, D.M.; Bond, W.J.; Pyne, S.J.; Alexander, M.E. Fire on Earth: An Introduction; Wiley Blackwell: Oxford, UK, 2013; 434p, ISBN 978-1-119-95356-2. [Google Scholar]
- Moreno, J.M. (Ed.) Forest Fires under Climate, Social and Economic Changes in Europe, the Mediterranean and Other Fire-Affected Areas of the World (FUME): Lessons Learned and Outlook; Calyptra Pty Ltd.: Adelaide, Australia, 2014; 56p, ISBN 978-84-695-9759-0. [Google Scholar]
- Rego, F.C.; Morgan, P.; Fernandes, P.; Hoffman, C. Fire Science: From Chemistry to Landscape Management; Springer Nature: Cham, Switzerland, 2021; 644p, ISBN 978-30-306-9814-0. [Google Scholar]
- Pyne, S.J. The Pyrocene: How We Created an Age of Fire, and What Happens Next; University of California Press: Berkeley, CA, USA, 2021; 192p, ISBN 978-05-203-8358-6. [Google Scholar]
- Dwyer, E.; Pereira, J.M.C.; Grégoire, J.-M.; DaCamara, C.C. Characterization of the spatio-temporal patterns of global fire activity using satellite imagery for the period April 1992 to March 1993. J. Biogeogr. 2000, 27, 57–69. [Google Scholar] [CrossRef]
- DaCamara, C.C.; Libonati, R.; Nunes, S.A.; de Zea Bermudez, P.; Pereira, J.M.C. Global-scale statistical modelling of the radiative power released by vegetation fires using a doubly truncated lognormal body distribution with generalized Pareto tails. Phys. A Stat. Mech. Appl. 2023, 625, 129049. [Google Scholar] [CrossRef]
- Andela, N.; Morton, D.C.; Giglio, L.; Paugam, R.; Chen, Y.; Hantson, S.; van der Werf, G.R.; Randerson, J.T. The Global Fire Atlas of individual fire size, duration, speed and direction. Earth Syst. Sci. Data 2019, 11, 529–552. [Google Scholar] [CrossRef]
- Andela, N.; Morton, D.C.; Giglio, L.; Chen, Y.; van der Werf, G.R.; Kasibhatla, P.S.; DeFries, R.S.; Collatz, G.J.; Hantson, S.; Kloster, S.; et al. A human-driven decline in global burned area. Science 2017, 356, 1356–1362. [Google Scholar] [CrossRef]
- Andreae, M.O. The Influence of Tropical Biomass Burning on Climate and the Atmospheric Environment. In Biogeochemistry of Global Change; Oremland, R.S., Ed.; Springer: New York, NY, USA, 1993; pp. 113–150. ISBN 978-04-120-3041-3. [Google Scholar]
- Crutzen, P.J.; Heidt, L.E.; Krasnec, J.P.; Pollock, W.H.; Seiler, W. Biomass Burning as a Source of Atmospheric Gases CO2, H2, N2O, NO, CH3Cl and COS. Nature 1979, 282, 253–256. [Google Scholar] [CrossRef]
- Cassou, C.; Cherchi, A.; Kosaka, Y. IPCC Annex IV: Modes of Variability. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 2153–2192. [Google Scholar] [CrossRef]
- Corte-Real, J.A.M.; Prates, F.; DaCamara, C.C. Sensitivity to Initial Conditions in Long-time Integrations of a Barotropic Unforced Flow Model. In Proceedings of the XVII General Assembly of the European Geophysical Society, Wiesbaden, Germany, 3–7 May 1993. [Google Scholar]
- Castanheira, J.M.; Graf, H.-F.; DaCamara, C.C.; Rocha, A. Using a physical reference frame to study global circulation variability. J. Atmos. Sci. 2002, 59, 1490–1501. [Google Scholar] [CrossRef]
- Le Page, Y.; Pereira, J.M.C.; Trigo, R.M.; DaCamara, C.C.; Oom, D.; Mota, B. Global fire activity patterns (1996–2006) and climatic influence: An analysis using the World Fire Atlas. Atmos. Chem. Phys. 2008, 8, 1911–1924. [Google Scholar] [CrossRef]
- DaCamara, C.C.; Kung, E.C.; Baker, W.E.; Lee, B.-C.; Corte-Real, J.A.M. Long-term analysis of planetary wave activities and blocking circulation in the Northern Hemisphere winter. Beiträge Zur Phys. Atm 1992, 64, 285–298. [Google Scholar]
- Trigo, R.M.; Trigo, I.F.; DaCamara, C.C.; Osborn, T.J. Climate impact of the European winter blocking episodes from the NCEP/NCAR Reanalyses. Clim. Dyn. 2004, 23, 17–28. [Google Scholar] [CrossRef]
- Damião, M.C.M.; Trigo, R.M.; Cavalcanti, I.F.A.; DaCamara, C.C. Blocking episodes in the Southern Hemisphere: Impact on the climate of adjacent continental areas. Pure Appl. Geophys. 2008, 165, 1941–1962. [Google Scholar] [CrossRef]
- Cruz, J.B.; Castanheira, J.M.; DaCamara, C.C. Local identification of equatorial Kelvin waves in real-time operational forecasts. Q. J. R. Meteorol. Soc. 2024, 150, 2440–2457. [Google Scholar] [CrossRef]
- Kung, E.C.; DaCamara, C.C.; Baker, W.E.; Susskind, J.; Park, C.-K. Simulations of winter blocking episodes using observed sea surface temperatures. Q. J. R. Meteorol. Soc. 1990, 116, 1053–1070. [Google Scholar] [CrossRef]
- Kung, E.C.; Susskind, J.; DaCamara, C.C. Prominent Northern Hemisphere winter blocking episodes and associated anomaly fields of sea surface temperatures. TAO 1993, 4, 273–291. [Google Scholar] [CrossRef]
- Dale, V.H.; Joyce, L.A.; McNulty, S.; Neilson, R.P.; Ayres, M.P.; Flannigan, M.D.; Hanson, P.J.; Irland, L.C.; Lugo, A.E.; Peterson, C.J.; et al. Climate Change and Forest Disturbances. BioScience 2001, 51, 723–734. [Google Scholar] [CrossRef]
- Silva, P.S.; Bastos, A.; Libonati, R.; Rodrigues, J.A.; DaCamara, C.C. Impacts of the 1.5 °C global warming target on future burned area in the Brazilian Cerrado. For. Ecol. Manag. 2019, 446, 193–203. [Google Scholar] [CrossRef]
- Silva, P.S.; Libonati, R.; Schmidt, I.B.; Nogueira, J.; DaCamara, C.C. Climate Change and Fire: The Case of Cerrado, the Brazilian Savanna. In Climate Change and Regional Socio-Economic Systems in the Global South; Mishra, M., de Lucena, A.J., Maharaj, B., Eds.; Springer: Singapore, 2014; pp. 87–105. [Google Scholar] [CrossRef]
- Libonati, R.; DaCamara, C.C.; Peres, L.F.; Sander de Carvalho, L.A.; Garcia, L.C. Rescue Brazil’s burning Pantanal wetlands. Nature 2020, 588, 217–219. [Google Scholar] [CrossRef] [PubMed]
- Chuvieco, E. (Ed.) Earth Observations of Wildland Fires in Mediterranean Ecosystems; Springer: Berlin/Heidelberg, Germany, 2009; 257p, ISBN 978-3-642-01753-7. [Google Scholar]
- Requardt, A.; Schuck, A.; Köhl, M. Means of combating forest dieback—EU support for maintaining forest health and vitality. iForest 2009, 2, 38–42. [Google Scholar] [CrossRef]
- Giorgi, F. Climate change hot-spots. Geophys. Res. Lett. 2006, 33, L08707. [Google Scholar] [CrossRef]
- Pausas, J.G.; Fernández-Muñoz, S. Fire regime changes in the Western Mediterranean Basin: From fuel-limited to drought-driven fire regime. Clim. Chang. 2011, 110, 215–226. [Google Scholar] [CrossRef]
- Lavorel, S.; Flannigan, M.D.; Lambin, E.F.; Scholes, M.C. Vulnerability of land systems to fire: Interactions among humans, climate, the atmosphere and ecosystems. Mitig. Adapt. Strat. Glob. Chang. 2006, 12, 33–53. [Google Scholar] [CrossRef]
- Fernandes, P.M. Fire-smart management of forest landscapes in the Mediterranean basin under global change. Landscape Urban Plan. 2013, 110, 175–182. [Google Scholar] [CrossRef]
- DaCamara, C.C.; Bento, V.A.; Nunes, S.A.; Lemos, G.; Soares, P.M.M.; Trigo, R.M. Impacts of fire prevention strategies in a changing climate: An assessment for Portugal. Environ. Res. Clim. 2024, 3, 045002. [Google Scholar] [CrossRef]
- Silva, P.S.; Rodrigues, J.A.; Nogueira, J.; Moura, L.C.; Enout, A.; Cuiabália, C.; DaCamara, C.C.; Pereira, A.A.; Libonati, R. Joining forces to fight wildfires: Science and management in a protected area of Pantanal, Brazil. Environ. Sci. Policy 2024, 159, 103818. [Google Scholar] [CrossRef]
- Forster, P.M.; Smith, C.; Walsh, T.; Lamb, W.F.; Lamboll, R.; Hall, B.; Hauser, M.; Ribes, A.; Rosen, D.; Gillett, N.P.; et al. Indicators of Global Climate Change 2023: Annual update of key indicators of the state of the climate system and human influence. Earth Syst. Sci. Data 2024, 16, 2625–2658. [Google Scholar] [CrossRef]
- Ward, D.S.; Kloster, S.; Mahowald, N.M.; Rogers, B.M.; Randerson, J.T.; Hess, P.G. The changing radiative forcing of fires: Global model estimates for past, present and future. Atmos. Chem. Phys. 2012, 12, 10857–10886. [Google Scholar] [CrossRef]




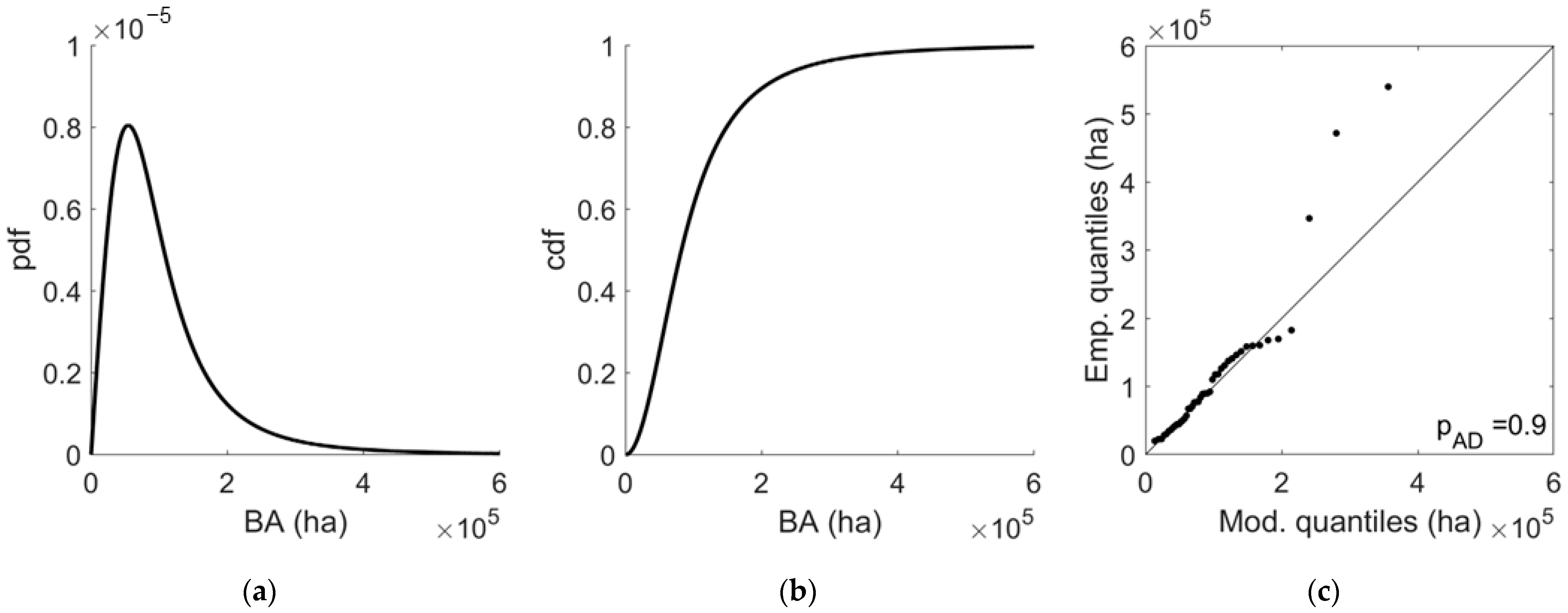
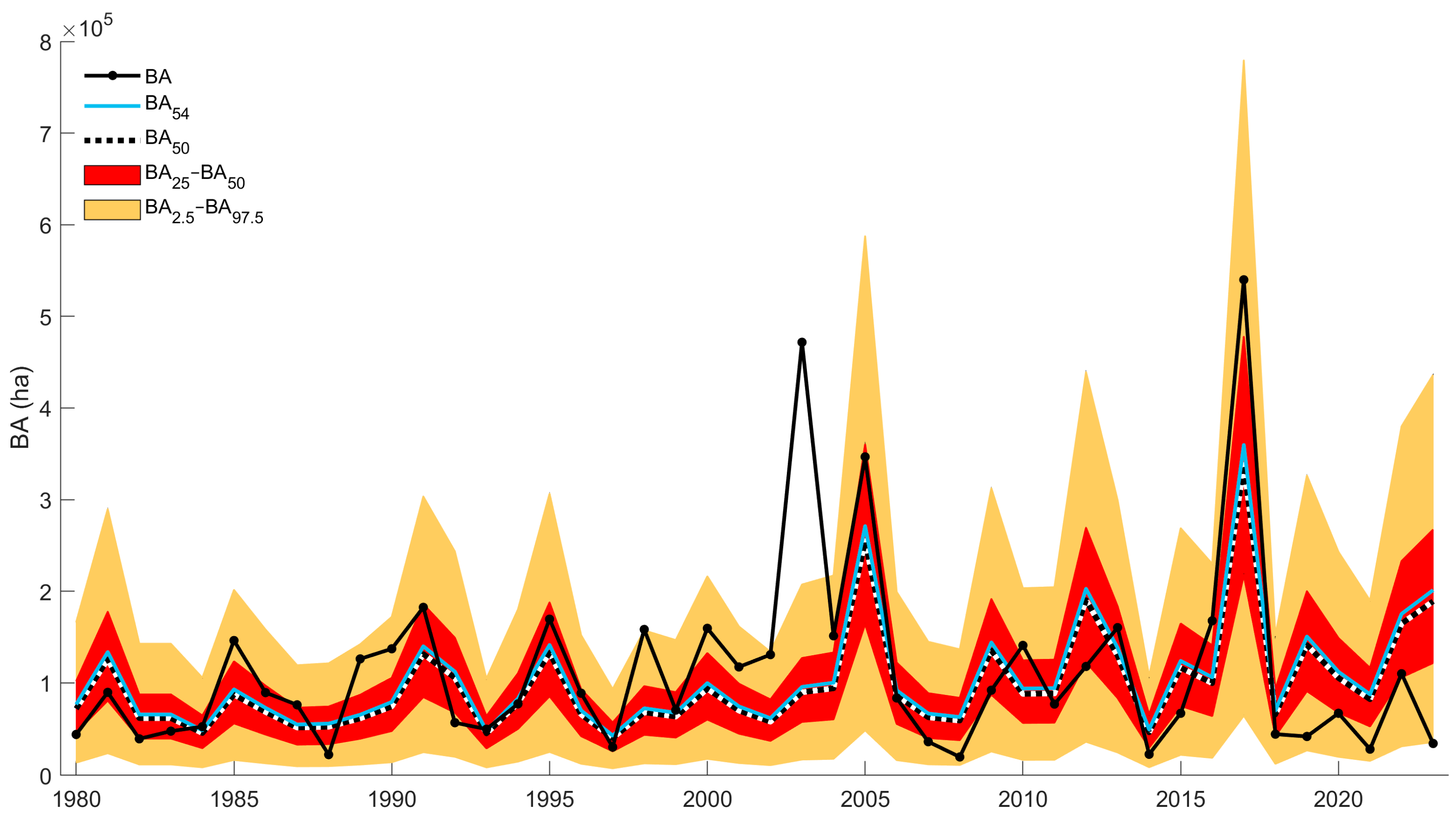
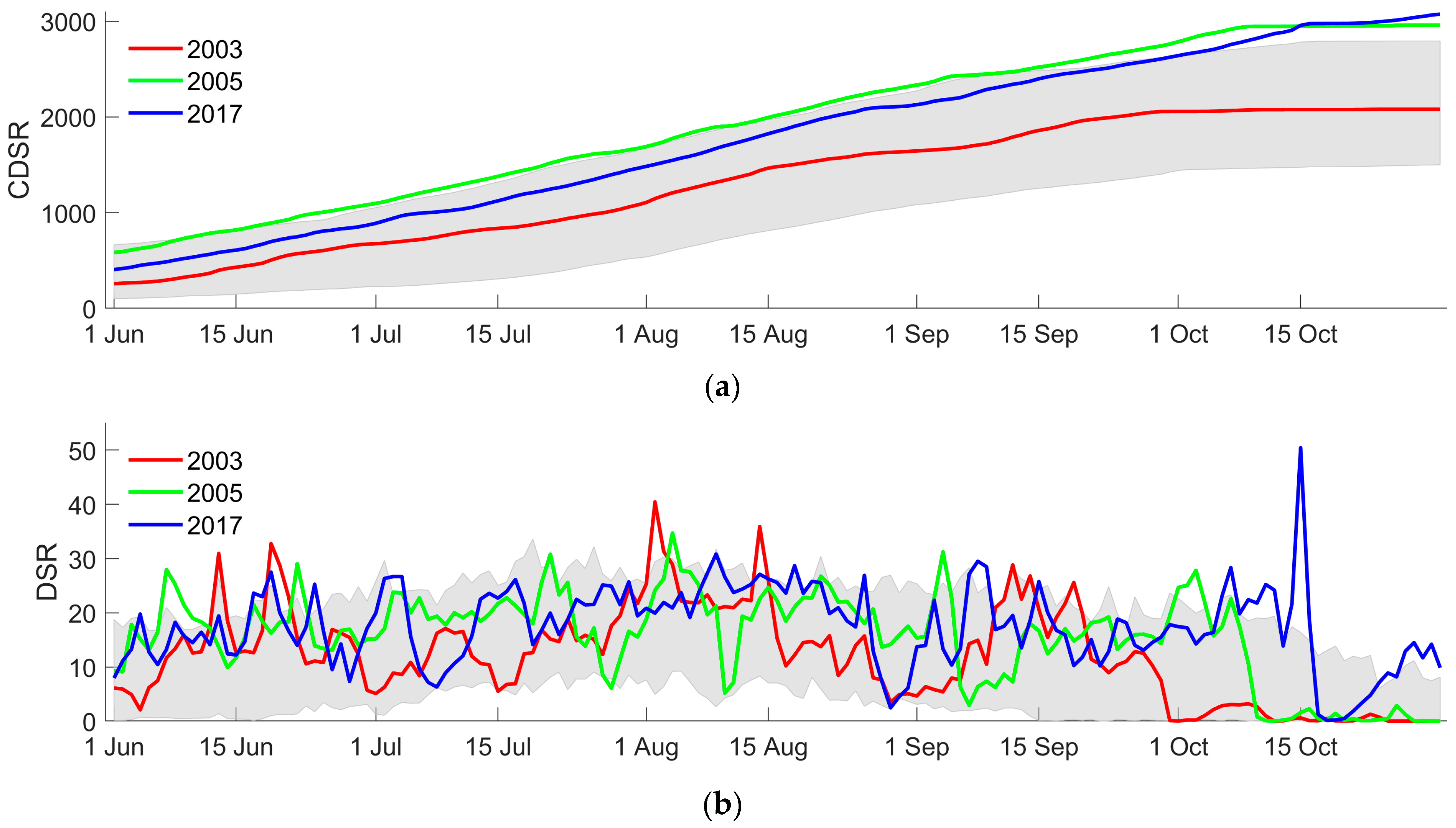
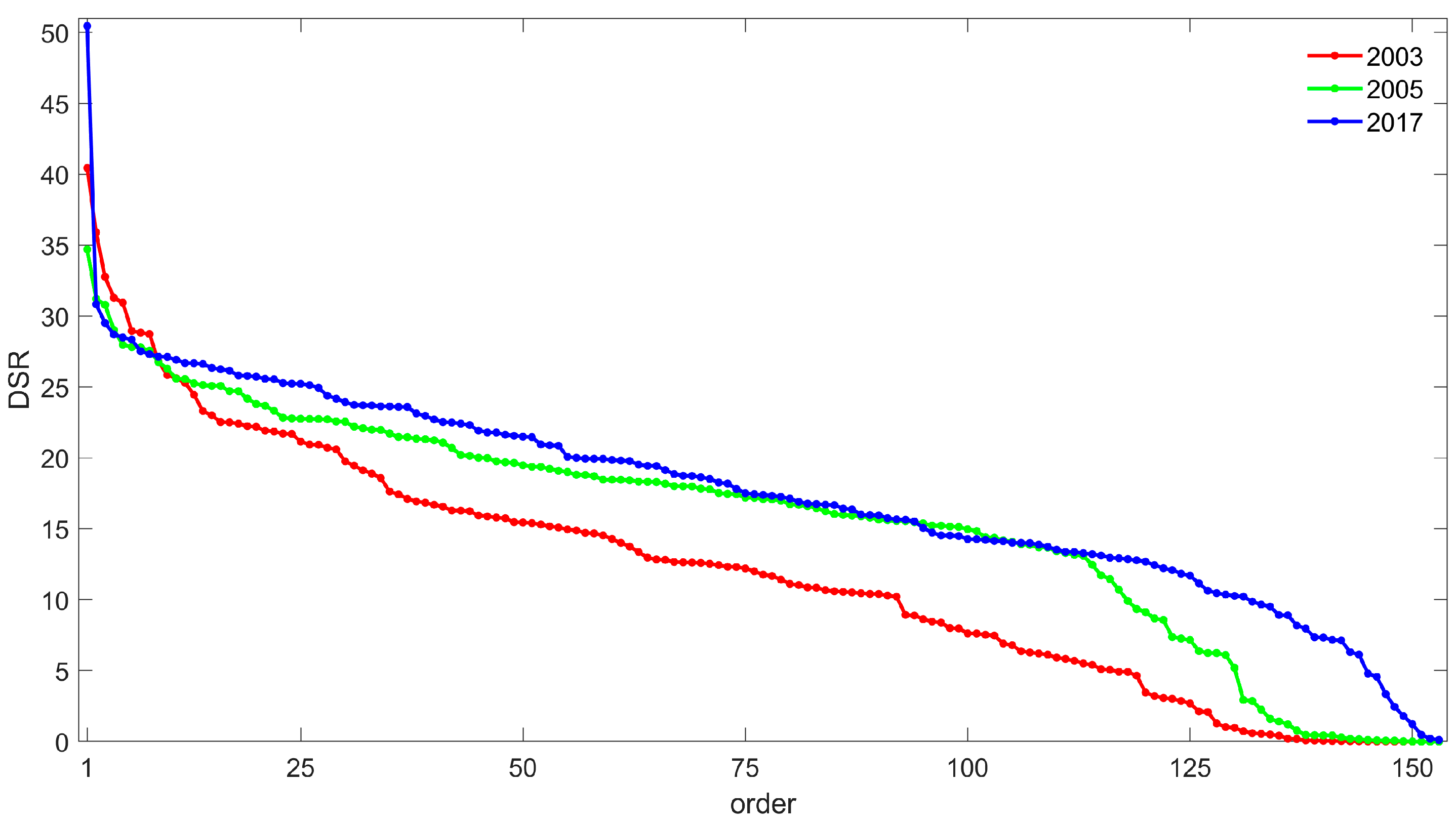

| Title 1 | 1980–2023 * | 1980–2001 | 2002–2023 |
|---|---|---|---|
| Mean () | 113,356 [88,519] ha | 92,450 ha | 134,263 |
| Median () | 86,287 [77,323] ha | 83,095 ha | 87,916 |
| 1st quartile () | 46,195 [44,496] ha | 49,963 ha | 42,084 ha |
| 2nd quartile () | 143,604 [132,450] ha | 137,252 ha | 151,370 ha |
| Standard deviation () | 106,343 [49,023] ha | 49,314 ha | 140,743 |
| Mean to median ratio () | 1.31 [1.14] | 1.11 | 1.53 |
| Coefficient of variation () | 0.94 [0.55] | 0.53 | 1.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
DaCamara, C.C. The Signature of Climate in Annual Burned Area in Portugal. Climate 2024, 12, 143. https://doi.org/10.3390/cli12090143
DaCamara CC. The Signature of Climate in Annual Burned Area in Portugal. Climate. 2024; 12(9):143. https://doi.org/10.3390/cli12090143
Chicago/Turabian StyleDaCamara, Carlos C. 2024. "The Signature of Climate in Annual Burned Area in Portugal" Climate 12, no. 9: 143. https://doi.org/10.3390/cli12090143
APA StyleDaCamara, C. C. (2024). The Signature of Climate in Annual Burned Area in Portugal. Climate, 12(9), 143. https://doi.org/10.3390/cli12090143






