Artificial Neural Networks for Drought Forecasting in the Central Region of the State of Zacatecas, Mexico
Abstract
1. Introduction
2. Materials and Methods
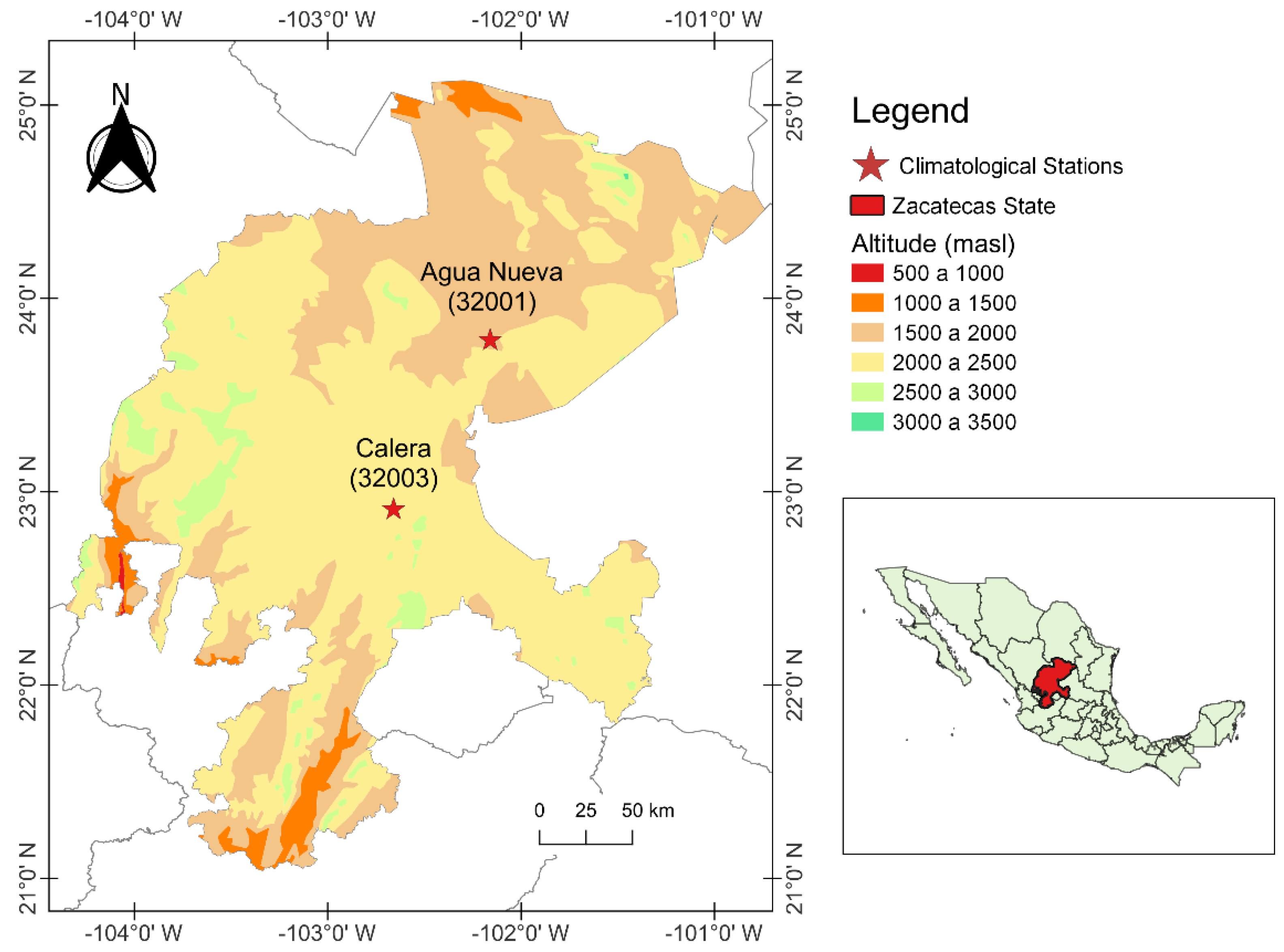
2.1. Description of the Study Area
2.2. Description of Data
2.3. Potential Evapotranspiration
2.4. Drought Indices
2.4.1. Standardized Precipitation Index
2.4.2. Standardized Precipitation and Evapotranspiration Index
2.4.3. Drought Reconnaissance Index
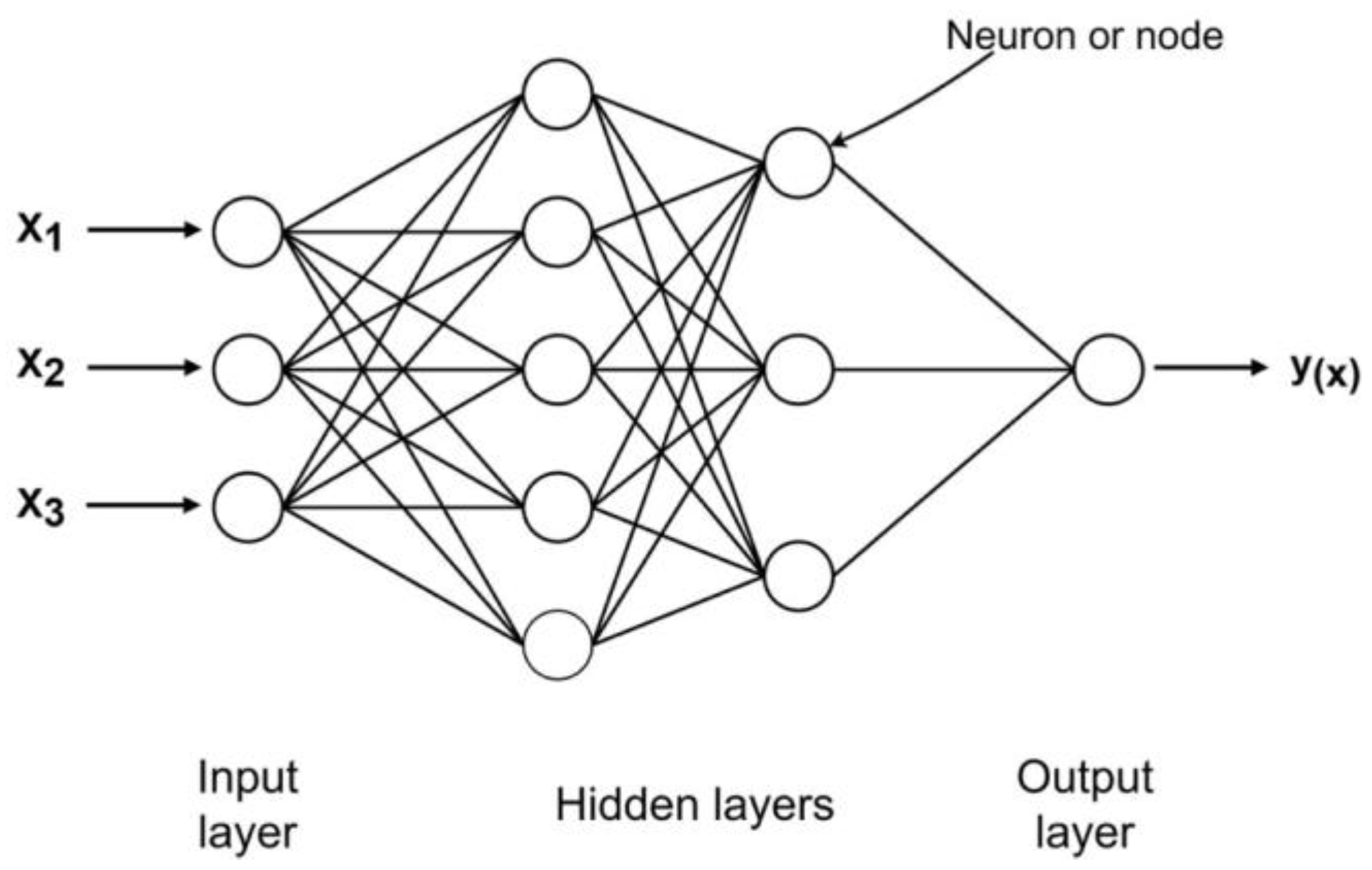
2.5. Artificial Neural Networks
2.6. Development of the MLP Models
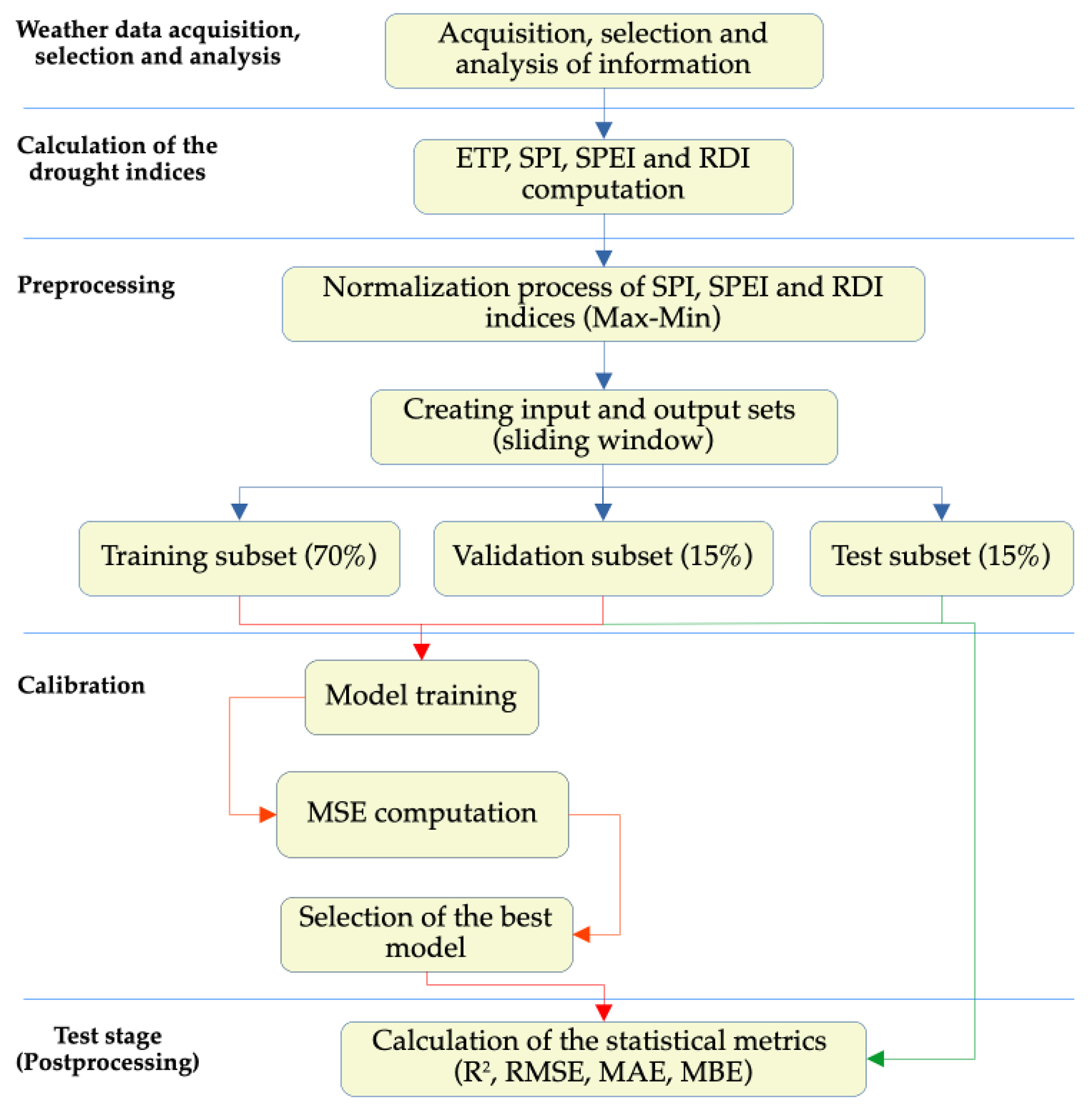
2.6.1. Data Preprocessing
2.6.2. Model Calibration
2.6.3. Model Evaluation
- Determination Coefficient
- Root Mean Squared Error
- Mean Absolute Error
- Mean Bias Error
2.7. Programming Tools
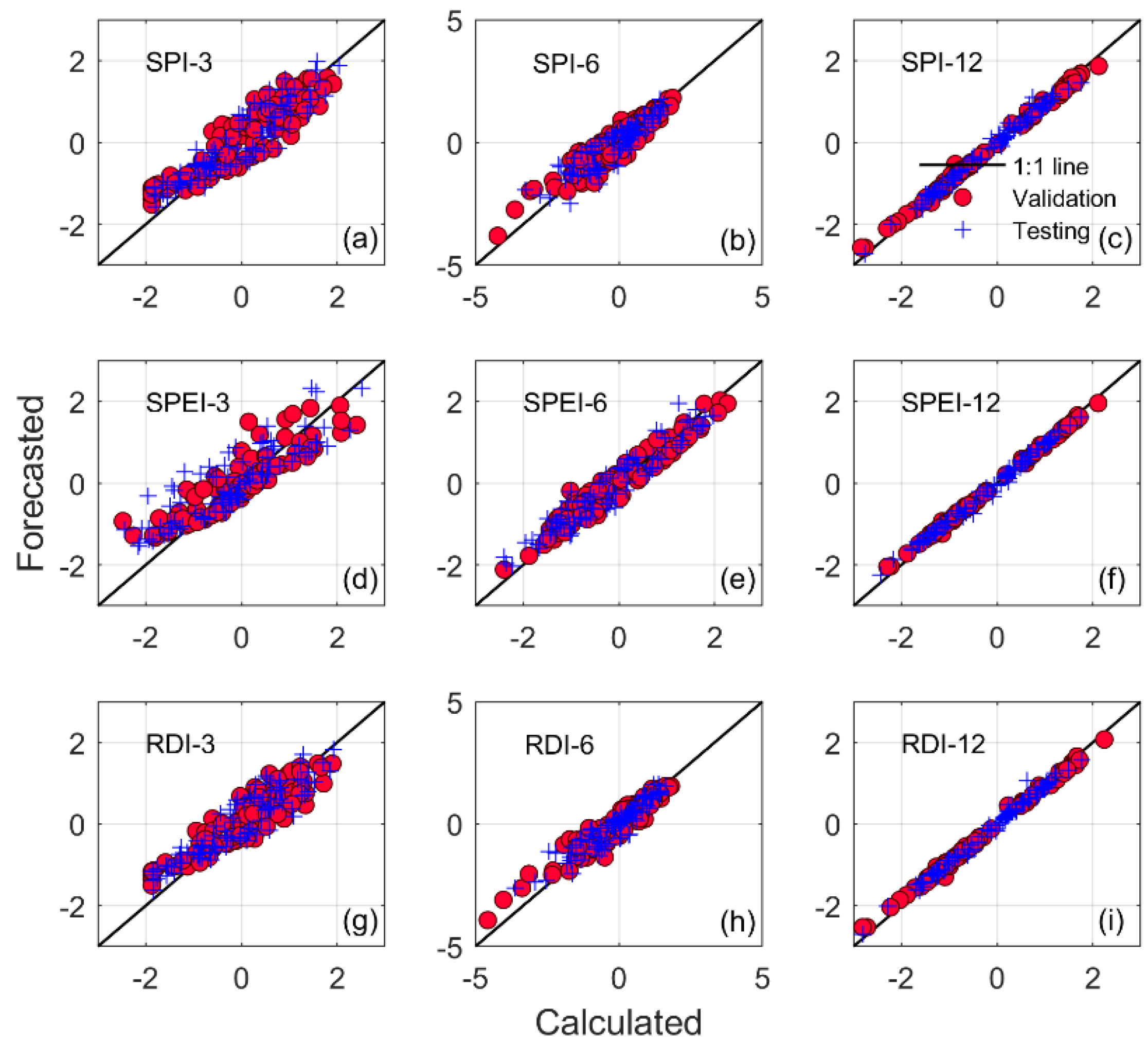
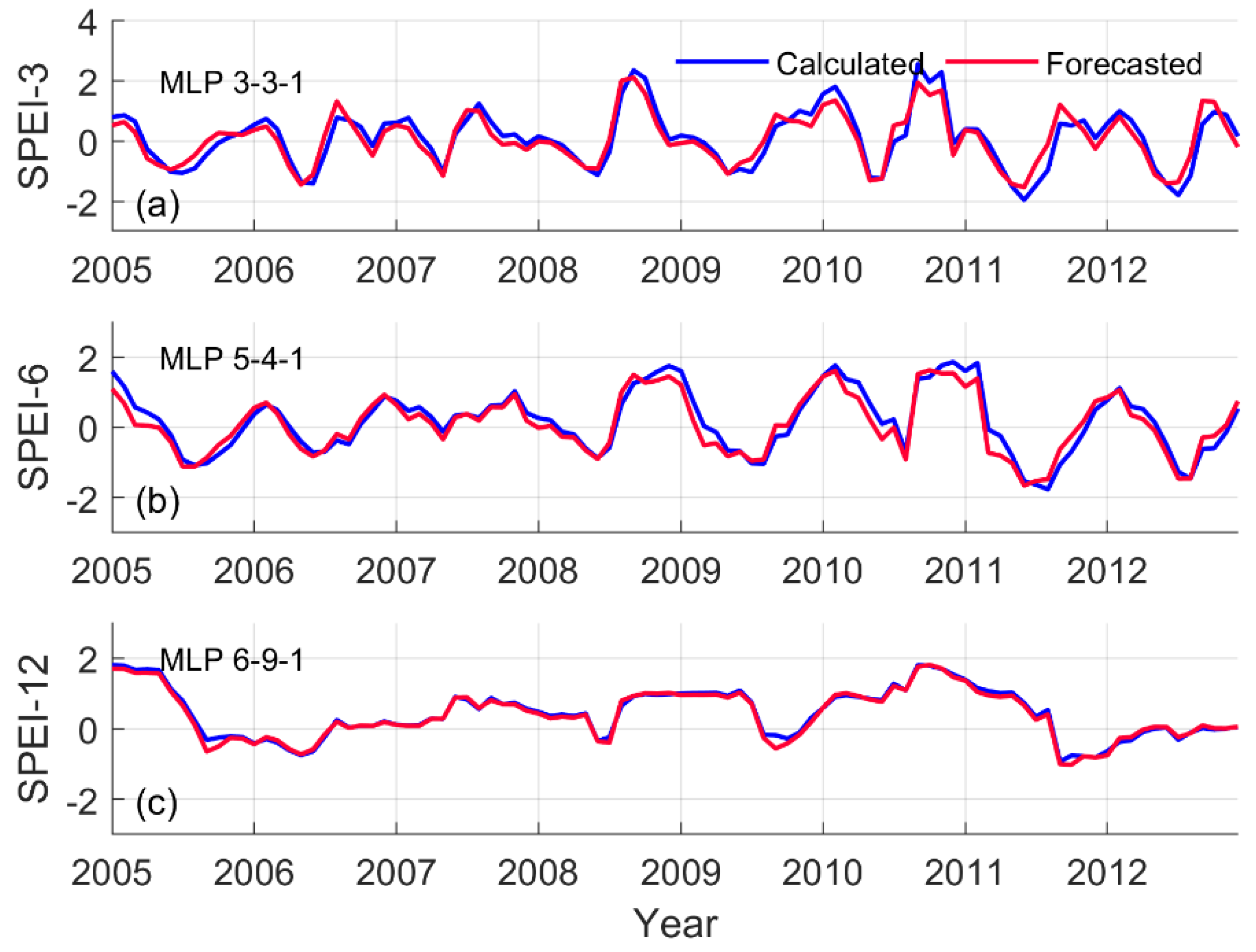
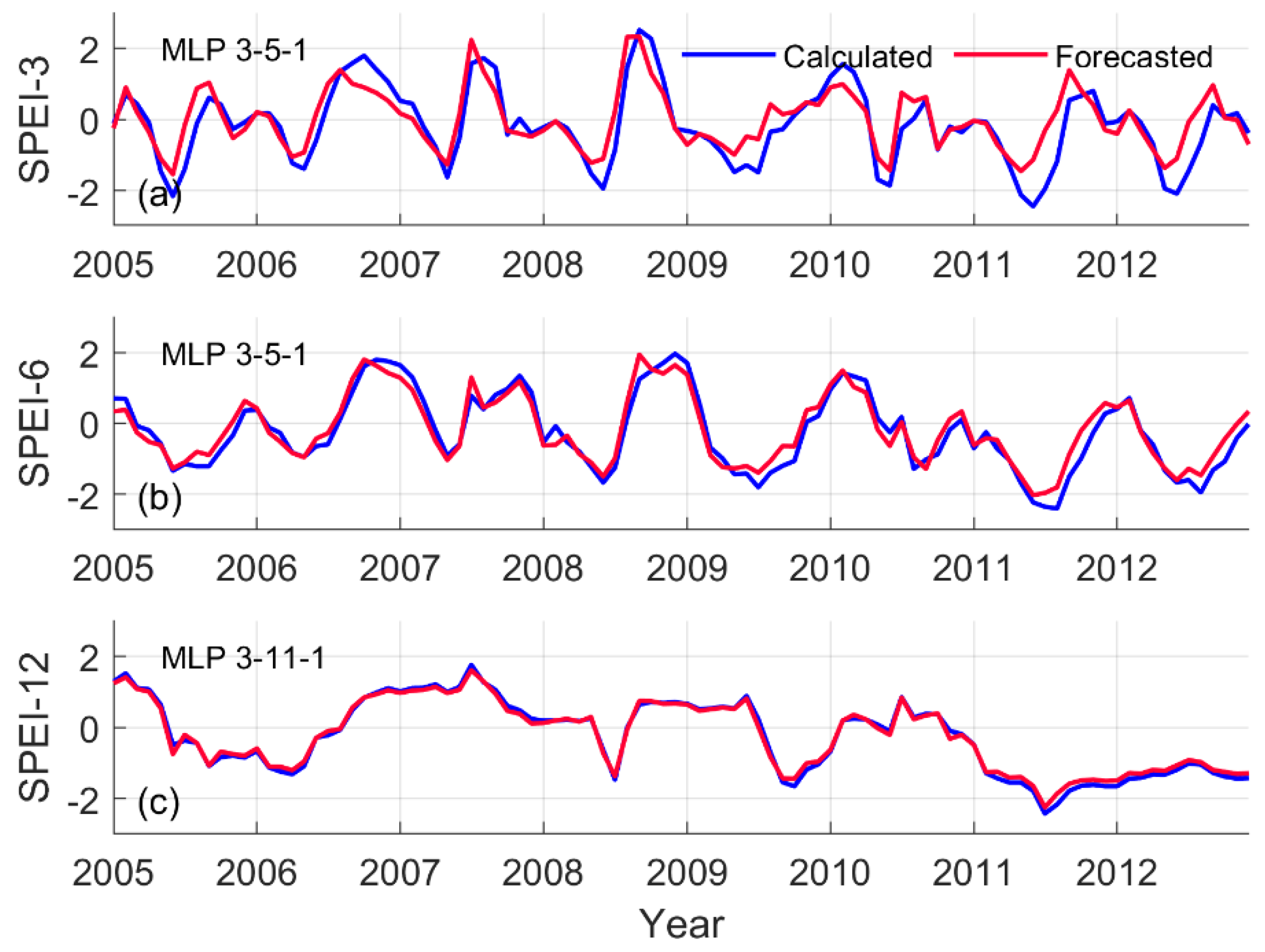
3. Results and Discussion
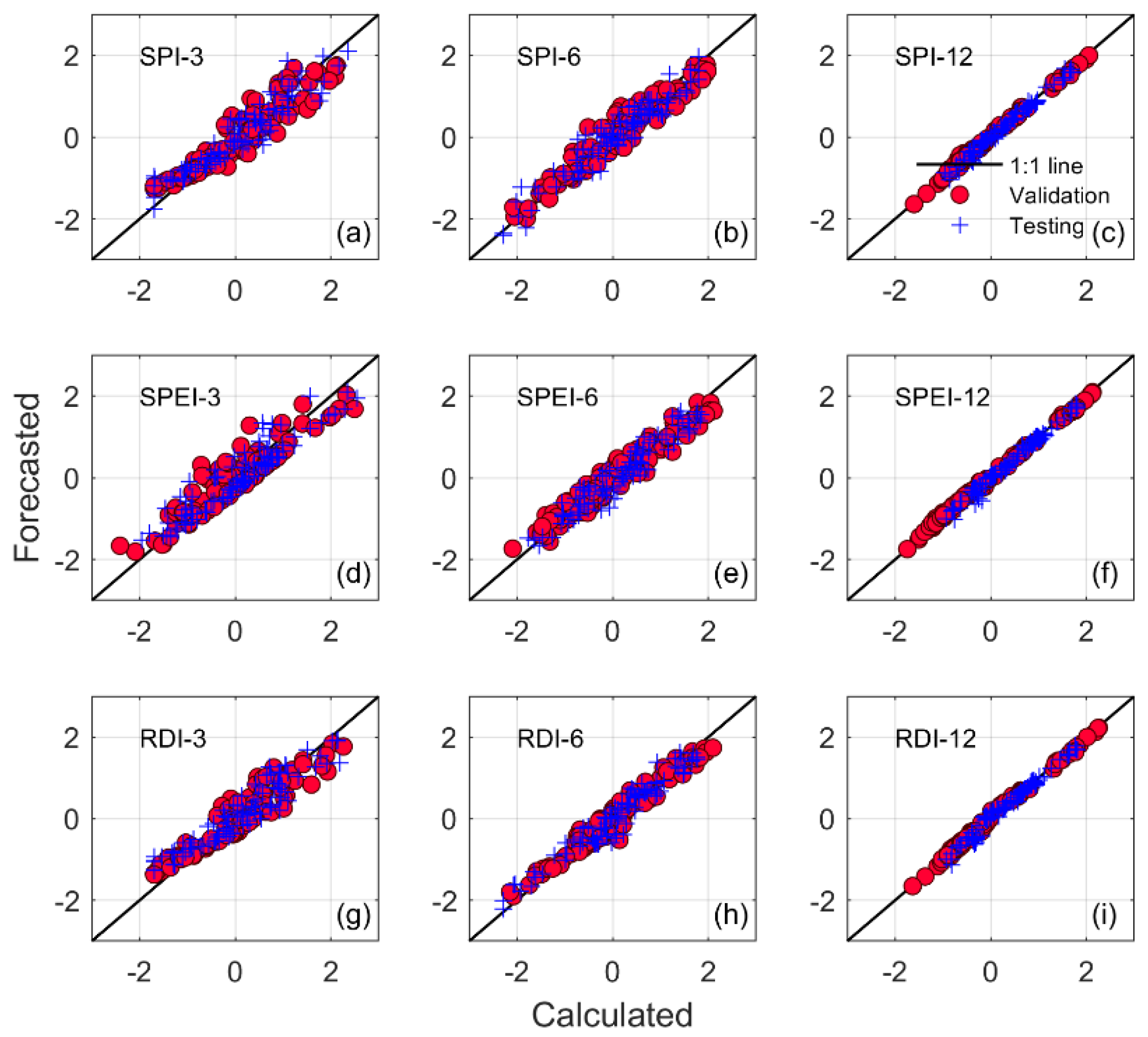
3.1. Calibration Stage
3.2. Trial Stage
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dukat, P.; Bednorz, E.; Ziemblińska, K.; Urbaniak, M. Trends in drought occurrence and severity at mid-latitude European stations (1951–2015) estimated using standardized precipitation (SPI) and precipitation and evapotranspiration (SPEI) indices. Meteorol. Atmos. Phys. 2022, 134, 20. [Google Scholar] [CrossRef]
- Dubrovsky, M.; Svoboda, M.D.; Trnka, M.; Hayes, M.J.; Wilhite, D.A.; Zalud, Z.; Hlavinka, P. Application of relative drought indices in assessing climate-change impacts on drought conditions in Czechia. Theor. Appl. Climatol. 2009, 96, 155–171. [Google Scholar] [CrossRef]
- Jiang, R.; Xie, J.; He, H.; Luo, J.; Zhu, J. Use of four drought indices for evaluating drought characteristics under climate change in Shaanxi, China: 1951–2012. Nat. Hazards 2014, 75, 2885–2903. [Google Scholar] [CrossRef]
- Xiao, M.; Zhang, Q.; Singh, V.P.; Chen, X. Probabilistic forecasting of seasonal drought behaviors in the Huai River basin, China. Theor. Appl. Climatol. 2017, 128, 667–677. [Google Scholar] [CrossRef]
- Dumitraşcu, M.; Mocanu, I.; Mitrică, B.; Dragotă, C.; Grigorescu, I.; Dumitrica, C. The assessment of socio-economic vulnerability to drought in Southern Romania (Oltenia Plain). Int. J. Disaster Risk Reduct. 2018, 27, 142–154. [Google Scholar] [CrossRef]
- Zhang, Q.; Yu, H.; Sun, P.; Singh, V.P.; Shi, P. Multisource data based agricultural drought monitoring and agricultural loss in China. Glob. Planet. Change 2019, 172, 298–306. [Google Scholar] [CrossRef]
- Zhao, C.; Brissette, F.; Chen, J.; Martel, J.-L. Frequency change of future extreme summer meteorological and hydrological droughts over North America. J. Hydrol. 2020, 584, 124316. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations (FAO). Impact of Disasters and Crises on Agriculture and Food Security, 2017; FAO: Roma, Italy, 2018; p. 143. [Google Scholar]
- Lobato Sánchez, R.; Altamirano del Carmen, M.Á.; Hoyos Reyes, C.; López Pérez, M.; Salas Salinas, M.A.; Rosario de la Cruz, J.G. Methodological procedure for a persistence drought monitor in Mexico. Tecnol. Cienc. Agua 2019, 10, 146–176. [Google Scholar] [CrossRef]
- Pendergrass, A.G.; Knutti, R.; Lehner, F.; Deser, C.; Sanderson, B.M. Precipitation variability increases in a warmer climate. Sci. Rep. 2017, 7, 17966. [Google Scholar] [CrossRef] [PubMed]
- Siddique, R.; Karmalkar, A.; Sun, F.; Palmer, R. Hydrological extremes across the Commonwealth of Massachusetts in a changing climate. J. Hydrol.-Reg. Stud. 2020, 32, 100733. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. [Google Scholar]
- Dai, A. Increasing drought under global warming in observations and models. Nat. Clim. Chang. 2013, 3, 52–58. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, J. Future global socioeconomic risk to droughts based on estimates of hazard, exposure, and vulnerability in a changing climate. Sci. Total Environ. 2021, 751, 142159. [Google Scholar] [CrossRef] [PubMed]
- Akhtari, R.; Morid, S.; Mahdian, M.H.; Smakhtin, V. Assessment of areal interpolation methods for spatial analysis of SPI and EDI drought indices. Int. J. Climatol. 2009, 29, 135–145. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J.; Khalil, B.; Ozga-Zielinski, B. Long-term SPI drought forecasting in the Awash River Basin in Ethiopia using wavelet neural networks and wavelet support vector regression models. J. Hydrol. 2014, 508, 418–429. [Google Scholar] [CrossRef]
- Kousari, M.R.; Hosseini, M.E.; Ahani, H.; Hakimelahi, H. Introducing an operational method to forecast long-term regional drought based on the application of artificial intelligence capabilities. Theor. Appl. Climatol. 2017, 127, 361–380. [Google Scholar] [CrossRef]
- Danandeh Mehr, A.; Kahya, E.; Özger, M. A gene–wavelet model for long lead time drought forecasting. J. Hydrol. 2014, 517, 691–699. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the Eighth Conference on Applied Climatology, American Meteorological Society, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- Tsakiris, G.; Vangelis, H. Establishing a drought index incorporating evapotranspiration. Eur. Water 2005, 9/10, 3–11. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Esquivel-Arriaga, G.; Cerano-Paredes, J.; Sánchez-Cohen, I.; Velásquez-Valle, M.A.; Flores-López, F.; Bueno-Hurtado, P. Temporal analysis of droughts (1922-2016) in the upper Nazas River Basin using SPI and its relationship with ENSO. Tecnol. Cienc. Agua 2019, 10, 126–153. [Google Scholar] [CrossRef]
- Magallanes-Quintanar, R.; Galván-Tejada, C.E.; Galván-Tejada, J.I.; Méndez-Gallegos, S.J.; Blanco-Macías, F.; Valdez-Cepeda, R.D. Artificial neural network models for prediction of standardized precipitation index in central Mexico. Agrociencia-Mexico 2023, 57, 177–207. [Google Scholar] [CrossRef]
- Hernández-Vásquez, C.C.; Ibáñez-Castillo, L.A.; Arteaga-Ramírez, R.; Monterroso-Rivas, A.I.; Cervantes-Osornio, R. Forecast of meteorological droughts with neural networks in Sonora watershed, Mexico. Tecnol. Cienc. Agua 2022, 13, 242–292. [Google Scholar] [CrossRef]
- Ortiz-Gómez, R.; Cardona-Diaz, J.C.; Ortiz-Robles, F.A.; Alvarado-Medellin, P. Characterization of droughts by comparing three multiscale indices in Zacatecas, Mexico. Tecnol. Cienc. Agua 2018, 9, 47–91. [Google Scholar] [CrossRef]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep learning with a long short-term memory networks approach for rainfall-runoff simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef]
- Mokhtar, A.; Jalali, M.; He, H.; Al-Ansari, N.; Elbeltagi, A.; Alsafadi, K.; Abdo, H.; Sammen, S.S.; Gyasi-Agyei, Y.; Rodrigo-Comino, J. Estimation of SPEI meteorological drought using machine learning algorithms. IEEE Access 2021, 9, 65503–65523. [Google Scholar] [CrossRef]
- Almikaeel, W.; Čubanová, L.; Šoltész, A. Hydrological drought forecasting using machine learning—Gidra River case study. Water 2022, 14, 387. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, W.; Chen, Q.; Pu, X.; Xiang, L. Multi-models for SPI drought forecasting in the north of Haihe River Basin, China. Stoch. Environ. Res. Risk Assess. 2017, 31, 2471–2481. [Google Scholar] [CrossRef]
- Maca, P.; Pech, P. Forecasting SPEI and SPI drought indices using the integrated artificial neural networks. Comput. Intell. Neurosci. 2016, 2016, 3868519. [Google Scholar] [CrossRef]
- Poornima, S.; Pushpalatha, M. Drought prediction based on SPI and SPEI with varying timescales using LSTM recurrent neural network. Soft Comput. 2019, 23, 8399–8412. [Google Scholar] [CrossRef]
- Yan, D.; Jiang, R.; Xie, J.; Zhao, Y.; Zhu, J.; Liang, J. Characteristics and prediction of extreme drought event using LSTM model in Wei River Basin. Terr. Atmos. Ocean. Sci. 2021, 32, 261–274. [Google Scholar] [CrossRef]
- Shrivastava, S.; Kiran, R.U.; Bal, P.K.; Singh, K.K. Estimation of the standardized precipitation evapotranspiration index (SPEI) using a multilayer perceptron artificial neural network model for Central India. Pure Appl. Geophys. 2022, 179, 1461–1473. [Google Scholar] [CrossRef]
- Choubin, B.; Malekian, A.; Golshan, M. Application of several data-driven techniques to predict a standardized precipitation index. Atmosfera 2016, 29, 121–128. [Google Scholar] [CrossRef]
- Achite, M.; Gul, E.; Elshaboury, N.; Jehanzaib, M.; Mohammadi, B.; Danandeh Mehr, A. An improved adaptive neuro-fuzzy inference system for hydrological drought prediction in Algeria. Phys. Chem. Earth 2023, 131, 103451. [Google Scholar] [CrossRef]
- Das, P.; Naganna, S.R.; Deka, P.C.; Pushparaj, J. Hybrid wavelet packet machine learning approaches for drought modeling. Environ. Earth Sci. 2020, 79, 221. [Google Scholar] [CrossRef]
- Fung, K.F.; Huang, Y.F.; Koo, C.H.; Mirzaei, M. Improved SVR machine learning models for agricultural drought prediction at downstream of Langat River Basin, Malaysia. J. Water Clim. Chang. 2020, 11, 1383–1398. [Google Scholar] [CrossRef]
- Shamshirband, S.; Hashemi, S.; Salimi, H.; Samadianfard, S.; Asadi, E.; Shadkani, S.; Kargar, K.; Mosavi, A.; Nabipour, N.; Chau, K.-W. Predicting standardized streamflow index for hydrological drought using machine learning models. Eng. Appl. Comput. Fluid Mech. 2020, 14, 339–350. [Google Scholar] [CrossRef]
- Mouatadid, S.; Raj, N.; Deo, R.C.; Adamowski, J.F. Input selection and data-driven model performance optimization to predict the standardized precipitation and evaporation index in a drought-prone region. Atmos. Res. 2018, 212, 130–149. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Ali, M.; Sharafati, A.; Al-Ansari, N.; Shahid, S. Forecasting standardized precipitation index using data intelligence models: Regional investigation of Bangladesh. Sci. Rep. 2021, 11, 3435. [Google Scholar] [CrossRef]
- Karbasi, M.; Karbasi, M.; Jamei, M.; Malik, A.; Azamathulla, H.M. Development of a new wavelet-based hybrid model to forecast multi-scalar SPEI drought index (case study: Zanjan city, Iran). Theor. Appl. Climatol. 2022, 147, 499–522. [Google Scholar] [CrossRef]
- Khan, M.M.H.; Muhammad, N.S.; El-Shafie, A. Wavelet based hybrid ANN-ARIMA models for meteorological drought forecasting. J. Hydrol. 2020, 590, 125380. [Google Scholar] [CrossRef]
- Truong, V.-H.; Ly, Q.V.; Le, V.-C.; Vu, T.-B.; Le, T.-T.-T.; Tran, T.-T.; Goethals, P. Machine learning-based method for forecasting water levels in irrigation and drainage systems. Environ. Technol. Innov. 2021, 23, 101762. [Google Scholar] [CrossRef]
- Kumar, V.; Kedam, N.; Sharma, K.V.; Mehta, D.J.; Caloiero, T. Advanced machine learning techniques to improve hydrological prediction: A comparative analysis of streamflow prediction models. Water 2023, 15, 2572. [Google Scholar] [CrossRef]
- Shams, M.Y.; Elshewey, A.M.; El-kenawy, E.-S.M.; Ibrahim, A.; Talaat, F.M.; Tarek, Z. Water quality prediction using machine learning models based on grid search method. Multimed. Tools Appl. 2024, 83, 35307–35334. [Google Scholar] [CrossRef]
- Khan, A.A.; Madendran, R.K.; Thirunavukkarasu, U.; Faheem, M. D2PAM: Epileptic seizures prediction using adversarial deep dual patch attention mechanism. CAAI Trans. Intell. Technol. 2023, 8, 755–769. [Google Scholar] [CrossRef]
- Onyango, A.; Okelo, B.; Omollo, R. Topological data analysis of COVID-19 using artificial intelligence and machine learning techniques in big datasets of hausdorff spaces. J. Data Sci. Intell. Syst. 2023, 1, 55–64. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, H.; Wu, Y.; Ren, S.; Diaty, D.M.; Fu, Y.; Zou, Y.; Zhang, L.; Wang, Z.; Wang, F.; et al. Predicting recurrence in osteosarcoma via a quantitative histological image classifier derived from tumour nuclear morphological features. CAAI Trans. Intell. Technol. 2023, 8, 836–848. [Google Scholar] [CrossRef]
- Achour, K.; Meddi, M.; Zeroual, A.; Bouabdelli, S.; Maccioni, P.; Moramarco, T. Spatio-temporal analysis and forecasting of drought in the plains of northwestern Algeria using the standardized precipitation index. J. Earth Syst. Sci. 2020, 129, 42. [Google Scholar] [CrossRef]
- Ravelo, A.C.; Sanz, R.R.; Douriet, C.J.C. Detección, evaluación y pronóstico de las sequías en la región del Organismo de Cuenca Pacífico Norte, México. Agriscientia 2014, 31, 11–24. [Google Scholar] [CrossRef]
- Instituto Nacional de Estadística y Geografía (INEGI). Anuario Estadístico y Geográfico de Zacatecas 2017; Instituto Nacional de Estadística y Geografía: Aguascalientes, Mexico, 2017. [Google Scholar]
- Ortiz-Gómez, R.; Muro-Hernández, L.J.; Flowers-Cano, R.S. Assessment of extreme precipitation through climate change indices in Zacatecas, Mexico. Theor. Appl. Climatol. 2020, 141, 1541–1557. [Google Scholar] [CrossRef]
- Comisión Nacional del Agua (CONAGUA). Base de datos climatológica nacional. CLIma COMpu-tarizado (CLICOM) system. Available online: https://smn.conagua.gob.mx/es/climatologia/informacion-climatologica/informacion-estadistica-climatologica (accessed on 6 June 2023).
- Mirza, M.M.Q. Hydrological changes in the Ganges system in Bangladesh in the post-Farakka period. Hydrol. Sci. J. 1997, 42, 613–631. [Google Scholar] [CrossRef]
- Hänsel, S.; Medeiros, D.M.; Matschullat, J.; Petta, R.A.; de Mendonça Silva, I. Assessing homogeneity and climate variability of temperature and precipitation series in the capitals of North-Eastern Brazil. Front. Earth Sci. 2016, 4, 29. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Edwards, D.C.; McKee, T.B. Characteristics of 20th Century Drought in the United States at Multiple Time Scales; Atmospheric Science Paper No. 634; Department of Atmospheric Science, Colorado State University: Fort Collins, CO, USA, 1997. [Google Scholar]
- Haied, N.; Foufou, A.; Chaab, S.; Azlaoui, M.; Khadri, S.; Benzahia, K.; Benzahia, I. Drought assessment and monitoring using meteorological indices in a semi-arid region. Energy Procedia 2017, 119, 518–529. [Google Scholar] [CrossRef]
- Burka, A.; Biazin, B.; Bewket, W. Drought characterization using different indices, theory of run and trend analysis in bilate river watershed, rift valley of Ethiopia. Front. Environ. Sci. 2023, 11, 1098113. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, P.; Chen, Y.; Yang, J.; Wu, D.; Ma, Y.; Huo, Z.; Liu, S. The optimal time-scale of Standardized Precipitation Index for early identifying summer maize drought in the Huang-Huai-Hai region, China. J. Hydrol.-Reg. Stud. 2023, 46, 101350. [Google Scholar] [CrossRef]
- Tsakiris, G.; Pangalou, D.; Vangelis, H. Regional drought assessment based on the Reconnaissance Drought Index (RDI). Water Resour. Manag. 2007, 21, 821–833. [Google Scholar] [CrossRef]
- Vangelis, H.; Tigkas, D.; Tsakiris, G. The effect of PET method on Reconnaissance Drought Index (RDI) calculation. J. Arid. Environ. 2013, 88, 130–140. [Google Scholar] [CrossRef]
- American Society of Civil Engineers (ASCE). Artificial neural networks in hydrology. I: Preliminary concepts. J. Hydrol. Eng. 2000, 5, 115–123. [Google Scholar] [CrossRef]
- Anshuka, A.; van Ogtrop, F.F.; Willem Vervoort, R. Drought forecasting through statistical models using standardised precipitation index: A systematic review and meta-regression analysis. Nat. Hazards 2019, 97, 955–977. [Google Scholar] [CrossRef]
- Ahmed, K.; Sachindra, D.A.; Shahid, S.; Iqbal, Z.; Nawaz, N.; Khan, N. Multi-model ensemble predictions of precipitation and temperature using machine learning algorithms. Atmos. Res. 2020, 236, 104806. [Google Scholar] [CrossRef]
- Nawi, N.M.; Khan, A.; Rehman, M.Z. A new Levenberg Marquardt based back propagation algorithm trained with Cuckoo search. Procedia Technol. 2013, 11, 18–23. [Google Scholar] [CrossRef]
- Deo, R.C.; Şahin, M. Application of the extreme learning machine algorithm for the prediction of monthly Effective Drought Index in eastern Australia. Atmos. Res. 2015, 153, 512–525. [Google Scholar] [CrossRef]
- Dimitriadou, S.; Nikolakopoulos, K.G. Artificial Neural Networks for the prediction of the reference evapotranspiration of the Peloponnese Peninsula, Greece. Water 2022, 14, 2027. [Google Scholar] [CrossRef]
- Vafaeipour, M.; Rahbari, O.; Rosen, M.A.; Fazelpour, F.; Ansarirad, P. Application of sliding window technique for prediction of wind velocity time series. Int. J. Energy Environ. Eng. 2014, 5, 105. [Google Scholar] [CrossRef]
- Jalalkamali, A.; Moradi, M.; Moradi, N. Application of several artificial intelligence models and ARIMAX model for forecasting drought using the standardized precipitation index. Int. J. Environ. Sci. Technol. 2015, 12, 1201–1210. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J.; Khalil, B. Short-term SPI drought forecasting in the Awash River Basin in Ethiopia using wavelet transforms and machine learning methods. Sustain. Water Resour. Manag. 2016, 2, 87–101. [Google Scholar] [CrossRef]
- Gao, S.; Huang, Y.; Zhang, S.; Han, J.; Wang, G.; Zhang, M.; Lin, Q. Short-term runoff prediction with GRU and LSTM networks without requiring time step optimization during sample generation. J. Hydrol. 2000, 589, 125188. [Google Scholar] [CrossRef]
- Lee, T.; Singh, V.P.; Cho, K.H. Data Preprocessing BT—Deep Learning for Hydrometeorology and Environmental Science, 1st ed.; Water Science and Technology Library; Springer: Cham, Switzerland, 2021; p. 220. [Google Scholar]
- Barua, S.; Perera, B.J.C.; Ng, A.W.M.; Tran, D. Drought forecasting using an aggregated drought index and artificial neural network. J. Water Clim. Chang. 2010, 1, 193–206. [Google Scholar] [CrossRef]
- Mishra, A.K.; Desai, V.R.; Singh, V.P. Drought forecasting using a hybrid stochastic and neural network model. J. Hydrol. Eng. 2007, 12, 626–638. [Google Scholar] [CrossRef]
- Zheng, A.; Casari, A. Feature Engineering for Machine Learning: Principles and Techniques for Data Scientists, 1st ed.; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2018; p. 200. [Google Scholar]
- Magallanes-Quintanar, R.; Galván-Tejada, C.E.; Galván-Tejada, J.I.; Méndez-Gallegos, S.J.; García-Domínguez, A.; Gamboa-Rosales, H. Narx neural networks models for prediction of standardized precipitation index in Central Mexico. Atmosphere 2022, 13, 1254. [Google Scholar] [CrossRef]
- Magallanes-Quintanar, R.; Galván-Tejada, C.E.; Galván-Tejada, J.I.; Gamboa-Rosales, H.; Méndez-Gallegos, S.d.J.; García-Domínguez, A. Auto-Machine-Learning Models for Standardized Precipitation Index Prediction in North–Central Mexico. Climate 2024, 12, 102. [Google Scholar] [CrossRef]
- Tuğrul, T.; Hinis, M.A. Improvement of drought forecasting by means of various machine learning algorithms and wavelet transformation. Acta Geophys. 2024. [Google Scholar] [CrossRef]
- Ghasemi, P.; Karbasi, M.; Nouri, A.Z.; Tabrizi, M.S.; Azamathulla, H.M. Application of Gaussian process regression to forecast multi-step ahead SPEI drought index. Alex. Eng. J. 2021, 60, 5375–5392. [Google Scholar] [CrossRef]
- Karbasi, M.; Jamei, M.; Malik, A.; Kisi, O.; Yaseen, Z.M. Multi-steps drought forecasting in arid and humid climate environments: Development of integrative machine learning model. Agric. Water Manag. 2023, 281, 108210. [Google Scholar] [CrossRef]
| Classification | SPI/SPEI/RDI Value |
|---|---|
| Extremely wet | ≥2 |
| Severely wet | 1.50 to 1.99 |
| Moderately wet | 1.00 to 1.49 |
| Slightly humid (close to normal) | 0 to 0.99 |
| Slight drought (close to normal) | 0 to −0.99 |
| Moderately drought | −1.00 to −1.49 |
| Severely drought | −1.50 to −1.99 |
| Extremely drought | ≤−2 |
| Model Output | Model Input | Window Size |
|---|---|---|
| 3 | ||
| 4 | ||
| 5 | ||
| 6 |
| Station | Index | Scale | MLP Architecture | Validation | Trial | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MSE | R2 | RMSE | MAE | MBE | R2 | RMSE | MAE | MBE | ||||
| Agua Nueva (32001) | SPI | 3 | 4-3-1 | 0.105 | 0.873 | 0.339 | 0.277 | −0.049 | 0.882 | 0.336 | 0.267 | −0.014 |
| 6 | 4-3-1 | 0.064 | 0.923 | 0.266 | 0.211 | −0.023 | 0.912 | 0.282 | 0.230 | −0.036 | ||
| 12 | 6-9-1 | 0.003 | 0.996 | 0.059 | 0.046 | 0.010 | 0.985 | 0.081 | 0.065 | −0.027 | ||
| SPEI | 3 | 3-3-1 | 0.129 | 0.856 | 0.363 | 0.305 | −0.022 | 0.866 | 0.346 | 0.297 | −0.043 | |
| 6 | 5-4-1 | 0.061 | 0.932 | 0.253 | 0.210 | −0.020 | 0.908 | 0.268 | 0.226 | −0.080 | ||
| 12 | 6-9-1 | 0.005 | 0.995 | 0.069 | 0.060 | 0.026 | 0.983 | 0.090 | 0.064 | −0.036 | ||
| RDI | 3 | 3-8-1 | 0.089 | 0.873 | 0.314 | 0.256 | −0.044 | 0.881 | 0.341 | 0.282 | 0.028 | |
| 6 | 3-5-1 | 0.039 | 0.950 | 0.204 | 0.163 | −0.014 | 0.936 | 0.240 | 0.189 | −0.017 | ||
| 12 | 6-11-1 | 0.003 | 0.996 | 0.057 | 0.043 | 0.006 | 0.979 | 0.099 | 0.072 | −0.019 | ||
| Calera (32003) | SPI | 3 | 3-10-1 | 0.191 | 0.817 | 0.443 | 0.370 | 0.068 | 0.822 | 0.412 | 0.352 | 0.076 |
| 6 | 3-10-1 | 0.198 | 0.853 | 0.450 | 0.362 | 0.077 | 0.804 | 0.452 | 0.359 | 0.066 | ||
| 12 | 4-10-1 | 0.010 | 0.993 | 0.102 | 0.082 | 0.019 | 0.987 | 0.111 | 0.091 | 0.005 | ||
| SPEI | 3 | 3-5-1 | 0.215 | 0.765 | 0.466 | 0.364 | 0.051 | 0.713 | 0.571 | 0.435 | 0.154 | |
| 6 | 3-5-1 | 0.072 | 0.929 | 0.268 | 0.227 | 0.049 | 0.914 | 0.313 | 0.268 | 0.075 | ||
| 12 | 3-11-1 | 0.009 | 0.993 | 0.094 | 0.082 | 0.033 | 0.988 | 0.109 | 0.089 | 0.024 | ||
| RDI | 3 | 3-10-1 | 0.163 | 0.831 | 0.409 | 0.336 | 0.070 | 0.834 | 0.402 | 0.343 | 0.095 | |
| 6 | 6-5-1 | 0.146 | 0.894 | 0.388 | 0.294 | 0.075 | 0.867 | 0.385 | 0.289 | 0.084 | ||
| 12 | 3-9-1 | 0.010 | 0.992 | 0.102 | 0.083 | 0.017 | 0.988 | 0.107 | 0.083 | 0.014 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esquivel-Saenz, P.J.; Ortiz-Gómez, R.; Zavala, M.; Flowers-Cano, R.S. Artificial Neural Networks for Drought Forecasting in the Central Region of the State of Zacatecas, Mexico. Climate 2024, 12, 131. https://doi.org/10.3390/cli12090131
Esquivel-Saenz PJ, Ortiz-Gómez R, Zavala M, Flowers-Cano RS. Artificial Neural Networks for Drought Forecasting in the Central Region of the State of Zacatecas, Mexico. Climate. 2024; 12(9):131. https://doi.org/10.3390/cli12090131
Chicago/Turabian StyleEsquivel-Saenz, Pedro Jose, Ruperto Ortiz-Gómez, Manuel Zavala, and Roberto S. Flowers-Cano. 2024. "Artificial Neural Networks for Drought Forecasting in the Central Region of the State of Zacatecas, Mexico" Climate 12, no. 9: 131. https://doi.org/10.3390/cli12090131
APA StyleEsquivel-Saenz, P. J., Ortiz-Gómez, R., Zavala, M., & Flowers-Cano, R. S. (2024). Artificial Neural Networks for Drought Forecasting in the Central Region of the State of Zacatecas, Mexico. Climate, 12(9), 131. https://doi.org/10.3390/cli12090131






