Quantifying Downstream Climate Impacts of Sea Surface Temperature Patterns in the Eastern Tropical Pacific Using Clustering
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Cluster Analysis
3. Results
3.1. Resulting SST Cluster Patterns
3.2. Analysis of the Oceanic Niño Index (ONI) and PMM
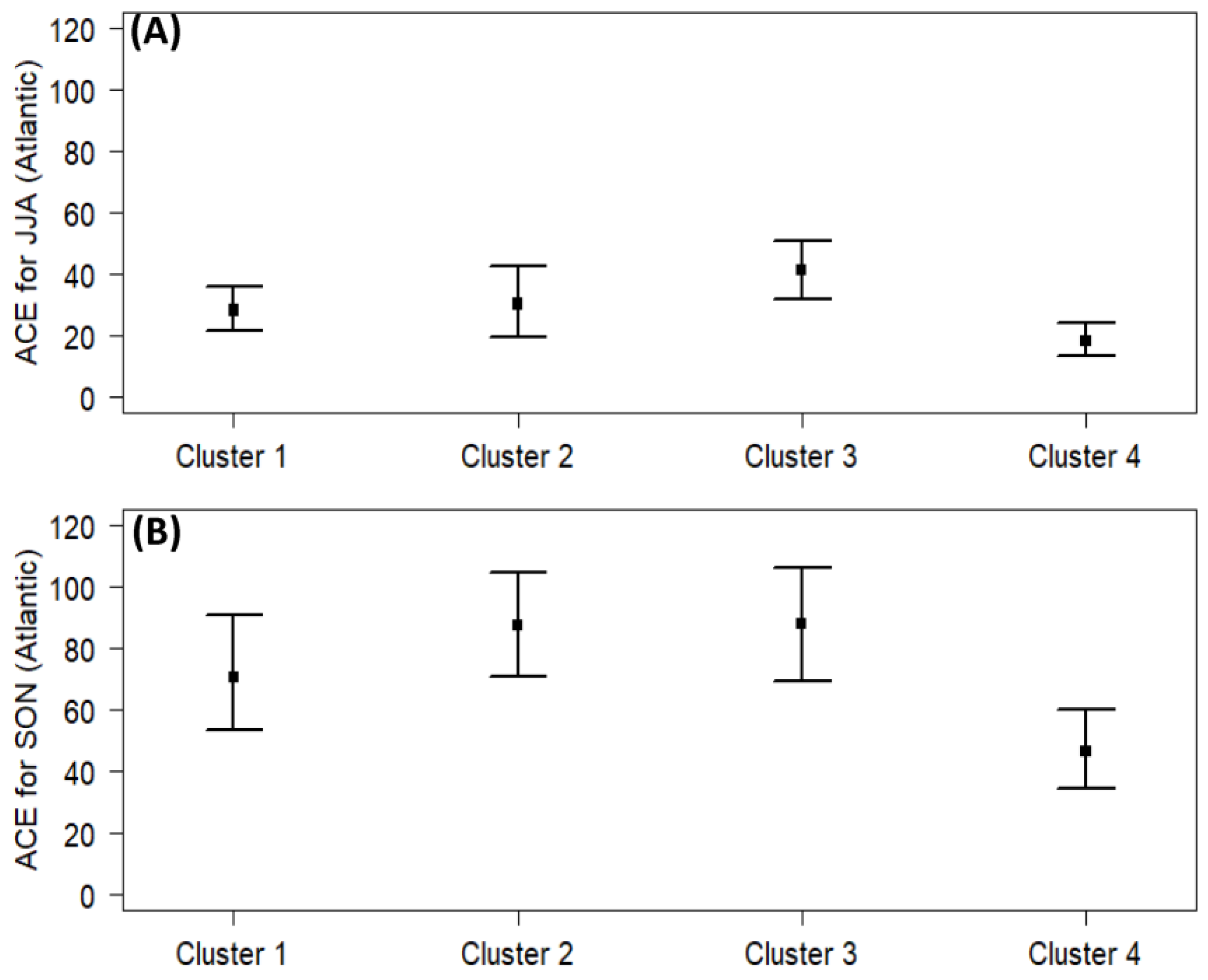
3.3. Accumulated Cyclone Energy (ACE) Case Study
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bjerknes, J. Atmospheric teleconnections from the equatorial pacific. Mon. Weather Rev. 1969, 97, 163–172. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Branstator, G.W.; Karoly, D.; Kumar, A.; Lau, N.-C.; Ropelewski, C. Progress during TOGA in understanding and modeling global teleconnections associated with tropical sea surface temperatures. J. Geophys. Res. 1998, 103, 14291–14324. [Google Scholar] [CrossRef]
- Alexander, M.A.; Bladé, I.; Newman, M.; Lanzante, J.R.; Lau, N.-C.; Scott, J.D. The atmospheric bridge: The influence of ENSO teleconnections on air–sea interaction over the global oceans. J. Clim. 2002, 15, 2205–2231. [Google Scholar] [CrossRef]
- McPhaden, M.J.; Zebiak, S.E.; Glantz, M.H. ENSO as an integrating concept in earth science. Science 2006, 314, 1740–1745. [Google Scholar] [CrossRef] [PubMed]
- Kump, L.R.; Kasting, J.F.; Crane, R.G. The Earth System, 3rd ed.; Pearson Education Inc.: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Johnson, N.C. How Many ENSO Flavors Can We Distinguish? J. Clim. 2013, 26, 4816–4827. [Google Scholar] [CrossRef]
- Henson, R. The Thinking Person’s Guide to Climate Change; American Meteorological Society: Boston, MA, USA, 2014. [Google Scholar]
- Capotondi, A.; Wittenberg, A.T.; Newman, M.; Di Lorenzo, E.; Yu, J.-Y.; Braconnot, P.; Cole, J.; Dewitte, B.; Giese, B.; Guilyardi, E.; et al. Understanding ENSO diversity. Bull. Am. Meteorol. Soc. 2015, 96, 921–938. [Google Scholar] [CrossRef]
- Bruun, J.T.; Allen, J.I.; Smyth, T.J. Heartbeat of the southern oscillation explains ENSO climatic resonances. J. Geophys. Res. 2017, 122, 6746–6772. [Google Scholar] [CrossRef]
- Larkin, N.K.; Harrison, D.E. Global seasonal temperature and precipitation anomalies during el niño autumn and winter. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Ashok, K.; Behera, S.K.; Rao, S.A. El Niño Modoki and its possible teleconnections. J. Geophys. Res. 2007, 112, 1–27. [Google Scholar] [CrossRef]
- Kao, H.Y.; Yu, J.Y. Contrasting eastern Pacific and central Pacific types of ENSO. J. Clim. 2009, 22, 615–632. [Google Scholar] [CrossRef]
- Kug, J.S.; Jin, F.F. Two types of El Niño events: Cold tongue El Niño and warm pool El Niño. J. Clim. 2009, 22, 1499–1515. [Google Scholar] [CrossRef]
- Su, H.; Neelin, J.D.; Meyerson, J.E. Mechanisms for lagged atmospheric response to ENSO SST forcing. J. Clim. 2005, 18, 4195–4215. [Google Scholar] [CrossRef]
- Navratil, J. ENSO Teleconnections—Analysis of Time Lag between Tropical Pacific Sea Surface Temperature and Climate and Vegetation Anomalies. Ph.D. Dissertation, Lunds Universitet, Lund, Sweden, 2020. [Google Scholar]
- Gill, A. Some simple solutions for heat-induced tropical circulation. Q. J. R. Meteorol. Soc. 1980, 106, 447–462. [Google Scholar] [CrossRef]
- Ratnam, J.; Behera, S.; Masumoto, Y.; Takahashi, K.; Yamagata, T. Anomalous climatic conditions associated with the El niño modoki during boreal winter of 2009. Clim. Dyn. 2011, 39, 227–238. [Google Scholar] [CrossRef]
- Williams, I.N.; Patricola, C.M. Diversity of ENSO events unified by convective threshold sea surface temperature: A nonlinear ENSO index. Geophys. Res. Lett. 2018, 45, 9236–9244. [Google Scholar] [CrossRef]
- Lutgens, F.K.; Tarbuck, E.J. The Atmosphere: An Introduction to Meteorology, 12th ed.; Pearson Education: Upper Saddle River, NJ, USA, 2013. [Google Scholar]
- Laing, A.; Evans, J. Introduction to Tropical Meteorology, 2nd ed. Available online: https://www.meted.ucar.edu/tropical/textbook_2nd_edition (accessed on 5 May 2024).
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 4th ed.; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Taschetto, A.S.; Haarsma, R.J.; Gupta, A.S.; Ummenhofer, C.C.; Hill, K.J.; England, M.H. Australian monsoon variability driven by a gill-matsuno type response to central west Pacific warming. J. Clim. 2010, 23, 4717–4736. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, G.; Yuan, D.; Zhang, Y. Linking the tropical Indian Ocean basin mode to the central-Pacific type of ENSO: Observations and CMIP5 reproduction. Clim. Dyn. 2023, 60, 1705–1727. [Google Scholar] [CrossRef]
- Vimont, D.J.; Alexander, M.A.; Newman, M. Optimal growth of Central and East Pacific ENSO events. Geophys. Res. Lett. 2014, 41, 4027–4034. [Google Scholar] [CrossRef]
- McCabe, G.J.; Betancourt, J.L.; Gray, S.T.; Palecki, M.A.; Hidalgo, H.G. Associations of multi-decadal sea-surface temperature variability with US drought. Quat. Int. 2008, 188, 31–40. [Google Scholar] [CrossRef]
- Hoell, A.; Funk, C. The ENSO-Related West Pacific sea surface temperature gradient. J. Clim. 2013, 26, 9545–9562. [Google Scholar] [CrossRef]
- Chiang, J.C.H.; Vimont, D.J. Analogous pacific and atlantic meridional modes of tropical atmosphere–ocean variability. J. Clim. 2004, 17, 4143–4158. [Google Scholar] [CrossRef]
- Chang, P.; Zhang, L.; Saravanan, R.; Vimont, D.J.; Chiang, J.C.H.; Ji, L.; Seidel, H.; Tippett, M.K. Pacific meridional mode and el niño–southern oscillation. Geophys. Res. Lett. 2007, 34, 1–5. [Google Scholar] [CrossRef]
- Ropelewski, C.; Halpert, M. Global and regional scale precipitation patterns associated with the El Niño Southern Oscillation. Mon. Weather Rev. 1987, 115, 1606–1626. [Google Scholar] [CrossRef]
- Stuecker, M.F. Revisiting the pacific meridional mode. Sci. Rep. 2018, 8, 3216. [Google Scholar] [CrossRef] [PubMed]
- Fan, H.; Yang, S.; Wang, C.; Lin, S. Revisiting the impacts of tropical Pacific SST anomalies on the Pacific Meridional Mode during the decay of strong eastern Pacific El Niño events. J. Clim. 2023, 36, 4987–5002. [Google Scholar] [CrossRef]
- Kao, P.; Hong, C.; Huang, A.-Y.; Chang, C.-C. Intensification of interannual cross-basin SST interaction between the North Atlantic tripole and Pacific Meridional Mode since the 1990s. J. Clim. 2022, 35, 5967–5979. [Google Scholar] [CrossRef]
- Messie, M.; Chavez, F. Global modes of sea surface temperature variability in relation to regional climate indices. J. Clim. 2011, 24, 4314–4331. [Google Scholar] [CrossRef]
- Schulte, J.A.; Georgas, N.; Saba, V.; Penelope, H. North Pacific influences on Long Island Sound temperature variability. J. Clim. 2018, 31, 2745–2769. [Google Scholar] [CrossRef]
- Tremblay, L.B. Can we consider the Arctic Oscillation independently from the Barents Oscillation? Geophys. Res. Lett. 2001, 28, 4227–4230. [Google Scholar] [CrossRef]
- Schulte, J.A.; Lee, S. Long Island Sound temperature variability and its associations with the ridge–trough dipole and tropical modes of sea surface temperature variability. Ocean Sci. 2019, 15, 161–178. [Google Scholar] [CrossRef]
- Su, J.; Lian, T.; Zhang, R.; Chen, D. Monitoring the pendulum between El Niño and La Niña events. Environ. Res. Lett. 2018, 13, 1–8. [Google Scholar] [CrossRef]
- Zhao, J.; Kug, J.-S.; Park, J.-H.; An, S.-I. Diversity of North Pacific Meridional Mode and Its Distinct Impacts on El Niño Southern Oscillation. Geophys. Res. Lett. 2020, 47, 1–8. [Google Scholar] [CrossRef]
- Huang, B.; Thorne, P.W.; Banzon, V.F.; Boyer, T.; Chepurin, G.; Lawrimore, J.H.; Menne, M.J.; Smith, T.M.; Vose, R.S.; Zhang, H.-M. Extended reconstructed sea surface temperature, version 5, (p ERSSTv5): Upgrades, validations, and intercomparisons. J. Clim. 2017, 30, 8179–8205. [Google Scholar] [CrossRef]
- L’Heureux, M.L.; Collins, D.C.; Hu, Z.-Z. Linear trends in sea surface temperature of the tropical Pacific Ocean and implications for the El Niño Southern Oscillation. Clim. Dyn. 2013, 40, 1223–1236. [Google Scholar] [CrossRef]
- Climate Prediction Center (CPC). Description of Changes to Ocean Niño Index (ONI). Available online: https://www.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ONI_change.shtml (accessed on 21 March 2022).
- Climate Prediction Center (CPC). Cold & Warm Episodes by Season. Available online: https://origin.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ONI_v5.php (accessed on 1 March 2023).
- Meng, J.; Fan, J.; Ashkenazy, Y.; Bunde, A.; Havlin, S. Forecasting the magnitude and onset of El Niño based on climate network. New J. Phys. 2018, 20, 043036. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Smith, C.; Wallace, J.M. An intercomparison of methods for finding coupled patterns in climate data. J. Clim. 1992, 5, 541–560. [Google Scholar] [CrossRef]
- Vimont, D.J. Meridional Mode Website. Available online: https://www.aos.wisc.edu/~dvimont/MModes/Home.html (accessed on 5 May 2024).
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Yu, J.-Y.; Chou, C.; Chiu, P.-G. A revised accumulated cyclone energy index. Geophys. Res. Lett. 2009, 36, 1–5. [Google Scholar] [CrossRef]
- Balaji, M.; Chakraborty, M.; Mandal, M. Changes in tropical cyclone activity in north Indian Ocean during satellite era (1981–2014). Int. J. Climatol. 2018, 38, 2819–2837. [Google Scholar] [CrossRef]
- Landsea, C.W.; Franklin, J.L. Atlantic hurricane database uncertainty and presentation of a new database format. Mon. Weather. Rev. 2013, 141, 3576–3592. [Google Scholar] [CrossRef]
- Singh, V.K.; Roxy, M.K.; Deshpande, M. Role of warm ocean conditions and the MJO in the genesis and intensification of extremely severe cyclone Fani. Sci. Rep. 2021, 11, 3607. [Google Scholar] [CrossRef] [PubMed]
- Hong, L.-C. Super El Niño. Ph.D. Dissertation, National Taiwan University, Taipei, Taiwan, 2016. [Google Scholar]
- Mercer, A.E. Dominant United States cold-season near surface temperature anomaly patterns derived from kernel methods. Int. J. Climatol. 2021, 41, 2383–2396. [Google Scholar] [CrossRef]
- Geng, T.; Cai, W.; Wu, L. Two types of ENSO varying in tandem facilitated by nonlinear atmospheric convection. Geophys. Res. Lett. 2020, 47, e2020. [Google Scholar] [CrossRef]
- Klotzbach, P.J.; Wood, K.M.; Schreck, C.J., III; Bowen, S.B.; Patricola, C.M.; Bell, M.M. Trends in the global tropical cyclone activity: 1990–2021. Geophys. Res. Lett. 2022, 49, 1–10. [Google Scholar] [CrossRef]
- Patricola, C.M.; Camargo, S.J.; Klotzbach, P.J.; Saravanan, R.; Chang, P. The influence of ENSO flavors on western north pacific tropical cyclone activity. J. Clim. 2018, 31, 5395–5416. [Google Scholar] [CrossRef]
- Seager, R.; Henderson, N.; Cane, M. Persistent discrepancies between observed and modeled trends in the tropical Pacific ocean. J. Clim. 2022, 35, 4571–4584. [Google Scholar] [CrossRef]
- Jin, F.F.; Boucharel, J.; Lin, I.I. Eastern Pacific tropical cyclones intensified by El Niño delivery of subsurface ocean heat. Nature 2014, 516, 82–85. [Google Scholar] [CrossRef] [PubMed]
- Klotzbach, P.J. El Niño–Southern Oscillation’s impact on Atlantic basin hurricanes and U.S. landfalls. J. Clim. 2011, 24, 1252–1263. [Google Scholar] [CrossRef]
- Larson, S.; Lee, S.-K.; Wang, C.; Chung, E.-S.; Enfield, D. Impacts of non-canonical El Niño patterns on Atlantic hurricane activity. Geophys. Res. Lett. 2012, 39, 1–6. [Google Scholar] [CrossRef]
- Patricola, C.M.; Chang, P.; Saravanan, R. Degree of simulated suppression of Atlantic tropical cyclones modulated by flavour of El Niño. Nat. Geosci. 2016, 9, 155–160. [Google Scholar] [CrossRef]
- Boucharel, J.; Jin, F.F.; Lin, I.I.; Huang, H.-C.; England, M.H. Different controls of tropical cyclone activity in the Eastern Pacific for two types of El Niño. Geophys. Res. Lett. 2016, 43, 1679–1686. [Google Scholar] [CrossRef]
- Wood, K.M.; Klotzbach, P.J.; Collins, J.M.; Schreck III, C.J. The record-setting 2018 Eastern North Pacific hurricane season. Geophys. Res. Lett. 2019, 46, 10072–10081. [Google Scholar] [CrossRef]
- Ren, H.-L.; Lu, B.; Wan, J.; Tian, B.; Zhang, P. Identification standard for ENSO events and its application for climate monitoring and prediction in China. J. Meteorol. Res. 2018, 32, 923–936. [Google Scholar] [CrossRef]
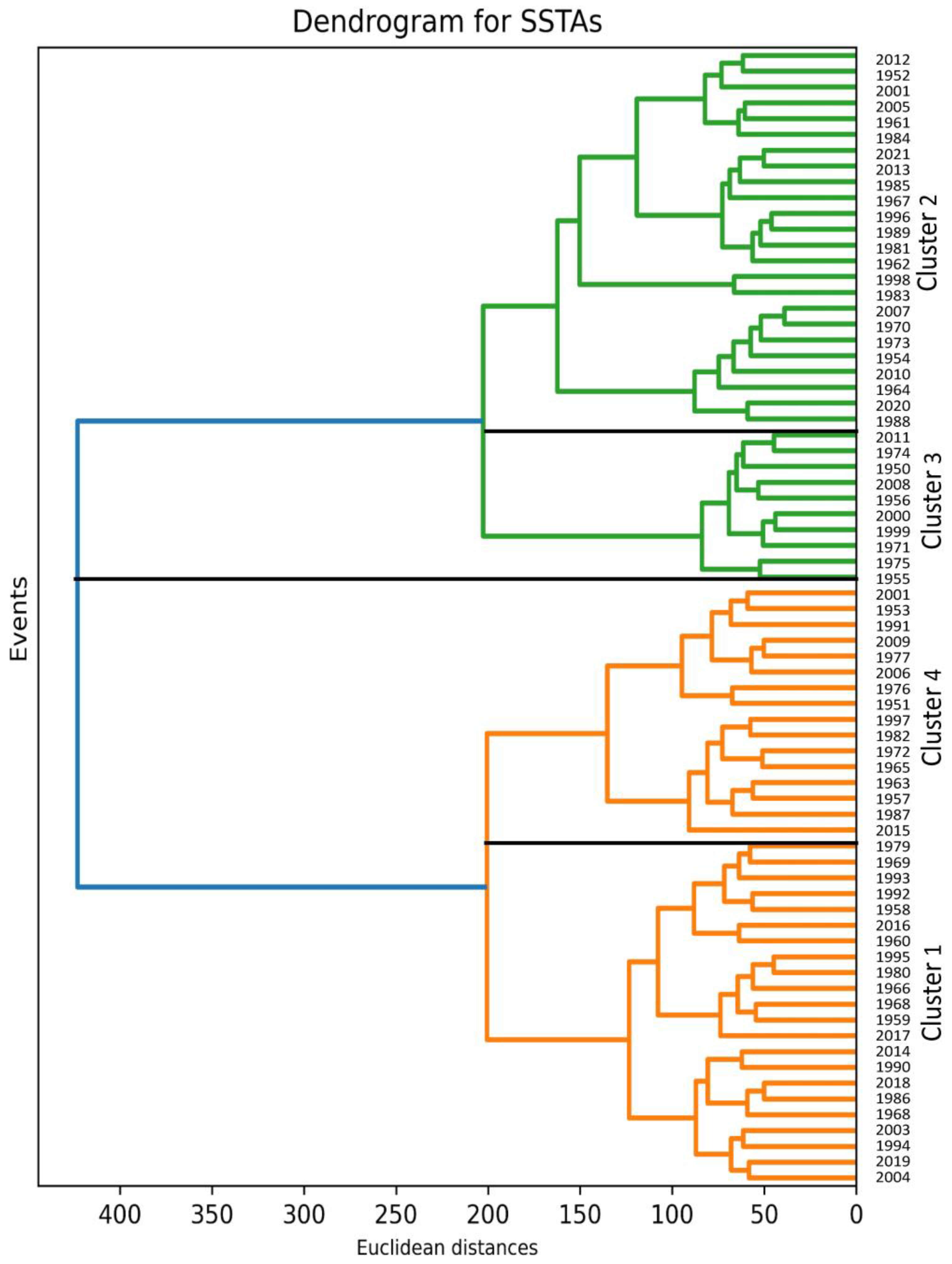
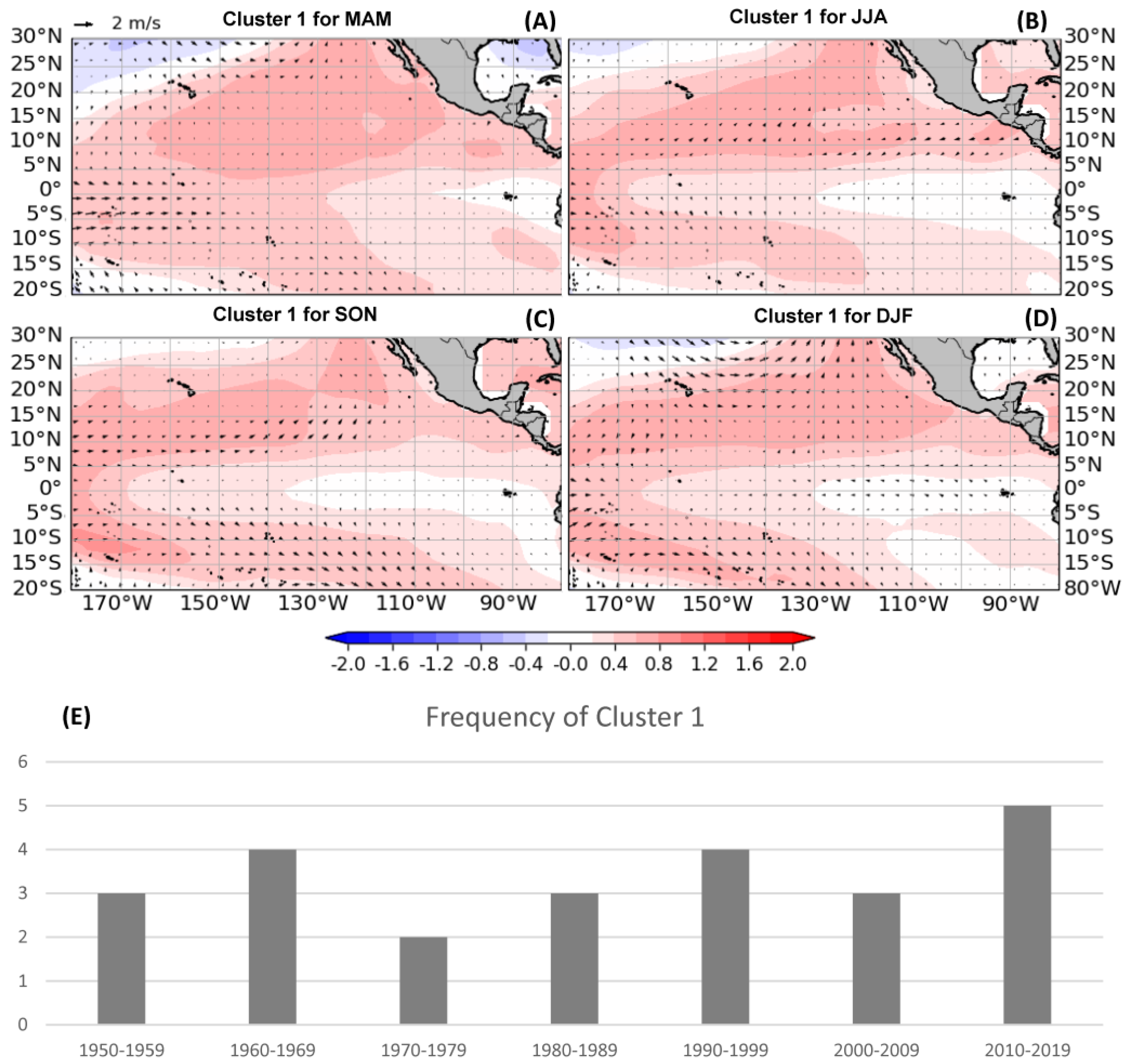

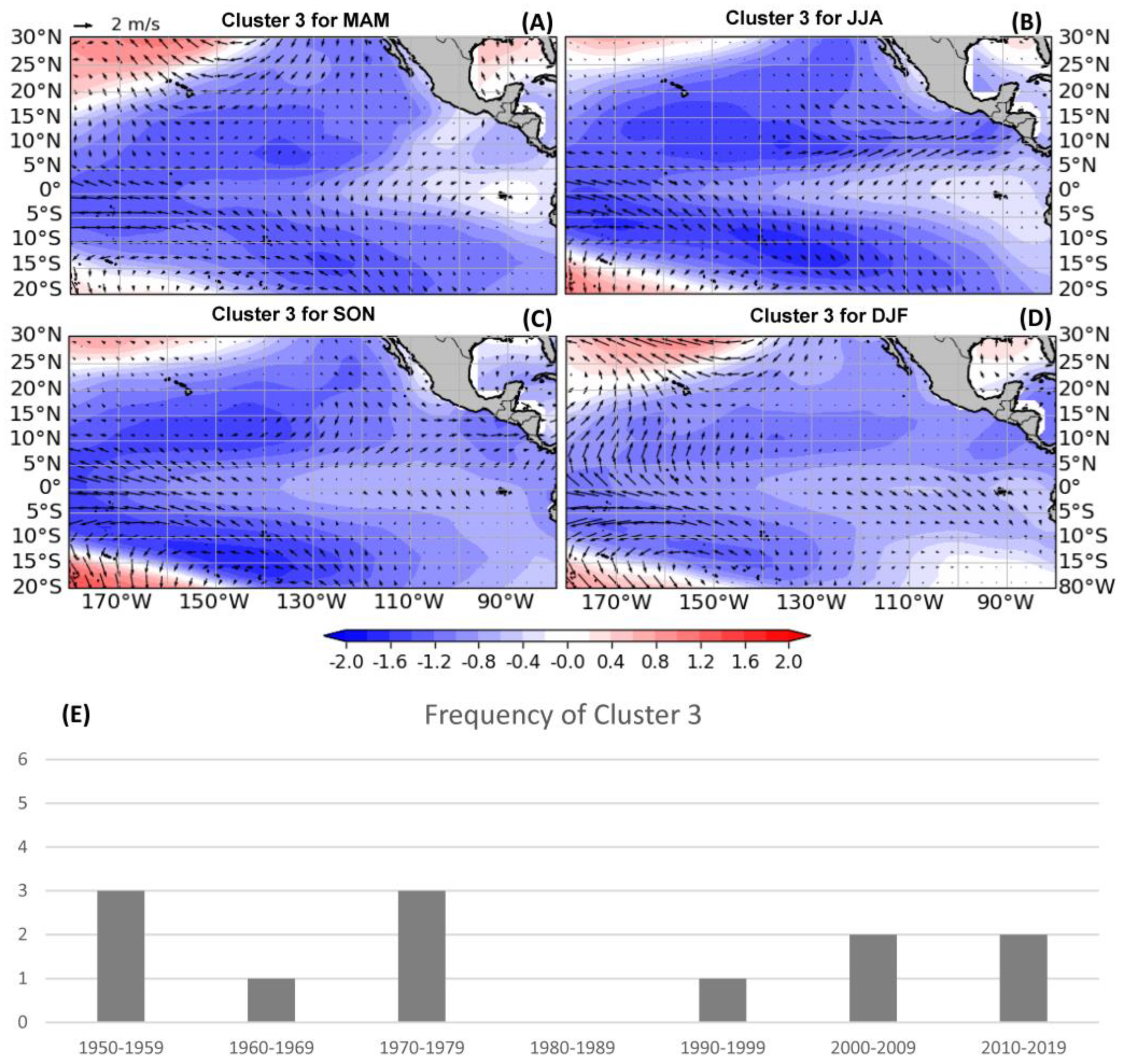
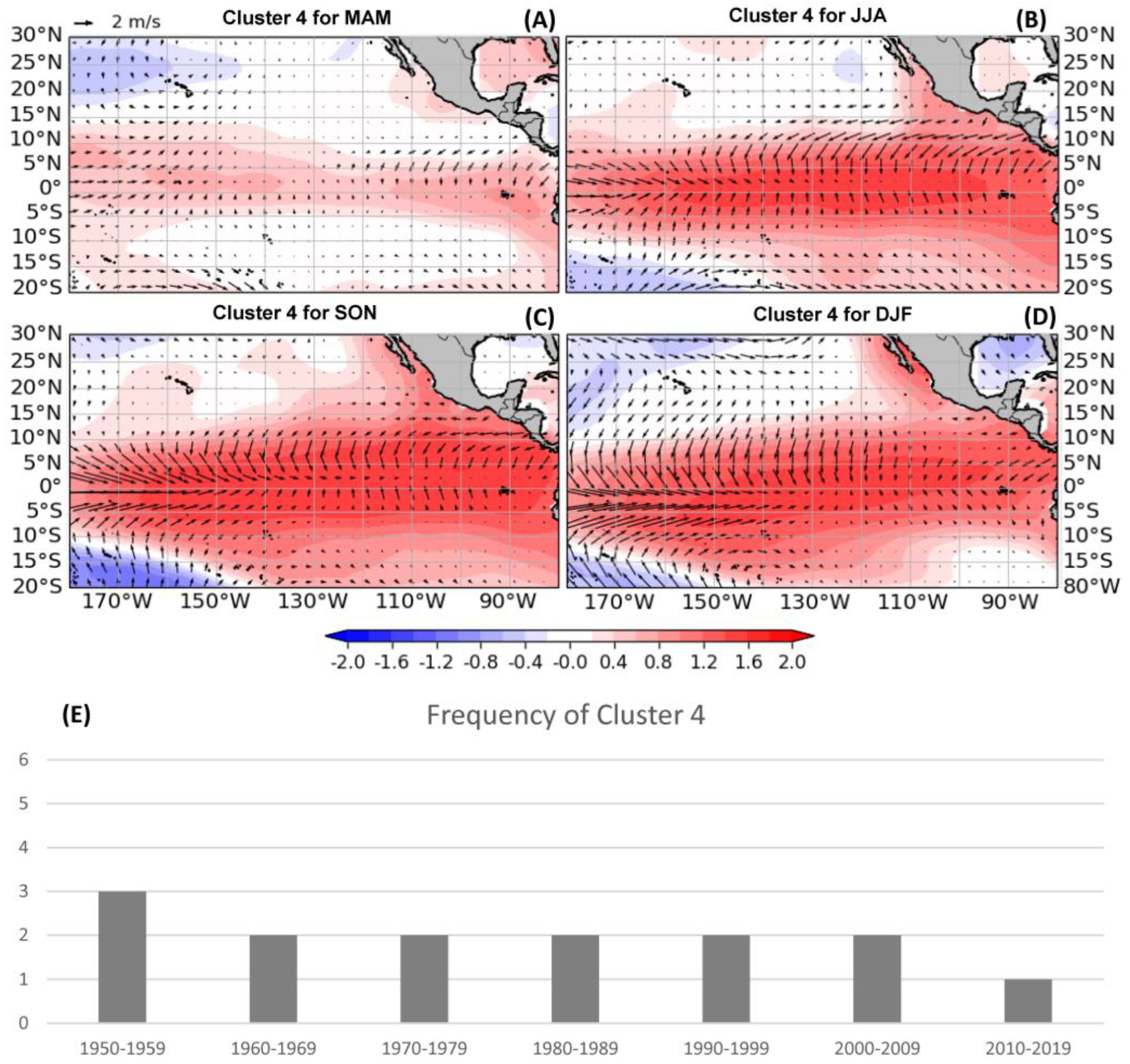
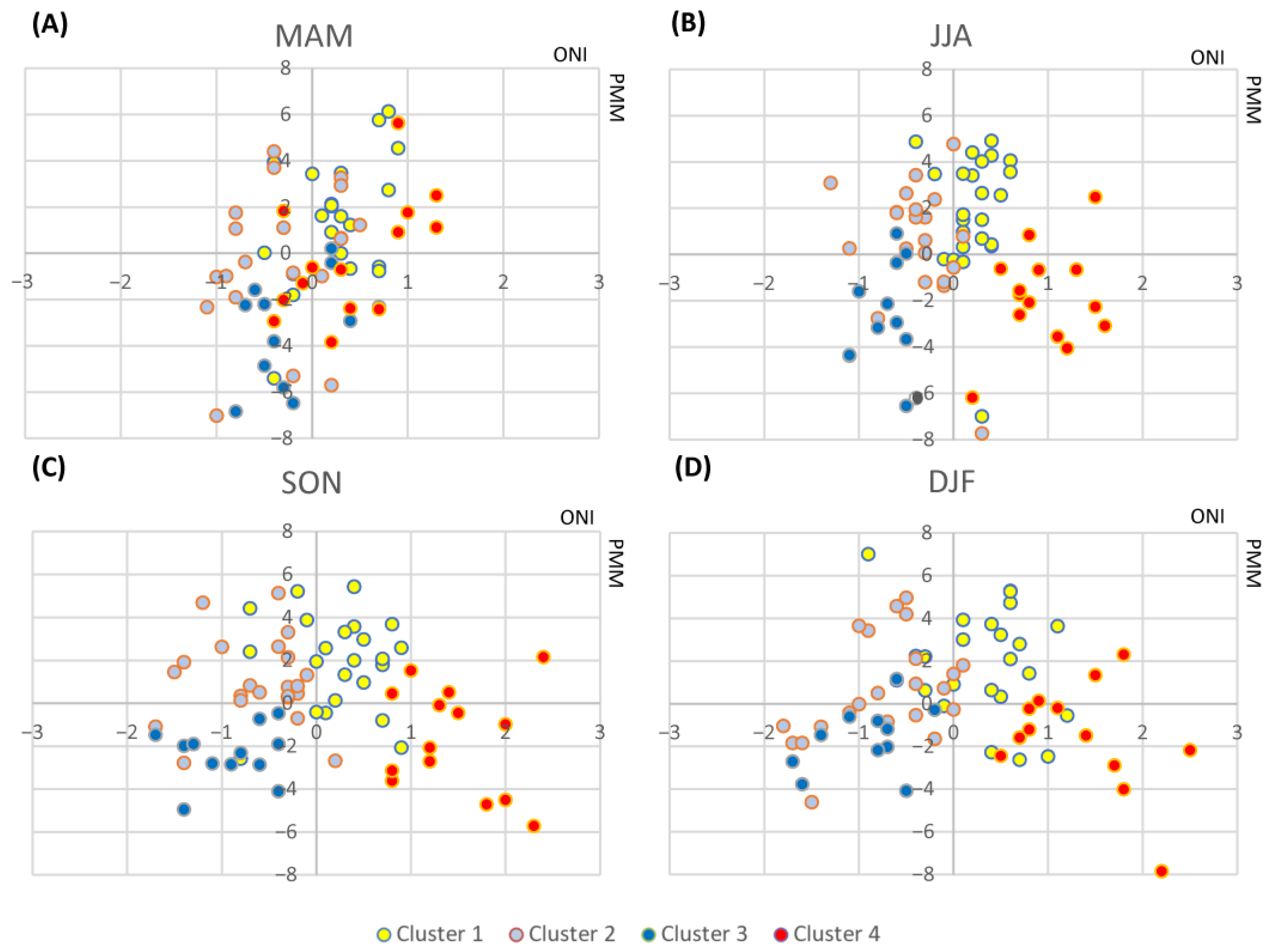

| Cluster Number | N | Season | La Niña | Neutral | El Niño | Negative PMM | Positive PMM |
|---|---|---|---|---|---|---|---|
| 1 | 24 | MAM | 1 | 17 | 6 | 7 | 17 |
| JJA | 0 | 21 | 3 | 4 | 20 | ||
| SON | 3 | 12 | 9 | 5 | 19 | ||
| DJF | 2 | 10 | 12 | 5 | 19 | ||
| 2 | 22 | MAM | 9 | 12 | 1 | 11 | 11 |
| JJA | 7 | 15 | 0 | 7 | 15 | ||
| SON | 10 | 12 | 0 | 4 | 18 | ||
| DJF | 14 | 8 | 0 | 11 | 11 | ||
| 3 | 12 | MAM | 5 | 6 | 1 | 11 | 1 |
| JJA | 11 | 1 | 0 | 10 | 2 | ||
| SON | 9 | 3 | 0 | 12 | 0 | ||
| DJF | 11 | 1 | 0 | 11 | 1 | ||
| 4 | 14 | MAM | 0 | 8 | 6 | 8 | 6 |
| JJA | 0 | 1 | 13 | 12 | 2 | ||
| SON | 0 | 0 | 14 | 10 | 4 | ||
| DJF | 0 | 0 | 14 | 11 | 3 |
| Cluster | SSTA Pattern | Dominant Climate Drivers | Trend (1950–2019) |
|---|---|---|---|
| 1 | Anomalous warming in the subtropical North Pacific, Central Pacific, and central and eastern South Pacific. | Positive PMM and CP El Niño | Increased |
| 2 | Anomalous cooling in the eastern and central equatorial Pacific with small regions of anomalous cooling off the coast of Mexico. | EP La Niña | Increased |
| 3 | Anomalous cooling in the Eastern and Central Pacific, with the most intense cooling in the equatorial Central and subtropical Central and Eastern Pacific. | Negative PMM and CP La Niña | Decreased |
| 4 | Anomalous warming in the Central and Eastern Pacific, with significant warming near the equator in the Central and Eastern Pacific. | EP El Niño | Decreased |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Finley, J.; Fosu, B.; Fuhrmann, C.; Mercer, A.; Rudzin, J. Quantifying Downstream Climate Impacts of Sea Surface Temperature Patterns in the Eastern Tropical Pacific Using Clustering. Climate 2024, 12, 71. https://doi.org/10.3390/cli12050071
Finley J, Fosu B, Fuhrmann C, Mercer A, Rudzin J. Quantifying Downstream Climate Impacts of Sea Surface Temperature Patterns in the Eastern Tropical Pacific Using Clustering. Climate. 2024; 12(5):71. https://doi.org/10.3390/cli12050071
Chicago/Turabian StyleFinley, Jason, Boniface Fosu, Chris Fuhrmann, Andrew Mercer, and Johna Rudzin. 2024. "Quantifying Downstream Climate Impacts of Sea Surface Temperature Patterns in the Eastern Tropical Pacific Using Clustering" Climate 12, no. 5: 71. https://doi.org/10.3390/cli12050071
APA StyleFinley, J., Fosu, B., Fuhrmann, C., Mercer, A., & Rudzin, J. (2024). Quantifying Downstream Climate Impacts of Sea Surface Temperature Patterns in the Eastern Tropical Pacific Using Clustering. Climate, 12(5), 71. https://doi.org/10.3390/cli12050071






