A Southeastern United States Warm Season Precipitation Climatology Using Unsupervised Learning
Abstract
1. Introduction
2. Data and Methods
2.1. Datasets
2.2. Cluster Analysis Methodology
3. Results
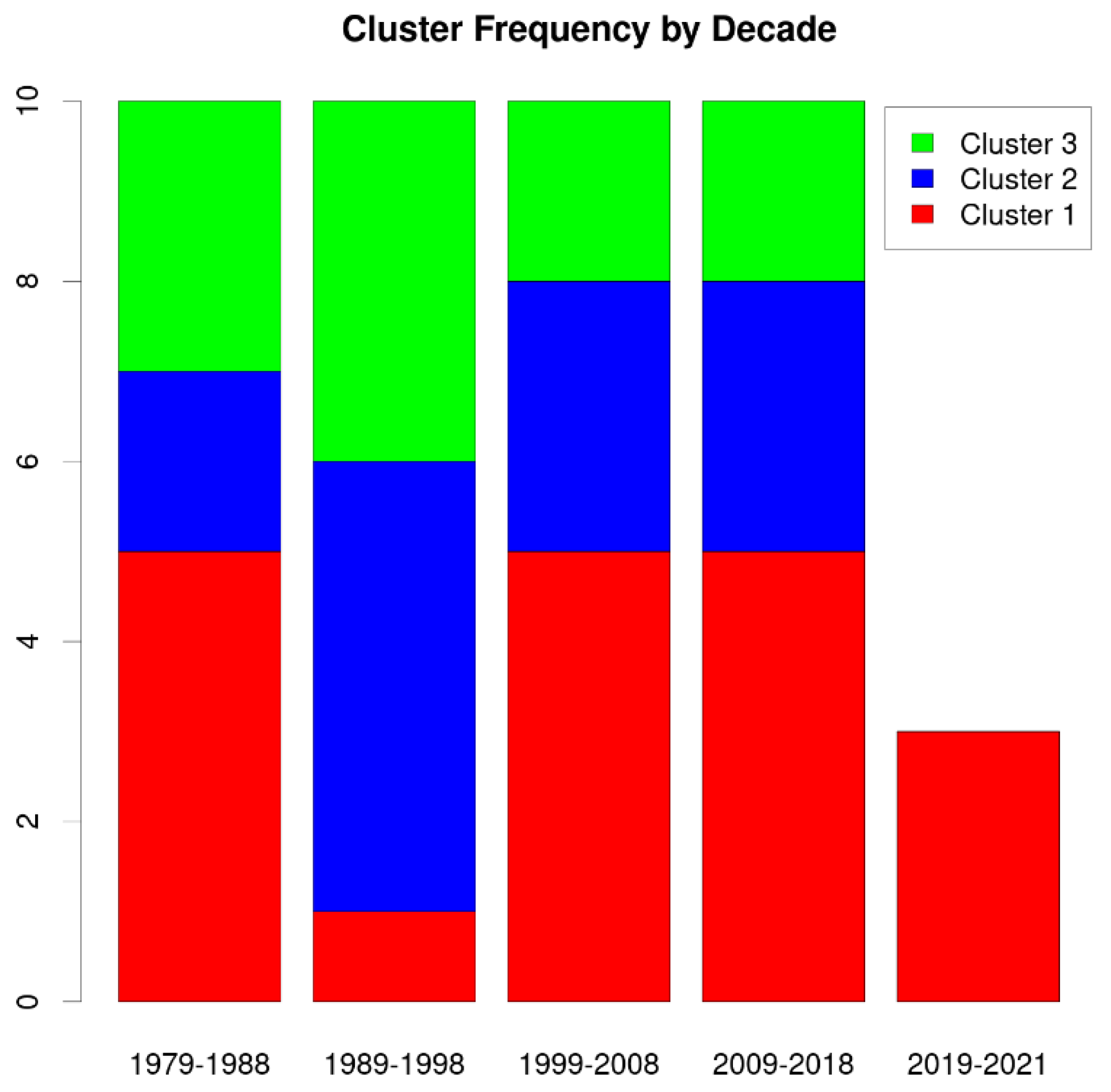
3.1. Cluster Analysis Overall Results
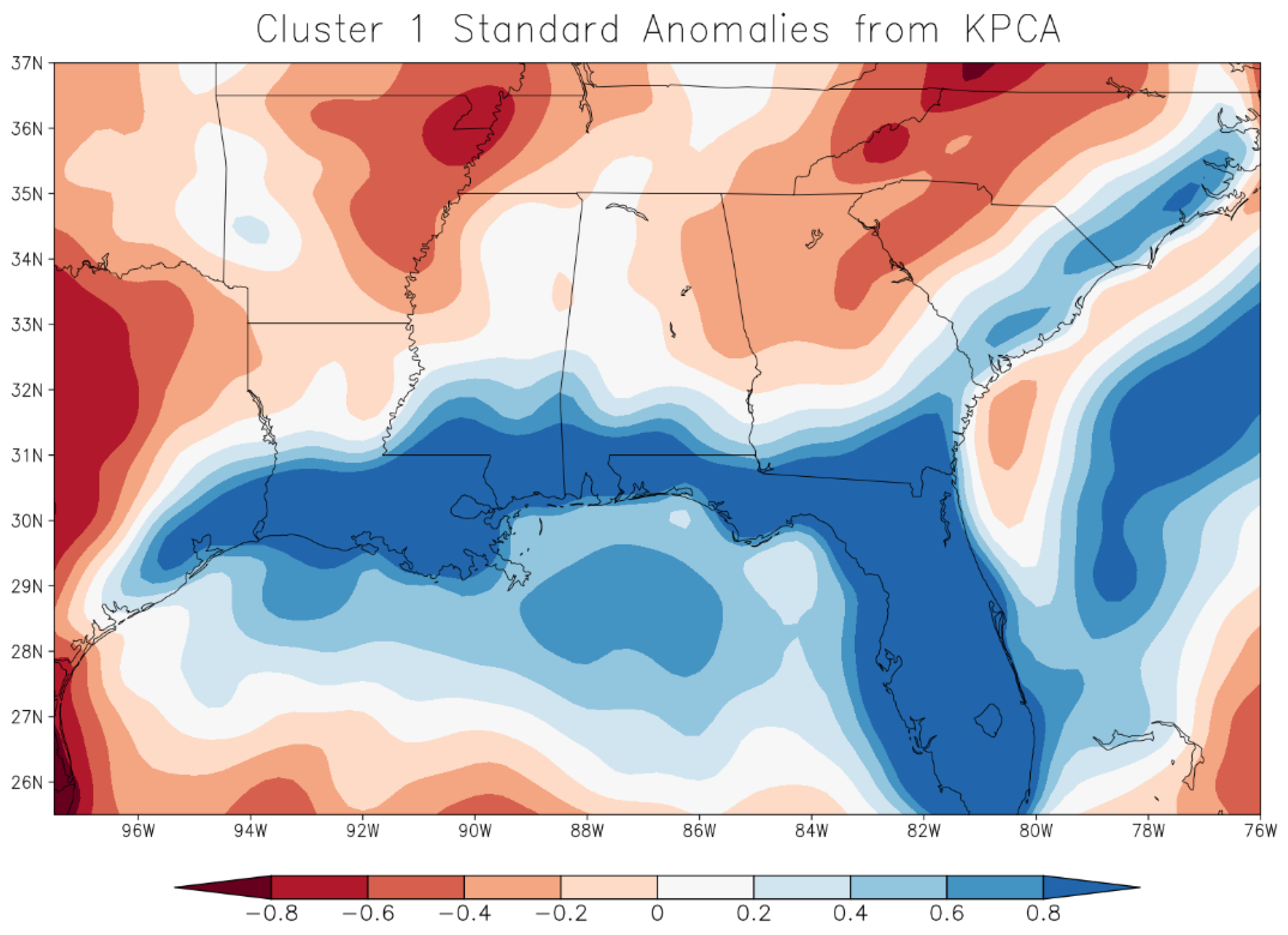
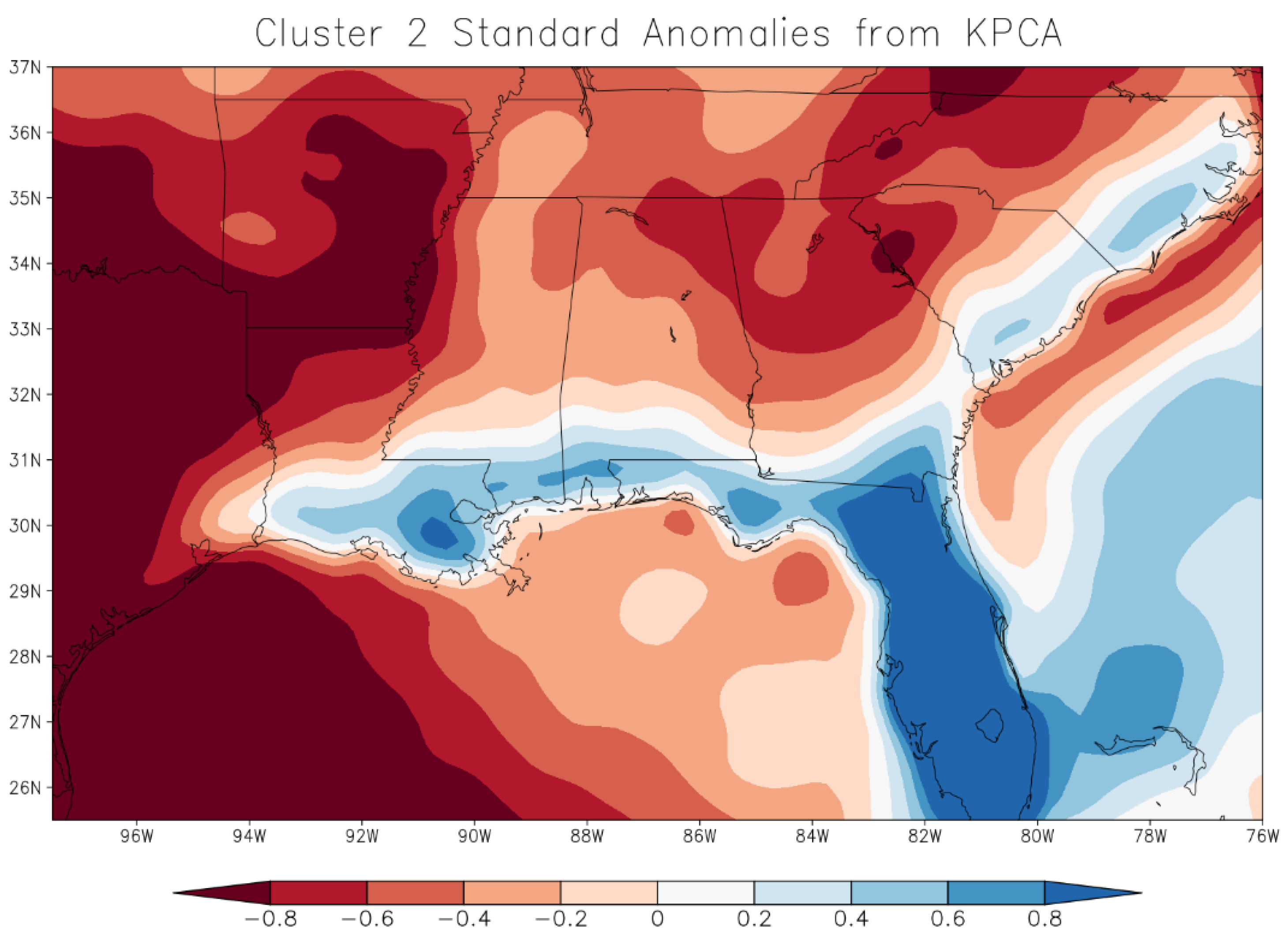
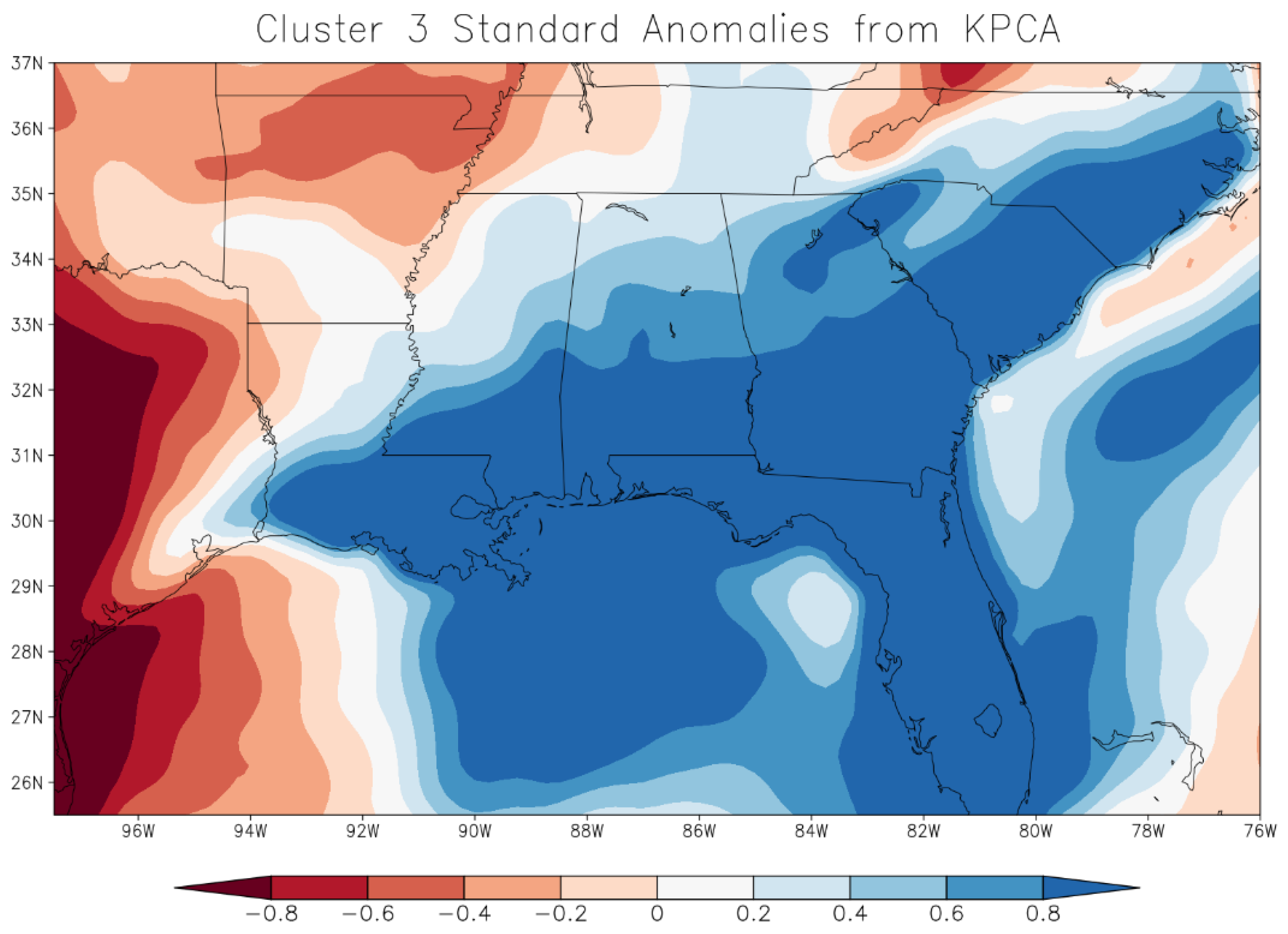
3.2. Cluster Map Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- United States Department of Agriculture. Quick Statistics. National Agricultural Statistics Service. 2021. Available online: https://quickstats.nass.usda.gov (accessed on 31 October 2022).
- Qian, J.; Viner, B.; Noble, S.; Werth, D. Precipitation characteristics of warm season weather types in the Southeastern United States of America. Atmosphere 2021, 12, 1001. [Google Scholar] [CrossRef]
- Lu, C.; Zhang, J.; Tian, H.; Crumpton, W.; Helmers, M.; Cai, W.; Hopkinson, C.; Lohrenz, S. Increased extreme precipitation challenges load management to the Gulf of Mexico. Nat. Commun. Earth Environ. 2020, 1, 1–10. [Google Scholar] [CrossRef]
- Dyer, J.; Mercer, A. Identification of recharge zones in the Lower Mississippi River alluvial aquifer using high-resolution precipitation estimates. J. Hydrol. 2015, 531, 360–369. [Google Scholar] [CrossRef]
- Tashie, A.; Mirus, B.; Pavelsky, T. Identifying long-term empirical relationships between storm characteristics and episodic groundwater recharge. Water Resour. Res. 2015, 52, 21–35. [Google Scholar] [CrossRef]
- Moore, B.; Mahoney, K.; Sukovich, E.; Cifelli, R.; Hamill, T. Climatology and environmental characteristics of extreme precipitation events in the Southeastern United States. Mon. Weather Rev. 2015, 143, 718–741. [Google Scholar] [CrossRef]
- Keim, B. Spatial, synoptic, and seasonal patterns of rainfall in the southeastern United States. Phys. Geogr. 1996, 17, 313–328. [Google Scholar] [CrossRef]
- Konrad, C. Synoptic-scale features associated with warm season heavy rainfall over the interior Southeastern United States. Weather Forecast. 1997, 12, 557–571. [Google Scholar] [CrossRef]
- Shepherd, J.; Grundstein, A.; Mote, T. Quantifying the contribution of tropical cyclones to extreme rainfall along the coastal southeastern United States. Geophys. Res. Lett. 2007, 34, L23810. [Google Scholar] [CrossRef]
- Knight, D.; Davis, R. Contribution of tropical cyclones to extreme rainfall events in the southeastern United States. J. Geophys. Res. 2009, 114, D23102. [Google Scholar] [CrossRef]
- Konrad, C.; Perry, L. Relationships between tropical cyclones and heavy rainfall in the Carolina region of the USA. Int. J. Climatol. 2010, 30, 522–534. [Google Scholar] [CrossRef]
- Seager, R.; Tzanova, A.; Nakamura, J. Drought in the southeastern United States: Causes, variability over the last millennium, and the potential for future hydroclimate change. J. Climate 2009, 22, 5021–5045. [Google Scholar] [CrossRef]
- Seager, R.; Ting, M.; Davis, M.; Cane, M.; Naik, N.; Nakamura, J.; Li, C.; Cook, E.; Stahle, D. Mexican drought: An observational modeling and tree ring study of variability and climate change. Atmósphera 2009, 22, 1–31. [Google Scholar]
- Schubert, S.; Chang, Y.; DeAngelis, A.; Wang, H.; Koster, R. On the development and demise of the Fall 2019 Southeast U.S. flash drought: Links to an extreme positive IOD. J. Climate 2021, 34, 1701–1723. [Google Scholar] [CrossRef]
- Dyer, J.; Mercer, A.; Raczynski, K. Quantifying spatial patterns of hydrologic drought over the Southeast US using retrospective National Water Model simulations. Water 2022, 14, 1525. [Google Scholar] [CrossRef]
- National Oceanic and Atmospheric Administration Office of Weather Prediction (OWP). The National Water Model. 2022. Available online: https://water.noaa.gov/about/nwm (accessed on 31 October 2022).
- Hsieh, W. Machine Learning Methods in the Environmental Sciences; Cambridge University Press: Cambridge, UK, 2009; pp. 16–18. [Google Scholar]
- Mercer, A.; Leslie, L.; Richman, M. Identification of severe weather outbreaks using kernel principal component analysis. Proc. Comp. Sci. 2011, 6, 231–236. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.; Müller, K. Kernel principal component analysis. In International Conference on Artificial Neural Networks; Springer: Berlin/Heidelberg, Germany, 1997; pp. 583–588. [Google Scholar]
- Wilks, D. Statistical Methods in the Atmospheric Sciences; Elsevier Press: Amsterdam, The Netherlands, 2019; pp. 721–738. [Google Scholar]
- Mercer, A.; Grimes, A.; Wood, K. Application of unsupervised learning techniques to identify Atlantic tropical cyclone rapid intensification environments. J. Appl. Meteorol. Clim. 2021, 60, 119–138. [Google Scholar] [CrossRef]
- Sugg, J.; Konrad, C. Defining hydroclimatic regions using daily rainfall characteristics in the southern Appalachian Mountains. Int. J. Digit. Earth 2019, 1–18. [Google Scholar] [CrossRef]
- Sugg, J.; Konrad, C. Relating warm season hydroclimatic variability in the Southern Appalachians to synoptic weather patterns using self-organizing maps. Clim. Res. 2017, 74, 145–160. [Google Scholar] [CrossRef]
- Dyer, J. Basin-scale precipitation analysis for southeast U.S. watersheds using high-resolution radar precipitation estimates. Phys. Geogr. 2008, 29, 320–340. [Google Scholar] [CrossRef]
- Mesinger, F.; DiMego, G.; Kalnay, E.; Mitchell, K.; Shafran, P.; Ebisuzaki, W.; Jović, D.; Woolen, J.; Rogers, E.; Berbery, E.; et al. North American Regional Reanalysis. Bull. Am. Meteorol. Soc. 2006, 87, 343–360. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines; Cambridge University Press: Cambridge, UK, 2000; pp. 1–182. [Google Scholar]
- Barnston, A.G.; Livezey, R.E. Classification, seasonality and persistence of low-frequency atmospheric circulation patterns. Mon. Weather Rev. 1987, 115, 1083–1126. [Google Scholar] [CrossRef]
- Mercer, A.; Richman, M. Assessing atmospheric variability using kernel principal component analysis. Proc. Comp. Sci. 2012, 7, 288–293. [Google Scholar] [CrossRef][Green Version]
- Rousseeuw, P. Silhouettes, a graphical aid for the interpretation and validation of cluster analysis. J. Comp. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Mercer, A. Dominant United States cold-season near surface temperature anomaly patterns derived from kernel principal component analysis. Int. J. Climatol. 2021, 41, 2383–2396. [Google Scholar] [CrossRef]
- Dyer, J. Evaluation of Surface and Radar-Estimated Precipitation Data Sources Over the Lower Mississippi River Alluvial Plain. Phys. Geogr. 2009, 30, 430–452. [Google Scholar] [CrossRef]
- Gaffin, D.; Hotz, D. A precipitation and flood climatology with synoptic features of heavy rainfall across the southern Appalachian mountains. Natl. Weather Dig. 2000, 24, 3–15. [Google Scholar]
- Chagnon, S. The 1988 drought, barges, and diversion. Bull. Am. Meteorol. Soc. 1989, 70, 1092–1104. [Google Scholar] [CrossRef]
- Lott, N. The summer of 1993: Flooding in the Midwest and drought in the Southeast. Nat. Clim. Data Center Tech. Rep. 1993, 17. [Google Scholar]
- Jong, B.; Ting, M.; Seager, R.; Anderson, W. ENSO teleconnections and impacts on U.S. summertime temperature during a multiyear La Niña life cycle. J. Climate 2020, 33, 6009–6024. [Google Scholar] [CrossRef]
- Cold & Warm Episodes by Season. Available online: https://origin.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ONI_v5.php (accessed on 31 October 2022).
- Efron, B.; Tibshirani, R. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1993; pp. 153–159. [Google Scholar]
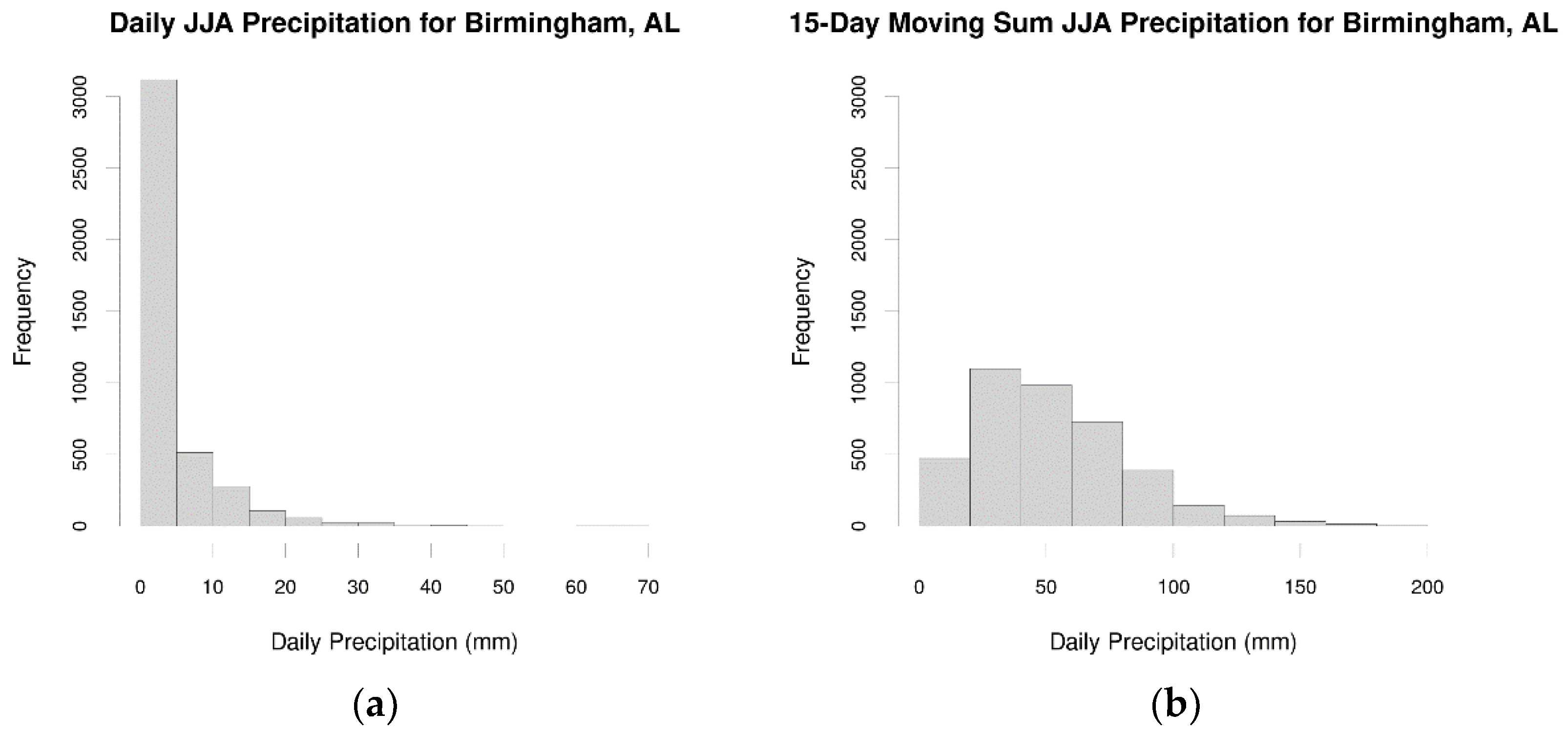
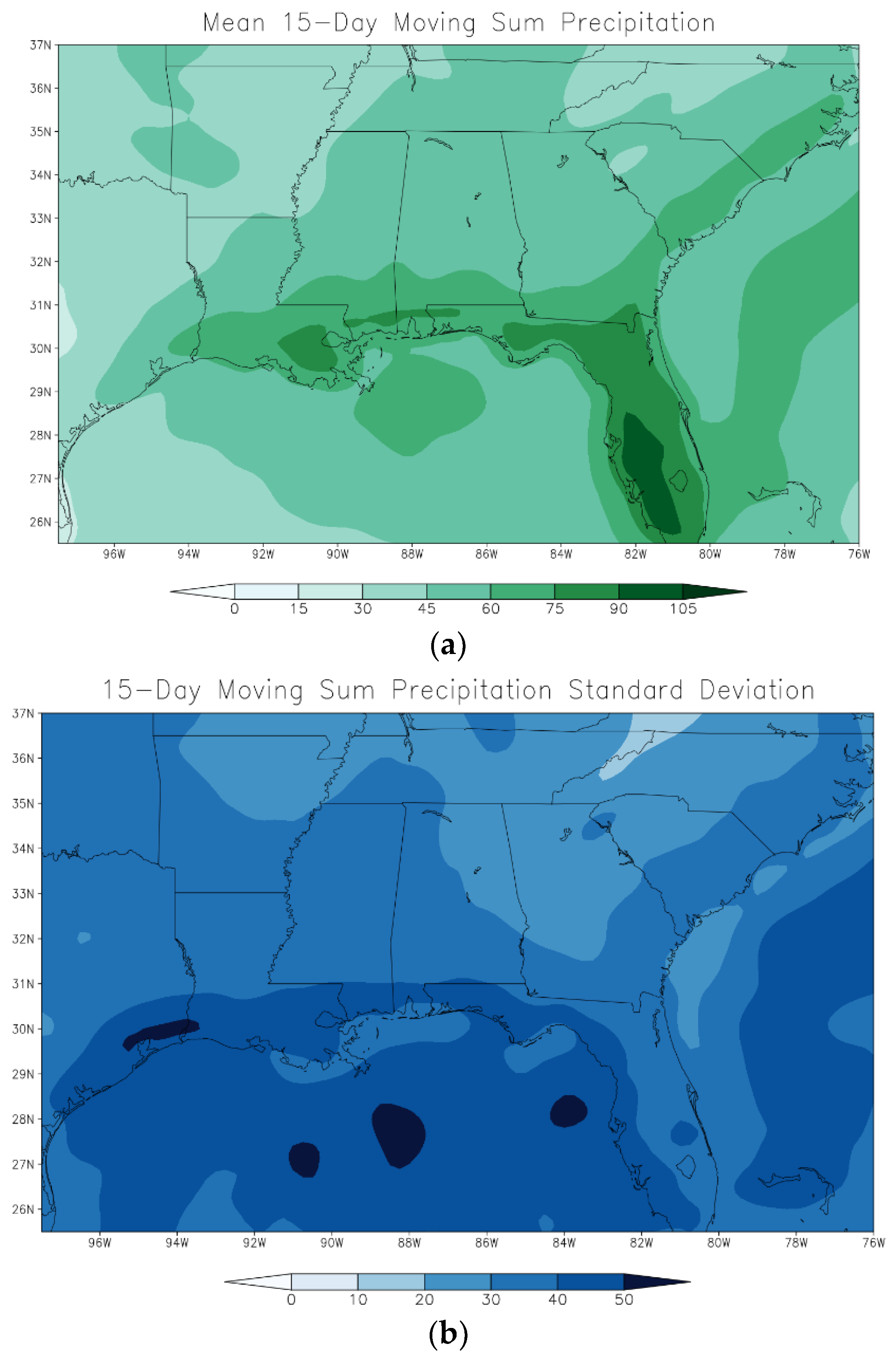
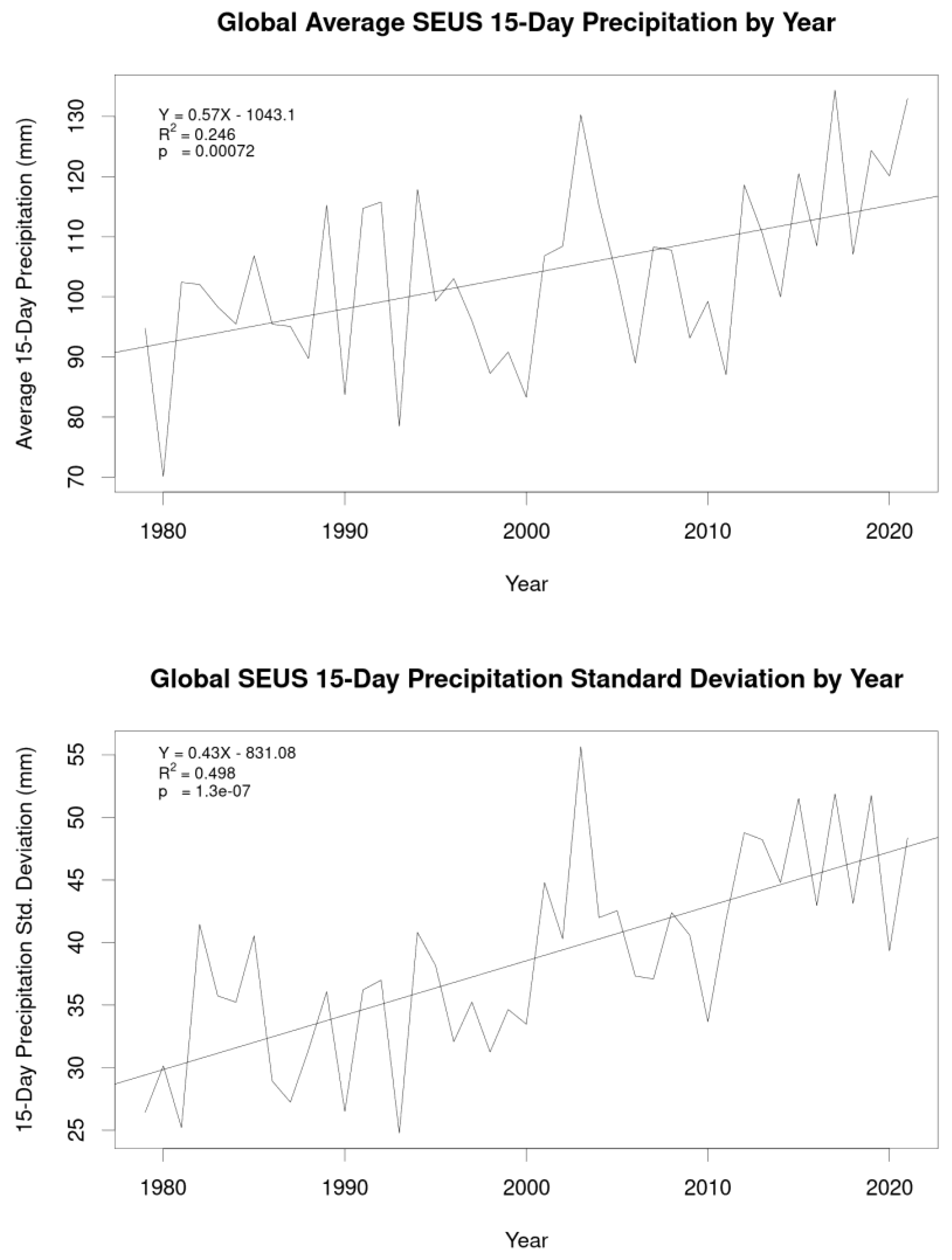
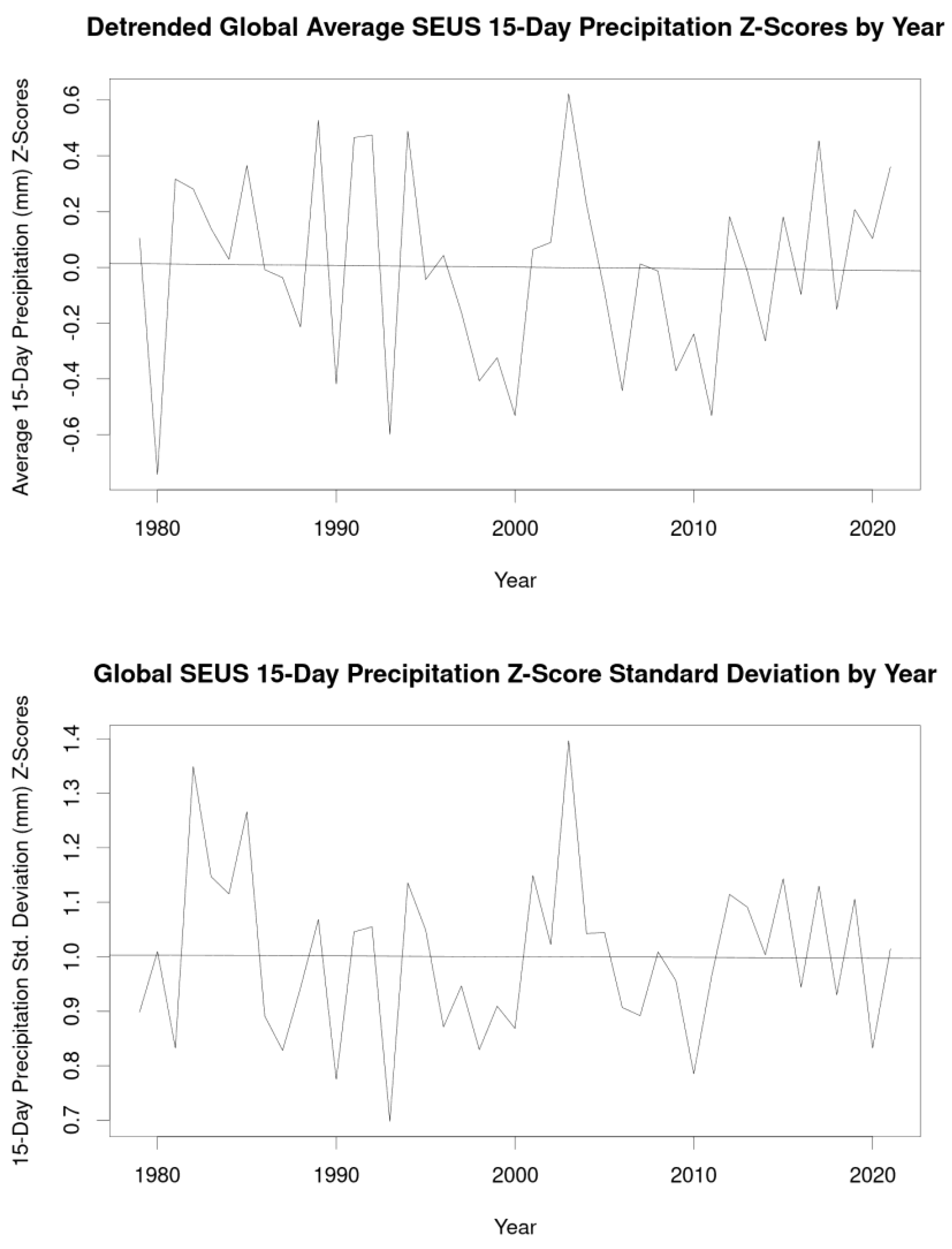



| Retained Clusters | Avg. Correlation | |
|---|---|---|
| 3 | 0.105 | 0.763 |
| 4 | 0.097 | 0.777 |
| 5 | 0.096 | 0.790 |
| 6 | 0.088 | 0.807 |
| 7 | 0.097 | 0.812 |
| 8 | 0.080 | 0.825 |
| Kernel | Loadings | Retained Clusters | Avg. Correlation | |
|---|---|---|---|---|
| Linear polynomial | 9 | 3 | 0.105 | 0.765 |
| RBF () | 24 | 4 | 0.100 | 0.788 |
| RBF () | 21 | 5 | 0.097 | 0.794 |
| RBF () | 36 | 8 | 0.081 | 0.829 |
| Percentile | Cluster 1 | Cluster 2 | Cluster 3 |
|---|---|---|---|
| 2.5% | 1.158 | 0.615 | 0.907 |
| 50% | 1.895 | 1.077 | 1.910 |
| 97.5% | 2.737 | 1.615 | 3.090 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mercer, A.; Dyer, J. A Southeastern United States Warm Season Precipitation Climatology Using Unsupervised Learning. Climate 2023, 11, 2. https://doi.org/10.3390/cli11010002
Mercer A, Dyer J. A Southeastern United States Warm Season Precipitation Climatology Using Unsupervised Learning. Climate. 2023; 11(1):2. https://doi.org/10.3390/cli11010002
Chicago/Turabian StyleMercer, Andrew, and Jamie Dyer. 2023. "A Southeastern United States Warm Season Precipitation Climatology Using Unsupervised Learning" Climate 11, no. 1: 2. https://doi.org/10.3390/cli11010002
APA StyleMercer, A., & Dyer, J. (2023). A Southeastern United States Warm Season Precipitation Climatology Using Unsupervised Learning. Climate, 11(1), 2. https://doi.org/10.3390/cli11010002






