Effect of Model Structure and Calibration Algorithm on Discharge Simulation in the Acısu Basin, Turkey
Abstract
1. Introduction
2. Materials and Methods
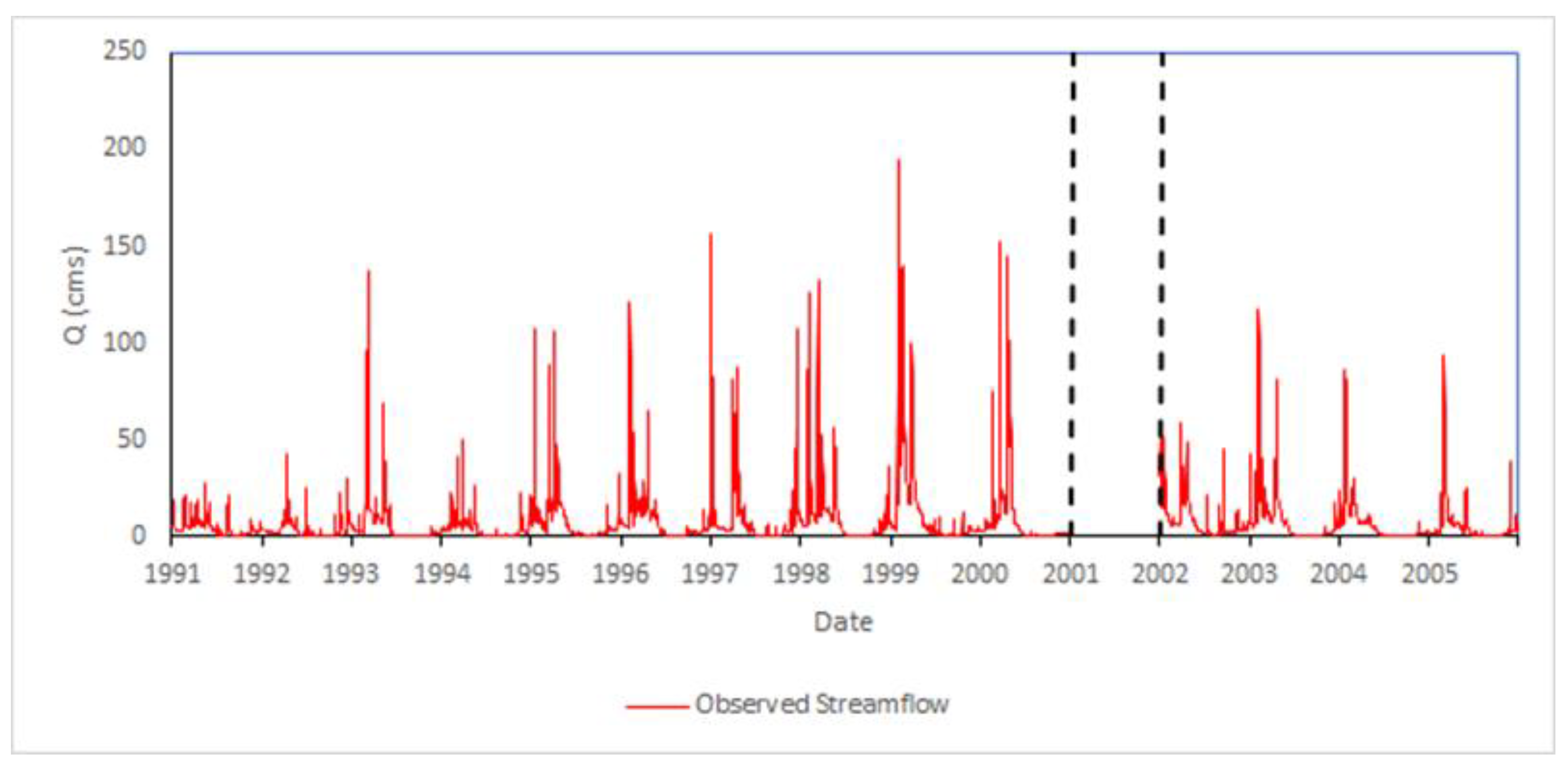
2.1. Study Area
2.2. Data
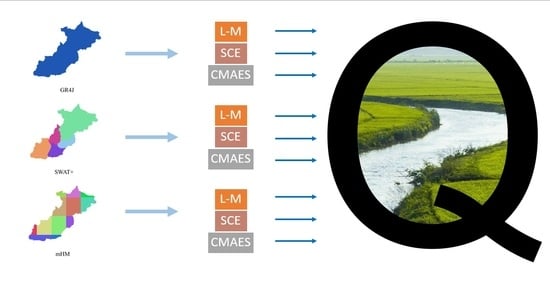
2.3. Hydrologic Models
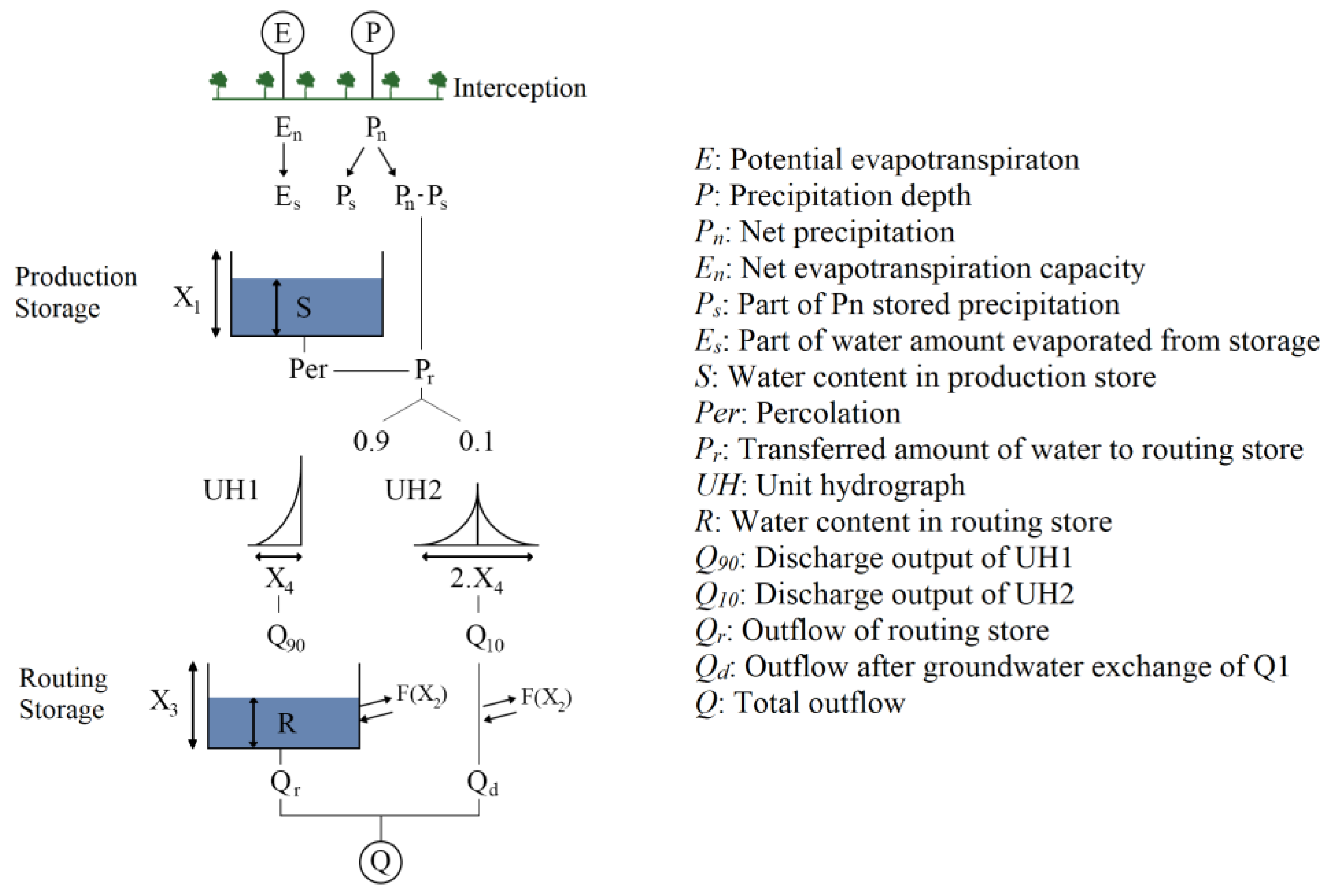
2.3.1. GR4J
2.3.2. SWAT+
2.3.3. mHM
2.4. Calibration of Models
2.4.1. Sensitivity Analysis
2.4.2. Calibration Algorithms
3. Results
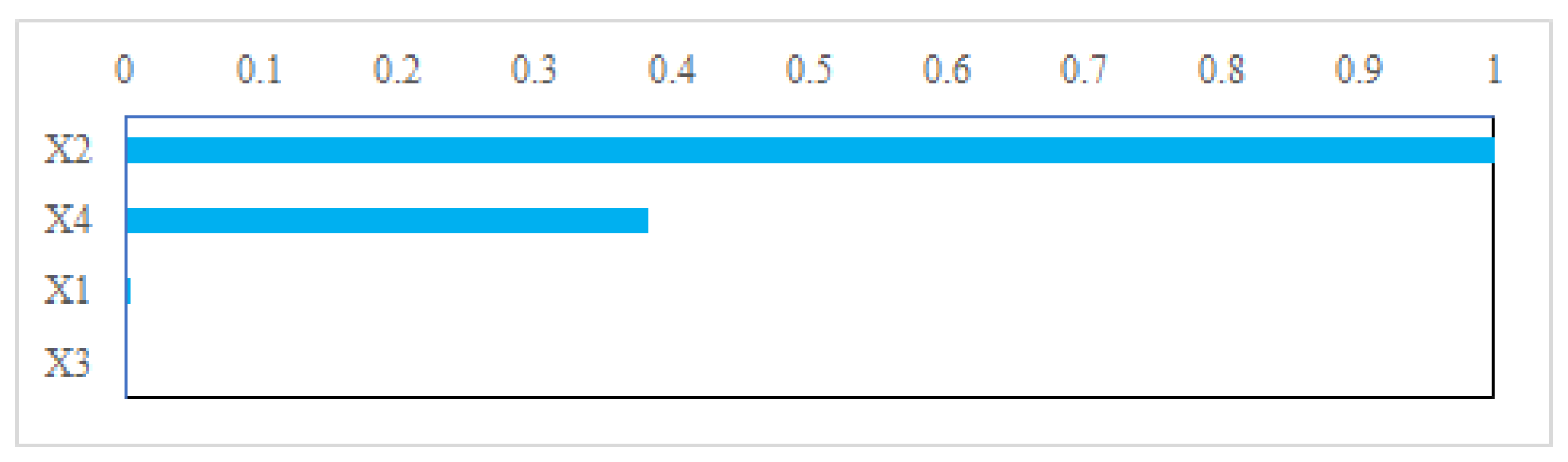
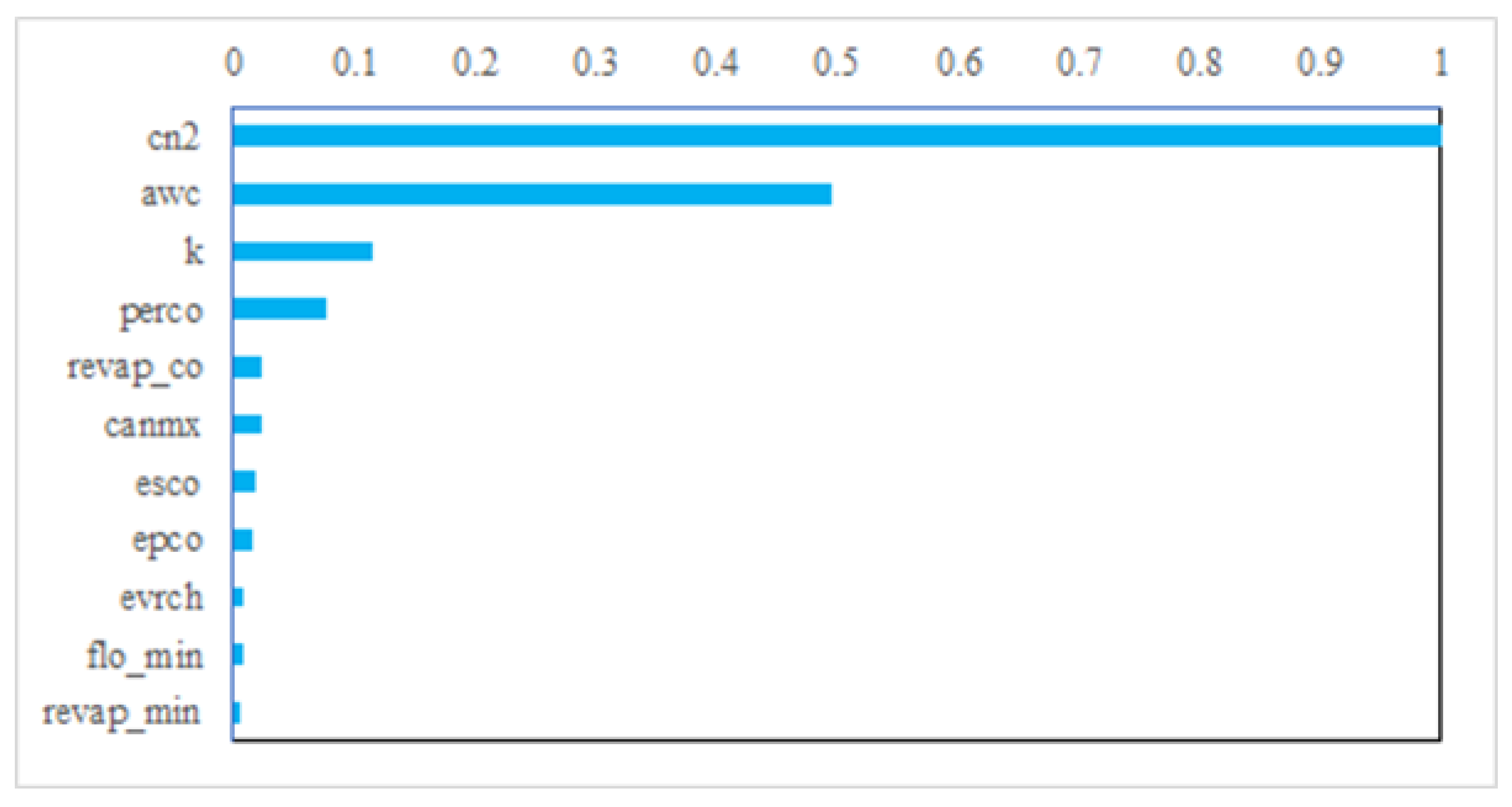
3.1. Sensitivity Analysis
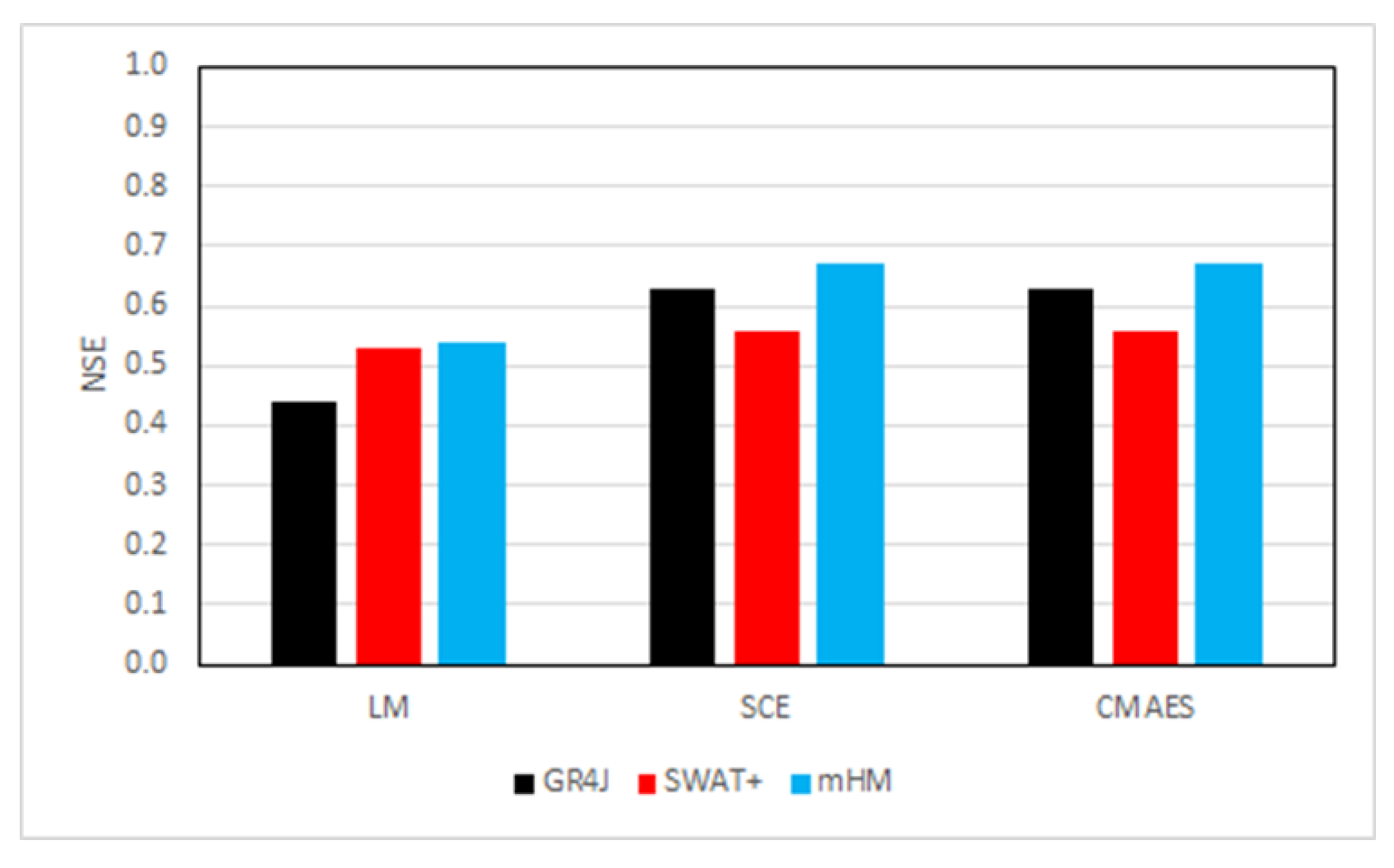
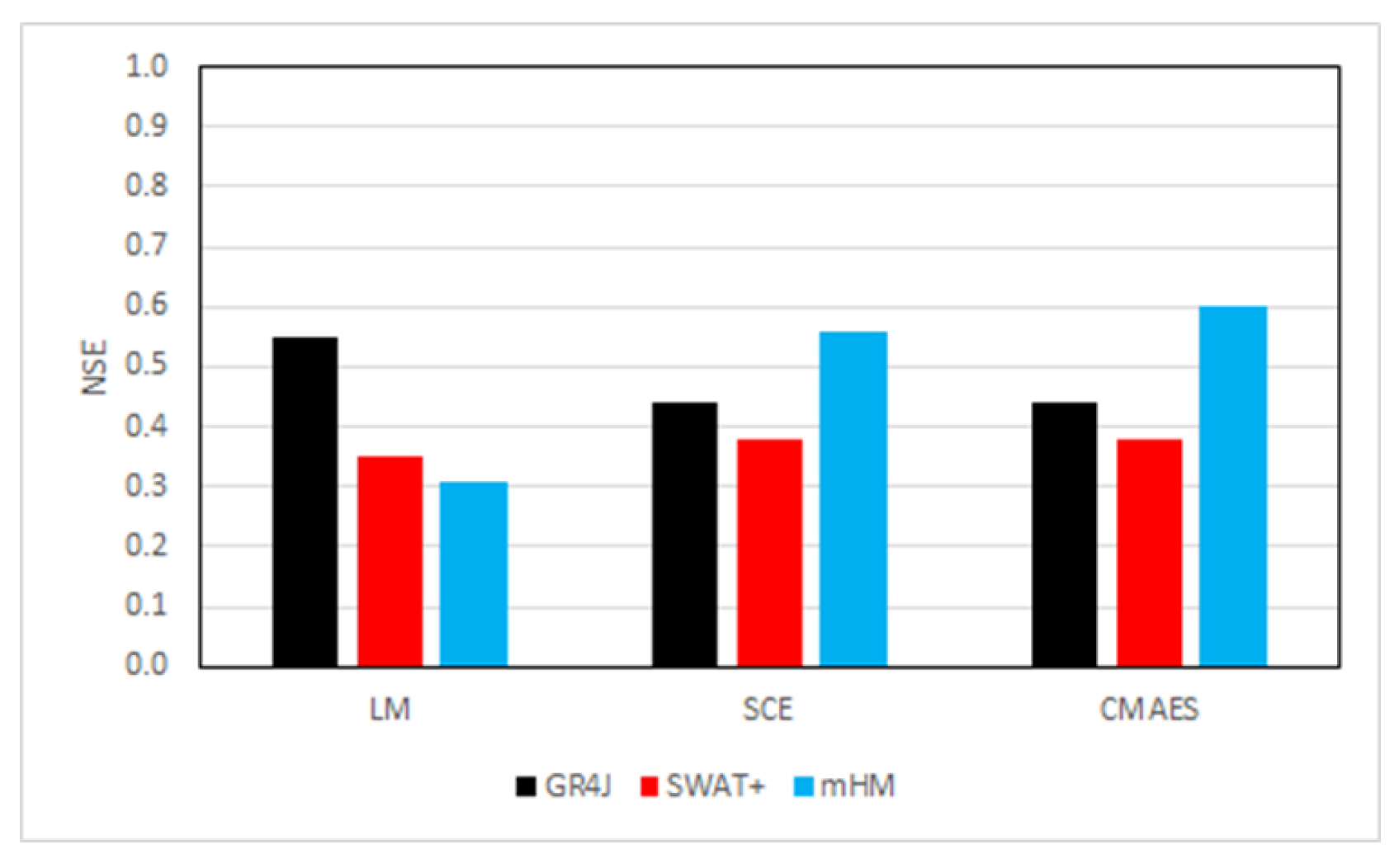
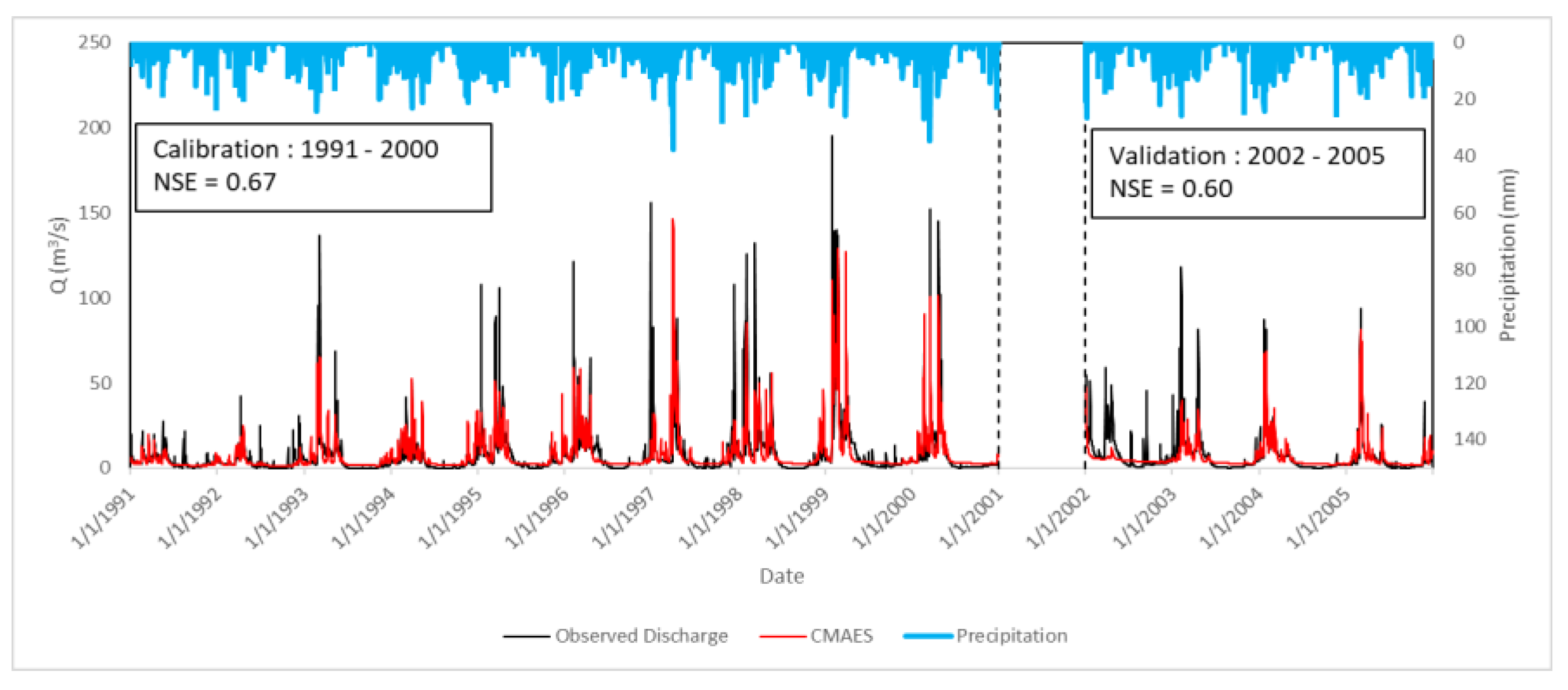
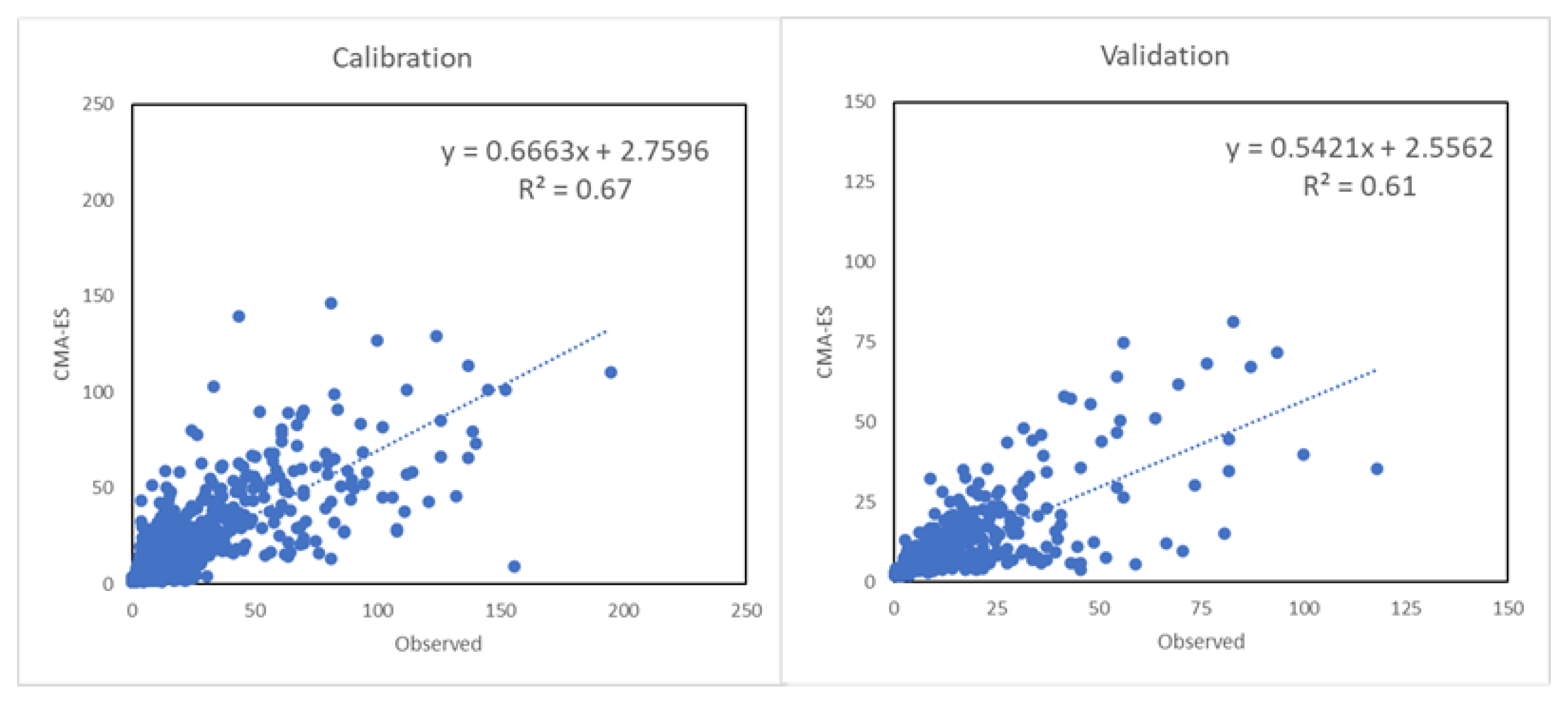
3.2. Calibration and Validation
4. Discussion
5. Conclusions
- In contrast to general findings, the distributed model (mHM) simulated the discharge with higher performance than the coarser models (SWAT+ and GR4J).
- Global optimization algorithms (CMAES and SCE) have extensive ability to search for the optimum parameter set compared to a local algorithm (LM). The highest performance was shown by CMAES based on average NSE through calibration and validation.
- In terms of time efficiency, each model has a different run-time for the study domain. A single run takes an average of 30 s for mHM, 2 min for SWAT+, and 4 s for GR4J.
- Since mHM and SWAT+ allows the drawing of outputs for any sub-basin located at the upstream, it is advantageous compared to GR4J under data-limited modelling conditions.
- The resultant hydrographs demonstrated that simulated discharge values were lower than observed values in general. The reason for this is related to the difference between ERA5 data and MGM measurements. The direct relationship between precipitation and discharge leads the models to simulate lower values.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pechlivanidis, I.G.; Jackson, B.M.; Mcintyre, N.R.; Wheater, H.S. Catchment scale hydrological modelling: A review of model types, calibration approaches and uncertainty analysis methods in the context of recent developments in technology and applications. Glob. Nest J. 2011, 13, 193–214. [Google Scholar] [CrossRef]
- Foughali, A.; Tramblay, Y.; Bargaoui, Z.; Carreau, J.; Ruelland, D. Hydrological Modeling in Northern Tunisia with Regional Climate Model Outputs: Performance Evaluation and Bias-Correction in Present Climate Conditions. Climate 2015, 3, 459–473. [Google Scholar] [CrossRef]
- Mulvaney, T.J. On the use of self registering rain and flood gauges in making observations of the relation of rainfall and flood discharges in given catchment. Trans. Instit. Civ. Eng. Irel. 1850, 4, 18–33. [Google Scholar]
- Crawford, N.H.; Linsley, R.K. Digital Simulation in Hydrology’Stanford Watershed Model 4; Stanford University: Stanford, CA, USA, 1966. [Google Scholar]
- De Luca, D.L.; Apollonio, C.; Petroselli, A. The Benefit of Continuous Hydrological Modelling for Drought Hazard Assessment in Small and Coastal Ungauged Basins: A Case Study in Southern Italy. Climate 2022, 10, 34. [Google Scholar] [CrossRef]
- Tegegne, G.; Park, D.K.; Kim, Y.O. Comparison of hydrological models for the assessment of water resources in a data-scarce region, the Upper Blue Nile River Basin. J. Hydrol. Reg. Stud. 2017, 14, 49–66. [Google Scholar] [CrossRef]
- Brulebois, E.; Ubertosi, M.; Castel, T.; Richard, Y.; Sauvage, S.; Sanchez-Perez, J.-M.; Moine, N.L.; Amiotte-Suchet, P. Robustness and performance of semi-distributed (SWAT) and global (GR4J) hydrological models throughout an observed climatic shift over contrasted French watersheds. Open Water J. 2018, 5, 41–56. [Google Scholar]
- Kunnath-Poovakka, A.; Eldho, T.I. A comparative study of conceptual rainfall-runoff models GR4J, AWBM and Sacramento at catchments in the upper Godavari river basin, India. J. Earth Syst. Sci. 2019, 128, 33. [Google Scholar] [CrossRef]
- Mai, J.; Tolson, B.A.; Shen, H.; Gaborit, É.; Fortin, V.; Gasset, N.; Awoye, H.; Stadnyk, T.A.; Fry, L.M.; Bradley, E.A.; et al. Great Lakes Runoff Intercomparison Project Phase 3: Lake Erie (GRIP-E). J. Hydrol. Eng. 2021, 26, 05021020. [Google Scholar] [CrossRef]
- Duan, Q.; Gupta, H.V.; Sorooshian, S.; Rousseau, A.N.; Turcotte, R. Calibration of Watershed Models; John Wiley & Sons: Hoboken, NJ, USA, 2003; Volume 6. [Google Scholar]
- Azar, A.T.; Khan, Z.I.; Amin, S.U.; Fouad, K.M. Hybrid Global Optimization Algorithm for Feature Selection. Comput. Mater. Contin. 2023, 74, 2021–2037. [Google Scholar] [CrossRef]
- Wallner, M.; Haberlandt, U.; Dietrich, J. Evaluation of different calibration strategies for large scale continuous hydrological modelling. Adv. Geosci. 2012, 31, 67–74. [Google Scholar] [CrossRef]
- Demirel, M.C.; Özen, A.; Orta, S.; Toker, E.; Demir, H.K.; Ekmekcioğlu, Ö.; Tayşi, H.; Eruçar, S.; Sağ, A.B.; Sarı, Ö.; et al. Additional Value of Using Satellite-Based Soil Moisture and Two Sources of Groundwater Data for Hydrological Model Calibration. Water 2019, 11, 2083. [Google Scholar] [CrossRef]
- Yılmaz, M.; Alp, H.; Tosunoğlu, F.; Aşıkoğlu, Ö.L.; Eriş, E. Impact of climate change on meteorological and hydrological droughts for Upper Coruh Basin, Turkey. Nat. Hazards 2022, 112, 1039–1063. [Google Scholar] [CrossRef]
- Kumanlioglu, A.A.; Fistikoglu, O. Performance Enhancement of a Conceptual Hydrological Model by Integrating Artificial Intelligence. J. Hydrol. Eng. 2019, 24, 04019047. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large Area Hydrologic Modeling and Assessment Part I: Model DevelopmenT. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Gebrechorkos, S.H.; Bernhofer, C.; Hülsmann, S. Climate change impact assessment on the hydrology of a large river basin in Ethiopia using a local-scale climate modelling approach. Sci. Total Environ. 2020, 742, 140504. [Google Scholar] [CrossRef]
- Peker, I.B.; Sorman, A.A. Application of SWAT using snow data and detecting climate change impacts in the mountainous eastern regions of Turkey. Water 2021, 13, 1982. [Google Scholar] [CrossRef]
- Anjum, M.N.; Ding, Y.; Shangguan, D. Simulation of the projected climate change impacts on the river flow regimes under CMIP5 RCP scenarios in the westerlies dominated belt, northern Pakistan. Atmos. Res. 2019, 227, 233–248. [Google Scholar] [CrossRef]
- Dile, Y.T.; Daggupati, P.; George, C.; Srinivasan, R.; Arnold, J. Introducing a New Open Source GIS User Interface for the SWAT Model. Environ. Model. Softw. 2016, 85, 129–138. [Google Scholar] [CrossRef]
- Rostamian, R.; Jaleh, A.; Afyuni, M.; Mousavi, S.F.; Heidarpour, M.; Jalalian, A.; Abbaspour, K.C. Application of a SWAT Model for Estimating Runoff and Sediment in Two Mountainous Basins in Central Iran. Hydrol. Sci. J. 2008, 53, 977–988. [Google Scholar] [CrossRef]
- Samaniego, L.; Kumar, R.; Attinger, S. Multiscale parameter regionalization of a grid-based hydrologic model at the mesoscale. Water Resour. Res. 2010, 46, W05523. [Google Scholar] [CrossRef]
- Kumar, R.; Samaniego, L.; Attinger, S. Implications of distributed hydrologic model parameterization on water fluxes at multiple scales and locations. Water Resour. Res. 2013, 49, 360–379. [Google Scholar] [CrossRef]
- Bergström, S. The HBV model—Its structure and applications. Swed. Meteorol. Hydrol. Inst. Norrköping 1992, 4, 1–33. [Google Scholar]
- Liang, X.; Wood, E.F.; Lettenmaier, D.P. Surface soil moisture parameterization of the VIC-2L model: Evaluation and modification. Glob. Planet. Change 1996, 13, 195–206. [Google Scholar] [CrossRef]
- Schweppe, R.; Thober, S.; Müller, S.; Kelbling, M.; Kumar, R.; Attinger, S.; Samaniego, L. MPR 1.0: A stand-alone multiscale parameter regionalization tool for improved parameter estimation of land surface models. Geosci. Model Dev. 2022, 15, 859–882. [Google Scholar] [CrossRef]
- Thober, S.; Cuntz, M.; Kelbling, M.; Kumar, R.; Mai, J.; Samaniego, L. The multiscale routing model mRM v1.0: Simple river routing at resolutions from 1 to 50 km. Geosci. Model Dev. 2019, 12, 2501–2521. [Google Scholar] [CrossRef]
- Demirel, M.C.; Mai, J.; Mendiguren, G.; Koch, J.; Samaniego, L.; Stisen, S. Combining satellite data and appropriate objective functions for improved spatial pattern performance of a distributed hydrologic model. Hydrol. Earth Syst. Sci. 2018, 22, 1299–1315. [Google Scholar] [CrossRef]
- Doherty, J.; Johnston, J.M. Methodologies for calibration and predictive analysis of a watershed model. J. Am. Water Resour. Assoc. 2003, 39, 251–265. [Google Scholar] [CrossRef]
- Mehrdoust, F.; Noorani, I.; Hamdi, A. Two-Factor Heston Model Equipped with Regime-Switching: American Option Pricing and Model Calibration by Levenberg–Marquardt Optimization Algorithm. Math. Comput. Simul. 2023, 204, 660–678. [Google Scholar] [CrossRef]
- Shoarinezhad, V.; Wieprecht, S.; Haun, S. Comparison of local and global optimization methods for calibration of a 3D morphodynamic model of a curved channel. Water 2020, 12, 1333. [Google Scholar] [CrossRef]
- Patel, S.; Eldho, T.I.; Rastogi, A.K.; Rabinovich, A. Groundwater Parameter Estimation Using Multiquadric-Based Meshfree Simulation with Covariance Matrix Adaptation Evolution Strategy Optimization for a Regional Aquifer System. Hydrogeol. J. 2022, 30, 2205–2221. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; van Griensven, A.; Van Liew, M.W.; et al. Swat: Model Use, Calibration, and Validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Feyereisen, G.W.; Strickland, T.C.; Bosch, D.D.; Sullivan, D.G. Evaluation of SWAT Manual Calibration and Input Parameter Sensitivity in the Little River Watershed. Trans. ASABE 2007, 50, 843–855. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar] [CrossRef]
- Okkan, U.; Ersoy, Z.B.; Ali Kumanlioglu, A.; Fistikoglu, O. Embedding machine learning techniques into a conceptual model to improve monthly runoff simulation: A nested hybrid rainfall-runoff modeling. J. Hydrol. 2021, 598, 126433. [Google Scholar] [CrossRef]
- Kilic, M.; Tuylu, G.I. Determination of water conveyance loss in the ahmetli regulator irrigation system in the lower Gediz Basin Turkey. Irrig. Drain. 2011, 60, 579–589. [Google Scholar] [CrossRef]
- Karatas, B.S.; Akkuzu, E.; Unal, H.B.; Asik, S.; Avci, M. Using satellite remote sensing to assess irrigation performance in Water User Associations in the Lower Gediz Basin, Turkey. Agric. Water Manag. 2009, 96, 982–990. [Google Scholar] [CrossRef]
- Tonkul, S.; Baba, A.; Şimşek, C.; Demirkesen, A.C. Groundwater recharge estımatıon ın the Alaşehir sub-basın usıng hydro-geochemical data; Alaşehir case study. Environ. Earth Sci. 2021, 80, 261. [Google Scholar] [CrossRef]

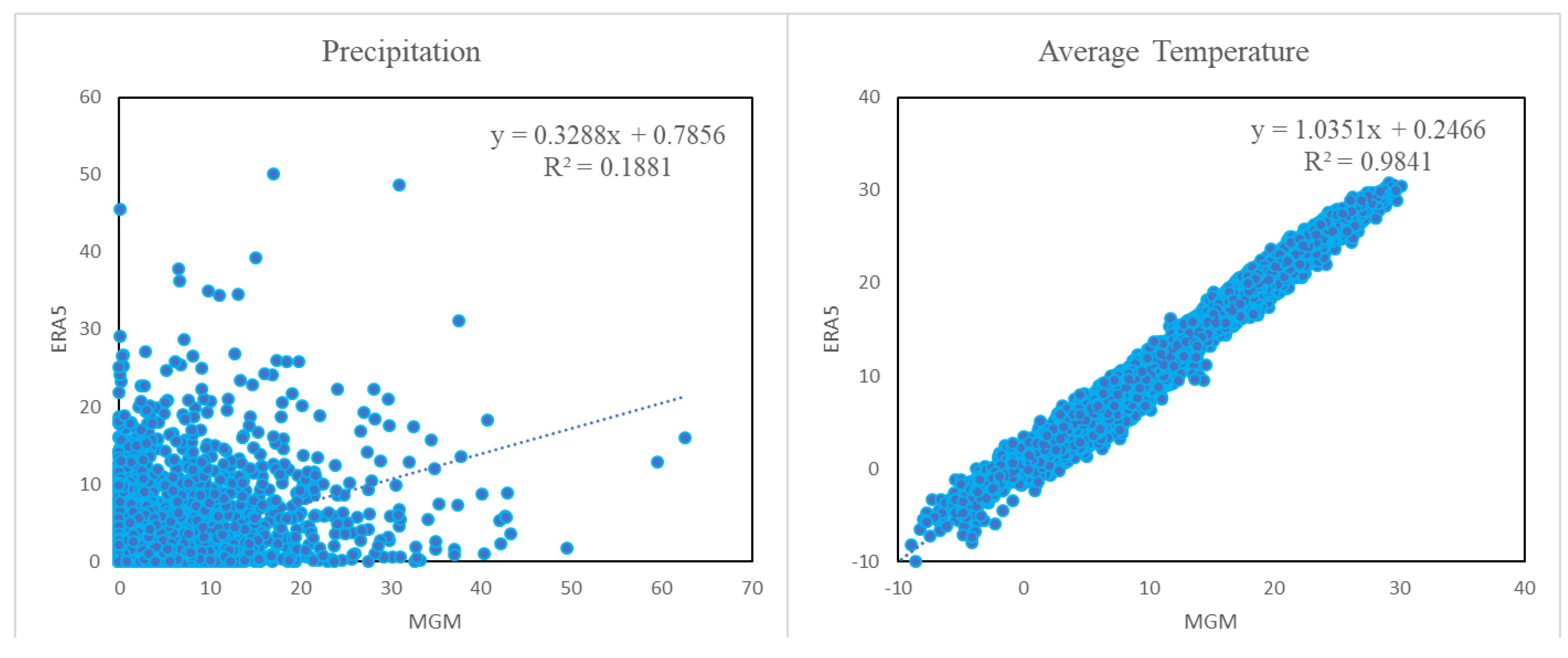



| Total Precipitation (mm) | Average Temperature (°C) | Maximum Temperature (°C) | Minimum Temperature (°C) | |||||
|---|---|---|---|---|---|---|---|---|
| MGM | ERA5 | MGM | ERA5 | MGM | ERA5 | MGM | ERA5 | |
| January | 69.2 | 59.7 | 3.2 | 3.2 | 12.8 | 12.3 | −10.6 | −9.4 |
| February | 62.2 | 56.1 | 3.4 | 3.9 | 14.4 | 14.2 | −8.9 | −9.9 |
| March | 60.0 | 58.6 | 6.5 | 7.2 | 19.2 | 18.8 | −6.5 | −5.2 |
| April | 63.5 | 56.6 | 11.0 | 11.9 | 21.5 | 21.6 | −1.2 | −0.1 |
| May | 43.7 | 40.2 | 15.6 | 16.8 | 23.3 | 24.9 | 4.2 | 5.2 |
| June | 19.8 | 17.9 | 19.8 | 21.4 | 27.3 | 28.6 | 9.9 | 9.6 |
| July | 17.4 | 10.2 | 23.3 | 24.6 | 30.2 | 30.8 | 12.8 | 15.5 |
| August | 12.4 | 7.6 | 23.3 | 24.3 | 29.7 | 30.4 | 15.9 | 17.3 |
| September | 14.7 | 10.1 | 19.2 | 20.0 | 26.9 | 28.3 | 9.4 | 11.1 |
| October | 37.5 | 27.2 | 14.2 | 14.6 | 22.8 | 23.0 | 3.1 | 4.1 |
| November | 74.0 | 58.4 | 8.4 | 8.3 | 18.3 | 17.2 | −2.9 | −1.8 |
| December | 88.3 | 69.3 | 4.7 | 4.6 | 13.9 | 13.2 | −5.4 | −5.6 |
| Annual | 562.8 | 472.0 | 12.8 | 13.5 | 30.2 | 30.8 | −10.6 | −9.9 |
| Parameter | Description |
|---|---|
| X1 | Production storage capacity (mm) |
| X2 | Groundwater exchange coefficient (mm) |
| X3 | One day ahead maximum capacity of the routing store (mm) |
| X4 | Time base of unit hydrograph (day) |
| Parameter | Desscription | Unit |
|---|---|---|
| cn2 | SCS curve number | - |
| awc | Soil water content | - |
| k | Hydraulic conductivity of saturated soil | mm/hr |
| perco | Percolation coefficient | - |
| revap | Evaporation coefficient from shallow aquifer to root | - |
| canmx | Maximum canopy storage | mm |
| esco | Soil evaporation compensation factor | - |
| epco | Plant uptake compensation factor | - |
| evrch | Reach evaporation adjustment factor | - |
| flomin | Minimum amount of water to be stored in the aquifer for return flow | mm |
| revap_min | Minimum water depth required in shallow aquifer for “revap” | mm |
| Parameter | Parameter Description |
|---|---|
| PTF_lower66_5_clay | Pedotransfer function (PTF) soil moisture constant for less than 66.5% clay |
| PTF_Ks_sand | PTF hydraulic conductivity constant for saturated sand |
| PTF_Ks_clay | PTF hydraulic conductivity constant for saturated clay |
| rootFractionCoefficient_pervious | Root fraction coefficient for pervious area |
| PTF_lower66_5_Db | PTF density constant for less than 66.5% sand |
| PTF_lower66_5_constant | PTF soil moisture constant for less than 66.5% sand |
| PTF_Ks_constant | PTF hydraulic conductivity constant for saturated soil |
| rootFractionCoefficient_forest | Root fraction coefficient for forest |
| infiltrationShapeFactor | Shape factor that divides effective precipitation into infiltration and surface flow |
| PET_a_forest | Forest—PET correction factor |
| PET_a_pervious | Pervious area—PET correction factor |
| PET_b | Agricultural land—PET correction factor |
| PET_c | Agricultural land—PET correction factor (2) |
| canopyInterceptionFactor | Canopy interception factor |
| exponentSlowInterflow | Slow interflow exponent |
| Model | Parameter | Calibrated Value | Limit | |||
|---|---|---|---|---|---|---|
| L-M | SCE-UA | CMAES | Min | Max | ||
| GR4J | X1 | 399.99 | 346.37 | 347.02 | 10 | 2000 |
| X2 | 0.00 | 0.46 | 0.47 | −8 | 6 | |
| X3 | 10.00 | 10.00 | 10.00 | 10 | 500 | |
| X4 | 1.77 | 1.32 | 1.33 | 1 | 4 | |
| SWAT+ | cn2 | 0.77 | 0.67 | 0.68 | 0.65 | 0.95 |
| awc | 0.02 | 0.01 | 0.01 | 0.01 | 0.51 | |
| k | 200.40 | 189.18 | 193.07 | 0.00 | 2000.00 | |
| perco | 0.28 | 0.16 | 0.20 | 0.00 | 1.00 | |
| revap | 0.20 | 0.05 | 0.16 | 0.02 | 0.20 | |
| canmx | 19.99 | 23.55 | 22.33 | 0.00 | 100.00 | |
| esco | 0.67 | 0.37 | 0.39 | 0.00 | 1.00 | |
| epco | 0.04 | 0.17 | 0.17 | 0.00 | 1.00 | |
| evrch | 0.67 | 0.75 | 0.56 | 0.50 | 1.00 | |
| flomin | 500.00 | 355.52 | 1059.35 | 0.00 | 1250.00 | |
| mHM | PTF_lower66_5_clay | 0.0017 | 0.0012 | 0.0019 | 0.0001 | 0.0029 |
| PTF_Ks_sand | 0.0083 | 0.0221 | 0.0158 | 0.0060 | 0.0260 | |
| PTF_Ks_clay | 0.0079 | 0.0130 | 0.0124 | 0.0030 | 0.0130 | |
| rootFractionCoefficient_pervious | 0.0608 | 0.0095 | 0.0460 | 0.0010 | 0.0900 | |
| PTF_lower66_5_Db | −0.3463 | −0.2141 | −0.2315 | −0.5513 | −0.0913 | |
| PTF_lower66_5_constant | 0.6877 | 0.6724 | 0.6750 | 0.5358 | 1.1232 | |
| PTF_Ks_constant | −0.7105 | −1.1978 | −1.0251 | −1.2000 | −0.2850 | |
| rootFractionCoefficient_forest | 0.9401 | 0.9623 | 0.9872 | 0.9000 | 0.9990 | |
| infiltrationShapeFactor | 1.9602 | 1.1113 | 1.0000 | 1.0000 | 4.0000 | |
| PET_a_forest | 0.7221 | 1.2466 | 1.2885 | 0.3000 | 1.3000 | |
| PET_a_pervious | 0.7414 | 0.3604 | 0.3176 | 0.3000 | 1.3000 | |
| PET_b | 0.6823 | 0.7020 | 0.5982 | 0.0000 | 1.5000 | |
| PET_c | −0.9670 | −0.0001 | −0.0427 | −2.0000 | 0.0000 | |
| canopyInterceptionFactor | 0.1520 | 0.1501 | 0.2135 | 0.1500 | 0.4000 | |
| exponentSlowInterflow | 0.1948 | 0.2324 | 0.2054 | 0.0500 | 0.3000 | |
| Calibratoin 1991–2000 | NSE | R2 | KGE | RSR | PBIAS | MSE | RMSE |
|---|---|---|---|---|---|---|---|
| mHM-CMAES | 0.67 | 0.66 | 0.74 | 0.58 | 2.0 | 77.84 | 8.82 |
| mHM-SCE | 0.67 | 0.67 | 0.74 | 0.57 | −1.9 | 76.59 | 8.75 |
| GR4J-SCE | 0.63 | 0.63 | 0.72 | 0.61 | 0.4 | 86.29 | 9.29 |
| GR4J-CMAES | 0.63 | 0.63 | 0.72 | 0.61 | 0.4 | 86.29 | 9.29 |
| SWAT+-SCE | 0.56 | 0.57 | 0.72 | 0.66 | −2.0 | 102.76 | 10.14 |
| SWAT+-CMAES | 0.56 | 0.57 | 0.72 | 0.67 | 2.8 | 103.13 | 10.16 |
| mHM-LM | 0.54 | 0.55 | 0.71 | 0.68 | −1.5 | 108.23 | 10.40 |
| SWAT+-LM | 0.53 | 0.55 | 0.70 | 0.68 | −3.4 | 108.32 | 10.41 |
| GR4J-LM | 0.44 | 0.59 | 0.22 | 0.75 | −55.5 | 131.05 | 11.45 |
| Validation 2002–2005 | NSE | R2 | KGE | RSR | PBIAS | MSE | RMSE |
|---|---|---|---|---|---|---|---|
| mHM-CMAES | 0.60 | 0.61 | 0.61 | 0.63 | −9.9 | 52.96 | 7.28 |
| mHM-SCE | 0.56 | 0.58 | 0.55 | 0.67 | −16.6 | 58.63 | 7.66 |
| GR4J-LM | 0.55 | 0.62 | 0.44 | 0.67 | −42.7 | 59.24 | 7.70 |
| GR4J-SCE | 0.44 | 0.67 | 0.60 | 0.75 | 23.5 | 73.77 | 8.59 |
| GR4J-CMAES | 0.44 | 0.67 | 0.60 | 0.75 | 23.5 | 73.50 | 8.57 |
| SWAT+-SCE | 0.38 | 0.41 | 0.57 | 0.79 | −2.4 | 81.58 | 9.03 |
| SWAT+-CMAES | 0.38 | 0.41 | 0.60 | 0.78 | 0.2 | 81.36 | 9.02 |
| SWAT+-LM | 0.35 | 0.40 | 0.54 | 0.81 | −9.4 | 86.29 | 9.29 |
| mHM-LM | 0.31 | 0.37 | 0.53 | 0.83 | −20.4 | 91.59 | 9.57 |
| Performance | RSR | NSE | PBIAS |
|---|---|---|---|
| Very Good | 0.00 ≤ RSR ≤ 0.50 | 0.70 < NSE ≤ 1.00 | PBIAS < ±10 |
| Good | 0.50 < RSR ≤ 0.60 | 0.65 < NSE ≤ 0.75 | ±10 ≤ PBIAS < ±15 |
| Satisfactory | 0.60 < RSR ≤ 0.70 | 0.50 < NSE ≤ 0.65 | ±15 ≤ PBIAS < ±25 |
| Poor | RSR > 0.70 | NSE ≤ 0.5 | PBIAS ≥ ±25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alp, H.; Demirel, M.C.; Aşıkoğlu, Ö.L. Effect of Model Structure and Calibration Algorithm on Discharge Simulation in the Acısu Basin, Turkey. Climate 2022, 10, 196. https://doi.org/10.3390/cli10120196
Alp H, Demirel MC, Aşıkoğlu ÖL. Effect of Model Structure and Calibration Algorithm on Discharge Simulation in the Acısu Basin, Turkey. Climate. 2022; 10(12):196. https://doi.org/10.3390/cli10120196
Chicago/Turabian StyleAlp, Harun, Mehmet Cüneyd Demirel, and Ömer Levend Aşıkoğlu. 2022. "Effect of Model Structure and Calibration Algorithm on Discharge Simulation in the Acısu Basin, Turkey" Climate 10, no. 12: 196. https://doi.org/10.3390/cli10120196
APA StyleAlp, H., Demirel, M. C., & Aşıkoğlu, Ö. L. (2022). Effect of Model Structure and Calibration Algorithm on Discharge Simulation in the Acısu Basin, Turkey. Climate, 10(12), 196. https://doi.org/10.3390/cli10120196