Analysis of Quadratic Correlation between Dryness Indices and Wine Grape Yield to Estimate Future Climate Impacts in Hungary
Abstract
1. Introduction
2. Materials and Methods
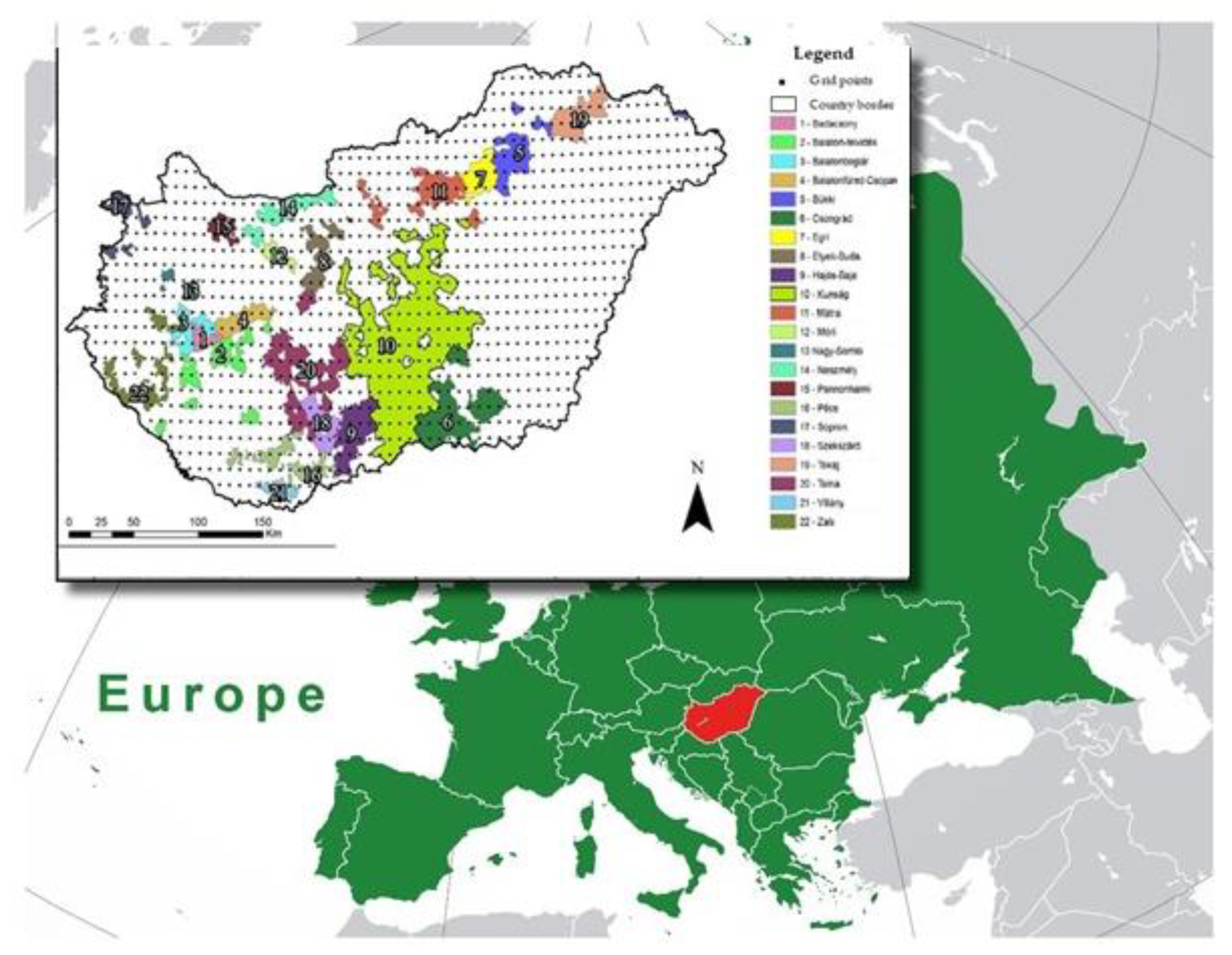
2.1. The Area of the Investigations
2.2. Observed Meteorological Data
2.3. Projected Meteorological Data
2.4. Dryness Indices
2.5. Grape Yield Database
2.6. Box Diagrams to Characterize Frequency Distributions
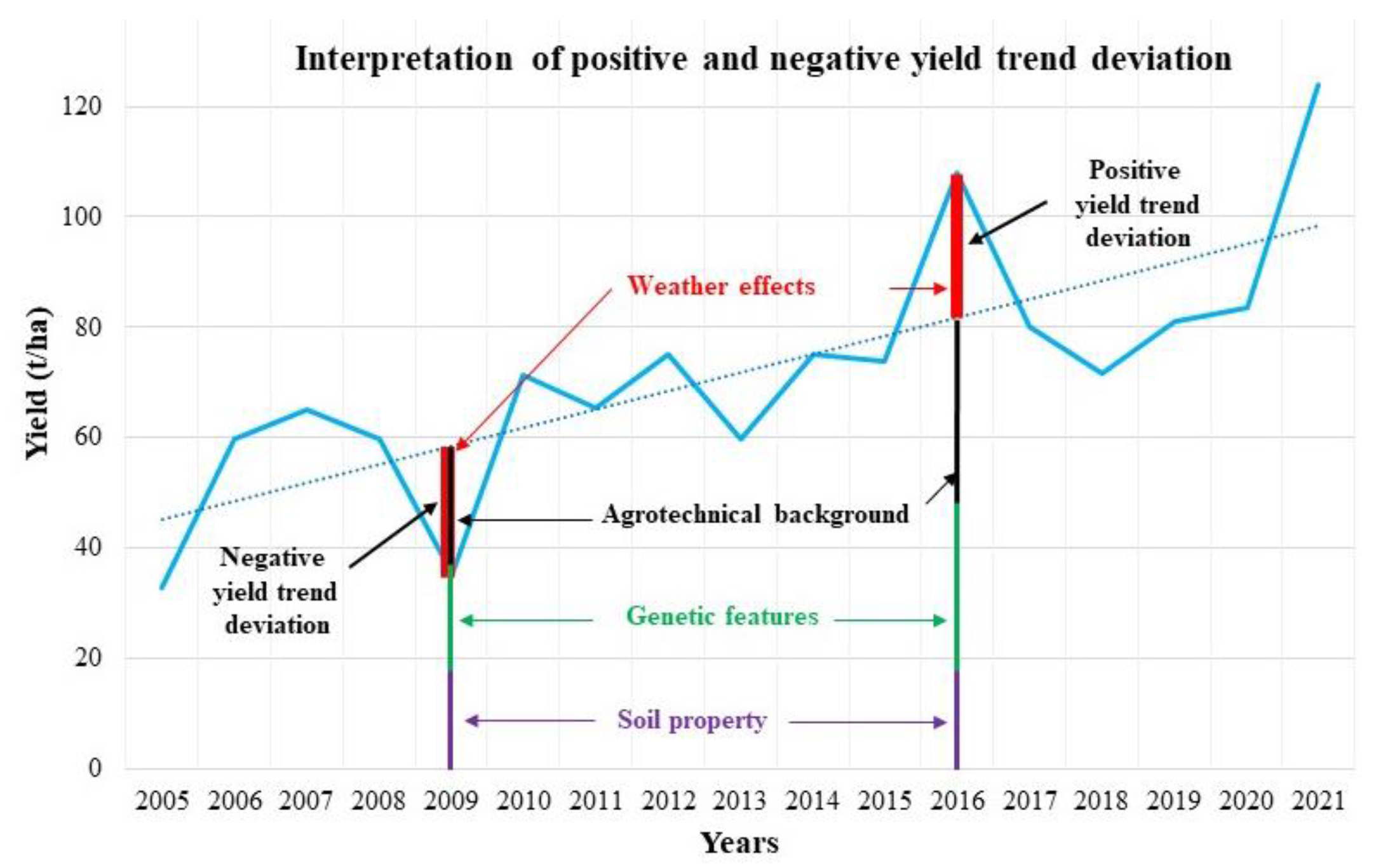
2.7. Method of Finding Statistical Correlations between the Dryness Indices and Yield Data
2.8. Estimation of Expected Future Yields
3. Results
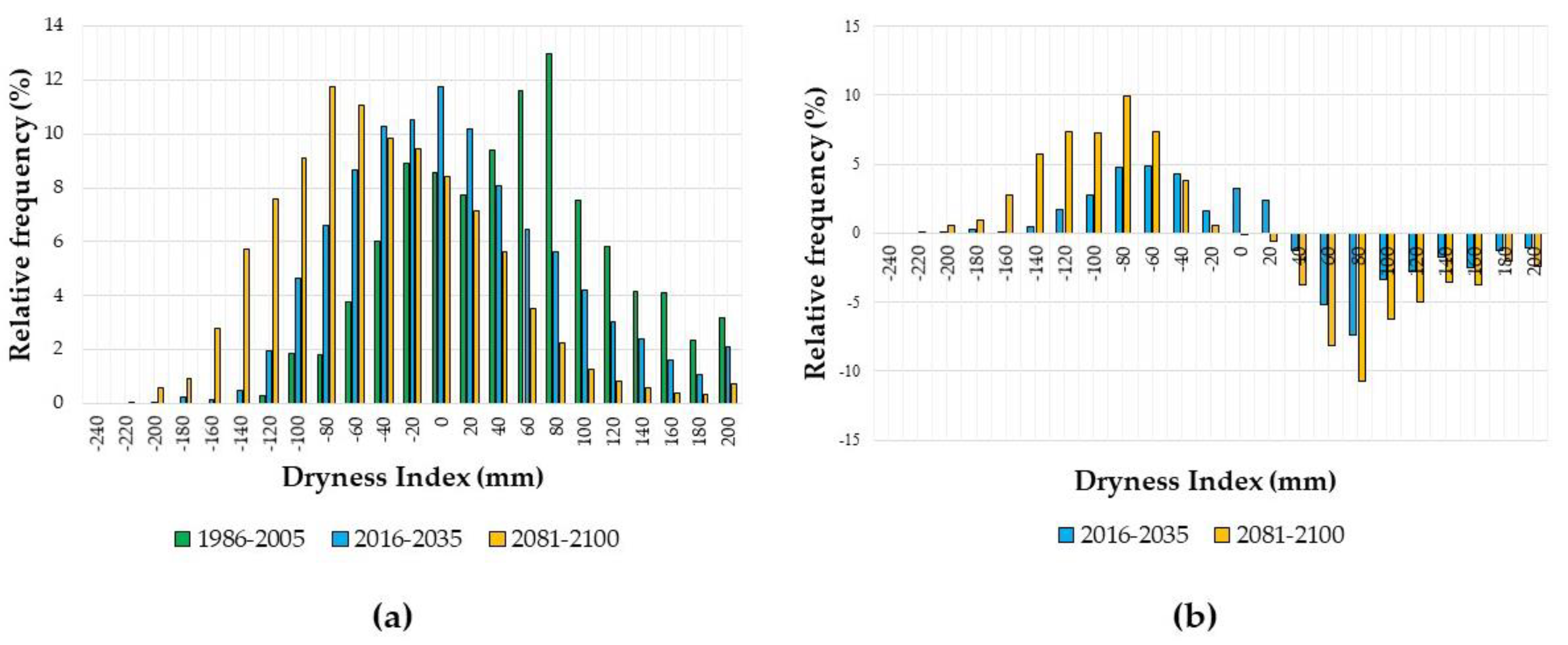
3.1. Statistical Distribution of the Dryness Indices
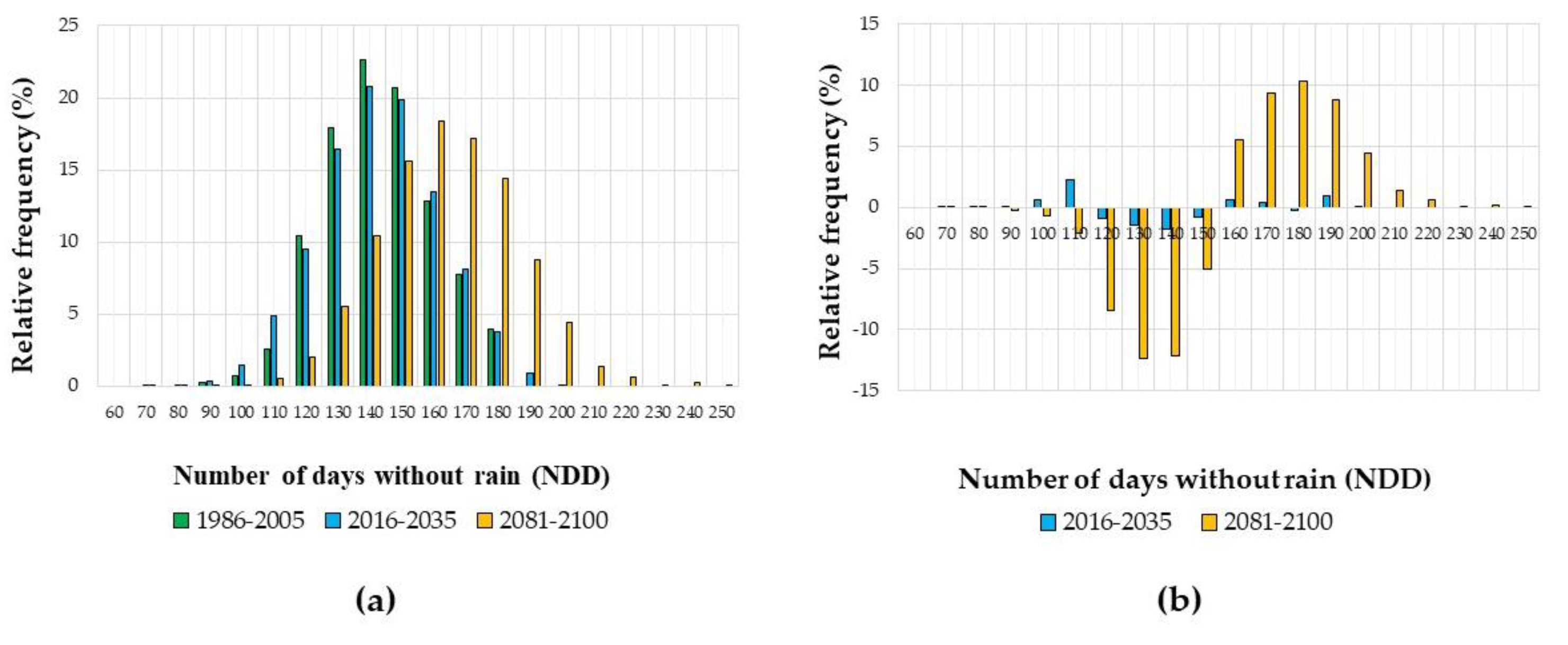
3.1.1. Number of Days without Rain (NDD)
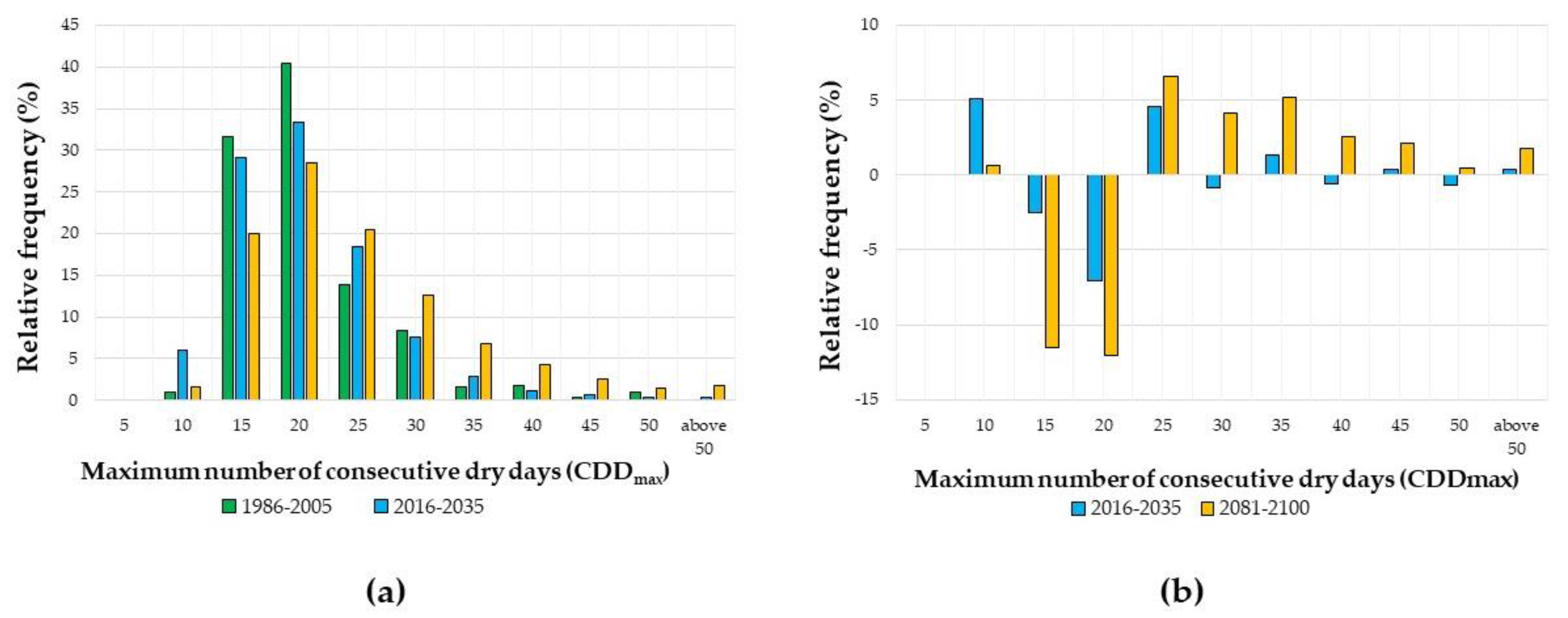
3.1.2. The Maximum Number of Consecutive Dry Days (CDDmax)
3.1.3. Climatic Water Balance (CWB)
3.1.4. Dryness Index (DI)
3.1.5. Vineyard Water Indicator (VWI)
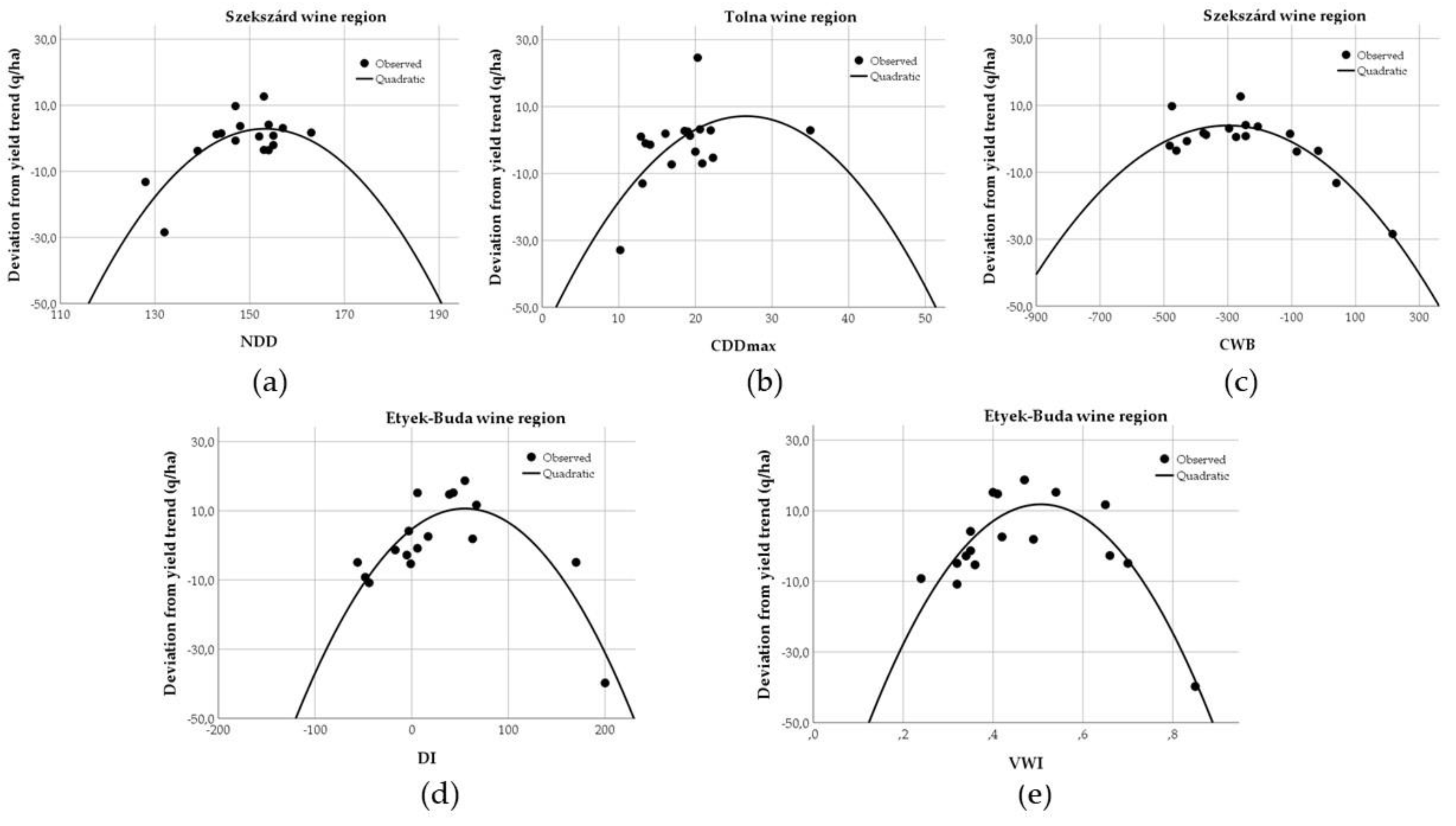
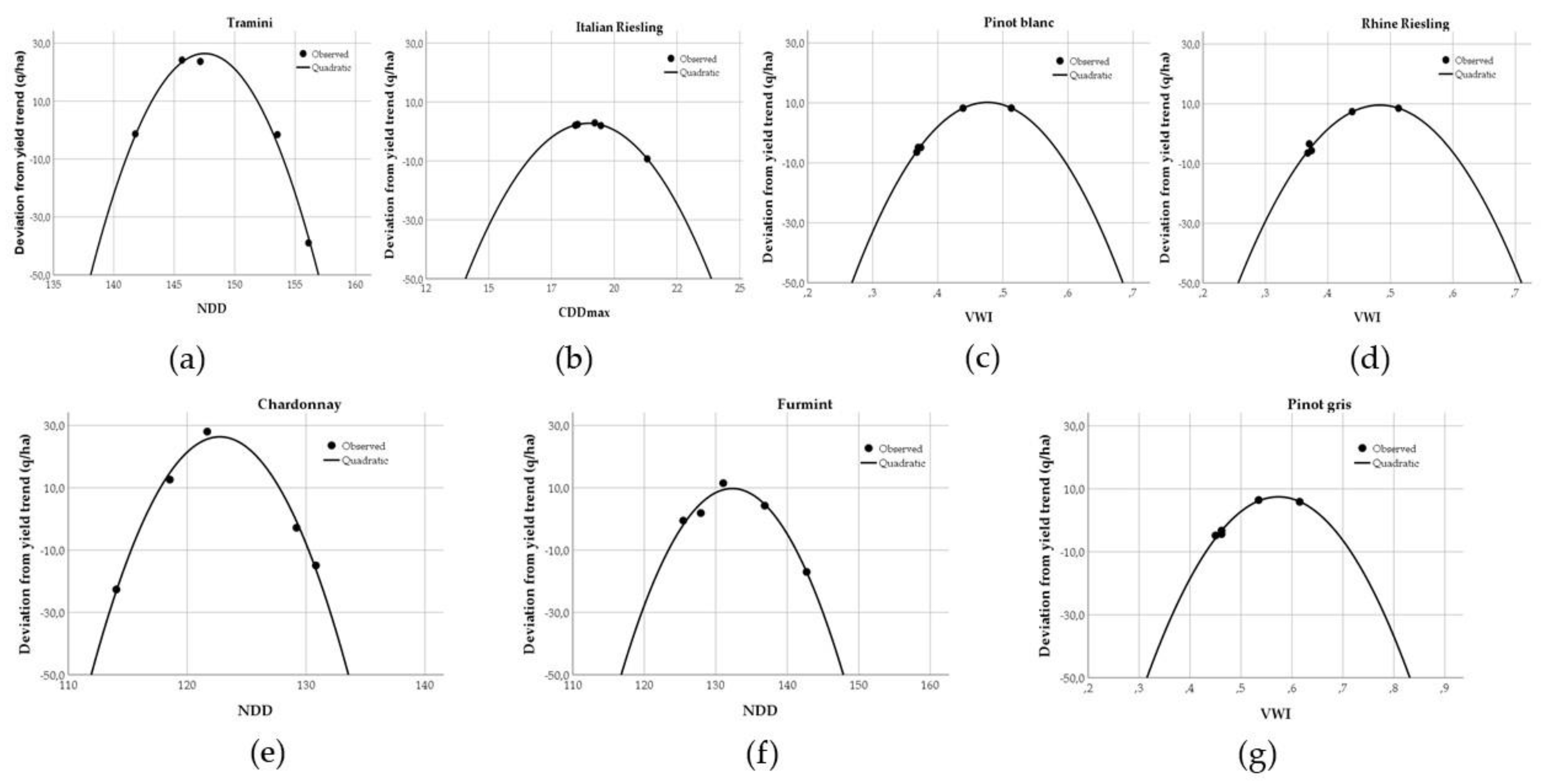
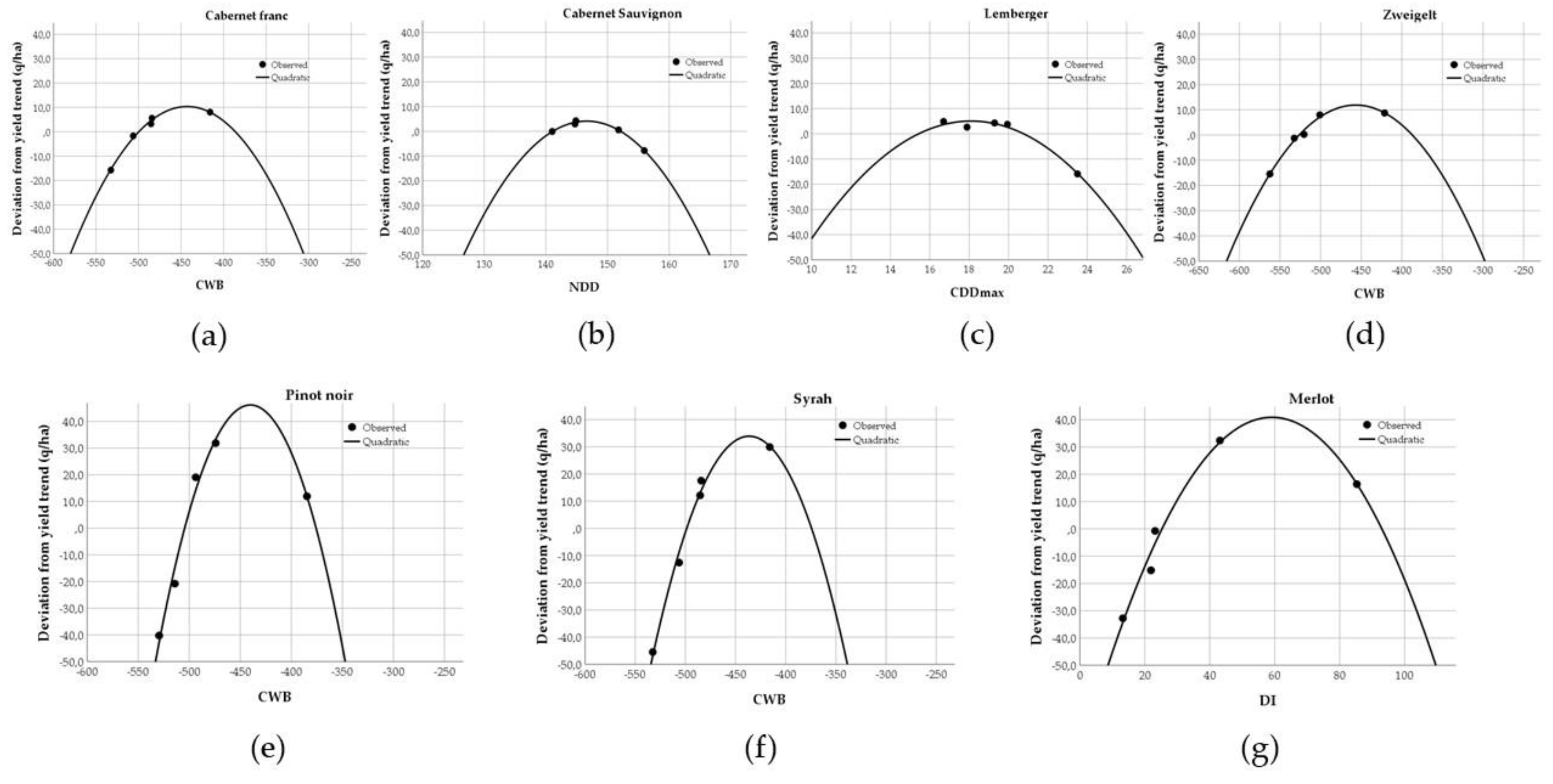
3.2. Quadratic Correlation of Wine Grape Yield with the Dryness Indices
3.3. Quadratic Relationships between the Yield Fluctuations and Indices
3.3.1. Analysis of More Extended Periods (2005–2021) without Grape Varieties
3.3.2. Analysis of Short Periods (2017–2021) with Grape Varieties
3.4. Estimation of the Expected Wine Grape Yield Fluctuation
3.4.1. Estimation Based on More Extended Yield Series
3.4.2. Estimation Based on Short Yield Series
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Phakula, S. Modelling Seasonal Rainfall Characteristics over South Africa. Master’s Thesis, University of Pretoria, Pretoria, South Afric, 2016. [Google Scholar]
- Mariotti, A. Recent changes in the Mediterranean water cycle: A pathway toward long-term regional hydroclimatic change? J. Clim. 2010, 23, 1513–1525. [Google Scholar] [CrossRef]
- Giorgi, F. Climate change hot spots. Geophys. Res. Lett. 2006, 33, L08707. [Google Scholar] [CrossRef]
- Ubeda, C.; Hornedo-Ortega, R.; Cerezo, A.B.; Garcia-Parrilla, M.C.; Troncoso, A.M. Chemical hazards in grapes and wine, climate change and challenges to face. Food Chem. 2020, 314, 126222. [Google Scholar] [CrossRef] [PubMed]
- Jones, G.V.; Alves, F. Impact of climate change on wine production: A global overview and regional assessment in the Douro Valley of Portugal. Int. J. Glob. Warm. 2012, 4, 383–406. [Google Scholar] [CrossRef]
- van Leeuwen, C.; Friant, P.; Chone, X.; Tregoat, O.; Koundouras, S.; Dubourdieu, D. Influence of climate, soil, and cultivar on terroir. Am. J. Enol. Vitic. 2004, 55, 207–217. [Google Scholar]
- Intrigliolo, D.S.; Castel, J.R. Response of grapevine cv. ‘Tempranillo’ to timing and amount of irrigation: Water relations, vine growth, yield and berry and wine composition. Irrig. Sci. 2010, 28, 113–125. [Google Scholar] [CrossRef]
- Deluc, L.G.; Quilici, D.R.; Decendit, A.; Grimplet, J.; Wheatley, M.D.; Schlauch, K.A.; Mérillon, J.M.; Cushman, J.C.; Cramer, G.R. Water deficit alters differentially metabolic pathways affecting important flavor and quality traits in grape berries of Cabernet Sauvignon and Chardonnay. BMC Genom. 2009, 10, 1–33. [Google Scholar] [CrossRef]
- Baeza, P.; Junquera, P.; Peiro, E.; Lissarrague, J.R.; Uriarte, D.; Vilanova, M. Effects of vine water status on yield components, vegetative response and must and wine composition. In Advances in Grape and Wine Biotechnology; IntechOpen: London, UK, 2019. [Google Scholar]
- Pellegrino, A.; Lebon, E.; Simonneau, T.; Wery, J. Towards a simple indicator of water stress in grapevine (Vitis vinifera L.) based on the differential sensitivities of vegetative growth components. Aust. J. Grape Wine Res. 2005, 11, 306–315. [Google Scholar] [CrossRef]
- Lovisolo, C.; Perrone, I.; Hartung, W.; Schubert, A. An abscisic acid-related reduced transpiration promotes gradual embolism repair when grapevines are rehydrated after drought. New Phytol. 2008, 180, 642–651. [Google Scholar] [CrossRef]
- Susilo, G.E.; Yamamoto, K.; Imai, T.; Ishii, Y.; Fukami, H.; Sekine, M. The effect of ENSO on rainfall characteristics in the tropical peatland areas of Central Kalimantan, Indonesia. Hydrol. Sci. J. 2013, 58, 539–548. [Google Scholar] [CrossRef]
- Polade, S.D.; Pierce, D.W.; Cayan, D.R.; Gershunov, A.; Dettinger, M.D. The key role of dry days in changing regional climate and precipitation regimes. Sci. Rep. 2014, 4, 4364. [Google Scholar] [CrossRef] [PubMed]
- Usman, M.T.; Reason, C.J.C. Dry spell frequencies and their variability 4012 over southern Africa. Clim. Res. 2004, 26, 199–211. [Google Scholar] [CrossRef]
- Frich, P.A.L.V.; Alexander, L.V.; Della-Marta, P.M.; Gleason, B.; Haylock, M.; Tank, A.K.; Peterson, T. Observed coherent changes in climatic extremes during the second half of the twentieth century. Clim. Res. 2002, 19, 193–212. [Google Scholar] [CrossRef]
- Kostopoulou, E.; Jones, P.D. Assessment of climate extremes in the Eastern Mediterranean. Meteorol. Atmos. Phys. 2005, 89, 69–85. [Google Scholar] [CrossRef]
- Nastos, P.T.; Zerefos, C.S. Spatial and temporal variability of consecutive dry and wet days in Greece. Atmos. Res. 2009, 94, 616–628. [Google Scholar] [CrossRef]
- Duan, Y.; Ma, Z.; Yang, Q. Characteristics of consecutive dry days variations in China. Theor. Appl. Climatol. 2017, 130, 701–709. [Google Scholar] [CrossRef]
- Ndlovu, M.; Clulow, A.D.; Savage, M.J.; Nhamo, L.; Magidi, J.; Madhaudhi, T. An assessment of the impacts of climate variability 3852 and change in Kwa-Zulu Natal province, South Africa. Atmosphere 2021, 12, 427. [Google Scholar] [CrossRef]
- Thomas, A. Spatial and temporal characteristics of potential evapotranspiration trends over China. Int. J. Climatol. 2000, 20, 381–396. [Google Scholar] [CrossRef]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land-atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- IPCC Climate Change. The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Paltineanu, C.; Mihailescu, I.F.; Seceleanu, I.; Dragota, C.; Vasenciuc, F. Using aridity indices to describe some climate and soil features in Eastern Europe: A Romanian case study. Theor. Appl. Climatol. 2007, 90, 263–274. [Google Scholar] [CrossRef]
- Paltineanu, C.R.; Mihailescu, I.F.; Prefac, Z.; Dragota, C.; Vasenciuc, F.; Claudia, N. Combining the standardized precipitation index and climatic water deficit in characterizing droughts: A case study in Romania. Theor. Appl. Climatol. 2009, 97, 219–233. [Google Scholar] [CrossRef]
- Prăvălie, R.; Bandoc, G. Aridity variability in the last five decades in the Dobrogea region, Romania. Arid. Land Res. Manag. 2015, 29, 265–287. [Google Scholar] [CrossRef]
- Hundertmark, W. Building drought management capacity in the Mekong River basin. Irrig. Drain. 2008, 57, 279–287. [Google Scholar] [CrossRef]
- Kranz, N.; Menniken, T.; Hinkel, J. Climate change adaptation strategies in the Mekong and Orange–Senqu basins: What determines the state-of-play? Environ. Sci. Pol. 2010, 13, 648–659. [Google Scholar] [CrossRef]
- Bastakoti, R.C.; Gupta, J.; Babel, M.S.; van Dijk, M.P. Climate risks and adaptation strategies in the Lower Mekong River basin. Reg. Environ. Change 2014, 14, 207–219. [Google Scholar] [CrossRef]
- Gaudillère, J.P.; Van Leeuwen, C.; Ollat, N. Carbon isotope composition of sugars in grapevine, and integrated indicator of vineyard water status. J. Exp. Bot. 2002, 53, 757–763. [Google Scholar] [CrossRef]
- Malheiro, A.C.; Santos, J.A.; Fraga, H.; Pinto, J.G. Climate change scenarios applied to viticultural zoning in Europe. Clim. Res. 2010, 43, 163–177. [Google Scholar] [CrossRef]
- Fraga, H.; Santos, J.A.; Malheiro, A.C.; Pereira, J.M. Climate change projections for the Portuguese viticulture using a multi-model ensemble. Ciência Téc. Vitiv. 2012, 27, 39–48. [Google Scholar]
- Conceição, M.A.F.; de Souza, R.T.; Tonietto, J. Estimating MCC System Dryness Index using the Vineyard Water Indicator. In Proceedings of the 39th World Congress of Vine and Wine, Bento Goncalves, Brazil, 24–28 October 2016; Volume 7, p. 01037. [Google Scholar]
- Tonietto, J.; Carbonneau, A. A multicriteria climatic classification system for grape-growing regions worldwide. Agric. For. Meteorol. 2004, 124, 81–97. [Google Scholar] [CrossRef]
- Fraga, H.; Malheiro, A.C.; Moutinho-Pereira, J.; Jones, G.V.; Alves, F.; Pinto, J.G.; Santos, J.A. Very high-resolution bioclimatic zoning of Portuguese wine regions: Present and future scenarios. Reg. Environ. Change 2014, 14, 295–306. [Google Scholar] [CrossRef]
- Moral, F.J.; Rebollo, F.J.; Paniagua, L.L.; García, A.; de Salazar, E.M. Application of climatic indices to analyze viticultural suitability in Extremadura, south-western Spain. Theor. Appl. Climatol. 2016, 123, 277–289. [Google Scholar] [CrossRef]
- Dobor, L.; Barcza, Z.; Hlásny, T.; Havasi, Á.; Horváth, F.; Ittzés, P.; Bartholy, J. Bridging the gap between climate models and impact studies: The FORESEE Database. Geosci. Data J. 2014, 2, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Cornes, R.C.; van der Schrier, G.; van den Besselaar, E.J.; Jones, P.D. An ensemble version of the E-OBS temperature and precipitation data sets. J. Geophys. Res. Atmos. 2018, 123, 9391–9409. [Google Scholar] [CrossRef]
- van der Linden, P. (Ed.) ENSEMBLES: Climate Change and Its Impacts at Seasonal, Decadal and Centennial Timescales; Summary of Research and Results from the ENSEMBLES Project. Met Office Hadley Centre. 2009. Available online: https://ensembles-eu.metoffice.gov.uk/docs/Ensembles_final_report_Nov09.pdf (accessed on 19 October 2022).
- Nakicenovic, N.; Alcamo, J.; Davis, G.; de Vries, B.; Fenhann, J.; Gaffin, S.; Gregory, K.; Grübler, A.; Jung, T.Y.; Kram, T.; et al. IKCC Special Report on Emissions Scenarios; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Gibelin, A.L.; Deque, M. Anthropogenic climate change over the Mediterranean region simulated by a global variable resolution model. Clim. Dynam. 2003, 20, 327–339. [Google Scholar] [CrossRef]
- Steppeler, J.; Doms, G.; Schattler, U.; Bitzer, H.W.; Gassmann, A.; Damrath, U.; Gregoric, G. Meso-gamma scale forecasts using the non-hydrostatic model LM. Meteorol. Atmos. Phys. 2003, 82, 75–96. [Google Scholar] [CrossRef]
- Jaeger, E.B.; Anders, I.; Luthi, D.; Rockel, B.; Schar, C.; Seneviratne, S.I. Analysis of ERA40-driven CLM simulations for Europe. Meteorol. Z. 2008, 17, 349–367. [Google Scholar] [CrossRef]
- Collins, M.; Booth, B.B.; Bhaskaran, B.; Harris, G.R.; Murphy, J.M.; Sexton, D.M.H.; Webb, M.J. Climate model errors, feedbacks and forcings: A comparison of perturbed physics and multi-model ensembles. Clim. Dynam. 2011, 36, 1737–1766. [Google Scholar] [CrossRef]
- Christensen, J.H.; Christensen, O.B.; Lopez, P.; van Meijgaard, E.; Botzet, M. The HIRHAM 4 Regional Atmospheric Climate Model; DMI Scientific Report 96-4; Danish Meteorological Institute: Copenhagen, Denmark, 1996. [Google Scholar]
- Lenderink, G.; van den Hurk, B.; van Meijgaard, E.; van Ulden, A.; Cuijpers, H. Simulation of Present-Day Climate in RACMO2: First Results and Model Developments; Ministerie van Verkeer en Waterstaat, Koninklijk Nederlands Meteorologisch Instituut: De Bilt, The Netherlands, 2003. [Google Scholar]
- Kjellström, E.; Bärring, L.; Gollvik, S.; Hansson, U.; Jones, C.; Samuelsson, P.; Rummukainen, M.; Ullerstig, A.; WillØn, U.; Wyser, K. A 140-Year Simulation of European Climate with the New Version of the Rossby Centre Regional Atmospheric Climate Model (RCA3); SMHI: Norrköping, Sweden, 2005; 54p. [Google Scholar]
- Samuelsson, P.; Jones, C.G.; Willen, U.; Ullerstig, A.; Gollvik, S.; Hansson, U.; Jansson, C.; Kjellstrom, E.; Nikulin, G.; Wyser, K. The Rossby Centre Regional Climate model RCA3: Model description and performance. Tellus A 2011, 63, 4–23. [Google Scholar] [CrossRef]
- Elguindi, N.; Bi, X.; Giorgi, F.; Nagarajan, B.; Pal, J.; Solmon, F.; Rauscher, S.; Zakey, A. RegCM Version 3.1 User’s Guide. PWCG Abdus Salam International Centre for Theoretical Physics (ICTP); Trieste, Italy, 58 p. 2007. Available online: http://kfs.ftj.agh.edu.pl/~zimnoch/files/dydaktyka/lato1112/L08/regcm.pdf (accessed on 25 October 2022).
- Pal, J.S.; Giorgi, F.; Bi, X.Q.; Elguindi, N.; Solomon, F.; Gao, X.J.; Rauscher, S.A.; Francisco, R.; Zakey, A.; Winter, J.; et al. Regional climate modeling for the developing world—The ICTP RegCM3 and RegCNET. Bull. Am. Met. Soc. 2007, 88, 1395–1409. [Google Scholar] [CrossRef]
- Jacob, D.; Podzun, R. Sensitivity studies with the regional climate model REMO. Meteorol. Atmos. Phys. 1997, 63, 119–129. [Google Scholar] [CrossRef]
- Jacob, D. A note to the simulation of the annual and interannual variability of the water budget over the Baltic Sea drainage basin. Meteorol. Atmos. Phys. 2001, 77, 61–73. [Google Scholar] [CrossRef]
- IPCC Climate Change. The Physical Science Basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Ed.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Uzun, H.I. Heat summation requirements of grape cultivars. Acta Hortic. 1997, 441, 383–386. [Google Scholar] [CrossRef]
- Jones, G.V.; Davis, R.E. Climate influences on grapevine phenology, grape composition, and wine production and quality for Bordeaux, France. Am. J. Enol. Viticult. 2000, 51, 249–261. [Google Scholar]
- Van Leeuwen, C.; Garnier, C.; Agut, C.; Baculat, B.; Barbeau, G.; Besnard, E.; Bois, B.; Boursiquot, J.-M.; Chuine, I.; Dessup, T.; et al. Heat requirements for grapevine cultivars are essential information to adapt plant material in a changing climate. In Proceedings of the 7th International Terroir Congress, (Agroscope Changins-Wädenswil: Switzerland), Changings, Switzerland, 19–23 May 2008; pp. 222–227. [Google Scholar]
- Cola, G.; Failla, O.; Mariani, L. BerryTone—A simulation model for the daily course of grape berry temperature. Agric. For. Meteorol. 2009, 149, 1215–1228. [Google Scholar] [CrossRef]
- Scarpare, F.V.; Scarpare, J.A.; Rodrigues, A.; Reichardt, K.; Angelocci, L.R. Growing degree-days for the Niagara Rosada grapevine pruned in different seasons. Int. J. Biometeorol. 2012, 56, 823–830. [Google Scholar] [CrossRef]
- Zapata, D.; Salazar, M.; Chaves, B.; Keller, M.; Hoogenboom, G. Estimation of the base temperature and growth phase duration in terms of thermal time for four grapevine cultivars. Int. J. Biometeorol. 2015, 59, 1771–1781. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Ambient Air Temperature; Microfiche collection; American Society of Agricultural Engineers: St. Joseph, MI, USA, 1985. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Guidelines for Computing Crop Water Requirements; FAO Irrigation and drainage paper 56; FAO—Food and Agriculture Organisation of the United Nations: Rome, Italy, 1998; p. 178. [Google Scholar]
- Szabo, A.; Gribovszki, Z.; Kalicz, P.; Szolgay, J.; Bolla, B. The soil moisture regime and groundwater recharge in aged forests in the Sand Ridge region of Hungary after a decline in the groundwater level: An experimental case study. J. Hydrol. Hydromech. 2022, 70, 308–320. [Google Scholar] [CrossRef]
- Paudel, B.; Acharya, B.S.; Ghimire, R.; Dahal, K.R.; Bista, P. Adapting agriculture to climate change and variability in Chitwan: Long-term trends and farmers’ perceptions. Agric. Res. 2014, 3, 165–174. [Google Scholar] [CrossRef]
- Lu, J.; Carbone, G.J.; Gao, P. Detrending crop yield data for spatial visualization of drought impacts in the United States 1895–2014. Agric. For. Meteorol. 2017, 237, 196–208. [Google Scholar] [CrossRef]
- Ansarifar, J.; Wang, L.; Archontoulis, S.V. An interaction regression model for crop yield prediction. Sci. Rep. 2021, 11, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Nicholls, N. Increased Australian wheat yield due to recent climate trends. Nature 1997, 387, 484–485. [Google Scholar] [CrossRef]
- McKillup, S.; Darby Dyar, M. Geostatistics Explained. An Introductory Guide for Earth Scientists; Cambridge University Press: Cambridge, UK, 2010; 396p. [Google Scholar]
- Hair, J.F., Jr.; Anderson, R.E.; Tatham, R.L.; Black, W.C. Multivariate Data Analysis, 5th ed.; Prentice Hall: Hoboken, NJ, USA, 1998; 730p. [Google Scholar]
- Marica, A.; Busuioc, A. The potential impacts of climate change on the main components of water balance relating to maize crop. Rom. J. Meteorol. 2004, 6, 40–49. [Google Scholar]
- Feng, S.; Fu, Q. Expansion of global drylands under a warming climate. Atmos. Chem. Phys. 2013, 13, 10081–10094. [Google Scholar] [CrossRef]
- Chaves, M.M.; Pereira, J.S.; Maroco, J.; Rodrigues, M.L.; Ricardo, C.P.P.; Osorio, M.L.; Carvalho, I.; Faria, T.; Pinheiro, C. How plants cope with water stress in the field. Photosynthesis and growth. Ann. Bot. 2002, 89, 907–916. [Google Scholar] [CrossRef] [PubMed]
- Roby, G.; Harbertson, J.F.; Adams, D.A.; Matthews, M.A. Berry size and vine water deficits as factors in winegrape composition: Anthocyanins and tannins. Aust. J. Grape Wine Res. 2004, 10, 100–107. [Google Scholar] [CrossRef]
- Chapman, D.M.; Roby, G.; Ebeler, S.E.; Guinard, J.-X.; Matthews, M.A. Sensory attributes of Cabernet Sauvignon wines made from vines with different water status. Aust. J. Grape Wine Res. 2005, 11, 329–347. [Google Scholar] [CrossRef]
- Wheeler, S.J.; Pickering, G.J. The effects of soil management techniques on grape and wine quality. In Fruits. Growth, Nutrition and Quality; WFL Publisher: Helsinki, Finland, 2006; pp. 195–208. [Google Scholar]
- Intrigliolo, D.S.; Pérez, D.; Risco, D.; Yeves, A.; Castel, J.R. Yield components and grape composition responses to seasonal water deficits in Tempranillo grapevines. Irrig. Sci. 2012, 30, 339–349. [Google Scholar] [CrossRef]
- Girona, J.; Marsal, J.; Mata, M.; Del Campo, J.; Basile, B. Phenological sensitivity of berry growth and composition of tempranillo grapevines (Vitis vinifera L) to water stress. Aust. J. Grape Wine Res. 2009, 15, 268–277. [Google Scholar] [CrossRef]
- Agosta, E.; Canziani, P.; Cavagnaro, M. Regional climate variability impacts on the annual grape yield in Mendoza, Argentina. J. Appl. Meteorol. Climatol. 2012, 51, 993–1009. [Google Scholar] [CrossRef]
- Dry, P.R.; Loveys, B.R. Factors influencing grapevine vigour and the potential for control with partial root-zone drying. Aust. J. Grape Wine Res. 1998, 4, 140–148. [Google Scholar] [CrossRef]
- Romero, P.; Gil-Muńoz, R.; Del Amor, F.M.; Valdés, E.; Fernández, J.I.; Martinez-Cutillas, A. Regulated deficit irrigation based upon optimum water status improves phenolic composition in Monastrell grapes and wines. Agric. Water Manag. 2013, 121, 85–101. [Google Scholar] [CrossRef]
- Vasconcelos, M.C.; Greven, M.; Winefield, C.S.; Trought, M.C.T.; Raw, V. The flowering process of Vitis vinifera: A review. Am. J. Enol. Vitic. 2009, 60, 411–434. [Google Scholar]
- Keller, M. Deficit irrigation and vine mineral nutrition. Am. J. Enol. Vitic. 2005, 56, 267–283. [Google Scholar]
- Illand, P.; Dry, P.; Proffitt, T.; Tyerman, S. The Grapevine from de Science to the Practice of Growing Vines for Wine; Patrick Illand Wine Promotions: Adelaide, Australian, 2011; p. 310. [Google Scholar]
- Williams, L.E.; Grimes, D.W.; Phene, C.J. The effects of applied water amounts at various fractions of measured evapotranspiration on water relations and vegetative growth of Thompson Seedless grapevines. Irrig Sci. 2010, 28, 221–232. [Google Scholar] [CrossRef]
- Williams, L.E.; Grimes, D.W.; Phene, C.J. The effects of applied water at various fractions of measured evapotranspiration on reproductive growth and water productivity of Thompson seedless grapevines. Irrig. Sci. 2009, 28, 233–243. [Google Scholar] [CrossRef]
- Junquera, P.; Lissarrague, J.R.; Jiménez, L.; Linares, R.; Baeza, P. Long-term effects of different irrigation strategies on yield components, vine vigour and grape composition in cv. Cabernetsauvignon (Vitis Vinifera L.). Irrig. Sci. 2012, 30, 351–361. [Google Scholar] [CrossRef]
- Romero, P.; Fernández-Fernández, J.I.; Martínez-Cutillas, A. Physiological thresholds for efficient regulated deficit irrigation management in wine grapes grown under semiarid conditions. Am. J. Enol. Vitic. 2010, 61, 300–312. [Google Scholar]
- Chacón-Vozmediano, J.L.; Gramaje, D.; León, M.; Armengol, J.; Moral, J.; Izquierdo-Cañas, P.M.; Martínez-Gascueña, J. Cultivar Susceptibility to Natural Infections Caused by Fungal Grapevine Trunk Pathogens in La Mancha Designation of Origin (Spain). Plants 2021, 10, 1171. [Google Scholar] [CrossRef]
- De La Fuente, M.; Fontaine, F.; Gramaje, D.; Armengol, J.; Smart, R.E.; Nagy, Z.A.; Borgo, M.; Rego, C.; Corio-Costet, M.-F. Grapevine Trunk Diseases: A Review, 1st ed.; OIV: Paris, France, 2016. [Google Scholar]
- Gessler, C.; Pertot, I.; Perazzolli, M. Plasmopara viticola: A review of knowledge on downy mildew of grapevine and effective disease management. Phytopathol. Mediterr. 2011, 50, 3–44. [Google Scholar]
- Wilcox, W.F.; Gubler, W.D.; Uyemoto, J.K. Compendium of Grape Diseases, Disorders, and Pests, 2nd ed.; Amer Phytopathological Society: St. Paul, MN, USA, 2015. [Google Scholar]
- Jones, D.S.; McManus, P.S. Susceptibility of cold-climate wine grape cultivars to downy mildew, powdery mildew, and black rot. Plant Dis. 2017, 101, 1077–1085. [Google Scholar] [CrossRef] [PubMed]
- Bois, B.; Zito, S.; Calonnec, A. Climate vs grapevine pests and diseases worldwide: The first results of a global survey. OENO ONE 2017, 51, 133–139. [Google Scholar] [CrossRef]
- Pérez-Álvarez, E.P.; Molina, D.I.; Vivaldi, G.A.; García-Esparza, M.J.; Lizama, V.; Álvarez, I. Effects of the irrigation regimes on grapevine cv. Bobal in a Mediterranean climate: I. Water relations, vine performance and grape composition. Agric. Water Manag. 2021, 248, 106772. [Google Scholar] [CrossRef]
- Battilani, A. Application of the regulated deficit of irrigation in grapevines (Vitis vinifera) in a sub-humid area. Acta Hortic. 2000, 537, 887–893. [Google Scholar] [CrossRef]
- Poni, S.; Bernizzoni, F.; Civardi, S. Response of ‘Sangiovese’grapevines to partial root-zone drying: Gas-exchange, growth and grape composition. Sci. Hort. 2007, 114, 96–103. [Google Scholar] [CrossRef]
- Dry, P.R.; Loveys, B.R.; McCarthy, M.G.; Stoll, M. Strategic irrigation management in Australian vineyards. OENO ONE 2001, 35, 129–139. [Google Scholar] [CrossRef]
- Stoll, M.; Loveys, B.; Dry, P. Hormonal changes induced by partial root-zone drying of irrigated grapevine. J. Exp. Bot. 2000, 51, 1627–1634. [Google Scholar] [CrossRef]
- Santos, T.; Lopes, C.M.; Rodrigues, M.L.; Souza, C.R.; Maroco, J.; Pereira, J.S.; Silva, J.R.; Chaves, M.M. Effects of deficit irrigation treatments on cluster microclimate for improving fruit composition of ‘Moscatel’ field-grown grapevines. Sci. Hort. 2007, 112, 321–330. [Google Scholar] [CrossRef]



| RCM | GCM | Institution | References |
|---|---|---|---|
| ALADIN | ARPEGE | Centre National de Recherches Météorologiques | [40] |
| CLM | HadCM3Q0 | Eidgenössische Technische Hochschule, Zürich | [41,42] |
| HadRM3Q0 | HadCM3Q0 | Hadley Centre | [43] |
| HIRHAM5 | ARPEGE | Danish Meteorological Institute | [44] |
| HIRHAM | ECHAM5 | Danish Meteorological Institute | [44] |
| RACMO2 | ECHAM5 | Koninklijk Nederlands Meteorologisch Instituut | [45] |
| RCA | ECHAM5 | Sweden’s Meteorological and Hydrological Institute | [46,47] |
| RCA | HadCM3Q3 | Sweden’s Meteorological and Hydrological Institute | [46,47] |
| RegCM3 | ECHAM5 | International Centre for Theoretical Physics | [48,49] |
| REMO | ECHAM5 | Max Planck Institute | [50,51] |
| White Wine Grapes | Red Wine Grapes |
|---|---|
| Tramini | Cabernet Franc |
| Italian Riesling | Cabernet Sauvignon |
| Pinot blanc | Lemberger |
| Rhine Riesling | Merlot |
| Chardonnay | Pinot noir |
| Furmint | Syrah |
| Pinot Gris | Zweigelt |
| CDDmax | Type of Dry Spell | 1986–2005 | 2016–2035 | 2081–2100 |
|---|---|---|---|---|
| 1–10 | weak dry spell | 1.2 | 7.9 | 2.6 |
| 11–20 | medium dry spell | 88.0 | 81.0 | 81.0 |
| >21 | strong dry spell | 10.8 | 11.1 | 16.3 |
| All types | 100.0 | 100.0 | 100.0 |
| Class of Viticultural Climate | Dryness Index (DI) | 1986–2005 | 2016–2035 | 2081–2100 |
|---|---|---|---|---|
| Very dry | DI ≤ −100 | 2.1 | 7.5 | 26.8 |
| Moderately dry | −100 < DI ≤ 50 | 51.5 | 69.4 | 65.3 |
| Sub-humid | 50 < DI ≤ 150 | 38.7 | 19.2 | 6.7 |
| Humid | 150 < DI | 7.6 | 3.9 | 1.2 |
| Dryness Indices | Rate (%) of Significant Quadratic Regression in the 22 Hungarian Wine Regions |
|---|---|
| NDD | 36.4 |
| CDDmax | 22.7 |
| CWB | 81.8 |
| DI | 72.7 |
| VWI | 68.2 |
| Five indices | 51.8 |
| White Wine Grapes | Rate of Significance | Red Wine Grapes | Rate of Significance |
|---|---|---|---|
| Tramini | 22.7 | Cabernet franc | 50.0 |
| Italian Riesling | 27.3 | Cabernet Sauvignon | 18.2 |
| Pinot blanc | 36.4 | Lemberger | 18.2 |
| Rhine Riesling | 27.3 | Merlot | 13.6 |
| Chardonnay | 27.3 | Pinor noir | 31.8 |
| Furmint | 31.8 | Syrah | 40.9 |
| Pinot gris | 31.8 | Zweigelt | 18.2 |
| White wines mean: | 29.2 | Red wines mean | 27.3 |
| Dryness Indices | Wine Region | Average Yield Deviation (1986–2005) | Average Yield Deviation (2016–2035) | Average Yield Deviation (2081–2100) |
|---|---|---|---|---|
| NDD | Szekszárd | −8.54 | −9.30 | −16.69 |
| CDDmax | Tolna | 0.83 | −0.80 | −1.43 |
| CWB | Szekszárd | 1.07 | 0.56 | −2.21 |
| DI | Etyek-Buda | 1.74 | −2.33 | −15.18 |
| VWI | Etyek-Buda | 4.39 | 0.39 | −1.87 |
| Average | −0.10 | −2.30 | −7.48 |
| Dryness Indices | Wine Region | The Average Standard Deviation of Yield 1986–2005 | The Average Standard Deviation of Yield 2016–2035 | The Average Standard Deviation of Yield 2081–2100 |
|---|---|---|---|---|
| NDD | Szekszárd | 12.18 | 15.35 | 31.30 |
| CDDmax | Tolna | 5.30 | 7.09 | 16.89 |
| CWB | Szekszárd | 3.51 | 4.65 | 8.40 |
| DI | Etyek-Buda | 11.20 | 14.69 | 25.26 |
| VWI | Etyek-Buda | 5.17 | 11.20 | 12.60 |
| Average | 7.47 | 10.60 | 18.89 |
| White Wine Grapes | Dryness Indices | Wine Region | Average Yield Deviation 1986–2005 | Average Yield Deviation 2016–2035 | Average Yield Deviation 2081–2100 |
|---|---|---|---|---|---|
| Tramini | NDD | Hajós-Baja | −26.29 | −27.97 | −109.84 |
| Italian Riesling | NDD | Balatonboglár | −12.87 | −12.60 | −50.95 |
| Pinot blanc | VWI | Pannonhalmi | −7.12 | −22.29 | −30.76 |
| Rhine Riesling | VWI | Pannonhalmi | −5.26 | −18.52 | −26.33 |
| Chardonnay | VWI | Zala | −12.69 | −35.59 | −51.34 |
| Furmint | NDD | Zala | −34.61 | −43.30 | −85.32 |
| Pinot gris | VWI | Sopron | −7.17 | −19.42 | −29.73 |
| Average | −15.15 | −25.67 | −54.90 |
| White Wine Grapes | Dryness Indices | Wine Region | The Average Standard Deviation of Yield 1986–2005 | The Average Standard Deviation of Yield 2016–2035 | The Average Standard Deviation of Yield 2081–2100 |
|---|---|---|---|---|---|
| Tramini | NDD | Hajós-Baja | 44.17 | 46.41 | 163.28 |
| Italian Riesling | NDD | Balatonboglár | 19.35 | 21.10 | 75.85 |
| Pinot blanc | VWI | Pannonhalmi | 15.62 | 37.86 | 50.61 |
| Rhine Riesling | VWI | Pannonhalmi | 13.69 | 32.18 | 43.28 |
| Chardonnay | VWI | Zala | 25.21 | 53.59 | 72.20 |
| Furmint | NDD | Zala | 47.31 | 78.79 | 193.09 |
| Pinot gris | VWI | Sopron | 24.59 | 31.14 | 42.06 |
| Red Wine Grapes | Dryness Indices | Wine Region | Average Yield Deviation 1986–2005 | Average Yield Deviation 2016–2035 | Average Yield Deviation 2081–2100 |
|---|---|---|---|---|---|
| Cabernet franc | NDD | Szekszárd | −54.48 | −65.52 | −169.64 |
| Cabernet Sauvignon | NDD | Villány | −26.38 | −31.56 | −94.75 |
| Lemberger | CDDmax | Pécs | −8.36 | −19.68 | −87.62 |
| Merlot | VWI | Balaton-felvidék | −28.51 | −52.99 | −167.85 |
| Pinot noir | VWI | Zala | −10.90 | −41.71 | −62.99 |
| Syrah | VWI | Bükki | −18.75 | −23.43 | −87.20 |
| Zweigelt | NDD | Bükki | −8.18 | −17.33 | −53.21 |
| Average | −22.22 | −36.03 | −103.32 |
| Red Wine Grapes | Dryness Indices | Wine Region | The Average Standard Deviation of Yield 1986–2005 | The Average Standard Deviation of Yield 2016–2035 | The Average Standard Deviation of Yield 2081–2100 |
|---|---|---|---|---|---|
| Cabernet franc | NDD | Szekszárd | 67.01 | 90.78 | 256.41 |
| Cabernet Sauvignon | NDD | Villány | 34.55 | 46.43 | 141.32 |
| Lemberger | CDDmax | Pécs | 27.33 | 54.30 | 233.73 |
| Merlot | VWI | Balaton-felvidék | 82.20 | 89.06 | 199.47 |
| Pinot noir | VWI | Zala | 26.88 | 64.12 | 88.02 |
| Syrah | VWI | Bükki | 30.83 | 37.51 | 129.65 |
| Zweigelt | NDD | Bükki | 21.74 | 28.89 | 65.39 |
| Average | 41.51 | 58.73 | 159.14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lakatos, L.; Mika, J. Analysis of Quadratic Correlation between Dryness Indices and Wine Grape Yield to Estimate Future Climate Impacts in Hungary. Climate 2022, 10, 165. https://doi.org/10.3390/cli10110165
Lakatos L, Mika J. Analysis of Quadratic Correlation between Dryness Indices and Wine Grape Yield to Estimate Future Climate Impacts in Hungary. Climate. 2022; 10(11):165. https://doi.org/10.3390/cli10110165
Chicago/Turabian StyleLakatos, László, and János Mika. 2022. "Analysis of Quadratic Correlation between Dryness Indices and Wine Grape Yield to Estimate Future Climate Impacts in Hungary" Climate 10, no. 11: 165. https://doi.org/10.3390/cli10110165
APA StyleLakatos, L., & Mika, J. (2022). Analysis of Quadratic Correlation between Dryness Indices and Wine Grape Yield to Estimate Future Climate Impacts in Hungary. Climate, 10(11), 165. https://doi.org/10.3390/cli10110165





