BACE and BMA Variable Selection and Forecasting for UK Money Demand and Inflation with Gretl
Abstract
:1. Introduction
2. The BACE Method
3. The BMA Method
BACE and BMA in Gretl
4. Autometrics
5. Empirical Results
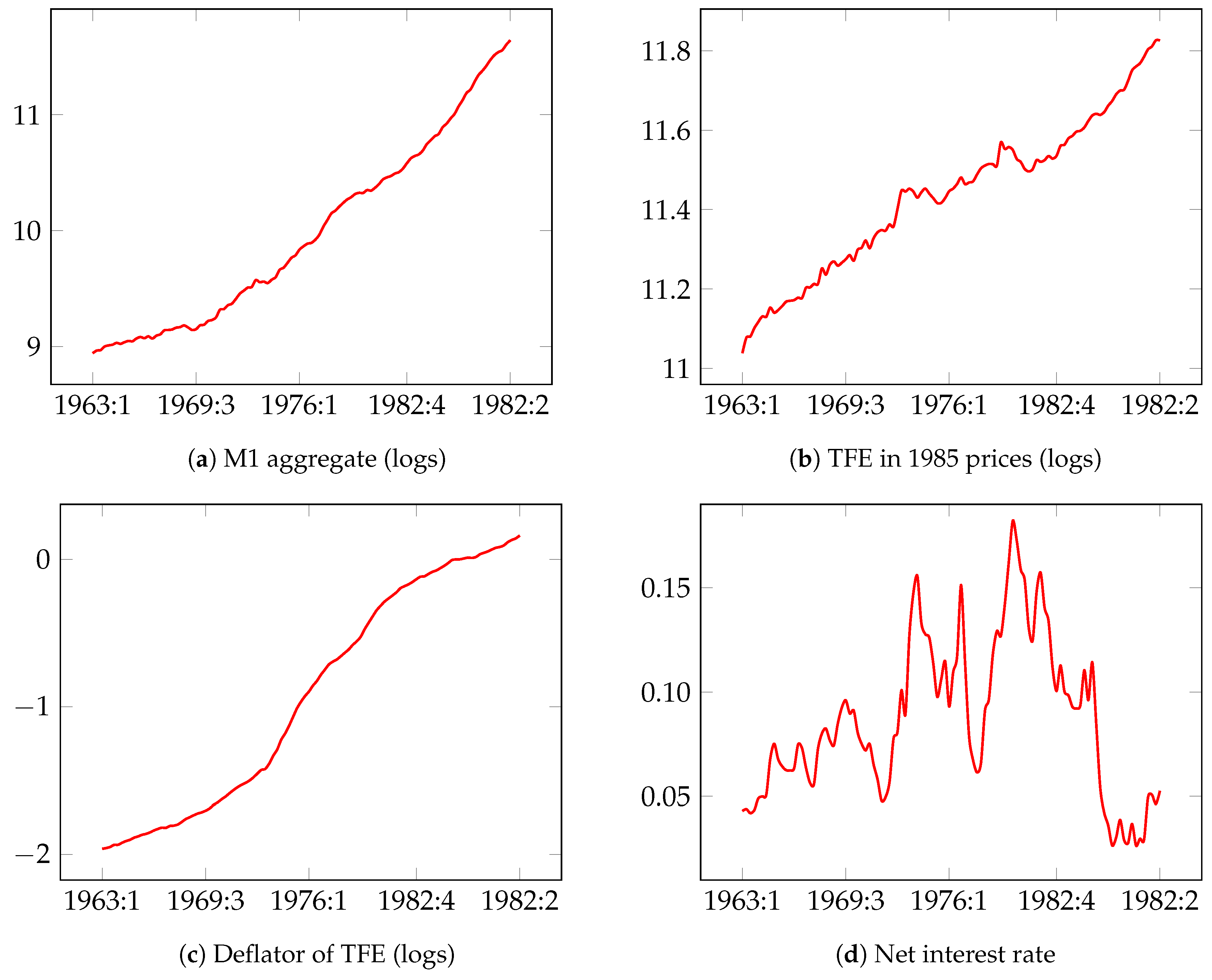
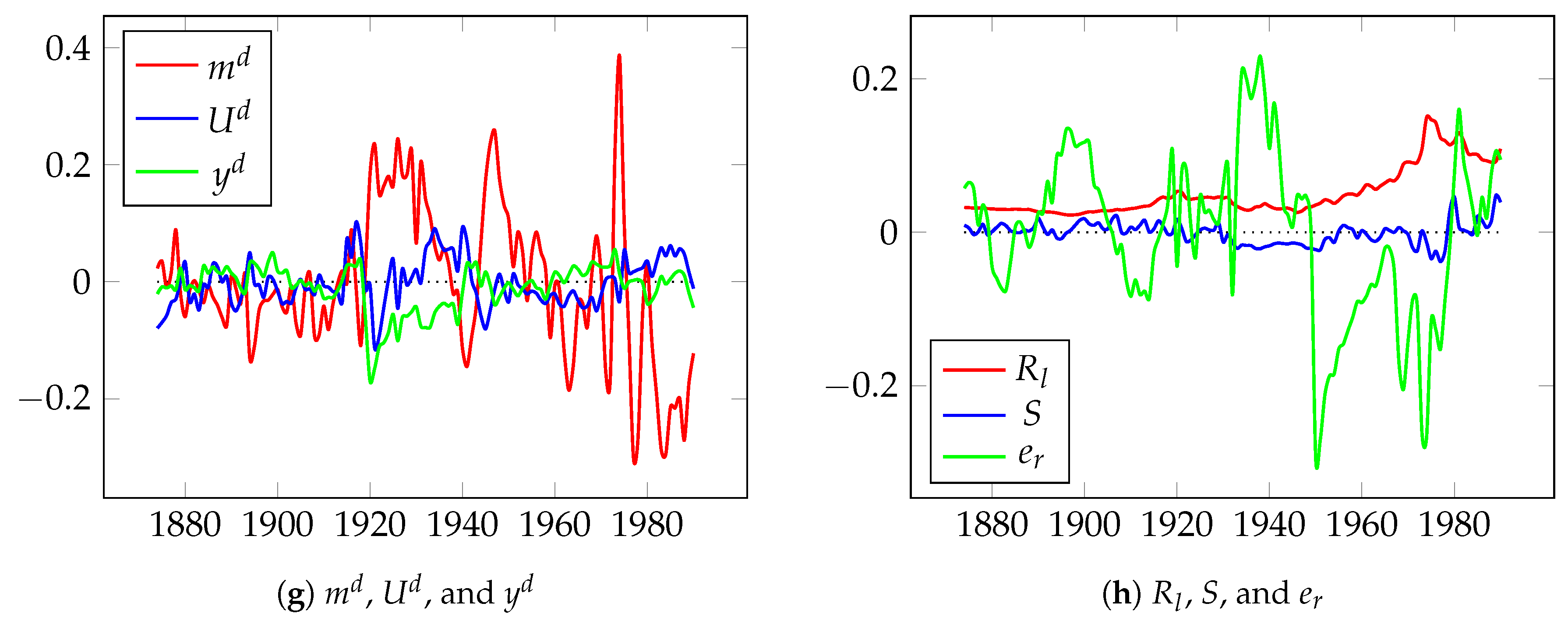
5.1. Modeling and Forecasting Demand for Narrow Money in the UK: UKM1
- : nominal narrow money, M1 aggregate in million £,
- : real total final expenditure (TFE) for 1985 prices in million £,
- : deflator of TFE,
- : net interest rate of the cost of holding money (calculated as the difference between the three-month interest rate and learning-adjusted own interest rate).
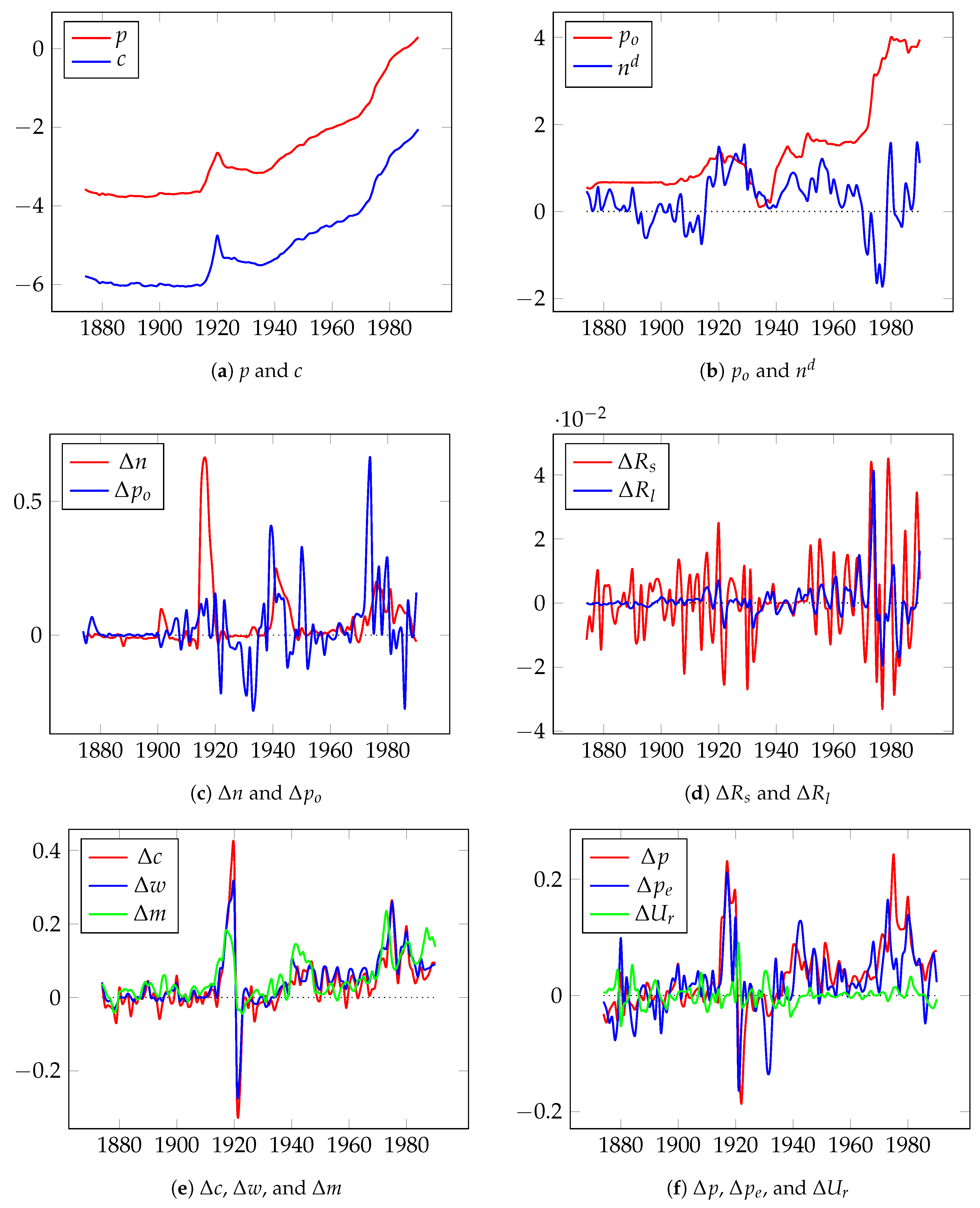
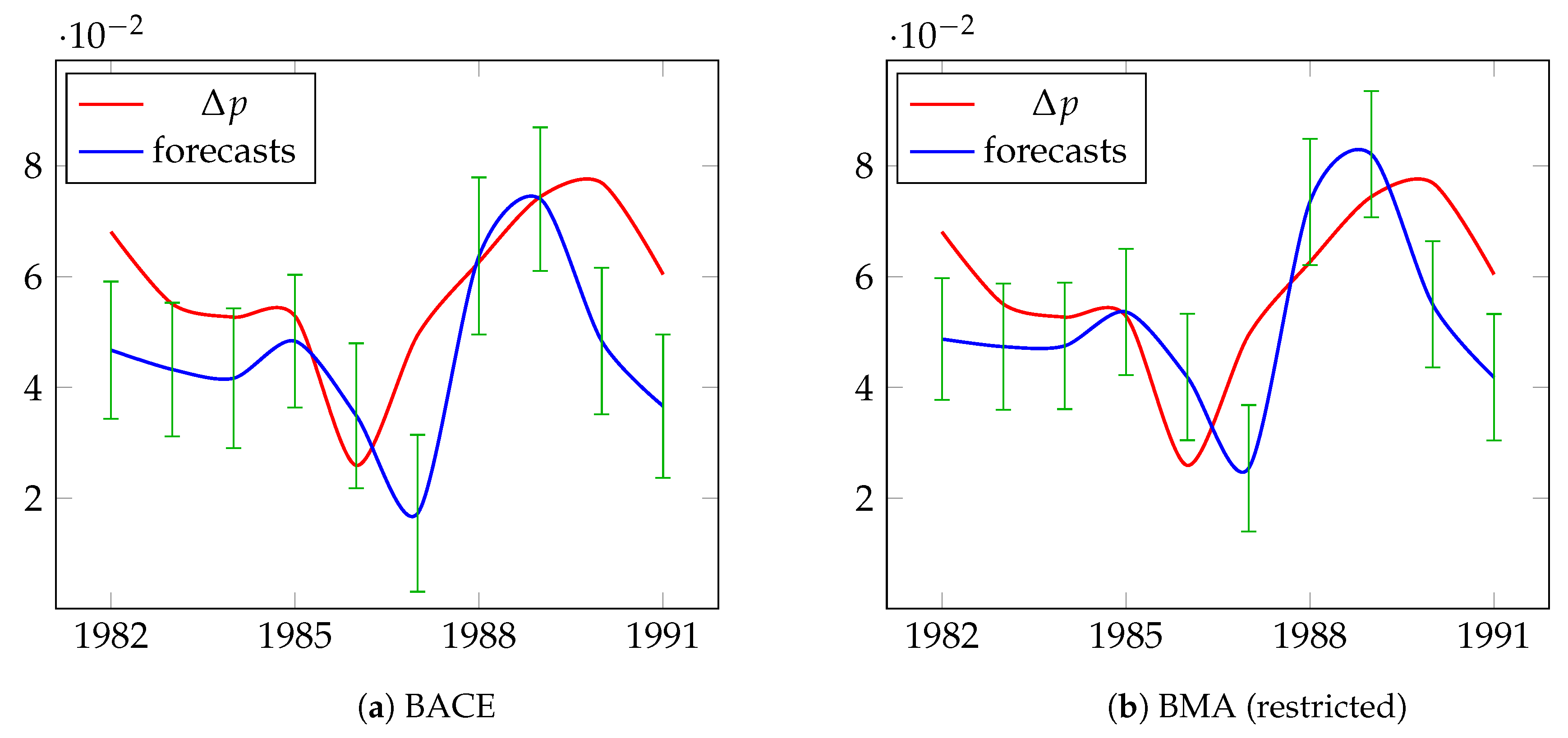
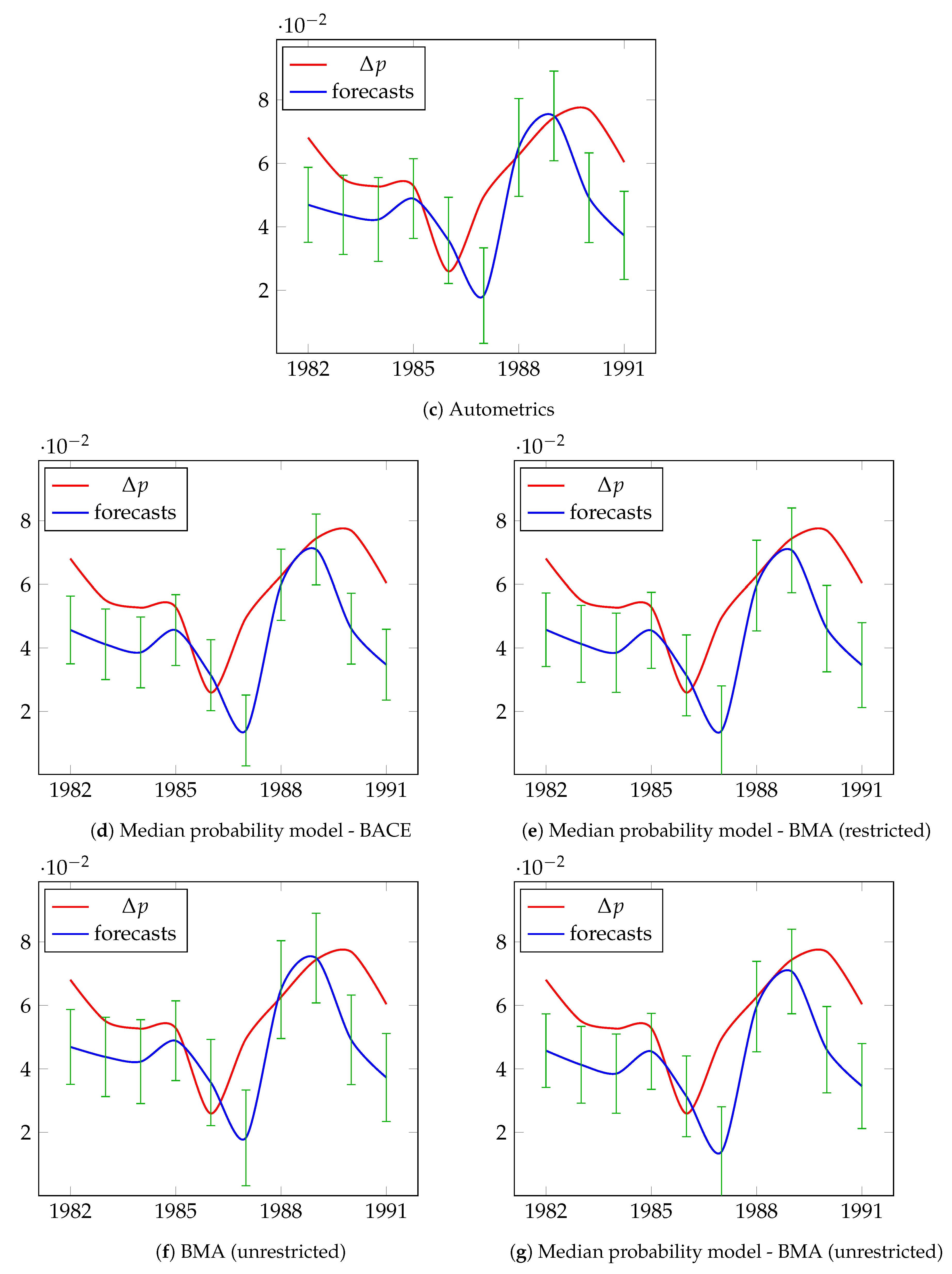
5.2. Modeling and Forecasting Long-Term UK Inflation
6. Robustness and Run Time Analysis
6.1. Robustness
6.2. BACE and BMA Run Times
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ADL | Autoregressive Distributed Lag |
| BACE | Bayesian Averaging of Classical Estimates |
| BMA | Bayesian Model Averaging |
| DGP | Data Generating Process |
| GDP | Gross Domestic Product |
| GUI | Graphical User Interface |
| GUM | General Unrestricted Model |
| LDGP | Local Data Generating Process |
| MAPE | Mean Absolute Percentage Error |
| MPI | Message Passing Interface |
| MC3 | Markov Chain Monte Carlo Model Composition |
| RMSE | Root-Mean-Square Error |
| TFE | Total Final Expenditure |
| UKM1 | Model for M1 Money Demand in UK |
References
- Ackah, Ishmael, and McCmari Asomani. 2015. Empirical Analysis of Renewable Energy Demand in Ghana with Autometrics. International Journal of Energy Economics and Policy 5: 754–58. [Google Scholar]
- Albis, Manuel Leonard F., and Dennis S. Mapa. 2014. Bayesian Averaging of Classical Estimates in Asymmetric Vector Autoregressive (AVAR) Models. MPRA Paper 55902. Munich: University Library of Munich. [Google Scholar]
- Barbieri, Maria Maddalena, and James O. Berger. 2004. Optimal predictive model selection. The Annals of Statistics 32: 870–97. [Google Scholar] [CrossRef]
- Bergh, Andreas, and Martin Karlsson. 2010. Government size and growth: Accounting for economic freedom and globalization. Public Choice 142: 195–213. [Google Scholar] [CrossRef] [Green Version]
- Białowolski, Piotr, Tomasz Kuszewski, and Bartosz Witkowski. 2014. Bayesian averaging of classical estimates in forecasting macroeconomic indicators with application of business survey data. Empirica 41: 53–68. [Google Scholar] [CrossRef]
- Błażejowski, Marcin, Jacek Kwiatkowski, and Jakub Gazda. 2019. Sources of Economic Growth: A Global Perspective. Sustainability 11: 275. [Google Scholar] [CrossRef] [Green Version]
- Błażejowski, Marcin, Paweł Kufel, and Jacek Kwiatkowski. 2020. Model simplification and variable selection: A Replication of the UK inflation model by Hendry (2001). In Journal of Applied Econometrics. forthcoming. [Google Scholar] [CrossRef] [Green Version]
- Błażejowski, Marcin, and Jacek Kwiatkowski. 2018. Bayesian Averaging of Classical Estimates (BACE) for gretl. Gretl Working Papers 6. Ancona, Italy: Dipartimento di Scienze Economiche e Sociali, Universita’ Politecnica delle Marche (I). [Google Scholar]
- Błażejowski, Marcin, and Jacek Kwiatkowski. 2020. Bayesian Model Averaging for Autoregressive Distributed Lag (BMA_ADL) in gretl. MPRA Paper 98387. Munich: University Library of Munich. [Google Scholar]
- Castle, Jennifer L., Jurgen A. Doornik, and David F. Hendry. 2012. Model selection when there are multiple breaks. Journal of Econometrics 169: 239–46. [Google Scholar] [CrossRef] [Green Version]
- Clements, Michael P., and David F. Hendry. 2008. Forecasting Annual UK Inflation Using an Econometric Model over 1875–1991. In Frontiers of Economics and Globalization. Bingley: Emerald Publishing, vol. 3, pp. 3–39. [Google Scholar] [CrossRef]
- Cottrell, Allin, and Riccardo Lucchetti. 2019a. Gretl + MPI. October. Available online: http://ricardo.ecn.wfu.edu/~cottrell/gretl/gretl-mpi.pdf (accessed on 27 April 2020).
- Cottrell, Allin, and Riccardo Lucchetti. 2019b. A Hansl Primer. December. Available online: http://ricardo.ecn.wfu.edu/pub/gretl/manual/PDF/hansl-primer-a4.pdf (accessed on 27 April 2020).
- Cottrell, Allin, and Riccardo Lucchetti. 2020. Gretl User’s Guide. January. Available online: http://ricardo.ecn.wfu.edu/pub/gretl/gretl-guide.pdf (accessed on 27 April 2020).
- Cuaresma, Jesus Crespo, and Gernot Doppelhofer. 2007. Nonlinearities in cross-country growth regressions: A Bayesian Averaging of Thresholds (BAT) approach. Journal of Macroeconomics 29: 541–54. [Google Scholar] [CrossRef] [Green Version]
- Desboulets, Loann David Denis. 2018. A Review on Variable Selection in Regression Analysis. Econometrics 6: 45. [Google Scholar] [CrossRef] [Green Version]
- Doan, Thomas, Robert Litterman, and Christopher Sims. 1984. Forecasting and conditional projection using realistic prior distributions. Econometric Reviews 3: 1–100. [Google Scholar] [CrossRef] [Green Version]
- Doornik, Jurgen A. 2009. Autometrics. In The Methodology and Practice of Econometrics: A Festschrift in Honour of David F. Hendry. Number 9780199237197 in OUP Catalogue. Edited by Jennifer Castle and Neil Shephard. Oxford: Oxford University Press. [Google Scholar] [CrossRef]
- Doornik, Jurgen A., and David F. Hendry. 2013. Empirical Econometric Modelling using PcGive: Volume I. London: Timberlake Consultants Press. [Google Scholar]
- Drachal, Krzysztof. 2018. Dynamic Model Averaging in Economics and Finance with fDMA: A Package for R. Warsaw: Faculty of Economic Sciences, University of Warsaw. [Google Scholar]
- Ericsson, Neil R., and Steven B. Kamin. 2009. Constructive Data Mining: Modelling Argentine Broad Money Demand. In The Methodology and Practice of Econometrics. Oxford: Oxford University Press, pp. 412–40. [Google Scholar] [CrossRef]
- Feldkircher, Martin. 2012. Forecast combination and Bayesian model averaging: A prior sensitivity analysis. Journal of Forecasting 31: 361–76. [Google Scholar] [CrossRef] [Green Version]
- Fernández, Carmen, Eduardo Ley, and Mark F. J. Steel. 2001a. Benchmark Priors for Bayesian Model Averaging. Journal of Econometrics 100: 381–427. [Google Scholar] [CrossRef] [Green Version]
- Fernández, Carmen, Eduardo Ley, and Mark F. J. Steel. 2001b. Model uncertainty in cross-country growth regressions. Journal of Applied Econometrics 16: 563–76. [Google Scholar] [CrossRef]
- Fragoso, Tiago M., Wesley Bertoli, and Francisco Louzada. 2018. Bayesian Model Averaging: A Systematic Review and Conceptual Classification. International Statistical Review 86: 1–28. [Google Scholar] [CrossRef] [Green Version]
- Hendry, David F. 1995. Dynamic Econometrics. Oxford: Oxford University Press. [Google Scholar] [CrossRef]
- Hendry, David F. 2001. Modelling UK Inflation, 1875–1991. Journal of Applied Econometrics 16: 255–75. [Google Scholar] [CrossRef]
- Hendry, David F. 2011. Revisiting UK consumers’ expenditure: Cointegration, breaks and robust forecasts. Applied Financial Economics 21: 19–32. [Google Scholar] [CrossRef]
- Hendry, David F. 2015. Introductory Macro-Econometrics: A New Approach. London: Timberlake Consultants. [Google Scholar]
- Hendry, David F., and Jurgen A. Doornik. 2014. Empirical Model Discovery and Theory Evaluation: Automatic Selection Methods in Econometrics. Cambridge: Mit Press. [Google Scholar]
- Hendry, David F., and Neil R. Ericsson. 1991. Modeling the demand for narrow money in the United Kingdom and the United States. European Economic Review 35: 833–81. [Google Scholar] [CrossRef] [Green Version]
- Hendry, David F., Massimiliano Marcellino, and Grayham E. Mizon. 2008. Special issue on encompassing. Oxford Bulletin of Economics and Statistics 70: 711–938. [Google Scholar] [CrossRef]
- Hendry, David F., and Bent Nielsen. 2012. Econometric Modeling: A Likelihood Approach. Princeton: Princeton University Press. [Google Scholar]
- Hoeting, Jennifer A., David Madigan, Adrian E. Raftery, and Chris T. Volinsky. 1999. Bayesian model averaging: A tutorial. Statistical Science 14: 382–401. [Google Scholar] [CrossRef]
- Jones, Garett, and W. Joel Schneider. 2006. Intelligence, human capital, and economic growth: A Bayesian Averaging of Classical Estimates (BACE) approach. Journal of Economic Growth 11: 71–93. [Google Scholar] [CrossRef]
- Kamarudin, Nur Azulia, and Suzilah Ismail. 2016. Model selection approaches of water quality index data. Global Journal of Pure and Applied Mathematics 12: 1821–29. [Google Scholar]
- Koop, Gary. 2003. Bayesian Econometrics. Chichester: John Wiley & Sons Ltd. [Google Scholar]
- Koop, Gary, Dale J. Poirier, and Justin L. Tobias. 2007. Bayesian Econometric Methods. New York: Cambridge University Press. [Google Scholar]
- Krolzig, Hans-Martin, and David F. Hendry. 2001. Computer automation of general-to-specific model selection procedures. Journal of Economic Dynamics and Control 25: 831–66. [Google Scholar] [CrossRef] [Green Version]
- Leamer, Edward. 1978. Specification Searches. Hoboken: John Wiley & Sons. [Google Scholar]
- Ley, Eduardo, and Mark F. J. Steel. 2009. On the effect of prior assumptions in Bayesian model averaging with applications to growth regression. Journal of Applied Econometrics 24: 651–74. [Google Scholar] [CrossRef] [Green Version]
- Mapa, Dennis S., and Kristine Joy S. Briones. 2007. Robustness procedures in economic growth regression models. Philippine Review of Economics 44: 71–84. [Google Scholar]
- Marczak, Martyna, and Tommaso Proietti. 2016. Outlier detection in structural time series models: The indicator saturation approach. International Journal of Forecasting 32: 180–202. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, Toby J., and John. J. Beauchamp. 1988. Bayesian variable selection in linear regression. Journal of the American Statistical Association 83: 1023–32. [Google Scholar] [CrossRef]
- Osiewalski, Jacek, and Mark F. J. Steel. 1993. Una perspectiva bayesiana en selección de modelos. Cuadernos Económicos de ICE 55: 327–51. [Google Scholar]
- Raftery, Adrian E., Miroslav Kárný, and Pavel Ettler. 2010. Online Prediction Under Model Uncertainty via Dynamic Model Averaging: Application to a Cold Rolling Mill. Technometrics 52: 52–66. [Google Scholar] [CrossRef] [Green Version]
- Raftery, Adrian E., David Madigan, and Jennifer A. Hoeting. 1997. Bayesian model averaging for linear regression models. Journal of the American Statistical Association 92: 179–91. [Google Scholar] [CrossRef]
- Sala-i-Martin, Xavier, Gernot Doppelhofer, and Ronald I. Miller. 2004. Determinants of Long-Term Growth: A Bayesian Averaging of Classical Estimates (BACE) Approach. American Economic Review 94: 813–35. [Google Scholar] [CrossRef] [Green Version]
- Simo-Kengne, Beatrice D. 2016. What Explains the Recent Growth Performance in Sub-Saharan Africa? Results from a Bayesian Averaging of Classical Estimates (BACE) Approach. Ersa Working Paper. Cape Town, South Africa: Economic Research Southern Africa. [Google Scholar]
- Steel, Mark F. J. 2019. Model Averaging and Its Use in Economics. Journal of Economic Literature. forthcoming. [Google Scholar]
- Theil, Henri. 1966. Applied Economic Forecasting. Amsterdam: North-Holland. [Google Scholar]
- van Dijk, Dick. 2004. Forecasting US Inflation Using Model Averaging. In Econometric Society 2004 Australasian Meetings. Cleveland: Econometric Society. [Google Scholar]
- Wasserman, Larry. 2000. Bayesian model selection and model averaging. Journal of Mathematical Psychology 44: 92–107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zellner, Arnold. 1971. An Introduction to Bayesian Inference in Econometrics. New York: John Wiley & Sons. [Google Scholar]
- Zellner, Arnold. 1986. On Assessing Prior Distributions and Bayesian Regression Analysis with g-Prior Distributions. In Bayesian Inference and Decision Techniques: Essays in Honor of Bruno de Finetti. Edited by Prem K. Goel and Arnold Zellner. Amsterdam and Holland: Elsevier. [Google Scholar]
| 1. | BACE is implicitly based on fixed Zellner’s g-prior, whereas, in the BMA framework, g-prior can be set explicitly. |
| 2. | The BACE 2.0 package is available at http://ricardo.ecn.wfu.edu/gretl/cgi-bin/gretldata.cgi?opt=SHOW_FUNCS and was developed by co-authors (see Błażejowski and Kwiatkowski 2018). |
| 3. | Gretl is an open-source software for econometric analysis and is available at http://gretl.sf.net. |
| 4. | The BMA_ADL package for gretl is available in Supplementary Materials along with scripts to replicate all analysis. |
| 5. | MPI is a standard that supports running a given program simultaneously on several CPU cores, so it supports a very flexible type of parallelism of Monte Carlo integration see (Cottrell and Lucchetti 2020, 2019a). |
| 6. | We used gretl version 2019d-git and PcGive version 14.2 with Ox Professional version 7.20 on a PC machine running under Debian GNU/Linux 64 bits. |
| 7. | Exogeneity of variables used in UKM1 model is discussed in (Hendry and Nielsen 2012, pp. 266–67; Hendry 1995, pp. 605–6; Hendry 2015, pp. 127–33) and the results show that modeling demand for narrow money in UK as a single equation is valid in general. |
| 8. | All data were retrieved from https://www.nuffield.ox.ac.uk/media/2502/dynects.zip. |
| 9. | Authors understand ‘reduction’ as a structured path of elimination insignificant variables based on t-statistics together with pre-search analysis and encompassing tests. |
| 10. | All series are freely available in the Journal of Applied Econometrics Data Archive at http://qed.econ.queensu.ca/jae/2001-v16.3/hendry. Exogeneity of variables used in this model is mentioned in (Hendry 2001, p. 261; Hendry 2015, p. 150). |
| 11. | The full replication of this model using the BACE approach, together with a detailed discussion on variable selection strategy and discovering the reduction path, is presented in Błażejowski et al. (2020). |
| 12. | All computations were performed on so-called haavelmo machine (located at Dipartimento di Scienze Economiche e Sociali (DiSES), Ancona, Italy) which consists on 20 Hyper-Threaded Intel® Xeon® CPU E5-2640 v4 @ 2.40GHz with 256 GB operational memory running under Debian GNU/Linux 64 bits. |
| Variable | BACE | BMA (Restricted) | BMA (Unrestricted) | Autometrics | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PIP | Avg. | Avg. | PIP | Avg. | Avg. | PIP | Avg. | Avg. | Coeff. | Std. | |
| Mean | Std. Dev. | Mean | Std. Dev. | Mean | Std. Dev. | Error | |||||
| 1.0000 | 0.7656 | 0.1233 | 1.0000 | 0.8334 | 0.0963 | 1.0000 | 0.8286 | 0.1003 | 0.8710 | 0.0221 | |
| 0.3590 | 0.0712 | 0.1186 | 0.1991 | 0.0357 | 0.0858 | 0.2138 | 0.0389 | 0.0894 | |||
| 0.1511 | −0.0101 | 0.0594 | 0.0565 | −0.0013 | 0.0284 | 0.0663 | −0.0020 | 0.0309 | |||
| 0.4107 | 0.0659 | 0.1003 | 0.1463 | 0.0170 | 0.0539 | 0.1759 | 0.0212 | 0.0601 | |||
| 0.6676 | 0.1590 | 0.1624 | 0.6164 | 0.1026 | 0.1164 | 0.6485 | 0.1129 | 0.1217 | 0.1140 | 0.0163 | |
| 0.3773 | 0.0804 | 0.2056 | 0.3521 | 0.0593 | 0.1490 | 0.3225 | 0.0545 | 0.1487 | |||
| 0.2991 | −0.0623 | 0.1754 | 0.1928 | −0.0266 | 0.1236 | 0.2009 | −0.0296 | 0.1285 | |||
| 0.2995 | −0.0559 | 0.1274 | 0.1643 | −0.0231 | 0.0823 | 0.1718 | −0.0249 | 0.0869 | |||
| 0.2138 | −0.0200 | 0.0757 | 0.1085 | −0.0081 | 0.0442 | 0.1161 | −0.0099 | 0.0488 | |||
| 0.2289 | 0.0182 | 0.0582 | 0.2021 | 0.0197 | 0.0523 | 0.2244 | 0.0212 | 0.0548 | |||
| 0.6495 | 0.1174 | 0.1198 | 0.5603 | 0.0866 | 0.0966 | 0.5449 | 0.0839 | 0.0965 | 0.1272 | 0.0203 | |
| 0.2425 | −0.0285 | 0.0896 | 0.1373 | −0.0093 | 0.0609 | 0.1447 | −0.0075 | 0.0609 | |||
| 0.1693 | −0.0048 | 0.0538 | 0.1127 | 0.0040 | 0.0382 | 0.1019 | 0.0031 | 0.0370 | |||
| 0.2150 | 0.0207 | 0.0570 | 0.2164 | 0.0229 | 0.0540 | 0.2061 | 0.0217 | 0.0530 | |||
| 0.9980 | −0.5192 | 0.1127 | 0.9975 | −0.5063 | 0.0945 | 0.9968 | −0.5099 | 0.0965 | −0.5053 | 0.0666 | |
| 0.2530 | −0.0625 | 0.1407 | 0.1018 | −0.0191 | 0.0829 | 0.1044 | −0.0208 | 0.0856 | |||
| 0.2798 | −0.0669 | 0.1416 | 0.1037 | −0.0191 | 0.0782 | 0.1107 | −0.0227 | 0.0870 | |||
| 0.1204 | 0.0045 | 0.0513 | 0.0508 | 0.0015 | 0.0281 | 0.0623 | 0.0021 | 0.0323 | |||
| 0.1149 | −0.0031 | 0.0384 | 0.0605 | −0.0034 | 0.0278 | 0.0528 | −0.0032 | 0.0274 | |||
| const | 0.2435 | −0.1639 | 0.3790 | 0.1435 | −0.1022 | 0.3150 | 0.1482 | −0.1042 | 0.3171 | ||
| Model | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1.53% | 0.64% | 0.60% | 0.59% | 0.46% | 0.44% | 0.38% | 0.37% | 0.33% | 0.32% | |
| 0.8710 | 0.8622 | 0.6691 | 0.7224 | 0.6760 | 0.8726 | 0.8689 | 0.8973 | 0.7056 | 0.7169 | |
| −0.5057 | −0.4758 | −0.5634 | −0.5531 | −0.5807 | −0.4843 | −0.4948 | −0.5489 | −0.5749 | −0.6301 | |
| 0.1140 | 0.3333 | 0.1207 | 0.3983 | 0.1126 | 0.1155 | 0.2208 | 0.0983 | 0.2786 | ||
| 0.1272 | 0.1353 | 0.1275 | 0.1333 | 0.1329 | 0.2699 | 0.1029 | 0.1765 | 0.0996 | ||
| 0.2070 | 0.1941 | |||||||||
| 0.1198 | ||||||||||
| 1.53% | 0.64% | 0.60% | 0.59% | 0.46% | 0.44% | 0.38% | 0.37% | 0.33% | 0.32% | |
| 0.1431 | 0.1761 | 0.1853 | ||||||||
| −0.2071 | ||||||||||
| −0.2685 | −0.1251 | −0.1826 | ||||||||
| −0.3563 | −0.3143 | |||||||||
| const | −0.6718 | |||||||||
| −0.1408 | ||||||||||
| 0.1255 |
| Model | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 8.09% | 3.55% | 2.82% | 2.06% | 1.35% | 1.30% | 1.19% | 1.18% | 1.07% | 0.91% | |
| 0.8710 | 0.8620 | 0.8725 | 0.8916 | 0.7228 | 0.8687 | 0.8645 | 0.8842 | 0.8861 | 0.8546 | |
| −0.5059 | −0.4756 | −0.4843 | −0.4912 | −0.5527 | −0.4955 | −0.4530 | −0.5132 | −0.4635 | −0.4463 | |
| 0.1141 | 0.1355 | 0.1126 | 0.0986 | 0.1208 | 0.1157 | 0.0961 | 0.1423 | |||
| 0.1273 | 0.1334 | 0.2695 | 0.1581 | |||||||
| 0.1200 | 0.1178 | 0.1020 | ||||||||
| 0.1425 | ||||||||||
| 0.1249 | ||||||||||
| const | −0.4988 | |||||||||
| -0.1402 | ||||||||||
| 0.1256 | 0.1329 | |||||||||
| 0.1083 | 0.1132 |
| Model | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 7.06% | 3.28% | 3.14% | 2.18% | 1.42% | 1.16% | 0.97% | 0.95% | 0.88% | 0.87% | |
| 0.8710 | 0.8725 | 0.8621 | 0.8914 | 0.7229 | 0.8878 | 0.8862 | 0.8991 | 0.8834 | 0.8687 | |
| −0.5051 | −0.4844 | −0.4763 | −0.4925 | −0.5528 | −0.4995 | −0.4630 | −0.5396 | −0.4997 | −0.4948 | |
| 0.1140 | 0.1126 | 0.0987 | 0.1206 | 0.1018 | 0.1774 | 0.1051 | 0.1157 | |||
| 7.06% | 3.28% | 3.14% | 2.18% | 1.42% | 1.16% | 0.97% | 0.95% | 0.88% | 0.87% | |
| 0.1273 | 0.1354 | 0.1332 | 0.1012 | 0.2710 | ||||||
| 0.1199 | 0.1019 | |||||||||
| 0.1256 | ||||||||||
| 0.1427 | ||||||||||
| 0.1158 | −0.1418 | |||||||||
| 0.1118 | ||||||||||
| 0.1085 | 0.1131 | |||||||||
| −0.0831 |
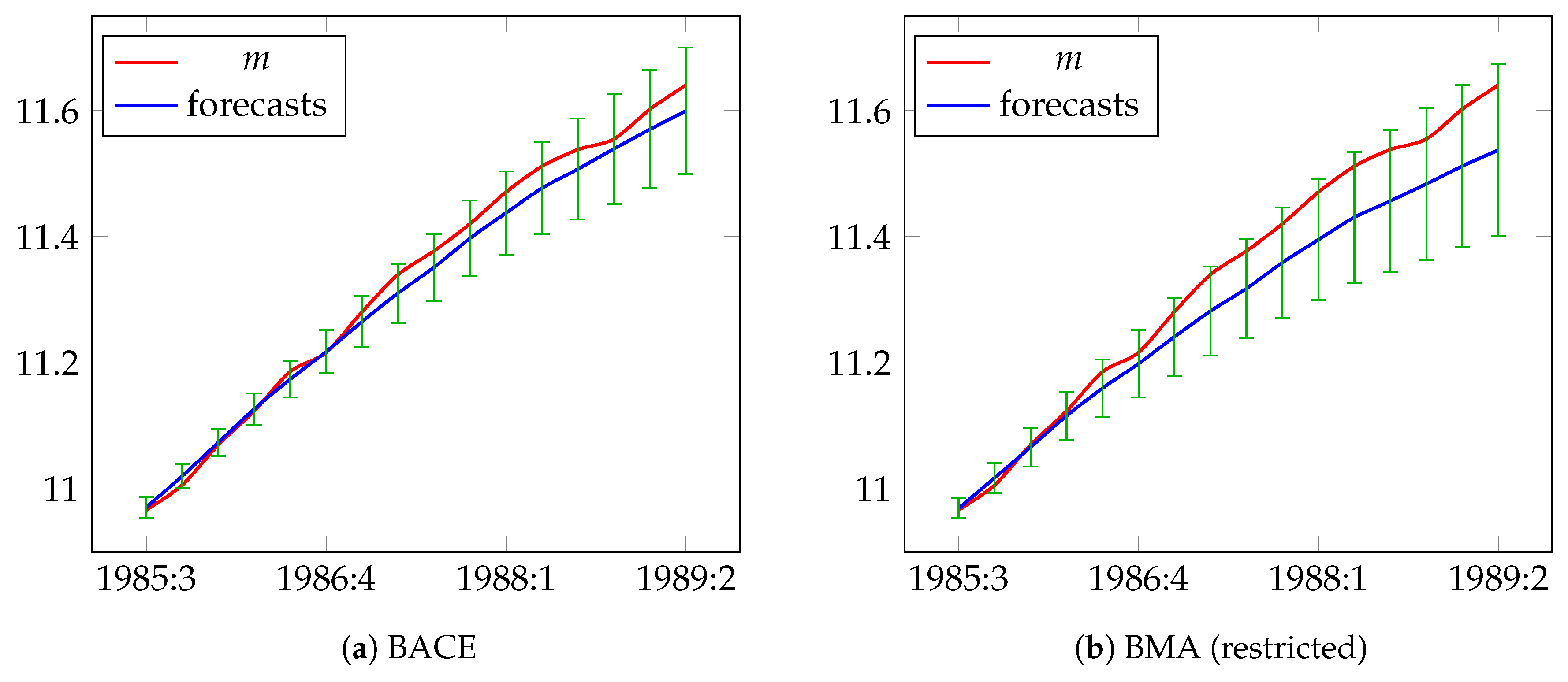
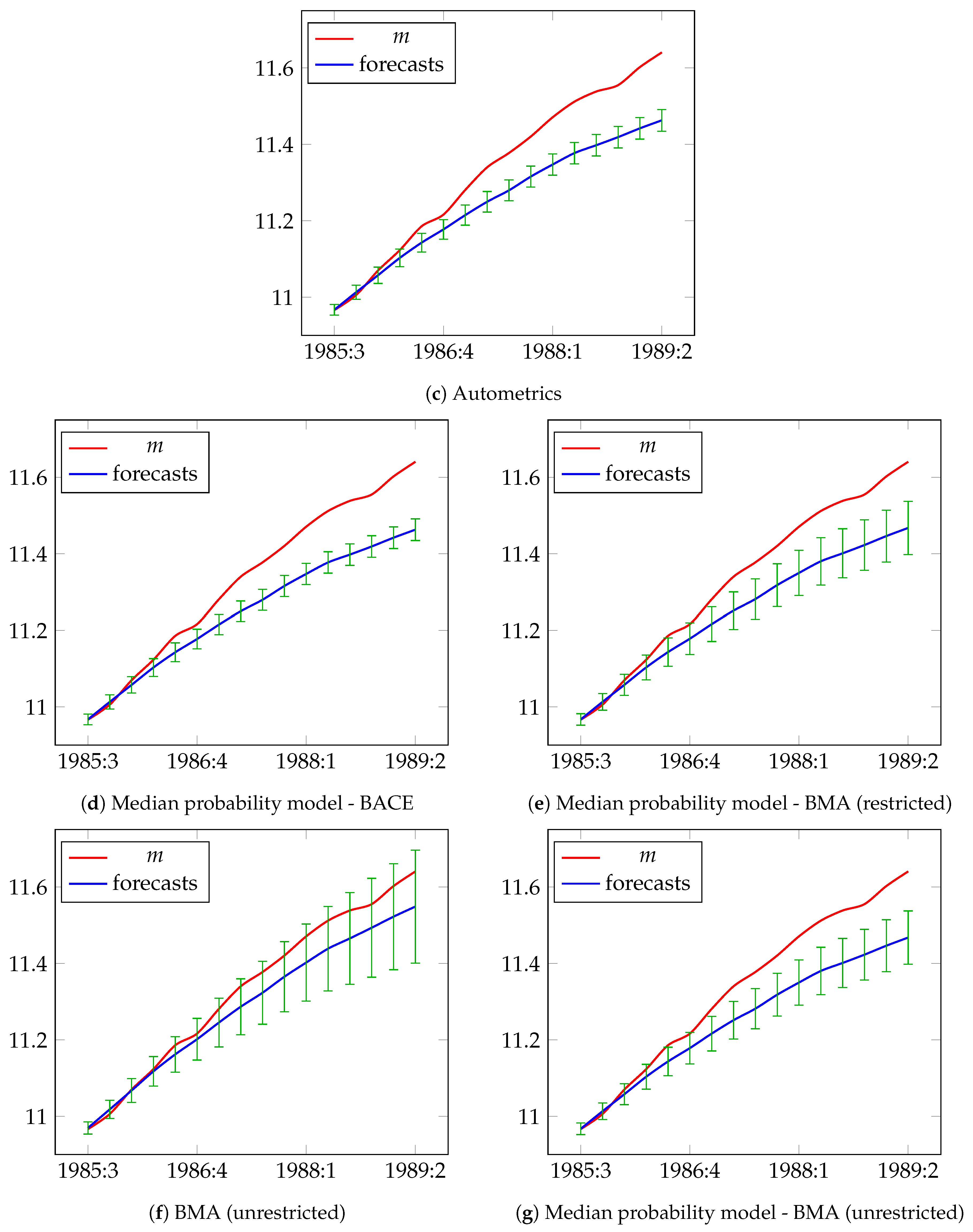
| Date | Actual | BACE | BMA (Restricted) | BMA (Unrestricted) | Autometrics | Median BACE | Median BMA (Restricted) | Median BMA (Unrestricted) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fcast. | SE | Fcast. | SE | Fcast. | SE | Fcast. | SE | Fcast. | SE | Fcast. | SE | Fcast. | SE | ||
| 1985:3 | 10.966 | 10.971 | 0.0167 | 10.969 | 0.0159 | 10.969 | 0.0160 | 10.967 | 0.0140 | 10.967 | 0.0140 | 10.967 | 0.0151 | 10.967 | 0.0151 |
| 1985:4 | 11.006 | 11.020 | 0.0185 | 11.017 | 0.0235 | 11.018 | 0.0237 | 11.013 | 0.0186 | 11.013 | 0.0186 | 11.013 | 0.0218 | 11.013 | 0.0218 |
| 1986:1 | 11.070 | 11.073 | 0.0212 | 11.066 | 0.0309 | 11.067 | 0.0312 | 11.058 | 0.0214 | 11.058 | 0.0214 | 11.058 | 0.0274 | 11.058 | 0.0274 |
| 1986:2 | 11.123 | 11.127 | 0.0247 | 11.116 | 0.0383 | 11.118 | 0.0387 | 11.103 | 0.0233 | 11.103 | 0.0233 | 11.103 | 0.0326 | 11.103 | 0.0326 |
| 1986:3 | 11.186 | 11.174 | 0.0288 | 11.160 | 0.0456 | 11.162 | 0.0464 | 11.143 | 0.0247 | 11.143 | 0.0247 | 11.143 | 0.0372 | 11.143 | 0.0372 |
| 1986:4 | 11.216 | 11.218 | 0.0340 | 11.199 | 0.0533 | 11.202 | 0.0546 | 11.178 | 0.0256 | 11.178 | 0.0256 | 11.178 | 0.0412 | 11.178 | 0.0412 |
| 1987:1 | 11.281 | 11.265 | 0.0403 | 11.241 | 0.0620 | 11.245 | 0.0638 | 11.215 | 0.0264 | 11.215 | 0.0264 | 11.216 | 0.0452 | 11.216 | 0.0452 |
| 1987:2 | 11.340 | 11.311 | 0.0468 | 11.282 | 0.0707 | 11.287 | 0.0732 | 11.250 | 0.0269 | 11.250 | 0.0269 | 11.251 | 0.0491 | 11.251 | 0.0491 |
| 1987:3 | 11.377 | 11.351 | 0.0534 | 11.318 | 0.0790 | 11.323 | 0.0823 | 11.280 | 0.0273 | 11.280 | 0.0273 | 11.282 | 0.0526 | 11.282 | 0.0526 |
| 1987:4 | 11.421 | 11.398 | 0.0600 | 11.359 | 0.0875 | 11.365 | 0.0917 | 11.316 | 0.0276 | 11.316 | 0.0276 | 11.318 | 0.0559 | 11.318 | 0.0559 |
| 1988:1 | 11.471 | 11.438 | 0.0662 | 11.395 | 0.0957 | 11.402 | 0.1009 | 11.347 | 0.0278 | 11.347 | 0.0278 | 11.350 | 0.0591 | 11.350 | 0.0591 |
| 1988:2 | 11.512 | 11.477 | 0.0730 | 11.431 | 0.1041 | 11.438 | 0.1104 | 11.377 | 0.0280 | 11.377 | 0.0280 | 11.380 | 0.0619 | 11.380 | 0.0619 |
| 1988:3 | 11.538 | 11.507 | 0.0801 | 11.457 | 0.1124 | 11.465 | 0.1198 | 11.398 | 0.0281 | 11.398 | 0.0281 | 11.401 | 0.0642 | 11.401 | 0.0642 |
| 1988:4 | 11.555 | 11.539 | 0.0872 | 11.484 | 0.1208 | 11.493 | 0.1294 | 11.419 | 0.0282 | 11.419 | 0.0282 | 11.423 | 0.0661 | 11.423 | 0.0661 |
| 1989:1 | 11.602 | 11.571 | 0.0937 | 11.512 | 0.1287 | 11.522 | 0.1387 | 11.442 | 0.0283 | 11.442 | 0.0283 | 11.446 | 0.0680 | 11.446 | 0.0680 |
| 1989:2 | 11.640 | 11.600 | 0.1003 | 11.538 | 0.1364 | 11.549 | 0.1478 | 11.463 | 0.0283 | 11.463 | 0.0283 | 11.468 | 0.0697 | 11.468 | 0.0697 |
| RMSE | 0.0224 | 0.0592 | 0.05317 | 0.1018 | 0.1018 | 0.0995 | 0.0995 | ||||||||
| MAPE | 0.17% | 0.43% | 0.39% | 0.74% | 0.74% | 0.72% | 0.72% | ||||||||
| UM (bias) | 49.5% | 64.4% | 63.6% | 67.3% | 67.3% | 67.4% | 67.4% | ||||||||
| UR (regression) | 40.0% | 34.0% | 34.4% | 31.9% | 31.8% | 31.9% | 31.8% | ||||||||
| UD (disturbance) | 10.5% | 1.6% | 2.0% | 0.8% | 0.8% | 0.8% | 0.8% | ||||||||
| Variable | Definition | Variable | Definition |
|---|---|---|---|
| real GDP, £ million, 1985 prices | world prices (1985 = 1) | ||
| implicit deflator of GDP (1985 = 1) | annual-average effective exchange rate | ||
| nominal broad money, million £ | deflator of net national income (1985 = 1) | ||
| three-month treasury bill rate, fraction p.a. | consumer price index (1985 = 1) | ||
| long-term bond interest rate, fraction p.a. | commodity price index, $ | ||
| opportunity cost of money measure | money excess demand | ||
| nominal National Debt, £ million | GDP excess demand | ||
| unemployment | short–long spread | ||
| working population | excess demand for debt | ||
| unemployment rate, fraction | real exchange rate | ||
| employment | profit markup | ||
| gross capital stock | excess demand for labor | ||
| wages | commodity prices in Sterling | ||
| normal hours (from 1920) | nominal unit labor costs |
| Variable | BACE | BMA (Restricted) | BMA (Unrestricted) | Autometrics | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PIP | Avg. | Avg. | PIP | Avg. | Avg. | PIP | Avg. | Avg. | Coeff. | Std. | |||
| Mean | Std. Dev. | Mean | Std. Dev. | Mean | Std. Dev. | Error | |||||||
| Hendry’s model (31) |  | 1.00 | 0.0380 | 0.0015 | 1.00 | 0.0379 | 0.0014 | 1.00 | 0.0379 | 0.0014 | 0.0377 | 0.0015 | |
| 1.00 | 0.2612 | 0.0248 | 1.00 | 0.2617 | 0.0236 | 1.00 | 0.2617 | 0.0236 | 0.2608 | 0.0247 | |||
| 1.00 | −0.9786 | 0.1060 | 1.00 | −0.9696 | 0.1024 | 1.00 | −0.9696 | 0.1024 | −0.9234 | 0.0997 | |||
| 1.00 | 0.1898 | 0.0381 | 1.00 | 0.1875 | 0.0352 | 1.00 | 0.1875 | 0.0352 | 0.1872 | 0.0330 | |||
| 1.00 | 0.2818 | 0.0353 | 1.00 | 0.2800 | 0.0322 | 1.00 | 0.2800 | 0.0322 | 0.2638 | 0.0264 | |||
| 0.99 | −0.1674 | 0.0295 | 1.00 | −0.1684 | 0.0281 | 1.00 | −0.1684 | 0.0281 | −0.1778 | 0.0273 | |||
| 0.99 | 0.6896 | 0.1273 | 0.99 | 0.6903 | 0.1199 | 0.99 | 0.6903 | 0.1199 | 0.6723 | 0.1182 | |||
| 0.99 | 0.0492 | 0.0111 | 0.99 | 0.0489 | 0.0106 | 0.99 | 0.0490 | 0.0106 | 0.0487 | 0.0110 | |||
| 0.99 | 0.1531 | 0.0325 | 0.99 | 0.1575 | 0.0309 | 0.99 | 0.1575 | 0.0309 | 0.1732 | 0.0293 | |||
| 0.71 | −0.0548 | 0.0443 | 0.60 | −0.0472 | 0.0449 | 0.60 | −0.0472 | 0.0449 | |||||
| 0.20 | 0.0006 | 0.0016 | 0.12 | 0.0004 | 0.0013 | 0.12 | 0.0004 | 0.0013 | |||||
| 0.15 | 0.0060 | 0.0217 | 0.09 | 0.0038 | 0.0170 | 0.09 | 0.0039 | 0.0170 | |||||
| 0.12 | 0.0030 | 0.0134 | 0.07 | 0.0017 | 0.0099 | 0.07 | 0.0018 | 0.0100 | |||||
| 0.12 | 0.0014 | 0.0063 | 0.06 | 0.0007 | 0.0044 | 0.06 | 0.0007 | 0.0044 | |||||
| const | 0.11 | 0.0001 | 0.0007 | 0.07 | 0.0001 | 0.0005 | 0.07 | 0.0001 | 0.0005 | ||||
| 0.10 | −0.0001 | 0.0132 | 0.05 | 0.0001 | 0.0083 | 0.05 | 0.0001 | 0.0083 | |||||
| 0.10 | −0.0009 | 0.0230 | 0.05 | −0.0001 | 0.0164 | 0.05 | −0.0001 | 0.0164 | |||||
| 0.10 | −0.0001 | 0.0043 | 0.05 | −0.0001 | 0.0028 | 0.05 | 0.0000 | 0.0029 | |||||
| 0.09 | 0.0003 | 0.0104 | 0.05 | 0.0001 | 0.0066 | 0.05 | 0.0001 | 0.0066 | |||||
| 0.09 | 0.0012 | 0.0839 | 0.05 | 0.0017 | 0.0591 | 0.05 | 0.0017 | 0.0590 | |||||
| Model | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 21.93% | 6.42% | 4.63% | 3.28% | 3.06% | 3.01% | 2.80% | 2.57% | 2.41% | 2.41% | |
| 0.0382 | 0.0377 | 0.0381 | 0.0383 | 0.0379 | 0.0378 | 0.0379 | 0.0380 | 0.0382 | 0.0382 | |
| 0.2639 | 0.2608 | 0.2619 | 0.2610 | 0.2581 | 0.2583 | 0.2623 | 0.2635 | 0.2634 | 0.2635 | |
| −0.9935 | −0.9234 | −1.0122 | −1.0002 | −0.9979 | −0.9607 | −0.9866 | −0.9896 | −0.9873 | −0.9946 | |
| 0.1788 | 0.1872 | 0.2069 | 0.1768 | 0.1858 | 0.2267 | 0.1829 | 0.1856 | 0.1785 | 0.1790 | |
| 0.2924 | 0.2638 | 0.2922 | 0.2837 | 0.2835 | 0.2676 | 0.2885 | 0.2930 | 0.2947 | 0.2952 | |
| 21.93% | 6.42% | 4.63% | 3.28% | 3.06% | 3.01% | 2.80% | 2.57% | 2.41% | 2.41% | |
| −0.1618 | −0.1778 | −0.1701 | −0.1642 | −0.1690 | −0.1875 | −0.1545 | −0.1619 | −0.1627 | −0.1620 | |
| 0.7149 | 0.6723 | 0.6605 | 0.6937 | 0.7248 | 0.5996 | 0.7165 | 0.7146 | 0.6998 | 0.7171 | |
| 0.0482 | 0.0487 | 0.0513 | 0.0479 | 0.0485 | 0.0532 | 0.0487 | 0.0488 | 0.0478 | 0.0480 | |
| 0.1555 | 0.1732 | 0.1468 | 0.1485 | 0.1482 | 0.1579 | 0.1470 | 0.1465 | 0.1547 | 0.1562 | |
| −0.0790 | −0.0710 | −0.0806 | −0.0814 | −0.0716 | −0.0744 | −0.0833 | −0.0794 | |||
| 0.0026 | 0.0038 | |||||||||
| 0.0254 | ||||||||||
| 0.0123 | ||||||||||
| 0.0253 | ||||||||||
| const | 0.0009 | |||||||||
| −0.0262 | ||||||||||
| −0.0028 |
| Model | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 32.66% | 17.63% | 3.74% | 3.24% | 2.95% | 2.80% | 2.39% | 1.94% | 1.92% | 1.90% | |
| 0.0381 | 0.0377 | 0.0378 | 0.0381 | 0.0373 | 0.0383 | 0.0379 | 0.0379 | 0.0375 | 0.0380 | |
| 0.2638 | 0.2609 | 0.2585 | 0.2616 | 0.2583 | 0.2610 | 0.2580 | −0.9864 | 0.2604 | 0.2636 | |
| −0.9948 | −0.9224 | −0.9602 | −1.0122 | −0.9228 | −1.0017 | −0.9973 | 0.2621 | −0.9241 | −0.9898 | |
| 0.1787 | 0.1874 | 0.2264 | 0.2067 | 0.1942 | 0.1767 | 0.1860 | 0.1825 | 0.2002 | 0.1855 | |
| 0.2927 | 0.2638 | 0.2676 | 0.2925 | 0.2614 | 0.2838 | 0.2831 | 0.2888 | 0.2687 | 0.2930 | |
| −0.1615 | −0.1782 | −0.1875 | −0.1699 | −0.1595 | −0.1639 | −0.1690 | −0.1544 | −0.1758 | −0.1619 | |
| 0.7163 | 0.6718 | 0.5991 | 0.6610 | 0.6844 | 0.6944 | 0.7237 | 0.7165 | 0.6779 | 0.7140 | |
| 0.0482 | 0.0488 | 0.0534 | 0.0514 | 0.0496 | 0.0478 | 0.0486 | 0.0487 | 0.0499 | 0.0488 | |
| 0.1554 | 0.1730 | 0.1576 | 0.1466 | 0.1517 | 0.1484 | 0.1484 | 0.1471 | 0.1515 | 0.1466 | |
| −0.0793 | −0.0711 | −0.0807 | −0.0812 | −0.0718 | −0.0746 | |||||
| 0.0038 | 0.0026 | |||||||||
| 0.0254 | ||||||||||
| 0.0124 | ||||||||||
| 0.0527 | 0.0251 | |||||||||
| const | 0.0018 | 0.0008 |
| Model | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 32.66% | 17.63% | 3.74% | 3.24% | 2.95% | 2.80% | 2.39% | 1.94% | 1.92% | 1.90% | |
| 0.0381 | 0.0377 | 0.0378 | 0.0381 | 0.0373 | 0.0383 | 0.0379 | 0.0379 | 0.0375 | 0.0380 | |
| 0.2638 | 0.2609 | 0.2585 | 0.2616 | 0.2583 | 0.2610 | 0.2580 | −0.9864 | 0.2604 | 0.2636 | |
| −0.9948 | −0.9224 | −0.9602 | −1.0122 | −0.9228 | −1.0017 | −0.9973 | 0.2621 | −0.9241 | −0.9898 | |
| 0.1787 | 0.1874 | 0.2264 | 0.2067 | 0.1942 | 0.1767 | 0.1860 | 0.1825 | 0.2002 | 0.1855 | |
| 0.2927 | 0.2638 | 0.2676 | 0.2925 | 0.2614 | 0.2838 | 0.2831 | 0.2888 | 0.2687 | 0.2930 | |
| −0.1615 | −0.1782 | −0.1875 | −0.1699 | −0.1595 | −0.1639 | −0.1690 | −0.1544 | −0.1758 | −0.1619 | |
| 0.7163 | 0.6718 | 0.5991 | 0.6610 | 0.6844 | 0.6944 | 0.7237 | 0.7165 | 0.6779 | 0.7140 | |
| 0.0482 | 0.0488 | 0.0534 | 0.0514 | 0.0496 | 0.0478 | 0.0486 | 0.0487 | 0.0499 | 0.0488 | |
| 0.1554 | 0.1730 | 0.1576 | 0.1466 | 0.1517 | 0.1484 | 0.1484 | 0.1471 | 0.1515 | 0.1466 | |
| −0.0793 | −0.0711 | −0.0807 | −0.0812 | −0.0718 | −0.0746 | |||||
| 0.0038 | 0.0026 | |||||||||
| 0.0254 | ||||||||||
| 0.0124 | ||||||||||
| 0.0527 | 0.0251 | |||||||||
| const | 0.0018 | 0.0008 |
| Date | Actual | BACE | BMA (Restricted) | BMA Median BMA (Unrestricted) | Autometrics | Median BACE (Restricted) | Median BMA (Unrestricted) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fcast. | SE | Fcast. | SE | Fcast. | SE | Fcast. | SE | Fcast. | SE | Fcast. | SE | Fcast. | SE | ||
| 1982 | 0.0681 | 0.0467 | 0.0124 | 0.0469 | 0.0118 | 0.0469 | 0.0118 | 0.0487 | 0.0110 | 0.0457 | 0.0107 | 0.0457 | 0.0116 | 0.0457 | 0.0116 |
| 1983 | 0.0551 | 0.0432 | 0.0120 | 0.0438 | 0.0125 | 0.0438 | 0.0125 | 0.0474 | 0.0114 | 0.0412 | 0.0111 | 0.0413 | 0.0121 | 0.0413 | 0.0121 |
| 1984 | 0.0527 | 0.0417 | 0.0126 | 0.0423 | 0.0132 | 0.0423 | 0.0132 | 0.0475 | 0.0114 | 0.0386 | 0.0112 | 0.0385 | 0.0125 | 0.0385 | 0.0125 |
| 1985 | 0.0529 | 0.0484 | 0.0120 | 0.0489 | 0.0126 | 0.0489 | 0.0126 | 0.0536 | 0.0114 | 0.0456 | 0.0112 | 0.0455 | 0.0120 | 0.0455 | 0.0120 |
| 1986 | 0.0259 | 0.0349 | 0.0131 | 0.0357 | 0.0136 | 0.0357 | 0.0136 | 0.0419 | 0.0114 | 0.0314 | 0.0112 | 0.0313 | 0.0127 | 0.0313 | 0.0127 |
| 1987 | 0.0495 | 0.0173 | 0.0142 | 0.0183 | 0.0151 | 0.0183 | 0.0151 | 0.0254 | 0.0114 | 0.0140 | −0.0112 | 0.0139 | 0.0142 | 0.0139 | 0.0142 |
| 1988 | 0.0626 | 0.0637 | 0.0142 | 0.0650 | 0.0154 | 0.0650 | 0.0154 | 0.0735 | 0.0114 | 0.0599 | 0.0112 | 0.0596 | 0.0143 | 0.0596 | 0.0143 |
| 1989 | 0.0744 | 0.0740 | 0.0129 | 0.0749 | 0.0141 | 0.0749 | 0.0141 | 0.0821 | 0.0114 | 0.0710 | 0.0112 | 0.0707 | 0.0133 | 0.0707 | 0.0133 |
| 1990 | 0.0769 | 0.0484 | 0.0132 | 0.0492 | 0.0141 | 0.0492 | 0.0141 | 0.0550 | 0.0114 | 0.0461 | 0.0112 | 0.0461 | 0.0136 | 0.0461 | 0.0136 |
| 1991 | 0.0604 | 0.0366 | 0.0129 | 0.0373 | 0.0139 | 0.0373 | 0.0139 | 0.0418 | 0.0114 | 0.0347 | 0.0112 | 0.0346 | 0.0134 | 0.0346 | 0.0134 |
| RMSE | 0.0179 | 0.0175 | 0.0175 | 0.0151 | 0.0196 | 0.0197 | 0.0197 | ||||||||
| MAPE | 26.06% | 25.85% | 25.85% | 25.06% | 28.31% | 28.41% | 28.41% | ||||||||
| UM (bias) | 54.5% | 51.3% | 51.3% | 21.9% | 65.0% | 65.3% | 65.3% | ||||||||
| UR (regression) | 0.3% | 0.3% | 0.3% | 1.2% | 0.2% | 0.2% | 0.2% | ||||||||
| UD (disturbance) | 45.2% | 48.3% | 48.3% | 76.9% | 34.8% | 34.5% | 34.5% | ||||||||
| Variable | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| PIP | Avg. | Avg. | PIP | Avg. | Avg. | PIP | Avg. | Avg. | |
| Mean | Std. Dev. | Mean | Std. Dev. | Mean | Std. Dev. | ||||
| 1.00 | 0.7695 | 0.1224 | 1.00 | 0.7676 | 0.1224 | 1.00 | 0.7734 | 0.1220 | |
| 0.35 | 0.0687 | 0.1161 | 0.35 | 0.0681 | 0.1157 | 0.34 | 0.0664 | 0.1144 | |
| 0.12 | −0.0074 | 0.0506 | 0.13 | −0.0073 | 0.0512 | 0.13 | −0.0068 | 0.0510 | |
| 0.39 | 0.0607 | 0.0962 | 0.40 | 0.0632 | 0.0976 | 0.38 | 0.0584 | 0.0950 | |
| 0.67 | 0.1562 | 0.1581 | 0.67 | 0.1582 | 0.1607 | 0.66 | 0.1541 | 0.1593 | |
| 0.37 | 0.0783 | 0.2002 | 0.37 | 0.0793 | 0.2028 | 0.37 | 0.0801 | 0.2049 | |
| 0.28 | −0.0598 | 0.1657 | 0.29 | −0.0628 | 0.1711 | 0.31 | −0.0657 | 0.1752 | |
| 0.29 | −0.0548 | 0.1207 | 0.29 | −0.0547 | 0.1219 | 0.27 | −0.0491 | 0.1172 | |
| 0.19 | −0.0178 | 0.0682 | 0.19 | −0.0179 | 0.0693 | 0.19 | −0.0174 | 0.0680 | |
| 0.22 | 0.0180 | 0.0555 | 0.22 | 0.0183 | 0.0561 | 0.23 | 0.0188 | 0.0570 | |
| 0.65 | 0.1155 | 0.1173 | 0.64 | 0.1143 | 0.1171 | 0.64 | 0.1148 | 0.1178 | |
| 0.22 | −0.0269 | 0.0860 | 0.22 | −0.0259 | 0.0856 | 0.23 | −0.0269 | 0.0878 | |
| 0.15 | −0.0031 | 0.0488 | 0.15 | −0.0030 | 0.0498 | 0.15 | −0.0024 | 0.0493 | |
| 0.20 | 0.0195 | 0.0544 | 0.20 | 0.0192 | 0.0540 | 0.20 | 0.0185 | 0.0534 | |
| 0.99 | −0.5208 | 0.1111 | 0.99 | −0.5187 | 0.1143 | 0.99 | −0.5195 | 0.1115 | |
| 0.23 | −0.0553 | 0.1334 | 0.24 | −0.0601 | 0.1395 | 0.23 | −0.0554 | 0.1334 | |
| 0.27 | −0.0650 | 0.1400 | 0.27 | −0.0658 | 0.1406 | 0.26 | −0.0610 | 0.1354 | |
| 0.10 | 0.0034 | 0.0435 | 0.10 | 0.0032 | 0.0436 | 0.10 | 0.0040 | 0.0453 | |
| 0.10 | −0.0030 | 0.0341 | 0.10 | −0.0026 | 0.0346 | 0.09 | −0.0028 | 0.0340 | |
| const | 0.23 | −0.1519 | 0.3652 | 0.22 | −0.1503 | 0.3661 | 0.22 | −0.1487 | 0.3626 |
| Variable | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| PIP | Avg. | Avg. | PIP | Avg. | Avg. | PIP | Avg. | Avg. | |
| Mean | Std. Dev. | Mean | Std. Dev. | Mean | Std. Dev. | ||||
| 1.00 | 0.0380 | 0.0015 | 1.00 | 0.0380 | 0.0015 | 1.00 | 0.0380 | 0.0015 | |
| 1.00 | 0.2612 | 0.0248 | 1.00 | 0.2612 | 0.0248 | 1.00 | 0.2612 | 0.0248 | |
| 1.00 | −0.9786 | 0.1060 | 1.00 | −0.9786 | 0.1060 | 1.00 | −0.9786 | 0.1060 | |
| 1.00 | 0.1898 | 0.0381 | 1.00 | 0.1898 | 0.0381 | 1.00 | 0.1898 | 0.0381 | |
| 1.00 | 0.2818 | 0.0352 | 1.00 | 0.2818 | 0.0352 | 1.00 | 0.2818 | 0.0352 | |
| 0.99 | −0.1674 | 0.0295 | 0.99 | −0.1673 | 0.0295 | 1.00 | −0.1674 | 0.0295 | |
| 0.99 | 0.6896 | 0.1272 | 0.99 | 0.6897 | 0.1272 | 0.99 | 0.6896 | 0.1273 | |
| 0.99 | 0.0492 | 0.0111 | 0.99 | 0.0492 | 0.0111 | 0.99 | 0.0492 | 0.0111 | |
| 0.99 | 0.1532 | 0.0325 | 0.99 | 0.1532 | 0.0325 | 0.99 | 0.1532 | 0.0325 | |
| 0.71 | −0.0549 | 0.0443 | 0.71 | −0.0549 | 0.0443 | 0.71 | −0.0549 | 0.0443 | |
| 0.20 | 0.0006 | 0.0016 | 0.20 | 0.0006 | 0.0016 | 0.20 | 0.0006 | 0.0016 | |
| 0.15 | 0.0059 | 0.0216 | 0.15 | 0.0059 | 0.0216 | 0.15 | 0.0059 | 0.0217 | |
| 0.12 | 0.0030 | 0.0133 | 0.12 | 0.0030 | 0.0133 | 0.12 | 0.0030 | 0.0133 | |
| 0.12 | 0.0014 | 0.0063 | 0.12 | 0.0014 | 0.0063 | 0.12 | 0.0014 | 0.0063 | |
| const | 0.11 | 0.0001 | 0.0007 | 0.11 | 0.0001 | 0.0007 | 0.11 | 0.0001 | 0.0007 |
| 0.10 | −0.0001 | 0.0130 | 0.10 | −0.0001 | 0.0130 | 0.10 | −0.0001 | 0.0130 | |
| 0.09 | −0.0009 | 0.0229 | 0.09 | −0.0009 | 0.0229 | 0.10 | −0.0009 | 0.0229 | |
| 0.09 | −0.0001 | 0.0042 | 0.10 | −0.0001 | 0.0042 | 0.09 | −0.0001 | 0.0042 | |
| 0.09 | 0.0003 | 0.0102 | 0.09 | 0.0003 | 0.0102 | 0.09 | 0.0003 | 0.0103 | |
| 0.09 | 0.0011 | 0.0831 | 0.09 | 0.0011 | 0.0832 | 0.09 | 0.0011 | 0.0833 | |
| Variable | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| PIP | Avg. | Avg. | PIP | Avg. | Avg. | PIP | Avg. | Avg. | |
| Mean | Std. Dev. | Mean | Std. Dev. | Mean | Std. Dev. | ||||
| 1.00 | 0.8318 | 0.0966 | 1.00 | 0.8292 | 0.0978 | 1.00 | 0.8298 | 0.0980 | |
| 0.20 | 0.0356 | 0.0857 | 0.20 | 0.0362 | 0.0865 | 0.20 | 0.0364 | 0.0863 | |
| 0.06 | −0.0011 | 0.0287 | 0.07 | −0.0014 | 0.0291 | 0.06 | −0.0013 | 0.0287 | |
| 0.15 | 0.0178 | 0.0550 | 0.16 | 0.0196 | 0.0572 | 0.16 | 0.0190 | 0.0570 | |
| 0.64 | 0.1069 | 0.1170 | 0.65 | 0.1090 | 0.1178 | 0.65 | 0.1091 | 0.1184 | |
| 0.33 | 0.0556 | 0.1450 | 0.33 | 0.0553 | 0.1483 | 0.33 | 0.0529 | 0.1455 | |
| 0.20 | −0.0279 | 0.1233 | 0.20 | −0.0286 | 0.1254 | 0.20 | −0.0275 | 0.1245 | |
| 0.15 | −0.0216 | 0.0789 | 0.15 | −0.0223 | 0.0797 | 0.15 | −0.0211 | 0.0783 | |
| 0.11 | −0.0083 | 0.0447 | 0.10 | −0.0082 | 0.0449 | 0.10 | −0.0085 | 0.0442 | |
| 0.18 | 0.0173 | 0.0498 | 0.21 | 0.0199 | 0.0526 | 0.19 | 0.0178 | 0.0505 | |
| 0.60 | 0.0911 | 0.0951 | 0.59 | 0.0906 | 0.0953 | 0.59 | 0.0907 | 0.0952 | |
| 0.13 | −0.0074 | 0.0585 | 0.13 | −0.0072 | 0.0592 | 0.14 | −0.0069 | 0.0594 | |
| 0.12 | 0.0041 | 0.0396 | 0.11 | 0.0034 | 0.0377 | 0.10 | 0.0030 | 0.0363 | |
| 0.19 | 0.0191 | 0.0497 | 0.17 | 0.0176 | 0.0478 | 0.19 | 0.0200 | 0.0505 | |
| 1.00 | −0.5090 | 0.0925 | 1.00 | −0.5081 | 0.0944 | 1.00 | −0.5080 | 0.0945 | |
| 0.09 | −0.0173 | 0.0758 | 0.10 | −0.0199 | 0.0829 | 0.10 | −0.0192 | 0.0822 | |
| 0.11 | −0.0212 | 0.0823 | 0.12 | −0.0220 | 0.0837 | 0.12 | −0.0224 | 0.0846 | |
| 0.05 | 0.0012 | 0.0274 | 0.05 | 0.0014 | 0.0276 | 0.05 | 0.0016 | 0.0287 | |
| 0.06 | −0.0030 | 0.0267 | 0.06 | −0.0026 | 0.0256 | 0.07 | −0.0033 | 0.0278 | |
| const | 0.14 | −0.0985 | 0.3076 | 0.14 | −0.0934 | 0.2985 | 0.14 | −0.0998 | 0.3097 |
| Variable | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| PIP | Avg. | Avg. | PIP | Avg. | Avg. | PIP | Avg. | Avg. | |
| Mean | Std. Dev. | Mean | Std. Dev. | Mean | Std. Dev. | ||||
| 1.00 | 0.0379 | 0.0014 | 1.00 | 0.0379 | 0.0014 | 1.00 | 0.0379 | 0.0014 | |
| 1.00 | 0.2617 | 0.0238 | 1.00 | 0.1879 | 0.0354 | 1.00 | 0.1879 | 0.0354 | |
| 1.00 | −0.9687 | 0.1024 | 1.00 | −0.9686 | 0.1024 | 1.00 | −0.9685 | 0.1024 | |
| 1.00 | 0.1877 | 0.0353 | 1.00 | 0.2617 | 0.0238 | 1.00 | 0.2617 | 0.0238 | |
| 1.00 | 0.2797 | 0.0324 | 1.00 | 0.2796 | 0.0324 | 1.00 | 0.2794 | 0.0324 | |
| 1.00 | −0.1685 | 0.0280 | 1.00 | −0.1687 | 0.0281 | 1.00 | −0.1687 | 0.0281 | |
| 0.99 | 0.6893 | 0.1196 | 0.99 | 0.6889 | 0.1201 | 0.99 | 0.6889 | 0.1198 | |
| 0.99 | 0.0490 | 0.0106 | 0.99 | 0.1577 | 0.0308 | 0.99 | 0.1577 | 0.0308 | |
| 0.99 | 0.1575 | 0.0310 | 0.99 | 0.0489 | 0.0107 | 0.99 | 0.0489 | 0.0106 | |
| 0.59 | −0.0465 | 0.0449 | 0.59 | −0.0463 | 0.0449 | 0.59 | −0.0460 | 0.0449 | |
| 0.12 | 0.0004 | 0.0013 | 0.12 | 0.0004 | 0.0013 | 0.12 | 0.0004 | 0.0013 | |
| 0.10 | 0.0042 | 0.0176 | 0.09 | 0.0039 | 0.0171 | 0.09 | 0.0040 | 0.0172 | |
| 0.07 | 0.0016 | 0.0096 | 0.07 | 0.0017 | 0.0097 | 0.07 | 0.0017 | 0.0097 | |
| 0.06 | 0.0008 | 0.0045 | 0.07 | 0.0008 | 0.0047 | 0.07 | 0.0008 | 0.0047 | |
| const | 0.07 | 0.0001 | 0.0005 | 0.07 | 0.0001 | 0.0006 | 0.07 | 0.0001 | 0.0006 |
| 0.05 | 0.0001 | 0.0086 | 0.05 | −0.0003 | 0.0165 | 0.05 | −0.0001 | 0.0163 | |
| 0.06 | −0.0003 | 0.0167 | 0.05 | 0.0002 | 0.0070 | 0.06 | 0.0001 | 0.0092 | |
| 0.05 | <0.0000 | 0.0028 | 0.05 | 0.0001 | 0.0085 | 0.05 | <0.0000 | 0.0028 | |
| 0.05 | 0.0002 | 0.0068 | 0.05 | 0.0022 | 0.0619 | 0.05 | 0.0023 | 0.0611 | |
| 0.05 | 0.0016 | 0.0591 | 0.05 | <0.0001 | 0.0029 | 0.05 | 0.0002 | 0.0069 | |
| Variable | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| PIP | Avg. | Avg. | PIP | Avg. | Avg. | PIP | Avg. | Avg. | |
| Mean | Std. Dev. | Mean | Std. Dev. | Mean | Std. Dev. | ||||
| 1.00 | 0.8320 | 0.0982 | 1.00 | 0.8332 | 0.0973 | 1.00 | 0.8315 | 0.0982 | |
| 0.20 | 0.0360 | 0.0861 | 0.20 | 0.0363 | 0.0865 | 0.21 | 0.0374 | 0.0875 | |
| 0.06 | −0.0013 | 0.0281 | 0.07 | −0.0014 | 0.0292 | 0.06 | −0.0013 | 0.0277 | |
| 0.16 | 0.0193 | 0.0573 | 0.15 | 0.0175 | 0.0545 | 0.15 | 0.0181 | 0.0554 | |
| 0.64 | 0.1102 | 0.1203 | 0.65 | 0.1089 | 0.1180 | 0.65 | 0.1112 | 0.1202 | |
| 0.33 | 0.0547 | 0.1486 | 0.33 | 0.0521 | 0.1451 | 0.33 | 0.0523 | 0.1472 | |
| 0.20 | −0.0286 | 0.1258 | 0.18 | −0.0247 | 0.1176 | 0.20 | −0.0264 | 0.1243 | |
| 0.16 | −0.0231 | 0.0809 | 0.16 | −0.0229 | 0.0806 | 0.17 | −0.0240 | 0.0849 | |
| 0.11 | −0.0098 | 0.0477 | 0.11 | −0.0097 | 0.0473 | 0.11 | −0.0093 | 0.0482 | |
| 0.20 | 0.0191 | 0.0517 | 0.20 | 0.0195 | 0.0522 | 0.20 | 0.0189 | 0.0514 | |
| 0.56 | 0.0857 | 0.0945 | 0.57 | 0.0880 | 0.0956 | 0.57 | 0.0873 | 0.0952 | |
| 0.13 | −0.0066 | 0.0575 | 0.14 | −0.0070 | 0.0591 | 0.13 | −0.0071 | 0.0591 | |
| 0.11 | 0.0039 | 0.0376 | 0.11 | 0.0030 | 0.0377 | 0.11 | 0.0030 | 0.0371 | |
| 0.20 | 0.0205 | 0.0511 | 0.19 | 0.0191 | 0.0493 | 0.20 | 0.0199 | 0.0500 | |
| 1.00 | −0.5099 | 0.0926 | 1.00 | −0.5087 | 0.0936 | 1.00 | −0.5089 | 0.0960 | |
| 0.09 | −0.0177 | 0.0773 | 0.09 | −0.0181 | 0.0792 | 0.09 | −0.0186 | 0.0814 | |
| 0.11 | −0.0221 | 0.0848 | 0.10 | −0.0192 | 0.0790 | 0.11 | −0.0210 | 0.0821 | |
| 0.05 | 0.0013 | 0.0265 | 0.06 | 0.0015 | 0.0287 | 0.06 | 0.0016 | 0.0299 | |
| 0.06 | −0.0029 | 0.0267 | 0.06 | −0.0028 | 0.0258 | 0.06 | −0.0031 | 0.0268 | |
| const | 0.14 | −0.0996 | 0.3097 | 0.14 | −0.0956 | 0.3035 | 0.13 | −0.0898 | 0.2958 |
| Variable | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| PIP | Avg. | Avg. | PIP | Avg. | Avg. | PIP | Avg. | Avg. | |
| Mean | Std. Dev. | Mean | Std. Dev. | Mean | Std. Dev. | ||||
| 1.00 | 0.0379 | 0.0014 | 1.00 | 0.0379 | 0.0014 | 1.00 | 0.0379 | 0.0014 | |
| 1.00 | 0.2617 | 0.0238 | 1.00 | 0.1879 | 0.0354 | 1.00 | 0.1879 | 0.0354 | |
| 1.00 | −0.9687 | 0.1024 | 1.00 | −0.9686 | 0.1024 | 1.00 | −0.9685 | 0.1024 | |
| 1.00 | 0.1877 | 0.0353 | 1.00 | 0.2617 | 0.0238 | 1.00 | 0.2617 | 0.0238 | |
| 1.00 | 0.2797 | 0.0324 | 1.00 | 0.2796 | 0.0324 | 1.00 | 0.2794 | 0.0324 | |
| 1.00 | −0.1685 | 0.0280 | 1.00 | −0.1687 | 0.0281 | 1.00 | −0.1687 | 0.0281 | |
| 0.99 | 0.6893 | 0.1196 | 0.99 | 0.6889 | 0.1201 | 0.99 | 0.6889 | 0.1198 | |
| 0.99 | 0.0490 | 0.0106 | 0.99 | 0.1577 | 0.0308 | 0.99 | 0.1577 | 0.0308 | |
| 0.99 | 0.1575 | 0.0310 | 0.99 | 0.0489 | 0.0107 | 0.99 | 0.0489 | 0.0106 | |
| 0.59 | −0.0465 | 0.0449 | 0.59 | −0.0463 | 0.0449 | 0.59 | −0.0460 | 0.0449 | |
| 0.12 | 0.0004 | 0.0013 | 0.12 | 0.0004 | 0.0013 | 0.12 | 0.0004 | 0.0013 | |
| 0.10 | 0.0042 | 0.0176 | 0.09 | 0.0039 | 0.0171 | 0.09 | 0.0040 | 0.0172 | |
| 0.07 | 0.0016 | 0.0096 | 0.07 | 0.0017 | 0.0097 | 0.07 | 0.0017 | 0.0097 | |
| 0.06 | 0.0008 | 0.0045 | 0.07 | 0.0008 | 0.0047 | 0.07 | 0.0008 | 0.0047 | |
| const | 0.07 | 0.0001 | 0.0005 | 0.07 | 0.0001 | 0.0006 | 0.07 | 0.0001 | 0.0006 |
| 0.05 | 0.0001 | 0.0086 | 0.05 | −0.0003 | 0.0165 | 0.05 | −0.0001 | 0.0163 | |
| 0.06 | −0.0003 | 0.0167 | 0.05 | 0.0002 | 0.0070 | 0.06 | 0.0001 | 0.0092 | |
| 0.05 | <0.0000 | 0.0028 | 0.05 | 0.0001 | 0.0085 | 0.05 | <0.0000 | 0.0028 | |
| 0.05 | 0.0002 | 0.0068 | 0.05 | 0.0022 | 0.0619 | 0.05 | 0.0023 | 0.0611 | |
| 0.05 | 0.0016 | 0.0591 | 0.05 | <0.0001 | 0.0029 | 0.05 | 0.0002 | 0.0069 | |
| CPUs | UKM1 | UK Inflation | ||||||
|---|---|---|---|---|---|---|---|---|
| without Forecasts | with Forecasts | without Forecasts | with Forecasts | |||||
| Nrep | Run Time | Nrep | Run Time | Nrep | Run Time | Nrep | Run Time | |
| 1 | 147 | 169 | 112 | 128 | ||||
| 4 | 128 | 143 | 49 | 54 | ||||
| 20 | 23 | 28 | 15 | 17 | ||||
| CPUs | UKM1 | UK Inflation | ||||||
|---|---|---|---|---|---|---|---|---|
| without Forecasts | with Forecasts | without Forecasts | with Forecasts | |||||
| Nrep | Run Time | Nrep | Run Time | Nrep | Run Time | Nrep | Run Time | |
| 1 | 10,554 | 275,165 | 1457 | 35,996 | ||||
| 4 | 2470 | 56,294 | 380 | 6829 | ||||
| 20 | 1169 | 14,771 | 136 | 3044 | ||||
| CPUs | UKM1 | UK Inflation | ||||||
|---|---|---|---|---|---|---|---|---|
| without Forecasts | with forecasts | without Forecasts | with Forecasts | |||||
| Nrep | Run Time | Nrep | Run Time | Nrep | Run Time | Nrep | Run Time | |
| 1 | 353 | 291,328 | 81 | 32,095 | ||||
| 4 | 167 | 65,862 | 54 | 6556 | ||||
| 20 | 103 | 16,630 | 55 | 1778 | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Błażejowski, M.; Kwiatkowski, J.; Kufel, P. BACE and BMA Variable Selection and Forecasting for UK Money Demand and Inflation with Gretl. Econometrics 2020, 8, 21. https://doi.org/10.3390/econometrics8020021
Błażejowski M, Kwiatkowski J, Kufel P. BACE and BMA Variable Selection and Forecasting for UK Money Demand and Inflation with Gretl. Econometrics. 2020; 8(2):21. https://doi.org/10.3390/econometrics8020021
Chicago/Turabian StyleBłażejowski, Marcin, Jacek Kwiatkowski, and Paweł Kufel. 2020. "BACE and BMA Variable Selection and Forecasting for UK Money Demand and Inflation with Gretl" Econometrics 8, no. 2: 21. https://doi.org/10.3390/econometrics8020021
APA StyleBłażejowski, M., Kwiatkowski, J., & Kufel, P. (2020). BACE and BMA Variable Selection and Forecasting for UK Money Demand and Inflation with Gretl. Econometrics, 8(2), 21. https://doi.org/10.3390/econometrics8020021





