Distributions You Can Count On …But What’s the Point? †
Abstract
1. Introduction
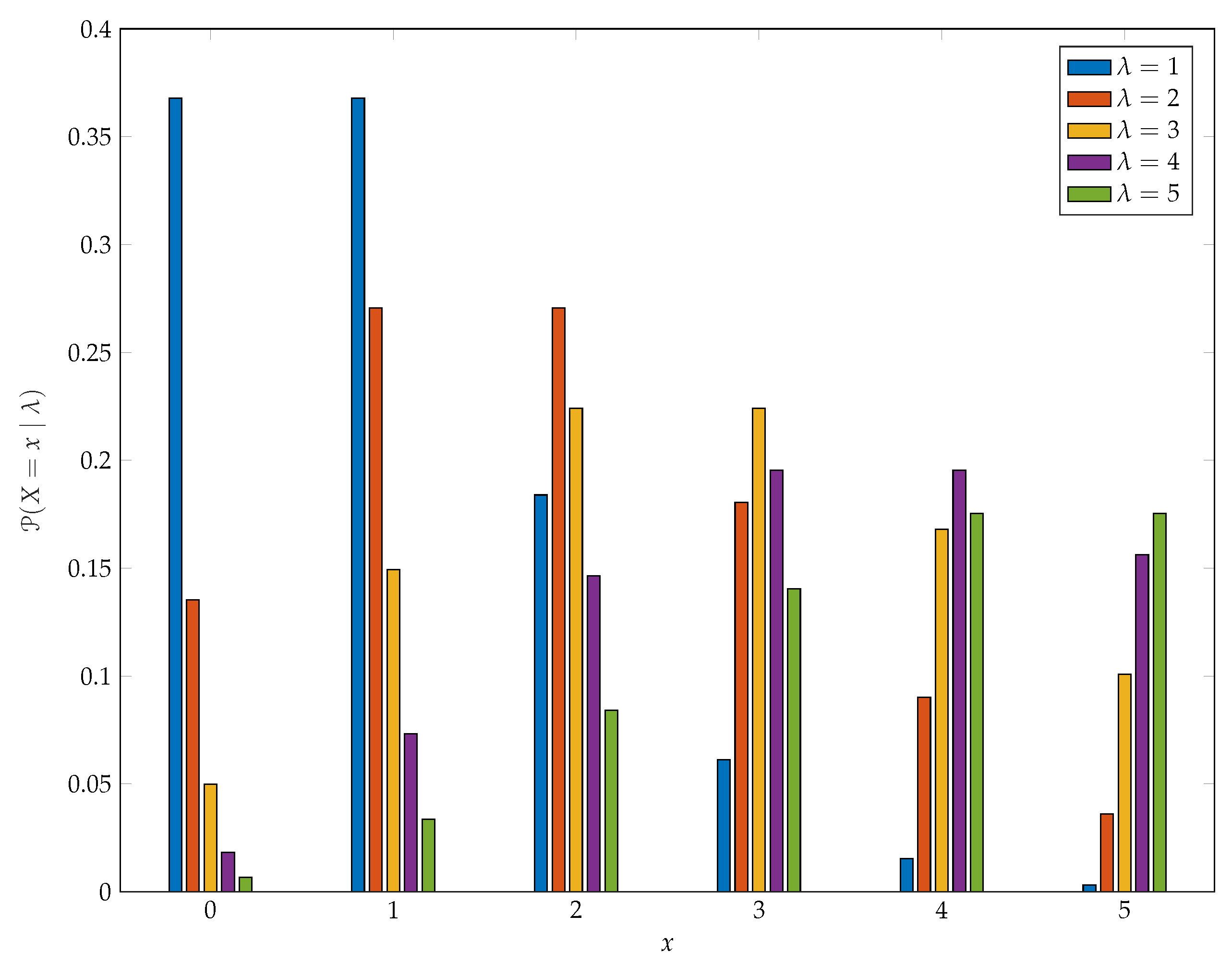
2. The Katz Family of Distributions
3. The Poisson, Negative Binomial, and Katz Regression Models
3.1. The Poisson Regression Model
3.2. The Classical Negative Binomial Regression Model
3.3. The Katz Regression Model
4. Testing for Over-dispersion in Poisson Regression model
4.1. The Katz Likelihood
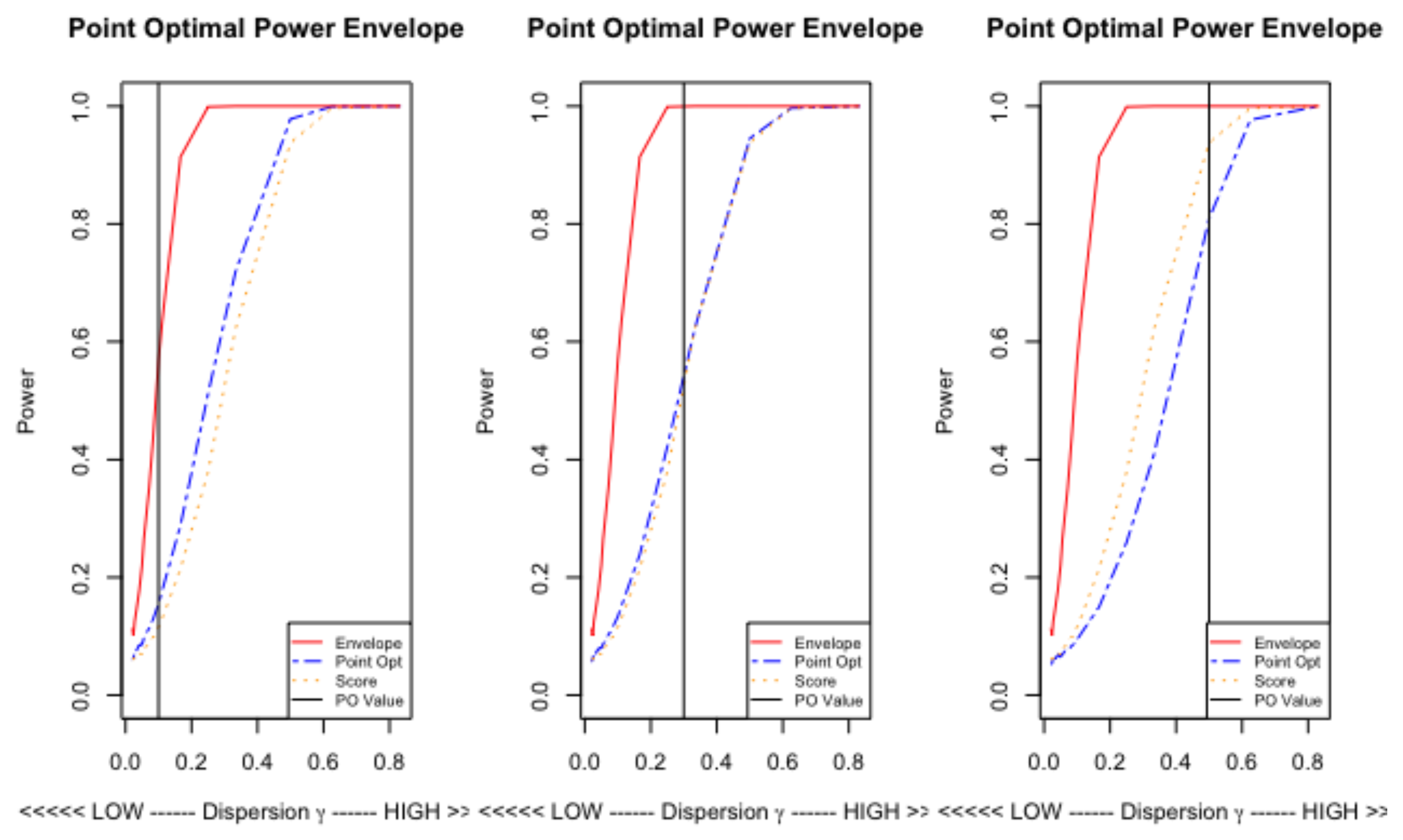
4.2. Point Optimal Tests
4.3. Score Test
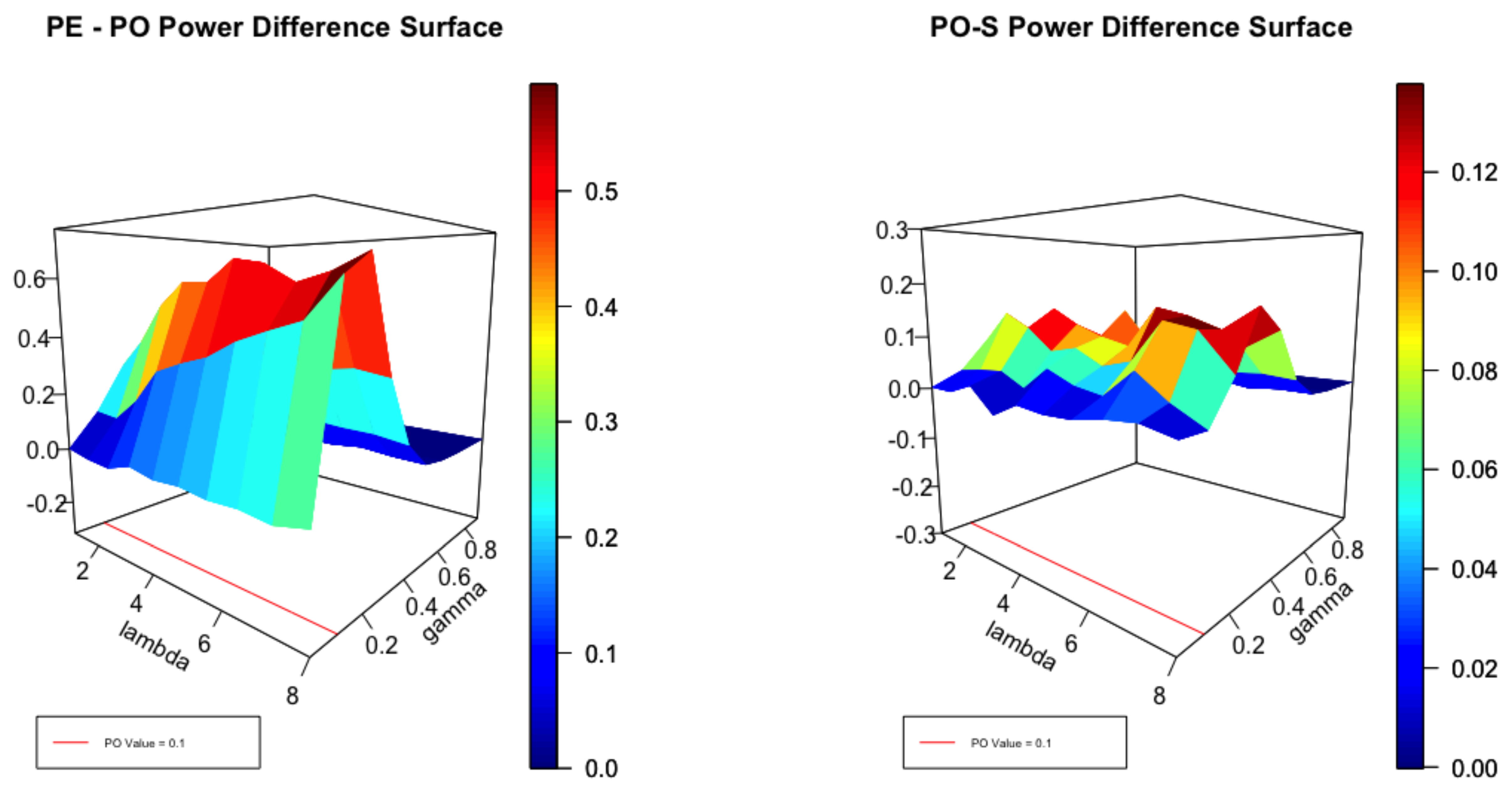
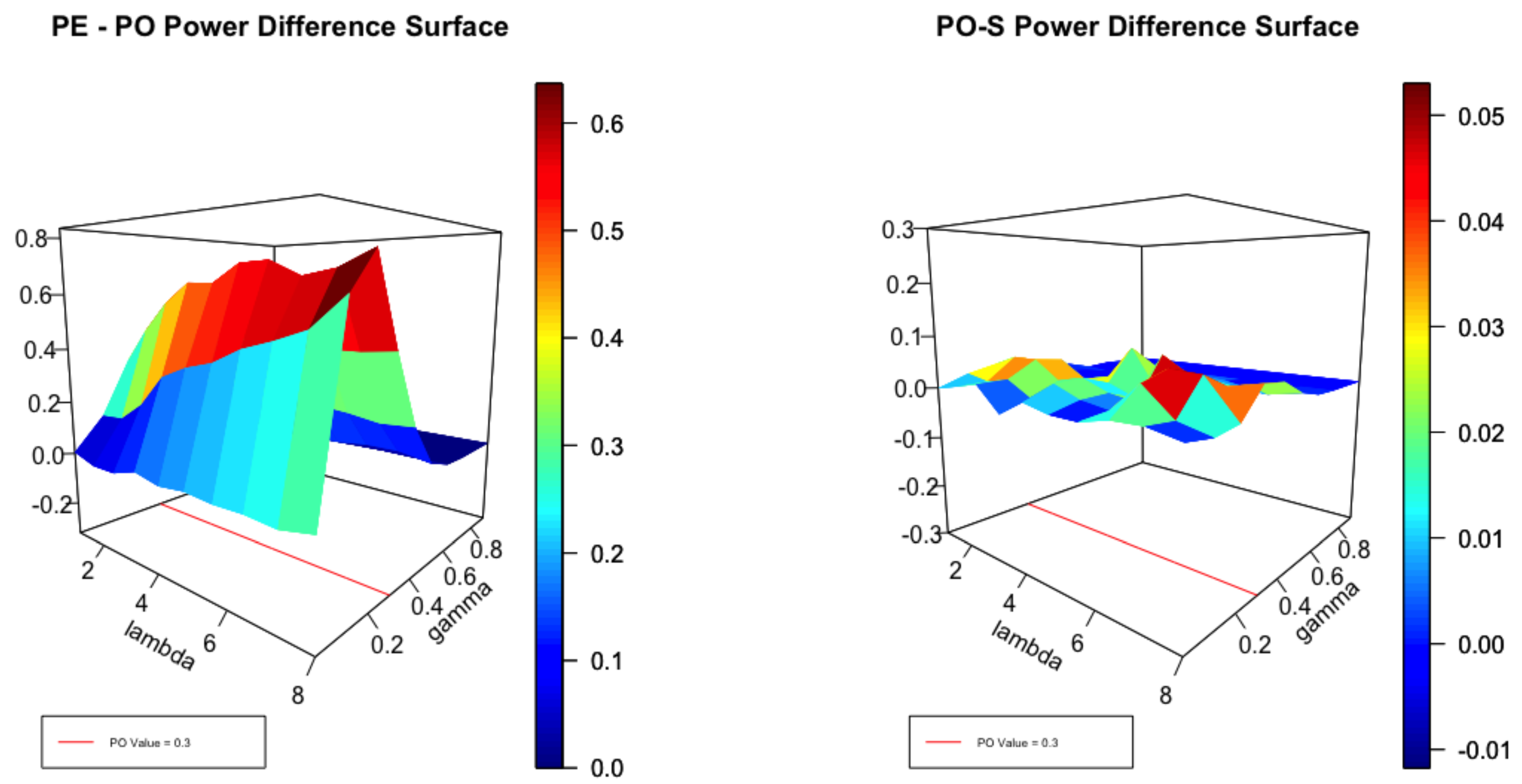
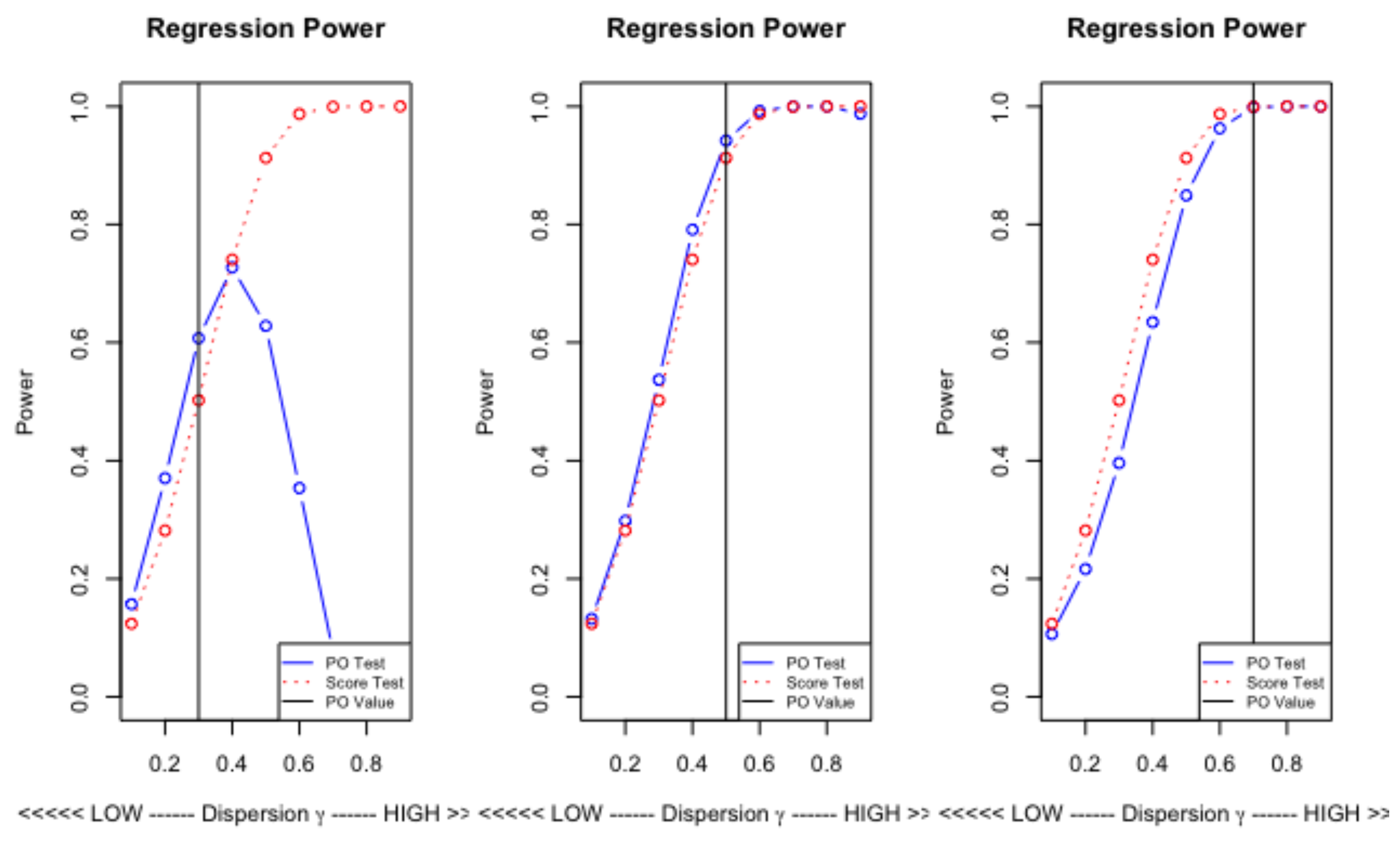
4.4. Simulation Experiments
4.4.1. The Unconditional Model
4.4.2. The Katz Regression
4.4.3. Summary
5. Hellinger Distance
5.1. The Poisson Distribution
5.2. The Katz Distribution
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. On Left-Truncated Katz Distributions
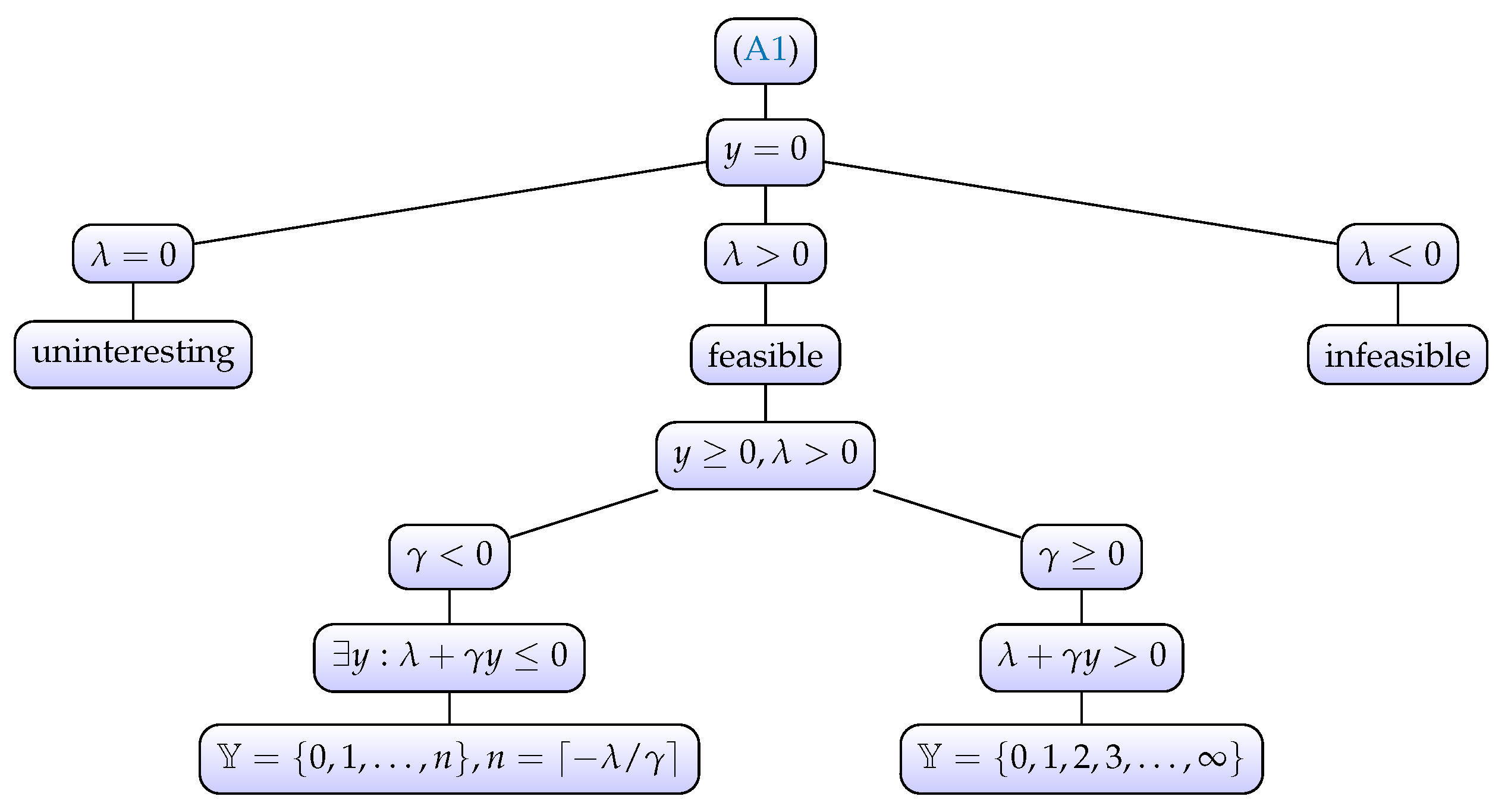
Appendix A.1. Support and Parameter Spaces
- [1]
- From (A1) we see that if for any then for all . In particular, if then for all . But this leads to violation of (4), that is, probabilities do not sum to unity, and so we exclude from further consideration. Equally, if , so that the pmf of Y is degenerate at L, which is a case that we have already excluded from further analysis. Hereafter, we assume that .
- [2]
- If and then we have a pmf degenerate at L unless , which will be assumed hereafter. In this case there is no implied restriction on the upper bound of , that is, . Of course, the concern when generating an infinite sequence of probabilities is to ensure that the associated series, , converges. This can be examined by considering the quantityand noting thatFrom the limit version of d’Alembert’s ratio test we see that the series converges because .
- [3]
- Similar in effect to the previous case, if then . Given , as assumed above, if and only if which will be assumed, hereafter, for all cases where .
- [4]
- Because , if and we see that for all and so here the support of the pmf of Y is unbounded from above and independent of the values taken by and . Again, we can establish convergence of the corresponding series. HereAppealing again to the limit version of d’Alembert’s ratio test we see that the series converges if , diverges if , but the test is inconclusive if . Expanding the denominator of in power series yieldsApplying Gauss’s test,23 we see that the series will converge absolutely if and only if but will otherwise diverge. Here we have assumed that and so . Hence, the series is divergent for .
- [5]
- In this case there is no value of y that satisfies and so cannot belong to . Moreover, this statement remains true even if . Consequently, in this case, the pmf of Y is degenerate at L, a situation that we have chosen to exclude from further consideration.
- [6]
- of different signIn this case we see that can change sign as y increases, unlike the situation of the previous two cases. Let n denote the smallest value of y such that . Then n is the largest value in . There are only two cases to consider here (having treated that of above): (i) , and (ii) .
- (a)
- If then the pmf of Y will be degenerate at L which, as explained above, is statistically uninteresting and a situation that we will assume away. That is, if then we will assume that . In particular, if then this requirement reduces to . As y increases, will approach zero from above. That value of y for which is first less than or equal to zero is the largest value of y in and shall be denoted by n, so that is well-defined but is not.24 That is, n is the smallest integer greater than or equal to . This is the definition of the so-called ceiling function, written . In summary, if then we see that the upper bound on the support of the pmf of Y is a function of the parameters and , with the space of subject to the constraint .
- (b)
- Here is an increasing function of y but the pmf of Y is non-degenerate at L if and only if . As we have already excluded from further consideration pmfs degenerate at L we here assume this to be the case. In particular, when we have a contradiction as we are assuming both , which is required when (see [3]), and ; we conclude that and can only arise when . As for all , will be unbounded from above provided that the series of probabilities so formed is convergent. Using the analysis outlined in [4], applying the ratio test we find convergence for all provided that . Moreover, if , Gauss’s test gives convergence provided that is strictly negative, that is, .
| n/a | n/a | |||
| n/a | n/a | n/a | ||
| n/a |
Appendix A.2. Probability Mass Functions and Their Properties
Appendix A.2.1. L = 0

Appendix A.2.2. L > 0
- (i)
- if then
- (ii)
- if then, on noting that ,
- (iii)
- if then
- (iv)
- If thenwhere the final equality follows on recognising the Mercator series andIn the special case , the quantity in the square brackets reduces to unity andwhich is the pmf of a logarithmic distribution. If then (A9) is recognizable as a left-truncated logarithmic distribution.
- (v)
- If thenandA comparison of this expression with that at (A8) reveals a remarkable similarity to the case where and . As in the earlier case we see that (i) the ratio is negative, (ii) there is a scale factor reflecting left-truncation, with the only substantial difference being that whereas here we have a series reducing to the term , in the earlier case we had a sum that only offers a similar simplification when is integer.
- (vi)
- The final case to consider is that where and . Herewhere the third equality is valid because , and

References
- Abadir, Karim M. 1999. An introduction to hypergeometric functions for economists. Econometric Reviews 18: 287–330. [Google Scholar] [CrossRef]
- Adamidis, Konstantinos. 1999. An EM algorithm for estimating negative binomial parameters. Australian & New Zealand Journal of Statistics 41: 213–21. [Google Scholar] [CrossRef]
- Al-Khasawneh, Mohanad F. 2010. Estimating the negative binomial dispersion parameter. Asian Journal of Mathematics & Statistics 3: 1–15. [Google Scholar] [CrossRef]
- Bardwell, George E., and Edwin L. Crow. 1964. A two-parameter family of hyper-Poisson distributions. Journal of the American Statistical Association 59: 133–41. [Google Scholar] [CrossRef]
- Boswell, M. T., and Ganapati P. Patil. 1970. Chance mechanisms generating the negative binomial distributions. In Random Counts in Models and Structures. Edited by G. P. Patil. London: University Press, vol. 1, chp. 1. pp. 3–22. [Google Scholar]
- Cameron, A. Colin, and Pravin K. Trivedi. 1986. Econometric models based on count data: Comparisons and applications of some estimators and tests. Journal of Applied Econometrics 1: 29–53. [Google Scholar] [CrossRef]
- Cameron, A. Colin, and Pravin K. Trivedi. 2013. Econometric Society Monographs No. In Regression Analysis of Count Data, 2nd ed. Econometric Society Monographs No. 53. Cambridge: Cambridge University Press. [Google Scholar]
- Consul, Prem C. 1989. Generalized Poisson Distribution: Properties and Applications. Statistics: Textbooks and Monographs 99. New York: Marcel Dekker Inc. [Google Scholar]
- Crow, Edwin L., and George E. Bardwell. 1965. Estimation of the parameters of the hyper-Poisson distributions. In Classical and Contagious Discrete Distributions. Proceedings of the International Symposium held at McGill University, Montreal, Canada, August 15–August 20, 1963. Edited by G. P. Patil. Calcutta: Statistical Publishing Society, Oxford: Pergamon Press, pp. 127–40. [Google Scholar]
- Dacey, Michael F. 1972. A family of discrete probability distributions defined by the generalized hypergeometric series. Sankhyā: The Indian Journal of Statistics, Series B 34: 243–50. [Google Scholar]
- Davidson, Russell, and James G. MacKinnon. 1987. Implicit alternatives and the local power of test statistics. Econometrica 55: 1305–29. [Google Scholar] [CrossRef]
- Dean, C. B. 1992. Testing for overdispersion in Poisson and binomial regression models. Journal of the American Statistical Association 87: 451–57. [Google Scholar] [CrossRef]
- Dean, C. B., and J. F. Lawless. 1989. Tests for detecting overdispersion in Poisson regression models. Journal of the American Statistical Association 84: 467–72. [Google Scholar] [CrossRef]
- Fang, Yue. 2003. GMM tests for the Katz family of distributions. Journal of Statistical Planning and Inference 110: 55–73. [Google Scholar] [CrossRef]
- Frome, Edward L., Michael H. Kutner, and John J. Beauchamp. 1973. Regression analysis of Poisson-distributed data. Journal of the American Statistical Association 68: 935–40. [Google Scholar] [CrossRef]
- Gart, John J. 1964. The analysis of Poisson regression with an application in virology. Biometrika 51: 517–21. [Google Scholar] [CrossRef]
- Ghahfarokhi, Mohammad Ali Baradaran, Hosseiyn Iravani, and M. R. Sepehri. 2008. Application of Katz family of distributions for detecting and testing overdispersion in Poisson regression models. World Academy of Science, Engineering and Technology 42: 514–19. [Google Scholar]
- Gilbert, Christopher L. 1979. Econometric models for discrete economic processes. Paper presented at Econometric Society European Meeting, Athens, Greece, September 3. [Google Scholar]
- Gilbert, Christopher L. 1982. Economic models for discrete (integer valued) economic processes. In Selected Papers on Contemporary Econometric Problems. Edited by E. G. Charatsis. Athens: Athens School of Economics and Business Science, pp. 255–83. [Google Scholar]
- Greene, William H. 2007. Functional form and heterogeneity in models for count data. Foundations and Trends ® in Econometrics 1: 113–218. [Google Scholar] [CrossRef]
- Greene, William H. 2008. Functional forms for the negative binomial model for count data. Economics Letters 99: 585–90. [Google Scholar] [CrossRef]
- Greenwood, M., and G. U. Yule. 1920. An inquiry into the nature of frequency distributions representative of multiple happenings with particular reference to the occurrence of multiple attacks or of repeated accidents. The Journal of the Royal Statistical Society, Series A 83: 255–79. [Google Scholar] [CrossRef]
- Gurland, John. 2006. Katz system of distributions. In Encyclopedia of Statistical Sciences. Edited by S. Kotz, N. Balakrishnan, C. B. Read and B. Vidakovic. New York: John Wiley & Sons, Inc., vol. 6, pp. 3824–25. [Google Scholar] [CrossRef]
- Haight, Frank A. 1967. Handbook of the Poisson Distribution. New York: John Wiley & Sons, Inc. [Google Scholar]
- Hausman, Jerry, Bronwyn H. Hall, and Zvi Griliches. 1984. Econometric models for count data with an application to the patents-r & d relationship. Econometrica 52: 909–38. [Google Scholar]
- Hellinger, Ernst. 1909. Neue begründung der theorie quadratischer formen von unendlichvielen veänderlichen. Journal für die reine und angewandte Mathematik 136: 210–71. [Google Scholar] [CrossRef]
- Hess, Klaus Th, Anett Liewald, and Klaus D. Schmidt. 2002. An extension of Panjer’s recursion. ASTIN Bulletin 32: 283–97. [Google Scholar] [CrossRef]
- Hilbe, Joseph M. 2011. Negative Binomial Regression, 2nd ed. Cambridge: Cambridge University Press. [Google Scholar]
- Hilbe, Joseph M. 2014. Modeling Count Data. New York: Cambridge University Press. [Google Scholar]
- Joe, Harry, and Rong Zhu. 2005. Generalized Poisson distribution: The property of mixture of Poisson and comparison with negative binomial distribution. Biometrical Journal 47: 219–29. [Google Scholar] [CrossRef]
- Johnson, Norman L., and Samuel Kotz. 1969. Discrete Distributions. New York: John Wiley & Sons, Inc. [Google Scholar]
- Johnson, Norman L., Samuel Kotz, and Adrienne W. Kemp. 1993. Univariate Discrete Distributions, 2nd ed. New York: John Wiley & Sons. [Google Scholar]
- Jorgenson, Dale W. 1961. Multiple regression analysis of a Poisson process. Journal of the American Statistical Association 56: 235–45. [Google Scholar] [CrossRef]
- Katz, Leo. 1945. Characteristics of Frequency Functions Defined by First Order Difference Equations. Ph. D. thesis, University of Michigan, Ann Arbor, MI, USA. [Google Scholar]
- Katz, Leo. 1946. On the class of functions defined by the difference equation (x + 1)f(x + 1) = (a + bx)f(x) (Abstract). Annals of Mathematical Statistics 17: 501. [Google Scholar]
- Katz, Leo. 1948. Frequency functions defined by the Pearson difference equation (Abstract). Annals of Mathematical Statistics 19: 120. [Google Scholar]
- Katz, Leo. 1965. Unified treatment of a broad class of discrete distributions. In Classical and Contagious Discrete Distributions. Proceedings of the International Symposium held at McGill University, Montreal, Canada, August 15–August 20, 1963. Edited by G. P. Patil. Calcutta: Statistical Publishing Society, Oxford: Pergamon Press, pp. 175–82. [Google Scholar]
- Kemp, Adrienne W. 1968. A wide class of discrete distributions and the associated differential equations. Sankhyā: The Indian Journal of Statistics, Series A (1961–2002) 30: 401–10. [Google Scholar]
- King, Gary. 1989. Variance specification in event count models: From restrictive assumptions to a generalized estimator. American Journal of Political Science 33: 762–84. [Google Scholar] [CrossRef]
- King, Maxwell L. 1987. Towards a theory of point optimal testing. Econometric Reviews 6: 169–218. [Google Scholar] [CrossRef]
- King, Maxwell L., and Sivagowry Sriananthakumar. 2015. Point optimal testing: A survey of the post 1987 literature. Model Assisted Statistics and Applications 10: 179–96. [Google Scholar] [CrossRef]
- Lawless, Jerald F. 1987a. Negative binomial and mixed Poisson regression. The Canadian Journal of Statistics 15: 209–25. [Google Scholar] [CrossRef]
- Lawless, J. F. 1987b. Regression methods for Poisson process data. Journal of the American Statistical Association 82: 808–15. [Google Scholar] [CrossRef]
- Lee, Lung-Fei. 1986. Specification test for Poisson regression models. International Economic Review 27: 689–706. [Google Scholar] [CrossRef]
- McCullagh, Peter, and John A. Nelder. 1989. Monographs On Statistics and Applied Probability 37. In Generalized Linear Models, 2nd ed. London: Chapman & Hall\CRC. [Google Scholar] [CrossRef]
- Miller, David W. 1998. Fitting Frequency Distributions Philosophy and Practice. Part 1: Discrete Distributions, 2nd ed. Self-published. [Google Scholar]
- Nelder, John A., and Robert W. M. Wedderburn. 1972. Generalized linear models. Journal of the Royal Statistical Society. Series A (General) 135: 370–84. [Google Scholar] [CrossRef]
- Ord, J. Keith. 1967a. On a system of discrete distributions. Biometrika 54: 649–56. [Google Scholar] [CrossRef]
- Ord, J. Keith. 1967b. On Families of Discrete Distributions. Ph. D. thesis, University of London, London, UK. [Google Scholar]
- Ord, J. Keith. 1972. Families of Frequency Distributions. London: Griffin. [Google Scholar]
- Panjer, Harry H. 1981. Recursive evaluation of a family of compound distributions. ASTIN Bulletin 12: 22–26. [Google Scholar] [CrossRef]
- Pearson, Karl. 1894. Contributions to the mathematical theory of evolution. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 185: 71–110 (+ 5 plates). [Google Scholar] [CrossRef]
- Pearson, Karl. 1895. Contributions to the mathematical theory of evolution. — II. Skew variation in homogeneous material. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 186: 343–414. [Google Scholar] [CrossRef]
- Pestana, Dinis D., and Sílvio F. Velosa. 2004. Extensions of Katz-Panjer families of discrete distributions. REVSTAT Statisical Journal 2: 145–62. [Google Scholar]
- Qu, Yinsheng, G. J. Beck, and G. W. Williams. 1990. Polya-Eggenberger distribution: Parameter estimation and hypothesis tests. Biometrical Journal 32: 229–42. [Google Scholar] [CrossRef]
- Raschke, Christian, and William H. Greene. 2010. Corrigendum to ”functional forms for the negative binomial model for count data”. Economics Letters 107: 313. [Google Scholar] [CrossRef]
- Slater, Lucy J. 1966. Generalized Hypergeometric Functions. Cambridge: Cambridge University Press. [Google Scholar]
- Staff, P. J. 1964. The displaced Poisson distribution. Australian Journal of Statistics 6: 12–20. [Google Scholar] [CrossRef]
- Staff, P. J. 1967. The displaced Poisson distribution. Region B. Journal of the American Statistical Association 62: 643–54. [Google Scholar]
- Sundt, Bjørn, and William S. Jewell. 1981. Further results on recursive evaluation of compound distributions. ASTIN Bulletin 12: 27–39. [Google Scholar] [CrossRef]
- Weisstein, Eric W. 2019. Gauss’s Test. From MathWorld — A Wolfram Web Resource. Available online: http://mathworld.wolfram.com/GausssTest.html (accessed on 21 December 2019).
- Willmot, Gordon. 1988. Sundt and Jewell’s family of discrete distributions. ASTIN Bulletin 18: 17–29. [Google Scholar] [CrossRef]
- Winkelmann, Rainer. 2008. Econometric Analysis of Count Data, 5th ed. Berlin: Springer. [Google Scholar] [CrossRef]
- Yang, Zhao, James W. Hardin, Cheryl L. Addy, and Quang H. Vuong. 2007. Testing approaches for overdispersion in Poisson regression versus the generalized Poisson model. Biometrical Journal 49: 565–84. [Google Scholar] [CrossRef] [PubMed]
- Yang, Zhao, James W. Hardin, and Cheryl L. Addy. 2009. A score test for overdispersion in Poisson regression based on the generalized Poisson-2 model. Journal of Statistical Planning and Inference 139: 1514–21. [Google Scholar] [CrossRef]
| 1. | |
| 2. | This family of distributions, and extensions to it, have proved important in the actuarial modelling of claims; see, for example, Hess et al. (2002); Panjer (1981); Sundt and Jewell (1981); Willmot (1988), and Pestana and Velosa (2004). Johnson et al. (1993, chp. 2) provides an extensive discussion of both the Katz family and various other, often related, families of discrete distributions. Although, in respect of the Katz family of distributions alone, the treatment in Johnson and Kotz (1969, chp. 2.4) is more complete; see also Gurland (2006) for a more recent treatment. |
| 3. | The one caveat to this observation is that the use of higher order moments may provide some power against models which share low order moments, thereby creating a class of implicit null hypotheses (Davidson and MacKinnon 1987). |
| 4. | Numerous extensions soon followed; see, for example, Bardwell and Crow (1964); Crow and Bardwell (1965); Ord (1967a, 1967b); Staff (1964, 1967) and Kemp (1968). Here we only briefly sketch some key ideas. For a more complete treatment of such families of distributions see, for example, any of Johnson et al. (1993, chp. 2.3), Ord (1972, chp. 5), or Dacey (1972). |
| 5. | Observe that the Pochhammer symbol , where y is a non-negative integer. Note that r can be negative. If r is a negative integer then for all . If r is a positive integer then . |
| 6. | When is integer the resulting pmfs are sometimes referred to as those of Pascal distributions, with the term negative binomial reserved for the more general case of not necessarily integer. |
| 7. | Similarly, the Poisson approximation to the Binomial reduces to for fixed , which is also a more intuitive statement of how parameters must evolve for the approximation to work than is typically encountered. |
| 8. | We shall persist with the abuse of notation inherent in expressions like rather than, say, a more complete notation along the lines of , for the sake of the notational economy it affords. |
| 9. | |
| 10. | Common variants of this argument include: (i) Lee (1986), who specifies the gamma distribution in terms of the shape and scale (or inverse rate) () parameters, that is, , and (ii) Cameron and Trivedi (1986), who use the so-called index form of the gamma distribution, which is specified in terms of the shape and mean () parameters, that is, . Cameron and Trivedi (1986) call the shape parameter () the index or precision parameter. |
| 11. | Moments for the gamma distribution specifications given in Footnote 10 follow immediately on making the appropriate substitution for . |
| 12. | Other values of k yield the Negbin P, or NBP, model (Greene 2008). |
| 13. | Strictly, it is not a generalized linear model as it stands but, conditioning on one of the parameters allows it to be treated so. This parameter can then be estimated conditional on the remaining parameters, which yields a two-step iterative estimation procedure. See, for example, either Hilbe (2011) or Hilbe (2014) for a discussion of the steps involved. |
| 14. | This latter model, of course, corresponds to the Negbin II model of Cameron and Trivedi (1986), and so provides a somewhat stronger theoretical basis for that model, which may explain some of its popularity in the literature. |
| 15. | Specifically, Greene (2008) discusses the broader class of models obtained when k is allowed to take values other than 0 or 1 in (14). He dubs this broad model the NBP model, seemingly because his notation uses p rather than the k used by Cameron and Trivedi (1986) (and here). |
| 16. | Alternatively, using similar averaging arguments to those seen previously for the NBRM, if we average with respect to , where and , then we obtain a more common form of the negative binomial pmf.
Note that the mean and variance of this distribution are given by (Appendix A.2.2). In contrast with the developments of (11), there is nothing in this model that requires that both the parameters of the mixing gamma distribution vary with the index i. Nor need they be linked in any restrictive way. Specifically, if we were to follow the developments of Greene (2008) who equates the parameters of the mixing distribution, we find that
|
| 17. | We note that Yang et al. (2007) and Yang et al. (2009) pursue a similar exercise against variants of the generalized Poisson distribution, see the discussions in Consul (1989) and Joe and Zhu (2005), although we shall not pursue these models further. |
| 18. | Strictly, Katz (1965) adopted an approach more in keeping with a method of moments test. Specifically, he looked at the difference between estimators for the mean and variance, which should be equal under the null and then scaled this difference appropriately to obtain a distribution under the null. In any event, the statistic so obtained is the same as the one proposed by Lee (1986) that we consider here. |
| 19. | Lee (1986) proposed other tests than the one considered here, although he did not compare them numerically The results recorded in Miller (1998) suggests that those involving third order moments may have better power properties. For now we are primarily concerned with proof of concept and do not explore these other tests in light of the simplicity of (17). |
| 20. | We also considered an alternative test based on the t-statistic in the regression of on a constant but there was little difference in performance. These tests correspond to the Negbin I and II cases above. |
| 21. | See, for example, https://en.wikipedia.org/wiki/Hellinger_distance. |
| 22. | In their extensions to this class of distributions, Panjer (1981); Sundt and Jewell (1981) and Willmot (1988) adopt a slightly different parameterization, specifically , . Equivalence with (A1) is seemingly established on setting and , although there are differences in the support of the resulting variables. In particular, is specifically excluded from this definition and hence many of the probability distributions claimed to satisfy the recursion in this form are not completely defined by it. |
| 23. | |
| 24. | In essence, this is the same as adopting the convention that any negative probabilities are set to zero. It might be argued that this is at odds with Katz’s original assumptions and should be excluded. Our justification for the inclusion in our analysis of these distributions where is non-integer, is that Katz himself included them.
|
| 25. | |
| 26. | |
| 27. | The condition integer obviously requires . |
| 28. | Note that Sundt and Jewell (1981, fig. 1)) provide a similar diagram although, as noted by Willmot (1988), they miss the possibility of . |

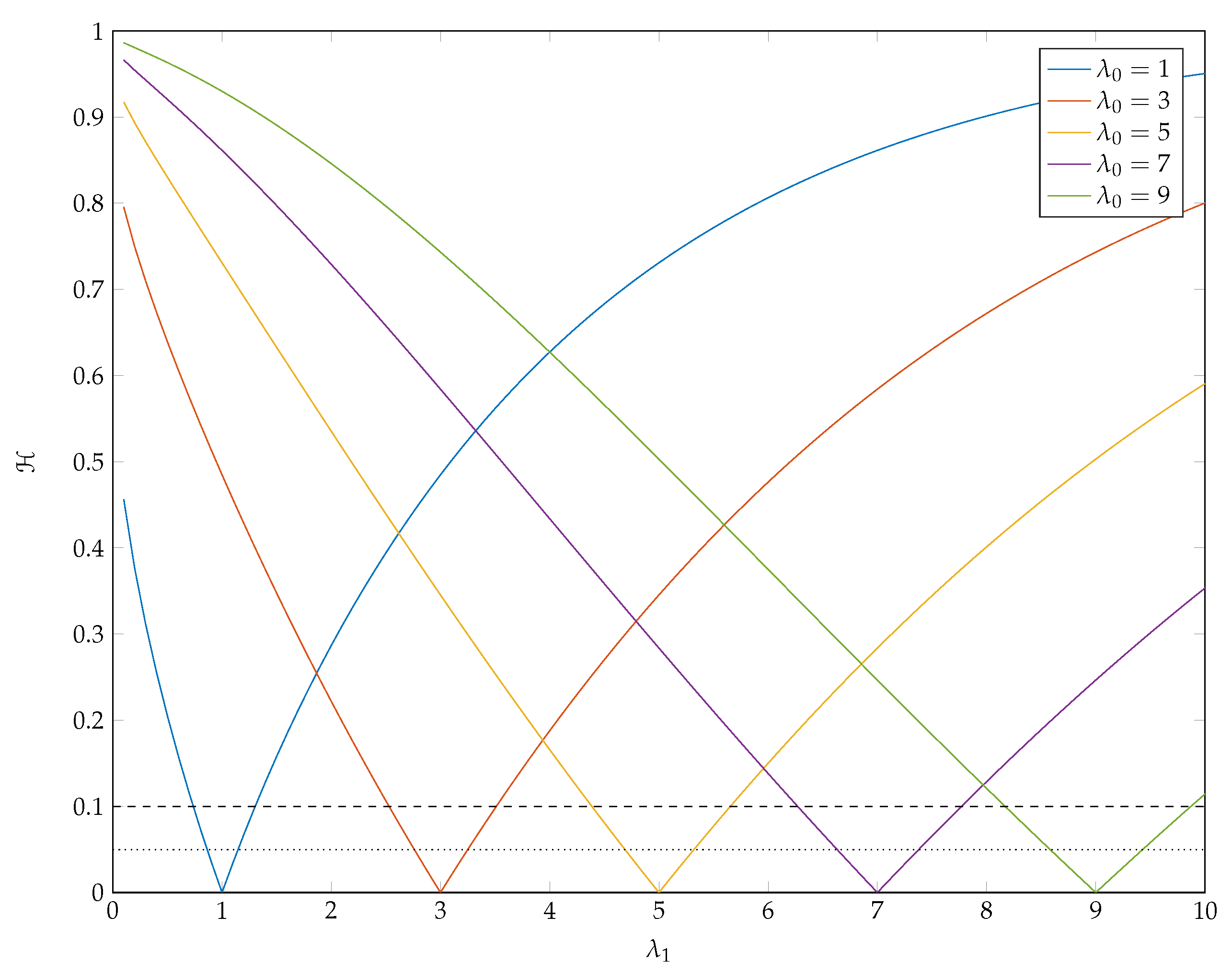
| ∖ | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 0.02 | 0.0348 | 0.0493 | 0.1261 | 0.1556 | 0.0147 |
| 0.04 | 0.0019 | 0.0121 | 0.0131 | 0.0250 | 0.0148 |
| 0.06 | 0.0032 | 0.0014 | 0.0115 | 0.0109 | 0.0136 |
| 0.08 | 0.0008 | 0.0033 | 0.0018 | 0.0061 | 0.0140 |
| 0.1 | 0.0027 | 0.0006 | 0.0022 | 0.0057 | 0.0072 |
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 0.02 | 0.0016 | 0.0008 | 0.0005 | 0.0004 | 0.0003 |
| 0.04 | 0.0064 | 0.0032 | 0.0021 | 0.0016 | 0.0013 |
| 0.06 | 0.0143 | 0.0072 | 0.0048 | 0.0036 | 0.0029 |
| 0.08 | 0.0252 | 0.0127 | 0.0085 | 0.0064 | 0.0051 |
| 0.1 | 0.0391 | 0.0198 | 0.0133 | 0.0100 | 0.0080 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
McCabe, B.P.M.; Skeels, C.L. Distributions You Can Count On …But What’s the Point? Econometrics 2020, 8, 9. https://doi.org/10.3390/econometrics8010009
McCabe BPM, Skeels CL. Distributions You Can Count On …But What’s the Point? Econometrics. 2020; 8(1):9. https://doi.org/10.3390/econometrics8010009
Chicago/Turabian StyleMcCabe, Brendan P. M., and Christopher L. Skeels. 2020. "Distributions You Can Count On …But What’s the Point?" Econometrics 8, no. 1: 9. https://doi.org/10.3390/econometrics8010009
APA StyleMcCabe, B. P. M., & Skeels, C. L. (2020). Distributions You Can Count On …But What’s the Point? Econometrics, 8(1), 9. https://doi.org/10.3390/econometrics8010009





