Abstract
The Poisson regression model remains an important tool in the econometric analysis of count data. In a pioneering contribution to the econometric analysis of such models, Lung-Fei Lee presented a specification test for a Poisson model against a broad class of discrete distributions sometimes called the Katz family. Two members of this alternative class are the binomial and negative binomial distributions, which are commonly used with count data to allow for under- and over-dispersion, respectively. In this paper we explore the structure of other distributions within the class and their suitability as alternatives to the Poisson model. Potential difficulties with the Katz likelihood leads us to investigate a class of point optimal tests of the Poisson assumption against the alternative of over-dispersion in both the regression and intercept only cases. In a simulation study, we compare score tests of ‘Poisson-ness’ with various point optimal tests, based on the Katz family, and conclude that it is possible to choose a point optimal test which is better in the intercept only case, although the nuisance parameters arising in the regression case are problematic. One possible cause is poor choice of the point at which to optimize. Consequently, we explore the use of Hellinger distance to aid this choice. Ultimately we conclude that score tests remain the most practical approach to testing for over-dispersion in this context.
Keywords:
Katz family of distributions; binomial distribution; negative binomial distribution; point optimal test; regression; score test; Hellinger distance JEL Classification:
C12; C25; C46
1. Introduction
The well-known Pearson family of continuous distributions, originally explored by Pearson (1895), is comprised of any solution to a particular differential equation. In his PhD thesis, Katz (1945) explored a family of discrete distributions that are solutions to a difference equation analogous to the Pearson differential equation.1 The Pearson family is a collection of four-parameter distributions and specializations thereof. Katz (1965, p. 175) observes that certain specializations ‘produce simpler and more manageable classes’ and restricts attention to a set of one- and two-parameter distributions. In particular, his restrictions result in a family of distributions that nest the two-parameter binomial and negative binomial (or Pascal) distributions, together with the one-parameter Poisson distribution.2 A defining characteristic of these distributions is that they arise when certain parameters, or parameter ratios, take integer values and so represent a set of measure zero in respect of the set of family members, which are defined in terms of real-valued parameters. The Katz family of distributions has proved important in the analysis of count data. It provides a framework within which practitioners can extend simple Poisson models to models that allow for individual heterogeneity, using the Poisson regression model (PRM). The PRM can, in turn, be extended to models that allow for either over-dispersion, using the negative binomial regression model (NBRM), or under-dispersion, using the binomial regression model. We shall, for the most part, defer consideration of under-dispersion to another time.
The problems of modelling and testing for over-dispersion have proved important in the count data literature. Essentially concurrently, papers by Cameron and Trivedi (1986); Lee (1986) and Lawless (1987a, 1987b) made substantial contributions to the literature on inference in the PRM, the NBRM, and testing for over-dispersion, with both Cameron and Trivedi (1986) and Lee (1986), in particular, couching substantial parts of their analysis within the context of the Katz family of distributions. This class of distributions is interesting because the binomial and negative binomial distributions are alternative specifications to the Poisson that allow under- and over-dispersion, respectively. Subsequent contributions to this literature include Dean (1992); Dean and Lawless (1989); Qu et al. (1990) and Fang (2003). Collectively they have explored likelihood ratio (LR), Lagrange multiplier (LM), and Wald tests, together with tests based on generalised method of moments (GMM) estimators, for over-dispersion in the PRM. Fang (2003) concludes that his preferred GMM test is that based on the fewest over-identifying assumptions offering essentially the same power as tests based on more over-identifying restrictions but having the greatest ease of calculation.3 Interestingly, this preferred test is that originally proposed by Katz (1965), on an ad hoc basis.
In this paper, we investigate a new family of tests for over-dispersion in the PRM by exploring point optimal tests where the alternative hypothesis lies in the Katz family of distributions. An analysis of the Katz likelihood reveals that maximum likelihood estimation may be problematic in the over-dispersed case, suggesting that the use of point optimal tests may have value. For overviews of the use of point optimal tests in econometrics see King (1987) and King and Sriananthakumar (2015). To the best of our knowledge they have not previously been used in the context of testing for over-dispersion.
This paper can be thought of as being comprised of three main parts. The first part provides a very brief description of the family of distributions introduced by Katz (1965), the second explores the role that these distributions can play in extending the PRM to allow for over-dispersion and, finally, we introduce a new class of point-optimal tests for over-dispersion. Specifically, in Section 2 we explore the Katz family of distributions, although most of the analysis is relegated to the Appendix A while Section 3 explores the PRM and NBRM. In particular, we highlight that the typical treatments of the NBRM really have little to do with what might be thought of as the canonical negative binomial distribution. Section 4 then focuses on the problem of testing for over-dispersion and the structure of the Katz likelihood. It is here that we introduce our family of point optimal tests and explore their small sample characteristics relative to some existing tests via a simulation study. We find that it is possible to choose a point optimal test which is better in the intercept only case, although the regression case proves problematic. One possible source of weakness in our point optimal tests is the choice of ‘point’ at which to optimize. In Section 5 we explore the use of Hellinger distance as a device to assist in choice of point. Although exact calculation of the Hellinger distance in this context is not tractable, it is straight-forward to obtain bounds on the distance. Using the upper bound, we find that the implied optimal points are extremely close to zero, implying that use of the score test is close to the optimal strategy in this context and so our advice to practitioners is to continue to use score tests to test for over-dispersion in this context. Section 6 concludes.
2. The Katz Family of Distributions
Among his many and varied interests, Karl Pearson was concerned with the problem of modelling (possibly) asymmetric empirical distributions. To this end, he developed a four-parameter family of skewed continuous distributions as solutions to a particular differential equation (Pearson 1895). The idea being that the distributions might be fitted to any data set using the method of moments approach that he had developed earlier (Pearson 1894). Perhaps surprisingly, the motivation for the choice of differential equation came from a difference equation that could be used to generate the hypergeometric distribution (Pearson 1895, pp.360–361); that is, from a discrete distribution. If we let denote the probability that the discrete random variable Y takes a value , where denotes the support of the distribution of Y, then the form of this difference equation was
with a, , , and denoting the various parameters of the distribution. We note that this expression is of the form
where P and Q are polynomials in y, and remark in passing that the sequence of probabilities so-defined are hypergeometric in that the ratio of adjacent terms in the sequence can be expressed as a ratio of polynomials in the index y.
Pearson did not pursue a discrete analogue to his family of distributions. Indeed, apart from some incidental investigations along these lines, Katz (1945) provided the first detailed analysis of the family of distributions arising from (1) although, apart from some abstracts (Katz 1946, 1948), it was not until Katz (1965) that this material was published. In the event, Katz (1965) focussed on a two-parameter special case of (1),4 which he expressed in the form
with , where denotes the set of non-negative integers and subject to the usual axiomatic properties of probability:
As we demonstrate in the Appendix A, there are circumstances where both and may include values that are positive, negative, or zero.
Although Katz himself included zero in , subsequent literature has not always done so, choosing instead to focus on the difference equation (2), whilst still referring to the resulting distributions as members of the Katz family; see, for example, Sundt and Jewell (1981); Willmot (1988) and Miller (1998). We too shall proceed in this latter manner, focussing on the what we call left-truncated Katz distributions, that include the original definition of Katz (1965) as the special case of no left-truncation. We relegate the technical analysis of these distributions to the Appendix A, which also gathers a number of other properties of this family of distributions.
Two members of this family that will be of particular interest to us are the Poisson and negative binomial distributions, which are commonly encountered in the modelling of counts and the possibility of over-dispersion. The probability mass functions (pmfs) of these distributions are the form:
respectively.5 Evidently, when , is the pmf of the Poisson distribution. When , if is integer then yields a standard representation of the negative binomial pmf, where the probability of success in any given trial is . Even if is not integer, is still the pmf of a negative binomial distribution — see, for example, (9) — although the interpretation of differs between the two cases.6 We shall, hereafter, denote the Poisson distribution with parameter , , and the negative binomial with parameters and , .
Before moving on, let us consider the well-known Poisson approximation to the negative binomial. A common statement of this result is as provided remains fixed. That is, at the same rate as diverges. One advantage of the parameterization adopted in (5) is that the somewhat convoluted requirement on how the parameters evolve in the approximation readily reduces to for fixed .7
3. The Poisson, Negative Binomial, and Katz Regression Models
3.1. The Poisson Regression Model
The PRM extends the Poisson distribution to allow for individual heterogeneity. It has played an important role in the analysis of count data in both econometrics and statistics — early references include Gart (1964); Jorgenson (1961), and Haight (1967, chp. 5) — and is readily available in standard software such as MATLABmathsizesmall, Stata, and R. The use of the PRM in econometrics became increasingly widespread following the significant contributions of Gilbert (1979, 1982) and Hausman et al. (1984). Recent summaries can be found in Greene (2007); Winkelmann (2008) and Cameron and Trivedi (2013).
The PRM is obtained from the Poisson distribution by replacing the fixed parameter with a function, denoted say, of the k-vector of characteristics that can vary across individuals. Specifically, in the language of generalized linear models (GLIMs), we have the link function
with regression coefficients . The work of Nelder and Wedderburn (1972) and Frome et al. (1973) shows how iterated least squares methods can be used to obtain maximum likelihood estimates of ; see also McCullagh and Nelder (1989).
One shortcoming of the PRM is the implied equality of mean and variance that is characteristic of the Poisson distribution. Specifically, on replacing with in (Appendix A.2.2), we obtain8
This is at odds with the observation that variability typically exceeds location in real world data, a feature known as over-dispersion. A common response to concerns about over-dispersion has been to explore extensions to the Poisson model that allow for different means and variances. To the extent that the Poisson regression model can be nested in such generalizations, this approach provides a framework within which one might test for either over-dispersion or underdispersion, although we will not explore this latter case here.
The fundamental characteristic of the PRM is that it is a function of the linear index, , only through the ‘parameter’ , as per (7). In the next two sub-sections we will consider different extensions to this model, the first being the classical NBRM and the second being what we dub the Katz regression model (KRM). Both models extend the PRM by nesting it within a richer model with an additional ‘parameter’. An important distinction between the NBRM and the KRM is the role of . In the case of the NBRM, remains the conditional mean of the count , whereas this is not the case in the KRM. A second distinction between the models is that the additional ‘parameter’ is typically treated as being a function of the linear index in the NBRM whereas in our treatment of the KRM it is not, it is a genuine parameter, although it is easy to envisage extensions where that requirement is relaxed.
3.2. The Classical Negative Binomial Regression Model
There are numerous paths leading to what might reasonably be called a negative binomial regression model.9 This is due, at least in part, to the variety of ways in which one might generate a negative binomial distribution. For example, Boswell and Patil (1970) provide 15 different derivations and, of course, there is a variety of parameterizations of the negative binomial distribution that can also lead to differences. Below we explore a fairly commonly adopted approach and consider some of its implications.
Our starting point is the following observation, originally due to Greenwood and Yule (1920). Suppose that , where is a random variable whose distribution is gamma with shape () and rate () parameters, written , so that the corresponding density function is,10
with and .11 Then, we obtain an unconditional distribution for Y on averaging with respect to , so that
If one imposes the restriction , where denotes the set of positive integers (or the natural numbers), then this is simply a form of the negative binomial (Pascal) pmf, with , see (A5). Note that
the same as for the gamma distribution (8), and that
One posible path to a NBRM is to extend the analysis of Greenwood and Yule (1920) to allow for individual heterogeneity; we follow the treatment of Cameron and Trivedi (1986, p. 32). Specifically, we replace by , where
with a disturbance term reflecting unobservables. Cameron and Trivedi (1986) then assume that either , or ‘equivalently’ , have a gamma distribution, conditional on the regressors. Their analysis then proceeds under the latter assumption, which is completely analogous to the developments of Greenwood and Yule (1920). Specifically, letting yields
Moreover,
and
It is immediately obvious that, in the final analysis, the functional form of (10) is a complete irrelevance, with only the parameters of the mixing Gamma distribution of any importance and we have made no assumptions about them beyond allowing the possibility of varying at the individual level. From here, Cameron and Trivedi (1986) argue that a variety of models are available on defining
for and arbitrary constant k, so that
Special cases of importance are then the Negbin I model (obtained when ) and the Negbin II model (),12 of which the latter is probably the more popular in the literature. This model nests the PRM as a limiting case where from above, a testable proposition, which is equivalent to diverging to ∞ for all i.
The specification (10) becomes more relevant if, instead, we assume that rather than . Define , so that . Thus, conditional on , is a scaled Gamma random variate which is, itself, a Gamma random variate. From the properties of the Gamma distribution we have immediately that . Moreover, analogs of results (11)–(13) are immediately available in this case on replacing by . In short, the differing distributional assumptions are ‘equivalent’ in that the structure of the results is the same in both cases, however, it is only in this latter case that (10) has any relevance, through the presence of in the various expressions.
The attraction of the formulation (11)–(13) of Cameron and Trivedi (1986) is its close resemblance to a GLIM, which simplifies estimation.13 As noted above, the null of a PRM obtains as , however, results in a relatively odd PRM with a potentially unbounded mean, unless is diverging to infinity at the same rate as is . Moreover, there is a Davies-type problem relating to the separate identification of both and when the null is true. Greene (2008) camouflages this difference by imposing the restriction .14 He refers to this restriction as being mean preserving, by which is meant that when , , as would be the case in the PRM. We should note that, in order to generate the same class of models as do Cameron and Trivedi (1986), Greene (2008) also allows to be replaced by , as defined by (14), but this means that must be replaced by too.15 Of course, the restriction that reduces the two parameter mixing gamma distribution to a single parameter distribution with the loss of modelling flexibility that implies. However, without this restriction, the conditional mean of is other than .
3.3. The Katz Regression Model
The fundamental difference between the NBRM, as described in the above, and what we refer to as the Katz regression model (KRM) lies in the generation of the underlying distribution. Specifically, the Katz family of distributions is not generated via a mixing argument and so, in contrast to the NBRM, the probabilistic quantities of interest (pmfs and moments) are not functions of the parameters of the mixing distribution; see (11)–(13). In this sense, the parameterization of the Katz family is more natural than that of the NBRM. Directly analogously with the PRM, the KRM can be generated from (A6) simply by replacing by , as per (6), which is analogous to our earlier development of the PRM.16 Equally, one might explore models that see replaced by functions of regressors, say, although we will not. Note that the conditional mean and variance of this distribution are given by (Appendix A.2.2), with replaced by . Contrast this structure with that for the NBRM described above. There we saw that the conditional mean of the dependent variable was not varying with , being a function of the linear index alone. Similarly, by construction, the variance exceeded the mean of the dependent variable, but the reduction to a Poisson model requires the shape parameter of the mixing gamma distribution to be unbounded, which yields a degenerate distribution for given rate parameter .
It is clear that it is not necessarily desirable to preserve the mean, in Greene’s sense of equating and (Greene 2008), because, as increases, the mean for both the NBRM and the KRM should be decreasing relative to that of the PRM.
We note in passing that this is the model that underlies the generalized event count (GEC) model of King (1989); this model was also considered by Ghahfarokhi et al. (2008). That they obtained more complicated models than that proposed here, resulting in the models being less popular than the NBRM in practice, stems from the fact that they did not have (A6) as the pmf implied by (2), which in part is due to working with (2) rather than (A1).
4. Testing for Over-dispersion in Poisson Regression model
There is a vast literature addressing the problem of over-dispersion and how to test for it. We will not attempt to provide a comprehensive survey of this literature, focussing instead on a few key contributions, although it should be noted that most of the references cited so far will have some discussion of the problem. We shall break our discussion into two parts. First, we shall restrict attention to the case where the only regressor in the model is an intercept, so that is a constant. Then we will extend the analysis to allow for additional regressors. In each case, the null hypothesis will be that the data have been generated by the PRM. We investigate the performance of tests whose preferred alternative is, variously, that the data have come from one of the Negbin I, Negbin II, or Katz regression models.17
4.1. The Katz Likelihood
For any positive real number , with and , the Katz pmf is given by
and hence
where products of the form for . In textbook cases, where n is known, the first and last terms in (15) are functions of the data only and is sufficient by the factorization theorem. But in the current context, when n is not known, there is no reduction to a fixed dimensional sufficient statistic. Even if is known there is no sufficiency reduction; the ratio n is required. Only the entire sample (or the order statistics) are sufficient but even they are are not complete so that different parameter configurations may give rise to the same data. We may surmise this from the likelihood (15) since any combination of and that preserves n gives the same likelihood. Adopting the convention that when , the log likelihood is
where the second line follows by substituting for n and simplifying.
In fact, (nonlinear) maximum likelihood estimators for n do not exist when the sample variance is less than the mean, that is, (see Al-Khasawneh (2010) and the references therein). Note that, even when drawing from a negative binomial, which by definition is over-dispersed, many individual samples will exhibit under-dispersion. We can see the difficulty explicitly by looking at simple moment estimates for and , that is, solve (Appendix A.2.2) to get
Hence, problems arise when since then , which is illegtimate when investigating over-dispersion. Even if , convergence issues arise if the difference is not great. This suggests that test procedures that use maximum likelihood estimates, such as Wald or Likelihood Ratio tests, can be problematic and that there may be a role for point optimal approaches.
4.2. Point Optimal Tests
Point optimal tests have had a long and varied career in econometrics; see King (1987) and King and Sriananthakumar (2015) for an overview. These tests optimize power at a particular parameter value under the alternative, the idea being to have good power at a point where incorrectly accepting the null really matters. This is in contrast to, say, a score test that is locally best, in that it has the steepest power function local to the null hypothesis. Although not an undesireable property in any way, the practical difference between a null model and some other model local to the null is often, although not always, vanishingly small. So, optimizing the ability to distiguish between such null model and another local to it is not necessarily all that desireable a property. Moreover, there is implicit in such an approach the notion that the power function will be monotonically increasing, which ideally it should be, and that it will remain near the power envelope as the data generating process diverges from the null. In many cases this is indeed what happens, although we know that power functions are likely to cross, as otherwise the test would be uniformly most powerful, which is a very rare property indeed. The divergence between the power function of a score test and the power envelope is then something that requires exploration on a case by case basis and we will explore this below.
The log likelihood ratio of the alternative to the Poisson (P) null is written
Assuming that both distributions are fully specified (with ), the Neyman-Pearson Lemma states that the test of versus is given by . Hence assuming known, the so-called power envelope is determined by computing over a range of values of . A test is constructed by choosing a fixed to be a ‘representative’ value under the alternative distribution, giving . It is desirable that be chosen so that the power of the test is as close as possible to the power of the family of tests , . That is, ideally, is chosen so that the power function of the resulting test is as close to the power envelope as possible.
4.3. Score Test
A common alternative to likelihood ratio approaches, which does not require maximum likelihood estimation of the parameter of interest, is to construct optimal tests local to the null . The so-called eficient score tests, or simply score test, are derived by differentiating the log likelihood with respect to and then setting . Such score tests are easily found for the Katz family using (16); see, for example, Katz (1965) and Lee (1986). Specifically, the score test is
4.4. Simulation Experiments
4.4.1. The Unconditional Model
In this section we simulate the powers of the point optimal and score tests and compare them to the benchmark power envelope. First we give details for the power envelope and this is followed by a description of the operational tests. We present results for a sample size of throughout.
In Figure 1, Figure 2 and Figure 3 below, we consider a range of values for and and look at the relative performance of the and S tests and the power envelope. For each pair we generate samples from the Katz family, . This is efficiently accomplished using along with the defining recurrence and then sampling from the inverse cumulative distribution function. Setting , for some very small positive , effectively simulates from the Poisson null. The null critical values are computed by simulation to avoid asymptotic approximations. This means that the sizes of tests are accurate (up to simulation error) and hence that the power comparisons are meaningful in smaller sample sizes.
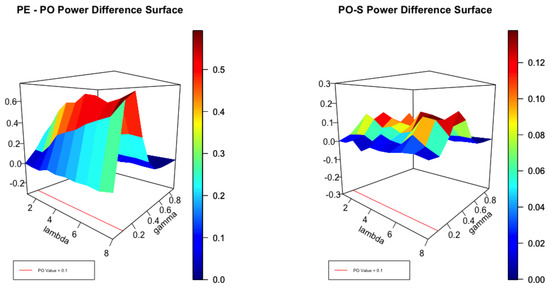
Figure 1.
Difference in Power of the Envelope and the PO test as well as the Difference between the PO and Score Tests at .
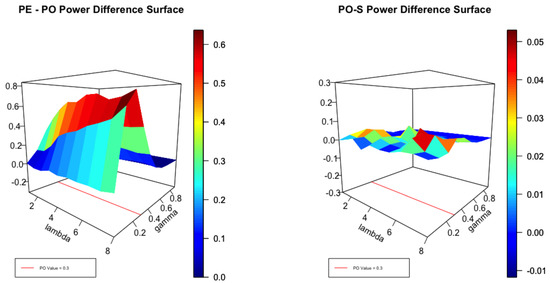
Figure 2.
Difference in Power of the Envelope and the PO test as well as the Difference between the PO and Score Tests at .
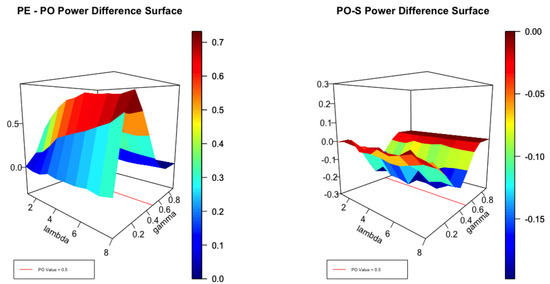
Figure 3.
Difference in Power of the Envelope and the PO test as well as the Difference between the PO and Score Tests at .
For the power envelope, we simulate from the null distribution, compute 10,000 values of and extract the quantile as a critical value, . The is the Katz family and we simulate replicates from the DGP and count the percentage of times the statistic, , exceeded the to calculate the power envelope.
The operational test estimates , and fixes at . To do this, we use simple moment based estimators, that is, compute , where and using the mean and variance of the data at hand. Should stray negative, we truncate and set . The test is computed as while the score test, using (17), is . The null is Poisson and we simulate from the null, computing and for each realization, to get ’s. We calculate the power by simulating from the DGP .
It is helpful to view Figure 1, Figure 2 and Figure 3 in the light of the cross sections displayed in Figure 4. It is clear that, for small values of , no test can be expected to perform well close to the null. Equally, for large values of , with high degrees of over-dispersion, all reasonable tests can be expected to be powerful. Thus, for small and large degrees of over-dispersion we expect to see little difference in the performance of the envelope and the test as the left panel of Figure 1 attests. For moderate values of , the power of the test can be significantly smaller than the envelope as the coloured scale suggests. In the left panel the difference in power between the and score tests is plotted for . The differences are not large but the test uniformly dominates as the scale indicates. Figure 2 plots the same surfaces for and the interesting feature is that both tests perform similarly but none dominates the other. In Figure 3, and the score test dominates by a small margin except where the corresponds to .
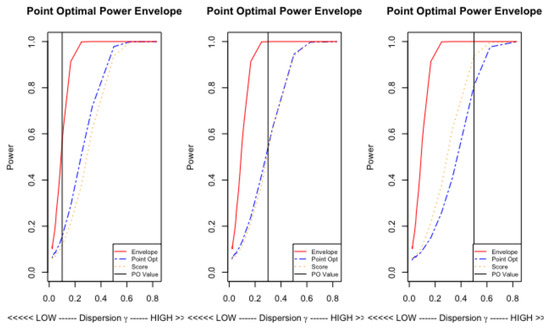
Figure 4.
Cross Section of the Power Envelope Surface and Power Surfaces of the Score and Point Optimal tests at .
Since the shapes of the surfaces are quite smooth over , we plot a cross-section at to look at absolute performance. There are three panels in Figure 4 each corresponding to a value of , , . The power envelope is shown in red, with those of the PO test in blue and the Score test in orange. Also shown (vertically) is the PO point .
The power envelope reaches unity at around . This corresponds to a degree of over-dispersion, in the distribution, of . For the tests to reach equivalent power requires with , roughly, and is required at . So, neither test can match the envelope unless the degree of over-dispersion is quite large. For less than the test performs better uniformly, at they perform equally well and for the score test is better. Thus, a choice of which is small will uniformly dominate.
4.4.2. The Katz Regression
In practice, the analysis of over-dispersion often takes place when covariates need to be taken into account. As explained in Section 3 there are many ways in which this may be approached. We work directly from the definition of the Katz family rather than mix over a kernel Poisson distribution. The log of the likelihood takes the form
with varying and fixed. This gives and .
The test, using , is based on the log likelihood ratio,
and the test needs to estimate the parameters and . Estimating may be problematic as trying to fit a regression when the data is Poisson can lead to identification/convergence problems, exacerbated by the fact that fitting these types of regressions requires nonlinear maximum likelihood estimation. We avoided this issue in the last sub-section by using Katz moment estimators. Here, we use a regression version of the same idea. First, estimate a Poisson regression (including a constant) which will return the mean estimate . Noting that we can write , where , we can set and hence to give the vector . To get we fit the Poisson without the constant term which returns the estimate , which gives , and hence .
As a comparator to the statistic, in the regression setting, we use the score test of Dean and Lawless (1989), which avoids the potential difficulties associated with maximum likelihood estimation. Thus, we estimate the Poisson regression (with a constant) to get the vector of predictors and, using , the test is computed as the t-statistic in the regression of on .20 Again critical values are computed by simulation. The null is generated as , with used to keep the means of the counts low. We used and the are kept fixed under replication. We generate simulated critical values, based on replications, for the tests and . To compute powers, the DGP is used, where and takes a selection of values in . As usual, . The results are presented in Figure 5.
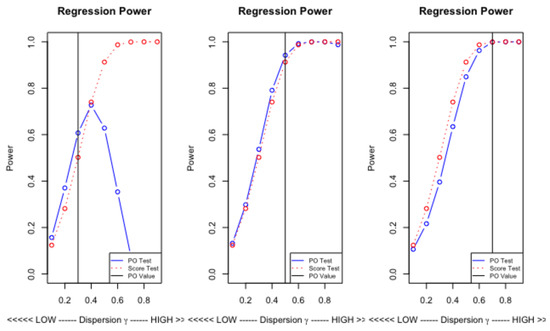
Figure 5.
Powers of the Regression Score and Point Optimal tests.
The test performs badly for very high degrees of over-dispersion when is less than approximately and is dominated by the score test for greater than . However, the choice does lead to superior performance albeit by not a great margin.
4.4.3. Summary
Our experimental results are mixed. In the unconditional model, the point optimal tests appeared to work best when was small, with their performance deteriorating relative to the score test as increased. In the regression model, the score test outperformed the point optimal tests suggesting that the null distribution of the score tests was more robust to the presence of nuisance parameters than was that of the point optimal tests, with none of the test statistics being pivotal. However, these rankings were also sensitive to the choice of point. This begs the question as to whether or not we are choosing the ‘point’ for the point optimal tests in a sensible way. It is to this question that we turn in the next section.
5. Hellinger Distance
The reasoning behind the use of point optimal tests is to put power where it is of greatest practical use. The immediate problem facing the use of point optimal tests is where to place the ‘point’. Sometimes the testing problem suggests a solution. Other times the choice is less clear and is often based an the outcome from a simulation study ‘run-off’, making the results somewhat ad hoc. The attraction of point optimal test in the context of testing for over-dispersion is that the parameter space of interest, namely that of , is bounded and so there is some hope of finding an appropriate point. One way of defining appropriate in this context is where the distribution under the alternative starts to depart from that under the null in some substantial way. The questions then reduces to one of how we might measure such a departure. In this section we explore the use of Hellinger distance for this purpose. We think that this is a novel use of such a distance measure and is of independent interest. We do not, however, assert that Hellinger distance is the only choice or even the best choice in this context, but it does yield some interesting results.
To begin, various definitions of Hellinger distance are available.21 Originally proposed in an integral form by Hellinger (1909), we will work with the following discrete variant:
Definition 1
(Hellinger Distance for Discrete Random Variables). The squared Hellinger distance between these two discrete distributions P and Q is
where and .
We note in passing that the Hellinger distance is bounded, . iff P assigns zero probability to anywhere that Q assigns positive probability and iff .
5.1. The Poisson Distribution
By way of example, to illustrate the basic idea and to help calibrate the procedure, suppose that we choose as our base case a Poisson distribution with parameter so that the implied standard deviation is . Writing , we are going to explore the behaviour of as we compare with for various . When comparing Poisson distributions, the squared Hellinger distance is readily shown to
Figure 6 provides some insight into the sensitivity of Poisson pmfs to changes in parameter values when the parameters are small and includes examples that are variously skewed to the right, (roughly) symmetric, and skewed to the left. Observe that, here we have used as the base case and that, as increases, it is by one standard deviation each time and so these changes are quite dramatic.
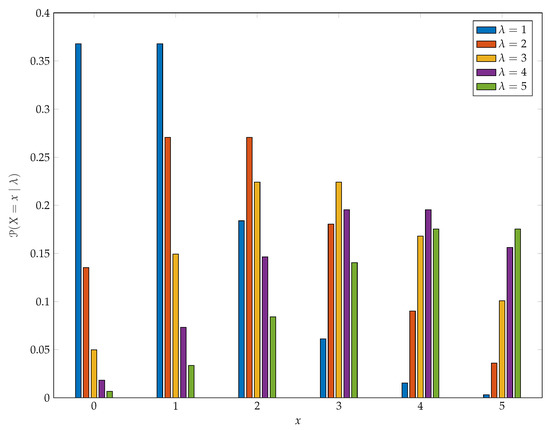
Figure 6.
Selected Poisson Probability Mass Functions.
In Figure 7 we present values for for various and . The dashed and dotted lines correspond to Hellinger distances of 0.1 and 0.05, respectively.
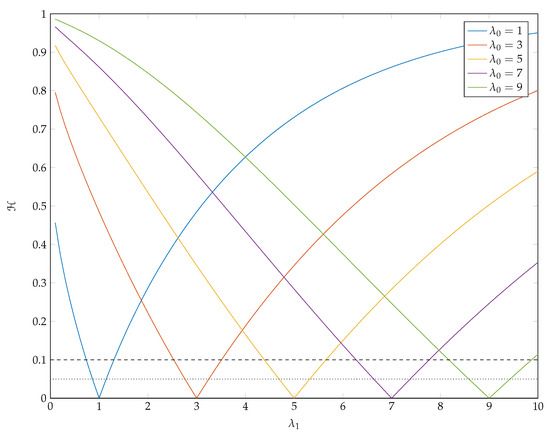
Figure 7.
Hellinger Distances ( Between and .
We observe that is asymmetric in for all considered, which reflects the skewed nature of Poisson distributions. Note that, as increases, so too does standard deviation of the base distribution. As this happens a given value of will admit great differences between and . For example, when a Hellinger distance of or greater is achieved for any . In contrast, when , for all , which is a much wider interval than the previous case. Given that we are seeking to construct point optimal tests that compete with locally best tests, these results suggest that we need to be looking at points for which the Hellinger distance is quite small.
5.2. The Katz Distribution
We will take the Poisson () as our base model. Moreover, as Poisson-ness, or otherwise, is completely determined by the value of , we will hold fixed across models. Here the support under both null (equi-dispersion) and alternative (over-dispersion) is and so
Although not amenable to direct solution we notice that
Therefore,
We can solve this non-linear equation for numerically for given and . Some results are reported in Table 1.

Table 1.
Values for Obtained From (21) For Given and (scaled by a factor of ).
We see that all values of are positive, albeit extremely to zero. Alternatively, from (20) we also have the result

Table 2.
Values for Obtained From (22) For Given and .
We see that is monotonically increasing in but monotonically decreasing in . That is, once becomes sufficiently large, even small departures of the hellinger distance from zero are consistent with .
All of the above said, however, the over-riding conclusion is that the optimal ‘points’ are going to be sufficiently close to zero that it is not clear that there is much benefit over just using the the score test, which is essentially point optimal at . The main reason for such a conclusion is our earlier results indicating that, in the regression context, the score test is much less subject to the influence of the regression coefficients, which are nuisance parameters in this testing problem.
6. Conclusions
At a fundamental level, this paper explores the use of point optimal tests in the problem of testing for over dispersion. Our basis of comparison is the score test of Lee (1986), which is the same as the earlier method of moments test proposed by Katz (1965). Our findings are somewhat disappointing and we are unable to recommend that practitioners change their current practices as the performance of the point optimal tests is, at best, mixed. It may be possible to improve the performance of the point optimal tests by a more refined analysis of (i) the problem of nuisance parameters and (ii) the construction of p-values, along the lines suggested by King and Sriananthakumar (2015). This we leave for further work.
Along the way, the paper has made two other contributions. First, in the Appendix A we have provided a reasonably exhaustive treatment of the family of distributions consistent with the difference equation of Katz (1965). To the best of our knowledge this treatment extends all known earlier results by allowing for arbitrary points of left truncation. This expands the class of distributions originally considered by Katz (1965), which can be characterized as including zero in the support of the count variable. The treatment is closest to that of Willmot (1988), although there are differences in the mode of analysis and he restricts attention to extensions where only zero is omitted from the support of the count variable. We note in passing that right truncation is a much easier problem to deal with as it neither expands nor contracts the members in the family, in the way that left-truncation does. Its only consequence is the introduction of a scale factor equal to , where R denotes the upper tail probability that has been truncated.
The other contribution that we have made is to introduce the use of Hellinger distance as a metric by which one might settle on the ‘points’ characterizing point optimal tests. This is novel and allows a more systematic treatment than the grid searches that have characterized such choices in the past.
Author Contributions
Both authors have contributed equally to all aspects of the preparation and writing of this paper. They have both read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. On Left-Truncated Katz Distributions
Certain properties of the family of distributions defined by (2)–(4) are available on inspection. In particular, the support of Y is, in certain circumstances, parameter dependent. Here we characterize those circumstances.
To begin, let us establish some notation. Our count variable is , where n may be either infinitely large or some finite integer and L is a non-negative integer integer. We will restrict because the case where yields a probability mass function degenerate at L, which is statistically uninteresting and shall, hereafter, be ignored. Next, write (2) as
This latter formulation has the advantage of being untroubled by the prospect of . It will also prove convenient to be able to express all probabilities in terms of , which we can do via back substitution in (A1). Thus, for all ,
Moving forward we shall break up our observations into three categories: (i) those relating to the support of the random variable and the parameter space of the associated distributions, (ii) statements of the probability mass functions belonging to the family, and (iii) certain properties of the various distributions. The results are ultimately the same as those of Willmot (1988) in the special case where , although our mode of analysis is different and we extend his results by allowing for arbitrary .22
Appendix A.1. Support and Parameter Spaces
From (A2), we see that the sequence of probabilities generated by the difference equation (A1) is governed by and by the terms , , as the ratio of factorials is a scale factor in the interval . Our subsequent analysis revolves around the behaviour of these quantities and the implications for of these behaviours. With the exception of [1], we shall hereafter assume that .
- [1]
- From (A1) we see that if for any then for all . In particular, if then for all . But this leads to violation of (4), that is, probabilities do not sum to unity, and so we exclude from further consideration. Equally, if , so that the pmf of Y is degenerate at L, which is a case that we have already excluded from further analysis. Hereafter, we assume that .
- [2]
- If and then we have a pmf degenerate at L unless , which will be assumed hereafter. In this case there is no implied restriction on the upper bound of , that is, . Of course, the concern when generating an infinite sequence of probabilities is to ensure that the associated series, , converges. This can be examined by considering the quantityand noting thatFrom the limit version of d’Alembert’s ratio test we see that the series converges because .
- [3]
- Similar in effect to the previous case, if then . Given , as assumed above, if and only if which will be assumed, hereafter, for all cases where .
- [4]
- Because , if and we see that for all and so here the support of the pmf of Y is unbounded from above and independent of the values taken by and . Again, we can establish convergence of the corresponding series. HereAppealing again to the limit version of d’Alembert’s ratio test we see that the series converges if , diverges if , but the test is inconclusive if . Expanding the denominator of in power series yieldsApplying Gauss’s test,23 we see that the series will converge absolutely if and only if but will otherwise diverge. Here we have assumed that and so . Hence, the series is divergent for .
- [5]
- In this case there is no value of y that satisfies and so cannot belong to . Moreover, this statement remains true even if . Consequently, in this case, the pmf of Y is degenerate at L, a situation that we have chosen to exclude from further consideration.
- [6]
- of different signIn this case we see that can change sign as y increases, unlike the situation of the previous two cases. Let n denote the smallest value of y such that . Then n is the largest value in . There are only two cases to consider here (having treated that of above): (i) , and (ii) .
- (a)
- If then the pmf of Y will be degenerate at L which, as explained above, is statistically uninteresting and a situation that we will assume away. That is, if then we will assume that . In particular, if then this requirement reduces to . As y increases, will approach zero from above. That value of y for which is first less than or equal to zero is the largest value of y in and shall be denoted by n, so that is well-defined but is not.24 That is, n is the smallest integer greater than or equal to . This is the definition of the so-called ceiling function, written . In summary, if then we see that the upper bound on the support of the pmf of Y is a function of the parameters and , with the space of subject to the constraint .
- (b)
- Here is an increasing function of y but the pmf of Y is non-degenerate at L if and only if . As we have already excluded from further consideration pmfs degenerate at L we here assume this to be the case. In particular, when we have a contradiction as we are assuming both , which is required when (see [3]), and ; we conclude that and can only arise when . As for all , will be unbounded from above provided that the series of probabilities so formed is convergent. Using the analysis outlined in [4], applying the ratio test we find convergence for all provided that . Moreover, if , Gauss’s test gives convergence provided that is strictly negative, that is, .
We summarize these findings in Table A1 and note in passing that, when , the only valid parameter configurations are those found in the row .

Table A1.
Parameter Configurations When .
Table A1.
Parameter Configurations When .
| n/a | n/a | |||
| n/a | n/a | n/a | ||
| n/a |
Appendix A.2. Probability Mass Functions and Their Properties
Having established the various restrictions on the parameter space and the support for the family of distributions generated by (A1), we now turn attention to the resulting pmfs and their properties. To begin, we will distinguish between two classes of distributions: (i) , the class originally explored by Katz (1965), and (ii) , which has subsequently been explored by others. In order to explore these pmfs, our first task is to evaluate which forms part of the normalizing constant in (A2).
Appendix A.2.1. L = 0
In the previous section we established that, when , we require . Moreover, we also required that , with unbounded from above if but that an upper bound of exists if . Summing the right-most side of (A2) over all and adding yields
where we have adopted the convention of
Recall that if then , otherwise . Thus, , where
where we have used the Pochhammer symbol to denote the rising factorial function
a polynomial of order n (n a non-negative integer) in a, with (including ), and where denotes the usual Gamma function.25 Note that the argument of the Pochhammer symbol can be negative and is in certain cases considered below. In the event that ‘a’ is a negative integer, the Pochhammer symbol will equal zero for all . The resulting pmfs are
There are two simplifications that arise when is integer. First, if one restricts attention to the case where is integer, r say, and then
On setting , the pmf reduces to
This form of the negative binomial distribution, also known as the Pascal distribution, admits an inverse sampling interpretation is available. Specifically, Y can be interpreted as a count of the number of failures in a sequence of independent Bernoulli trials, each with probability of success , before the rth success is observed. Interestingly, we note that
and so the negative binomial representation in (A4) can be thought of as valid for all cases , recognizing that the case must be thought of as a limit. Finally, when is non-integer, the pmf in (A4) still gives the probability that given the parameters and , it just no longer admits the inverse sampling interpretation usually ascribed to a count variable with a negative binomial distribution.
Second, if and is a negative integer, so that , then
so that
and
On setting , so that , we can recognize the resulting pmf
as that of a binomial random variable where, again, denotes the success of a single Bernoulli trial and gives the probability of y successes in a sequence of n independent Bernoulli trials. That is, . These findings are summarized in Figure A1.
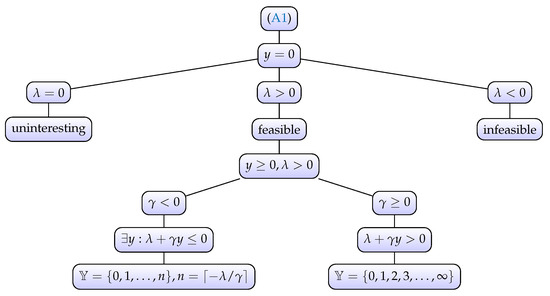
Figure A1.
Restrictions on Parameters and Support Implied by (A1).
The Poisson, Pascal, and Binomial distributions, being those cases where is integer, were the cases originally explored in Katz (1965, fig. 1). Figure A2, which is a variant of Katz (1965), provides a graphical representation of these distributions.
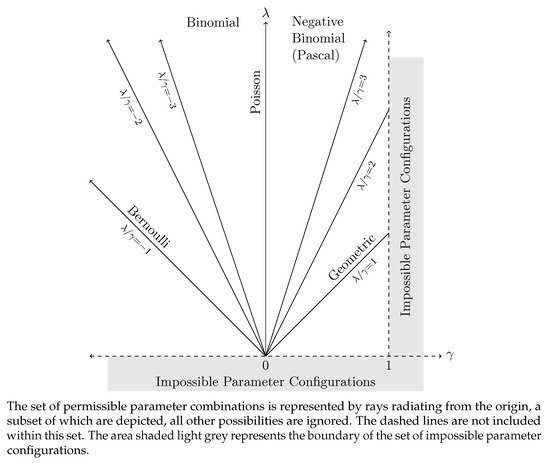
Figure A2.
Parameter Space for the Katz Family in Special Cases.
Kemp (1968) observed that the family of distributions depicted in Figure A2 could all be expressed in terms of hypergeometric functions on noting that
and that, specifically,
so that
subject to the requirement that is integer if . This characterization of the probability function makes two things clear. First, the restriction that follows immediately from the standard convergence criteria for hypergeometric functions; see, inter alios, Abadir (1999, p. 292). Second, it is clear that, for , the restriction that be integer is completely unnecessary as the probability function is perfectly well defined for non-integer values of this ratio.26
It is straight-forward to show that the probability generating function for this family of distributions is of the form
In the special cases where either or where is a positive integer, reduces to
Moments for all members of the family can be calculated directly from (A1), without reference to the exact form of the pmf. A slight re-arrangement of (A1) allows us to sum over , the support of Y, thus
The left-hand side of (A7) can be written
The right-hand side becomes
Solving for yields
and similar arguments lead to
From Katz (1965, p. 176) we have the following inverse parametric relationships
which yields a potentially useful alternative parameterization of the distributions in terms of mean and variance rather than the somewhat more nebulous and . Observe that if then , a situation termed equi-dispersion. If , then , which is called over-dispersion and, if then , which is called under-dispersion. Importantly, if we consider the ratio then we see that under-dispersion, equi-dispersion, and over-dispersion are determined by the value of alone, and so is a nuisance parameter for the testing problems of interest in this paper. Finally, observe that is an increasing function of . Specifically,
Appendix A.2.2. L > 0
This case differs from that of in two key ways: (i) there are three more cases to consider, all related to and, obviously, (ii) zero is no longer in . To begin the analysis, let us first determine by summing over (A2). Noting that n may be infinite (depending on parameter configuration) and adopting the convention (A3), we see that
so that
The exact definition of , as noted above, is parameter dependent. Hence,
- (i)
- if then
- (ii)
- if then, on noting that ,
- (iii)
- if then
These first three results correspond to those examined in the case and they have the same simplifications for integer as mentioned in that case.27 The structure of the result is clear, with the normalizing constant scaled by a factor of , so that the resulting probabilities are simply left-truncated versions of those encountered previously. In particular, we see that, for and ,
Before moving it is worth reminding ourselves of cases that we need not consider further. If and then the only case leading to valid, non-degenerate distributions are those where . The next three cases have no corresponding result when .
- (iv)
- If thenwhere the final equality follows on recognising the Mercator series andIn the special case , the quantity in the square brackets reduces to unity andwhich is the pmf of a logarithmic distribution. If then (A9) is recognizable as a left-truncated logarithmic distribution.
- (v)
- If thenandA comparison of this expression with that at (A8) reveals a remarkable similarity to the case where and . As in the earlier case we see that (i) the ratio is negative, (ii) there is a scale factor reflecting left-truncation, with the only substantial difference being that whereas here we have a series reducing to the term , in the earlier case we had a sum that only offers a similar simplification when is integer.
- (vi)
- The final case to consider is that where and . Herewhere the third equality is valid because , andThis somewhat surprising result reduces to that of Willmot (1988) when , in which case the denominator reduces to unity.
We will not go through all the properties considered in the case , although we note in passing that contributes nothing to any of the expectations used to calculate either the mean or variance of Y and so the expressions provided remain valid, except in the special case of where finite moments do not appear to exist. We can, however, update Figure A2 to reflect what we have learned in these cases where , see Figure A3.28 In essence, the major change is that the parameter space now admits non positive values of , provided that they exceed and , but only when .
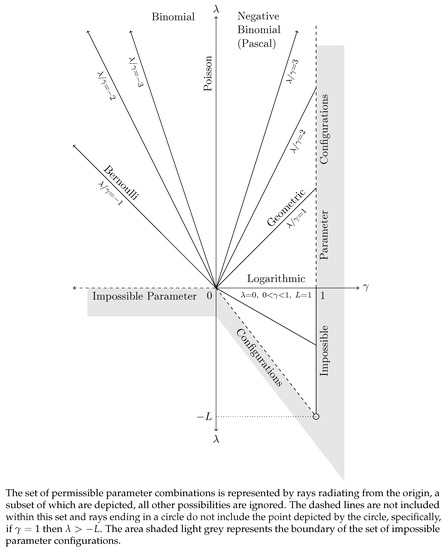
Figure A3.
Parameter Space for the Extended Katz Family For .
References
- Abadir, Karim M. 1999. An introduction to hypergeometric functions for economists. Econometric Reviews 18: 287–330. [Google Scholar] [CrossRef]
- Adamidis, Konstantinos. 1999. An EM algorithm for estimating negative binomial parameters. Australian & New Zealand Journal of Statistics 41: 213–21. [Google Scholar] [CrossRef]
- Al-Khasawneh, Mohanad F. 2010. Estimating the negative binomial dispersion parameter. Asian Journal of Mathematics & Statistics 3: 1–15. [Google Scholar] [CrossRef]
- Bardwell, George E., and Edwin L. Crow. 1964. A two-parameter family of hyper-Poisson distributions. Journal of the American Statistical Association 59: 133–41. [Google Scholar] [CrossRef]
- Boswell, M. T., and Ganapati P. Patil. 1970. Chance mechanisms generating the negative binomial distributions. In Random Counts in Models and Structures. Edited by G. P. Patil. London: University Press, vol. 1, chp. 1. pp. 3–22. [Google Scholar]
- Cameron, A. Colin, and Pravin K. Trivedi. 1986. Econometric models based on count data: Comparisons and applications of some estimators and tests. Journal of Applied Econometrics 1: 29–53. [Google Scholar] [CrossRef]
- Cameron, A. Colin, and Pravin K. Trivedi. 2013. Econometric Society Monographs No. In Regression Analysis of Count Data, 2nd ed. Econometric Society Monographs No. 53. Cambridge: Cambridge University Press. [Google Scholar]
- Consul, Prem C. 1989. Generalized Poisson Distribution: Properties and Applications. Statistics: Textbooks and Monographs 99. New York: Marcel Dekker Inc. [Google Scholar]
- Crow, Edwin L., and George E. Bardwell. 1965. Estimation of the parameters of the hyper-Poisson distributions. In Classical and Contagious Discrete Distributions. Proceedings of the International Symposium held at McGill University, Montreal, Canada, August 15–August 20, 1963. Edited by G. P. Patil. Calcutta: Statistical Publishing Society, Oxford: Pergamon Press, pp. 127–40. [Google Scholar]
- Dacey, Michael F. 1972. A family of discrete probability distributions defined by the generalized hypergeometric series. Sankhyā: The Indian Journal of Statistics, Series B 34: 243–50. [Google Scholar]
- Davidson, Russell, and James G. MacKinnon. 1987. Implicit alternatives and the local power of test statistics. Econometrica 55: 1305–29. [Google Scholar] [CrossRef]
- Dean, C. B. 1992. Testing for overdispersion in Poisson and binomial regression models. Journal of the American Statistical Association 87: 451–57. [Google Scholar] [CrossRef]
- Dean, C. B., and J. F. Lawless. 1989. Tests for detecting overdispersion in Poisson regression models. Journal of the American Statistical Association 84: 467–72. [Google Scholar] [CrossRef]
- Fang, Yue. 2003. GMM tests for the Katz family of distributions. Journal of Statistical Planning and Inference 110: 55–73. [Google Scholar] [CrossRef]
- Frome, Edward L., Michael H. Kutner, and John J. Beauchamp. 1973. Regression analysis of Poisson-distributed data. Journal of the American Statistical Association 68: 935–40. [Google Scholar] [CrossRef]
- Gart, John J. 1964. The analysis of Poisson regression with an application in virology. Biometrika 51: 517–21. [Google Scholar] [CrossRef]
- Ghahfarokhi, Mohammad Ali Baradaran, Hosseiyn Iravani, and M. R. Sepehri. 2008. Application of Katz family of distributions for detecting and testing overdispersion in Poisson regression models. World Academy of Science, Engineering and Technology 42: 514–19. [Google Scholar]
- Gilbert, Christopher L. 1979. Econometric models for discrete economic processes. Paper presented at Econometric Society European Meeting, Athens, Greece, September 3. [Google Scholar]
- Gilbert, Christopher L. 1982. Economic models for discrete (integer valued) economic processes. In Selected Papers on Contemporary Econometric Problems. Edited by E. G. Charatsis. Athens: Athens School of Economics and Business Science, pp. 255–83. [Google Scholar]
- Greene, William H. 2007. Functional form and heterogeneity in models for count data. Foundations and Trends ® in Econometrics 1: 113–218. [Google Scholar] [CrossRef]
- Greene, William H. 2008. Functional forms for the negative binomial model for count data. Economics Letters 99: 585–90. [Google Scholar] [CrossRef]
- Greenwood, M., and G. U. Yule. 1920. An inquiry into the nature of frequency distributions representative of multiple happenings with particular reference to the occurrence of multiple attacks or of repeated accidents. The Journal of the Royal Statistical Society, Series A 83: 255–79. [Google Scholar] [CrossRef]
- Gurland, John. 2006. Katz system of distributions. In Encyclopedia of Statistical Sciences. Edited by S. Kotz, N. Balakrishnan, C. B. Read and B. Vidakovic. New York: John Wiley & Sons, Inc., vol. 6, pp. 3824–25. [Google Scholar] [CrossRef]
- Haight, Frank A. 1967. Handbook of the Poisson Distribution. New York: John Wiley & Sons, Inc. [Google Scholar]
- Hausman, Jerry, Bronwyn H. Hall, and Zvi Griliches. 1984. Econometric models for count data with an application to the patents-r & d relationship. Econometrica 52: 909–38. [Google Scholar]
- Hellinger, Ernst. 1909. Neue begründung der theorie quadratischer formen von unendlichvielen veänderlichen. Journal für die reine und angewandte Mathematik 136: 210–71. [Google Scholar] [CrossRef]
- Hess, Klaus Th, Anett Liewald, and Klaus D. Schmidt. 2002. An extension of Panjer’s recursion. ASTIN Bulletin 32: 283–97. [Google Scholar] [CrossRef]
- Hilbe, Joseph M. 2011. Negative Binomial Regression, 2nd ed. Cambridge: Cambridge University Press. [Google Scholar]
- Hilbe, Joseph M. 2014. Modeling Count Data. New York: Cambridge University Press. [Google Scholar]
- Joe, Harry, and Rong Zhu. 2005. Generalized Poisson distribution: The property of mixture of Poisson and comparison with negative binomial distribution. Biometrical Journal 47: 219–29. [Google Scholar] [CrossRef]
- Johnson, Norman L., and Samuel Kotz. 1969. Discrete Distributions. New York: John Wiley & Sons, Inc. [Google Scholar]
- Johnson, Norman L., Samuel Kotz, and Adrienne W. Kemp. 1993. Univariate Discrete Distributions, 2nd ed. New York: John Wiley & Sons. [Google Scholar]
- Jorgenson, Dale W. 1961. Multiple regression analysis of a Poisson process. Journal of the American Statistical Association 56: 235–45. [Google Scholar] [CrossRef]
- Katz, Leo. 1945. Characteristics of Frequency Functions Defined by First Order Difference Equations. Ph. D. thesis, University of Michigan, Ann Arbor, MI, USA. [Google Scholar]
- Katz, Leo. 1946. On the class of functions defined by the difference equation (x + 1)f(x + 1) = (a + bx)f(x) (Abstract). Annals of Mathematical Statistics 17: 501. [Google Scholar]
- Katz, Leo. 1948. Frequency functions defined by the Pearson difference equation (Abstract). Annals of Mathematical Statistics 19: 120. [Google Scholar]
- Katz, Leo. 1965. Unified treatment of a broad class of discrete distributions. In Classical and Contagious Discrete Distributions. Proceedings of the International Symposium held at McGill University, Montreal, Canada, August 15–August 20, 1963. Edited by G. P. Patil. Calcutta: Statistical Publishing Society, Oxford: Pergamon Press, pp. 175–82. [Google Scholar]
- Kemp, Adrienne W. 1968. A wide class of discrete distributions and the associated differential equations. Sankhyā: The Indian Journal of Statistics, Series A (1961–2002) 30: 401–10. [Google Scholar]
- King, Gary. 1989. Variance specification in event count models: From restrictive assumptions to a generalized estimator. American Journal of Political Science 33: 762–84. [Google Scholar] [CrossRef]
- King, Maxwell L. 1987. Towards a theory of point optimal testing. Econometric Reviews 6: 169–218. [Google Scholar] [CrossRef]
- King, Maxwell L., and Sivagowry Sriananthakumar. 2015. Point optimal testing: A survey of the post 1987 literature. Model Assisted Statistics and Applications 10: 179–96. [Google Scholar] [CrossRef]
- Lawless, Jerald F. 1987a. Negative binomial and mixed Poisson regression. The Canadian Journal of Statistics 15: 209–25. [Google Scholar] [CrossRef]
- Lawless, J. F. 1987b. Regression methods for Poisson process data. Journal of the American Statistical Association 82: 808–15. [Google Scholar] [CrossRef]
- Lee, Lung-Fei. 1986. Specification test for Poisson regression models. International Economic Review 27: 689–706. [Google Scholar] [CrossRef]
- McCullagh, Peter, and John A. Nelder. 1989. Monographs On Statistics and Applied Probability 37. In Generalized Linear Models, 2nd ed. London: Chapman & Hall\CRC. [Google Scholar] [CrossRef]
- Miller, David W. 1998. Fitting Frequency Distributions Philosophy and Practice. Part 1: Discrete Distributions, 2nd ed. Self-published. [Google Scholar]
- Nelder, John A., and Robert W. M. Wedderburn. 1972. Generalized linear models. Journal of the Royal Statistical Society. Series A (General) 135: 370–84. [Google Scholar] [CrossRef]
- Ord, J. Keith. 1967a. On a system of discrete distributions. Biometrika 54: 649–56. [Google Scholar] [CrossRef]
- Ord, J. Keith. 1967b. On Families of Discrete Distributions. Ph. D. thesis, University of London, London, UK. [Google Scholar]
- Ord, J. Keith. 1972. Families of Frequency Distributions. London: Griffin. [Google Scholar]
- Panjer, Harry H. 1981. Recursive evaluation of a family of compound distributions. ASTIN Bulletin 12: 22–26. [Google Scholar] [CrossRef]
- Pearson, Karl. 1894. Contributions to the mathematical theory of evolution. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 185: 71–110 (+ 5 plates). [Google Scholar] [CrossRef]
- Pearson, Karl. 1895. Contributions to the mathematical theory of evolution. — II. Skew variation in homogeneous material. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 186: 343–414. [Google Scholar] [CrossRef]
- Pestana, Dinis D., and Sílvio F. Velosa. 2004. Extensions of Katz-Panjer families of discrete distributions. REVSTAT Statisical Journal 2: 145–62. [Google Scholar]
- Qu, Yinsheng, G. J. Beck, and G. W. Williams. 1990. Polya-Eggenberger distribution: Parameter estimation and hypothesis tests. Biometrical Journal 32: 229–42. [Google Scholar] [CrossRef]
- Raschke, Christian, and William H. Greene. 2010. Corrigendum to ”functional forms for the negative binomial model for count data”. Economics Letters 107: 313. [Google Scholar] [CrossRef]
- Slater, Lucy J. 1966. Generalized Hypergeometric Functions. Cambridge: Cambridge University Press. [Google Scholar]
- Staff, P. J. 1964. The displaced Poisson distribution. Australian Journal of Statistics 6: 12–20. [Google Scholar] [CrossRef]
- Staff, P. J. 1967. The displaced Poisson distribution. Region B. Journal of the American Statistical Association 62: 643–54. [Google Scholar]
- Sundt, Bjørn, and William S. Jewell. 1981. Further results on recursive evaluation of compound distributions. ASTIN Bulletin 12: 27–39. [Google Scholar] [CrossRef]
- Weisstein, Eric W. 2019. Gauss’s Test. From MathWorld — A Wolfram Web Resource. Available online: http://mathworld.wolfram.com/GausssTest.html (accessed on 21 December 2019).
- Willmot, Gordon. 1988. Sundt and Jewell’s family of discrete distributions. ASTIN Bulletin 18: 17–29. [Google Scholar] [CrossRef]
- Winkelmann, Rainer. 2008. Econometric Analysis of Count Data, 5th ed. Berlin: Springer. [Google Scholar] [CrossRef]
- Yang, Zhao, James W. Hardin, Cheryl L. Addy, and Quang H. Vuong. 2007. Testing approaches for overdispersion in Poisson regression versus the generalized Poisson model. Biometrical Journal 49: 565–84. [Google Scholar] [CrossRef] [PubMed]
- Yang, Zhao, James W. Hardin, and Cheryl L. Addy. 2009. A score test for overdispersion in Poisson regression based on the generalized Poisson-2 model. Journal of Statistical Planning and Inference 139: 1514–21. [Google Scholar] [CrossRef]
| 1. | An abstract to this thesis appeared in Katz (1946). |
| 2. | This family of distributions, and extensions to it, have proved important in the actuarial modelling of claims; see, for example, Hess et al. (2002); Panjer (1981); Sundt and Jewell (1981); Willmot (1988), and Pestana and Velosa (2004). Johnson et al. (1993, chp. 2) provides an extensive discussion of both the Katz family and various other, often related, families of discrete distributions. Although, in respect of the Katz family of distributions alone, the treatment in Johnson and Kotz (1969, chp. 2.4) is more complete; see also Gurland (2006) for a more recent treatment. |
| 3. | The one caveat to this observation is that the use of higher order moments may provide some power against models which share low order moments, thereby creating a class of implicit null hypotheses (Davidson and MacKinnon 1987). |
| 4. | Numerous extensions soon followed; see, for example, Bardwell and Crow (1964); Crow and Bardwell (1965); Ord (1967a, 1967b); Staff (1964, 1967) and Kemp (1968). Here we only briefly sketch some key ideas. For a more complete treatment of such families of distributions see, for example, any of Johnson et al. (1993, chp. 2.3), Ord (1972, chp. 5), or Dacey (1972). |
| 5. | Observe that the Pochhammer symbol , where y is a non-negative integer. Note that r can be negative. If r is a negative integer then for all . If r is a positive integer then . |
| 6. | When is integer the resulting pmfs are sometimes referred to as those of Pascal distributions, with the term negative binomial reserved for the more general case of not necessarily integer. |
| 7. | Similarly, the Poisson approximation to the Binomial reduces to for fixed , which is also a more intuitive statement of how parameters must evolve for the approximation to work than is typically encountered. |
| 8. | We shall persist with the abuse of notation inherent in expressions like rather than, say, a more complete notation along the lines of , for the sake of the notational economy it affords. |
| 9. | The NBRM was explored in Adamidis (1999); Greene (2008); Lawless (1987a, 1987b), and Raschke and Greene (2010); Hilbe (2011) and Hilbe (2014) provide useful recent surveys of the NBRM. |
| 10. | Common variants of this argument include: (i) Lee (1986), who specifies the gamma distribution in terms of the shape and scale (or inverse rate) () parameters, that is, , and (ii) Cameron and Trivedi (1986), who use the so-called index form of the gamma distribution, which is specified in terms of the shape and mean () parameters, that is, . Cameron and Trivedi (1986) call the shape parameter () the index or precision parameter. |
| 11. | Moments for the gamma distribution specifications given in Footnote 10 follow immediately on making the appropriate substitution for . |
| 12. | Other values of k yield the Negbin P, or NBP, model (Greene 2008). |
| 13. | Strictly, it is not a generalized linear model as it stands but, conditioning on one of the parameters allows it to be treated so. This parameter can then be estimated conditional on the remaining parameters, which yields a two-step iterative estimation procedure. See, for example, either Hilbe (2011) or Hilbe (2014) for a discussion of the steps involved. |
| 14. | This latter model, of course, corresponds to the Negbin II model of Cameron and Trivedi (1986), and so provides a somewhat stronger theoretical basis for that model, which may explain some of its popularity in the literature. |
| 15. | Specifically, Greene (2008) discusses the broader class of models obtained when k is allowed to take values other than 0 or 1 in (14). He dubs this broad model the NBP model, seemingly because his notation uses p rather than the k used by Cameron and Trivedi (1986) (and here). |
| 16. | Alternatively, using similar averaging arguments to those seen previously for the NBRM, if we average with respect to , where and , then we obtain a more common form of the negative binomial pmf.
Note that the mean and variance of this distribution are given by (Appendix A.2.2). In contrast with the developments of (11), there is nothing in this model that requires that both the parameters of the mixing gamma distribution vary with the index i. Nor need they be linked in any restrictive way. Specifically, if we were to follow the developments of Greene (2008) who equates the parameters of the mixing distribution, we find that
|
| 17. | We note that Yang et al. (2007) and Yang et al. (2009) pursue a similar exercise against variants of the generalized Poisson distribution, see the discussions in Consul (1989) and Joe and Zhu (2005), although we shall not pursue these models further. |
| 18. | Strictly, Katz (1965) adopted an approach more in keeping with a method of moments test. Specifically, he looked at the difference between estimators for the mean and variance, which should be equal under the null and then scaled this difference appropriately to obtain a distribution under the null. In any event, the statistic so obtained is the same as the one proposed by Lee (1986) that we consider here. |
| 19. | Lee (1986) proposed other tests than the one considered here, although he did not compare them numerically The results recorded in Miller (1998) suggests that those involving third order moments may have better power properties. For now we are primarily concerned with proof of concept and do not explore these other tests in light of the simplicity of (17). |
| 20. | We also considered an alternative test based on the t-statistic in the regression of on a constant but there was little difference in performance. These tests correspond to the Negbin I and II cases above. |
| 21. | See, for example, https://en.wikipedia.org/wiki/Hellinger_distance. |
| 22. | In their extensions to this class of distributions, Panjer (1981); Sundt and Jewell (1981) and Willmot (1988) adopt a slightly different parameterization, specifically , . Equivalence with (A1) is seemingly established on setting and , although there are differences in the support of the resulting variables. In particular, is specifically excluded from this definition and hence many of the probability distributions claimed to satisfy the recursion in this form are not completely defined by it. |
| 23. | See, for example, Weisstein (2019). |
| 24. | In essence, this is the same as adopting the convention that any negative probabilities are set to zero. It might be argued that this is at odds with Katz’s original assumptions and should be excluded. Our justification for the inclusion in our analysis of these distributions where is non-integer, is that Katz himself included them.
|
| 25. | A useful collection of results on Pochhammer symbols can be found in Slater (1966, Appendix I). |
| 26. | We note that Katz (1965) was perfectly well aware of the possibility of non-integer values of , see the quote in Footnote 24. |
| 27. | The condition integer obviously requires . |
| 28. | Note that Sundt and Jewell (1981, fig. 1)) provide a similar diagram although, as noted by Willmot (1988), they miss the possibility of . |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).