Pitfalls of Two-Step Testing for Changes in the Error Variance and Coefficients of a Linear Regression Model
Abstract
:1. Introduction
2. Models and Test Statistics
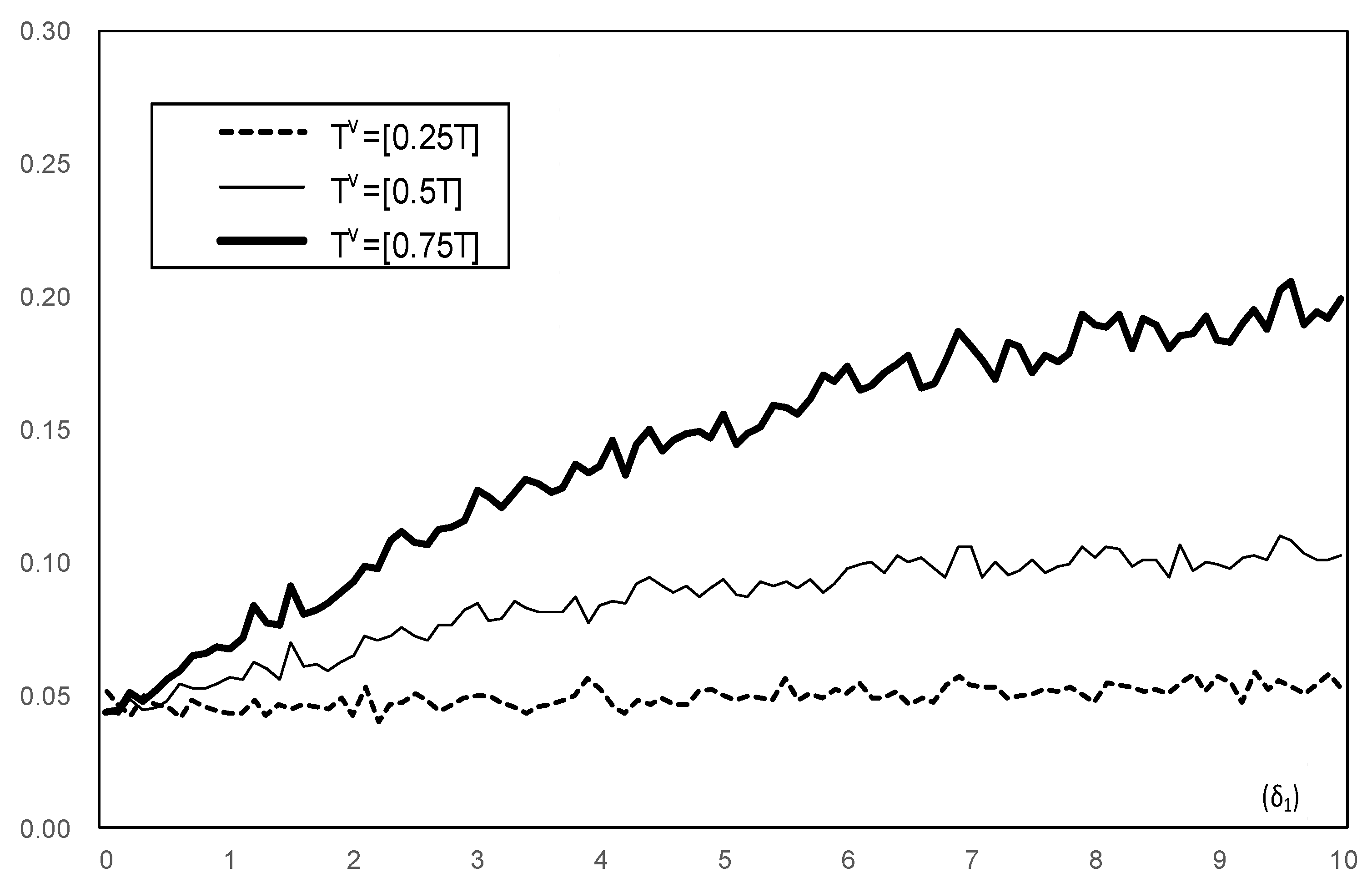
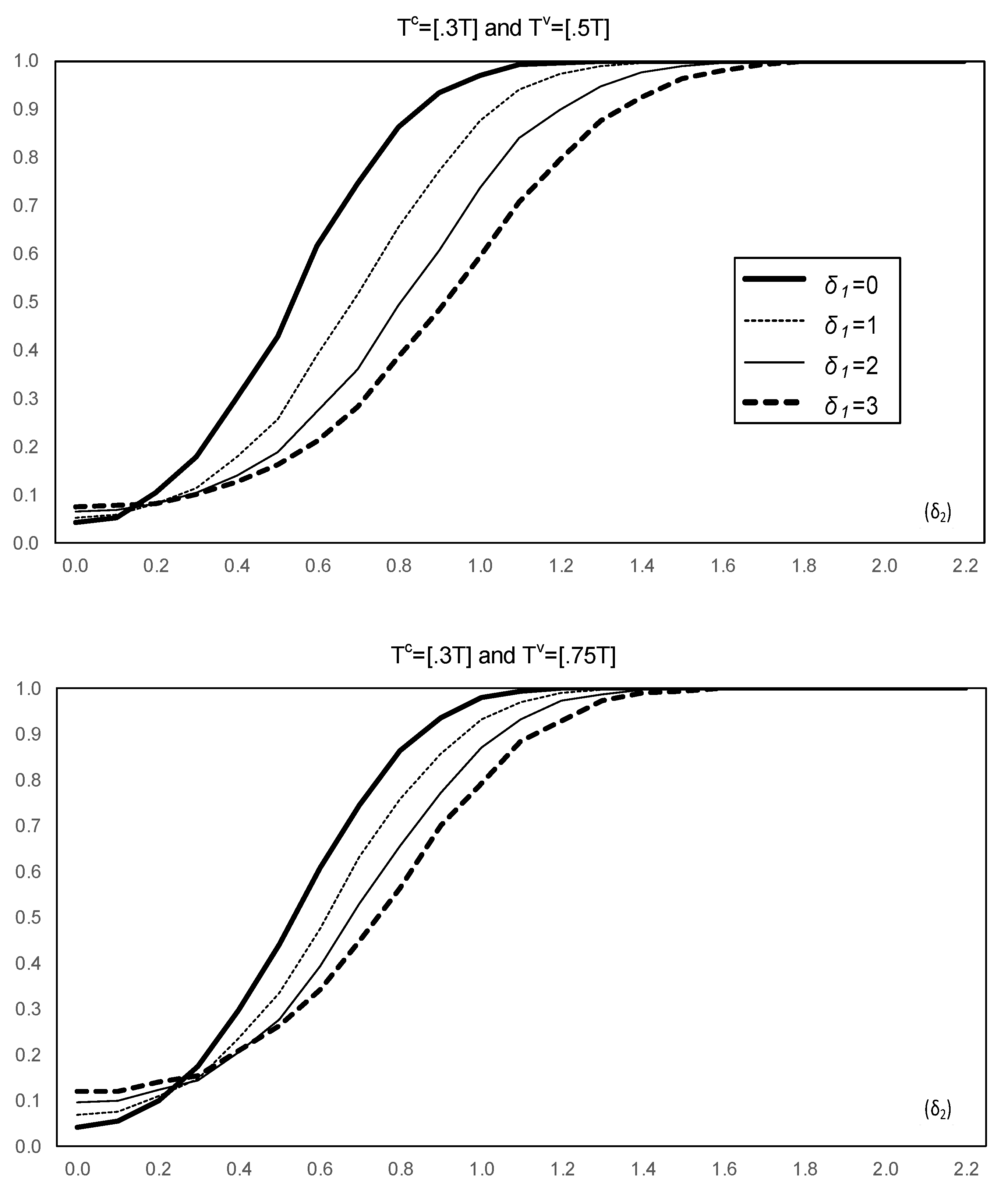
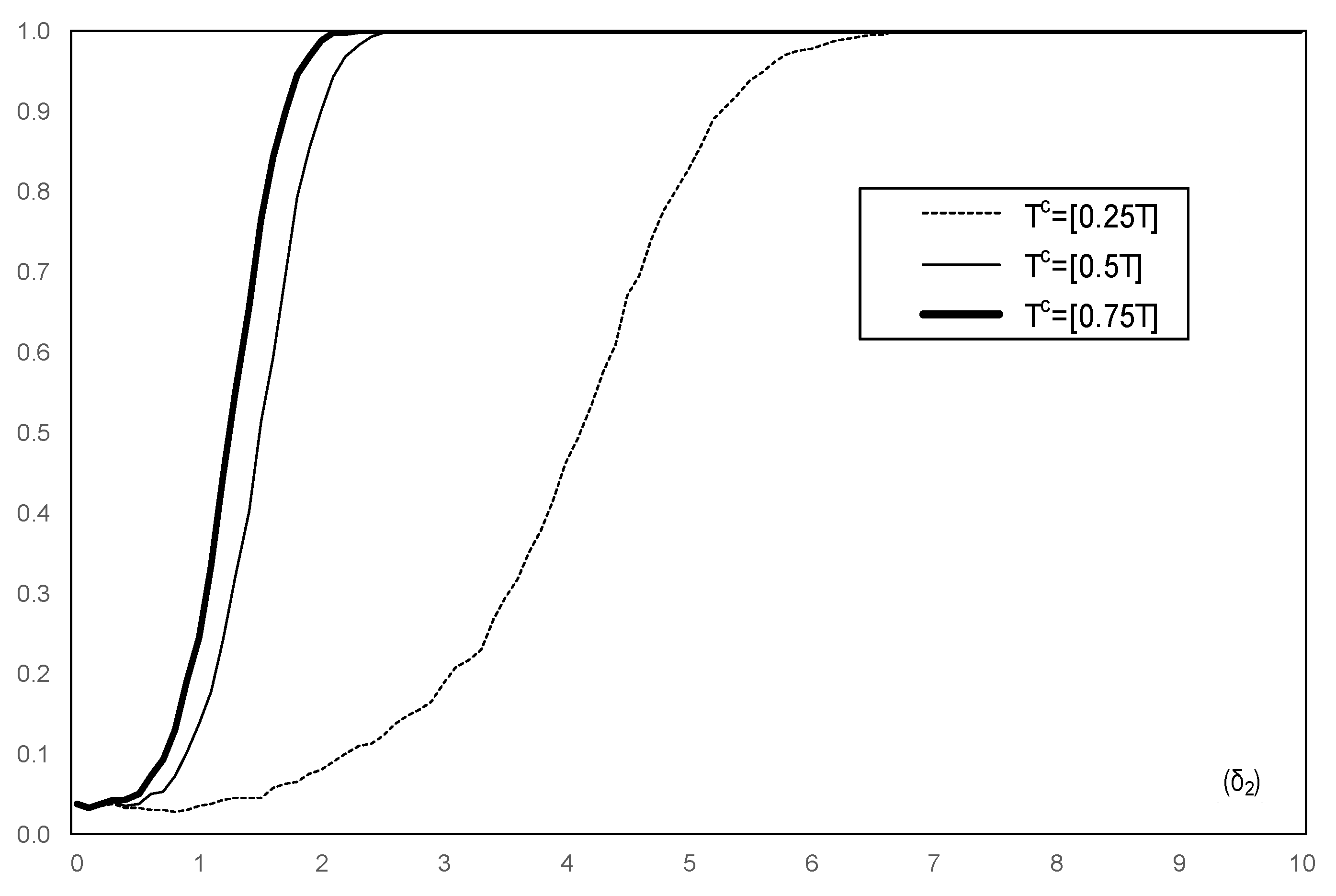
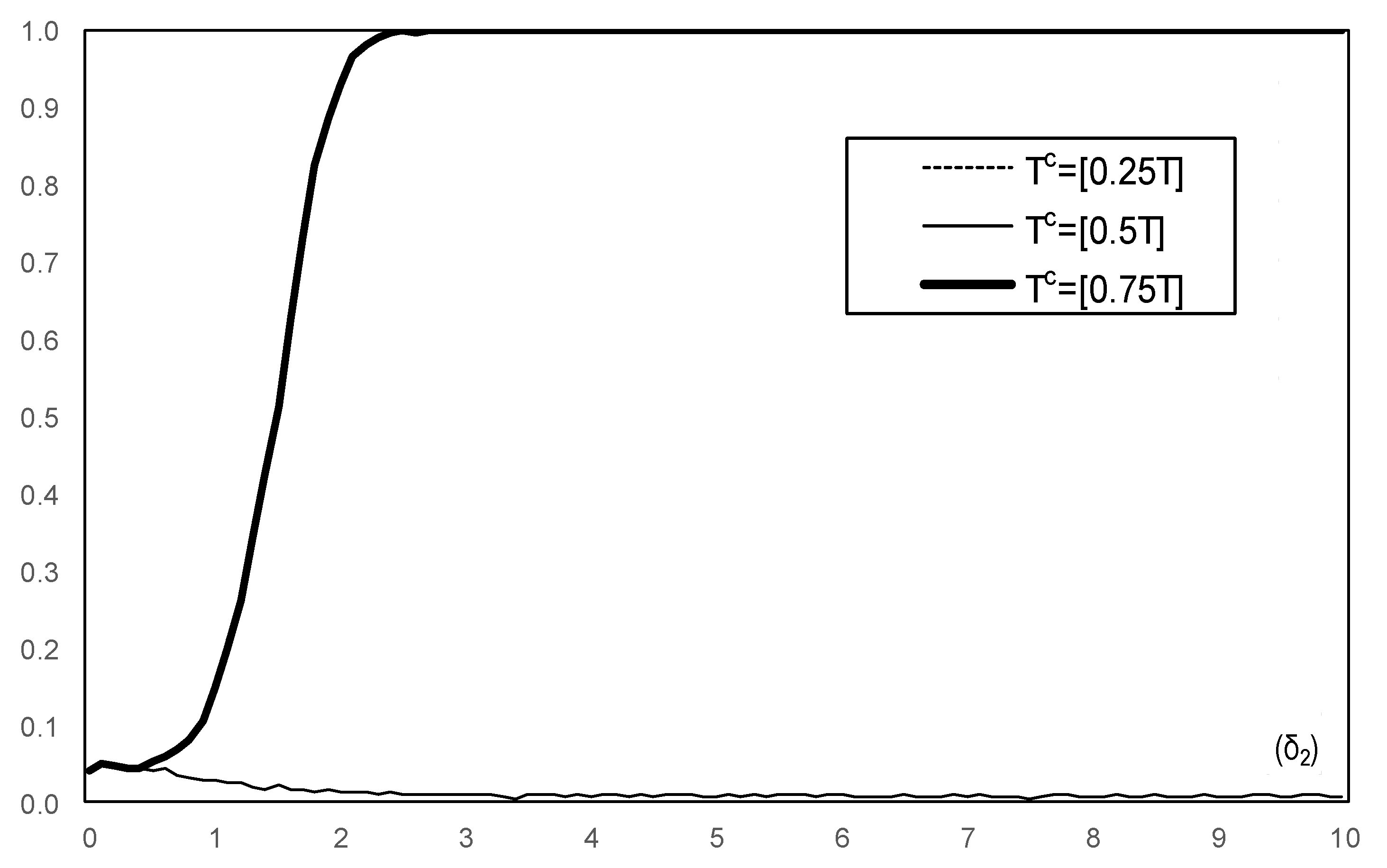
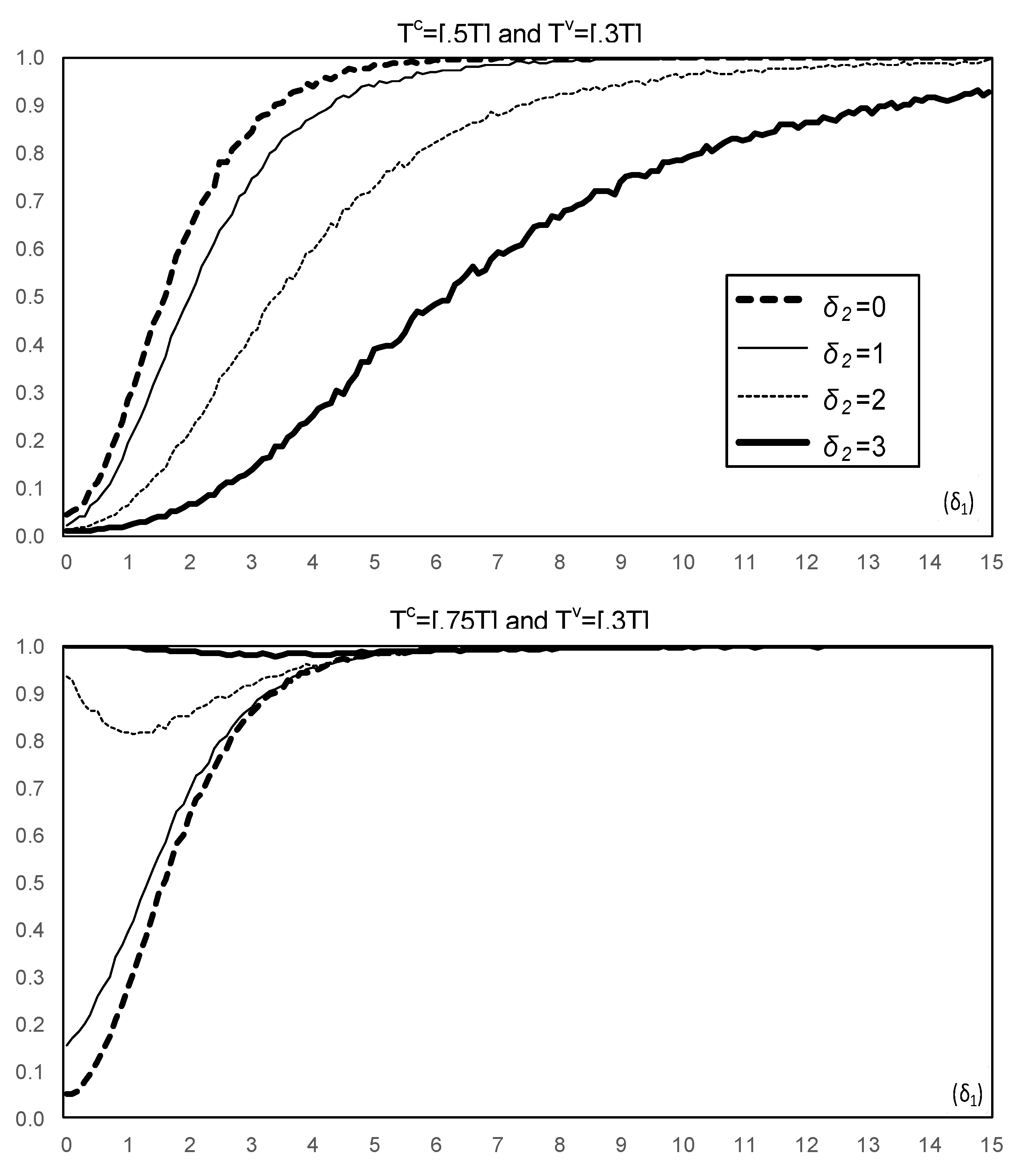
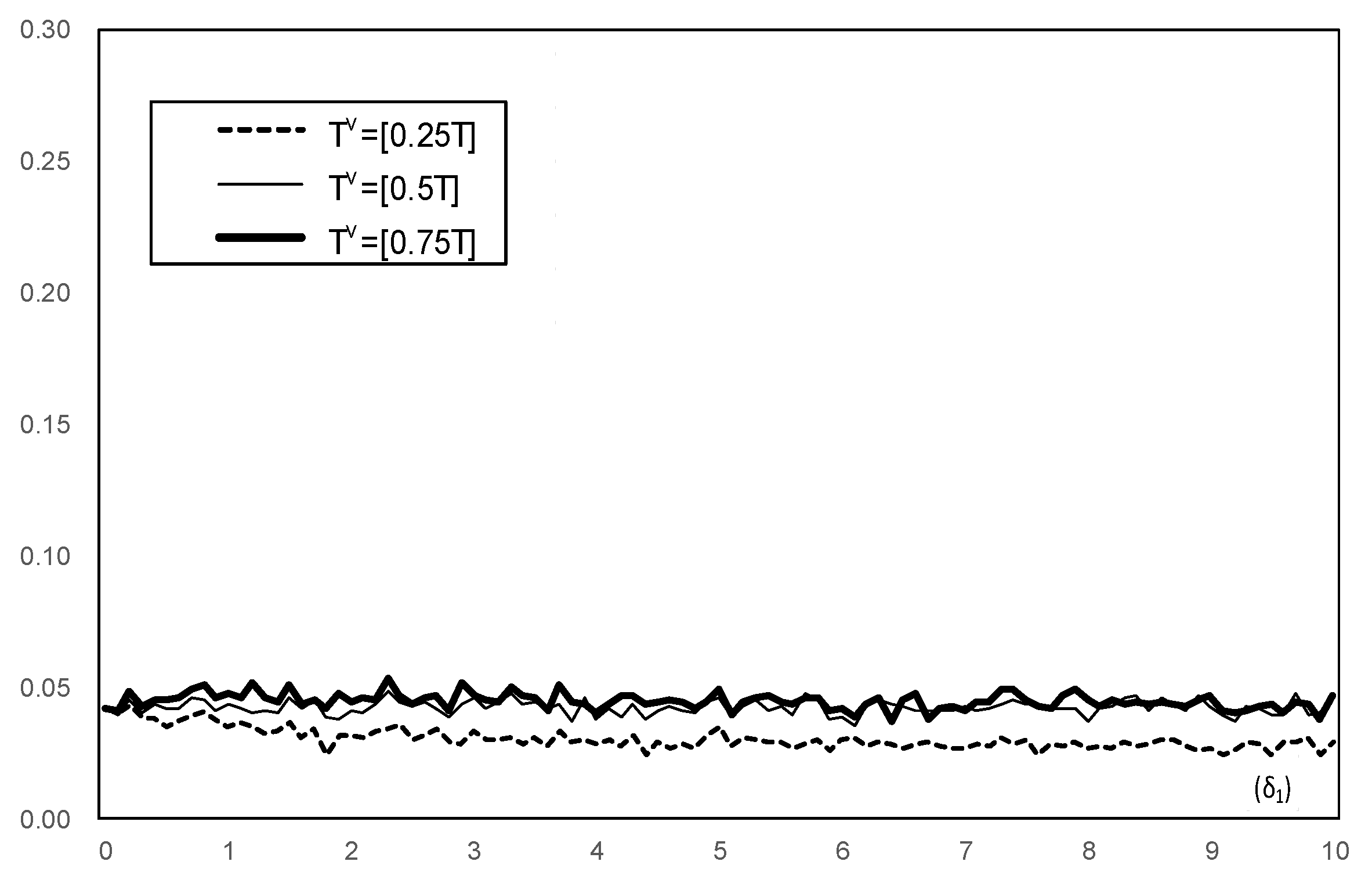
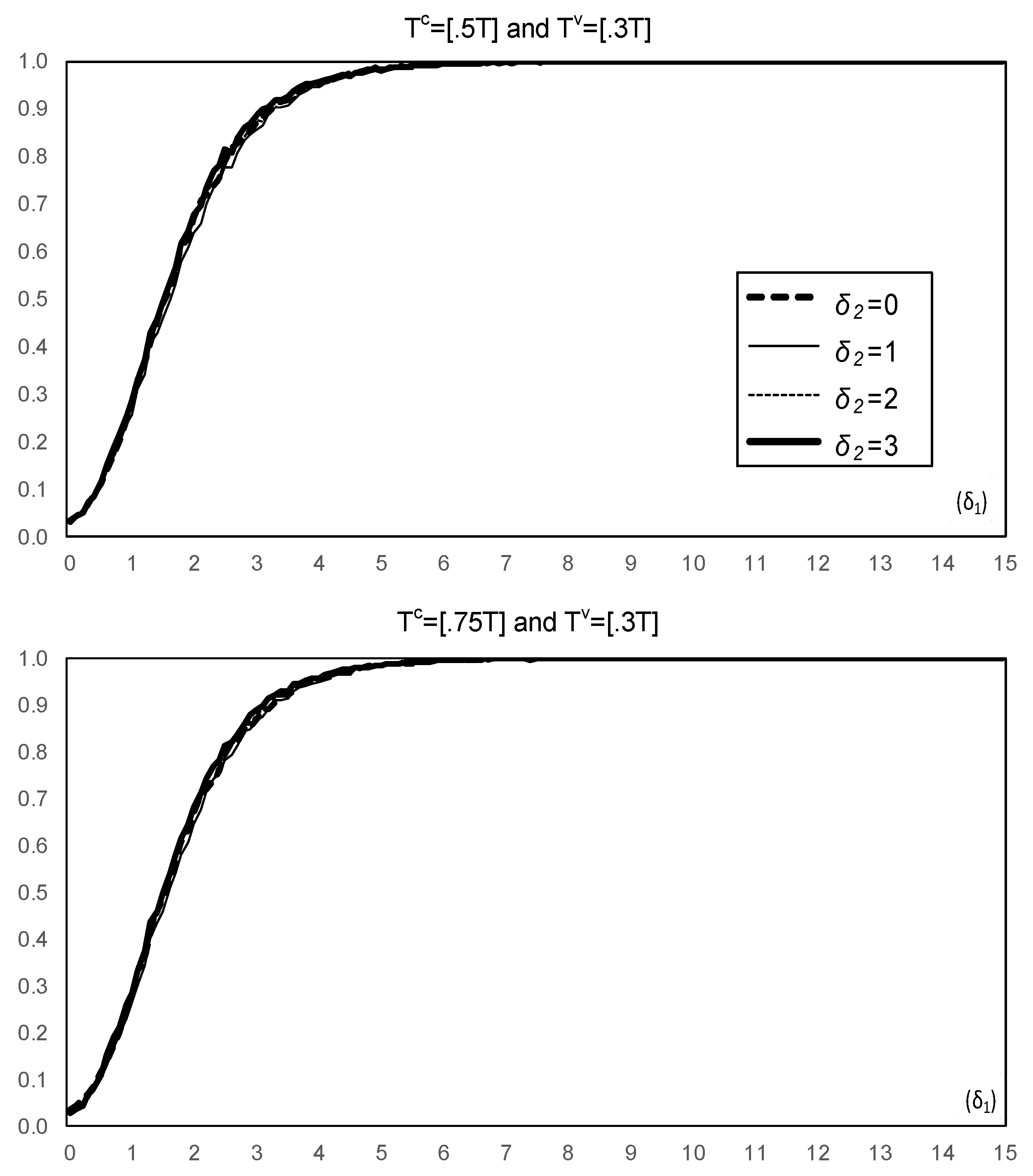
3. Results
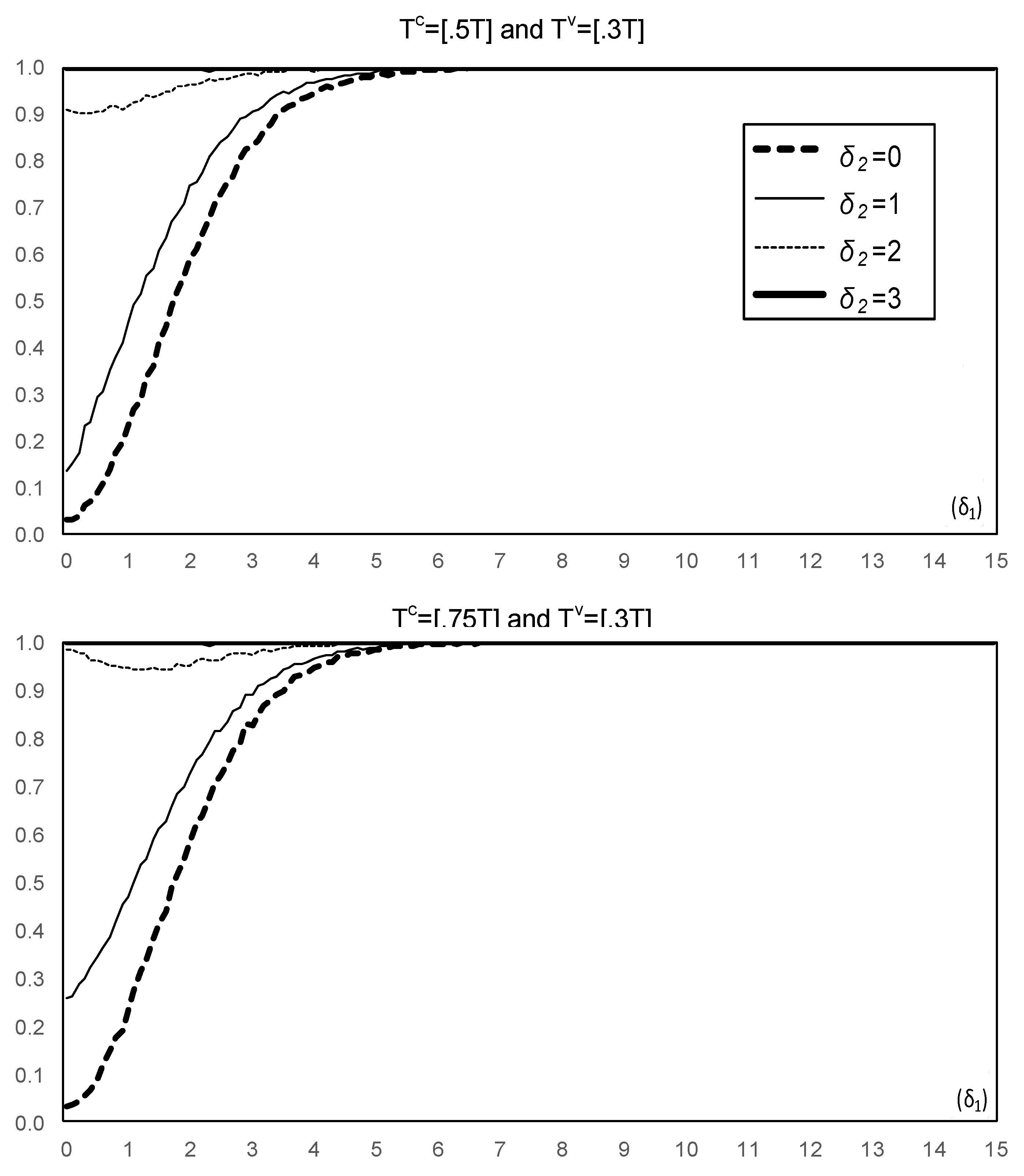
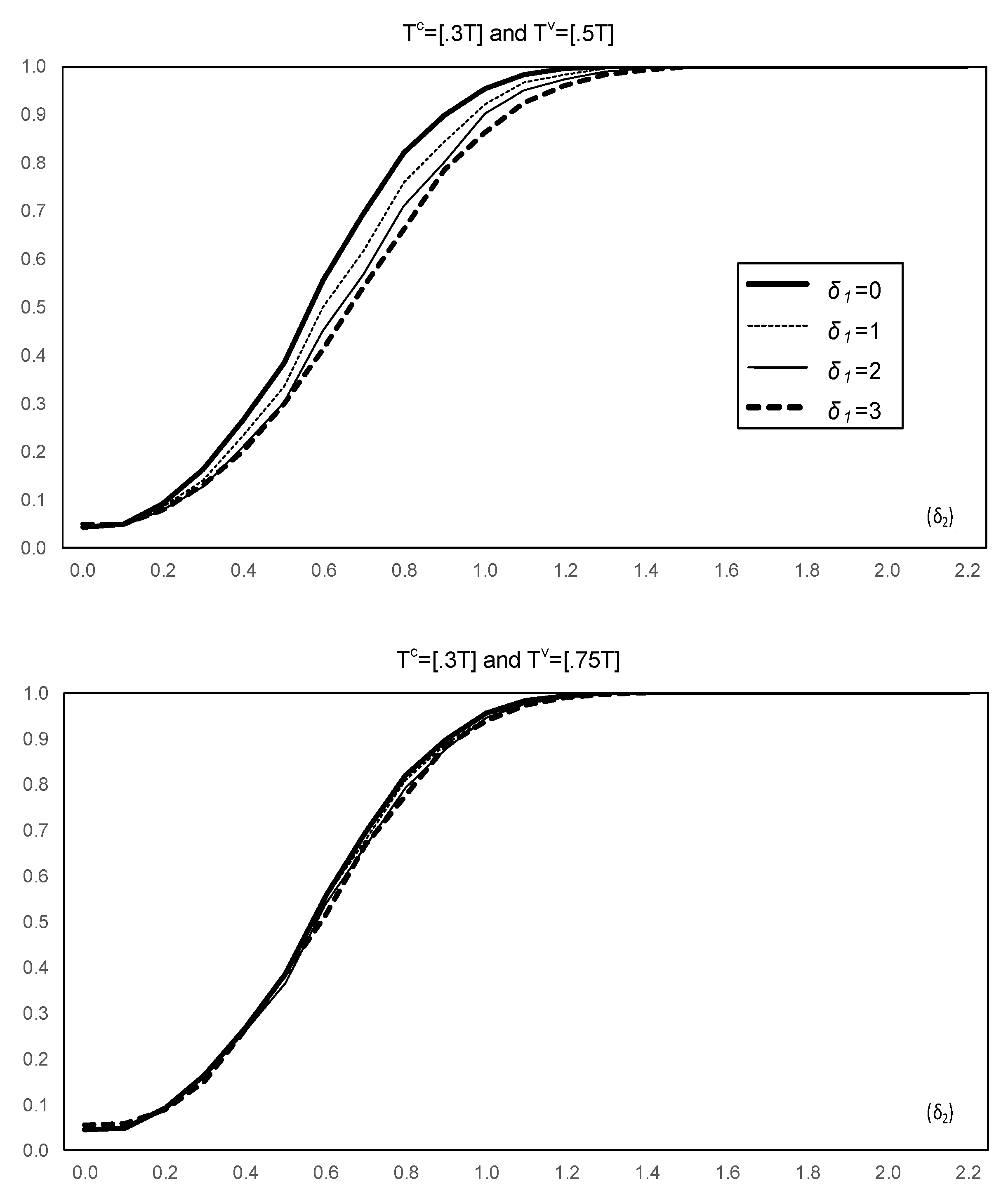
4. Tests Allowing for Joint Changes
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Andrews, Donald W. K. 1993. Tests for parameter instability and structural change with unknown change point. Econometrica 61: 821–856. [Google Scholar] [CrossRef]
- Bai, Jushan, and Pierre Perron. 1998. Estimating and testing linear models with multiple structural changes. Econometrica 66: 47–78. [Google Scholar] [CrossRef]
- Brown, Robert L., James Durbin, and James M. Evans. 1975. Techniques for testing the constancy of regression relationships over time. Journal of the Royal Statistical Society B 37: 149–63. [Google Scholar] [CrossRef]
- Deng, Ai, and Pierre Perron. 2008a. The limit distribution of the CUSUM of squares test under general mixing conditions. Econometric Theory 24: 809–22. [Google Scholar] [CrossRef]
- Deng, Ai, and Pierre Perron. 2008b. A non-local perspective on the power properties of the CUSUM and CUSUM of squares tests for structural change. Journal of Econometrics 142: 212–40. [Google Scholar] [CrossRef]
- Herrera, Ana Maria, and Elena Pesavento. 2005. The decline in U.S. output volatility: structural changes and inventory investment. Journal of Business & Economic Statistics 23: 462–72. [Google Scholar]
- Inclán, Carla, and George C. Tiao. 1994. Use of cumulative sums of squares for retrospective detection of changes of variance. Journal of the American Statistical Association 89: 913–23. [Google Scholar]
- Perron, Pierre, Yohei Yamamoto, and Jing Zhou. 2019. Testing Jointly for Structural Changes in the Error Variance and Coefficients of a Linear Regression Model. Unpublished Manuscript, Boston University, Boston, MA, USA. Available online: http://people.bu.edu/perron/ (accessed on 16 April 2019).
- Pitarakis, Jean-Yves. 2004. Least-squares estimation and tests of breaks in mean and variance under misspecification. Econometrics Journal 7: 32–54. [Google Scholar] [CrossRef]
- Qu, Zhongjun, and Pierre Perron. 2007. Estimating and testing multiple structural changes in multivariate regressions. Econometrica 75: 459–502. [Google Scholar] [CrossRef]
- Stock, James H., and Mark W. Watson. 2002. Has the business cycle changed and why? In NBER Macroeconomics Annual 17. Edited by M. Gertler and K. Rogoff. Cambridge: MIT press, pp. 159–218. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perron, P.; Yamamoto, Y. Pitfalls of Two-Step Testing for Changes in the Error Variance and Coefficients of a Linear Regression Model. Econometrics 2019, 7, 22. https://doi.org/10.3390/econometrics7020022
Perron P, Yamamoto Y. Pitfalls of Two-Step Testing for Changes in the Error Variance and Coefficients of a Linear Regression Model. Econometrics. 2019; 7(2):22. https://doi.org/10.3390/econometrics7020022
Chicago/Turabian StylePerron, Pierre, and Yohei Yamamoto. 2019. "Pitfalls of Two-Step Testing for Changes in the Error Variance and Coefficients of a Linear Regression Model" Econometrics 7, no. 2: 22. https://doi.org/10.3390/econometrics7020022
APA StylePerron, P., & Yamamoto, Y. (2019). Pitfalls of Two-Step Testing for Changes in the Error Variance and Coefficients of a Linear Regression Model. Econometrics, 7(2), 22. https://doi.org/10.3390/econometrics7020022




