Interval-Based Hypothesis Testing and Its Applications to Economics and Finance
Abstract
Genuinely interesting hypotheses are neighbourhoods, not points. No parameter is exactly equal to zero; many may be so close that we can act as if they were zero.
1. Introduction
2. Current Paradigm and Its Deficiencies
2.1. A Simple t-Test for a Point Null Hypothesis
2.2. Shortcomings of the p-Value Criterion
2.3. Zero-Probability Paradox
2.4. Problems and Consequences
When a researcher tries many ways to do a study, including various combinations of explanatory factors, various periods, and various models, we often say, he is “data mining.” If he reports only the more successful runs, we have a hard time interpreting any statistical analysis he does. We worry that he selected, from the many models tried, only the ones that seem to support his conclusions. With enough data mining, all the results that seem significant could be just accidental.
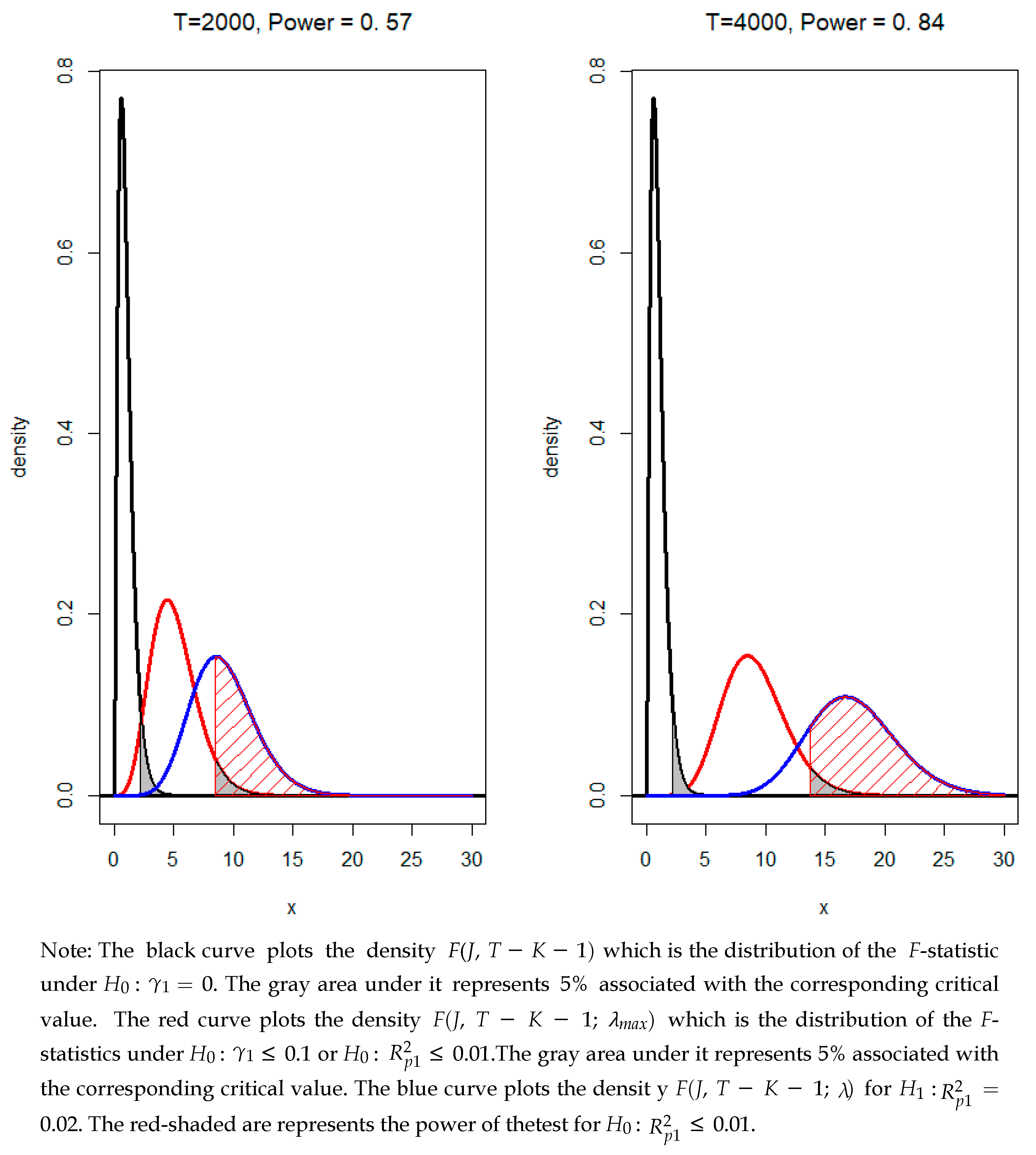
3. Tests for Minimum-Effect, Equivalence, and Non-Inferiority
3.1. Test for Minimum Effect
- against alternative and
- against alternative .
3.2. Test for Equivalence
- against alternative and
- against alternative .
3.3. Test for Non-Inferiority
3.4. Interval Tests in the Linear Regression Model
3.5. Bootstrap Implementation
3.6. Model Equivalence Test
3.7. Equivalence Test for Model Validation
3.8. Choosing the Limits of Economic Significance
4. Empirical Applications
4.1. A SAD Stock Market Cycle
4.1.1. Evaluating the Results of Kamstra et al.
4.1.2. Replicating the Results of Kamstra et al.
4.2. Empirical Validity of an Asset-Pricing Model
4.2.1. GRS Test: Minimum-Effect
4.2.2. LR Test: Model Equivalence
4.3. Testing for Persistence of a Time Series
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Arrow, Kenneth. 1960. Decision theory and the choice of a level of significance for the t-test. In Contributions to Probability and Statistics: Essays in Honor of Harold Hotelling. Edited by Ingram Olkin. Stanford: Stanford University Press, pp. 70–78. [Google Scholar]
- Basu, Sudipta, and Han-Up Park. 2014. Publication Bias in Recent Empirical Accounting Research, Working Paper. Available online: http://ssrn.com/abstract=2379889 (accessed on 31 May 2018).
- Berger, James O., and Thomas Sellke. 1987. Testing a Point Null Hypothesis: The Irreconcilability of p-Values and Evidence. Journal of the American Statistical Association 82: 112–22. [Google Scholar] [CrossRef]
- Black, Fischer. 1993. Beta and return. The Journal of Portfolio Management 20: 8–18. [Google Scholar] [CrossRef]
- Box, George E. P. 1976. Science and Statistics. Journal of the American Statistical Association 71: 791–99. [Google Scholar] [CrossRef]
- Campbell, John Y., and N. Gregory Mankiw. 1987. Are Output Fluctuations Transitory? Quarterly Journal of Economics 102: 857–80. [Google Scholar] [CrossRef]
- Campbell, John Y., Andrew W. Lo, and Archie Craig MacKinlay. 1997. The Econometrics of Financial Markets. Princeton: Princeton University Press. [Google Scholar]
- Carhart, Mark M. 1997. On persistence in mutual fund performance. Journal of Finance 52: 57–82. [Google Scholar] [CrossRef]
- Choi, In. 2015. Almost All about Unit Roots. New York: Cambridge University Press. [Google Scholar]
- Cohen, Jacob. 1977. Statistical Power Analysis for the Behavioral Sciences, 2nd ed. New York: LBA. [Google Scholar]
- Cohen, Kalman J., and Richard M. Cyert. 1961. Computer Models in Dynamic Economics. The Quarterly Journal of Economics 75: 112–27. [Google Scholar] [CrossRef]
- De Long, J. Bradford, and Kevin Lang. 1992. Are All Economic Hypotheses False? Journal of Political Economy 100: 1257–72. [Google Scholar] [CrossRef]
- DeJong, David N., John C. Nankervis, N. E. Savin, and Charles H. Whiteman. 1992. Integration versus trend stationary in time series. Econometrica 60: 423–33. [Google Scholar] [CrossRef]
- Dickey, David A., and Wayne A. Fuller. 1979. Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association 74: 427–31. [Google Scholar]
- Efron, Bradley, and Robert J. Tibshirani. 1994. An Introduction to the Bootstrap. Boca Raton: Chapman & Hall, CRC Monographs on Statistics & Applied Probability. [Google Scholar]
- Fama, Eugene F., and Kenneth R. French. 1993. Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33: 3–56. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2015. A five-factor asset-pricing model. Journal of Financial Economics 116: 1–22. [Google Scholar] [CrossRef]
- Freitas, Wilson. 2018. Bizdays: Business Days Calculations and Utilities. R Package Version 1.0.6. Available online: https://CRAN.R-project.org/package=bizdays (accessed on 31 May 2018).
- Gibbons, Michael R., Stephen A. Ross, and Jay Shanken. 1989. A test of the efficiency of a given portfolio. Econometrica 57: 1121–52. [Google Scholar] [CrossRef]
- Gigerenzer, Gerd. 2004. Mindless statistics: Comment on “Size Matters”. Journal of Socio-Economics 33: 587–606. [Google Scholar] [CrossRef]
- Grossman, Sanford J., and Joseph E. Stiglitz. 1980. On the impossibility of informationally efficient markets. The American Economic Review 70: 393–408. [Google Scholar]
- Harvey, Campbell R. 2017. Presidential Address: The Scientific Outlook in Financial Economics. Journal of Finance 72: 1399–440. [Google Scholar] [CrossRef]
- Harvey, Campbell R., Yan Lin, and Heqing Zhu. 2016. … and the cross-section of expected returns. Review of Financial Studies 29: 5–68. [Google Scholar] [CrossRef]
- Hirshleifer, David, and Tyler Shumway. 2003. Good day sunshine: Stock returns and the weather. Journal of Finance 58: 1009–32. [Google Scholar] [CrossRef]
- Hodges, J. L., Jr., and E. L. Lehmann. 1954. Testing the Approximate Validity of Statistical Hypotheses. Journal of the Royal Statistical Society, Series B (Methodological) 16: 261–68. [Google Scholar] [CrossRef]
- Johnstone, D. J., and D. V. Lindley. 1995. Bayesian Inference Given Data Significant at Level α: Tests of Point Hypotheses. Theory and Decision 38: 51–60. [Google Scholar] [CrossRef]
- Kamstra, Mark J., Lisa A. Kramer, and Maurice D. Levi. 2003. Winter blues: A sad stock market cycle. American Economic Review 93: 324–43. [Google Scholar] [CrossRef]
- Kandel, Shmuel., and Robert F. Stambaugh. 1996. On the Predictability of Stock Returns: An Asset-Allocation Perspective. The Journal of Finance 51: 385–424. [Google Scholar] [CrossRef]
- Keuzenkamp, Hugo A., and Jan Magnus. 1995. On tests and significance in econometrics. Journal of Econometrics 67: 103–28. [Google Scholar] [CrossRef]
- Kilian, Lutz. 1998a. Small sample confidence intervals for impulse response functions. The Review of Economics and Statistics 80: 218–30. [Google Scholar] [CrossRef]
- Kilian, Lutz. 1998b. Accounting for lag-order uncertainty in autoregressions: The endogenous lag order bootstrap algorithm. Journal of Time Series Analysis 19: 531–38. [Google Scholar] [CrossRef]
- Kim, Jae H. 2004. Bootstrap Prediction Intervals for Autoregression using Asymptotically Mean-Unbiased Parameter Estimators. International Journal of Forecasting 20: 85–97. [Google Scholar] [CrossRef]
- Kim, Jae H. 2017. Stock Returns and Investors’ Mood: Good Day Sunshine or Spurious Correlation? International Review of Financial Analysis 52: 94–103. [Google Scholar] [CrossRef]
- Kim, Jae H. 2019. Tackling False Positives in Business Research: A Statistical Toolbox with Applications. Journal of Economic Surveys. [Google Scholar] [CrossRef]
- Kim, Jae H., and In Choi. 2017. Unit Roots in Economic and Financial Time Series: A Re-evaluation at the Decision-based Significance Levels. Econometrics 5: 41. [Google Scholar] [CrossRef]
- Kim, Jae H., and In Choi. 2019. Choosing the Level of Significance: A Decision-Theoretic Approach. Abacus: A Journal of Accounting, Finance and Business Studies. forthcoming. [Google Scholar]
- Kim, Jae H., and Philip Inyeob Ji. 2015. Significance Testing in Empirical Finance: A Critical Review and Assessment. Journal of Empirical Finance 34: 1–14. [Google Scholar] [CrossRef]
- Kim, Jae. H., Kamran Ahmed, and Philip Inyeob Ji. 2018. Significance Testing in Accounting Research: A Critical Evaluation based on Evidence. Abacus: A Journal of Accounting, Finance and Business Studies 54: 524–46. [Google Scholar] [CrossRef]
- Kleijnen, Jack P. C. 1995. Verification and validation of simulation models. European Journal of Operational Research 82: 145–62. [Google Scholar] [CrossRef]
- Labes, Detlew, Helmut Schuetz, and Benjamin Lang. 2018. Power and Sample Size Based on Two One-Sided t-Tests (TOST) for (Bio)Equivalence Studies, R Package Version: 1.4-7. Available online: https://cran.r-project.org/web/packages/PowerTOST/index.html (accessed on 31 May 2018).
- Lakens, Daniel, Anne M. Scheel, and Peder M. Isager. 2018. Equivalence Testing for Psychological Research: A Tutorial. Advances in Methods and Practices in Psychological Science 1: 259–69. [Google Scholar] [CrossRef]
- Lavergne, Pascal. 2014. Model Equivalence Tests in a Parametric Framework. Journal of Econometrics 178: 414–25. [Google Scholar] [CrossRef]
- Leamer, Edward. 1978. Specification Searches: Ad Hoc Inference with Nonexperimental Data. New York: Wiley. [Google Scholar]
- Leamer, Edward. 1988. Things that bother me. Economic Record 64: 331–35. [Google Scholar] [CrossRef]
- Lehmann, Erich L., and Joseph P. Romano. 2005. Testing Statistical Hypotheses, 3rd ed. New York: Springer. [Google Scholar]
- Lo, Andrew W., and A. Craig MacKinlay. 1990. Data Snooping in Tests of Financial Asset Pricing Models. Review of Financial Studies 10: 431–67. [Google Scholar] [CrossRef]
- Lothian, James R., and Mark P. Taylor. 1996. Real exchange rate behavior: The recent float from the perspective of the past two centuries. Journal of Political Economy 104: 488–510. [Google Scholar] [CrossRef]
- McCloskey, Deirdre N., and Stephen T. Ziliak. 1996. The standard error of regressions. Journal of Economic Literature 34: 97–114. [Google Scholar]
- Murphy, Kevin R., and Brett Myors. 1999. Testing the Hypothesis That Treatments Have Negligible Effects: Minimum-Effect Tests in the General Linear Model. Journal of Applied Psychology 84: 234–48. [Google Scholar] [CrossRef]
- Murphy, Kevin R., Brett Myors, and Allen Wolach. 2014. Statistical Power Analysis: A Simple and General Model for Traditional and Modern Hypothesis Tests, 4th ed. New York: Routledge. [Google Scholar]
- Nelson, Charles R., and Charles R. Plosser. 1982. Trends and random walks in macroeconomic time series. Journal of Monetary Economics 10: 139–62. [Google Scholar] [CrossRef]
- Ohlson, James A. 2018. Researchers’ Data Analysis Choices: An Excess of False Positives? Available online: https://ssrn.com/abstract=3089571 (accessed on 31 May 2018).
- Open Science Collaboration. 2015. Estimating the reproducibility of psychological science. Science 349: 6251. [Google Scholar] [CrossRef]
- Peng, Roger. 2015. The Reproducibility Crisis in Science: A Statistical Counterattack. Significance 12: 30–32. [Google Scholar] [CrossRef]
- Peracchi, Franco. 2001. Econometrics. New York: Wiley. [Google Scholar]
- R Core Team. 2017. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 31 May 2018).
- Rao, Calyampudi Radhakrishna, and Miodrag M. Lovric. 2016. Testing Point Null Hypothesis of a Normal Mean and the Truth: 21st Century Perspective. Journal of Modern Applied Statistical Methods 15: 2–21. [Google Scholar] [CrossRef]
- Robinson, Andrew P. 2016. Equivalence: Provides Tests and Graphics for Assessing Tests of Equivalence. R Package Version 0.7.2. Available online: https://cran.r-project.org/web/packages/equivalence/index.html (accessed on 31 May 2018).
- Robinson, Andrew P. 2019. Testing Simulation Models Using Frequentist Statistics. In Computer Simulation Validation: Fundamental Concepts, Methodological Frameworks, and Philosophical Perspectives. Edited by Claus Beisbart and Nicole Saam. Berlin: Springer. [Google Scholar]
- Robinson, Andrew P., and Robert E. Froese. 2004. Model validation using equivalence tests. Ecological Modelling 176: 349–58. [Google Scholar] [CrossRef]
- Robinson, Andrew P., Remko A. Duursma, and John D. Marshall. 2005. A regression-based equivalence test for model validation: Shifting the burden of proof. Tree Physiology 25: 903–13. [Google Scholar] [CrossRef] [PubMed]
- Saunders, Edward M. 1993. Stock prices and wall street weather. American Economic Review 83: 1337–45. [Google Scholar]
- Schotman, Peter C., and Herman K. van Dijk. 1991. On Bayesian routes to unit roots. Journal of Applied Econometrics 6: 387–401. [Google Scholar] [CrossRef]
- Shaman, Paul, and Robert A. Stine. 1988. The bias of autoregressive coefficient estimators. Journal of the American Statistical Association 83: 842–48. [Google Scholar] [CrossRef]
- Spanos, Aris. 2017. Mis-specification testing in retrospect. Journal of Economic Surveys 32: 541–77. [Google Scholar] [CrossRef]
- Startz, Richard. 2014. Choosing the More Likely Hypothesis. Foundations and Trends in Econometrics 7: 119–89. [Google Scholar] [CrossRef]
- van der Laan, Mark, Jiann-Ping Hsu, Karl E. Peace, and Sherri Rose. 2010. Statistics ready for a revolution: Next generation of statisticians must build tools for massive data sets. Amstat News 399: 38–39. [Google Scholar]
- Walker, Esteban, and Amy S. Nowacki. 2011. Understanding Equivalence and Noninferiority Testing. Journal of General Internal Medicine 26: 192–96. [Google Scholar] [CrossRef] [PubMed]
- Wasserstein, Ronald L., and Nicole A. Lazar. 2016. The ASA’s statement on p-values: Context, process, and purpose. The American Statistician 70: 129–33. [Google Scholar] [CrossRef]
- Wellek, Stefan. 2010. Testing Statistical Hypotheses of Equivalence and Noninferiority, 2nd ed. New York: CRC Press. [Google Scholar]
- Wellek, Stefan, and Peter Ziegler. 2017. EQUIVNONINF: Testing for Equivalence and Noninferiority. R Package Version 1.0. Available online: https://CRAN.R-project.org/package=EQUIVNONINF (accessed on 31 May 2018).
- Winer, Ben J. 1962. Statistical Principles in Experimental Design. New York: McGraw-Hill. [Google Scholar]
- Ziliak, Steve T., and Deirdre Nansen McCloskey. 2008. The Cult of Statistical Significance: How the Standard Error Costs Us Jobs, Justice, and Lives. Ann Arbor: The University of Michigan Press. [Google Scholar]
| 1 | There are two other R packages for equivalence and non-inferiority tests. One is EQUIVNONINF (Wellek and Ziegler 2017) which accompanies the book by Wellek (2010), and the other is PowerTOST (Labes et al. 2018), which contains functions to calculate power and sample size for various study designs used for bio-equivalence studies. |
| 2 | |
| 3 |
| Market | T | F | |||||
|---|---|---|---|---|---|---|---|
| US1 | 18,380 | 0.011 | 20.43 | 1.83 | 26.87 | 120.25 | 245.15 |
| US2 | 9688 | 0.027 | 29.84 | 1.88 | 15.76 | 66.27 | 133.20 |
| US3 | 7083 | 0.033 | 26.82 | 1.88 | 12.33 | 49.83 | 99.26 |
| US4 | 9688 | 0.091 | 107.66 | 1.88 | 15.77 | 66.27 | 133.20 |
| SWE | 4836 | 0.017 | 9.28 | 1.88 | 9.29 | 35.46 | 69.70 |
| UK | 4534 | 0.009 | 4.57 | 1.88 | 8.87 | 33.51 | 65.69 |
| GER | 9411 | 0.008 | 8.42 | 1.88 | 15.40 | 64.53 | 129.61 |
| CAN | 8308 | 0.030 | 28.52 | 1.88 | 13.96 | 57.58 | 115.26 |
| NZ | 2627 | 0.010 | 3.31 | 1.94 | 6.79 | 23.49 | 45.04 |
| JAP | 12,783 | 0.002 | 3.20 | 1.94 | 22.11 | 96.18 | 194.77 |
| AUS | 5521 | 0.010 | 6.19 | 1.88 | 10.22 | 39.86 | 78.75 |
| SA | 7247 | 0.010 | 8.12 | 1.88 | 12.54 | 50.87 | 101.41 |
| Model | GRS | Ratio | ||||
|---|---|---|---|---|---|---|
| CAPM | 4.41 | 0.74 | 0.25 | 1.52 | 1.88 | 0.25 |
| 3-factor | 3.61 | 0.92 | 0.10 | 1.52 | 2.62 | 0.46 |
| 4-factor | 3.07 | 0.92 | 0.09 | 1.52 | 3.70 | 0.63 |
| 5-factor | 2.79 | 0.92 | 0.09 | 1.52 | 4.03 | 0.67 |
| T | p-Value | t-Stat | ||||
|---|---|---|---|---|---|---|
| R.GNP | 80 | 0.05 | −0.140 | −0.66 | −0.298 | −0.037 |
| N.GNP | 80 | 0.58 | −0.010 | 2.96 | −0.147 | −0.0001 |
| P.GNP | 80 | 0.04 | −0.150 | −0.82 | −0.304 | −0.043 |
| IP | 129 | 0.26 | −0.098 | −0.21 | −0.274 | −0.002 |
| Emp | 99 | 0.18 | −0.118 | −0.21 | −0.242 | −0.031 |
| Uemp | 99 | 0.01 | −0.214 | −1.53 | −0.430 | −0.074 |
| Def | 100 | 0.70 | −0.003 | 5.56 | −0.081 | −0.0001 |
| CPI | 129 | 0.91 | −0.002 | 13.22 | −0.019 | −0.0001 |
| Wages | 89 | 0.53 | −0.026 | 2.81 | −0.144 | −0.0002 |
| Rwages | 89 | 0.75 | −0.010 | 1.90 | −0.183 | −0.0002 |
| MS | 100 | 0.18 | −0.037 | 3.83 | −0.110 | −0.0016 |
| Vel | 120 | 0.78 | −0.001 | 4.65 | −0.099 | −0.0001 |
| Rate | 89 | 0.98 | −0.025 | 2.35 | −0.191 | −0.0004 |
| S&P | 118 | 0.64 | −0.021 | 2.15 | −0.144 | −0.0002 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.H.; Robinson, A.P. Interval-Based Hypothesis Testing and Its Applications to Economics and Finance. Econometrics 2019, 7, 21. https://doi.org/10.3390/econometrics7020021
Kim JH, Robinson AP. Interval-Based Hypothesis Testing and Its Applications to Economics and Finance. Econometrics. 2019; 7(2):21. https://doi.org/10.3390/econometrics7020021
Chicago/Turabian StyleKim, Jae H., and Andrew P. Robinson. 2019. "Interval-Based Hypothesis Testing and Its Applications to Economics and Finance" Econometrics 7, no. 2: 21. https://doi.org/10.3390/econometrics7020021
APA StyleKim, J. H., & Robinson, A. P. (2019). Interval-Based Hypothesis Testing and Its Applications to Economics and Finance. Econometrics, 7(2), 21. https://doi.org/10.3390/econometrics7020021






