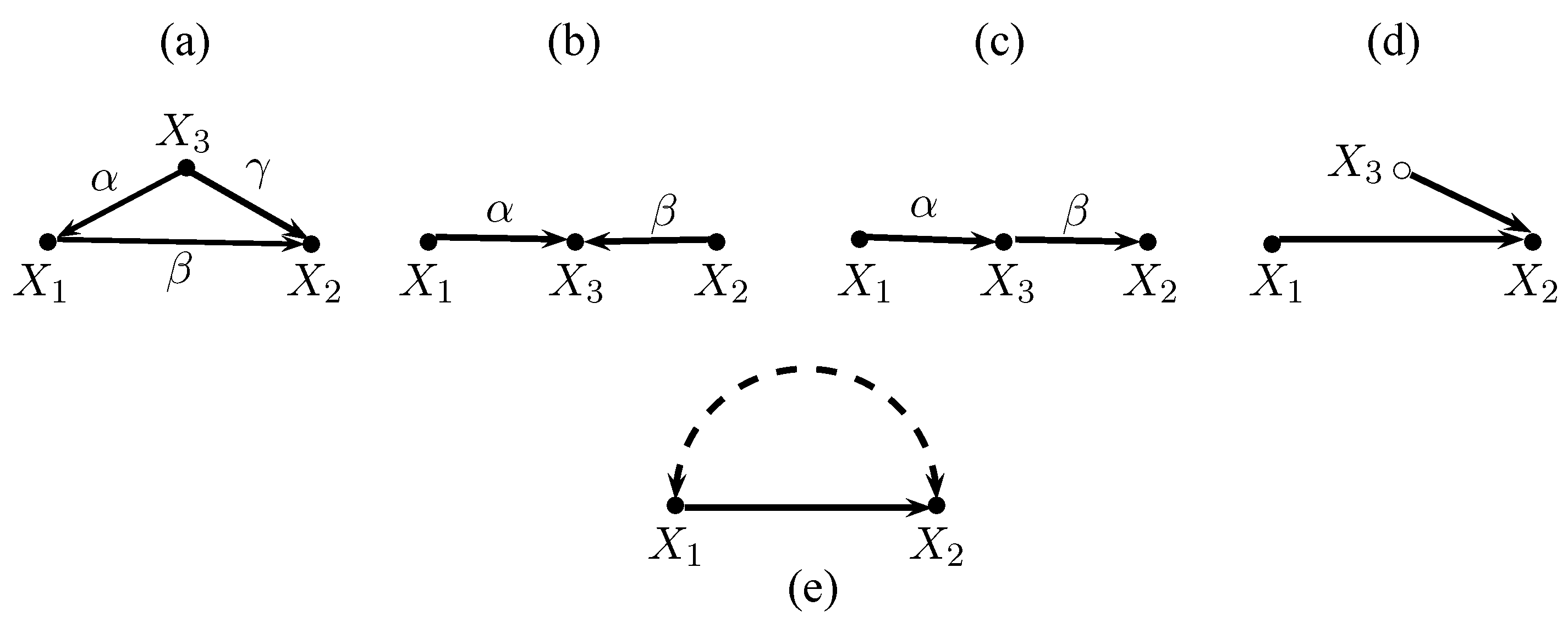1. Introduction
A popular strategy for estimating the causal effect of a latent variable in a linear structural model is to replace the latent variable with an indicator. It is usually assumed that the indicator variable is driven by the latent variable and some random noise.
1 The effect of the latent variable is then estimated from the resulting auxiliary model.
It is well known that the ordinary least squares (OLS) method does not provide consistent coefficient estimates because the indicator becomes endogenous in the auxiliary model. In contrast, instrumental variable (IV) methods provide consistent estimates when a valid instrument is used for the indicator.
This paper looks at indicators of latent variables that violate the classical assumptions. In contrast to ordinary effect indicators, these indicators are also systematically influenced by variables that are not part of the structural model of interest. Such “background indicators” deserve attention because in empirical work they can easily be confused with ordinary effect indicators. This paper studies how background indicators affect the identification and estimation of causal effects of latent variables in linear models.
Background indicators are subtle. As just mentioned, background indicators are influenced by “background variables” that do not belong to the structural model of interest. Thus, background indicators do not directly affect the dependent variable. However, a background indicator can, in contrast to an ordinary effect indicator, also be a cause of the latent variable. In this case, the background indicator affects the dependent variable only indirectly via the latent variable. Background indicators can invalidate otherwise perfectly valid instruments for the latent variable. This happens because of the chosen indicator and not because there is something fundamentally wrong with the instrument. Moreover, in certain cases one must control for the background variable in an IV estimation although the indicator has neither a direct nor an indirect effect on the dependent variable, and although the instrument for the latent variable is valid. Furthermore, when a background indicator causes the latent variable it can happen that IV estimation yields the causal effect of the indicator rather than the causal effect of the latent variable. The objective of this paper is to explain these notable results in detail.
Background indicators can in principle occur in any empirical study in which latent variables are replaced by indicators. The following two examples from economics are cases where background indicators might occur. The discussion aims to highlight possible scenarios and should not be understood as a critique of the empirical results of these studies.
The first example is about the impact of financial development on economic growth. Financial development is an unobservable variable. Therefore, bank credit relative to gross domestic product (GDP) is often used as an indicator for the development of the banking sector of a country.
2 However, credit to GDP ratios may capture more than domestic financial development. International financial integration may also affect credit to GDP ratios, in particular in developing economies where foreign lending is important (
Giannetti and Ongena 2009). Furthermore, international financial integration may also directly affect the financial sector of a country via entry, or the thread of entry of foreign banks. Thus, credit to GDP ratios may be background indicators of financial development, and international financial integration may be a background variable.
The second example deals with uncertainty and economic activity. Empirical studies about the impact of uncertainty on economic activity often use stock market volatility to measure uncertainty.
3 For example,
Bloom (
2009) finds that stock market volatility rises sharply after bad events such as war or terror. However, these bad events may simultaneously affect stock market volatility and economic uncertainty. Moreover, high levels of stock market volatility may amplify uncertainty when people see the stock market as a predictor of future economic activity (
Farmer 2015;
Romer 1990). Stock market volatility could therefore be a background indicator of uncertainty that sometimes reinforces economic uncertainty even further.
The analysis in this paper builds on causal graphs and path-tracing rules (
Chen and Pearl 2014;
Morgan and Winship 2007;
Pearl 2009). Causal graphs make modeling assumptions transparent, and the path-tracing rules yield algebraic expressions for OLS and IV estimates when the model is linear.
Graphical methods for studying structural models are well known in statistics, computer science, and sociology, but are relatively unknown in economics.
4 Therefore, the next section provides a gentle introduction to the graphical methods that are used in this paper. The book of
Pearl (
2009) provides a comprehensive and much more general treatment of graphical methods and causal inference.
The graphical analysis proceeds in two steps. The analysis first presents some results about identification of effects of latent variables with IV methods and ordinary effect indicators through the lens of graphical methods. Additional control variables can play an important role in the identification of the causal effect of a latent variable. The exposition therefore explains what types of control variables enable or prevent identification of effects of latent variables. The results about control variables also apply when IV methods are used to identify effects of observable variables. Some of these results are not all widely known and are not discussed in standard econometrics texts. The main point of this first step is to equip the reader with general results that are also relevant in the analysis of background indicators.
Then the analysis moves on to background indicators. The analysis shows that background indicators complicate the identification of effects of latent variables. Moreover, background indicators often produce inconsistent estimates in empirically relevant cases. The last part of the graphical analysis shows that a background indicator can nevertheless be a useful instrument for an effect indicator.
5A simple simulation experiment in which stock market volatility is used to estimate the effect of uncertainty on consumption illustrates how background indicators can affect OLS and IV estimates. The experiment shows that the negative impact of uncertainty on consumption may be overestimated when stock market volatility is a background indicator.
2. Graphs and Path-Tracing Rules
This section introduces causal graphs and the path-tracing rules that are used in this paper.
Figure 1 shows five graphs. Solid nodes represent observed variables, hollow nodes represent unobserved variables, solid arrows indicate causal links, and curved dashed bi-directed arrows indicate covariances that arise from unspecified causes. Hence, all variables in
Figure 1a–c are observed,
is unobserved in
Figure 1d, and
causes
in
Figure 1e but the variables are also correlated because of other unmodeled causes.
A
path is a sequence of nodes connected by arrows. A path is
d-connected if it does not traverse any collider.
6 A variable is a
collider on a path if two arrows are pointing into it. Thus, the paths
and
in
Figure 1a are d-connected. The path
in
Figure 1b is not d-connected because
is a collider that blocks the path.
A path between two variables and can be blocked or d-separated by a set of variables S in two ways. The path can be blocked by conditioning when the path contains a chain or a fork and the middle variable is in the conditioning set S. The path between and is also blocked when the path contains a collider and the collider (or any of its descendants) is not in the conditioning set S. As a consequence, two variables and are d-connected conditional on a set of variablesS if there is a collider-free path between them that does not traverse any member of S, or if there is a path between them where a collider is in the conditioning set S.
Two simple
path-tracing rules (
Pearl 2013) yield analytical expressions for covariances between variables in a graph.
7 The resulting expressions for the covariances can be substituted into other formulas.
The first path-tracing rule applies to standardized variables (i.e., variables that have been normalized to have zero mean and unit variance). Let be the product of the path coefficients along a path i that d-connects two standardized variables A and B, say. Path coefficients can either be structural coefficients or covariances. The first rule states that the covariance between A and B is the sum of the products of the path coefficients along all d-connected paths between A and B, i.e., .
The second path-tracing rule extends the first path-tracing rule to non-standardized variables. The product associated with a path i of non-standardized variables A and B must be multiplied by the variance of the variable from which path i originates. Double arrows serve as their own origin. Thus, when A and B are non-standardized variables, then .
It is instructive to use the path-tracing rules to derive the covariance between
and
conditional on
in
Figure 1a–c, because the results show how conditioning on a third variable may affect the covariance between the other two variables. Equation (
1) expresses the covariance between
and
conditional on
,
in terms of the unconditional covariances. For convenience, let us assume that
,
, and
are standardized multivariate normally distributed random variables.
8 Thus,
.
In
Figure 1a conditioning uncovers the causal effect of
on
. Fixing
blocks the path
. Path-tracing yields
,
and
. Plugging these expressions into (
1) yields
.
In
Figure 1b the variables
and
are independent. Thus,
, but conditioning on the common outcome
creates dependence between
and
. Intuitively, information about one of the causes makes the other cause more or less likely, given that we know the outcome. Here,
,
, and (
1) yields
.
In
Figure 1c the variable
mediates the effect of
on
. The unconditional covariance is
. Conditioning on
breaks this link, and
.
3. Effect Indicators
In empirical studies it is common that a model for the dependent variable contains one or more explanatory variables of interest and some additional control variables that should help to identify causal effects of the explanatory variables of interest. Here we are interested in the causal effect of a latent variable
L. In this paper,
I always denotes an indicator of the latent variable. In this section,
I is an effect indicator. Later, in
Section 4 and
Section 5, the letter
I will denote a background indicator that is affected by a background variable
B.
Let us now consider a linear structural model
where
Y is the dependent variable,
L is a latent variable,
X is a column vector of control variables,
is a row vector of coefficients, and
u is an error term. The coefficient
measures the effect of
L on
Y.
If
L were observable, OLS would provide a consistent estimate for
if in the population there is no exact linear relationship between the regressors and the error
u has mean zero and is uncorrelated with each of the regressors.
9 However, here we cannot observe
L.
A standard solution to this problem is to find an indicator
I of the latent variable of the form
where the error
e is assumed to be uncorrelated with
L. Most latent variables have no natural scale. It is, therefore, common to set
, so that the observable indicator and the latent variable have the same scale.
Rearranging (
3) and plugging in for
L in (
2) yields
where
=
and
.
10 It is easy to show that the indicator
I is correlated with the compound error
and therefore endogenous. Thus, OLS is inconsistent.
Let us now turn to IV estimation of model (
4). For simplicity, let us assume that the structural model (
2) has only a single control variable
X and that all variables are demeaned such that
. Let
Z be an instrument for the latent variable
L. The IV estimator for
in the auxiliary model (
4) is (
Bowden and Turkington 1984)
When
Z is uncorrelated with
X (i.e.,
) then Equation (
5) collapses to the simple IV estimator
that arises when model (
4) is estimated without
X.
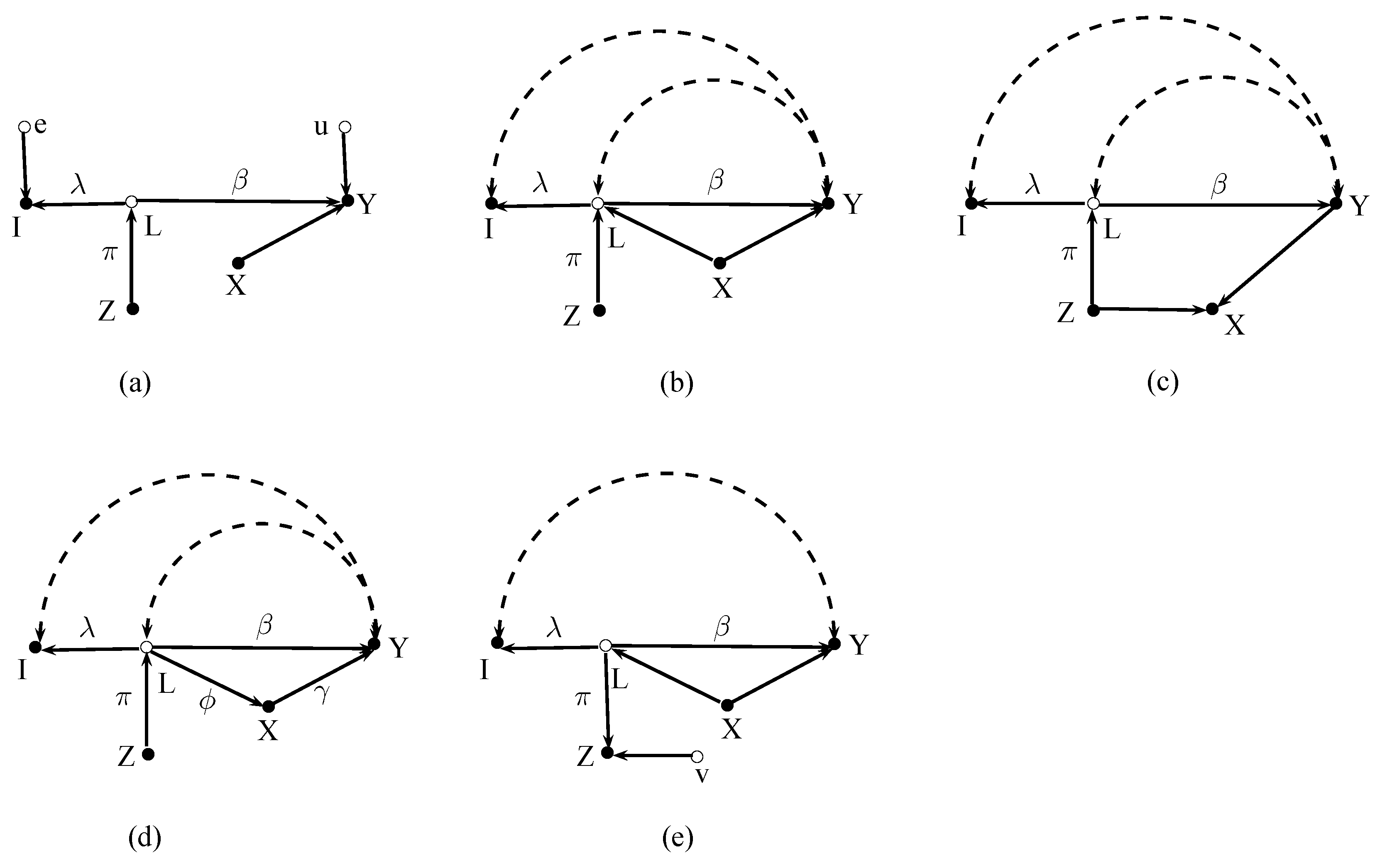
11Figure 2 depicts five causal graphs where
I is an effect indicator of the latent variable
L.
Figure 2a shows a case where the error
e in
I and the error
u in the structural model (
2) are uncorrelated. This is the standard assumption made in applied work. One path connects
Z and
Y via
L, and one path runs from
Z via
L to
I. Hence,
and
=
. Moreover,
because the only path between
Z and
X is blocked by
Y. Thus, the simple IV estimator applies. Plugging the expressions for
and
into (
6) yields
and hence
by imposing
= 1 in (
3).
12 Figure 2b relaxes the standard assumption of uncorrelated errors because the errors
e and
u are correlated. Furthermore,
X is now a confounding variable, and the latent variable
L in the structural model is endogenous because of neglected other joint causes of
L and
Y. These complications appear to be substantial, but they have no effect because
L and
I are colliders. In particular,
. The simple IV estimator still applies, and there is no need to control for the confounding variable
X.
Figure 2c shows a case where
X is an outcome of
Z and
Y. Including
X in the regression would now be harmful because the “back-door” path between
Z and
Y would be opened.
Z is only a valid instrument for
I without controlling for
X. Path-tracing verifies that the simple IV estimator (
6) works, but the IV estimator (
5) that takes
X into account does not.
In
Figure 2d the latent variable affects the dependent variable directly and indirectly via the mediating variable
X. Now, the IV estimator
yields the direct effect of the latent variable
L. The simple IV estimator yields
, which is the total effect (i.e., the direct + the indirect effect) of
L on
Y. Hence, identification of the direct effect of the latent variable requires controlling for the mediating variable
X.
In the former cases the instrument
Z caused the latent variable
L.
Figure 2e shows a situation where the instrument
Z is a second effect indicator of
L. This apparently minor difference to the former cases has important consequences. First, the errors
e and
u may be correlated but the error
v in
Z must be uncorrelated with both errors. Second, the latent variable
L must now be exogenous in the structural model (i.e., there must be no double arrows between
L and
Y). Third, one must control for all
L –
Y confounding variables. Then the ratio
is identified. While conditioning
L –
Y confounders is necessary for identification, conditioning on
L –
Y mediators (such as the
X variable in
Figure 2d) is only necessary if one wants to disentangle direct and indirect effects of the latent variable and not to obtain the total effect. Thus, IV estimates of the effect of the latent variable that are based on two effect indicators require stronger assumptions than estimates where the instrument causes the latent variable.
4. Background Indicators
As already explained, background indicators are, in contrast to ordinary indicators, also systematically affected by variables that are not part of the original structural model. Background variables could be joint causes of the latent variable and the indicator, or they could be variables that mediate effects of the latent variable to the indicator.
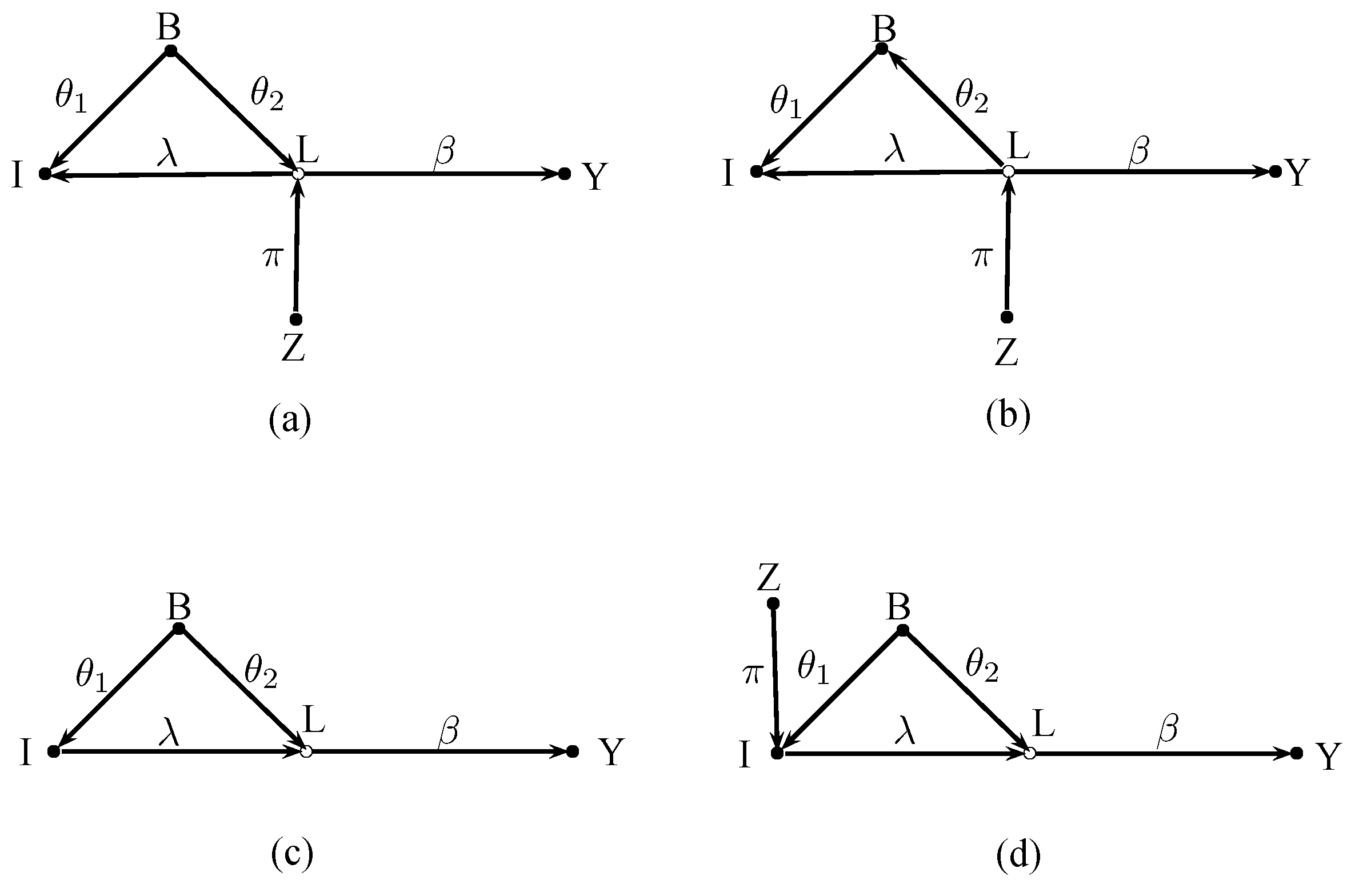
Figure 3 shows four cases with background indicators. For clarity, the graphs now abstract from error terms and additional control variables because these issues have already been discussed in the previous section.
Figure 3a,b describe cases that could occur in studies on the link between financial development and economic growth. In these examples
Y is economic growth and
L is financial development, which is the latent variable we are interested in. The variable
I is a ratio of bank credit to GDP,
B is a background variable such as international financial integration, and
Z is an instrument for financial development. Empirical studies have for instance used the origin of the legal system of a country as an instrument for the development of its financial system (
Levine et al. 2000).
In
Figure 3a the background variable
B causes the latent variable
L and the indicator
I. The covariance between
Z and
Y is
, and the covariance between
I and
Z is
. The resulting IV estimate is therefore
As can be seen, this estimate is not affected by the background indicator. The usual practice of setting may be more difficult to justify, however.
Figure 3b shows a situation where the latent variable affects the indicator directly and indirectly via the mediating background variable
B. The covariances are now
and
. The IV estimate becomes
Thus, the presence of
B biases the simple IV estimate. This bias can only be removed by controlling for
B, as can be verified by computing the IV estimate
using (
5). Remarkably, in case (b) the background variable
B must be included in the regression, even though
B does not affect the dependent variable
Y in the structural model.
Figure 3c,d shows two cases that could for example occur in studies about effects of uncertainty on economic activity. Here,
Y is economic activity,
L is the unobservable uncertainty,
I is stock market volatility, a frequently used indicator of uncertainty, and
B is a background variable.
Figure 3c,d depict a situation, as considered in
Romer (
1990), where a stock market crash or extreme stock market volatility becomes an additional source of uncertainty in an economy. Certain events
B such as terrorist attacks, wars, or other bad events may raise uncertainty in the economy. Without a stock market there would be no further source of uncertainty. However, here a stock market exists, and the events
B may also affect the uncertainty of stock traders about the future course of the economy. This uncertainty is reflected in the volatility of the stock market. Please note that the traders may sit anywhere (i.e., in large international financial institutions) and may not necessarily belong to the economy of interest. While people may not own stocks themselves, they interpret the stock market as a predictor of their future income, and they become nervous when they see extreme stock market volatility. Stock market volatility now becomes an additional source of uncertainty that amplifies the uncertainty in the economy even further.
As already mentioned, background indicators may easily get confused with ordinary effect indicators.
Figure 3c depicts such a case. The background variable
B captures exogenous events that simultaneously drive uncertainty
L and stock market volatility
I, but volatility amplifies uncertainty further. Variables that cause only the latent variable do not work as instruments here because such variables are necessarily uncorrelated with the indicator. Thus, one is tempted to use the exogenous variable
B that is correlated with the indicator
I as an instrument.
Using
B mistakenly as an instrument for
I yields
and
. The resulting IV estimate
is inconsistent. The estimate captures three distinct effects, namely the effect
of
I on
Y, the effect
of
B on
Y, and the strength
of the effect of
B on
I. The estimate tends to the causal effect of
I on
Y when
is small. When
is close to zero the estimate blows up, because
B becomes a weak instrument.
What does OLS yield when stock market volatility amplifies uncertainty? Since
the OLS estimate
is also biased and inconsistent because the background variable
B has been omitted. The second term in (
11) reflects this bias.
Regressing
Y on
I and
B removes the omitted variable bias in (
11), but the resulting estimate
is the causal effect of
I on
Y. In this example one would therefore estimate the causal effect of stock market volatility on output rather than the effect of uncertainty on output.
Let us now assume that
. In this case, exogenous bad events affect the uncertainty of traders and the public to the same extent and stock market volatility fully amplifies uncertainty. Let us further assume that the effect of uncertainty on output is negative, as theory predicts.
13 The IV estimate given in (
10) becomes
and the OLS estimate (
11) is
where
r denotes the ratio of
. Both quantities overestimate the magnitude of the (negative) effect of uncertainty, but OLS can get close to
when
r is small. In contrast, a weaker link (i.e.,
) between
B and
I would inflate the IV estimate further.
Figure 3d shows a case where
Z is indeed a valid instrument for stock market volatility
I. Even if such an instrument could be found it would not solve the problem. Path-tracing yields
and
. The resulting IV estimate
would capture the causal effect of stock market volatility on output rather than the effect of uncertainty on output.
7. Conclusions
Background indicators of latent variables have until now been neglected although they might easily be confused with ordinary effect indicators. This paper studied simple linear models to gain a conceptual understanding of background indicators.
The analysis showed that background indicators produce inconsistent estimates of effects of latent variables in empirically relevant cases. In the simulation experiment, for instance, the estimated effects of uncertainty are too large when stock market volatility is a background indicator of uncertainty. Background indicators may be useful instruments, but they should not replace latent variables in a structural model. The results also suggest that the choice of indicators should, just like the choice credibility of instruments, be guided by theoretical considerations and careful judgment.
Future work could extend the analysis to nonlinear models. Analytical results are then of course more difficult to obtain. Another possible extension would be to investigate the usefulness of causal search algorithms for identifying background indicators. These issues are, however, beyond the scope of this paper and are left for future research.