1. Introduction
In many applications, the available data are not of quantitative nature (e.g., real numbers or counts) but consist of observations from a given finite set of categories. In the present article, we are concerned with data about political goals in Germany, fear states in the stock market, and phrases in a bird’s song. For stochastic modeling, we use a
categorical random variable
X, i.e. a qualitative random variable taking one of a finite number of categories, e.g.
categories with some
. If these categories are unordered,
X is said to be a
nominal random variable, whereas an
ordinal random variable requires a natural order of the categories (
Agresti 2002). To simplify notations, we always assume the possible outcomes to be arranged in a certain order (either lexicographical or natural order), i.e. we denote the range (state space) as
. The stochastic properties of
X can be determined based on the vector of marginal probabilities by
, where
(probability mass function, PMF). We abbreviate
for
, where
has to hold. The subscripts “
” are used for
and
p to emphasize that only
m of the probabilities can be freely chosen because of the constraint
.
Well-established dispersion measures for quantitative data, such as variance or inter quartile range, cannot be applied to qualitative data. For a categorical random variable
X, one commonly defines dispersion with respect to the uncertainty in predicting the outcome of
X(
Kvålseth 2011b;
Rao 1982;
Weiß and Göb 2008). This uncertainty is maximal for a uniform distribution
on
(a reasonable prediction is impossible if all states are equally probable, thus maximal dispersion), whereas it is minimal for a one-point distribution
(i.e., all probability mass concentrates on one category, so a perfect prediction is possible). Obviously, categorical dispersion is just the opposite concept to the concentration of a categorical distribution. To measure the dispersion of the categorical random variable
X, the most common approach is to use either the (normalized)
Gini index (also
index of qualitative variation, IQV) (
Kvålseth 1995;
Rao 1982) defined as
or the (normalized)
entropy (
Blyth 1959;
Shannon 1948) given by
Both measures are minimized by a one-point distribution and maximized by the uniform distribution on . While nominal dispersion is always expressed with respect to these extreme cases, it has to be mentioned that there is an alternative scenario of maximal ordinal variation, namely the extreme two-point distribution; however, this is not further considered here.
If considering a (stationary) categorical process
instead of a single random variable, then not only marginal properties are relevant but also information about the serial dependence structure (
Weiß 2018). The (signed) autocorrelation function (ACF), as it is commonly applied in case of real-valued processes, cannot be used for categorical data. However, one may use a type of
Cohen’s κ instead (
Cohen 1960). A
-measure of signed serial dependence in categorical time series is given by (see
Weiß 2011,
2013;
Weiß and Göb 2008);
Equation (
3) is based on the lagged bivariate probabilities
for
.
for serial independence at lag
h, and the strongest degree of positive (negative) dependence is indicated if all
(
), i.e., if the event
is necessarily followed by
(
).
Motivated by a mobility index discussed by
Shorrocks (
1978), a simplified type of
-measure, referred to as the
modified κ, was defined by
Weiß (
2011,
2013):
Except the fact that the lower bound of the range differs from the one in Equation (
3) (note that this lower bound is free of distributional parameters), we have the same properties as stated before for
. The computation of
is simplified compared to the one of
and, in particular, its sample version
has a more simple asymptotic normal distribution, see
Section 5 for details. Unfortunately,
is not defined if only one of the
equals 0, whereas
is well defined for any marginal distribution not being a one-point distribution. This issue may happen quite frequently for the sample version
if the given time series is short (a possible circumvention is to replace all summands with
by 0). For this reason,
appear to be of limited use for practice as a way of quantifying signed serial dependence. It should be noted that a similar “zero problem” happens with the entropy
in Equation (
2), and, actually, we work out a further relation between
and
below.
In the recent work by
Lad et al. (
2015),
extropy was introduced as a complementary dual to the entropy. Its normalized version is given by
Here, the zero problem obviously only happens if one of the
equals 1 (i.e., in the case of a one-point distribution). Similar to the Gini index in Equation (
1) and the entropy in Equation (
2), the extropy takes its minimal (maximal) value 0 (1) for
(
), thus also Equation (
5) constitutes a normalized measure of nominal variation. In
Section 2, we analyze its properties in comparison to Gini index and entropy. In particular, we focus on the respective sample versions
,
and
(see
Section 3). To be able to do statistical inference based on
,
and
, knowledge about their distribution is required. Up to now, only the asymptotic distribution of
and (to some part) of
has been derived; in
Section 3, comprehensive results for all considered dispersion measures are provided. These asymptotic distributions are then used as approximations to the true sample distributions of
,
and
, which is further investigated with simulations and a real application (see
Section 4).
The second part of this paper is dedicated to the analysis of serial dependence. As a novel competitor to the measures in Equations (
3) and (
4), a new type of modified
is proposed, namely
Again, this constitutes a measure of signed serial dependence, which shares the before-mentioned (in)dependence properties with
. However, in contrast to
, the newly proposed
does not have a division-by-zero problem: except for the case of a one-point distribution,
is well defined. Note that, in
Section 3.2, it turns out that
is related to
in some sense, e.g.
is related to
and
to
. In
Section 5, we analyze the sample version of
in comparison to those of
, and we derive its asymptotic distribution under the null hypothesis of serial independence. This allows us to test for significant dependence in categorical time series. The performance of this
-test, in comparison to those based on
, is analyzed in
Section 6, where also two further real applications are presented. Finally, we conclude in
Section 7.
2. Extropy, Entropy and Gini Index
As extropy, entropy and Gini index all serve for the same task, it is interesting to know their relations and differences. An important practical issue is the “
”-problem, as mentioned above, which never occurs for the Gini index, only occurs in the case of a (deterministic) one-point distribution for the extropy, and always occurs for the entropy if only one
.
Lad et al. (
2015) further compared the non-normalized versions of extropy and entropy, and they showed that the first is never smaller than the latter. Actually, using the inequality
for
from
Love (
1980), it follows that
(see
Appendix B.1 for further details).
Things change, however, if considering the normalized versions
,
and
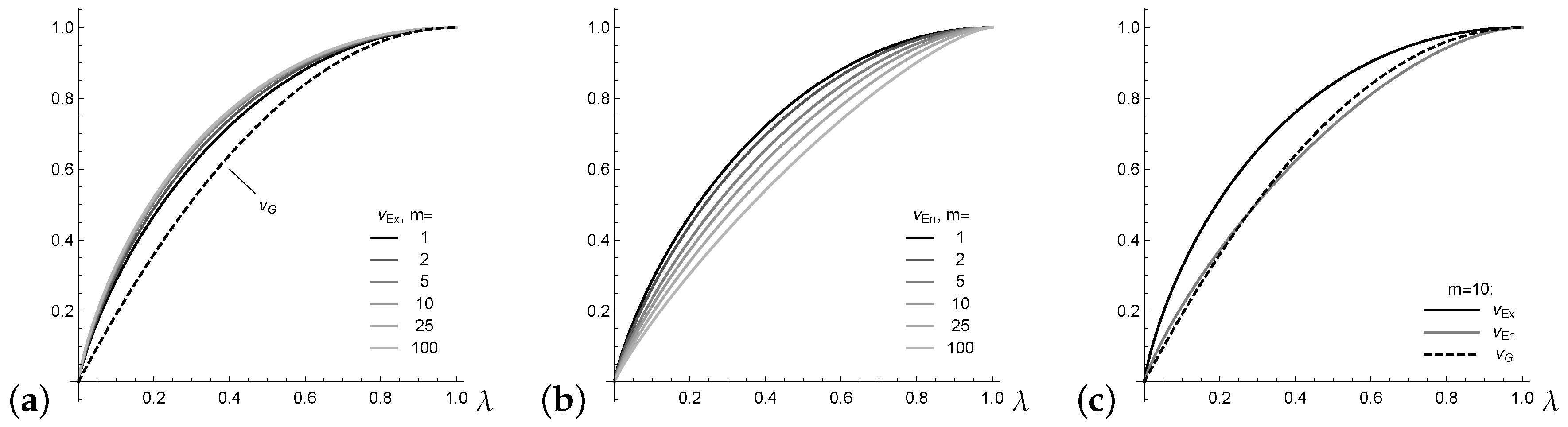
. For illustration, assume an underlying Lambda distribution
with
defined by the probability vector
(
Kvålseth 2011a). Note that
leads to a one-point distribution, whereas
leads to the uniform distribution; actually,
can be understood as a mixture of these boundary cases. For
, the Gini index satisfies
for all
(see
Kvålseth (
2011a)). In addition, the extropy
has rather stable values for varying
m (see
Figure 1a), whereas the entropy values in
Figure 1b change greatly. This complicates the interpretation of the actual level of normalized entropy.
Finally, the example
plotted in
Figure 1c shows that, in contrast to Equation (
7), there is no fixed order between the normalized entropy
and Gini index
. In this and many further numerical experiments, however, it could be observed that the inequalities
and
hold. These inequalities are formulated as a general conjecture here.
From now on, we turn towards the sample versions
of
. These are obtained by replacing the probabilities
by the respective estimates
, which are computed as relative frequencies from the given sample data
. As detailed in
Section 3,
are assumed as time series data, but we also consider the case of independent and identically distributed (i.i.d.) data.
5. Measures of Signed Serial Dependence
After having discussed the analysis of marginal properties of a categorical time series, we now turn to the analysis of serial dependencies. In
Section 1, two known measures of signed serial dependence, Cohen’s
in Equation (
3) and a modification of it,
in Equation (
4), are briefly surveyed, and, in
Section 3.2, we realize a connection to
and
, respectively. Motivated by a zero problem with
, a new type of modified
is proposed in Equation (
6), the measure
, and this turns out to be related to
.
If replacing the (bivariate) probabilities in Equations (
3), (
4) and (
6) by the respective (bivariate) relative frequencies computed from
, we end up with sample versions of these dependence measures. Knowledge of their asymptotic distribution is particularly relevant for the i.i.d.-case, because this allows us to test for significant serial dependence in the given time series. As shown by
Weiß (
2011,
2013),
then has an asymptotic normal distribution, and it holds approximately that
The sample version of
has a more simple asymptotic normal distribution with
Weiß (
2011,
2013)
but it suffers from the before-mentioned zero problem, especially for short time series.
Thus, it remains to derive the asymptotics of the novel
under the null of an i.i.d. sample
. The starting point is an extension of the limiting result in Equation (
8). Under appropriate mixing assumptions (see
Section 3),
Weiß (
2013) derived the joint asymptotic distribution of
all univariate and equal-bivariate relative frequencies, i.e. of all
and
, which is the
-dimensional normal distribution
. The covariance matrix
consists of four blocks with entries
where always
, and where
This rather complex general result simplifies greatly special cases such as an NDARMA- DGP (
Weiß 2013) and, in particular, for an i.i.d. DGP:
Now, the asymptotic properties of
can be derived, as done in
Appendix B.3.
is asymptotically normally distributed, and mean and variance can be approximated by plugging Equation (
18) into
In the i.i.d.-case, we simply have
Comparing Equations (
16), (
17) and (
21), we see that all three measures have the same asymptotic bias
, but their asymptotic variances generally differ. An exception to the latter statement is obtained in the case of a uniform distribution, then also the asymptotic variances coincide (see
Appendix B.3).