Abstract
We propose an Aitken estimator for Gini regression. The suggested -Gini estimator is proven to be a U-statistics. Monte Carlo simulations are provided to deal with heteroskedasticity and to make some comparisons between the generalized least squares and the Gini regression. A Gini-White test is proposed and shows that a better power is obtained compared with the usual White test when outlying observations contaminate the data.
JEL Classification:
C14; C3
1. Introduction
Among regressions, the Gini regression initiated by Olkin and Yitzhaki (1992) is increasingly used in econometrics. It enables traditional hypotheses to be relaxed such as the linearity of the model. Moreover, it is well suited for the study of variables contaminated by outliers or measurement errors. The reader is referred to Yitzhaki and Schechtman (2013) for a complete overview of the Gini methodology.
Shelef and Schechtman (2011) and Carcea and Serfling (2015) investigated independently the use of the Gini autocovariance functions to estimate, respectively, the parameter of AR(1) and ARMA processes in the case of heavy tailed distributions such as Pareto processes. Recently, Mussard and Ndiaye (2018) investigated the semi-parametric Gini regression for vector autoregressive models in which non-spherical disturbances occur. They showed that premultiplying the model by a matrix that neutralizes the Gini covariance of the error terms may produce non-biased Gini estimators.
In the context of semi-parametric Gini regressions, we showed that the Aitken transformation (Aitken 1935) for non-spherical disturbances based on the variance provides exactly the same estimator obtained by neutralizing the Gini covariance of the error term. However, the convergence of the former estimator requires the existence of the second moment of the error term, whereas the latter is a U-statistics. Monte Carlo simulations are addressed in order to show the superiority of the Aitken-Gini estimator compared with the traditional GLS estimator in the presence heteroskedasticity. It is also shown that the usual White test to detect heteroskedasticity should be done in the Gini sense, that is, by testing the Gini covariance of the regressors instead of their variance. In this case, more power is obtained for small samples. Finally, a feasible generalized Gini regression is provided. It consists in estimating the residuals of the regression (with the semi-parametric Gini regression) and to plug those residuals in the model to purge the heteroskedasticity (with a Gini instrumental variable regression). Monte Carlo simulations prove the superiority of this algorithm in the presence of outlying observations compared with the usual White algorithm based on generalized least squares.
The remainder of this paper is outlined as follows. We begin in Section 2 with the two versions of the Aitken-Gini estimator based, respectively, on the variance and on the Gini covariance, before showing their equivalence. Section 3 is devoted to the convergence property. Section 4 presents Monte Carlo simulations. It is shown that the combination of nonspherical disturbances and outliers (measurement errors) imply a loss of efficiency, which is not so important in the Gini case compared with GLS. In addition, the power of White’s test is analyzed in the presence of outlying observations. Section 5 closes the article.
2. Aitken-Gini Estimators
It is common practice to deal with heteroskedasticity and autocorrelation with generalized least squares. However, if the data are contaminated by outliers, the loss of efficiency can drastically affect the coefficient estimates. In the following, outliers are assumed to be contaminated data, such as measurement errors, which lead to bad estimates. It is shown that the employ of the Aitken-Gini estimator may be preferred to GLS when the data are contaminated by outlying observations. The model is the following:
where is the dependent variable ( vector), is the matrix of the regressors (of size with a first column of ones), is the vector of parameters to be estimated, and is the vector of perturbation terms (of size ). Following Olkin and Yitzhaki (1992), the semi-parametric Gini regression yields an estimator of ,
where is the rank matrix of . The rank matrix is the matrix in which, for each regressor (), the observations () are replaced by their rank within (the smallest value of is replaced by 1, and the highest one by n). Olkin and Yitzhaki (1992) showed that Gini estimators may be of particular relevance when outliers arise in the data. It is worth mentioning that, in the sequel, only the semi-parametric Gini regression is investigated. The parametric Gini regression is a numerical technique relying on the minimization of the Gini index of the residuals, which yields the same estimator as the semi-parametric Gini regression when the model is linear.
2.1. Mimicking the Usual Aitken Estimator
The generalized least squares (GLS) technique requires, in the case of heteroskedasticity and non serial correlation, the traditional following hypotheses , for all , and , such that with
Let us denote by the variance of the error term such that . Let , then setting , and yields:1
Thereby, a first Aitken-Gini estimator may be derived.
Proposition 1.
Proof.
The application of the semi-parametric Gini regression to the model in Equation (3) is obvious. Note that:
□
We obtain a result quite close to Equation (2), which has the form of estimators by instrumental variables (IV) (see Yitzhaki and Schechtman (2004) for the link between Gini regressions and IV). Indeed, setting , we get an IV estimator:
The Gini estimator in Equation (4) is derived by mimicking the usual Aitken estimator, which may be used if, and only if, the variability of the error term is defined with respect to the variance, i.e., . However, the Gini methodology is employed whenever the underlying variability is the covariance-Gini defined by Schechtman and Yitzhaki (1987), the co-Gini from now on, which is examined in the next subsection.
2.2. The Aitken-Gini Estimator
The usual Aitken estimator described in the previous subsection is valid whenever the second moments of are known and when no outliers occur in , for which the first moments exist. The Gini estimator may be one solution to overcome this difficulty without invoking the existence of the second moment of . For that purpose, we must define the transformed model,
such that there is no heteroskedasticity in the Gini sense, that is, the co-Gini of remains constant for all . Let the co-Gini operator be defined such that:
where is the cumulative distribution function of . In this respect, we have with such that,
The Aitken-Gini estimator must be defined according to the -rank idempotent property of the transformation matrix .
Definition 1.
A squared matrix is said to be -rank idempotent if, for any given real random variable X, such that ,
where and stand for the cumulative distribution functions of X and Z, respectively.
For estimation purposes, this assumption implies that the rank vector of X remains invariant after any given transformation . This assumption is necessary to obtain spherical disturbances.
Proposition 2.
Proof.
If is supposed to be -rank idempotent, then . From the transformed model in Equation (5):
Since , then
Note that the invertibility of is ensured since it is positive semi-definite. □
2.3. A Reconciliation
In the previous subsections, two Aitkien-Gini estimators have been derived. We can actually show that the Gini estimator that mimics the GLS is equivalent to the Aitken-Gini estimator .
Proposition 3.
Let be an i.i.d. process such thatand. Let such that for some real-valued function and assume that and . Then, the following assertions hold:
- (i)
- .
- (ii)
- .
- (iii)
- and .
Proof.
(i) Let us remark that . Consequently,
Thus, by Proposition 1 we get that , consequently the transformed model provides . Hence, .
(ii) We have . Thereby, and so:
By Proposition 2, we get that . The transformed model yields . Hence, .
(iii) Considering Assertions (i) and (ii), it follows that . Note that both estimators and are issued from with , and the rank matrix of . Note that is employed in the first case and in the second one. Since , then , which concludes the proof. □
The previous results are all based on the rank matrix of ; consequently, as shown by Olkin and Yitzhaki (1992), the semi-parametric Gini regression is robust to outliers. Although the previous proposition indicates that an equivalence exists between the two Aitken-Gini estimators and ; it is noteworthy that requires fewer assumptions, since the first moment of has to be known only, whereas is based on the existence of the two first moments of .
3. Sampling Properties
The aim of this section is to show, as above, that two strategies are available to get the sampling variance of the Aitken-Gini estimator. The first one is to consider that the second moment of exists, as usual in the case of least squares regression, to derive the asymptotic variance of . The second one assumes that the second moment of does not exist, thus the variance of is derived by jackknife. For this purpose, one needs additional assumptions.
We start again with the transformed model:
The hypotheses of the model are the following:
H1:.
H2: Whenever is a non null matrix, the perturbation term is linearly approximated as follows:2
H3: The perturbation term is independent of .
H4: is a positive definite matrix.
H5: The matrix is diagonal and it contains finite elements .
H6: The second moment of exists for all such that .
Hypothesis H2 is necessary because the semi-parametric Gini regression does not rely on the usual linearity assumption of the regressors. First, we prove that the estimators and are unbiased. The proof is made for only, since it is similar in both cases.
Proposition 4.
Under HypothesesH1–H5, is an unbiased estimator of .
Proof.
From Equation (6), and , with being invertible by Hypothesis H4, and with being invertible by Hypothesis . Let , then we have by Hypothesis H2:
Since , therefore, by Hypotheses H1 and H3:
Note that Hypothesis H3 is respected whenever outliers do not contaminate the sample. □
3.1. Convergence
We suppose that the second moments of exists [Hypothesis H6] in order to derive the asymptotic variance of and to check for its convergence. By the result of Proposition 3, we set .
Proposition 5.
Under HypothesesH1–H6, the following assertions hold.
- (i)
- .
- (ii)
- is convergent.
Proof.
(i) From Equation (7), we deduce that:
(ii) From Proposition 4, is an unbiased estimate of . We have . The matrix exists since is invertible by Hypothesis H5. Thus by Hypothesis H4,
is a positive definite matrix (with and being rows of and , respectively). Then, the asymptotic variance covariance matrix exists and amounts to:
Letting n tend towards infinity, we get that . □
As mentioned by Yitzhaki and Schechtman (2013), the inference on the regressors of the semi-parametric Gini regression has to be performed with U-statistics. In this case, the convergence is ensured without invoking Hypothesis H6.
3.2. Convergence with U-Statistics
As shown by Yitzhaki and Schechtman (2013), Gini estimators are U-statistics. The main advantage of dealing with the class of U-statistics, based on the generalized notion of average, is to find unbiased estimators and to derive their asymptotic property. The reader is referred to Serfling (1980, chp. 5) for more details. A brief review of this chapter is provided below.
Let , be independent observations from a population on a distribution F. The parameter of the population is a parametric function for which an unbiased estimator exists. It is expressed as:
where , called the kernel, is a symmetric function3. The U-statistics of is an estimator based on a sample of size n, , such that . Averaging the kernel , the U-statistics is written as:
where denotes the sum over all combinations of m elements from . The U-statistic for the parameter is an unbiased estimator of and the distribution of tends to a normal distribution as under the condition that . The variance of a U-statistic also relies on the existence of second moments. Let the sets and be composed of m distinct integers among the set , with c the number of common integers of sets A and B. Let , then, by symmetry of as well as the independence of the observations of the sample:
Defining
the variance of a U-statistic is given by:
with the number of possibilities for sets A and B to get c elements in common, and with the hypothesis . The estimation by jackknife of the variance of does not necessitate such an assumption:
where is the estimator based on a sample of size , without the ith observation.
Proposition 6.
Each element of the Aitken-Gini estimator is a function of U-statistics, thus estimating the variance of by jackknife for all implies that is a consistent estimator of such that for all , neither invoking the existence of the second moments of nor those of [H6].
Proof.
See Appendix A. □
4. Tests and Simulations
In this section, it is shown that the semi-parametric Aitken-Gini estimator is more robust than the usual GLS one when the data are contaminated by outliers with being known. Furthermore, a feasible generalized Gini regression is proposed to deal with the case where is unknown.
4.1. Monte Carlo Simulations
We performed Monte Carlo simulations to assess the robustness of the semi-parametric Gini regression with outlying observations in and the presence of heteroskedasticity. In this section, we assume that the heteroskedasticity shape is known. The steps of the Monte Carlo simulation were as follows.
Step 1: Generate three independent normal distributions of size such that , with and .
Step 2: Sort the matrix by ascending order according to the vector (the second column of ). Multiply the last row of by (with increments of 100) in order to inflate the most important value of : .
Step 3: For each outlier , perform simulations, i.e., generate B × 3 independent normal distributions for all with one outlier valued to be .
Step 4: Generate heteroskedasticity as follows and fix a vector to compute with independent of and with .
Step 5: Regress on with the semi-parametric Gini regression and with GLS in order to estimate . Compute the standard deviation of by jackknife in the first case, and the standard deviation of the GLS estimators in the second case (for each value of ). Measure the mean squared error of the coefficient estimates over B replications (for each ) for both techniques: Gini and GLS.
The jackknife standard deviations of the estimators for are reported in Figure 1 for each value of the outlier . As depicted in Figure 1, jackknife standard deviations of the Aitken-Gini estimator are lower than those of the GLS estimator, which are drastically affected by the introduction of one outlier in a sample of observations. This corresponds to a contamination of the sample of only . Since the outlying observation corresponds to the last row of (), in which there is the most important value of , the vector is the most contaminated regressor. Therefore, as shown in Figure 1 (top right), important variations of the standard deviation of are recorded, especially for the GLS estimator (red curve) compared with the Gini one (black curve).
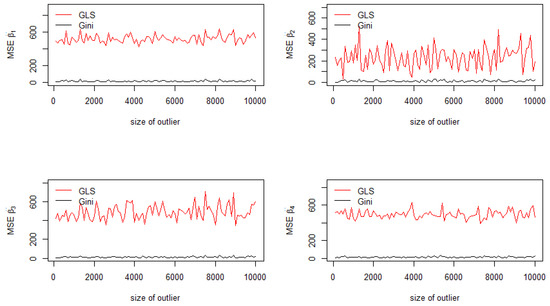
Figure 1.
Standard deviations of the coefficients.
In addition, it is possible to compute the mean squared errors of the GLS estimator and the Aitken-Gini one. The contamination process is the same as before.
The Aitken-Gini estimator is better than the usual GLS estimator for the constant of the model (Figure 2, top left) and for the second regressor (Figure 2, top right), as depicted in Figure 2. This is due to the fact that the outlier is generated by multiplying by , which corresponds to inflating the most important value of (Step 2). Consequently, the Aitken-Gini estimator yields a robust estimation compared with GLS. For the other cases, the MSE of the generalized least squares estimator are less important.
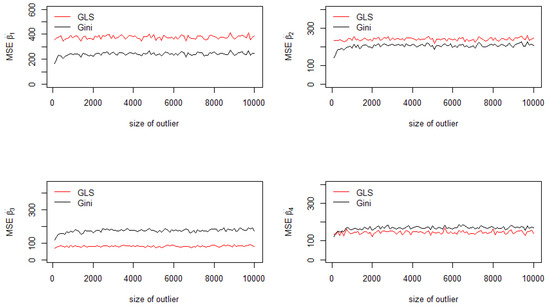
Figure 2.
Mean squared errors of the coefficients.
4.2. Tests
The aim of this subsection is to prove that the usual White test for heteroskedasticity has a low power whenever outlying observations arise in the sample, even if the contamination rate is around 1%. Another test is proposed based on the co-Gini operator, and it is shown that a good power may be obtained compared with the standard White test.
Although GLS estimators may be affected by outliers, it is worth mentioning that Aitken-Gini estimators and GLS estimators are based on two different notions of heteroskedasticity. The Aitken-Gini one captures another type of variability, the co-Gini based on ranks, compared with GLS based on the variance. In the following, focus is put on White’s test since it is commonly employed in the literature.
White’s model and its Gini counterpart are given by,
and,
where is the rank of and is the rank of (within the vector ). The intuition of the White-Gini test is to exhibit the variables that depend on the rank of the individuals. This is the case for example when we regress incomes on age. We have the same intuition for White’s test performed with OLS. However, the squared residuals and the squared covariates may be inflated because of the outliers. In this respect, it is possible to use Eq.(White-Gini) to test for heteroskedasticity. It is noteworthy that this equation cannot be estimated by the semi-parametric Gini regression since the rank vector of and the rank vector of are collinear (⊗ being the Hadamard product). Consequently, both equations are estimated by OLS. The advantage of dealing with Eq.(White-Gini) is to capture the shape of heteroskedasticity in the presence of outliers. The standard White-OLS equation aims at capturing quadratic shapes in the covariates. However, the model fails to achieve this goal in the presence of outliers because outliers are squared. In the White-Gini equation, the product allows the quadratic shape to be detected, while the intensity of the outliers are attenuated by the role of the rank vector .
In the following tables, we provide the mean of each model over the number of Monte Carlo experiments . We provide in parenthesis the power of the Fisher test related to the significance of the in each model. The Monte Carlo simulations with contamination were based on the same simulation process described in Algorithm 1.
In Table 1, one observation is contaminated for a sample size , that is 3.33% of the sample. The same generating process was used as in the Monte Carlo simulations performed in the previous section. The outlying observation consists in multiplying the most important value of by . Without outlier, the White-Gini model provides an of 0.17 (in mean over B) with a very low test power around 2%, whereas the White-OLS model yields an of 0.26 with a power of 14%. However, when is valued to be 100, the White-Gini model performs quite well with an of 0.45 and a power of 51%, whereas the power decreases slightly in the White-OLS model. In the White-Gini model, thanks to the rank vector of as a regressor, the regression curve stays distant from the outlying observation and becomes closer to the other points. Then, the variability of the model explained by the regression curve increases (and then increases). On the contrary, for the standard model (White-OLS), the regression curve moves toward the outlying observation so that the variability of the residuals increases, and in this case decreases.

Table 1.
Power of the White-Gini test: small sample .
In Table 2, the sample size is so that the contamination represents 1% of the sample. Without outlier, the White-Gini model provides a very low test power around 7%, compared with 64–70% for White-OLS model. The test power increases to reach 70% in the first case against 59% in the second case.

Table 2.
Power of the White-Gini test: .
Finally, in Table 3, and test power remain quite equivalent in both models. As mentioned in the literature, for large samples, White-OLS provides an excellent power. When the outliers are dilute in the sample, for instance when the contamination of the sample is only concerned with % of the sample, because the sample size is large and the number of outliers very low, both tests produce the same power.

Table 3.
Power of the White-Gini test: .
4.3. The Feasible Generalized Gini Regression
After testing the presence of heteroskedasticity with outlying observations, a new procedure is proposed to estimate . The so-called feasible generalized least squares (FGLS), introduced by Zellner (1962), was adapted to the Gini regression, the feasible generalized Gini regression (FGGR). Aitken’s theorem no longer applies if is unknown and must be estimated. The feasible generalized least squares estimator is not the best linear unbiased estimator, nevertheless Kakwani (1967) proved that it is still unbiased under general conditions, and Schmidt (1976) discussed the fact that most of the properties of generalized least squares estimation remain intact in large samples, when plugging in an estimator of . The form of the heteroskedasticity is unknown, but it can be approximated with a flexible model as,
in a “Breusch–Pagan” version (in the sense that we consider a linear form of heteroskedasticity), such that and independent of . Instead of using the least squared estimator, the semi-parametric Gini estimator in Equation (2) is employed to deal with contaminated data in :
Then,
such that,
From , we deduce an estimation of denoted . Thus, we get that . Let be the rank matrix of , hence the FGGR estimator is given by:
On the contrary, the usual FGLS estimator is given by,
with estimated by generalized least squares in the first step [Equation (9)]. However, in Proposition 2, it is shown that the Aitken-Gini estimator is based on the -rank idempotent hypothesis. This assumption states that the rank vector of the residuals must remain invariant after the transformation of the model with respect to matrix , thereby an Aitken estimator is obtained. However, whenever one outlier occurs in the sample, e.g., the ith row of is such that ), then it comes that so that the respect of the -rank idempotent hypothesis is not necessarily ensured for the outlying observation. Consequently, the FGGR estimator is biased. Indeed, the semi-parametric Gini estimator in Equation (10) is based on the rank matrix of which contains errors since is computed on the basis of contaminated data. Replacing by , being the rank matrix of , avoids such a contamination. It is worth mentioning that replacing the rank matrix of the covariates by another rank matrix of some data correlated to the covariates corresponds to the Gini instrumental variable estimator introduced by Yitzhaki and Schechtman (2004). In this respect, the FGGR estimator becomes a feasible generalized Gini regression by instrumental variable (FGGR-IV):
Because is the rank matrix of the initial contaminated data, it comes that the residuals of the transformed model issued from the FGGR-IV estimator are more likely to respect the -rank idempotent hypothesis compared with FGGR based on because both matrices are contaminated.
We performed some Monte Carlo simulations to compare the mean squared errors of the FGGR-IV and FGLS estimators.4
Step 1: Generate three independent normal distributions of size for all with .
Step 2: As in the previous simulation, sort the matrix by ascending order according to , except multiply the last row of by (with increments of 1 to avoid problems of matrix invertibility) to inflate the most important value of .
Step 3: For each outlier , perform simulations, i.e., generate B × 3 independent normal distributions for all with one outlier valued to be .
Step 4: Fix a vector to compute with , that is, suppose that the heteroskedasticity comes from .
Step 5: Compute the coefficients estimated based on FGGR-IV and FGLS with their MSEs over replications.
Figure 3 depicts an interesting correction of heteroskedasticity performed by the FGGR-IV estimator when outliers contaminate only 1% of the sample. The FGGR-IV estimator provides MSEs close to 0 except for the constant and for . Because the model has been specified such that , then the outlier is even more inflated in this case (bottom left in Figure 3).
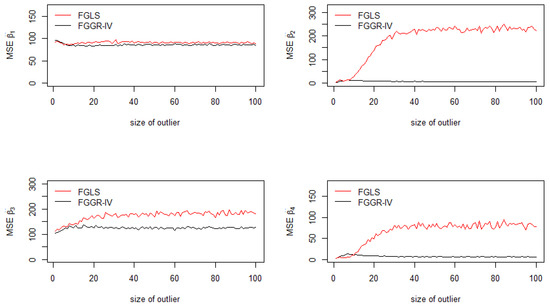
Figure 3.
Mean squared errors of the coefficients: FGGR-IV and FGLS.
To show that the FGGR-IV estimator is relevant with other forms of heteroskedasticity, Step 4 was replaced by Step 4’, in which an ARCH(1) is modeled (see Figure 4):
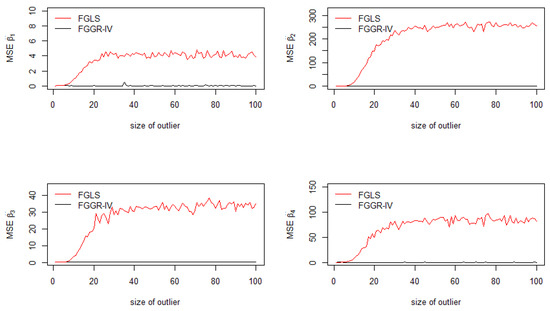
Figure 4.
Mean squared errors of the coefficients: FGGR-IV and FGLS with ARCH(1).
Step 4’: Fix a vector to compute with and .
The results depicted in Figure 4 are even more clear: the MSEs of all FGGR-IV estimators tend toward 0, consequently the bias of those estimators also tend toward 0.
5. Concluding Remarks
In this paper, we have demonstrated that two equivalent Gini estimators may be proposed to deal with heteroskedasticity: the former deals with heteroskedasticity in the variance sense and the latter with heteroskedasticity in the Gini sense. The jackknife variance of these estimators are shown to be robust in the presence of outlying observations compared with the usual GLS technique, i.e., the loss of efficiency is less important in the Gini case. The simulations presented in Table 1, Table 2 and Table 3 show that a contamination of 1% of the sample may drastically affect the power of the White-OLS test, so that the White-Gini test may be preferred to detect the presence of heteroskedasticity when outlying observations occur in the sample.
Author Contributions
Conceptualization, S.M. and N.K.; methodology, A.C.; software, A.C. and S.M.; validation, O.H.N.; writing–original draft preparation, all authors; writing–review and editing, all authors.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Proof of Proposition 6:
We follow the proof obtained by Ka and Mussard (2016) in the case of fixed effects panel Gini regressions. Let be the kth column of and the kth column of , for all . Let . From Equation (3), we get that:
Hence, the following identities hold:5
Setting , and , and dividing the three last equations by, respectively, , and yields:
Now, we define the two following columns vectors and . Then, it comes:
The previous expression shows that the Aitken-Gini estimator is a function of slope coefficients of semi-parametric simple Gini regressions . Consequently, it is a semi-parametric Gini estimator.
Note that , and are all ratios of U-statistics. Indeed, consider a continuous bivariate distribution with F and G the marginal cumulative distribution functions of X and Y, respectively. By Proposition 9.2 of Yitzhaki and Schechtman (2013), there exists an unbiased and consistent estimator of :
where is the value of y concomitant to the ith order statistic of . On the other hand, the U-statistic of is (Proposition 9.1 of Yitzhaki and Schechtman 2013):
Estimators and are unbiased and consistent estimators of and , respectively.6 The estimators , and are ratios of two dependent U-statistics, such as . By Slutzky’s theorem, because and are consistent estimators, then is also a consistent estimator. By Theorem 10.4 in Yitzhaki and Schechtman (2013), if there exists a real-valued function of parameters of the population, and if there exist U-statistics corresponding to such that g and its derivatives are continuous in the neighbourhood of , then . Because the estimation of the variance of can be made by jackknife, there is no need to postulate the existence of the second moments . From Equation (A1), since each element of is a function of ratios of U-statistics being consistent, then applying Theorem 10.4 in Yitzhaki and Schechtman (2013), it comes that is a consistent estimator of such that , for all . □
References
- Aitken, Alexander Craig. 1935. On least squares and combinations of observations. Proceedings of the Royal Society of Edinburgh 55: 42–48. [Google Scholar] [CrossRef]
- Carcea, Marcel, and Robert Serfling. 2015. A Gini autocovariance function for time series modeling. Journal of Time Series Analysis 36: 817–38. [Google Scholar] [CrossRef]
- Ka, Ndéné, and Stéphane Mussard. 2016. ℓ1 Regressions: Gini estimators for fixed effects panel data. Journal of Applied Statistics 43: 1436–46. [Google Scholar] [CrossRef]
- Kakwani, Nanak. 1967. The unbiasedness of Zellner’s seemingly unrelated regression equation estimators. Journal of the American Statistical Association 82: 141–42. [Google Scholar] [CrossRef]
- Mussard, Stéphane, and Oumar Hamady Ndiaye. 2018. Vector autoregressive models: A Gini approach. Physica A 492: 1967–79. [Google Scholar] [CrossRef]
- Olkin, Ingram, and Shlomo Yitzhaki. 1992. Gini regression analysis. International Statistical Review 60: 185–96. [Google Scholar] [CrossRef]
- Schechtman, Edna, and Shlomo Yitzhaki. 1987. A Measure of association based on Gin’s mean difference. Communications in Statistics—Theory and Methods 16: 207–31. [Google Scholar] [CrossRef]
- Schmidt, Peter. 1976. Econometrics. New York: Marcel Dekker. [Google Scholar]
- Serfling, Robert J. 1980. Approximation Theorems of Mathematical Statistics. New York: John Wiley & Sons. [Google Scholar]
- Shelef, Amit, and Edna Schechtman. 2011. A Gini-based methodology for identifying and analyzing time series with non-normal innovations. SSNR Electronic Journal, 1–26. [Google Scholar] [CrossRef]
- Yitzhaki, Shlomo, and Edna Schechtman. 2004. The Gini Instrumental Variable or the “double instrumental variable” estimator. Metron LXII: 287–313. [Google Scholar]
- Yitzhaki, Shlomo, and Edna Schechtman. 2013. The Gini Methodology. A Primer on a Statistical Methodology. New York: Springer. [Google Scholar]
- Zellner, Arnold. 1962. An efficient method of estimating seemingly unrelated regressions and tests for aggregation bias. Journal of the American Statistical Association 57: 348–68. [Google Scholar] [CrossRef]
| 1 | This technique corresponds to the weighted least squares. Mathematically, things can be extended to the case where is not diagonal using the singular value decomposition, but interpretation is much harder. Only the diagonal case is studied here. |
| 2 | The regression curve of the Gini regression does not require any linear assumption of the model. Only a linear approximation is necessary to estimate the error term. |
| 3 | If is not symmetric in its arguments, we can also average over the permutations
|
| 4 | The results of FGGR are not reported because of their bad results compared with FGLS. |
| 5 | This technique was introduced by Yitzhaki and Schechtman (2013, chp. 8) in the case of the standard Gini regression. |
| 6 | Note that, for small samples, both and are biased downward. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).