A Hybrid MCMC Sampler for Unconditional Quantile Based on Influence Function
Abstract
:1. Introduction
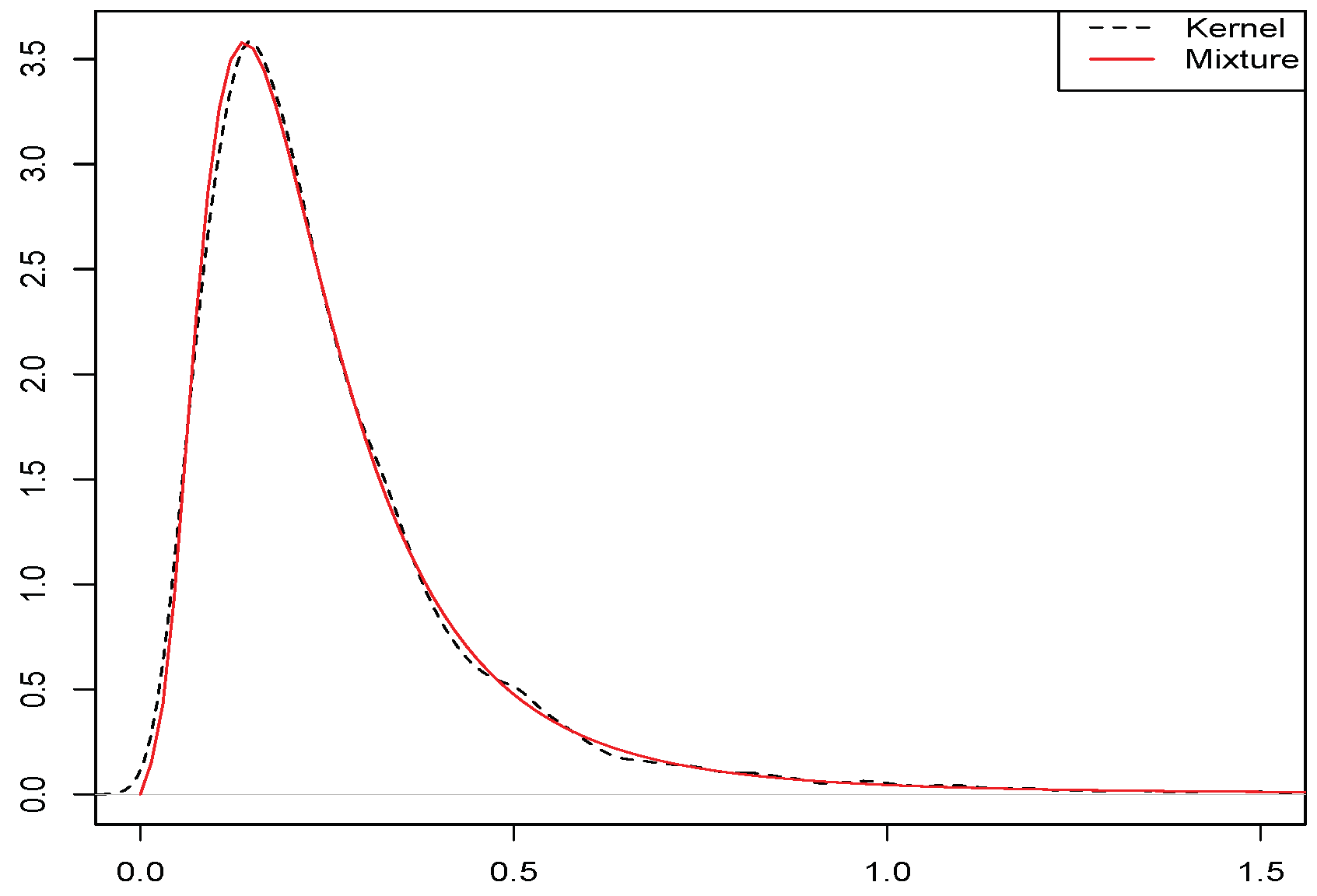
2. Unconditional Quantile Regression Models
2.1. RIF-Regression Models
2.2. Bayesian Estimation of the RIF-Regression
- Estimate the density function of y by Gibbs sampling to obtain
- Initialization: run a linear probability model to set , and compute .
- Iteration: for
- Generate
- Compute the acceptance probability
- With probability , set otherwise
- Compute
- Average to obtain the estimates of the RIF-regression coefficient, .
3. Empirical Analysis
3.1. Data and Descriptive Statistics
3.2. Real Consumption Expenditure Per Capita Distribution
4. Empirical Application
5. Conclusions and Policy Implications
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Comparison with Conditional Quantile Regression Model
| Lowest | Lower Middle | Median | Upper Middle | Highest | |
|---|---|---|---|---|---|
| 0.10 | 0.25 | 0.50 | 0.75 | 0.90 | |
| Intercept | |||||
| primary | |||||
| secondary | |||||
| tertiary | |||||
| age | |||||
| age2 | |||||
| size | |||||
| female | |||||
| rural | |||||
| married |
References
- ANSD. 2007. ANSD, Enquête de Suivi de la Pauvreté au Sénégal, ESPS. Technical Report. Dakar: Agence Nationale de la Statistique et de la Démographie (ANSD). [Google Scholar]
- Bahadur, R. R., and Leonard J. Savage. 1956. The Nonexistence of Certain Statistical Procedures in Nonparametric Problems. Annals of Statistics 27: 1115–22. [Google Scholar] [CrossRef]
- Boccanfuso, Dorothée, Bernard Decaluwé, and Luc Savard. 2008. Poverty, income distribution and CGE micro-simulation modeling: Does the functional form of distribution matter? Journal of Economic Inequality 6: 149–84. [Google Scholar] [CrossRef]
- Boccanfuso, Dorothée, Antonio Estache, and Luc Savard. 2009. A macro-micro analysis of the effects of electricity reform in Senegal on poverty and distribution. Journal of Development Studies 45: 351–68. [Google Scholar] [CrossRef]
- Buchinsky, Moshe. 1994. Changes in the U.S. Wage Structure 1963–1987: An application of Quantile Regression. Econometrica 62: 405–58. [Google Scholar] [CrossRef]
- Chamberlain, Gary. 1994. Quantile Regression Censoring and the Structure Of Wages. In Advances in Econometrics. Edited by Sims Christopher. Oxford: Cambridge University Press. [Google Scholar]
- Davidson, Russell. 2012. Statistical inference in the presence of heavy tails. Econometrics Journal 15: C31–53. [Google Scholar] [CrossRef]
- Deaton, Angus. 1997. The Analysis of Household Surveys. Baltimore and London: The John Hopkins University Press. [Google Scholar]
- Deaton, Angus, and John Muellbauer. 1980. An Almost Ideal Demand System. The American Economic Review 70: 312–26. [Google Scholar]
- Delaunay, Karine. 2012. Education in Senegal: Inequality in Development. Discussion Paper 397. Marseille, France: Institution de Recherche Pour le Development (IRD). [Google Scholar]
- Diawara, Barassou. 2012. Schooling and Assets Ownership. Modern Economy 3: 126–38. [Google Scholar] [CrossRef]
- DSRP. 2005. Document de Stratégie de Réduction de la Pauvreté (2003–2005). Ministère de l’Économie et des Finances du Sénégal, Unité de Coordination et de Suivi de la politique Economique; Technical Report. DSRP. Available online: http://www.bameinfopol.info/IMG/pdf/DSRP.pdf (accessed on 2 May 2017).
- Firpo, Sergio, Nicole M. Fortin, and Thomas Lemieux. 2009. Unconditional Quantile Regressions. Econometrica 77: 953–73. [Google Scholar]
- IMF. 2007. Republic of Senegal: Poverty Reduction Strategy Paper. Technical Report 07/316. Washington: International Monetary Fund, IMF. [Google Scholar]
- Koenker, Roger, and Gilbert Bassett. 1978. Regression Quantiles. Econometrica 46: 33–50. [Google Scholar] [CrossRef]
- Kozumi, Hideo, and Genya Kobayashi. 2011. Gibbs sampling methods for Bayesian quantile regression. Journal of Statistical Computation and Simulation 81: 1565–78. [Google Scholar] [CrossRef]
- Lubrano, Michel, and Abdoul Aziz J. Ndoye. 2014. Bayesian Unconditional Quantile Regression: An Analysis of Recent Expansions in Wage Structure and Earnings Inequality in the US 1992–2009. Scottish Journal of Political Economy 61: 129–53. [Google Scholar] [CrossRef]
- Lubrano, Michel, and Abdoul Aziz J. Ndoye. 2016. Income inequality decomposition using a finite mixture of log-normal distributions: A Bayesian approach. Computational Statistics & Data Analysis 100: 830–46. [Google Scholar] [CrossRef]
- Machado, José A. F., and José Mata. 2001. Earning functions in Portugal 1982–1994: Evidence from quantile regressions. Empirical Economics 26: 115–34. [Google Scholar] [CrossRef]
- Marin, Jean-Michel, and Christian P. Robert. 2001. Bayesian Core: A Practical Approach to Computational Bayesian Statistics. New York: Springer-Verlag Inc. [Google Scholar]
- Mincer, Jacob. 1974. Schooling, Experience and Earnings. New York: The Natural Bureau of Economic Research. [Google Scholar]
- Newey, Whitney K. 1994. The Asymptotic Variance of Semiparametric Estimators. Econometrica 62: 1349–82. [Google Scholar] [CrossRef]
- Psacharopoulos, George. 1994. Returns to investment in education: A global update. World Development 22: 325–43. [Google Scholar] [CrossRef]
- Psacharopoulos, George, and Harry A. Patrinos. 2002. Returns to Investment in Education: A Further Update. Policy Research Working paper 2881. Washington, DC, USA: Education Sector Unit, World Bank. [Google Scholar]
- Ravallion, Martin. 2001. Growth, Inequality and Poverty: Looking beyond Averages. Washington: Development Research Group, World Bank. [Google Scholar]
- Yang, Yunwen, Huixia J. Wang, and Xuming He. 2016. Posterior Inference in Bayesian Quantile Regression with Asymmetric Laplace Likelihood. International Statistical Review 84: 327–44. [Google Scholar] [CrossRef]
- Yu, Keming, and Rana A. Moyeed. 2001. Bayesian quantile regression. Statistics & Probability Letters 84: 437–47. [Google Scholar]
| 1 | |
| 2 | Unlike conditional means, conditional quantiles do not average up to their unconditional population counterparts. |
| 3 | Mixture models provide flexible extensions of parametric models, and the Bayesian approach takes into account the uncertainty related to the first step of the estimation. |
| 4 | The consumption expenditure is considered as an indicator of a household’s income. |
| 5 | Source: published reports and papers; see for instance (IMF 2007; Delaunay 2012). These ratios correspond to the number of students formally registered in primary school. |
| 6 | ESPS, “Enquête Suivie de la Pauvreté au Sénégal”, 2005–2006; ANSD, “Agence National de la Statistique et de la Démographie”. |
| 7 | Among the studies using the ESPS datasets, we can cite Boccanfuso et al. (2008); Boccanfuso et al. (2009); Diawara (2012), among others, and the national and institutional reports: DSRP 2005; IMF 2007; ANSD 2007. |
| 8 | The standard (Mincer 1974) earnings equation linearly regresses the log of wage on the year of education and the quadratic function of labor market experience. |
| 9 | The Gibbs sampler for the mixture of lognormal densities was developed in Lubrano and Ndoye (2016); see also Marin and Robert (2007) for the mixture of normal distributions. |
| 10 | CFA (Communauté Financière Africaine (African Financial Community)). CFA franc had a fixed exchange rate with the Euro (1 euro = 656 CFA) in 2013. |
| 11 | West African Economic and Monetary Union. |
| 12 | Primary education corresponds to 6 years or less, secondary between 7 and 13 years and tertiary more than 13 years. |
| 13 | We consider the quadratic function of age to capture the fact that on-the-job training investments decline over time in a standard life-cycle human capital model. This quadratic form of age is implied by a model in which investments decline linearly over time. |
| 14 | Considering the three age values (30, 50, 65)/100, the following marginal effects for the four quantiles are (−0.679 −0.402 −0.300 −0.2482); (−0.667 −0.395 −0.294 −0.243) and (−0.658 −0.390 −0.290 −0.239), respectively. |
| 15 | Details of Bayesian inference for quantile regression based on Gibbs sampling can be found in: Yu and Moyeed 2001; Kozumi and Kobayashi 2011; Yang et al. 2016. |
| Education Level of the Head | Age | ||
|---|---|---|---|
| Illiterate | 71.22 | Mean | 50.62 |
| Primary | 12.63 | less 40 | 21.97 |
| Secondary | 11.58 | 40–65 | 57.92 |
| Tertiary | 4.57 | 65 and plus | 30.11 |
| Gender | Occupation of the head | ||
| Female | 22.55 | Employed | 70.6 |
| Marital status of the head | Size of the household | ||
| Monogamy | 57.03 | Mean | 9.01 |
| Polygamy | 25.39 | 1–4 | 20.13 |
| Single | 3.40 | 5–9 | 49.25 |
| Widower | 11.71 | 10–14 | 18.33 |
| Divorced | 2.39 | 15, + | 12.29 |
| 8.89 | |
| 13.54 | |
| Median | 20.71 |
| Mean | 27.11 |
| 32.40 | |
| 50.07 | |
| N | 13,326 |
| Gini | 0.388 |
| Lowest | Lower Middle | Median | Upper Middle | Highest | |
|---|---|---|---|---|---|
| 0.10 | 0.25 | 0.50 | 0.75 | 0.90 | |
| RIF-Logit Regression Using Flat Prior | |||||
| Intercept | |||||
| primary | |||||
| secondary | |||||
| tertiary | |||||
| age | |||||
| age2 | |||||
| size | |||||
| female | |||||
| rural | |||||
| married | |||||
| Lowest | Lower Middle | Median | Upper Middle | Highest | |
|---|---|---|---|---|---|
| 0.10 | 0.25 | 0.50 | 0.75 | 0.90 | |
| RIF-Logit Regression Using Zellner’s Non-Informative Prior | |||||
| Intercept | |||||
| primary | |||||
| secondary | |||||
| tertiary | |||||
| age | |||||
| age2 | |||||
| size | |||||
| female | |||||
| rural | |||||
| married | |||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laghlal, E.M.; Ndoye, A.A.J. A Hybrid MCMC Sampler for Unconditional Quantile Based on Influence Function. Econometrics 2018, 6, 24. https://doi.org/10.3390/econometrics6020024
Laghlal EM, Ndoye AAJ. A Hybrid MCMC Sampler for Unconditional Quantile Based on Influence Function. Econometrics. 2018; 6(2):24. https://doi.org/10.3390/econometrics6020024
Chicago/Turabian StyleLaghlal, El Moctar, and Abdoul Aziz Junior Ndoye. 2018. "A Hybrid MCMC Sampler for Unconditional Quantile Based on Influence Function" Econometrics 6, no. 2: 24. https://doi.org/10.3390/econometrics6020024
APA StyleLaghlal, E. M., & Ndoye, A. A. J. (2018). A Hybrid MCMC Sampler for Unconditional Quantile Based on Influence Function. Econometrics, 6(2), 24. https://doi.org/10.3390/econometrics6020024





