4.1. Model Comparisons
Recall that our model is designed in part to capture the optimal window of data history for model estimation. Therefore, benchmark models to compare can be those using fixed windows of data history. Without any possible model changes, statistical analysis suggests using all data available to improve the precision of the parameter estimation. On the other hand, it has been common practice in industry to use only a fixed number of recent observations for estimation; perhaps due to the same intuition about model change that we have discussed for our case of forecasting variances and correlations. That is, old data histories can be misleading when there are model changes and can introduce bias to forecasts. Therefore, following the commonly-used practitioner’s approach, our second benchmark is to use a 60-period rolling window.
For ease of notation, we denote by the benchmark model using the entire available data history weighted equally. Subscript 1 references that data begin from Time Period 1. Similarly, we denote by the alternative benchmark model, which following popular practitioner’s practice, uses the most recent 60 observations. Lastly, we use the notation to denote our model that uses the time-varying weights of different submodels at each time.
Our approach is designed to forecast the entire unconditional distribution rather than focusing on specific moments of the distribution. Nevertheless, to compare how each model performs with respect to forecasting the first moment of our variables of interest (realized variances and realized correlations), we use the conventional Mincer–Zarnowitz regressions to assess forecast bias and the efficiency of each model. The Mincer–Zarnowitz regression is designed to assess a model’s ability to fit the observed data point. Therefore, it only focuses on the model’s ability to forecast the first moment of the data. Although the first moment may be the most interesting one to forecast, higher moments of the distributions will also matter depending on the application. As discussed further below, we also use tests for the fit of the entire distribution.
The following MZ regressions are used for each model to estimate the slope and intercept coefficients, as well as the proportion of the variability in the target that is explained by the forecasts (the
of the regression). For model
and
, the forecast is simply the sample average of the data history used, that is
and
, respectively. For model
, the forecast is computed using historical data with time-varying weights on each submodel following the approach described in the previous section. The detailed implementation is discussed in
Appendix B (Equation (
A.9)).
Analogous regressions are also run for FisRCorr.
The top panel of
Table 2 summarizes the results using monthly log
RV from 1885–2013. The last column is a robustness check for the initial prior on
, which is set to a much higher level to check whether the result is driven by the initial choice of the prior on the
process. The intercept and slope coefficients estimate the bias of the forecasting model. Having an intercept equal to zero and slope equal to one corresponds to unbiased forecasts. Thus, we assess each model by comparing how close the intercept and slope coefficients are to zero and one, respectively. Moreover, the
metric is used to assess the efficiency of model fit.
Note first that the performance of model
is very disappointing. It only generates
of 0.14% with heavily biased coefficients. It was somewhat expected as we anticipate frequent model changes for the monthly
process as discussed in
Section 2. Once we use the most recent 60 time periods, or five years of observation, as in the forecasting model
, the performance increases significantly, in that the
is much higher (16.14%) and the forecasts are much less biased.
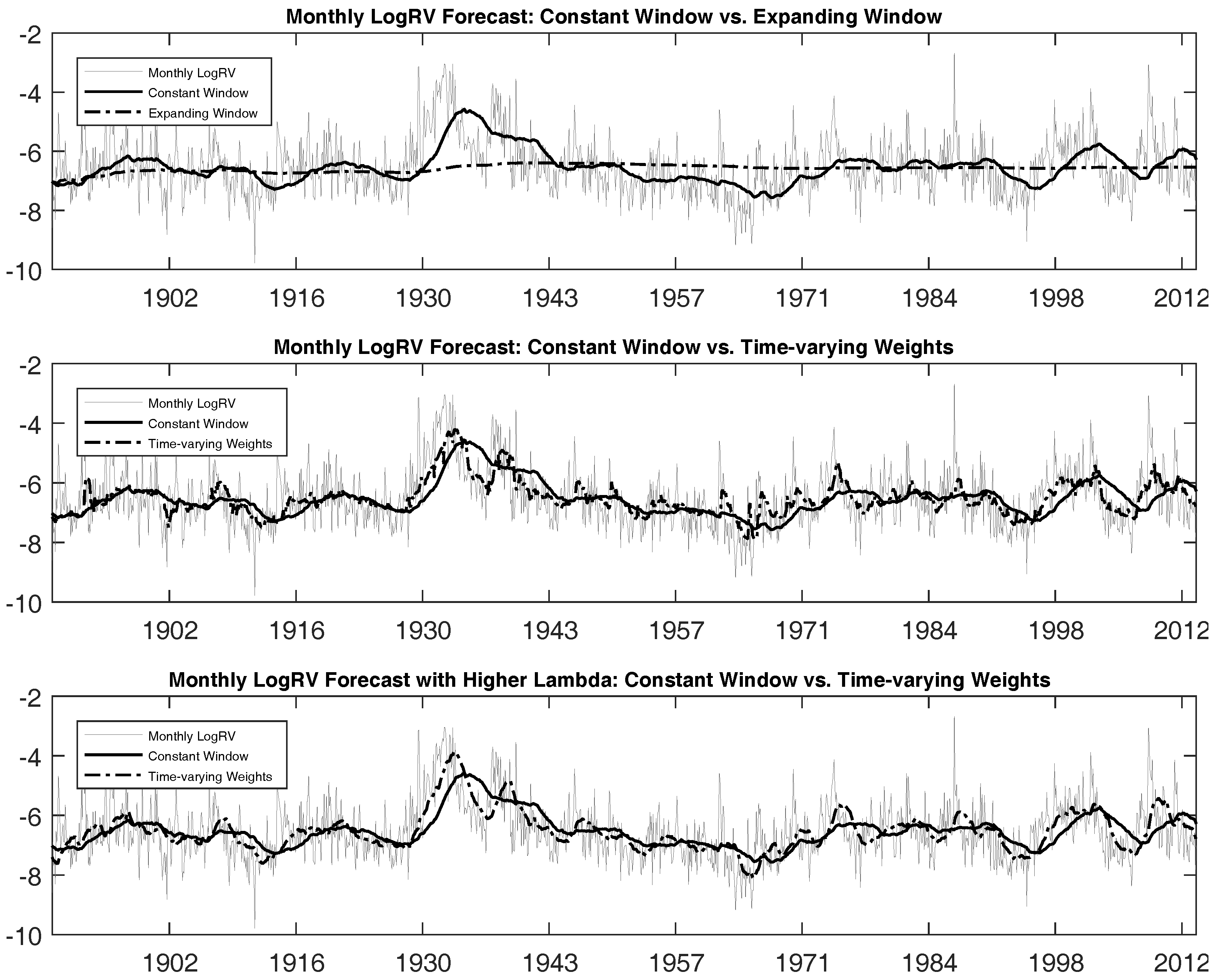
Figure 3 graphically illustrates these results by plotting the target log
RV against model predictions. We see that using the entire data sample weighted equally as in the
model generates forecasts that are too smooth, being unable to capture the frequently-occurring model changes of the log
RV process. In contrast, taking the recent five years of observations allows forecasts to respond to the model changes in a better fashion. However, this
model still lacks the ability to react fast enough.
Now, we turn our attention to the our model that uses data histories associated with submodels each period. Improvement in the forecasting performance is quite noticeable with respect to both the bias and efficiency metrics. The , that is the proportion of variability in out-of-sample RV explained by forecasts using the model, increases to 33.21%, which is more than double that of the model, and the forecasts are much less biased than those for the other two models as indicated by the intercept and slope coefficients.
Figure 3 illustrates these differences graphically. We see that the model
is able to react faster to capture possible model change. Note again that all three models we compare are the same model in the statistical sense. They only differ in the data sample we use to estimate the parameters; thus, the difference in the performance should solely come from the difference in data samples used to estimate the parameters and generate the forecasts. Our results, even for the first moment of the monthly realized variance forecasts, illustrate the improvements originating from being able to select time-varying weights of different data histories at each point in time. That is, choosing a fixed-length moving window generates additional bias and forecasts that track our target less efficiently. Overall, this result confirms the importance of using the time-varying weights when making forecasts. We will discuss this in more detail in the next subsection.
In the bottom panel of
Table 2, we report the same analyses performed for forecasts of daily log
RV from April 2007–February 2015 for three futures. The daily futures
RV were constructed from 15-min intraday futures prices as discussed in
Section 2 above. For all three SP, GC and CL futures, the model
performs poorly as before, while the model
does a much better job. The model
still remains dominant, particularly providing much less biased forecasts. However, a less dramatic increase in
is observed when compared to the model
, perhaps indicating that 60 days is close to the best fixed window-length to use for daily realized variance data. It is not too surprising since 60 days has been found to be a good ad hoc number to use by many practitioners. Figures similar to
Figure 3 for daily forecasts of three Futures’ log
RV exhibit similar findings and are omitted for brevity. More or less, we see the same pattern as for monthly data that the model
is the best at reacting to model changes in the underlying data.
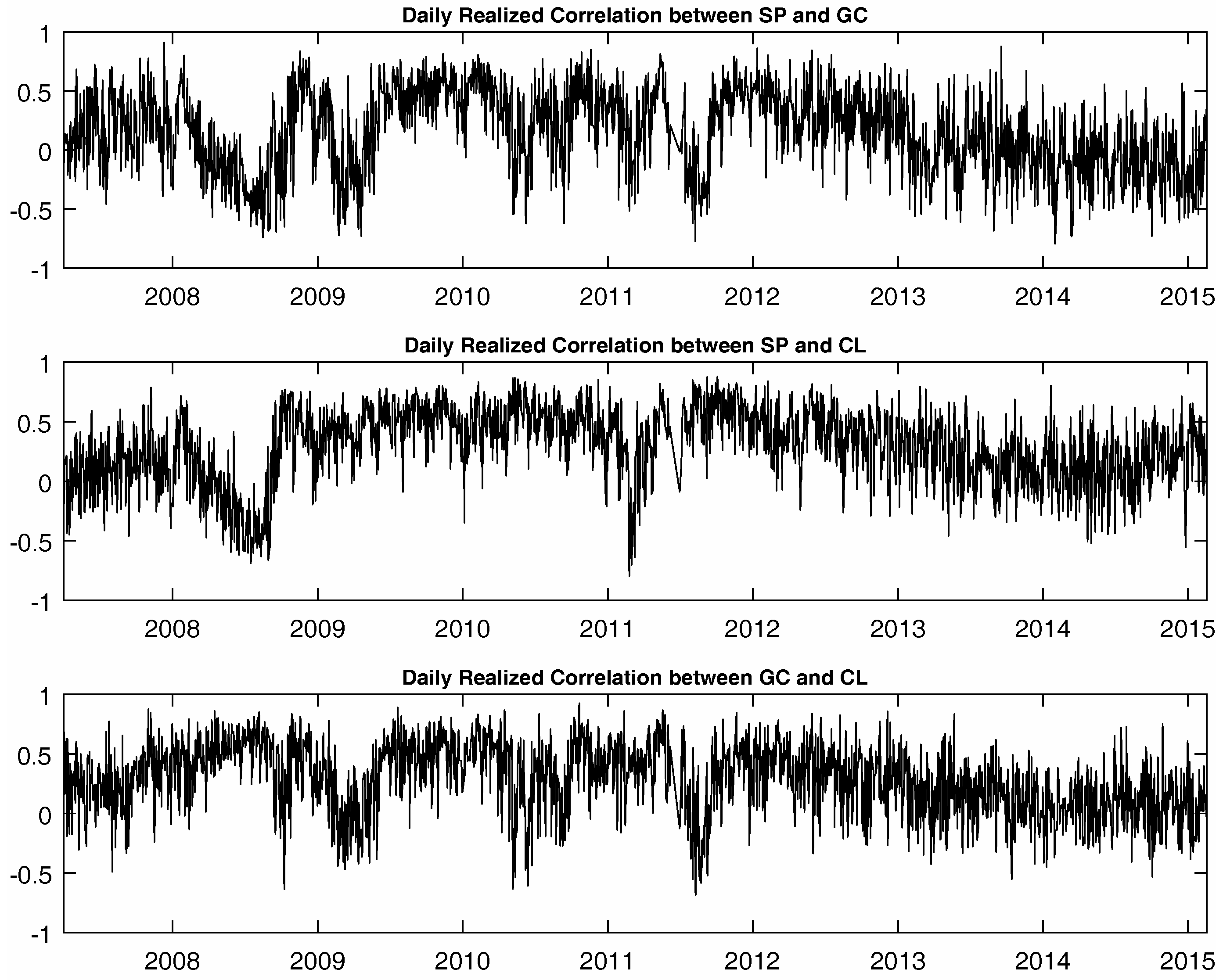
Next, we perform the same analyses of the Fisher transformed daily realized correlations for the three futures.
Table 3 reports results using the same period of data from April 2007–February 2015 as for the realized variances. Again, the same broad conclusions can be drawn from the realized correlations forecasts. However, improvements in both the bias and the
associated with the
model are more pronounced. In particular, the estimated intercept and slope coefficients are such that forecasts are strikingly close to being unbiased. In addition, the
model forecasts provide a much better fit in general compared to those for the log of realized variance. It is likely the case that the realized correlations exhibit more variation in the length between the occurrence of model changes. In that case, our model using the time-varying weights is better suited for capturing the realized correlation than the realized variance.
Figure 4 again illustrates the differences between the forecasted values and realized values for correlation between SP and GC futures. The other two cases are omitted for brevity where the same conclusions hold in all cases.
So far, we have been focusing on assessing each model’s ability to forecast the first moment of the underlying process. We now turn our attention to the statistical measure that can assess higher moments, as well, that is the distributions of log(
RV)and Fis
RCorr. Given the normality assumption of the underlying process, the marginal predictive likelihood at each point of time only requires the forecasts of mean and variance of
. For the case of model
, we compute the forecasts of mean and variance using Equation (
A.9), while the sample mean and sample variance of the corresponding data history are used for the benchmark models. Then, the sum of log marginal predictive likelihood is computed by the expression below.
Table 4 summarizes these results. Cases with higher prior values on
are again included to make sure our approach is robust to the initial choice of
. The results again heavily favour the model
over the two benchmark models. A dramatic increase in the log-likelihood is observed for all the datasets. The results here are not directly comparable to the MZ regression results discussed above, but they indicate that
model has superior forecasts of the distributions of realized variance and correlation relative to the benchmark models. Using a Bayes factor criterion for comparison of the log(
ML) across models indicates very strong or decisive evidence in favour of the
model.
Overall, all of the above statistical tests heavily support the model over the other two models. Again, the differences are purely coming from the fact that each model uses different data histories, thus highlighting the importance of having a flexible framework to capture model changes in the underlying data.
4.3. Time-Varying Window Length
Given the results in the previous section, we now turn to a the deeper analysis of why the model performs so well. In order to do so, we introduce the measure that we call time-varying window length (), designed to suggest a length of data history to be used at each time period. Loosely speaking, we can think that the model corresponds to the case where is equal to 60 in all time periods.
To construct
, recall from Equation (
19) that we have the posterior submodel probabilities for each submodel
. Since each submodel
corresponds to the model using the data window of length
, we can compute the average length of the data window at time
t by averaging these by the submodel probabilities. Thus, we define
at time
t as follows:
For example, consider the following artificial case. Suppose that and the submodel probabilities are calibrated to be , and . In this case, using the above formula, we have . Note that the model in this case not only uses the submodel , but also uses the submodels and with lower probability weights. However, since the highest weight is placed on the submodel , the measure turns out to be two to represent that the average length of the data history is two at that point in time. Therefore, , at each t, provides a convenient measure of a time-varying window length.
Table 5 summarizes the descriptive statistics of the
measures over the sample period. We see that the mean
for monthly log
RV is around 24, being much smaller than 60. Meanwhile, the mean
for daily Fis
RCorr data are closer to 60 days for the (SP, GC) and (SP, CL) pairs and a bit larger than 60 days for the (GC, CL) pair. This provides an explanation as to the difference in performance for each dataset we observed using MZ regressions. If the mean
is close to 60, the model
will perform much better relative to the
model than the case for which the mean
is far from 60, as in the case of monthly log
RV.
Table 6 provides two analyses of the characteristics of the underlying data that influence the mean
. To have a valid comparison, we only present the results for Fis
RCorr as they have equal sample periods. We first observe that Fis
RCorr (GC, CL) has the smallest standard deviation of the three series and exhibits the longest length for the mean
measure. Moreover, the levels of persistence, as measured by the first two autocorrelation coefficients, show that the less persistent time series have a longer mean window length. This is particularly pronounced for Fis
RCorr (GC, CL).
We next examine potential sources of the time series variability of
. Our forecasting approach was designed to capture probabilistic model change, such as regime switches, varying importance of economic fundamentals, etc., as revealed in the changing data generating process (DGP). We chose CBOE (Chicago Board Options Exchange) Volatility Index, VIX, as an indicator or representative variable to proxy the business conditions or economic regime at each point of time. Larger VIX values are interpreted as bad states, while smaller VIX values are viewed as good states. Panel B of
Table 6 reports the results of simple linear regressions to test the relationship between the VIX index and three
time series of interest. The estimated coefficients associated with the VIX index are all negative and statistically significant, indicating that high VIX periods are associated with low
values, and vice versa. This finding suggests that our forecasting approach adjusts the length of data history to be used at each point of time (time-variation in the
data), at least partly in response to changes in the DGP.
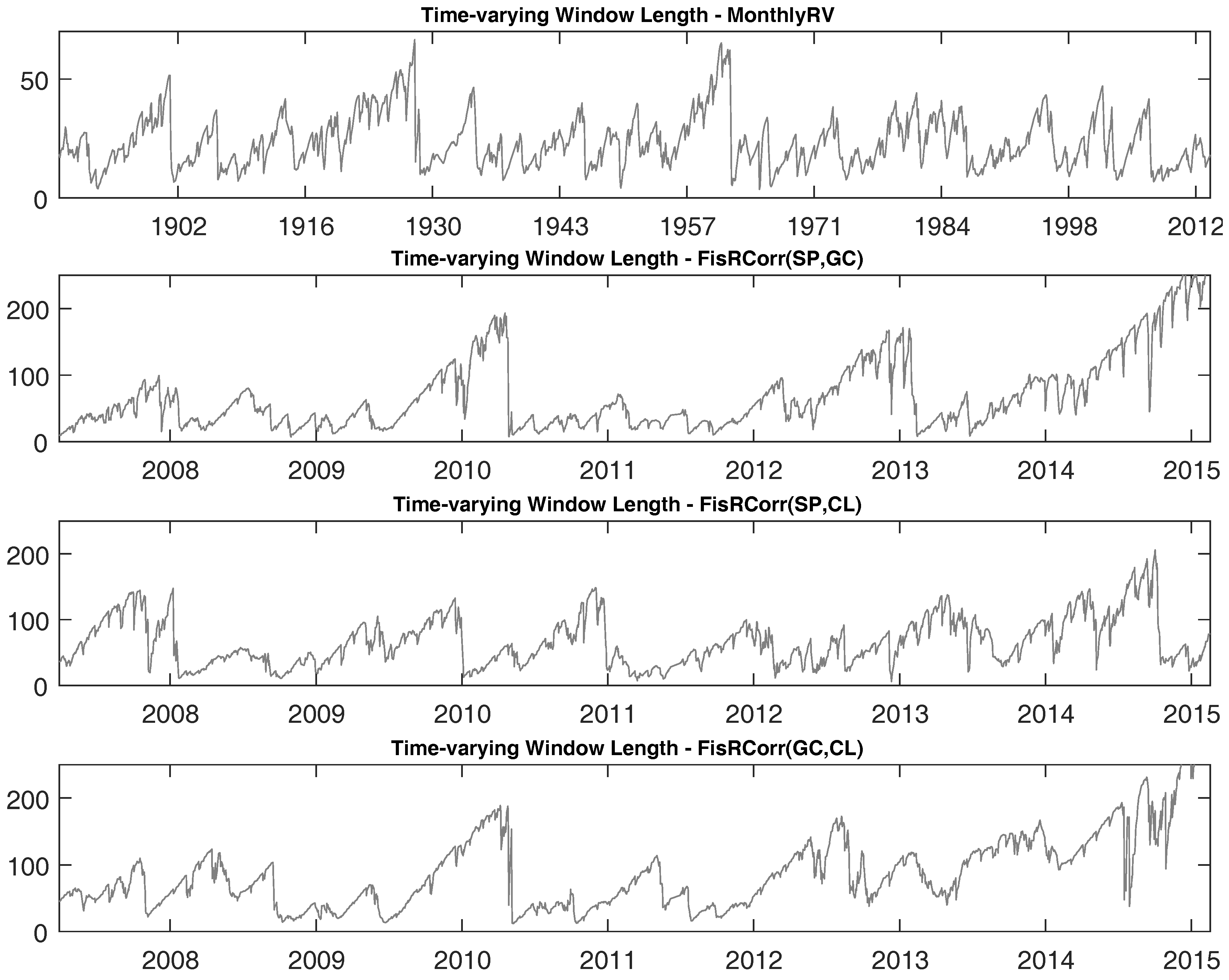
To observe how
varies over time, we plot the time series of
in
Figure 6. There is significant time variation revealed for the
time series for all of our realized variance and correlation datasets. For the case of realized correlations,
can be as small as a single digit and can be as large as almost 250 days, roughly a year, depending on the time period. Our forecasting approach was designed to learn about changes in the DGP and update the submodel probabilities accordingly. When the submodel probabilities change, the time-varying window
measure will change.
4.4. Time-Varying Window Model
Recall that our optimal data-use model, , generates forecasts using information from all of the submodels, appropriately weighted by their time-varying submodel probabilities that maximize the forecasting power. That is, assigns probability weights to the available submodels (data histories) where each submodel is estimated separately, then the resulting submodel forecast are aggregated by the submodel probability weights (in combination with the estimated model change probability). Thus, that approach uses the entire data history available from , but assigns different weights to each data history covered by each submodel.
Alternatively, we can truncate the data history, every period, at the point of most mass for the submodel probability distribution for that period, which we estimate as the time-varying window length (). Then, we can fix the length of the data window, each period, using this measure and compute our forecasts using that data window. In other words, in contrast to , we switch the order of aggregation in that we aggregate the data histories to the length of the window first and then estimate the model and forecast using data corresponding to that window length. Of course, the length of this window will vary over time as varies period-by-period. We will write this model as .
Table 7 reports comparison between these two time-varying data-use models. Interestingly, we see that
of the Mincer–Zarnowitz regression is higher using the
model in almost all datasets, but at the same time, as indicated by the intercept and slope coefficients, the forecasts are more biased than the
forecasts, but still significantly less biased than in the two benchmark models.
The only difference between the forecasts associated with model and the forecasts from the benchmark models, and , is the length of the data window. The fact that the forecasts are better than the benchmark model with respect to both bias and (that is, the proportion of the variation in the target explained by the forecast) confirms that it uses the better length of data window, period-by-period, that drives the superior performance of our approach.
Note that when we compare the log-likelihoods across the two models in
Table 7, the time-varying weights model
forecasts the distributions slightly better than the time-varying window model
. This is not surprising given that the
model updates all submodel probabilities period-by-period based on their predictive content and uses those optimal weights to compute out-of-sample forecasts; whereas the
model first finds the submodel (data history) that has the most predictive content and then fixes the forecast estimation window at that value for that period.
It is clear from comparing the log-likelihood results reported in
Table 7 to those for the benchmark models reported in Columns 2 and 3 of
Table 4, as well as from the Mincer–Zarnowitz forecast regression results presented in earlier tables and figures, the forecasts from both the time-varying weights model
and the time-varying window model
are far superior to the conventional benchmark forecasts.