Abstract
We propose a new method to implement the Business Time Sampling (BTS) scheme for high-frequency financial data. We compute a time-transformation (TT) function using the intraday integrated volatility estimated by a jump-robust method. The BTS transactions are obtained using the inverse of the TT function. Using our sampled BTS transactions, we test the semi-martingale hypothesis of the stock log-price process and estimate the daily realized volatility. Our method improves the normality approximation of the standardized business-time return distribution. Our Monte Carlo results show that the integrated volatility estimates using our proposed sampling strategy provide smaller root mean-squared error.
Keywords:
autoregressive conditional duration model; high-frequency data; integrated volatility; time-transformation function JEL Codes:
G410; G120
1. Introduction
In high-frequency financial data analysis, researchers usually do not use all available data but would select a subgrid of transactions. To choose the subgrid, two issues have to be considered: selecting the sampling scheme and choosing the target average sampling frequency. Three sampling schemes are commonly used in the literature: Calendar Time Sampling (CTS), Tick Time Sampling (TTS) and Business Time Sampling (BTS). Under the CTS scheme, transactions are selected by regularly spaced calendar time, such as every 5 s/min. The TTS scheme selects transactions with regularly spaced number of ticks, e.g., every 5 or 10 ticks. The BTS transactions are often selected to ensure approximately equal volatility for the returns over each interval. Thus, the CTS and TTS schemes are implemented based on explicit criteria (i.e., regular calendar-time length or number of ticks, respectively). In contrast, the BTS scheme depends on the unobserved volatility. As a result, the CTS and TTS schemes have been used widely in the literature, while the BTS scheme is used less frequently.
The BTS scheme possesses some desirable properties for high-frequency financial data analysis. It dates back to Dacorogna et al. (1993), and see also Zhou (1998), Peters and De Vilder (2006), and Mykland (2012). In particular, the BTS scheme yields independently and identically distributed (iid) normal returns for a semimartingale price process even when there is leverage or feedback effect.1 In contrast, due to the leverage effect or varying volatility, the calendar-time returns may not be iid normal even if the price process is a continuous local martingale. The assumption of iid Gaussian returns is required for the Gaussian-likelihood approach Nowman (1997) and several widely used integrated volatility estimates, including the multipower variation (MPV) estimate of Barndorff-Nielsen et al. (2006), the quantile realized volatility (QRV) method of Christensen et al. (2010) and the nearest neighbor truncation method of Andersen et al. (2012, 2014). However, in the implementation, researchers often sample transactions under the CTS or TTS scheme. Andersen et al. (2007, 2010) find that the normalized daily and weekly returns sampled in business time accord well with the standard normal distribution. To sample the time points, they use a sequential method to include intraday returns until the cumulative squared returns exceeds the average daily or weekly realized volatility.
One drawback of the method in Andersen et al. (2007, 2010) is that its performance in obtaining returns with approximately equal volatility over each interval deteriorates as the sampling frequency increases. In addition, researchers need to choose a threshold to obtain sampled returns at the target frequency. In this paper, we propose a new method to implement the BTS scheme, which has better performance as the sampling frequency increases and needs no threshold. We estimate the intraday integrated volatility using the jump-robust Tripower Realized Volatility (TRV) method of Barndorff-Nielsen et al. (2006) and calculate a time-transformation (TT) function over the investigated time period. The value of the TT function corresponds to the cumulative increments of the estimated intraday integrated volatility over time and the sampled BTS transactions are obtained using the inverse of the TT function.
We test the semi-martingale hypothesis on the BTS returns of 40 stocks selected from the New York Stock Exchange (NYSE). Our proposed BTS method improves the normality approximation of the empirical standardized return distribution. We further explore the use of the BTS scheme in estimating integrated volatility. First, we consider the Realized Volatility (RV) estimates for daily integrated volatility when the returns are sampled using the BTS, CTS and TTS schemes. Our Monte Carlo simulation shows that the TRV estimates (with and without subsampling) using the BTS returns provide the smallest root mean-squared error (RMSE). Second, we modify the ACD-ICV method of Tse and Yang (2012), making use of the BTS scheme. Our modified ACD-ICV estimator performs better than the Realized Kernel (RK) estimates Barndorff-Nielsen et al. (2008) and the method of Tse and Yang (2012), which uses price-event sampling.
The rest of this paper is as follows. Section 2 outlines our proposed implementation of the BTS scheme. Section 3 reports some empirical results on testing the semi-martingale hypothesis. In Section 4, we outline the estimation methods of daily volatility examined in this paper. We report the results of our Monte Carlo study in Section 5 and draw conclusions in Section 6. The Appendix A provides further details of the jump detection procedure and computation of the BT time-transformation function. Some additional results can be found in the accompanying online supplementary material.
2. Intraday Periodicity and the BTS Scheme
The stylized fact of intraday periodicity is a well known phenomenon in high-frequency financial data analysis. Trading activities are usually high at the beginning and close of the trading day and low around lunch time. Modifications are needed to get rid of this pattern before data are fitted into high-frequency models. To adjust for the intraday periodicity of transaction activity, Tse and Dong (2014) use a time-transformation function computed by pooling all transactions over all trading days in the sample. The TT function transforms all observed transactions from the calendar time to a transformed time for which transactions are evenly observed. However, the time-transformation function proposed by Tse and Dong (2014) will not be appropriate for BT sampling if volatility and transaction activity exhibit different intraday periodicity patterns.
Figure 1 presents the intraday periodicity in volatility and trading activity of the stock JP Morgan (JPM) from January 2010 to April 2013. Figure 1A plots the means of the 1 min intraday realized volatilities over all trading days in the sample period, expressed in annualized standard deviation in percent, while Figure 1B plots the total number of transactions at each second from 9:30 a.m. to 4:00 p.m. over all trading days in the sample. We observe that the realized volatility at the beginning of the trading day is approximately two to three times larger than that near the end of the trading day. In contrast, the number of transactions at the end of the trading day is two to three times larger than that in the morning. This finding is quite regular across other stocks in our sample, which shows that intraday periodicity patterns in volatility and trading activity are quite different.2 Thus, TTS returns in the morning will have larger volatility than those in the afternoon. In contrast, by construction, BTS returns will have nearly constant volatility over the whole trading day.
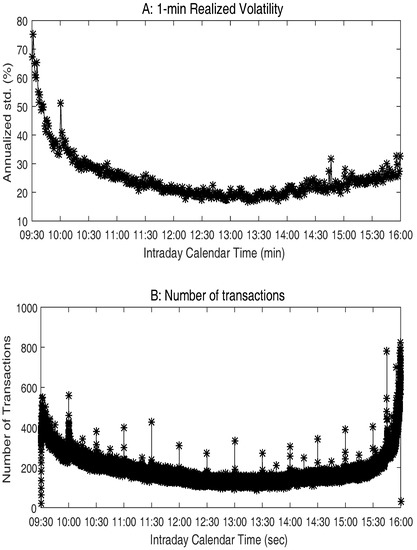
Figure 1.
Intraday volatility and trading activity of JPMorgan Chase (JPM), January 2010 to April 2013.
To implement the BTS scheme, Peters and De Vilder (2006) select transactions based on increments of estimated quadratic volatility. To alleviate the microstructure noise effect, transactions are selected sparsely, such as at 2 min frequency, to calculate the volatility. One drawback of this method is that it assumes away the price jumps, although this assumption is often rejected in the literature (see, e.g., Barndorff-Nielsen and Shephard (2004, 2006), Huang and Tauchen (2005), Lee and Mykland (2008) and Boudt et al. (2011)).3 Another drawback of this method (also in Andersen et al. 2010) is that researchers need to select a threshold value to obtain transactions at the target sampling frequency. The procedure of choosing the threshold has to be iterated, especially when the target frequency is high.
In this paper, we adopt the time-transformation approach to implement the BTS scheme. Let T denote the calendar-time length in seconds aggregated over all trading days in the sample. The time-transformation function at calendar time t (in sec), for , is computed as the empirical proportion of the intraday integrated volatility up to time t.4 The diurnally transformed time corresponding to calendar time t is denoted by , with . Thus, returns over equal intervals of diurnally transformed time will have approximately equal integrated volatility. To obtain BTS transactions at a given frequency, we can select equally spaced transactions at the diurnally transformed time and choose the corresponding BTS transactions using the inverse function . In contrast to the methods in the literature, we do not need to choose a threshold value when implementing the BTS scheme.
We outline our method to obtain the BTS transactions as follows. Consider a sequence of estimated intraday integrated volatility for K consecutive time intervals over the period , with the end point in each time interval represented by , for .5 Denote the collection of points by and define and for . The time-transformation function is calculated as , for . at any calendar-time point t can then be computed using a cubic interpolation that preserves monotonicity in t.6 To sample a sequence of calendar-time points with BTS duration h, we take equally spaced diurnally transformed BT points , with and . Then, are the required calendar-time points for the BTS scheme.
Figure 2A,B present the time-transformation functions for stock JPM based on intraday volatility and trading activity, respectively. These functions are computed by merging the data over the complete sample period, resulting in representative one-day time-transformation functions.7 Note that the two transformation functions exhibit different intraday patterns, with the compression of diurnally transformed time during market open more prominent for volatility than for trading activity.
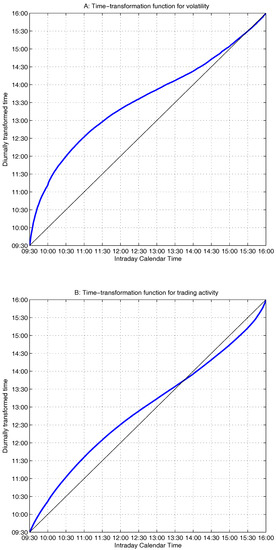
Figure 2.
Time-transformation functions for JPM.
3. Testing the Semi-Martingale Hypothesis Using BTS Returns
As discussed above, BTS returns are iid normal for a semi-martingale price process even when there is leverage and/or feedback effect, whereas the CTS returns may not be iid normal even if the price process is a continuous local martingale. We now examine empirically the behavior of the BTS returns following the study of Andersen et al. (2010).
3.1. The Semi-Martingale Hypothesis
Let be the jump-adjusted returns over the time interval .8 If the log-price follows a jump-diffusion process9 with no leverage and volatility feedback, standardized by the integrated volatility will follow a standard normal distribution, i.e.,
where is the instantaneous volatility function. The above result, however, will not hold if exhibits correlation over time (feedback effect) or with the log-price innovation (leverage effect). On the other hand, if the jump-adjusted returns are sampled over business time so that, over each business-time interval , we have
for a given volatility threshold ,10 Then, the jump-adjusted returns over the business-time intervals () satisfy
To sample a sequence of BTS returns, Andersen et al. (2010) include intraday returns until the cumulative squared 5-min returns exceed a threshold, defined as the average daily or weekly realized volatility in calendar time (ABFN method hereafter). They report improved accuracy of the normal approximation under this sampling scheme.
3.2. Empirical Results of the Tests
To examine empirically the performance of our proposed BTS method versus the ABFN method, we use data of the top 40 market-capitalization stocks from the NYSE in 2010. We extract the tick-by-tick transaction data of these stocks from the TAQ database from January 2010 to April 2013. To clean the raw data, we follow the steps described in Tse and Dong (2014). Using the sequential jump-detection procedure of Andersen et al. (2010), we investigate the proportion of detected jumps (number of the detected jumps over the total number of sampled returns) when different sampling intervals and sampling schemes are used.11
We test the normality assumption of the drift-corrected and jump-adjusted BTS returns (returns with jumps removed). For each trading day, all BTS returns with jumps are deleted and the jump-adjusted 30-min, daily or weekly BTS returns are then computed by summing the remaining consecutive jump-adjusted BTS returns. We apply the Lilliefors (1967) test for normality to the jump-adjusted CTS returns, ABFN returns, and BTS returns. The results are reported in Table 1. It can be seen that the BTS method and the ABFN method substantially improve the normality approximation of the standardized return distribution over the Calendar-Time method. While the results for the weekly data are similar for the BTS method and the ABFN method, the BTS sampling scheme at higher frequencies restores normality for several stocks.

Table 1.
Test of normality hypothesis for no-jump returns of 40 New York Stock Exchange (NYSE) stocks.
We further compare the performance of various methods by computing the moments of 30 min returns with jump-adjustment. In addition to using the Lilliefors (1967) test for normality, we also examine the skewness and kurtosis of the sampled returns of the 40 stocks and compute the average of the absolute difference of the calculated skewness and kurtosis versus 0 and 3, respectively. The results are reported in Table 2. We observe that, for high-frequency returns, the BTS method performs the best in restoring normality, while the TTS method performs the worst. This observation confirms our finding in Section 2 that we cannot use the TTS scheme to approximate the BTS scheme to select intraday returns. For illustration, Figure 3 presents the QQ (Quantile-Quantile) plots of the 30 min jump-adjusted ABFN returns and BTS returns for the JPM stock data. Our proposed BTS method performs better than the ABFN method in restoring normality for returns sampled at high frequency.12

Table 2.
Mean of the absolute difference for no-jump 30 min returns of 40 New York Stock Exchange (NYSE) stocks.
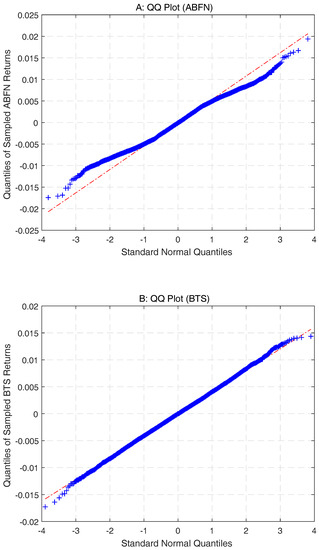
Figure 3.
QQ (Quantile-Quantile) plots of sampled 30 min returns for JPMorgan Chase (JPM), January 2010–April 2013.
4. Estimation of Integrated Volatility
We now examine the use of the BTS scheme for estimating integrated volatility. We consider two methods of estimating daily volatility: Realized Volatility (RV) method and Autoregressive Conditional Duration-Integrated Conditional Volatility (ACD-ICV) method. The literature on RV estimation has grown tremendously since its inception. In this paper, we select the Tripower Realized Volatility (TRV) estimate of Barndorff-Nielsen et al. (2006) for its robustness to price jumps.13 We compare the performance of the TRV estimates when returns are sampled by BTS, CTS and TTS schemes, with and without subsampling. With the same estimator used, the performance of the estimates is only differentiated by the sampling method. We also consider the use of the ACD-ICV approach, with some modifications based on the BTS methodology.
4.1. Integrated Volatility Estimation Using BT Returns
For a given subgrid , the TRV estimate is computed as
where for and for , with denoting the gamma function and denoting the elements following in . We define as number of points in grid minus 1. For the CTS scheme, the previous-tick method is adopted when there is no transaction at the selected time point. For the TTS scheme, the number of subsampling grids S is selected to ensure that each subgrid has transactions at the target sampling frequency. To implement the subsampling method under the BTS scheme, we select BTS transactions with the sampling frequency being twice the average transaction duration. Subsampling is then implemented to obtain subgrids at the target sampling frequency.
4.2. Integrated Volatility Estimation Using the Modified ACD-ICV Method
Tse and Yang (2012) propose the ACD-ICV method to estimate daily and intraday volatility by modeling the price durations parametrically. They point out that, for short intraday intervals, such as an hour or 15 min, the RV methods use only local data for the period of interest. Thus, the infill sample size may not be large enough to justify the applicability of the asymptotics of the RV estimates. In contrast, the ACD-ICV method estimates the conditional volatility using data beyond the period of interest and produces better estimates of volatility over short intraday intervals. Their simulation results show that the ACD-ICV method performs better than other methods (such as the Realized Kernel method of Barndorff-Nielsen et al. (2008) in estimating the daily, 1 h and 15 min integrated volatility.
The ACD-ICV method samples observations from the observed transaction data based on a pre-specified price threshold . That is, transactions are selected whenever the absolute price change exceeds the threshold , which are the price events. Suppose is the selected price events and the ith price duration is . Let denote the information set upon the price event at time . Denote as the conditional expectation of the price duration and assume that the standardized durations are iid positive random variables with a mean of unity. Given the information at time , the conditional instantaneous return variance per unit time at time , denoted by , is
where is the hazard function of . Assuming to be iid standard exponential distributed, the integrated conditional variance (ICV) over time period is calculated as
The conditional expectation of the price durations can be estimated by various methods, such as the ACD method of Engle and Russell (1998) or the Augmented ACD method of Fernandes and Grammig (2006).
The original ACD-ICV method models the price durations obtained by the threshold by assuming that these durations have equal volatility, and this assumption may not be true. In this paper, we modify the ACD-ICV method in two ways. First, instead of modeling the durations of the price events, we model the BTS durations that are obtained based on volatility change (instead of the absolute price change). The BTS returns are sampled as in Section 2. Second, we replace in Equation (6) by an estimate of the mean volatility over each sampled BTS return. Suppose there are K BTS returns over m trading days, and the estimated integrated volatility over these m trading days is equal to . Then, each BTS return has an approximately constant integrated volatility of . Instead of using as an approximation of the integrated volatility of each price event as in Tse and Yang (2012), we use to replace in Equation (6) to obtain a new ACD-ICV estimate.
Thus, for the ACD-ICV approach, we consider three variations of estimates. We first select transactions using the price-event sampling method (where transactions are selected based on absolute price change) and estimate the daily integrated volatility using the ACD-ICV method as in Tse and Yang (2012). We denote this method by ME1. We then replace in equation (6) by , which is the integrated volatility estimated using TRV with subsampling at 3-min sampling frequency. We call this method ME2.14 Finally, we sample data using the BTS scheme (not by price events) and repeat the computation as in ME2, which is called ME3. We compare the daily volatility estimates using the ACD-ICV methods against the RK method.15
5. Monte Carlo Study
We conduct a Monte Carlo (MC) study to examine the performances of different integrated volatility estimates. Our MC set-up draws upon other models in the literature.
5.1. Simulation Models
We consider five simulation models, which are summarized in Table 3. Models MD1 and MD2 are the Heston models (Heston (1993) and Aït-Sahalia and Mancini (2008) with some modifications) with high and low volatility, respectively. MD3 is the two-factor afine stochastic volatility model with an intraday U-shape pattern Hasbrouck (1999) and Andersen et al. (2012). MD4 is a deterministic volatility set-up Tse and Yang (2012). Finally, MD5 is MD1 with price jumps.

Table 3.
Summary of simulation models.
For all set-ups above, we set the initial price to 60 and the initial value of to 30%. We introduce sparsity of trade to the data by simulating exponentially distributed calendar-time transaction durations.16 We first simulate transactions second by second and then generate exponentially distributed transaction durations with mean equal to 5 s, 10 s and 20 s, respectively. For simplicity, we only investigate iid market microstructure noise with constant noise-signal ratio (NSR). Based on the findings in Dong and Tse (2017), we consider cases with NSR = 0.005%, 0.01% and 0.02%. We introduce a 0.01 price rounding error in all simulations. The intraday duration periodicity is adjusted by the time-transformation method in Tse and Dong (2014) before we fit all price durations and BTS durations to the ACD model. Each model is simulated over 60 trading days, with the simulation repeated 1000 times.
5.2. Simulation Results
We first report our results on the TRV estimates. For each model set-up, sampling frequencies of 1, 2, 3, 5 and 10 min are considered. We compute TRV based on the CTS, TTS and BTS returns, with and without subsampling. To save space, we present only the results for the BTS scheme with subsampling in Table 4. Table 5 summarizes the average difference in RMSE of the CTS and TTS schemes versus the BTS scheme over all models and parameter set-ups, with subsampling, in both absolute and relative terms. All results can be found in the supplementary material (Tables S4–S9). The BTS returns perform the best in reporting generally smaller root mean-squared error (RMSE), especially for methods with no subsampling. When the subsampling method is used, the RMSE decreases substantially. Generally, the BTS scheme still performs the best and its advantage is especially obvious for MD3 and MD4 when there is intraday volatility periodicity in the simulated price process.17 Under all sampling schemes, the TRV estimates suffer from the market microstructure noise problems when the NSR is large, resulting in high mean error (ME) at high sampling frequency. When sparsity and NSR are both low, high sampling frequency at 1 min interval produces the lowest RMSE. Overall, the BTS returns outperform the CTS and TTS returns in estimating the integrated volatility.

Table 4.
Mean error (ME) and root mean-squared error (RMSE) of estimates of daily volatility using the Tripower Realized Volatility (TRV) method under the Business Time Sampling (BTS) scheme with subsampling.

Table 5.
Comparison of the Tripower Realized Volatility (TRV) estimates under different sampling schemes with subsampling.
We now turn to the results of the ACD-ICV method. Table 6 and Table 7 report the ME and RMSE of the RK and the ACD-ICV estimates for MD1 and MD5, respectively. Results for other models can be found in the online supplementary material (Tables S10–S12). Table 8 summarizes the average RMSE of Realized Kernel estimate versus the ACD-ICV estimates over all models and parameter set-ups. The RK method performs quite well for the unbiasedness property, reporting small ME for all models except MD5 (model with price jump). ME1 reports quite big absolute ME and RMSE values among all the sampling frequencies considered and it often performs worse than the RK method except for MD5.18 In contrast, the modified ACD-ICV methods, ME2 and ME3, report quite small ME and RMSE. ME3 consistently reports smaller RMSE than ME2 except for few cases in MD3 and MD5 at the 3 min and 5 min sampling frequencies. Moreover, ME2 varies more across different sampling frequencies. This demonstrates the superiority of the BTS durations over the price durations when they are fitted to the ACD model to estimate the integrated volatility. The better performance of ME3 over ME2 is mainly due to the fact that the BTS scheme performs better in yielding returns with constant volatility compared against the ACD-ICV method using the price events.

Table 6.
Mean error (ME) and root mean-squared error (RMSE) of daily volatility estimates of the realized kernel (RK) and Autoregressive Conditional Duration-Integrated Conditional Variance (ACD-ICV) methods for Model MD1.

Table 7.
Mean error (ME) and root mean-squared error (RMSE) of daily volatility estimates of the realized kernel (RK) and Autoregressive Conditional Duration-Integrated Conditional Variance (ACD-ICV) methods for Model MD5.

Table 8.
Comparison of the root mean-squared error (RMSE) of daily volatility estimates of the realized kernel (RK) and Autoregressive Conditional Duration-Integrated Conditional Variance (ACD-ICV) methods.
Our modified ACD-ICV method ME3 consistently produces lower RMSE over all models and parameter set-ups than the RK estimates. Its performance is robust over a wide range of sampling frequencies of up to 15 min. It also outperforms the TRV estimates with subsampling, except possibly for MD5, in which case their performances are comparable.19
6. Conclusions
We propose an easy-to-use time-transformation method to implement the BTS scheme at a prespecified average sampling frequency. Using 40 stocks from the NYSE, we perform normality test to the jump-adjusted daily and weekly BTS returns. Our results show that stock prices can be considered discrete observations from a continuous-time jump-diffusion process. The BTS scheme performs better than other sampling methods in yielding iid Gaussian returns, and it also performs better than the CTS and TTS schemes in estimating daily realized volatility using the TRV method. We also show the superiority of the BTS durations over the price durations in estimating the daily integrated volatility using the ACD-ICV method. Our modified ACD-ICV estimate, ME3, which models the high-frequency BTS durations using the ACD model, performs the best in reporting smaller RMSE values.
Finally, we note that there are other possible applications of the BTS scheme. For example, we can estimate the conditional instantaneous volatility or intraday integrated volatility (such as over 30 min intervals) by modeling the high-frequency BTS durations using the ACD model. Moreover, we can estimate the integrated quarticity () by using a method similar to that implemented in this paper. That is, we first obtain transactions with approximately equal quarticity increments. The conditional instantaneous quarticity or integrated quarticity can be estimated further by modeling clustering of the corresponding durations using the ACD model. Please refer to Jacod and Rosenbaum (2013) and Andersen et al. (2014), among others, for theories and empirical applications of the asset price quarticity.
Supplementary Materials
The following are available online at www.mdpi.com/2225-1146/5/4/51/s1, Figure S1: 1-min Realized Volatility and number of transactions, 2010–2013. Table S1: Proportion of detected jumps. Table S2: Rejection proportion of the normality hypothesis for no-jump returns under different sampling schemes. Table S3: Rejection proportion of the normality hypothesis for returns under different sampling schemes. Table S4: ME and RMSE of daily volatility estimates using the TRV method without subsampling under the CTS scheme. Table S5: ME and RMSE of daily volatility estimates using the TRV method without subsampling under the TTS scheme. Table S6: ME and RMSE of daily volatility estimates using the TRV method without subsampling under the BTS scheme. Table S7: ME and RMSE of daily volatility estimates using the TRV method with subsampling under the CTS scheme. Table S8: ME and RMSE of daily volatility estimates using the TRV method with subsampling under the TTS scheme. Table S9: ME and RMSE of daily volatility using the TRV method with subsampling under the BTS scheme. Table S10: ME and RMSE of daily volatility estimates of the RK and ACD-ICV methods for Model MD2. Table S11: ME and RMSE of daily volatility estimates of the RK and ACD-ICV methods for Model MD3. Table S12: ME and RMSE of daily volatility estimates of the RK and ACD-ICV methods for Model MD4.
Acknowledgments
Yingjie Dong acknowledges support provided by the Fundamental Research Funds for the Central Universities in University of International Business and Economics (UIBE) (CXTD8-01).
Author Contributions
Yingjie Dong and Yiu-Kuen Tse contributed equally to this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. Jump Detection Procedure
We remove price jumps using the sequential jump-adjustment procedure of Andersen et al. (2010) with some minor modifications. The test statistic for day t is computed as
where , is the realized volatility, is the realized bipower volatility and is the realized tripower quarticity, and is the grid on day t. The realized tripower quarticity is computed as
where for and Under the condition of no jumps, is approximately standard normal. At the significance level , a jump is considered to be significant if , where is the -quantile of the standard normal distribution. When , we delete the return that has the maximum absolute value among all returns and repeat the jump test again for the remaining returns. This recursive procedure stops when .
Appendix A.2. Computation of the BT Time-Transformation Function
To compute the BT transformation function , where for , we need to calculate the intraday integrated volatility . To alleviate the effects of market microstructure noise and price jumps we adopt the Tripower Realized Volatility (TRV) method of Barndorff-Nielsen et al. (2006). Suppose there are S subsampling grids and the sth subgrid is denoted by . Under subgrid , for trading day d, denote the returns by . We define
for , where for and is the gamma function. Moreover, and . Since the estimate may have large fluctuations, we group every g together to obtain the estimated intraday integrated volatility at 10-min average sampling frequency. Thus, the pth intraday integrated volatility on day d under subgrid is . The corresponding end point of is the end point of and is denoted by . Finally, the estimated pth intraday integrated volatility and its corresponding end point can be obtained by taking the average over all subsamples. That is, and . and pooled over all m trading days form for and , respectively, for the computation of the time-transformation function . The number of subsamples S is selected to obtain subgrids of approximately 1 min sampling frequency.
References
- Aït-Sahalia, Yacine, and Loriano Mancini. 2008. Out of sample forecasts of quadratic variation. Journal of Econometrics 147: 17–33. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, and Dobrislav Dobrev. 2007. No-arbitrage semi-martingale restrictions for continuous-time volatility models subject to leverage effects, jumps and iid noise: Theory and testable distributional implications. Journal of Econometrics 138: 125–80. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, Per Frederiksen, and Ørregaard Nielsen. 2010. Continuous-time models, realized volatilities, and testable distributional implications for daily stock returns. Journal of Applied Econometrics 25: 233–61. [Google Scholar] [CrossRef]
- Andersen, Torben G., Dobrislav Dobrev, and Ernst Schaumburg. 2012. Jump-robust volatility estimation using nearest neighbor truncation. Journal of Econometrics 169: 75–93. [Google Scholar] [CrossRef]
- Andersen, Torben G., Dobrislav Dobrev, and Ernst Schaumburg. 2014. A robust neighborhood truncation approach to estimation of integrated quarticity. Econometric Theory 30: 3–59. [Google Scholar] [CrossRef]
- Bajgrowicz, Pierre, Olivier Scaillet, and Adrien Treccani. 2016. Jumps in high-frequency data: Spurious detections, dynamics, and news. Management Science 62: 2198–217. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2004. Power and bipower variation with stochastic volatility and jumps. Journal of Financial Econometrics 2: 1–37. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2006. Econometrics of testing for jumps in financial economics using bipower variation. Journal of financial Econometrics 4: 1–30. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., Neil Shephard, and Matthias Winkel. 2006. Limit theorems for multipower variation in the presence of jumps. Stochastic Processes and Their Applications 116: 796–806. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., Peter Reinhard Hansen, Asger Lunde, and Neil Shephard. 2008. Designing realized kernels to measure the ex post variation of equity prices in the presence of noise. Econometrica 76: 1481–536. [Google Scholar]
- Boudt, Kris, Christophe Croux, and Sébastien Laurent. 2011. Robust estimation of intraweek periodicity in volatility and jump detection. Journal of Empirical Finance 18: 353–67. [Google Scholar] [CrossRef]
- Christensen, Kim, Roel Oomen, and Mark Podolskij. 2010. Realised quantile-based estimation of the integrated variance. Journal of Econometrics 159: 74–98. [Google Scholar] [CrossRef]
- Dacorogna, Michael M., Ulrich A. Müller, Robert J. Nagler, Richard B. Olsen, and Olivier V. Pictet. 1993. A geographical model for the daily and weekly seasonal volatility in the foreign exchange market. Journal of International Money and Finance 12: 413–38. [Google Scholar] [CrossRef]
- Dambis, Karl E. 1965. On the decomposition of continuous submartingales. Theory of Probability & Its Applications 10: 401–10. [Google Scholar]
- Dong, Yingjie, and Yiu-Kuen Tse. 2017. On estimating market microstructure noise variance. Economics Letters 150C: 59–62. [Google Scholar] [CrossRef]
- Dubins, Lester E., and Gideon Schwarz. 1965. On continuous martingales. Proceedings of the National Academy of Sciences of the United States of America 53: 913. [Google Scholar] [CrossRef] [PubMed]
- Engle, Robert F., and Jeffrey R. Russell. 1998. Autoregressive conditional duration: A new model for irregularly spaced transaction data. Econometrica 66: 1127–62. [Google Scholar] [CrossRef]
- Fernandes, Marcelo, and Joachim Grammig. 2006. A family of autoregressive conditional duration models. Journal of Econometrics 130: 1–23. [Google Scholar] [CrossRef]
- Hasbrouck, Joel. 1999. The dynamics of discrete bid and ask quotes. The Journal of Finance 54: 2109–42. [Google Scholar] [CrossRef]
- Heston, Steven L. 1993. A closed-form solution for options with stochastic volatility with applications to bond and currency options. Review of Financial Studies 6: 327–43. [Google Scholar] [CrossRef]
- Huang, Xin, and George Tauchen. 2005. The relative contribution of jumps to total price variance. Journal of Financial Econometrics 3: 456–99. [Google Scholar] [CrossRef]
- Jacod, Jean, and Mathieu Rosenbaum. 2013. Quarticity and other functionals of volatility: Efficient estimation. The Annals of Statistics 41: 1462–84. [Google Scholar] [CrossRef]
- Lee, Suzanne S., and Jan Hannig. 2010. Detecting jumps from Lévy jump diffusion processes. Journal of Financial Economics 96: 271–90. [Google Scholar] [CrossRef]
- Lee, Suzanne S., and Per A. Mykland. 2008. Jumps in financial markets: A new nonparametric test and jump dynamics. The Review of Financial Studies 21: 2535–63. [Google Scholar] [CrossRef]
- Lilliefors, Hubert W. 1967. On the Kolmogorov-Smirnov test for normality with mean and variance unknown. Journal of the American Statistical Association 62: 399–402. [Google Scholar] [CrossRef]
- Mykland, Per A. 2012. A Gaussian calculus for inference from high frequency data. Annals of Finance 8: 235–58. [Google Scholar] [CrossRef]
- Nowman, Khalid B. 1997. Gaussian Estimation of Single-Factor Continuous Time Models of The Term Structure of Interest Rates. The Journal of Finance 52: 1695–706. [Google Scholar] [CrossRef]
- Oomen, Roel C. A. 2006. Properties of realized variance under alternative sampling schemes. Journal of Business & Economic Statistics 24: 219–37. [Google Scholar]
- Peters, Remco T., and Robin G. De Vilder. 2006. Testing the continuous semimartingale hypothesis for the S&P 500. Journal of Business & Economic Statistics 24: 444–54. [Google Scholar]
- Tse, Yiu-Kuen, and Thomas Tao Yang. 2012. Estimation of high-frequency volatility: An autoregressive conditional duration approach. Journal of Business & Economic Statistics 30: 533–45. [Google Scholar]
- Tse, Yiu-Kuen, and Yingjie Dong. 2014. Intraday Periodicity Adjustments of Transaction Duration and Their Effects on High-Frequency Volatility Estimation. Journal of Empirical Finance 28: 352–61. [Google Scholar] [CrossRef]
- Zhou, Bin. 1998. F-consistency, De-volatilization and normalization of high-frequency financial data. In Nonlinear Modelling of High Frequency Financial Time Series. Edited by Christian Dunis and Bin Zhou. New York: Wiley, pp. 109–23. [Google Scholar]
| 1. | Dambis (1965) and Dubins and Schwarz (1965) show that a process compiled from a continuous local martingale with equal quadratic-variation increments is a Brownian motion. Leverage effect refers to the asymmetry between equity returns and volatility. That is, large negative returns tend to be associated with higher future volatility than positive returns of the same magnitude. Feedback effect refers to the case when the volatility function is correlated over time. |
| 2. | Results for other stocks can be found in the online supplementary material (Figure S1). |
| 3. | One drawback of the jump detection methods is the presence of the spurious detections due to multiple testing issues. See Bajgrowicz et al. (2016) for a discussion. |
| 4. | As there are 6.5 h of trades in a trading day for the NYSE, for m trading days we have s. at calendar time t (in s) is an increasing function of t, with , and . |
| 5. | Here, are calendar-time points which need not to be regularly spaced. We outline the detailed steps in calculating and , for , in the Appendix A. can be any suitable estimates of intraday integrated volatility. In this paper we use the TRV method of Barndorff-Nielsen et al. (2006) to calculate for its robustness to jumps. |
| 6. | We use the Matlab (2015a, Mathworks, Natick, MA, United States) command pchip in this paper. Given and the calendar-time point t, the diurnally transformed time is . Conversely, given and a diurnally transformed time , the corresponding calendar time is . |
| 7. | In the empirical applications in this paper, the time-transformation function for BTS is extended over the whole sample period, which takes account of varying volatility over different trading days. |
| 8. | The jump-adjustment procedure can be found in the Appendix A. |
| 9. | The Brownian semimartingale process can be defined as , where is the drift term, the instantaneous volatility process is càdlàg, and denotes a standard Brownian motion independent of the drift. In this paper, we further add jumps to the Brownian semimartingale and assume the price process to be a generic jump-diffusion process. That is, , where when there is a jump at time t, and otherwise, and denotes the jump size if a jump occurs at time t. We assume the jump component to be a finite activity jump process. Note that when there are infinite number of jumps in the data, our BTS method will work if we select BTS transactions based on estimated integrated volatility that are robust to the presence of Lévy-type jumps. See Lee and Hannig (2010) for the evidence of the presence of the Lévy-type jumps and see Barndorff-Nielsen et al. (2006) for an analysis of the multipower variation estimates when there are infinite number of jumps. |
| 10. | Note that, given and , is the minimum business time so that the integrated volatility over the interval reaches . |
| 11. | As our focus here is the testing of the semi-martingale hypothesis, the results of the jump detection are not presented. Details of the selected stocks and results of the jump tests can be found in the supplementary material (Tables S1–S3) for which sampling frequencies of 1 min, 5 min and 10 min are used. When the sampling frequency is equal to 1 min, more than 12 stocks report jump proportions with values exceeding 10% under all sampling schemes. This suggests that sampling frequency that is too high (such as 1 min) may render misleading results when they are used for jump detection using the method of Andersen et al. (2010). See Oomen (2006) for an analysis of the performance of the realized variance estimator among alternative sampling schemes. |
| 12. | QQ plots of the jump-adjusted ABFN returns and BTS returns at daily and weekly frequencies are very similar. We also calculate the ACF values of the sampled 30 min returns up to lag 150. All returns sampled using various methods exhibit no periodicity. The correlation between the ABFN returns and BTS returns increases as the sampling frequency decreases, and the value is around 13.5% at weekly frequency. |
| 13. | We do not use the bipower realized volatility method here since the TRV method is more robust to the presence of jumps, especially when the sampling frequency is high. |
| 14. | Note that, for ME1 and ME2, the returns are sampled by price events and the ACD models are fitted to diurnally transformed durations using the time-transformation function based on the number of trades. |
| 15. | The RK method is selected for comparison due to its superior performance among the RV estimators (see Barndorff-Nielsen et al. (2008)). To calculate the bandwidth of the RK method, we use the subsampling realized volatility estimator and 3 min TTS returns. For the ACD-ICV methods, all results in this paper are based on conditional duration models fitted using the power ACD (PACD) model (see Fernandes and Grammig 2006). |
| 16. | Sparsity occurs as empirically transactions are not observed sec by sec. Inactive stocks typically have more sparse transactions. |
| 17. | When there is intraday volatility periodicity, the BTS returns resemble more closely to normal distribution than the CTS and TTS returns. |
| 18. | This is in contrast to the findings in Tse and Yang (2012), which shows the superiority of the ACD-ICV method over the RK method via simulation using second-by-second transactions (sparsity of 1 s). The poor performance of ME1 is mainly due to the transaction sparsity, since using as the proxy for integrated volatility over one price event becomes unreliable when transactions are sparse. Supporting evidence is provided in our simulation study that the RMSE of ME1 increases when observed transactions are more sparse. |
| 19. | MD5 is a model with price jumps, and the TRV method is constructed to be robust to price jumps. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).