Do Seasonal Adjustments Induce Noncausal Dynamics in Inflation Rates?
Abstract
1. Introduction
2. Mixed Causal-Noncausal Models
2.1. Model Representation
2.2. Estimation
3. Seasonal Adjustment Methods
3.1. The Linear X-11 Seasonal Filter
3.2. Properties of Seasonal Adjustment
3.3. Seasonal Adjustment for Mixed Processes
4. Simulation Study
4.1. Purely Causal and Noncausal Processes
4.1.1. Case 1: X-11 Seasonally Adjusted Series
4.1.2. Case 2: Deterministic Seasonal Adjustment
4.2. Mixed Causal-Noncausal Processes
5. Seasonal Adjustment, Noncausality and Inflation Rates
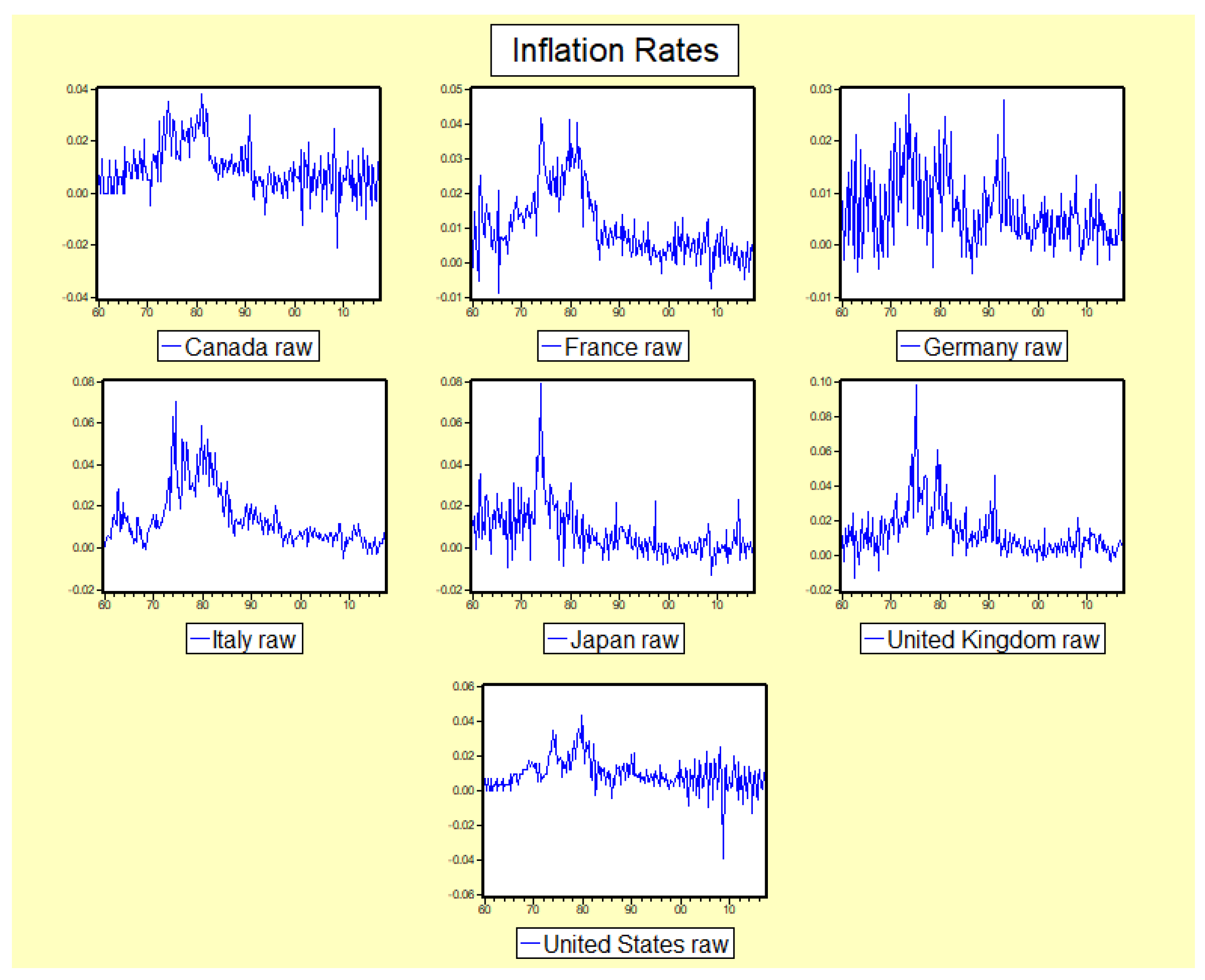
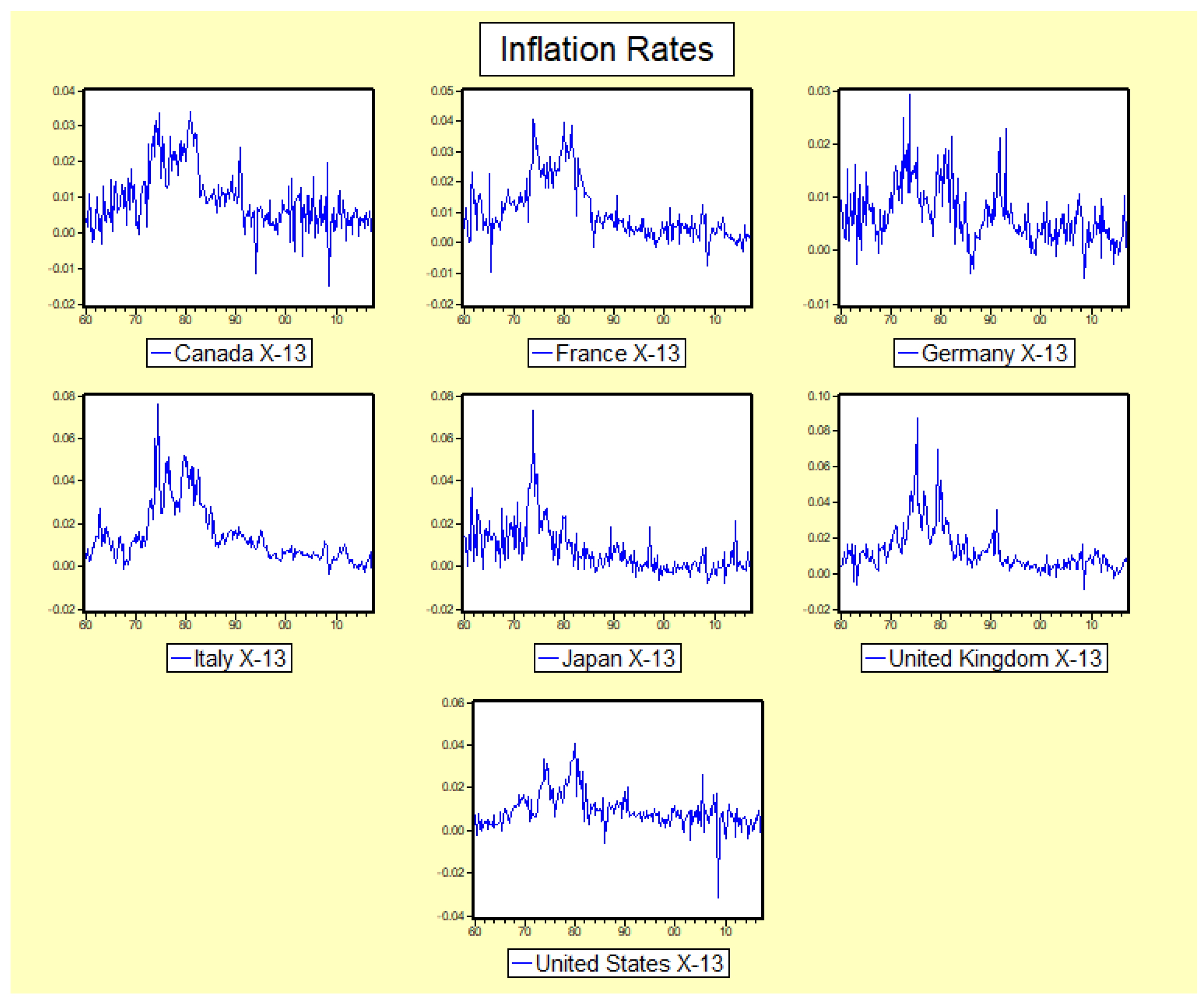
5.1. Data
5.2. Results
5.3. Considerations
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Autocovariances and Spectra
Appendix A.1. White Noise with Seasonal Dummies
Appendix A.2. AR(1) with Seasonal Dummies
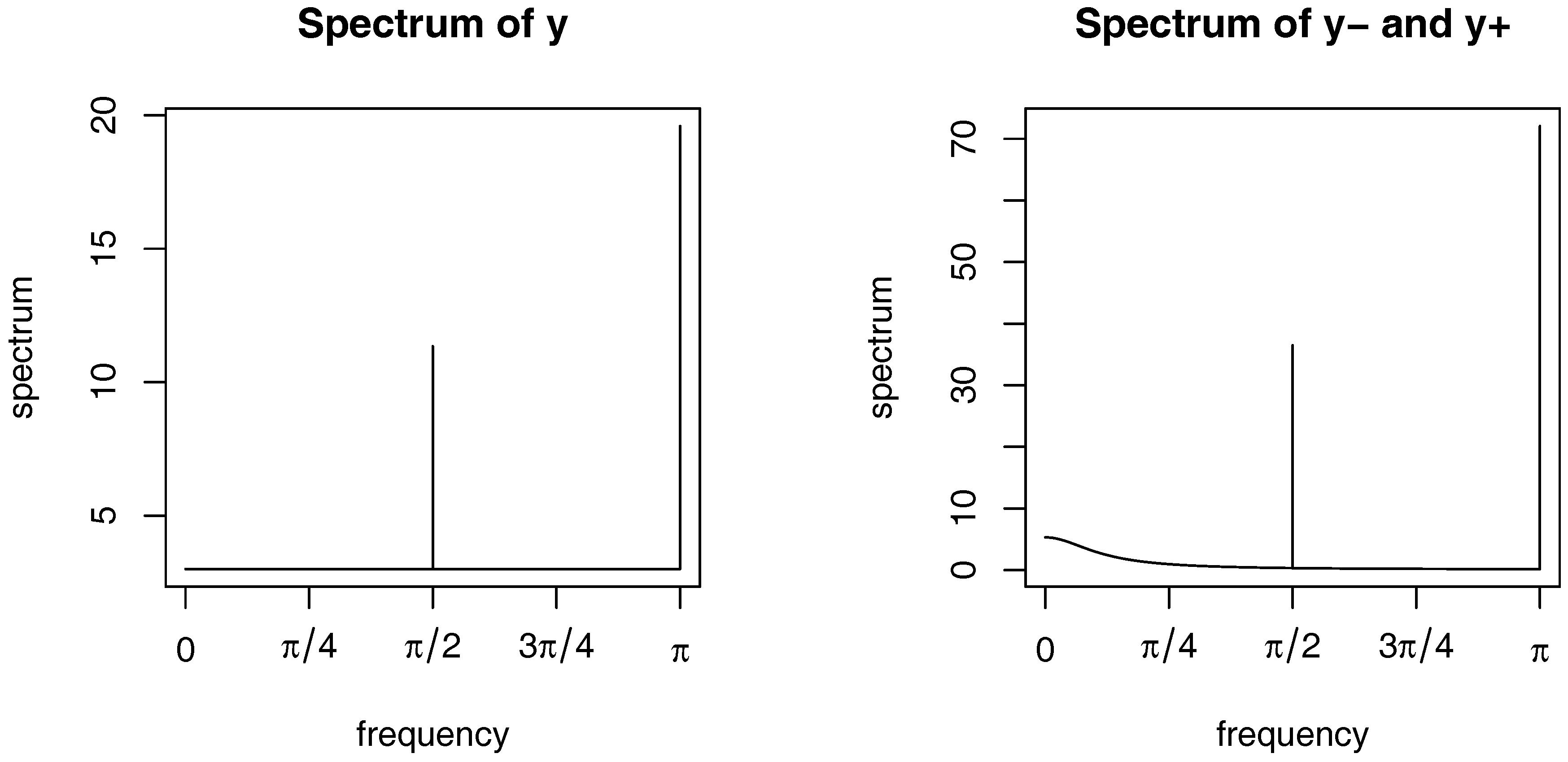
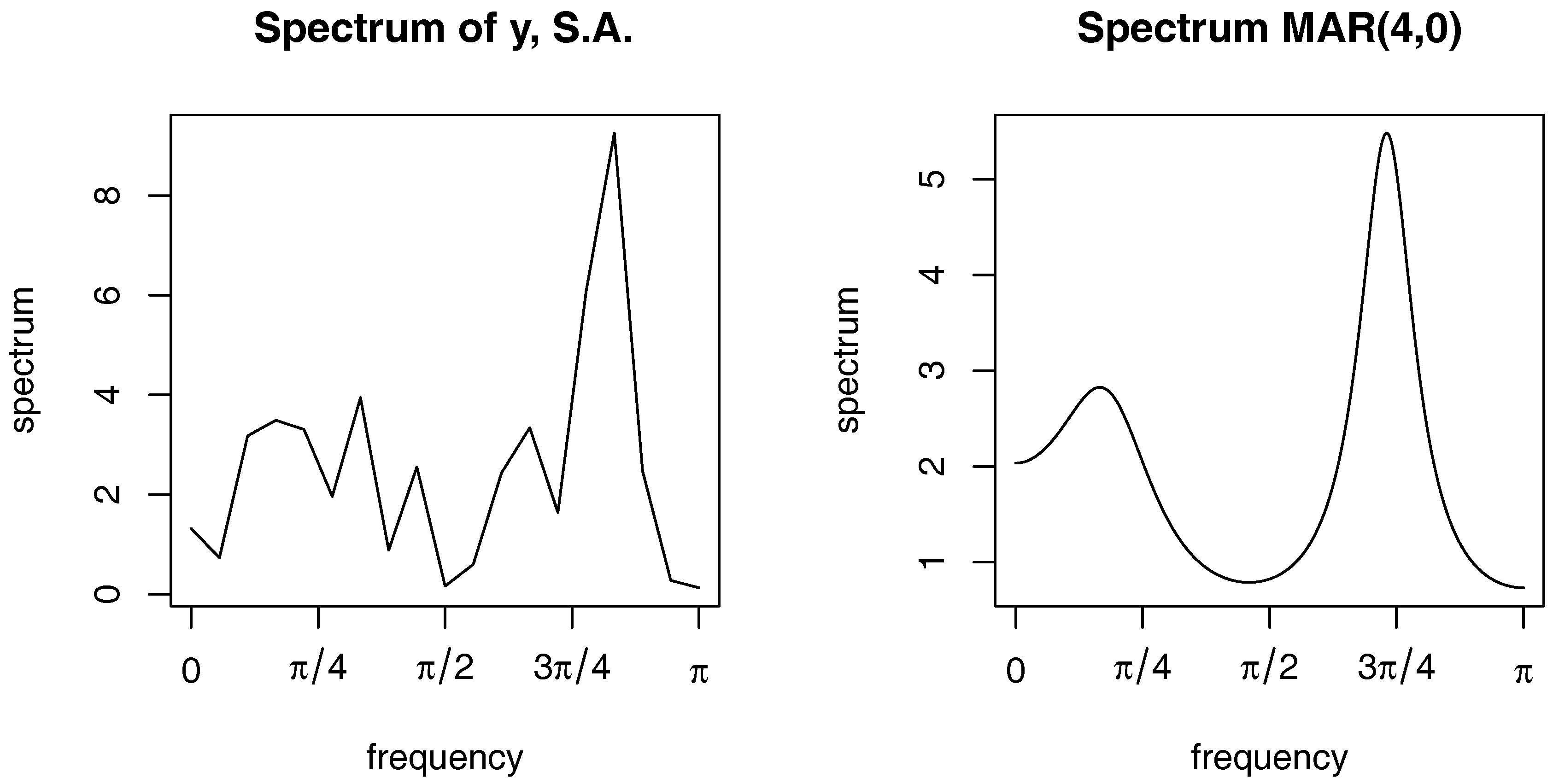
Appendix B. Graphs
References
- Abeln, Barend, and Jan Jacobs. 2015. Seasonal Adjustment With and Without Revisions: A Comparison of X-13 ARIMA-SEATS and CAMPLET. CAMA Working Papers. Canberra, Australia: Australian National University. [Google Scholar]
- Alessi, Lucia, Matteo Barigozzi, and Marco Capasso. 2011. Non-Fundamentalness in Structural Econometric Models: A Review. International Statistical Review 79: 1. [Google Scholar] [CrossRef]
- Bell, William. 1987. A Note on Overdifferencing and the Equivalence of Seasonal Time Series Models with Monthly Means and Models with (0,1,1)12 Seasonal Parts when Θ = 1. Journal of Business and Economic Statistics 5: 383–87. [Google Scholar] [CrossRef]
- Bell, William, and Steven Hillmer. 2002. Issues Involved with the Seasonal Adjustment of Economic Time Series. Journal of Business & Economic Statistics 20: 98–127. [Google Scholar]
- Breidt, F. Jay, Richard Davis, Keh-Shin Lii, and Murray Rosenblatt. 1991. Maximum Likelihood Estimation for Noncausal Autoregressive Processes. Journal of Multivariate Analysis 36: 175–98. [Google Scholar] [CrossRef]
- Brockwell, Peter, and Richard Davis. 1991. Time Series: Theory and Methods, 2nd ed. New York: Springer. [Google Scholar]
- Cavaliere, Giuseppe, Heino Bohn Nielsen, and Anders Rahbek. 2017. Bootstrapping Non-Causal Autoregressions: with an Application to Explosive Bubble Modelling. Working Paper. Copenhagen, Denmark: University of Copenhagen. [Google Scholar]
- De Jong, Robert, and Neslihan Sakarya. 2016. The Econometrics of the Hodrick-Prescott Filter. The Review of Economics and Statistics 98: 310–17. [Google Scholar] [CrossRef]
- Del Barrio Castro, Tomás, and Denise Osborn. 2004. The Consequences of Seasonal Adjustment for Periodic Autoregressive Processes. Econometrics Journal 7: 207–31. [Google Scholar] [CrossRef]
- Del Barrio Castro, Tomás, Paolo M. M. Rodrigues, and A. M. Robert Taylor. 2017. Semi-Parametric Seasonal Unit Root Tests. Econometric Theory, 1–30. [Google Scholar] [CrossRef]
- Franses, Philip Hans, and Bart Hobijn. 1997. Critical Values for Unit Root Tests in Seasonal Time Series. Journal of Applied Statistics 24: 25–47. [Google Scholar] [CrossRef]
- Fries, Sébastien, and Jean-Michel Zakoïan. 2017. Mixed Causal-Noncausal AR Processes and the Modelling of Explosive Bubbles. MPRA Paper 81345. Munich, Germany: University Library of Munich. [Google Scholar]
- Ghysels, Eric. 1990. Unit Root Tests and the Statistical Pitfalls of Seasonal Adjustment: The Case of U.S. Post War Real GNP. Journal of Business and Economic Statistics 8: 145–52. [Google Scholar]
- Ghysels, Eric, Hahn S. Lee, and Pierre L. Siklos. 1993. On the (Mis)specification of Seasonality and its Consequences: An Empirical Investigation with U.S. Data. Empirical Economics 18: 191–204. [Google Scholar] [CrossRef]
- Ghysels, Eric, and Perron Pierre. 1993. The Effect of Seasonal Adjustment Filters on Tests for a Unit Root. Journal of Econometrics 55: 57–98. [Google Scholar] [CrossRef]
- Gouriéroux, Christian, and Joann Jasiak. 2017. Misspecification of Noncausal Order in Autoregressive Processes. Journal of Econometrics. forthcoming. [Google Scholar]
- Gouriéroux, Christian, Joann Jasiak, and Alain Monfort. 2016. Stationary Bubble Equilibria in Rational Expectation Models. CRESTWorking Paper. Paris, France: Centre de Recherche en Economie et Statistique. [Google Scholar]
- Gouriéroux, Christian, and Jean-Michel Zakoïan. 2016. Local Explosion Modelling by Noncausal Process. Journal of the Royal Statistical Society, Series B. [Google Scholar] [CrossRef]
- Hamilton, James D. 1994. Time Series Analysis. Princeton: Princeton University Press. [Google Scholar]
- Hecq, Alain. 1996. IGARCH Effects on Autoregressive Lag Length Selection and Causality Tests. Applied Economic Letters 3: 317–23. [Google Scholar] [CrossRef]
- Hecq, Alain, Lenard Lieb, and Sean Telg. 2016. Identification of Mixed Causal-Noncausal Models in Finite Samples. Annals of Economics and Statistics 123/124: 307–31. [Google Scholar]
- Hecq, Alain, Lenard Lieb, and Sean Telg. 2017. Simulation, Estimation and Selection of Mixed Causal-Noncausal Autoregressive Models: The MARX Package. Working Paper. Available online: https://ssrn.com/abstract=3015797 (accessed on 8 October 2017).
- Hylleberg, Svend, Robert F. Engle, Clive W.J. Granger, and Byung Sam Yoo. 1990. Seasonal Integration and Cointegration. Journal of Econometrics 44: 215–38. [Google Scholar] [CrossRef]
- Kaiser, Regina, and Agustin Maravall. 2001. Measuring Business Cycles in Economic Time Series. New York: Springer. [Google Scholar]
- Lanne, Markku, and Jani Luoto. 2012. Has U.S. Inflation Really Become Harder To Forecast? Economics Letters 155: 383–86. [Google Scholar] [CrossRef]
- Lanne, Markku, and Jani Luoto. 2013. Autoregression-Based Estimation of the New Keynesian Phillips Curve. Journal of Economic Dynamics & Control 37: 561–70. [Google Scholar]
- Lanne, Markku, Janni Luoto, and Pentti Saikkonen. 2012a. Optimal Forecasting of Noncausal Autoregressive Time Series. International Journal of Forecasting 28: 623–31. [Google Scholar] [CrossRef]
- Lanne, Markku, Henri Nyberg, and Erkka Saarinen. 2012b. Does Noncausality Help in Forecasting Economic Time Series? Economics Bulletin 32: 2849–59. [Google Scholar]
- Lanne, Marrku, and Pentti Saikkonen. 2011. Noncausal Autoregressions for Economic Time Series. Journal of Time Series Econometrics 3. [Google Scholar] [CrossRef]
- Maravall, Agustin. 1993. Stochastic linear trends, models and estimators. Journal of Econometrics 56: 5–37. [Google Scholar] [CrossRef]
- Maravall, Agustin. 1997. Use and (Mostly) Abuse of Time Series Techniques in Economic Analysis. Paper Presented at the 5th CEMAPRE Conference, Lisbon, Portugal, May 26–28. [Google Scholar]
- Maravall, Agustin. 2006. An Application of the TRAMO-SEATS Automatic Procedure; Direct Versus Indirect Adjustment. Computational Statistics & Data Analysis 50: 2167–90. [Google Scholar]
- Nelson, Charles, and Heejoon Kang. 1981. Spurious Periodicity in Inappropriately Detrended Time Series. Econometrica 49: 741–51. [Google Scholar] [CrossRef]
- Saikkonen, Pentti, and Rickard Sandberg. 2016. Testing for a Unit Root in Noncausal Autoregressive Models. Journal of Time Series Analysis 37: 99–125. [Google Scholar] [CrossRef]
- Wei, William W. S. 2006. Time Series Analysis. Boston: Pearson Addison Wesley. [Google Scholar]
| 1. | The term ‘approximate’ stems from the fact that the sample used in the likelihood contains only terms. As shown in Breidt et al. (1991), this quantity is only an approximation of the true joint density of the data vector . |
| 2. | Taking degrees of freedom equal to 1,2,...,5 give similar qualitative results. As shown in Hecq et al. (2016), identification in finite samples becomes more difficult when the degrees of freedom parameter is high. In practice, a value around 10 might already be considered troublesome. |
| 3. | The height of the peaks in this theoretical spectrum can be controlled by adjusting the autoregressive parameters. Here we chose to obtain a spectrum similar to the process . |
| 4. | The same simulation exercise has been done based on a seasonal adjustment method called CAMPLET (see Abeln and Jacobs 2015), which is not based on linear filters. Results show that MAR() with are selected in most of the cases. Causality and noncausality is mostly preserved, but not to the same extent as for the X-11. Results are available upon request. |
| 5. | Simulation results are available upon request. |
| 6. | In order to conserve space, we only report the models that were selected at least once for any . |
| 7. | Alternatively, modified () seasonal unit root tests, see e.g., Del Barrio Castro et al. (2017), could be used. It has been shown that these tests have good finite sample size and power properties. However, as we only apply the seasonal unit root test for illustrative purposes, we restrict ourselves to the original HEGY test. |
| 8. | The package MARX used in this study is freely available in the CRAN package repository. See Hecq et al. (2017) for instructions on how to use the package. |
| 9. | Since the Jarque-Bera test is based on the sample skewness and kurtosis, which might not exist for fat-tailed processes, we also performed the Kolmogorov-Smirnov and Anderson-Darling test to check for normality. These tests confirmed the reported results for the Jarque-Bera test. |
| 10. | The same investigation has been done using the TRAMO/SEATS seasonal adjustment method (see Maravall 1997) which is merely used by Eurostat. This method is based on unobserved components decomposition but is not free from filters. In particular, a truncated version of the two-sided, centered, symmetric Wiener-Kolmogorov filter is used to estimate the signal in an observed process (for more details, see e.g., Maravall 2006). As the results are very similar, we do not report them here. |
| 11. | We performed the one-step method on the raw and seasonally adjusted inflation rates. In many cases, the one- and two-step procedure select the same model. However, the one-step procedure is more sensitive to numerical inaccuracies in the optimization routine, as the number of different models to be estimated heavily increases even when p goes up from e.g., 4 to 8 (from 15 to 45 models). The model selected in the two-step approach is, however, often among the second or third best when ranked by the values of the information criteria. An advantage of the two-step approach is that p is bounded and numerical inaccuracies only play a role for all models estimated within this p. |
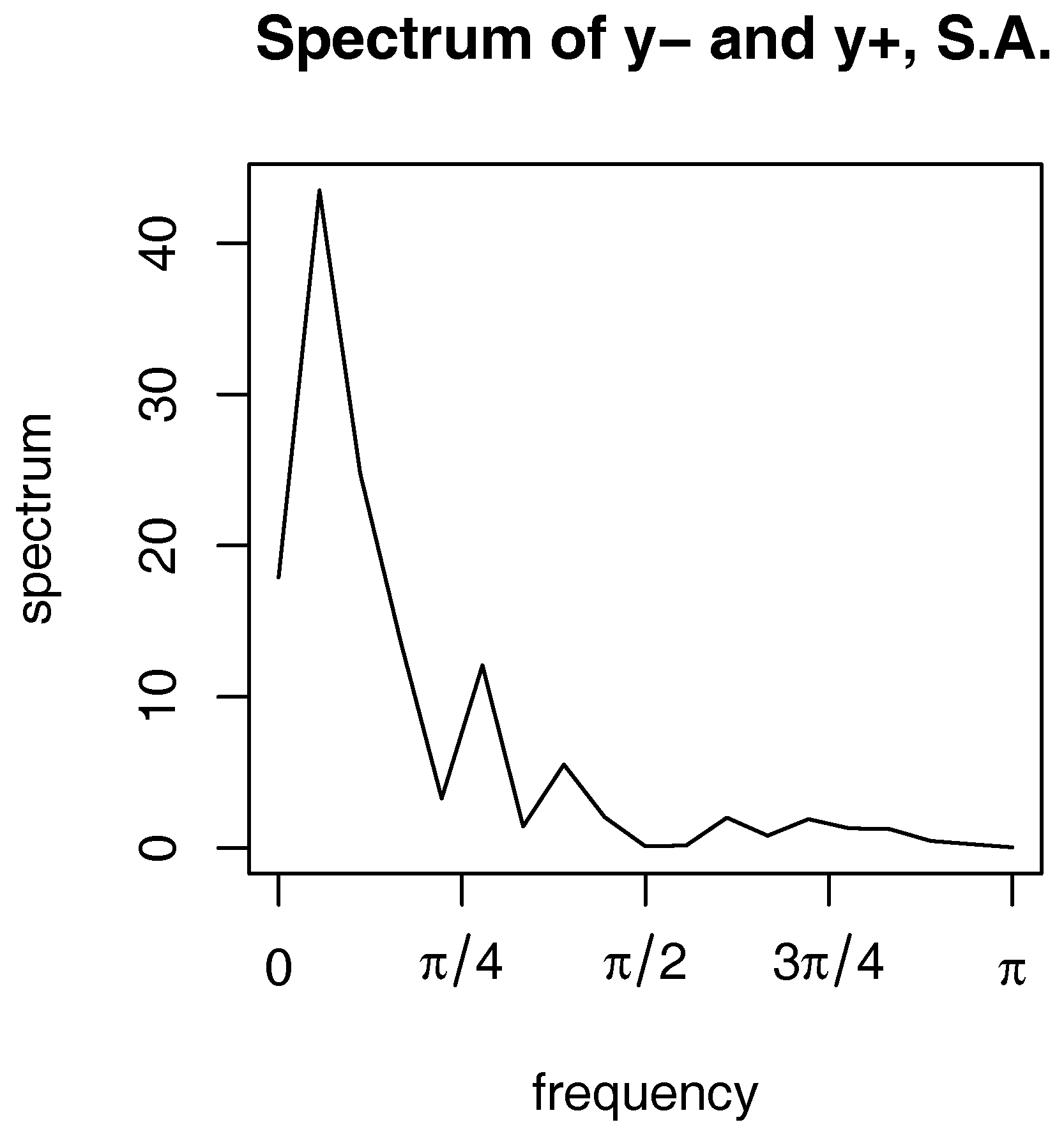
| Lags/Leads | Lags/Leads | Lags/Leads | |||
|---|---|---|---|---|---|
| 0 | 0.856 | 10 | 0.025 | 20 | |
| 1 | 0.051 | 11 | 0.012 | 21 | <0.001 |
| 2 | 0.041 | 12 | 22 | 0.002 | |
| 3 | 0.050 | 13 | 0.021 | 23 | <0.001 |
| 4 | 14 | 0.016 | 24 | <0.001 | |
| 5 | 0.055 | 15 | 25 | <0.001 | |
| 6 | 0.034 | 16 | 26 | <0.001 | |
| 7 | 0.029 | 17 | <0.001 | 27 | <0.001 |
| 8 | 18 | 0.008 | 28 | <0.001 | |
| 9 | 0.038 | 19 |
| MAR(0,0) | 75.5 | 0.0 | 0.0 | 19.5 | 0.0 | 0.0 | 1.9 | 0.0 | 0.0 |
| MAR(1,0) | 6.4 | 82.1 | 4.4 | 4.3 | 83.1 | 0.0 | 0.3 | 73.8 | 0.0 |
| MAR(0,1) | 5.1 | 5.4 | 82.7 | 3.8 | 0.0 | 84.5 | 0.5 | 0.0 | 72.2 |
| MAR(2,0) | 0.6 | 4.1 | 0.2 | 0.2 | 1.8 | 0.0 | 0.0 | 1.9 | 0.0 |
| MAR(1,1) | 0.5 | 3.2 | 3.6 | 0.0 | 4.4 | 4.3 | 0.0 | 5.2 | 5.4 |
| MAR(0,2) | 0.2 | 0.4 | 3.6 | 0.4 | 0.0 | 1.9 | 0.0 | 0.0 | 1.9 |
| MAR(3,0) | 0.6 | 0.8 | 0.0 | 0.0 | 0.6 | 0.0 | 0.0 | 0.2 | 0.0 |
| MAR(2,1) | 0.1 | 0.3 | 0.3 | 0.0 | 0.2 | 1.0 | 0.0 | 0.0 | 1.2 |
| MAR(1,2) | 0.0 | 0.0 | 0.3 | 0.0 | 0.4 | 0.1 | 0.0 | 0.6 | 0.1 |
| MAR(0,3) | 0.1 | 0.0 | 0.7 | 0.0 | 0.0 | 0.8 | 0.0 | 0.0 | 0.7 |
| MAR(4,0) | 4.8 | 2.6 | 0.2 | 38.3 | 8.3 | 0.0 | 50.6 | 16.9 | 0.0 |
| MAR(3,1) | 0.0 | 0.2 | 0.8 | 0.2 | 0.0 | 0.9 | 0.0 | 0.0 | 1.8 |
| MAR(2,2) | 0.7 | 0.3 | 0.3 | 0.0 | 0.0 | 0.1 | 0.0 | 0.1 | 0.0 |
| MAR(1,3) | 0.3 | 0.3 | 0.1 | 0.0 | 1.2 | 0.0 | 0.0 | 1.3 | 0.0 |
| MAR(0,4) | 5.1 | 0.3 | 2.8 | 33.3 | 0.0 | 6.4 | 46.7 | 0.0 | 16.7 |
| MAR(0,0) | 75.5 | 1.6 | 1.3 | 19.5 | 0.0 | 0.0 | 1.9 | 0.0 | 0.0 |
| MAR(1,0) | 6.4 | 73.1 | 7.9 | 4.3 | 58.1 | 0.4 | 0.3 | 25.4 | 0.0 |
| MAR(0,1) | 5.1 | 9.1 | 75.8 | 3.8 | 0.1 | 58.5 | 0.5 | 0.1 | 26.6 |
| MAR(2,0) | 0.6 | 2.5 | 0.5 | 0.2 | 1.2 | 0.0 | 0.0 | 0.7 | 0.0 |
| MAR(1,1) | 0.5 | 1.7 | 1.8 | 0.0 | 2.4 | 1.4 | 0.0 | 1.1 | 1.0 |
| MAR(0,2) | 0.2 | 0.2 | 1.3 | 0.4 | 0.0 | 1.3 | 0.0 | 0.0 | 0.6 |
| MAR(3,0) | 0.6 | 0.3 | 0.1 | 0.0 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 |
| MAR(2,1) | 0.1 | 0.3 | 0.2 | 0.0 | 0.1 | 0.4 | 0.0 | 0.2 | 0.4 |
| MAR(1,2) | 0.0 | 0.0 | 0.0 | 0.0 | 0.2 | 0.2 | 0.0 | 0.2 | 0.0 |
| MAR(0,3) | 0.1 | 0.0 | 0.4 | 0.0 | 0.0 | 0.1 | 0.0 | 0.0 | 0.0 |
| MAR(4,0) | 4.8 | 7.6 | 1.9 | 38.3 | 36.2 | 0.6 | 50.6 | 71.2 | 0.2 |
| MAR(3,1) | 0.0 | 0.1 | 0.4 | 0.2 | 0.0 | 0.7 | 0.0 | 0.0 | 0.5 |
| MAR(2,2) | 0.7 | 0.6 | 1.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| MAR(1,3) | 0.3 | 0.4 | 0.0 | 0.0 | 0.9 | 0.0 | 0.0 | 0.9 | 0.1 |
| MAR(0,4) | 5.1 | 2.5 | 7.3 | 33.3 | 0.7 | 36.4 | 46.7 | 0.2 | 70.6 |
| MAR(0,0) | 92.9 | 0.0 | 0.0 | 93.9 | 0.0 | 0.0 | 96.6 | 0.0 | 0.0 |
| MAR(1,0) | 2.5 | 89.2 | 2.9 | 2.7 | 95.8 | 0.0 | 1.3 | 96.4 | 0.0 |
| MAR(0,1) | 3.2 | 3.2 | 90.3 | 2.9 | 0.0 | 96.4 | 1.9 | 0.0 | 97.3 |
| MAR(2,0) | 0.3 | 3.6 | 0.1 | 0.2 | 2.1 | 0.0 | 0.1 | 1.5 | 0.0 |
| MAR(1,1) | 0.4 | 2.4 | 2.4 | 0.2 | 1.8 | 1.8 | 0.0 | 1.5 | 0.7 |
| MAR(0,2) | 0.2 | 0.3 | 2.7 | 0.1 | 0.0 | 1.6 | 0.1 | 0.0 | 1.8 |
| MAR(3,0) | 0.1 | 0.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.0 |
| MAR(2,1) | 0.1 | 0.2 | 0.5 | 0.0 | 0.3 | 0.1 | 0.0 | 0.2 | 0.0 |
| MAR(1,2) | 0.1 | 0.2 | 0.3 | 0.0 | 0.0 | 0.1 | 0.0 | 0.2 | 0.0 |
| MAR(0,3) | 0.0 | 0.0 | 0.4 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.2 |
| MAR(4,0) | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| MAR(3,1) | 0.0 | 0.0 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| MAR(2,2) | 0.0 | 0.2 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.0 |
| MAR(1,3) | 0.0 | 0.2 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| MAR(0,4) | 0.2 | 0.0 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| MAR(0,0) | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| MAR(1,0) | 9.6 | 2.2 | 0.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| MAR(0,1) | 18.2 | 0.4 | 1.9 | 0.4 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| MAR(2,0) | 2.4 | 61.7 | 2.8 | 0.0 | 24.5 | 0.0 | 0.0 | 5.0 | 0.0 |
| MAR(1,1) | 57.2 | 5.0 | 5.0 | 92.3 | 0.0 | 0.0 | 90.6 | 0.0 | 0.0 |
| MAR(0,2) | 4.7 | 2.2 | 62.0 | 0.0 | 0.0 | 26.9 | 0.0 | 0.0 | 6.5 |
| MAR(3,0) | 0.6 | 2.3 | 0.2 | 0.0 | 0.2 | 0.0 | 0.0 | 0.1 | 0.0 |
| MAR(2,1) | 1.7 | 2.8 | 0.4 | 3.8 | 1.5 | 0.0 | 5.3 | 0.6 | 0.0 |
| MAR(1,2) | 2.0 | 0.7 | 2.5 | 2.1 | 0.0 | 1.5 | 3.5 | 0.0 | 0.8 |
| MAR(0,3) | 0.9 | 0.1 | 2.6 | 0.0 | 0.0 | 0.4 | 0.0 | 0.0 | 0.1 |
| MAR(4,0) | 0.4 | 16.8 | 1.4 | 0.1 | 72.9 | 0.1 | 0.0 | 94.1 | 0.0 |
| MAR(3,1) | 0.3 | 1.4 | 1.4 | 0.3 | 0.5 | 0.4 | 0.4 | 0.1 | 0.0 |
| MAR(2,2) | 0.4 | 1.0 | 1.2 | 0.0 | 0.3 | 0.6 | 0.0 | 0.1 | 0.3 |
| MAR(1,3) | 0.3 | 2.1 | 1.1 | 0.0 | 0.1 | 0.5 | 0.0 | 0.0 | 0.2 |
| MAR(0,4) | 1.3 | 1.3 | 17.3 | 0.4 | 0.0 | 69.6 | 0.2 | 0.0 | 92.1 |
| MAR(1,0) | 8.6 | 0.0 | 0.0 | MAR(4,2) | 1.1 | 0.5 | 0.0 |
| MAR(0,1) | 11.6 | 0.0 | 0.0 | MAR(3,3) | 0.2 | 0.0 | 0.0 |
| MAR(2,0) | 1.5 | 0.0 | 0.0 | MAR(2,4) | 1.0 | 0.3 | 0.0 |
| MAR(1,1) | 36.2 | 12.2 | 0.4 | MAR(1,5) | 4.7 | 34.5 | 44.4 |
| MAR(0,2) | 3.2 | 0.0 | 0.0 | MAR(0,6) | 1.1 | 0.2 | 0.0 |
| MAR(3,0) | 0.2 | 0.0 | 0.0 | MAR(6,1) | 0.1 | 1.7 | 1.7 |
| MAR(2,1) | 0.9 | 0.1 | 0.0 | MAR(5,2) | 0.4 | 1.8 | 1.8 |
| MAR(1,2) | 3.8 | 0.7 | 0.0 | MAR(4,3) | 0.1 | 0.3 | 0.0 |
| MAR(0,3) | 1.5 | 0.0 | 0.0 | MAR(3,4) | 0.1 | 0.1 | 0.0 |
| MAR(4,0) | 0.4 | 0.0 | 0.0 | MAR(2,5) | 0.8 | 0.5 | 1.2 |
| MAR(3,1) | 0.5 | 0.0 | 0.0 | MAR(1,6) | 1.5 | 4.4 | 3.5 |
| MAR(2,2) | 0.4 | 0.0 | 0.0 | MAR(0,7) | 0.3 | 0.0 | 0.0 |
| MAR(1,3) | 0.8 | 0.0 | 0.0 | MAR(8,0) | 0.1 | 0.0 | 0.0 |
| MAR(0,4) | 0.8 | 0.0 | 0.0 | MAR(7,1) | 0.1 | 0.0 | 0.0 |
| MAR(5,0) | 1.1 | 0.0 | 0.0 | MAR(6,2) | 0.1 | 0.0 | 0.0 |
| MAR(4,1) | 3.8 | 6.6 | 1.6 | MAR(5,3) | 0.1 | 0.1 | 0.2 |
| MAR(2,3) | 0.6 | 0.1 | 0.0 | MAR(4,4) | 0.4 | 0.0 | 0.0 |
| MAR(1,4) | 5.5 | 3.2 | 1.0 | MAR(3,5) | 0.2 | 0.1 | 0.2 |
| MAR(0,5) | 1.4 | 0.2 | 0.0 | MAR(2,6) | 0.2 | 0.0 | 0.0 |
| MAR(6,0) | 0.1 | 0.0 | 0.0 | MAR(1,7) | 1.1 | 1.4 | 0.8 |
| MAR(5,1) | 2.2 | 30.6 | 43.0 | MAR(0,8) | 1.2 | 0.4 | 0.2 |
| Country | | | | Pseudo Model | Jarque-Bera: : Normality | ARCH-LM: : no-ARCH | MAR() |
|---|---|---|---|---|---|---|---|
| Canada | −0.91 | −6.39 * | 36.03 * | AR(4) | 9.99 * | 1.35 | MAR(0,4) |
| France | −1.51 | −5.80 * | 50.62 * | AR(3) | 40.26 * | 20.42 * | MAR(3,0) |
| Germany | −1.05 | −5.85 * | 27.47 * | AR(4) | 6.33 * | 1.77 | MAR(0,4) |
| Italy | −0.86 | −9.91 * | 142.52 * | AR(3) | 292.63 * | 66.78 * | MAR(3,0) |
| Japan | −1.29 | −3.66 * | 25.94 * | AR(4) | 121.72 * | 10.46 * | MAR(4,0) |
| United Kingdom | −1.06 | −6.21 * | 43.70 * | AR(4) | 191.87 * | 17.06 * | MAR(1,3) |
| United States | −0.86 | −6.60 * | 33.44 * | AR(4) | 816.86 * | 0.82 | MAR(2,2) |
| c.v. (5%) | −3.49 | −2.91 | 6.57 | 5.99 | 3.00 |
| Country | ADF-Statistic Unit Root | Pseudo Model | Jarque-Bera: : Normality | ARCH-LM: : no-ARCH | MAR() |
|---|---|---|---|---|---|
| Canada | AR(3) | 28.11 * | 2.39 | MAR(0,3) | |
| France | AR(3) | 166.52 * | 14.21 * | MAR(3,0) | |
| Germany | AR(3) | 51.33 * | 0.22 | MAR(0,3) | |
| Italy | AR(6) | 754.96 * | 45.54 * | MAR(2,4) | |
| Japan | AR(3) | 76.95 * | 23.30 * | MAR(3,0) | |
| United Kingdom | AR(2) | 538.86 * | 13.05 * | MAR(0,2) | |
| United States | AR(3) | 1320.34 * | 0.64 | MAR(0,3) | |
| c.v. (5%) | 5.99 | 3.00 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hecq, A.; Telg, S.; Lieb, L. Do Seasonal Adjustments Induce Noncausal Dynamics in Inflation Rates? Econometrics 2017, 5, 48. https://doi.org/10.3390/econometrics5040048
Hecq A, Telg S, Lieb L. Do Seasonal Adjustments Induce Noncausal Dynamics in Inflation Rates? Econometrics. 2017; 5(4):48. https://doi.org/10.3390/econometrics5040048
Chicago/Turabian StyleHecq, Alain, Sean Telg, and Lenard Lieb. 2017. "Do Seasonal Adjustments Induce Noncausal Dynamics in Inflation Rates?" Econometrics 5, no. 4: 48. https://doi.org/10.3390/econometrics5040048
APA StyleHecq, A., Telg, S., & Lieb, L. (2017). Do Seasonal Adjustments Induce Noncausal Dynamics in Inflation Rates? Econometrics, 5(4), 48. https://doi.org/10.3390/econometrics5040048






