1. Introduction
One of the main objectives of quantitative research is the modelling and approximation of multivariate distributions. A multivariate model should be flexible enough to capture the stylized facts of empirical finance. Moreover, increasing interest in short-term quantitative risk management requires the time-variability of such models. The current paper builds on two actively developing areas of financial econometrics: copulae and high-frequency data. On the one hand, copulae appear to be a helpful tool to analyse complex dependence structures, evaluate the risk, and are therefore widely used to price financial derivatives, see
Embrechts et al. (
2003),
Rodriguez (
2007),
Hofert and Scherer (
2011),
Krämer et al. (
2013). On the other hand, models based on high-frequency data yield superior predictions in comparison to approaches based on daily data. Among others,
Andersen et al. (
2002),
Barndorff-Nielsen and Shephard (
2004) and
Zhang et al. (
2005) made it possible to compute the daily realized covariances from high-frequency data. Many researchers have implemented the obtained realized measures to model financial time series. Most of those studies, however, employ models where the realized correlation matrix directly characterizes the multivariate distribution, see, for example,
Bauer and Vorkink (
2011),
Chiriac and Voev (
2011),
Jin and Maheu (
2012), or address GARCH type models, for example,
Hansen et al. (
2014),
Bauwens et al. (
2012),
Noureldin et al. (
2012),
Bollerslev et al. (
2016). There are only a limited number of studies which discuss the implementation of high-frequency data in copula models.
Breymann et al. (
2003) and
Dias and Embrechts (
2004) employ copulae to study the properties of intraday log-returns.
Creal et al. (
2013) consider an autoregressive updating equation and improve the predictive power in
Salvatierra and Patton (
2015) by including the lagged realized volatility in the equation.
To the best of our knowledge, the only model that parameterizes the whole Archimedean copula (AC) by the realized variance-covariance matrix is in
Fengler and Okhrin (
2016), who introduced the realized copula parameter. The authors suggested capturing time-varying dependence by using high-frequency intraday data to estimate the parameter of an AC daily. It has been demonstrated empirically that the realized copula model outperforms the list of benchmark models in one-day-ahead out-of-sample VaR prediction. The realized copula model of
Fengler and Okhrin (
2016) has, however, several limitations. First, their realized copula is driven by one single parameter, which limits the flexibility of the model. Second, the estimation procedure is performed by applying a method of moments kind of estimator, which suffers from the curse of dimensionality.
We propose to extend the work of
Fengler and Okhrin (
2016) by introducing the realized hierarchical Archimedean copula (rHAC), which allows more flexibility and is applicable to managing high-dimensional portfolios. We adapt the estimation procedures described in
Segers and Uyttendaele (
2014) and
Górecki et al. (
2016a) to high-frequency data, which allows estimating the structure and the parameters of a copula based only on a realized covariance matrix. As a result, the estimate does not suffer from microstructure noise or jumps. Moreover, it can be applied to high-dimensional portfolios since the computationally expensive optimization procedure proposed in
Fengler and Okhrin (
2016) is reduced to a set of simple tasks. This result is of particular importance in many financial applications, especially in risk management.
This paper is structured as follows.
Section 2 contains a literature review of the theory of the copula and introduces the concept of a realized copula. An estimator of the structure and the parameters of an rHAC is presented in
Section 3. Simulation studies and a comparison with the benchmark models are provided in
Section 4.
Section 5 discusses the construction of the rHAC, and gives a short summary of competing models.
Section 6 describes an application of the proposed models to one-day-ahead VaR prediction for a multidimensional portfolio. Finally, we summarize the main contribution of the paper.
2. The Concept of the Realized Copula
The concept of the copula was introduced to the statistical literature by
Sklar (
1959) and further popularized in the world of finance by
Embrechts et al. (
1999) in the context of risk management. Sklar’s theorem, see
Sklar (
1959), states that a
d-dimensional distribution function
with marginals
can be represented as
where
is a
d-dimensional copula. In addition, it states that the continuity of the marginal distributions
ensures the uniqueness of the copula.
Having a huge number of classes of bivariate copulae, see
Nelsen (
2007), there is still a lack of multivariate ones. The most popular classes of multivariate copulae currently are elliptical, factor, pair-copula constructions, and HAC. The first class is often used in practice due to its simplicity and intuitive interpretation. However, elliptical copulae are not able to capture the stylized facts observed in financial data. The factor approach overcomes this limitation and has attracted attention in the copula literature over the last decade, see, for example,
Andersen and Sidenius (
2004),
Van der Voort (
2007),
Krupskii and Joe (
2013),
Oh and Patton (
2017). The limitation of the factor copula models is that the likelihood function is often not known in closed form, which complicates the estimation of the parameters. Pair-copula constructions are discussed in more detail by
Joe (
1996),
Bedford and Cooke (
2001),
Czado (
2010), and
Kurowicka (
2011), and are increasing in popularity. Another popular copula class is AC, which contains, among others, the Clayton, Gumbel and Frank copulae. The AC parametrized by the parameter
is defined as
,
with
being non-decreasing and convex on
for
, where
.
,
and the pseudo inverse is defined as
for
and 0 otherwise. The generators and the densities of some AC are given in
Appendix A.
Due to the lack of flexibility of AC, caused by the fact that the whole copula is driven by just one parameter
, generalizations such as nested copulae have been introduced. This paper employs a flexible multivariate copula family, HAC, a special case of which may be defined recursively in the following way:
where
is the parameter vector of the HAC and
s is the structure of the HAC. As is evident from (
2), the current study assumes that all generators of the HAC belong to the same parametric family and each of them depends on one single parameter. For simplicity, we compress the notation of (
2) and denote the
d-dimensional HAC with
k generators which is parametrized by the structure
s and the parameter vector
as
. The structure
s is the merging ordering
, where
,
is a reordering of the indices of the variables
,
. The structure of a
d-dimensional HAC
s can be seen as a tree with
non-leaf nodes that correspond to the generators and
d leaves representing the variables
. The leaves correspond to the lowest level of the tree. The root corresponding to the variable
is assumed to be the highest level of the tree. The nodes, which are not the leaves are called internal nodes, each corresponds to the generator. A node which is directly connected to another node when moving away from the root is called the child node. A node which is directly connected to another node when moving from the leaves to the root is called the parent node. Descendants are the children nodes of the node, children of these children, etc. The set of ancestors includes the parent node of the node, parents of the parents, etc. The structure of the HAC is called binary if it corresponds to the binary tree, i.e., if each internal node has exactly two children. Further on, we denote the nodes associated with the generators by
, where
is the set of leaves (variables) that are descendant nodes of the node
,
. Assuming this notation, the node
is an ancestor of the node
(the leave associated with the variable
) if
(
),
,
. Another concept that will be used later on is the concept of the lowest common ancestor (lca). The lca of the nodes
(the leave
) and
(the leave
) is the node
that is the lowest node satisfying
(
) and
(
),
,
.
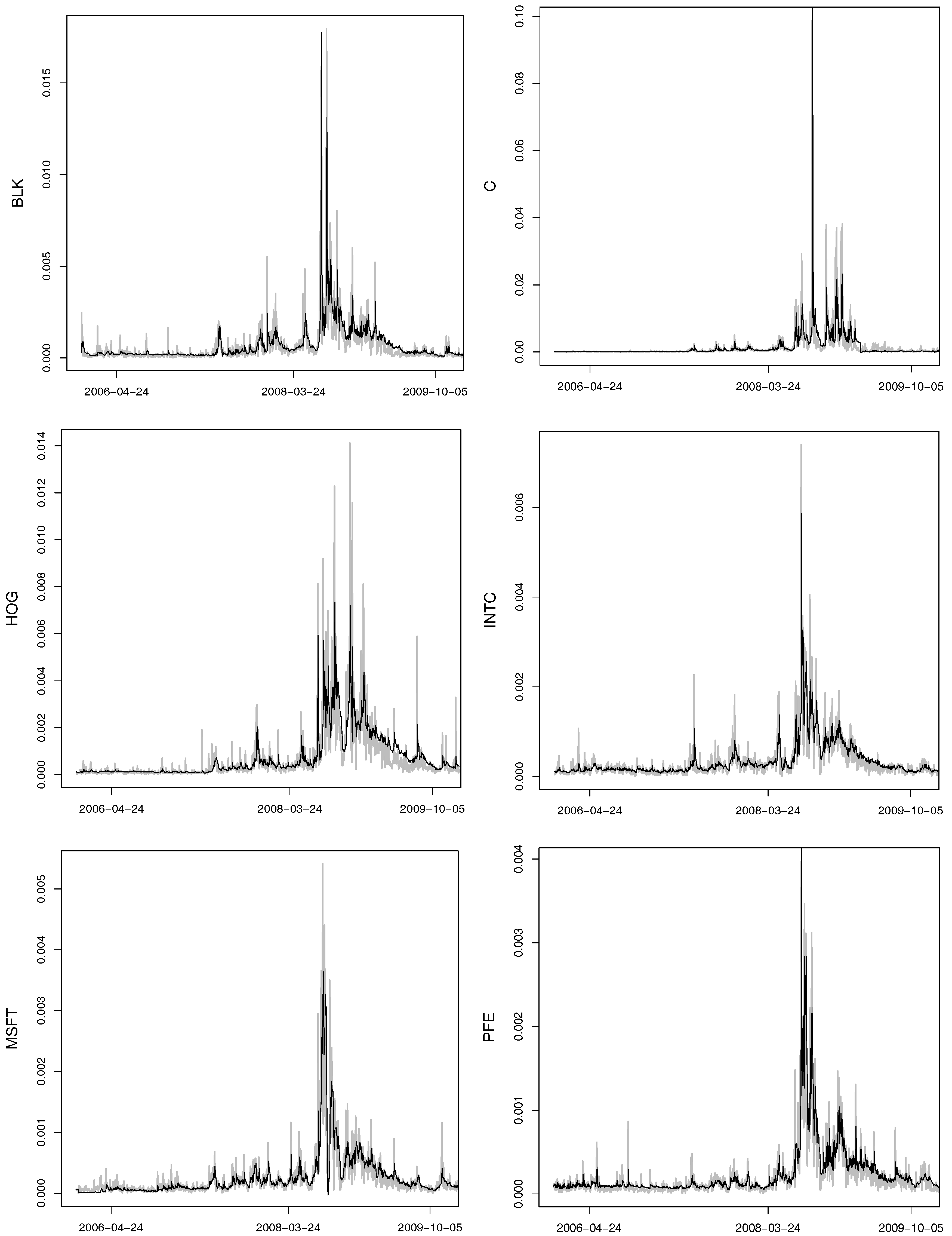
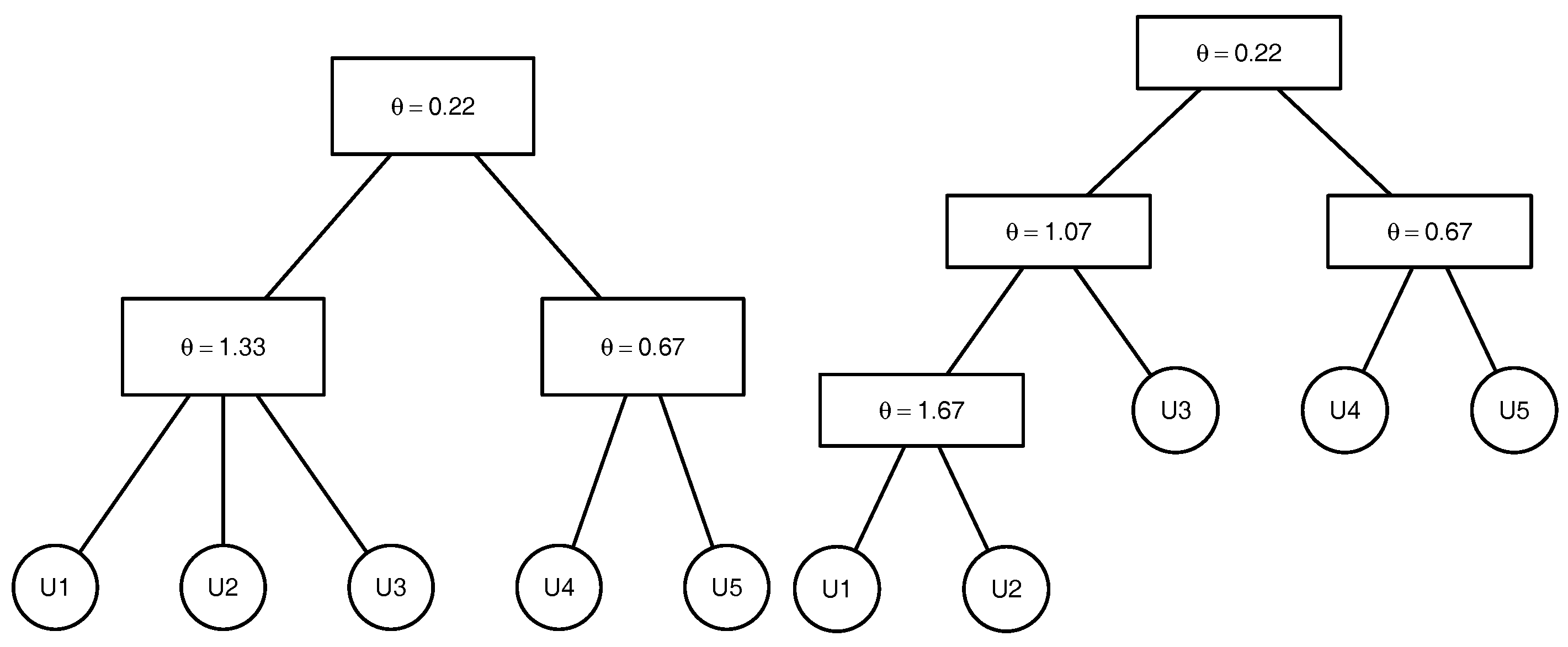
To clarify the above-mentioned definitions and avoid introducing the comprehensive notation of the graph theory, we illustrate the above-named concepts by an example. Consider the 5-dimensional copula
that can be written as
, where
with
being the parameters of the marginal distributions
,
. The tree corresponding to this copula is presented in the
Figure 1. This copula has the binary structure
. There are
non-leaf (internal) nodes. The leaves which correspond to the lowest level of the copula tree are given by the variables
,
,
,
and
. The root
which represents the highest level of the copula tree corresponds to the variable
, where
. The root node is the parent node for the node corresponding to the variable
and the node
associated with the variable generated by
, where
. The root node is the ancestor for all other nodes of the given copula tree. The lca of the nodes associated with the variables
and
is the node
that corresponds to the variable
, where
. The lca of the nodes corresponding to the variables
and
is the root node
as it is the lowest node satisfying
and
,
.
Although copula models are flexible enough to capture nonlinear dependencies, many empirical applications require the time variability of the parameters (and the structure) of the whole copula. For example, the empirical evidence makes it reasonable to assume that the dependence between asset log-returns gets stronger during periods of financial turbulence. A vast amount of literature is devoted to dynamic copula models, including the parsimonious rolling window approach and more sophisticated models, such as, for example, the local change point procedure of
Härdle et al. (
2013). Recent developments in time-varying copula models take advantage of the rapidly growing availability of high-frequency observations and include the realized measures (volatility and correlations) in the copula models to improve their predictive power, see, for example,
Salvatierra and Patton (
2015). The improvement is obtained due to the fact that the actual realizations of the volatility of log-returns which are not directly observable can be estimated by the sum of finely-sampled squared realizations of log-return over a fixed time interval when the high-frequency observations are available. Such a nonparametric ex-post measurement of the log-return variation is called the realized volatility. In an analog manner, the realized covariances are defined by summing all the cross products of intraday log-returns. The formal definition of the realized measures is given in
Appendix B. Despite the constantly growing research on incorporating the realized measures into multivariate Gaussian models, discussed in
Chiriac and Voev (
2011) and
Bauer and Vorkink (
2011), and into GARCH type models, for example,
Hansen et al. (
2014) and
Bollerslev et al. (
2016), there is still a gap in the literature on how the parameters of non-Gaussian copula can be estimated daily based on high-frequency observations. It is important to note here that such standard copula estimation techniques as the Maximum Likelihood (ML) method or the inversion of Kendall’s
can not be directly applied to tick-by-tick observations. Estimating the copula by applying these approaches to high-frequency data would estimate the multivariate distribution of high-frequency log-returns, which in general does not coincide with the multivariate distribution of daily log-returns. Such a model would estimate the intraday dependence and produce the forecast of the multivariate distribution of log-returns in the next second and could not be used for one-day-ahead VaR forecasts. For further details on the standard estimation procedures, refer to
Nelsen (
2007),
Trivedi and Zimmer (
2007),
Jaworski et al. (
2013),
Cherubini et al. (
2011),
Joe (
2014) and
Durante and Sempi (
2015). In contrast to the direct application of the ML approach to tick-by-tick data or high-frequency estimator of Kendall’s
, there is a considerable literature discussing how to estimate the correlation matrix of daily log-returns via a realized correlation matrix or similar methods, see
Barndorff-Nielsen et al. (
2004),
Barndorff-Nielsen and Shephard (
2004),
Zhang et al. (
2005),
Hayashi and Yoshida (
2005),
De Pooter et al. (
2008). The idea of using the information concentrated in the realized covariance matrix to estimate the parameters of a copula daily has been employed by
Fengler and Okhrin (
2016), who used a combination of the results from a lemma of
Hoeffding (
1940) and Sklar’s theorem (
1) to express the covariance
between two random variables
and
in terms of the marginal distributions
and
and the copula
where
is the parameter of the copula and
,
are the parameters of the marginal distributions
and
. In the high-frequency framework, the covariance
in (
3) is replaced by the element
of the realized covariance matrix
computed at day
t. From now on, we denote the diagonal elements of matrix
by
instead of
,
. As has been shown in
Breymann et al. (
2003) and discussed in more detail in
Hautsch (
2011), with an increasing sampling frequency, the marginal distributions of log-returns can be assumed to be Gaussian with zero mean and the standard deviation equal to
,
, this leads us to assume throughout this study that margins are
. Thus, if the realized covariance matrix
can be computed, according to
Fengler and Okhrin (
2016), it can be assumed that for the Archimedean copula driven by one single parameter
the integral in (
3) depends on just the parameter of the copula which belongs to some parametric family
. Therefore, after replacing the covariances in (
3) by their realized counterparts and standardizing the variables, the expression (
3) can be rewritten for the realized correlations as
where
is the cdf of the standard normal distribution and
is the element of the realized correlation matrix
calculated at day
t,
. According to (
4), the realized correlations depend solely on the copula parameter, under the assumption of some parametric family. Based on (
4), the parameter of the copula can be estimated based on just the realized correlation matrix:
where
is a vector of length
where all the
are stacked together and
W is a
-dimensional positive definite weighting matrix. When the copula parameter is estimated from (
5) and the diagonal elements of the realized covariance matrix
are calculated, the multivariate distribution of
is fully specified. It is important to note that
Fengler and Okhrin (
2016) consider the restrictive setting of AC. Therefore, all bivariate copulae in (
4) coincide and are driven by one single parameter
.
In practice, one is usually interested in predicting a multivariate distribution, rather than just estimating it. This can be done in two ways. The parameter of the realized copula can be estimated daily and predicted using some time-series model. Alternatively, the realized correlation matrix can be predicted and the parameter of the copula can be estimated from
, which is one-day-ahead prediction of the realized correlation matrix
obtained by applying the specific time series model in the spirit of
Bauer and Vorkink (
2011) or
Chiriac and Voev (
2011). The limitation of both approaches comes from the estimation procedure (
5), which suffers from the curse of dimensionality and enables the estimation of the realized copula only in moderate dimensions. Moreover, as was mentioned earlier, the whole realized copula in
Fengler and Okhrin (
2016) is driven by just one parameter
, which might be too restrictive for multivariate portfolios.
We propose to overcome these limitations by using the HAC instead of the simple AC. This extension is not straightforward, as in addition to the parameter vector
of
, the structure of the copula
s needs to be estimated. The estimation of the parameter vector
of a
d-dimensional copula
should be addressed as well. The procedure of
Fengler and Okhrin (
2016) allows the estimation of the parameters at the bottom level of the copula. The estimation of the parameters of the higher levels is not trivial, as the realized correlation among the original variables and the variables determined by the copulae of the bottom levels can not be specified. This motivates the estimation of the structure and the parameters of the hierarchical copula based just on the realized correlation matrix. Recent studies in the copula literature address the question of how the structure (or the structure and the parameters) of a hierarchical copula can be estimated based on Kendall’s
correlation matrix, see, for example,
Segers and Uyttendaele (
2014),
Górecki et al. (
2016a,
2016b),
Uyttendaele (
2016). We propose to combine the methods discussed in
Segers and Uyttendaele (
2014) and
Górecki et al. (
2016a) and adapt them to the realized correlation matrix with the final goal of improving one-day-ahead VaR prediction for multivariate portfolios.
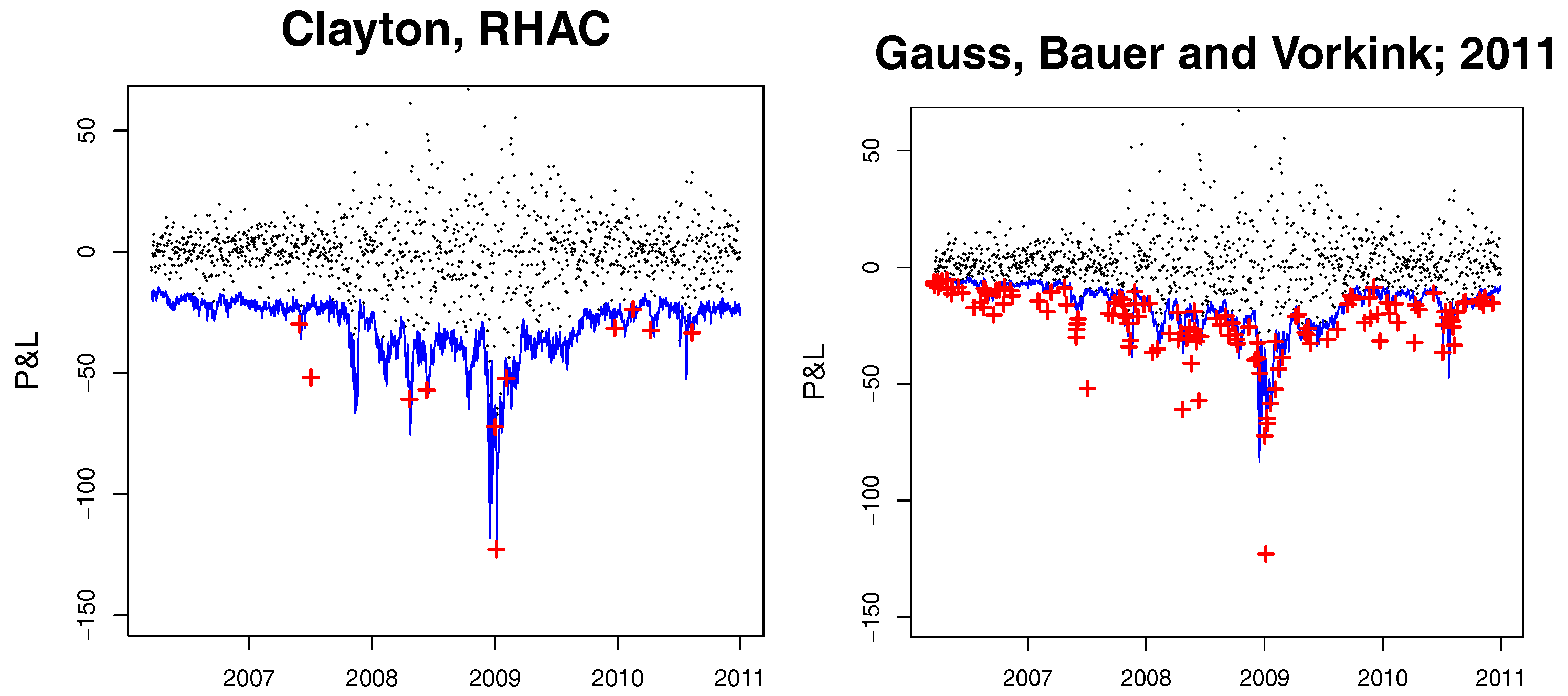
4. Simulation Results
In this section, we show the validity of the clustering estimator (CE) presented in Algorithms 2 and 3 and compare it to the adaptation of the method of
Segers and Uyttendaele (
2014) (SU) and the approach of
Okhrin et al. (
2013) (OOS) which was improved by
Górecki et al. (
2014) and was implemented in the
R package
HAC by
Okhrin and Ristig (
2014). We compare the introduced estimator only to a couple of currently available studies and leave the recent advances discussed in, for example,
Górecki et al. (
2014,
2016b),
Uyttendaele (
2016) and
Okhrin et al. (
2015) outside the scope of this study since the objective of the simulation studies is rather to answer the question whether the proposed algorithm is valid in the case of linear correlation, than to find the best possible estimator of an HAC. We are aware of the fact that the linear correlation based estimator might be not as efficient as an ML approach or a nonlinear correlation based estimator, as it contains information only about linear dependencies among the variables. However, in the framework of high-frequency data, this is so far the only possible way to proceed. Moreover, we aim to define a minimal recommended sample size.
In the current simulation study no high-frequency observations are presented. In order to compare different methods, CE is applied to the Kendall’s correlation matrix and to the linear correlation matrix estimated in the usual manner over the whole sample path that corresponds to the correlation matrices of the daily log-returns. In the case of the SU estimator, the parameters are estimated by the sequential inversion of Kendall’s
. For the estimation of the structure according to Algorithms 1 and 2, we set
and
. A full ML is applied to the structures estimated by OOS. For illustrative purposes, the 5-dimensional copulae structures presented in
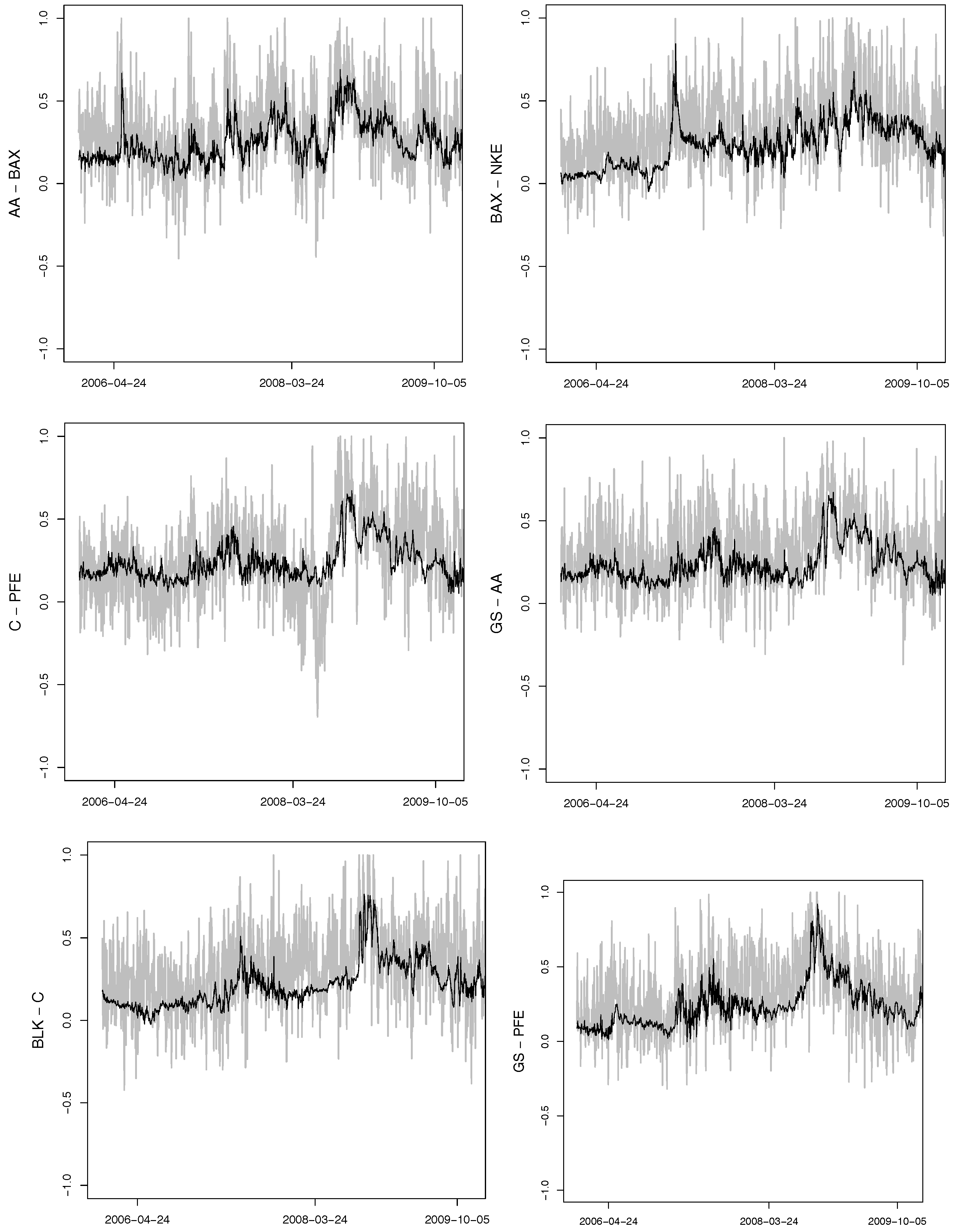
Figure 4 are considered. For each structure, Clayton, Gumbel and Frank copulae are analysed with the parameters corresponding to
and
. The marginal distributions are assumed to be known. For each of the above mentioned estimators, we proceed as follows: a sample of size
n is simulated from the copula, and the structure is estimated. If the estimated structure coincides with the true one, the parameters are estimated. The procedure is repeated
m times until 200 structures are estimated correctly. Thus, the estimators of the structure are compared in terms of the proportion of correctly estimated structures 200/m. For the comparison of the estimation of the parameters, we introduce the characteristic
, which is the Euclidean norm of the difference between the vector of true parameters and the estimated ones.
Table 1 and
Table 2 present the mean
, the variance
and the 25%
, 50%
and 75%
quantiles of
E for different structures.
Table 1 shows the simulation results for the 5-dimensional Clayton copula presented in
Figure 4 with sample sizes
. The results make evident that the OOS method outperforms all the competitors for small samples for the Clayton copula with the structure
. However, there are some outliers, which can be seen from the sample variance of
E. This means that the full ML estimate had a large deviation from the true value of the parameter for a few samples. The interquantile range
is still smaller for the ML in small samples. The same results for the variance are observed for the CE
, therefore, this estimator is not recommended for small samples. In contrast,
Table 2 shows that for the structure
, OOS is not the best method for estimating the structure in small samples. This is due to the fact that the performance of this estimator depends on the choice of the merging parameter. The results for the other copulae are presented in
Appendix C and show that there is no leading method in terms of estimating the structure. The method to choose depends on the type of the copula and the values of the parameters. For a large enough sample, all the methods perform similarly. The general conclusion to be drawn for the estimation of the parameters is that the variance of the CE
r estimator is the highest for small samples and that the full ML has the smallest variance, however, some exceptions are observed. It is worth noting that the simulation results are used just for comparison purposes, as the difference in the parameters influences the proportion of the correctly estimated structures more severely than does the type of the copula. Additionally, the dimension of the copula should always be taken into consideration in order to select the minimal sufficient sample size. The question of convergence of the estimator to the true structure still needs to be addressed in the literature.
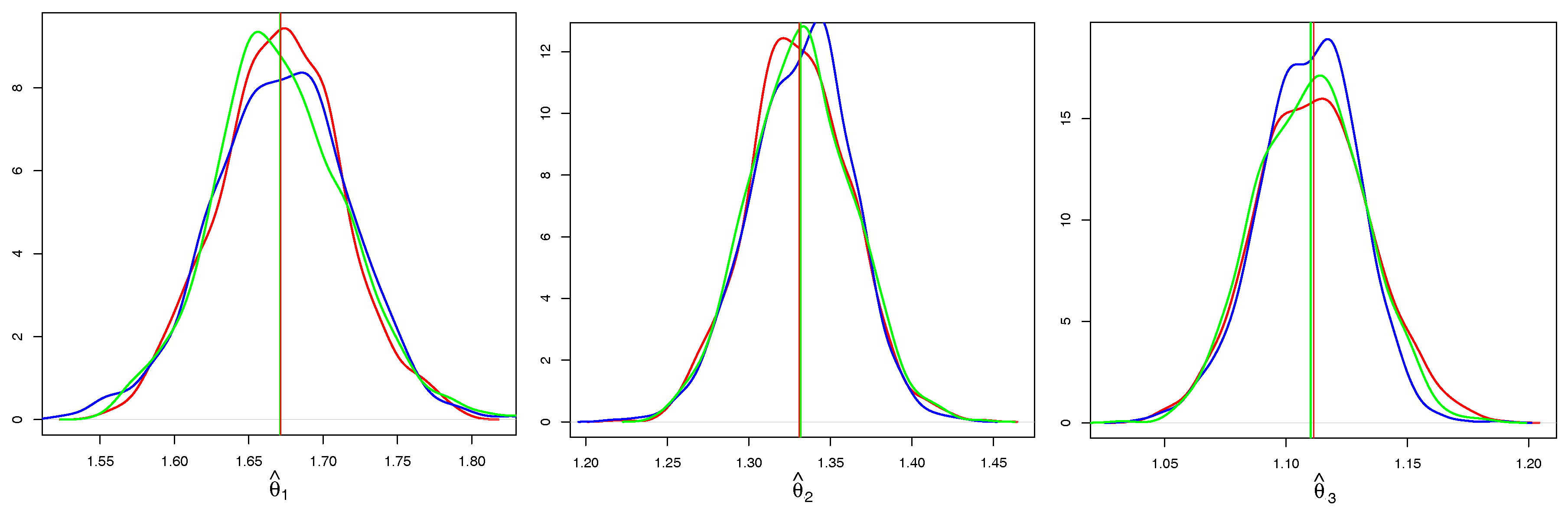
In
Figure 5, we take a closer look at the individual components of
. We compare only CE based on Kendall’s correlation and the full ML, as the CE
and SU behave very similarly in terms of the properties of
. It is evident that both estimators are asymptotically unbiased, however, CE has a higher variance. In addition to the kernel density estimates of CE and ML, we add a kernel density estimate of the Gaussian sample (blue line) with the mean
and the variance estimated from (
14) and observe that it coincides with the kernel density estimate of CE.
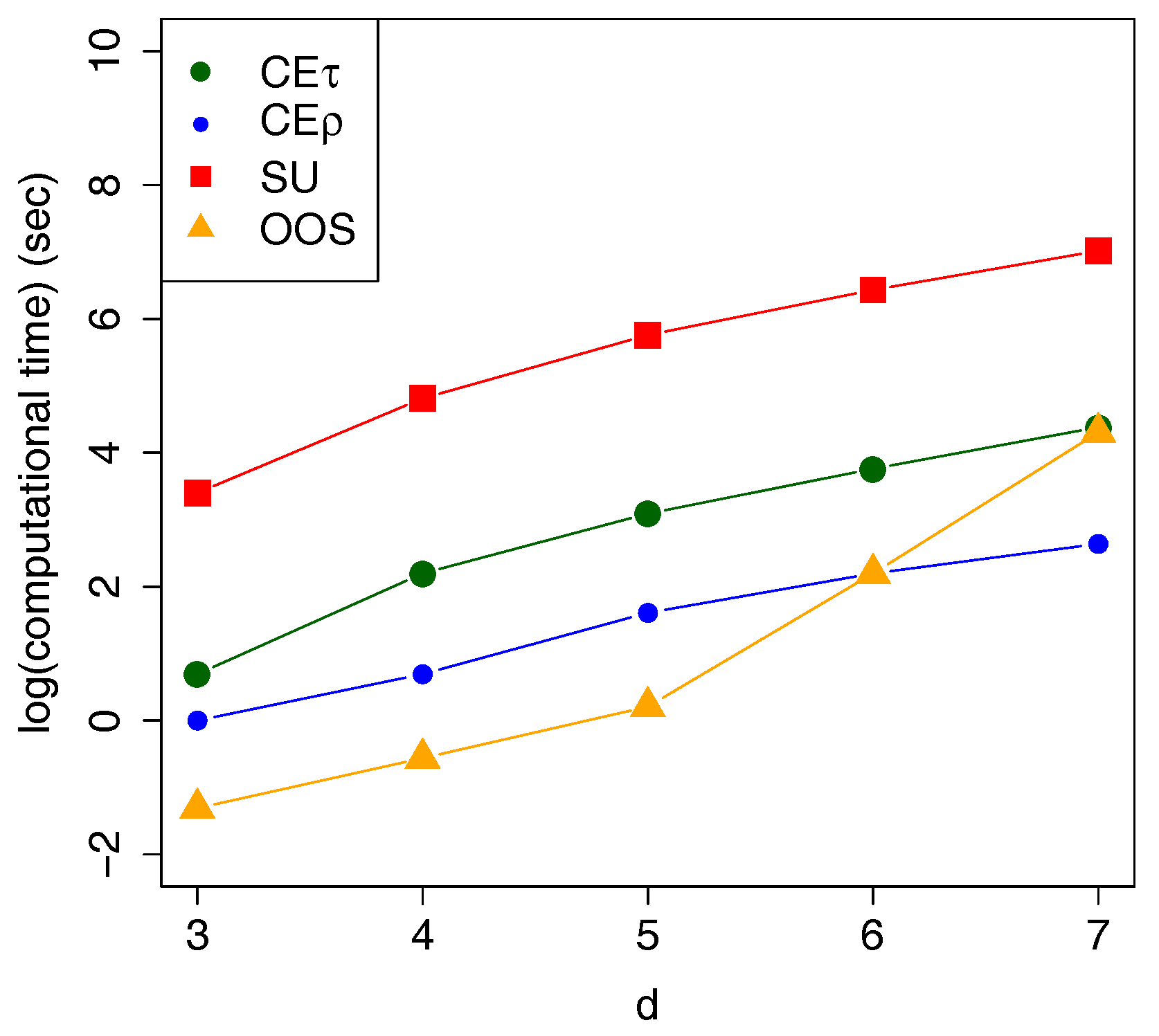
It is worth noting that the computational advantage is on the side of CE.
Figure 6 shows the average computational time in seconds for all the above mentioned estimators over 100 trials. The difference in the computational time becomes crucial with growing dimensions, for example, in
Segers and Uyttendaele (
2014), the SU estimation of a 7-dimensional copula needs roughly 20 min versus 15 s for the proposed clustering estimator (CE).
The main conclusion of this section is that the linear correlation based clustering estimator is applicable in practice and can be applied to high-frequency data, where moderate samples are atypical.