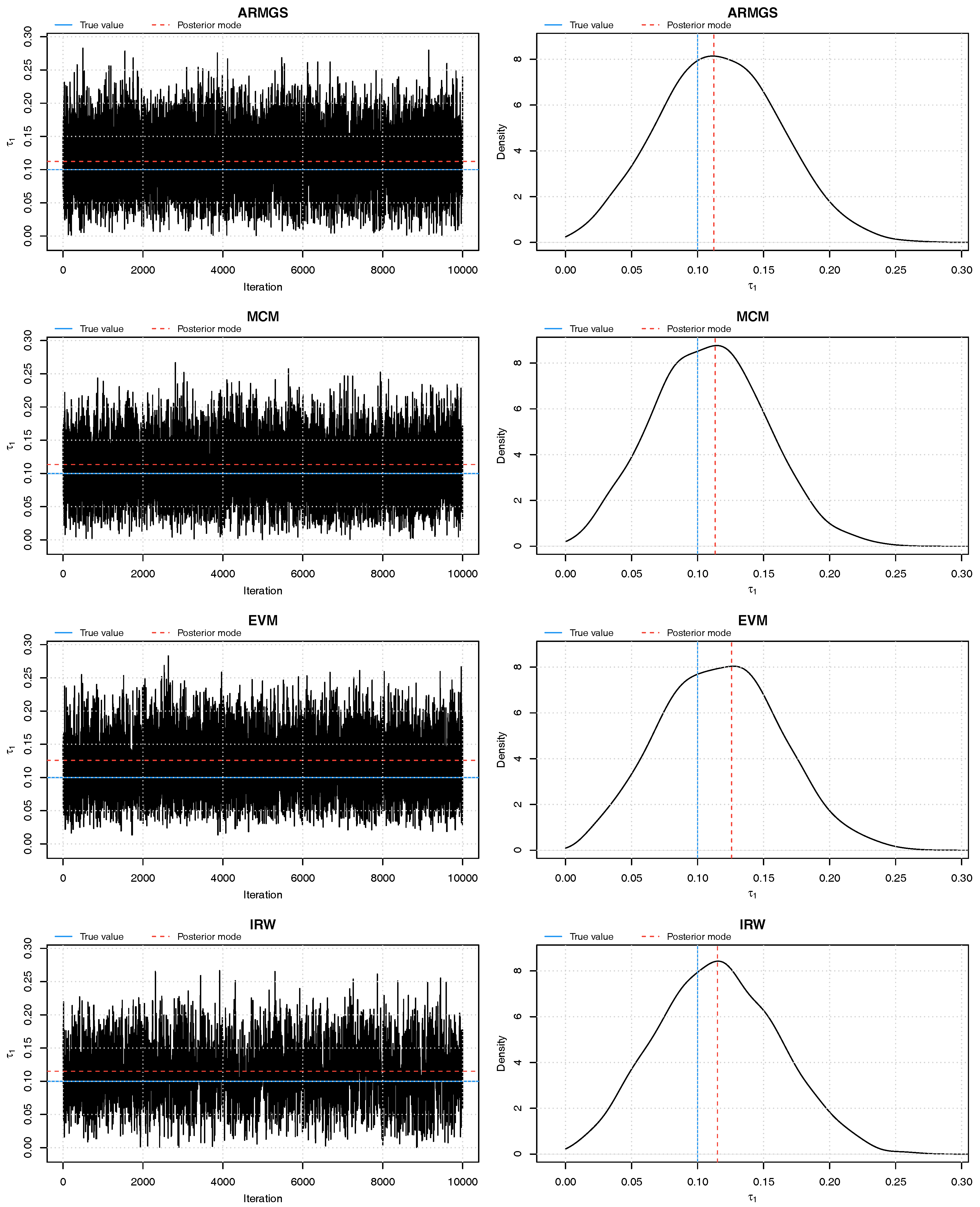
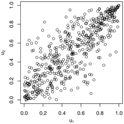
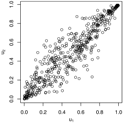
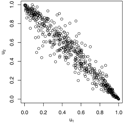
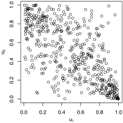
Figure 1.
Trace plots and density plots of a single run from each of our four sampling methods on Kendall’s scale. The output is based on posterior samples of in the mixed scenario.
Figure 1.
Trace plots and density plots of a single run from each of our four sampling methods on Kendall’s scale. The output is based on posterior samples of in the mixed scenario.
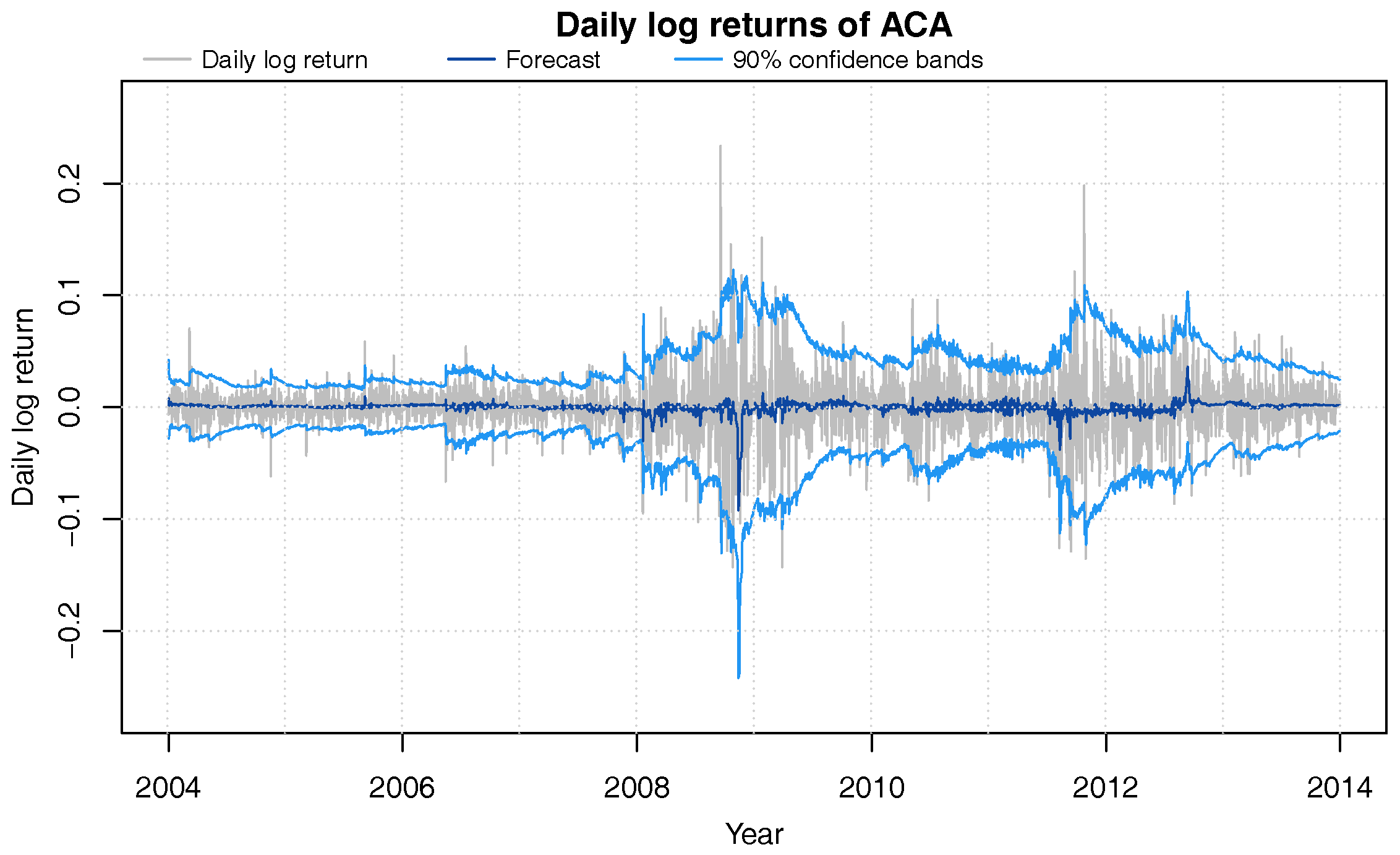
Figure 2.
Daily log-returns (grey) of ACA from 2004 through 2013 with DLM one-day ahead 90% confidence bands (blue) and forecast value (dark blue).
Figure 2.
Daily log-returns (grey) of ACA from 2004 through 2013 with DLM one-day ahead 90% confidence bands (blue) and forecast value (dark blue).
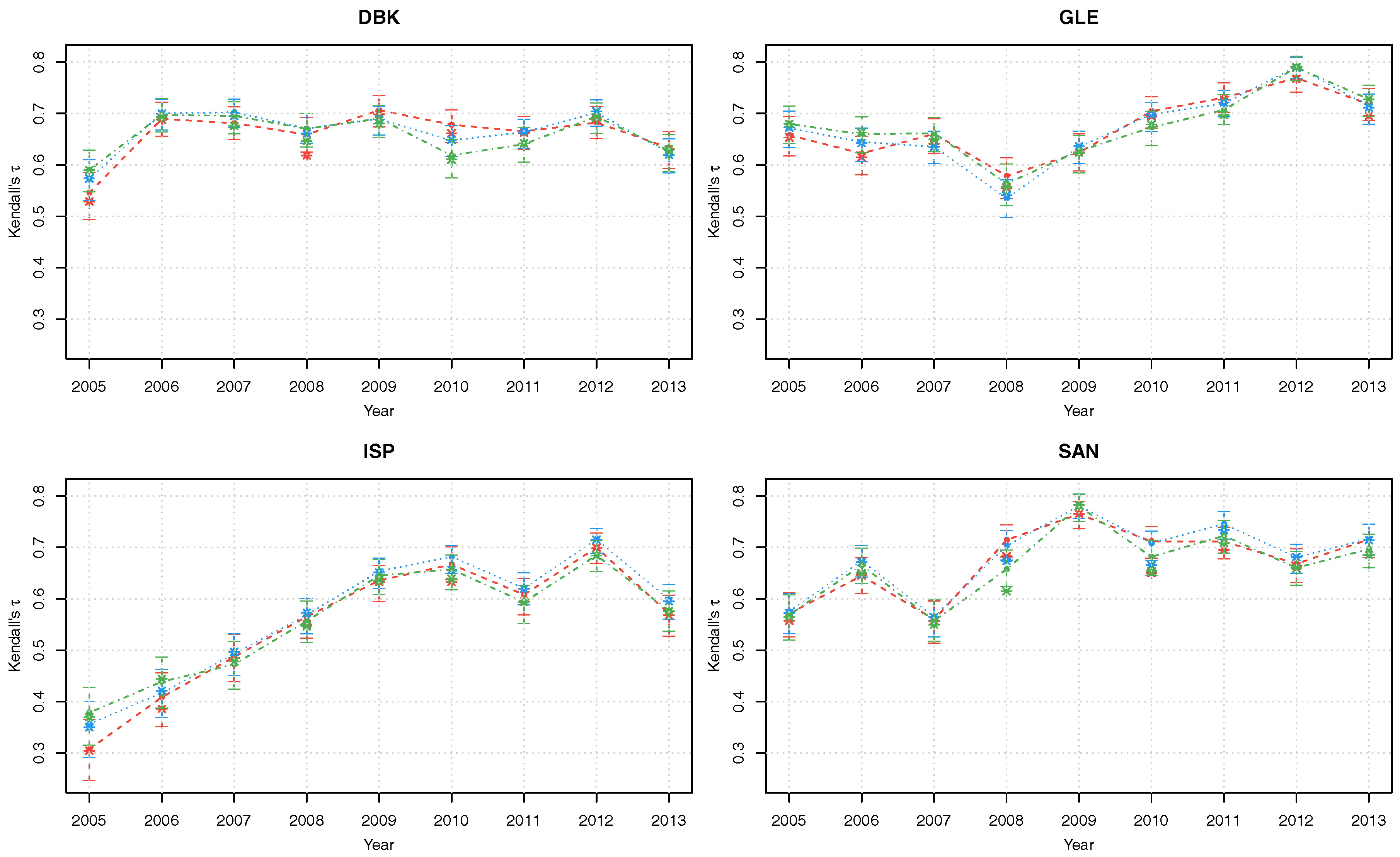
Figure 3.
Kendall’s posterior modes with corresponding 90% credible intervals of copula parameters of the latent factor copula model with Gumbel (red), Gaussian (blue) and survival Gumbel (green) linking copulas.
Figure 3.
Kendall’s posterior modes with corresponding 90% credible intervals of copula parameters of the latent factor copula model with Gumbel (red), Gaussian (blue) and survival Gumbel (green) linking copulas.
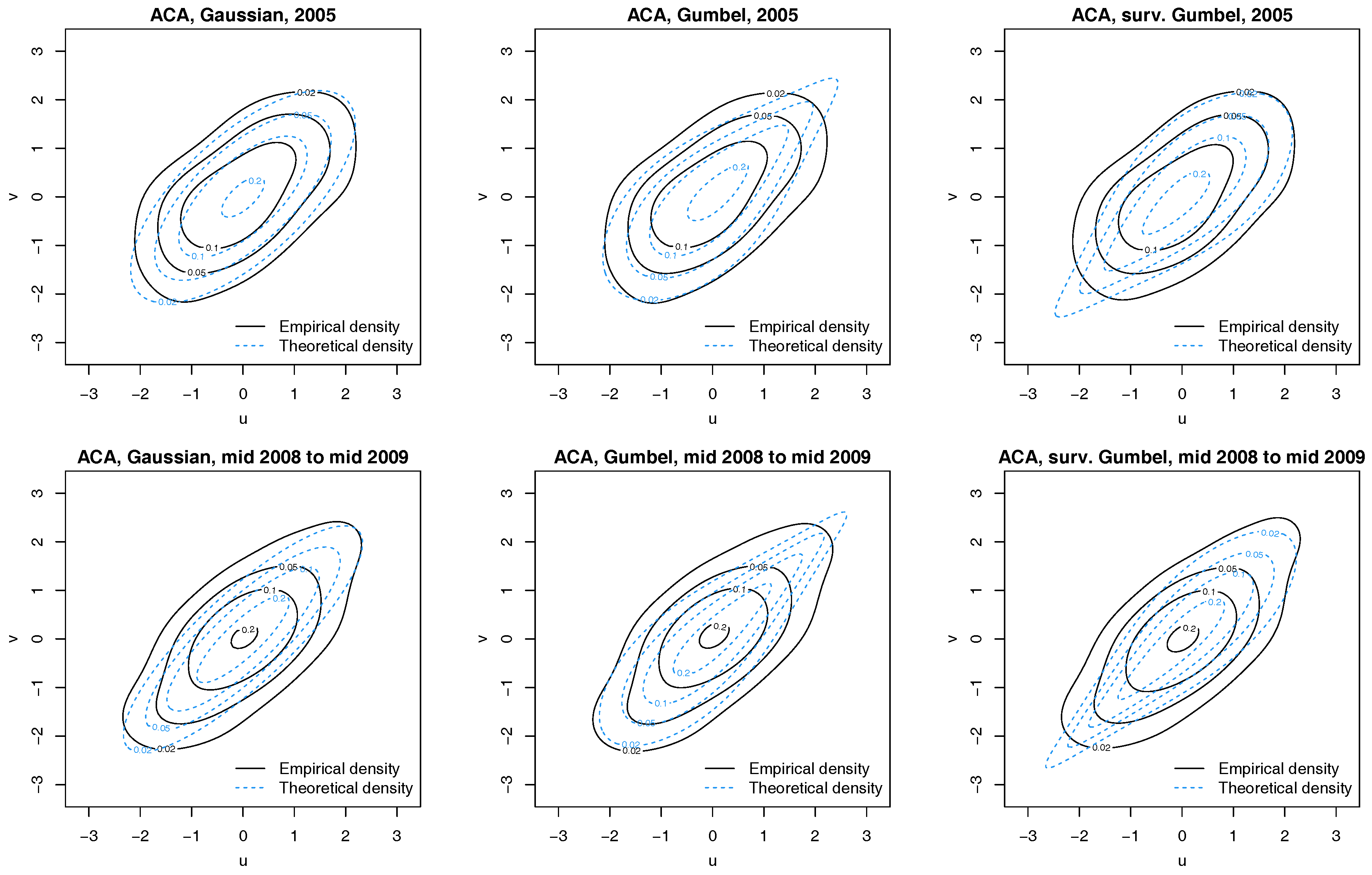
Figure 4.
Contour plots with standard normal margins for ACA and latent factor pairs for 2005 (Top) and 1 July 2008 to 30 June 2009 (Bottom). Empirical densities are indicated by solid black lines, while dotted blue lines show the theoretical densities.
Figure 4.
Contour plots with standard normal margins for ACA and latent factor pairs for 2005 (Top) and 1 July 2008 to 30 June 2009 (Bottom). Empirical densities are indicated by solid black lines, while dotted blue lines show the theoretical densities.
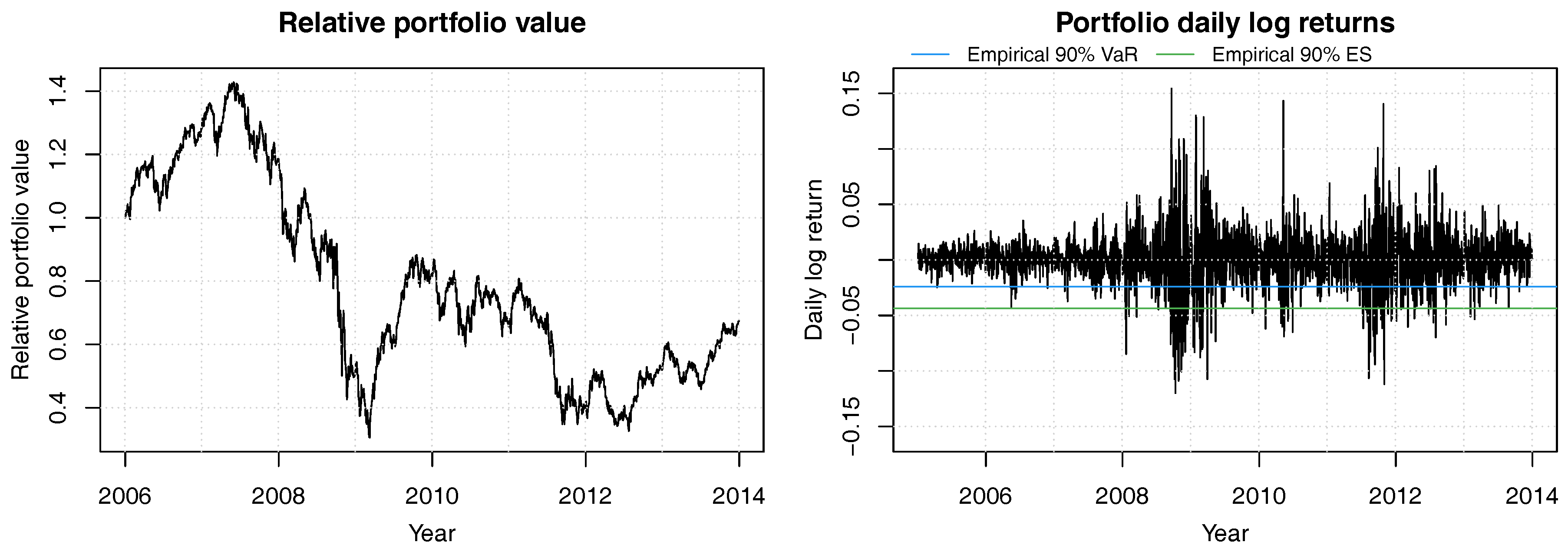
Figure 5.
Historical relative portfolio value of a constant mix strategy with equal weights in the 8 bank stocks ACA, BBVA, BNP, CBK, DBK, GLE, ISP and SAN for years 2006 to 2013. Portfolio weights are readjusted daily. The 90% empirical VaR is shown in blue and the 90% empirical ES is in green.
Figure 5.
Historical relative portfolio value of a constant mix strategy with equal weights in the 8 bank stocks ACA, BBVA, BNP, CBK, DBK, GLE, ISP and SAN for years 2006 to 2013. Portfolio weights are readjusted daily. The 90% empirical VaR is shown in blue and the 90% empirical ES is in green.
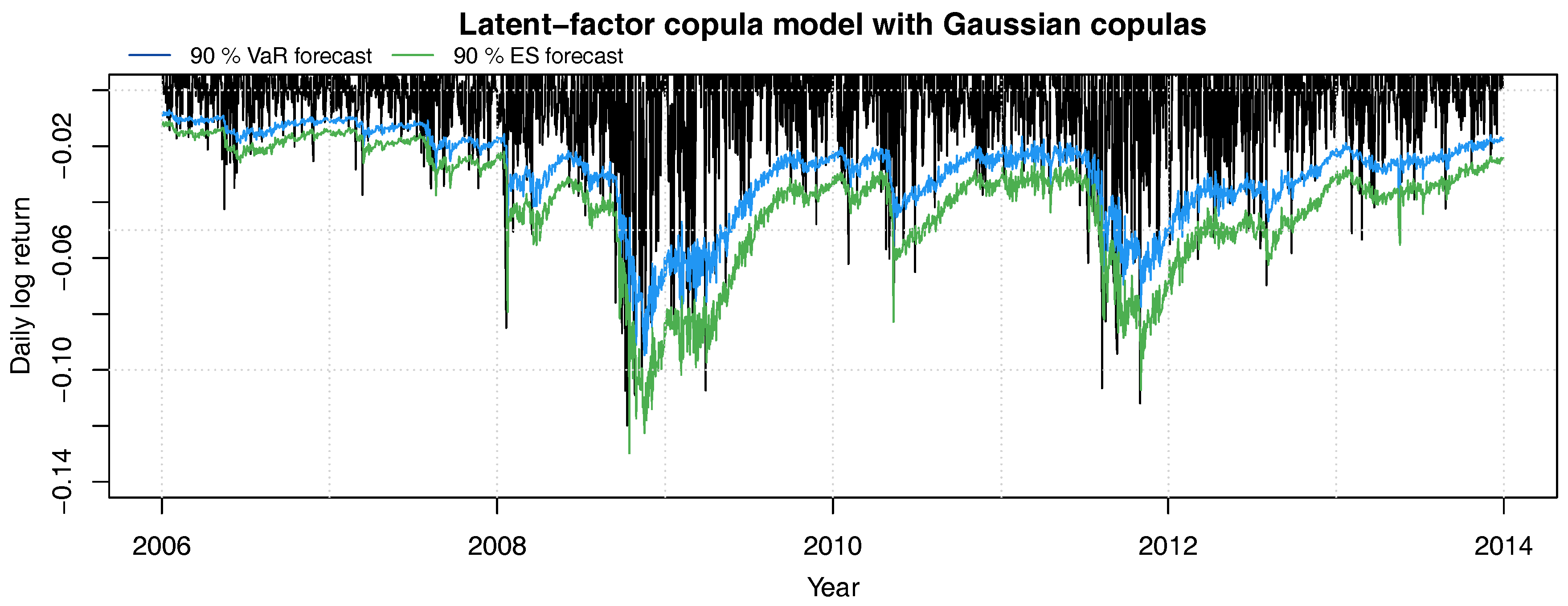
Figure 6.
Daily log-returns of the equally weighted constant mix portfolio with (negative) 90% VaR (blue line) and ES (green line) forecasts.
Figure 6.
Daily log-returns of the equally weighted constant mix portfolio with (negative) 90% VaR (blue line) and ES (green line) forecasts.
Table 1.
Density functions and Kendall’s as a function of the parameter of the Gaussian and Gumbel pair copulas.
Table 1.
Density functions and Kendall’s as a function of the parameter of the Gaussian and Gumbel pair copulas.
| Copula | Density Function | |
|---|
| Gaussian | | |
| Gumbel | , where and | |
| Survival Gumbel | | |
Table 2.
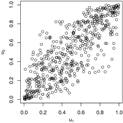
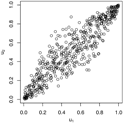
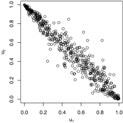
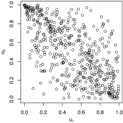
Pairs plots for the Gaussian, Gumbel and survival Gumbel copulas for different parameter values. As the Gumbel and survival Gumbel copulas only exhibit positive dependence, the and rotations of the Gumbel copulas are shown for negative Fisher z parameters.
Table 3.
Copula parameters used in the simulation to model the dependence between each marginal series and the latent factor .
Table 3.
Copula parameters used in the simulation to model the dependence between each marginal series and the latent factor .
| | | | | | |
|---|
| | Low |
| 0.10 | 0.12 | 0.15 | 0.18 | 0.20 |
| 1.11 | 1.14 | 1.18 | 1.21 | 1.25 |
| z | 0.10 | 0.13 | 0.15 | 0.18 | 0.20 |
| | High |
| 0.50 | 0.57 | 0.65 | 0.73 | 0.80 |
| 2.00 | 2.35 | 2.86 | 3.64 | 5.00 |
| z | 0.55 | 0.65 | 0.78 | 0.92 | 1.10 |
| | Mixed |
| 0.10 | 0.28 | 0.45 | 0.62 | 0.80 |
| 1.11 | 1.38 | 1.82 | 2.67 | 5.00 |
| z | 0.10 | 0.28 | 0.48 | 0.73 | 1.10 |
Table 4.
Mean absolute deviation (MAD), mean squared error (MSE), effective sample size (ESS) per minute, and realized coverage of 95% credible intervals (C.I.) averaged across all variables and replications. Runtime is for 10,000 MCMC iterations on a 16-core node.
Table 4.
Mean absolute deviation (MAD), mean squared error (MSE), effective sample size (ESS) per minute, and realized coverage of 95% credible intervals (C.I.) averaged across all variables and replications. Runtime is for 10,000 MCMC iterations on a 16-core node.
| | ARMGS | MCM | EVM | IRW | MLE |
|---|
| | Low |
| MAD | 0.1088 | 0.0900 | 0.1105 | 0.1032 | 0.0739 |
| MSE | 0.0314 | 0.0129 | 0.0327 | 0.0262 | 0.0105 |
| ESS/min | 6.1 | 0.5 | 0.2 | 9.2 | n/a |
| 95% C.I. | 0.96 | 0.61 | 0.94 | 0.93 | n/a |
| | High |
| MAD | 0.0292 | 0.0292 | 0.0293 | 0.0294 | 0.0212 |
| MSE | 0.0014 | 0.0014 | 0.0014 | 0.0014 | 0.0007 |
| ESS/min | 23.7 | 1.6 | 1.4 | 22.2 | n/a |
| 95% C.I. | 0.95 | 0.91 | 0.95 | 0.95 | n/a |
| | Mixed |
| MAD | 0.0509 | 0.0434 | 0.0517 | 0.0506 | 0.0339 |
| MSE | 0.0043 | 0.0030 | 0.0045 | 0.0042 | 0.0017 |
| ESS/min | 21.4 | 1.9 | 1.1 | 29.2 | n/a |
| 95% C.I. | 0.93 | 0.84 | 0.93 | 0.90 | n/a |
| | Average across All Scenarios |
| Runtime | 165s | 664s | 776s | 55s |
Table 5.
Mean absolute deviation (MAD), mean squared error (MSE), effective sample size (ESS) per minute, and realized coverage of 95% credible intervals (C.I.) averaged across all latent variables and replications.
Table 5.
Mean absolute deviation (MAD), mean squared error (MSE), effective sample size (ESS) per minute, and realized coverage of 95% credible intervals (C.I.) averaged across all latent variables and replications.
| | ARMGS | MCM | EVM | IRW |
|---|
| | Low |
| MAD | 0.2808 | 0.2975 | 0.2805 | 0.2811 |
| MSE | 0.1248 | 0.1397 | 0.1248 | 0.1251 |
| ESS/min | 25.7 | 0.5 | 1.1 | 63.5 |
| 95% C.I. | 0.91 | 0.71 | 0.89 | 0.88 |
| | High |
| MAD | 0.0709 | 0.0678 | 0.0710 | 0.0709 |
| MSE | 0.0095 | 0.0087 | 0.0095 | 0.0095 |
| ESS/min | 43.7 | 1.6 | 2.6 | 38.8 |
| 95% C.I. | 0.95 | 0.80 | 0.95 | 0.94 |
| | Mixed |
| MAD | 0.0828 | 0.0898 | 0.0824 | 0.0826 |
| MSE | 0.0132 | 0.0154 | 0.0131 | 0.0131 |
| ESS/min | 25.8 | 1.5 | 2.0 | 34.3 |
| 95% C.I. | 0.88 | 0.78 | 0.87 | 0.83 |
Table 6.
Ticker symbol, company name and exchange of the selected bank stocks.
Table 6.
Ticker symbol, company name and exchange of the selected bank stocks.
| Ticker | Company Name | Exchange |
|---|
| ACA.PA | Credit Agricole S.A. | Euronext - Paris |
| BBVA.MC | Banco Bilbao Vizcaya Argentaria | Madrid Stock Exchange |
| BNP.PA | BNP Paribas SA | Euronext - Paris |
| CBK.DE | Commerzbank AG | XETRA |
| DBK.DE | Deutsche Bank AG | XETRA |
| GLE.PA | Societe Generale Group | Euronext - Paris |
| ISP.MI | Intesa Sanpaolo S.p.A. | Borsa Italiana |
| SAN.MC | Banco Santander | Madrid Stock Exchange |
Table 7.
Percentage of observed log-returns above and below sequentially out-of-sample 90% forecast interval.
Table 7.
Percentage of observed log-returns above and below sequentially out-of-sample 90% forecast interval.
| | ACA | BBVA | BNP | CBK | DBK | GLE | ISP | SAN |
|---|
| Above 95% bound | 4.90% | 4.90% | 4.43% | 4.86% | 4.22% | 4.73% | 4.73% | 4.61% |
| Below 5% bound | 4.35% | 5.07% | 4.65% | 4.43% | 5.29% | 4.78% | 5.33% | 5.16% |
Table 8.
Frequency of 90% VaR violations and 90% ES of an equals weights portfolio of all eight selected financial stocks, and p-values of conditional coverage test of VaR violations. denotes the multivariate regular vine copula model; the other columns are for the dynamic factor copula model with the respective linking copula families. The best values are emphasized in bold.
Table 8.
Frequency of 90% VaR violations and 90% ES of an equals weights portfolio of all eight selected financial stocks, and p-values of conditional coverage test of VaR violations. denotes the multivariate regular vine copula model; the other columns are for the dynamic factor copula model with the respective linking copula families. The best values are emphasized in bold.
| | | Gumbel | Gaussian | Survival Gumbel | |
|---|
| | | ARMGS | MLE | ARMGS | MLE | ARMGS | MLE |
|---|
| 90% VaR viol. | 9.64% | 10.17% | 10.60% | 9.59% | 9.36% | 9.35% | 9.17% |
| 90% ES | 4.07% | 4.00% | 3.88% | 4.10% | 4.08% | 4.13% | 4.08% |
| p-value, cond. coverage test | 0.24 | 0.44 | 0.07 | 0.30 | 0.01 | 0.10 | 0.03 |