Copula-Based Factor Models for Multivariate Asset Returns

Abstract

Recently, several copula-based approaches have been proposed for modeling stationary multivariate time series. All of them are based on vine copulas, and they differ in the choice of the regular vine structure. In this article, we consider a copula autoregressive (COPAR) approach to model the dependence of unobserved multivariate factors resulting from two dynamic factor models. However, the proposed methodology is general and applicable to several factor models as well as to other copula models for stationary multivariate time series. An empirical study illustrates the forecasting superiority of our approach for constructing an optimal portfolio of U.S. industrial stocks in the mean-variance framework.

1. Introduction

It took almost four decades before the statistical usefulness and attractiveness of copulas was widely recognized after the seminal papers by Frees and Valdez (1998), Li (2000), and Embrechts et al. (2002). Copulas are now a standard tool for modeling a dependence structure of multivariate iid data in applied science. The foundation of the copula theory was laid by the famous Sklar’s theorem (see Sklar 1959), which states that any multivariate distribution can be represented through its copula and marginal distributions. If marginal distributions are continuous, then the copula of a multivariate distribution is unique. This approach is particularly flexible, since margins and the dependence structure—which is dictated by the copula—can be modeled independently.

To our knowledge, Darsow et al. (1992) initiated a theoretical application of copulas to specify univariate Markov processes of first order. Thus, conditional independence can be stated in terms of copulas, and this results in a copula counterpart of the Chapman–Kolmogorov equations for the transition probabilities of a Markov process. Ibragimov (2009) generalized their approach for univariate Markov processes of higher order as well as for non-Markov processes. Furthermore, he introduced new classes of copulas for modeling univariate time series. Estimation of copula-based stationary time series models can still be pursued in the classical framework as for iid data. For example, Chen and Fan (2006) investigated theoretical aspects of the two-step estimation when marginal distributions are fitted non-parametrically in the first step and copula parameters are then estimated by maximum likelihood.

The first non-Gaussian VAR models were introduced by Biller and Nelson (2003), where smartly chosen Gaussian VAR time series were transformed to achieve desired autocorrelation structure and marginal distributions. Recently, Brechmann and Czado (2015), Beare and Seo (2015), and Smith (2015) simultaneously developed copula-based models for stationary multivariate time series. Although these models differ from each other, their generality consists of an underlying R-vine pair-copula construction (see Aas et al. 2009) to describe the cross-sectional and temporal dependence jointly. To capture the cross-sectional dependence, Brechmann and Czado (2015) employ C-Vine, while Beare and Seo (2015) and Smith (2015) consider D-vine. Further, Brechmann and Czado (2015) and Beare and Seo (2015) assume the existence of a key variable, whose temporal dependence was explicitly modeled, and this assumption combined with C- or D-vine for the cross-sectional dependence results in a corresponding R-vine for a multivariate time series. In contrast, Smith (2015) explicitly modeled the temporal dependence between multivariate observations and constructed a general D-vine for them consisting of D-vines for the cross-sectional dependence.

In the time of big data, factor models offer an elegant solution to describe a high-dimensional panel data with a few unobservable (latent) variables, called factors. The idea behind factor models is that observable variables are driven by two orthogonal, hidden processes: one captures their co-movements and arises from a linear combination of the latent factors, whereas the other covers their individual nature in the form of idiosyncratic shocks. The dimension of the observed data usually significantly exceeds the number of factors, and so a reduction in dimension takes place.

In the seminal works of Stock and Watson (1999, 2002a, 2002b), factor models supported the forecasting of univariate time series. It was shown for large panel data that the unobserved factors can be consistently estimated, and this served for a consistent forecasting framework. In particular, Stock and Watson (2002a) illustrated that the forecasting of several macroeconomic variables based on factor models can outperform those obtained from competing models such as autoregression (AR), VAR, and leading indicators. In the literature, factor models are classified as static or dynamic with respect to the stochastic dynamics of the unobserved factors. Static factor models suppose iid normally distributed factors, while dynamic factor models assume that the factor obeys a VAR model of order $p\ge 1$.

In this paper, we apply the copula autoregressive (COPAR) model of Brechmann and Czado (2015) to quantify the dependence structure of estimated unobserved factors in dynamic factor models. More precisely, we consider two dynamic factor models and estimate them separately with the maximum likelihood by employing the Kalman filter and smoother. The estimated factors are then combined with a COPAR model, from which latent factors are simulated for a forecasting purpose. Thus, our approach allows several estimated dynamic factor models to be coupled with a copula and admits a non-Gaussian dependence structure of simulated latent factors. To gain information from the estimated factors, a forecasted variable of each market is regressed on the corresponding simulated factors and its previous value.

It should be noted that our modeling approach is different from the factor copula modeling of Krupskii and Joe (2013) and Oh and Patton (2017). We first estimate unobserved factors and then fit copula for them as for observable data. With factor models, we reduce the data dimension, and using autoregressive structure of factors we decrease the number of copula parameters essentially. In contrast, Krupskii and Joe (2013) and Oh and Patton (2017) treat iid data and reduce the dimension of copula parameters by considering conditional independence with respect to unobserved factors. Numerically integrating the unobserved factors, a copula with low dimensional parameters for observed iid data is obtained. For multivariate time series, Oh and Patton (2016) extended the factor copula models with time-varying parametric copulas.

In the empirical application, we consider monthly U.S. financial and macroeconomic panel data to filter driving factors later employed for a mean-variance portfolio optimization. Our main contribution is a new method to improve portfolio performance using factor predictions sampled from the COPAR model. In contrast to dynamic factor models, we explicitly allow for non-Gaussian cross-sectional and temporal dependence between factors. The forecasted factors with non-linear dependence structure are used to assess the future variability of multivariate asset returns. This allows us to construct an optimal portfolio in the mean-variance framework. For comparison, three benchmark portfolios are constructed using dynamic factor models as well as empirical moments of observed asset returns. Thus, our optimal portfolio outperforms the benchmark portfolios according to several risk-adjusted performance measures.

The rest of the paper is organized as follows. Section 2 outlines dynamic factor models and their estimation in the maximum likelihood framework. Section 3 briefly considers vine copulas. Section 4 reviews COPAR models and discusses an algorithm to extend COPAR(1) model for another multivariate observation. Section 5 presents our proposed methodology for an optimal asset allocation of 35 industrial stocks from S&P500 listed in Appendix A and compares it with three benchmark portfolios. Finally, we conclude and discuss further research. Appendix B gives an overview on the considered monthly panel data. Appendix C presents bivariate pair-copulas considered in a model selection procedure for cross-sectional dependence. Appendices Appendix D and Appendix E contain detailed numerical results for portfolio comparisons. Appendix F summarizes testing results of Granger causality between estimated factors.

2. Factor Models

In our application, we deal only with dynamic factor models (DFMs). Further, we restrict our exposition to the simplest factor dynamics of order 1, since any VAR$\left(p\right)$ can be written in VAR$\left(1\right)$ form (see Lütkepohl 2005, p. 15).

Definition 1. 

(Dynamic Factor Model) For any point in time t, let ${\mathit{X}}_t\in {\mathbb{R}}^m$ be a stationary vector process with zero mean. Let ${\mathit{F}}_t\in {\mathbb{R}}^q,q\le m,$ denote the multivariate factor at time t, and let the vector ${\mathit{\epsilon }}_t\in {\mathbb{R}}^m$ collect all idiosyncratic shocks. Then, a dynamic factor model of order 1 is given by

$$\begin{array}{cc}\hfill {\mathit{X}}_t& =\Lambda {\mathit{F}}_t+{\mathit{\epsilon }}_t,\hfill \\ \hfill {\mathit{F}}_t& =A{\mathit{F}}_{t-1}+{\mathit{u}}_t,\hfill \end{array}$$

with constant matrices $\Lambda \in {\mathbb{R}}^{m\times q}$ and $A\in {\mathbb{R}}^{q\times q}$. The idiosyncratic shocks ${\mathit{\epsilon }}_t$ are iid Gaussian with zero mean and covariance matrix $R\in {\mathbb{R}}^{m\times m}$ and the error vectors ${\mathit{u}}_t\in {\mathbb{R}}^q$ are iid Gaussian with zero mean and covariance matrix $Q\in {\mathbb{R}}^{q\times q}$.

Since ${\mathit{X}}_t$ is a stationary process, Definition 1 implicitly assumes that unobserved factor process ${\mathit{F}}_t$ is also stationary. The stationarity of ${\mathit{F}}_t$ can be ensured if the roots of the characteristic polynomial $\left|I_q-Az\right|$ lie outside of the complex unit circle. In this case, the moving average representation for ${\mathit{F}}_t$ yields its stationary $q-$ dimensional zero-mean Gaussian distribution (see Lütkepohl 2005, pp. 18–21) given by

$$N_q(\mathbf{0},{\Sigma }_{\mathbf{F}})\mathrm{with}{\Sigma }_{\mathbf{F}}=\sum _{i=1}^{\infty }{A}^{i}Q{\left(A^i\right)}^{\prime }.$$

(1)

For known or estimated Q and A, the factors can be drawn from (1) by truncating the infinite sum for a pre-specified error tolerance of ${10}^{-5}$ for all entries of ${\Sigma }_{\mathbf{F}}$.

Parameters $\Lambda ,A,R$, and Q of the dynamic factor model in Definition 1 can be estimated in the maximum likelihood framework with Expectation-Maximization Algorithm (EM-Algorithm) of Dempster et al. (1977). This was first done by Shumway and Stoffer (1982) and Watson and Engle (1983), though Shumway and Stoffer (1982) assumed a known $\Lambda$, and Watson and Engle (1983) did not directly maximize the log-likelihood of dynamic factor models. Recently, Bork (2009) and Bańbura and Modugno (2014) derived the EM-Algorithm for the dynamic factor models in Definition 1, on which we rely in our empirical application. Note that the convergence properties of the EM-Algorithm has been theoretically shown for an exponential family by Wu (1983).

For the convenience of the reader, we outline the estimation procedure of Bork (2009) and Bańbura and Modugno (2014). and refer to the original works for further details. Ignoring the unobservability of the factors, the log-likelihood function of the model in Definition 1 for a data sample of length T can be derived by iterative conditioning on observations (e.g., in Bork 2009, p. 45 or Bańbura and Modugno 2014, p. 156). However, the factors ${\mathit{F}}_t$ are unobservable, and therefore the log-likelihood is integrated out with respect to the factor distribution. This results in the expected log-likelihood conditioned on the observed panel data, which constitutes the expectation step of the EM-Algorithm. In contrast to the unconditioned log-likelihood, here factors are replaced by their corresponding conditional moments of first and second order, which a single run of the Kalman filter and smoother given in (Bork 2009, p.43) can provide.

In the maximization step of the EM-Algorithm, Bork (2009) and Bańbura and Modugno (2014) treat the conditional factor moments as constants, when the partial derivatives of the conditional expectation of the log-likelihood with respect to the model parameters are computed. Next, they search for the zeros of the arising system of linear equations to determine the maximum of the expected log-likelihood function. The iterative parameter updates of the EM-Algorithm from Bork (2009) and Bańbura and Modugno (2014) is summarized in Theorem 1.

Theorem 1. 

(EM-Algorithm as in Bork (2009) and Bańbura and Modugno (2014)) Assume the dynamic factor model in Definition 1 and let the matrix $X=\left[{\mathit{X}}_1,\dots ,{\mathit{X}}_T\right]\in {\mathbb{R}}^{m\times T}$ collect all panel data. Let the index $l\ge 0$ indicate the current loop of the EM-Algorithm and let $\mathbb{E}\left[·|X,{\theta }_{\left(l\right)}\right]$ denote the expectation conditioned on the panel data and the parameters estimated in loop l. Then, the parameter updates in loop $(l+1)$ are given as follows:

$$\begin{array}{cc}\hfill {\Lambda }_{\left(l+1\right)}& =\left(\sum _{t=1}^T{\mathit{X}}_t\mathbb{E}\left[{\mathit{F}}_t^{\prime }|X,{\theta }_{\left(l\right)}\right]\right){\left(\sum _{t=1}^T\mathbb{E}\left[{\mathit{F}}_t{\mathit{F}}_t^{\prime }|X,{\theta }_{\left(l\right)}\right]\right)}^{-1},\hfill \\ \hfill A_{\left(l+1\right)}& =\left(\sum _{t=1}^T\mathbb{E}\left[{\mathit{F}}_t{\mathit{F}}_{t-1}^{\prime }|X,{\theta }_{\left(l\right)}\right]\right){\left(\sum _{t=1}^T\mathbb{E}\left[{\mathit{F}}_{t-1}{\mathit{F}}_{t-1}^{\prime }|X,{\theta }_{\left(l\right)}\right]\right)}^{-1},\hfill \\ \hfill R_{\left(l+1\right)}& =\frac{1}{T}\left(\sum _{t=1}^T{\mathit{X}}_t{\mathit{X}}_t^{\prime }-{\Lambda }_{\left(l+1\right)}\sum _{t=1}^T\mathbb{E}\left[{\mathit{F}}_t|X,{\theta }_{\left(l\right)}\right]{\mathit{X}}_t^{\prime }\right),\hfill \\ \hfill Q_{\left(l+1\right)}& =\frac{1}{T}\left(\sum _{t=1}^T\mathbb{E}\left[{\mathit{F}}_t{\mathit{F}}_t^{\prime }|X,{\theta }_{\left(l\right)}\right]-A_{\left(l+1\right)}\sum _{t=1}^T\mathbb{E}\left[{\mathit{F}}_{t-1}{\mathit{F}}_t^{\prime }|X,{\theta }_{\left(l\right)}\right]\right),\hfill \end{array}$$

where $Z^{-1}$ stands for the inverse matrix and conditional factor moments are computed using the Kalman filter and smoother for each loop l.

The iterative estimation procedure in Theorem 1 requires a termination criterion. In our application, we terminate the above EM-Algorithm as soon as the change in log-likelihood is smaller than ${10}^{-8}$. Finally, note that the estimated factors are unique up to rotation with orthogonal matrices. For forecasting purposes, one can ignore this fact, since estimated parameters of factors in forecasting equations will then be transformed correspondingly with no effect on forecasting variable. We illustrate this point later in our application.

3. Vine Copulas

Since the statistical applicability of vine copulas with non-Gaussian building bivariate copulas was recognized by Aas et al. (2009), vine copulas became a standard tool to describe the dependence structure of multivariate data (see Aas 2016 for a recent review). Moreover, Brechmann and Czado (2015), Beare and Seo (2015), and Smith (2015) have applied vine copulas to model temporal dependence of multivariate time series as well as the cross-sectional dependence between univariate time series. In this section, we review the COPAR model of Brechmann and Czado (2015), which is used to describe the stochastic dynamics and the dependence structure of the estimated factors from Section 2. We start with the concept of regular vines from Kurowicka and Cooke (2006). We do not consider illustrating examples on pair-copula constructions, and refer instead to Aas (2016) or Czado (2010) for more intuition on them.

Definition 2. 

(Regular vine) A collection of trees $\mathcal{V}=\left(T_1,\dots ,T_{d-1}\right)$ is a regular vine on d elements if

1. 

$T_1$ is a tree with nodes $N_1=\left\{1,\dots ,d\right\}$ connected by a set of non-looping edges $E_1$.

2. 

For $i=2,\dots ,d-1$, $T_i$ is a connected tree with edge set $E_i$ and node set $N_i=E_{i-1}$, where $\left|N_i\right|=d-\left(i-1\right)$ and $\left|E_i\right|=d-i$ are the number of edges and nodes, respectively.

3. 

For $i=2,\dots ,d-1$, $\forall e=\left\{a,b\right\}\in E_i$: $\left|a\cap b\right|=1$ (two nodes $a,b\in N_i$ are connected by an edge e in $T_i$ if the corresponding edges a and b in $T_{i-1}$ share one node (proximity condition)).

A tree $T=\left(N,E\right)$ is an acyclic graph, where N is its set of nodes and E is its set of edges. Acyclic means that there exits no path such that it cycles. In a connected tree we can reach each node from all other nodes on this tree. R-vine is simply a sequence of connected trees such that the edges of $T_i$ are the nodes of $T_{i+1}$. A traditional example of these structures are canonical vines (C-vines) and drawable vines (D-vines) (see Czado (2010) and Aas et al. 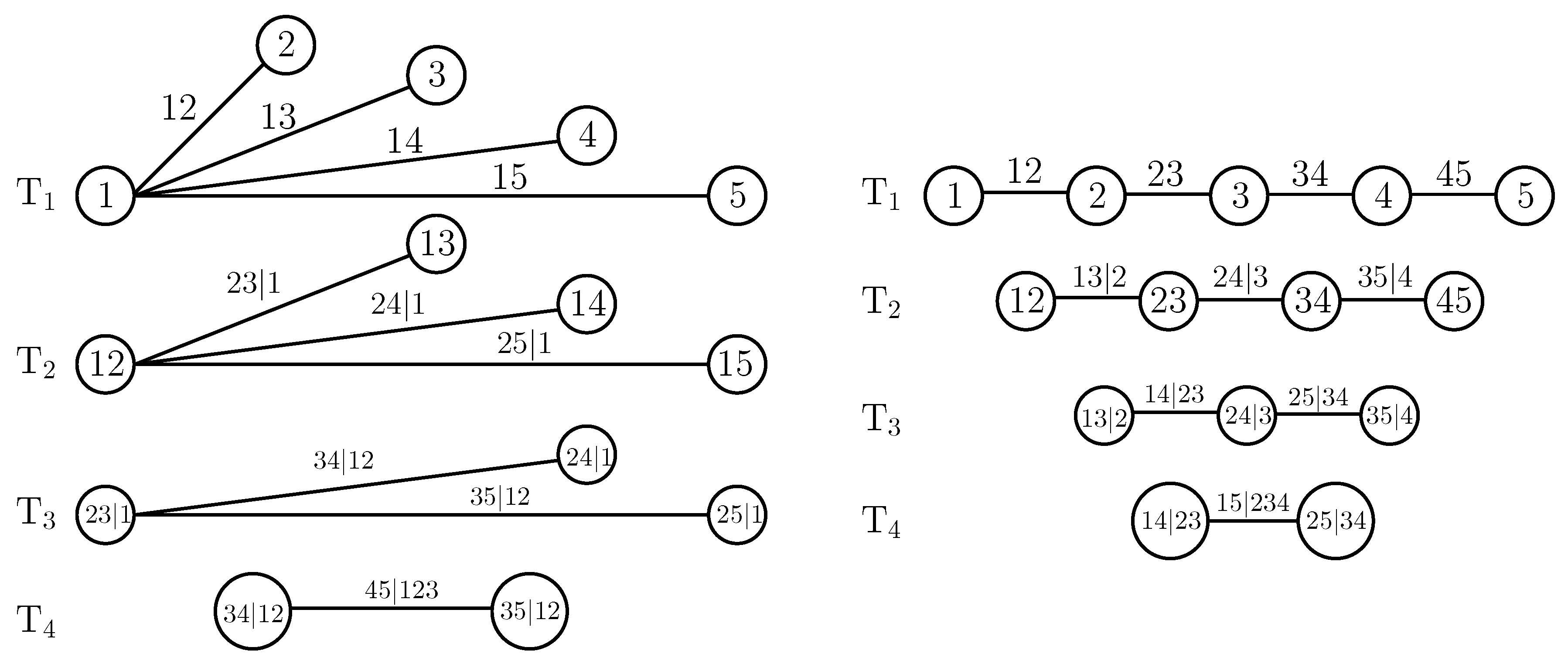(2009)) in Figure 1. Every tree of a C-vine is defined by a root node, which has $d-i$ incoming edges, in each tree $T_i$, $i\in \left\{1,\dots ,d-1\right\}$, whereas a D-vine is solely defined through its first tree, where each node has at most two incoming edges.

Regular vines are a powerful tool to systemize all possible factorizations of a $d-$dimensional density as a product of d univariate marginal densities with a product of $d(d-1)/2$ conditional and unconditional bivariate copulas (see Theorem 4.2 in Kurowicka and Cooke (2006)). Thus, the unconditional and conditional bivariate copulas—called pair-copulas—of a given factorization can be uniquely mapped onto the edge set E of a particular regular vine, and vice versa. Then, the conditional copulas and their arguments depend on conditioned values. The dependence of conditional copulas on conditioned values is crucial, and allows for statistical applications only for a subclass of elliptical distributions (see Stöber et al. (2013)), since in this case, conditioned pair-copulas depend on conditioned values only through their arguments. Aas et al. (2009) first developed this observation further and went beyond the elliptical world. Thus, they considered regular vine factorizations with arbitrary fixed conditional copulas and showed that this results in valid multivariate distributions and copulas. In this paper, we also assume that conditional copulas depend on conditioned values only through their arguments, and so they can be chosen from bivariate copula families.

The number of possible vine structures on d random variables can be immense. For $d\le 4$, only C- and D-vines are possible. For $d>4$, there are $\frac{d!}{2}$ different C- and D-vines. The total amount of regular vine structures has been computed by Morales-Nápoles et al. (2010), and is equal to $\frac{d!}{2}·2^{\left(\genfrac{}{}{0pt}{}{d-2}{2}\right)}$. To select conditional copulas on these graphical structures, we define the following sets as in Czado (2010).

Definition 3. 

(Conditioned and conditioning sets) For any edge $e=\left\{a,b\right\}\in E_i$ of a regular vine $\mathcal{V}$, the complete union of e is the subset

$$A_e=\left\{v\in N_1:\forall m=1,\dots ,i-1,\exists e_{j_m}\in E_{m}s.t.v\in e_{j_1}\in \cdots \in e_{j_{i-1}}\in e\right\}.$$

The conditioning set associated with e is

$$D_e=A_a\cap A_b.$$

The conditioned sets associated with e are

$$\begin{array}{ccc}\hfill i\left(e\right)& =& A_a\backslash D_e\hfill \\ \hfill j\left(e\right)& =& A_b\backslash D_e.\hfill \end{array}$$

The copula for this edge will be denoted by

$$C_e≔C_{i\left(e\right),j\left(e\right)\mid D\left(e\right)}.$$

Given a regular vine, we specify a regular vine copula by assigning a (conditional) pair copula (with parameters) to each edge of the regular vine. In doing so, we follow Czado et al. (2012).

Definition 4. 

(Regular vine copula). A regular vine copula $C=\left(\mathcal{V},\mathcal{B}\left(\mathcal{V}\right),\theta \left(\mathcal{B}\left(\mathcal{V}\right)\right)\right)$ in d dimensions is a multivariate distribution function such that for a random vector $\mathbf{U}={\left(U_1,\dots ,U_d\right)}^{\prime }\sim C$ with uniform margins

• $\mathcal{V}$ is a regular vine on d elements,
• $\mathcal{B}\left(\mathcal{V}\right)=\left\{C_e\mid e\in E_m,m=1,\dots ,d-1\right\}$ is a set of $d\left(d-1\right)/2$ copula families identifying the unconditional distributions of ${\mathbf{U}}_{i\left(e\right),j\left(e\right)}$ as well as the conditional distributions of ${\mathbf{U}}_{i\left(e\right),j\left(e\right)}\mid {\mathbf{U}}_{D\left(e\right)},$
• $\theta \left(\mathcal{B}\left(\mathcal{V}\right)\right)=\left\{{\theta }_e\mid e\in E_m,m=1,\dots ,d-1\right\}$ is the set of parameter vectors corresponding to the copulas in $\mathcal{B}\left(\mathcal{V}\right).$

To facilitate statistical inference, a matrix representation of R-vines was proposed by Morales-Nápoles et al. (2010) and further developed by Dissmann et al. (2013). To specify a d-dimensional R-vine in matrix form, one needs several lower triangular $d\times d$ matrices: one that stores the structure of the R-vine, one with copula families, and another two with the first and second parameters.

For a d-dimensional R-vine, the matrix with the structure has the following form

$$M=\left(\begin{array}{c}{m}_{1,1}\\ ⋮& \ddots \\ m_{d-1,1}& \cdots & m_{d-1,d-1}\\ m_{d,1}& \cdots & m_{d,d-1}& m_{d,d}\end{array}\right),$$

where $m_{i,j}\in \left(1,\dots ,d\right)$. The rules for reading from this matrix are as follows. The conditioned set for an entry $m_{i,j}$ is the entry itself and the diagonal entry of the column $m_{j,j}$, whereas the conditioning set is composed of variables under the entry; i.e., for $m_{i,j}$, the conditioned set will be $\left(m_{i,j},m_{j,j}\right)$, the conditioning set is $\left(m_{i+1,j},\dots ,m_{d,j}\right)$. Thus, $m_{i,j}$ denotes the node $\left(m_{j,j},m_{i,j}\mid m_{i+1,j},\dots ,m_{d,j}\right)$. We will assume that the diagonal of M is sorted in descending order, which can always be achieved by reordering the node labels, so that we have $m_{i,i}=n-i+1$. To illustrate the R-vine matrix notation, we consider the C-vine from Figure 1 and give below its R-vine matrix representation.

$$\left(\begin{array}{c}5\\ 4& 4\\ 3& 3& 3\\ 2& 2& 2& 2\\ 1& 1& 1& 1& 1\end{array}\right)$$

The first column encodes the following nodes

• Node $54\mid 321$ is saved through $m_{1,1},m_{2,1}$ given $m_{3,1},m_{4,1}$ and $m_{5,1}$;
• Node $53\mid 21$ is saved through $m_{1,1},m_{3,1}$ given $m_{4,1}$ and $m_{5,1}$;
• Node $52\mid 1$ is saved through $m_{1,1},m_{4,1}$ given $m_{5,1}$;
• Node 51 is saved through $m_{1,1},m_{5,1}$.

In the sequel, we utilize C-vines to capture the cross-sectional dependence of a multivariate time series at any time point t. To capture the dependence between multivariate observations, the first tree of the C-vine for multivariate observation at time point t is connected to the first trees of the C-vines for existing neighboring multivariate observations at time points $t-1$ and $t+1$ with one edge, correspondingly. This results in the first tree of an R-vine for all multivariate observations treated as one huge sample point. Depending on the choice of C-vines and the connection of the first trees, the copula autoregressive model of Brechmann and Czado (2015) from the next section can be obtained.

Finally, note that the information on copula families and their parameters is similarly stored in lower triangular $d\times d$ matrices. Each element of the R-vine matrix below the diagonal specifies a conditional or unconditional pair-copula depending on the diagonal entry above it. The family and parameters of this pair-copula are now entered at the same entry place of matrices for copula families and parameters. Since the diagonal entries of the R-vine matrix alone do not determine any pair-copulas, no entries for copula family and parameters matrices are needed on the diagonal. To avoid confusion with space character, we fill the main diagonal with * sign.

4. Copula Autoregressive Model

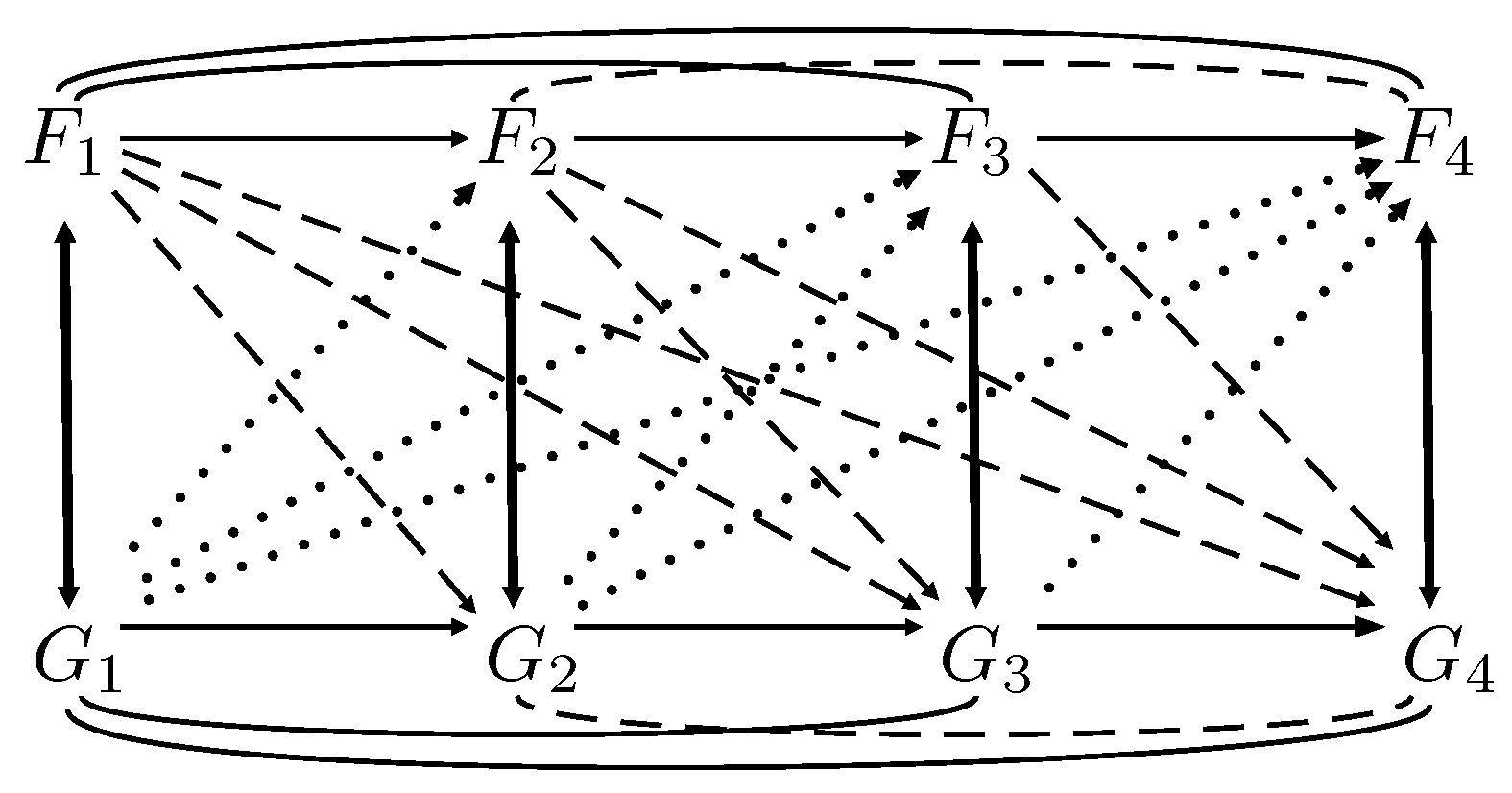
R-vines have been mostly used to model contemporaneous dependence. We now present a special R-vine structure called copula autoregressive (COPAR) model from Brechmann and Czado (2015) which is designed to capture cross-sectional, serial, and cross-serial dependence in multivariate time series, and allows a general Markovian structure. Let ${\left\{F_t,G_t\right\}}_{t=1,\dots ,T}$ be an observable bivariate stationary time series. To illustrate how the two individual time series are interdependent, consider the mapping of dependencies for $T=4$ in Figure 2. Vertical solid lines represent the cross-sectional dependence, horizontal solid lines and curved lines represent the serial dependence for each time series, and dotted and dashed lines represent the cross-serial dependence.

Traditionally, R-vines were used to model only the cross-sectional dependence (pictured by the vertical solid lines in Figure 2), but under the assumption that other dependencies are absent (i.e., data is iid). The COPAR model is designed to additionally capture serial and cross-serial dependence. The following definition of a COPAR model without Markovian structure for two time series adopted to our notation is taken from Brechmann and Czado (2015). The vectors $\left(F_s,\dots ,F_t\right)$ and $\left(G_s,\dots ,G_t\right)$ are denoted as ${\mathbf{F}}_{s:t}$ and ${\mathbf{G}}_{s:t}$, respectively.

Definition 5. 

(COPAR model for the bivariate case) The COPAR model for stationary continuous time series ${\left\{F_t\right\}}_{t=1,\dots ,T}$ and ${\left\{G_t\right\}}_{t=1,\dots ,T}$ has the following components.

(i) 

Unconditional marginal distributions of each time series are independent of time.

(ii) 

An R-vine for the serial and between-series dependence of ${\left\{F_t\right\}}_{t=1,\dots ,T}$ and ${\left\{G_t\right\}}_{t=1,\dots ,T}$, where the following pairs are selected.

1. 

Serial dependence of ${\left\{F_t\right\}}_{t=1,\dots ,T}$: The pairs of serial D-vine copula for $F_1,\dots ,F_T$; that is,

$$F_s,F_t\mid {\mathbf{F}}_{\left(s+1\right):\left(t-1\right)},1\le s<t\le T.$$

(2)

2. 

Between-series dependence:

$$F_s,G_t\mid {\mathbf{F}}_{\left(s+1\right):t},1\le s\le t\le T,$$

(3)

and

$$G_s,F_t\mid {\mathbf{F}}_{1:\left(t-1\right)},{\mathbf{G}}_{\left(s+1\right):\left(t-1\right)},1\le s<t\le T.$$

(4)

3. 

Conditional serial dependence of ${\left\{G_t\right\}}_{t=1,\dots ,T}$: The pairs of a serial D-vine copula for $G_1,\dots ,G_T$ conditioned on all previous values of ${\left\{F_t\right\}}_{t=1,\dots ,T}$; that is,

$$G_s,G_t\mid {\mathbf{F}}_{1:t},{\mathbf{G}}_{\left(s+1\right):\left(t-1\right)},1\le s<t\le T.$$

(5)

Pair copulas of the same lag length $t-s$, $t\ge s$, are identical. We associate

1. 

copula $C_{t-s}^F≔C_{F_s,F_t\mid {\mathbf{F}}_{\left(s+1\right):\left(t-1\right)}}$ with (2),

2. 

copulas $C_{t-s}^{FG}≔C_{F_s,G_t\mid {\mathbf{F}}_{\left(s+1\right):t}}$ and $C_{t-s}^{GF}≔C_{G_s,F_t\mid {\mathbf{F}}_{1:\left(t-1\right)},{\mathbf{G}}_{\left(s+1\right):\left(t-1\right)}}$ with (3) and (4), respectively, and

3. 

copula $C_{t-s}^G≔C_{G_s,G_t\mid {\mathbf{F}}_{1:t},{\mathbf{G}}_{\left(s+1\right):\left(t-1\right)}}$ with (5).

Let us explain the above definition on an example of a bivariate time series ${\left\{F_t,G_t\right\}}_{t=1,\dots ,4}$ with four observations. Using a D-vine, Equation (2) captures the dependence structure of $F_1$, $F_2$, $F_3$, and $F_4$ expressed by the top lines connecting them in Figure 2. For $s=1$ and $t=4$, Equation (3) describes the conditional dependence between $F_1$ and $G_4$ conditioned on $F_2$, $F_3$, and $F_4$. Thus, Equation (3) captures the conditional dependence between $F_s$ and $G_t$ for $s<t$ reflected by the dashed lines in Figure 2. For $s=t$, Equation (3) models the unconditional dependence between $F_t$ and $G_t$ expressed by the vertical lines. Similarly, Equation (4) describes the conditional serial dependence between univariate time series illustrated by the dotted lines in Figure 2. However, Equations (3) and (4) are not symmetric with respect to conditioned sets. In particular, the conditional distribution of $F_s$ and $G_t$ for $s<t$ is independent of $G_1,\dots ,G_{t-1}$. This already indicates that the first time series ${\left\{F_t\right\}}_{t=1,\dots ,T}$ plays a key role in the stochastic dynamics of the time series, since it is sufficient to describe the conditional dependence between $F_s$ and $G_t$ for $s<t$. Therefore, the univariate time series are not interchangeable. Using a D-vine, Equation (5) finally describes the dependence structure of $G_1,G_2,\dots ,G_T$ (connecting bottom lines in Figure 2) conditioned on $F_1,F_2,\dots ,F_T$. Due to the property that copulas of same lag length are identical, the COPAR model defines a stationary bivariate time series.

Now, we expand the COPAR model to an arbitrary number of variables with Markov structure. We consider q univariate time series observed at T time points; that is, ${\left\{F_{1,t}\right\}}_{t=1,\dots ,T},\dots ,{\left\{F_{q,t}\right\}}_{t=1,\dots ,T}$. We denote a random vector of q variables observed at times $t=1,\dots ,T$ as ${\mathbf{F}}_t={\left(F_{1,t},\dots ,F_{q,t}\right)}^{\prime }$, time series of individual variables for $i=1,\dots ,q$ as ${\mathbf{F}}^{\left(i\right)}=\left(F_{i,1},\dots ,F_{i,T}\right)$, and also introduce a vector ${\mathbf{F}}_{l:q,s:t}=\left(F_{l,s},\dots ,F_{l,t},\dots ,F_{q,s},\dots ,F_{q,t}\right)$. Finally, we define a COPAR$\left(k\right)$ model, which is COPAR model for a multivariate time series with a Markovian structure of the k-th order. Since unobservable factors in Section 2 are also denoted by ${\mathbf{F}}_t$, our notation above should not lead to a confusion. Our modeling approach utilizes estimated factors even if they are not observed. Therefore, for reader convenience, we denote here multivariate time series with ${\mathbf{F}}_t$ and present COPAR models in terms of ${\mathbf{F}}_t$.

Definition 6. 

(COPAR$\left(k\right)$ model for q time series of length T) The COPAR$\left(k\right)$ model for a q-dimensional stationary time series ${\mathbf{F}}_t\in {\mathbb{R}}^{q\times 1}$, $t=1,\cdots ,T$ has the following components.

(i) 

Unconditional marginal distributions of each time series are independent of time.

(ii) 

An R-vine for the serial and between-series dependence of ${\mathbf{F}}_t\in {\mathbb{R}}^{q\times 1}$, $t=1,\cdots ,T$, where the following pairs are selected.

1. 

Serial dependence of ${\mathbf{F}}^{\left(1\right)}$: The pairs of serial D-vine copula for $F_{1,1},\dots ,F_{1,T}$; that is,

$$F_{1,s},F_{1,t}\mid {\mathbf{F}}_{1,\left(s+1\right):\left(t-1\right)},1\le s<t\le T.$$

2. 

Between-series dependence of ${\mathbf{F}}^{\left(i\right)}$ and ${\mathbf{F}}^{\left(j\right)}$ for $i<j$, $i,j=1,\dots ,q$:

$$F_{i,s},F_{j,t}\mid {\mathbf{F}}_{1:\left(i-1\right),1:t},{\mathbf{F}}_{i,\left(s+1\right):t}1\le s\le t\le T,$$

and

$$F_{j,s},F_{i,t}\mid {\mathbf{F}}_{1:\left(i-1\right),1:t},{\mathbf{F}}_{i:\left(j-1\right),1:\left(t-1\right)},{\mathbf{F}}_{j,\left(s+1\right):\left(t-1\right)}1\le s<t\le T,$$

3. 

Conditional serial dependence of ${\mathbf{F}}^{\left(i\right)}$ for $2\le i\le q$:

$$F_{i,s},F_{i,t}\mid {\mathbf{F}}_{1:\left(i-1\right),1:t},{\mathbf{F}}_{i,\left(s+1\right):\left(t-1\right)},1\le s<t\le T,$$

whereas

(a) 

copulas $\forall i$ and for lag length $t-s>k$ are independent copulas,

(b) 

copulas for $i,j=1,\dots ,q$ for the same lag length $t-s$, $t\ge s$ are identical.

Definition 6 introduces the COPAR model, if a) is neglected. The dependence of ${\mathbf{F}}^{\left(i\right)}$ is modeled conditioned on ${\mathbf{F}}^{\left(1\right)},\dots ,{\mathbf{F}}^{\left(i-1\right)}$, and consequently, the order of variables cannot be simply interchanged. The number of pair copulas in COPAR models for time series with Markovian structure does not depend on T, and is less than the number needed for a general R-vine. With respect to the number of pair-copulas, the following result from Brechmann and Czado (2015) holds.

Lemma 1.

The number of copulas needed for a COPAR$\left(k\right)$ model of q univariate time series is $q^{2}k+\frac{q\left(q-1\right)}{2}$.

Note, the number of parameters in a VAR$\left(k\right)$ for the between-series dependence of q time series—not counting parameters for marginal distributions—is equal to the number of pair-copulas in a COPAR$\left(k\right)$ model. Therefore, the number of parameters in a COPAR$\left(k\right)$ model is bounded by a multiple of the number of VAR parameters, depending on the number of parameters of the involved copula families. In contrast, a general R-vine requires $\frac{qT\left(qT-1\right)}{2}$ pair-copulas, resulting in a huge number of parameters.

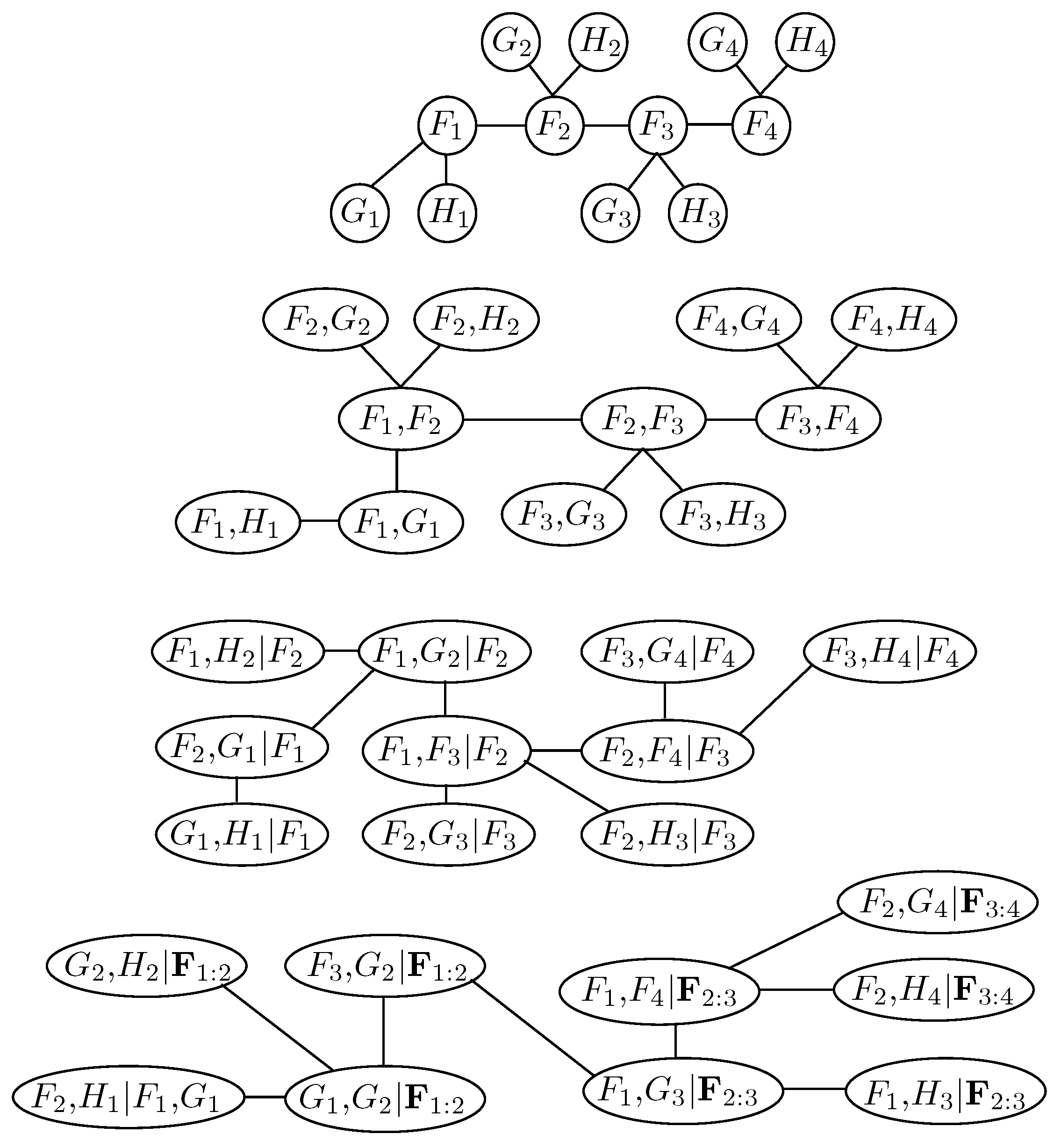
Figure 3 illustrates the first 4 trees of a COPAR model for three univariate time series $F_t$, $G_t$, and $H_t$ with $T=4$ (i.e., for four observations). Examining the first tree, we observe that it is a sequence of connected C-vines, where the central nodes are the time points of the first factor $F_t$. Thus, unconditional contemporaneous dependence is modeled with a C-vine.

The matrix representation of the R-vine structure of this COPAR model is given by

$$\left(\begin{array}{c}{H}_4\\ H_1& G_4\\ H_2& H_1& F_4\\ H_3& H_2& H_1& H_3\\ G_1& H_3& H_2& H_1& G_3\\ G_2& G_1& H_3& H_2& H_1& F_3\\ G_3& G_2& G_1& G_1& H_2& H_1& H_2\\ G_4& G_3& G_2& G_2& G_1& H_2& H_1& G_2\\ F_1& F_1& G_3& G_3& G_2& G_1& G_1& H_1& F_2\\ F_2& F_2& F_1& F_1& F_1& G_2& G_2& G_1& H_1& H_1\\ F_3& F_3& F_2& F_2& F_2& F_1& F_1& F_1& G_1& G_1& G_1\\ F_4& F_4& F_3& F_3& F_3& F_2& F_2& F_2& F_1& F_1& F_1& F_1\end{array}\right)$$

and the matrix of copulas for three-dimensional COPAR model is given by

$$\left(\begin{array}{c}*\\ C_3^H& *\\ C_2^H& C_3^{HG}& *\\ C_1^H& C_2^{HG}& C_3^{HF}& *\\ C_3^{GH}& C_1^{HG}& C_2^{HF}& C_2^H& *\\ C_2^{GH}& C_3^G& C_1^{HF}& C_1^H& C_2^{GH}& *\\ C_1^{GH}& C_2^G& C_3^{GF}& C_2^{GH}& C_1^{GH}& C_2^{HF}& *\\ C^{GH}& C_1^G& C_2^{GF}& C_1^{GH}& C_2^G& C_1^{HF}& C_1^H& *\\ C_3^{FH}& C_3^{FG}& C_1^{GF}& C^{GH}& C_1^G& C_2^{GF}& C_1^{GH}& C_1^{GH}& *\\ C_2^{FH}& C_2^{FG}& C_3^F& C_2^{FH}& C_2^{FG}& C_1^{GF}& C^{GH}& C_1^G& C_1^{HF}& *\\ C_1^{FH}& C_1^{FG}& C_2^F& C_1^{FH}& C_1^{FG}& C_2^F& C_1^{FH}& C_1^{FG}& C_1^{GF}& C^{GH}& *\\ C^{FH}& C^{FG}& C_1^F& C^{FH}& C^{FG}& C_1^F& C^{FH}& C^{FG}& C_1^F& C^{FH}& C^{FG}& *\end{array}\right).$$

If a COPAR$\left(k\right)$ model is estimated based on the first T multivariate observations, then it can easily be extended to $T+1$ observations. This allows us to sample the $(T+1)$-th observation according to the estimated dependence structure between the $k-$th subsequent multivariate observations. Let us illustrate this point for a COPAR$\left(1\right)$ model and the above example with three univariate time series. The matrix representation of the R-vine structure of this COPAR$\left(1\right)$ model remains unchanged, and the matrix of copulas for three-dimensional COPAR$\left(1\right)$ model is now simplified to the matrix in (6), where 0 stands for independence copula

$$\begin{array}{c}\hfill \left(\begin{array}{c}*\\ 0& *\\ 0& 0& *\\ C_1^H& 0& 0& *\\ 0& C_1^{HG}& 0& 0& *\\ 0& 0& C_1^{HF}& C_1^H& 0& *\\ C_1^{GH}& 0& 0& 0& C_1^{GH}& 0& *\\ C^{GH}& C_1^G& 0& C_1^{GH}& 0& C_1^{HF}& C_1^H& *\\ 0& 0& C_1^{GF}& C^{GH}& C_1^G& 0& C_1^{GH}& C_1^{GH}& *\\ 0& 0& 0& 0& 0& C_1^{GF}& C^{GH}& C_1^G& C_1^{HF}& *\\ C_1^{FH}& C_1^{FG}& 0& C_1^{FH}& C_1^{FG}& 0& C_1^{FH}& C_1^{FG}& C_1^{GF}& C^{GH}& *\\ C^{FH}& C^{FG}& C_1^F& C^{FH}& C^{FG}& C_1^F& C^{FH}& C^{FG}& C_1^F& C^{FH}& C^{FG}& *\end{array}\right).\end{array}$$

(6)

Now, if we want to expand this COPAR$\left(1\right)$ model by adding a new time point (i.e., $T\to T+1$—in our case, $4\to 5$), the matrix representation will be changed as follows

• Add three blank columns to the left of the matrix and add $\left(H_{T+1},G_{T+1},F_{T+1}\right)$ to the diagonal;
• Under $F_{T+1}$ comes ${\left(H_1,\dots ,H_T\right)}^{\prime }$, then ${\left(G_1,\dots ,G_T\right)}^{\prime }$ and ${\left(F_1,\dots ,F_T\right)}^{\prime }$;
• Under $G_{T+1}$ comes ${\left(H_1,\dots ,H_T\right)}^{\prime }$, then ${\left(G_1,\dots ,G_T\right)}^{\prime }$ and ${\left(F_1,\dots ,F_{T+1}\right)}^{\prime }$;
• Under $H_{T+1}$ comes ${\left(H_1,\dots ,H_T\right)}^{\prime }$, then ${\left(G_1,\dots ,G_{T+1}\right)}^{\prime }$ and ${\left(F_1,\dots ,F_{T+1}\right)}^{\prime }$.

The expanded matrix representation is as follows, where the new columns are marked in bold:

$$\left(\begin{array}{ccc}{\mathbf{H}}_{\mathbf{5}}& & \\ {\mathbf{H}}_{\mathbf{1}}& {\mathbf{G}}_{\mathbf{5}}& \\ {\mathbf{H}}_{\mathbf{2}}& {\mathbf{H}}_{\mathbf{1}}& {\mathbf{F}}_{\mathbf{5}}\\ {\mathbf{H}}_{\mathbf{3}}& {\mathbf{H}}_{\mathbf{2}}& {\mathbf{H}}_{\mathbf{1}}& H_4\\ {\mathbf{H}}_{\mathbf{4}}& {\mathbf{H}}_{\mathbf{3}}& {\mathbf{H}}_{\mathbf{2}}& H_1& G_4\\ {\mathbf{G}}_{\mathbf{1}}& {\mathbf{H}}_{\mathbf{4}}& {\mathbf{H}}_{\mathbf{3}}& H_2& H_1& F_4\\ {\mathbf{G}}_{\mathbf{2}}& {\mathbf{G}}_{\mathbf{1}}& {\mathbf{H}}_{\mathbf{4}}& H_3& H_2& H_1& H_3\\ {\mathbf{G}}_{\mathbf{3}}& {\mathbf{G}}_{\mathbf{2}}& {\mathbf{G}}_{\mathbf{1}}& G_1& H_3& H_2& H_1& G_3\\ {\mathbf{G}}_{\mathbf{4}}& {\mathbf{G}}_{\mathbf{3}}& {\mathbf{G}}_{\mathbf{2}}& G_2& G_1& H_3& H_2& H_1& F_3\\ {\mathbf{G}}_{\mathbf{5}}& {\mathbf{G}}_{\mathbf{4}}& {\mathbf{G}}_{\mathbf{3}}& G_3& G_2& G_1& G_1& H_2& H_1& H_2\\ {\mathbf{F}}_{\mathbf{1}}& {\mathbf{F}}_{\mathbf{1}}& {\mathbf{G}}_{\mathbf{4}}& G_4& G_3& G_2& G_2& G_1& H_2& H_1& G_2\\ {\mathbf{F}}_{\mathbf{2}}& {\mathbf{F}}_{\mathbf{2}}& {\mathbf{F}}_{\mathbf{1}}& F_1& F_1& G_3& G_3& G_2& G_1& G_1& H_1& F_2\\ {\mathbf{F}}_{\mathbf{3}}& {\mathbf{F}}_{\mathbf{3}}& {\mathbf{F}}_{\mathbf{2}}& F_2& F_2& F_1& F_1& F_1& G_2& G_2& G_1& H_1& H_1\\ {\mathbf{F}}_{\mathbf{4}}& {\mathbf{F}}_{\mathbf{4}}& {\mathbf{F}}_{\mathbf{3}}& F_3& F_3& F_2& F_2& F_2& F_1& F_1& F_1& G_1& G_1& G_1\\ {\mathbf{F}}_{\mathbf{5}}& {\mathbf{F}}_{\mathbf{5}}& {\mathbf{F}}_{\mathbf{4}}& F_4& F_4& F_3& F_3& F_3& F_2& F_2& F_2& F_1& F_1& F_1& F_1\end{array}\right).$$

We also expand the matrix of copulas by adding three columns to the left of (6), as follows:

$$\left(\begin{array}{c}*\\ \mathbf{0}& *& \\ \mathbf{0}& \mathbf{0}& *\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& *\\ {\mathbf{C}}_{\mathbf{1}}^{\mathbf{H}}& \mathbf{0}& \mathbf{0}& 0& *\\ \mathbf{0}& {\mathbf{C}}_{\mathbf{1}}^{\mathbf{HG}}& \mathbf{0}& 0& 0& *\\ \mathbf{0}& \mathbf{0}& {\mathbf{C}}_{\mathbf{1}}^{\mathbf{HF}}& C_1^H& 0& 0& *\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& 0& C_1^{HG}& 0& 0& *\\ {\mathbf{C}}_{\mathbf{1}}^{\mathbf{GH}}& \mathbf{0}& \mathbf{0}& 0& 0& C_1^{HF}& C_1^H& 0& *\\ {\mathbf{C}}^{\mathbf{GH}}& {\mathbf{C}}_{\mathbf{1}}^{\mathbf{G}}& \mathbf{0}& C_1^{GH}& 0& 0& 0& C_1^{GH}& 0& *\\ \mathbf{0}& \mathbf{0}& {\mathbf{C}}_{\mathbf{1}}^{\mathbf{GF}}& C^{GH}& C_1^G& 0& C_1^{GH}& 0& C_1^{HF}& C_1^H& *\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& 0& 0& C_1^{GF}& C^{GH}& C_1^G& 0& C_1^{GH}& C_1^{GH}& *\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& 0& 0& 0& 0& 0& C_1^{GF}& C^{GH}& C_1^G& C_1^{HF}& *\\ {\mathbf{C}}_{\mathbf{1}}^{\mathbf{FH}}& {\mathbf{C}}_{\mathbf{1}}^{\mathbf{FG}}& \mathbf{0}& C_1^{FH}& C_1^{FG}& 0& C_1^{FH}& C_1^{FG}& 0& C_1^{FH}& C_1^{FG}& C_1^{GF}& C^{GH}& *\\ {\mathbf{C}}^{\mathbf{FH}}& {\mathbf{C}}^{\mathbf{FG}}& {\mathbf{C}}_{\mathbf{1}}^{\mathbf{F}}& C^{FH}& C^{FG}& C_1^F& C^{FH}& C^{FG}& C_1^F& C^{FH}& C^{FG}& C_1^F& C^{FH}& C^{FG}& *\end{array}\right).$$

Thus, the three new columns are just replications of the previous three columns by expanding the uninterrupted sequences of zeros with an additional zero.

5. Empirical Application

The idea to model asset returns with factors arising from some observed data and idiosyncratic components is quite popular in modern finance theory. The most prominent example is the capital asset-pricing model (CAPM) of Sharpe (1964), Litner (1965), Mossin (1966), and Treynor (2012), which is a one-factor model with the market return as the only common driver of asset prices. Another well-known approach is the arbitrage pricing theory (APT) of Ross (1976). In this case, a multi-factor model describes the return of an asset as the sum of an asset-specific return, an exposure to systematic risk factors, and an error term. A third example is Stock and Watson (2002a), who extracted factors from a large number of predictors to forecast the log-returns of the Federal Reserve Board’s Index of Industrial Production. Ando and Bai (2014) provide further empirical evidence that stock returns are related to macro- and microeconomic factors. In this section, latent factors from U.S. macroeconomic data are extracted and then used for portfolio optimization. We consider 35 assets from S&P 500, which are classified as “Industrials” according to Global Industry Classification Standard. We assume that the estimated factors have the most prediction power for these assets.

The U.S. panel data includes such economic indicators as government bond yields along the curve, currency index, main commodity prices, indicators of money stock, inflation, consumer consumption, and industrial production gauges. Altogether, we have 22 time series listed in Appendix B. Each series contains monthly data from 31 January 1986 to 30 November 2016, 371 data points in total. Next, we split the panel data into financial and macroeconomic groups according to

Table A2. U.S. financial indicators.

Indicator	Description	Transformation	Source
USA Treasury 3 m	Yield of U.S. government bonds with maturity of 3 months	Monthly change	FRED
USA Treasury 1y	Yield of U.S. government bonds with maturity of 1 year	Monthly change	FRED
USA Treasury 2y	Yield of U.S. government bonds with maturity of 2 years	Monthly change	FRED
USA Treasury 3y	Yield of U.S. government bonds with maturity of 3 years	Monthly change	FRED
USA Treasury 5y	Yield of U.S. government bonds with maturity of 5 years	Monthly change	FRED
USA Treasury 7y	Yield of U.S. government bonds with maturity of 7 years	Monthly change	FRED
USA Treasury 10y	Yield of U.S. government bonds with maturity of 10 years	Monthly change	FRED
Gold	Gold Fixing Price 10:30 A.M. (London time) in London Bullion Market, based in U.S. Dollars.	Return	FRED
WTI Crude	Crude Oil Prices: West Texas Intermediate (WTI)—Cushing, Oklahoma.	Return	FRED

and

Table A3. U.S. macroeconomical indicators.

Indicator	Description	Transformation	Source
M1 U.S.	Narrow money (M1) includes currency, i.e., banknotes and coins, as well as balances which can immediately be converted into currency or used for cashless payments, i.e., overnight deposits.	Return	FRED
M2 U.S.	“Intermediate” money (M2) comprises narrow money (M1) and, in addition, deposits with a maturity of up to two years and deposits redeemable at a period of notice of up to three months.	Return	FRED
Unemployment	Unemployment rate	Return	FRED
CPI	Consumer Price Index (CPI) measures changes in the price level of a market basket of consumer goods and services purchased by households.	Return	FRED
PPI	Producer Price Index (PPI) measures the average changes in prices received by domestic producers for their output	Return	FRED
PCE	Measures goods and services purchased by U.S. residents	Return	FRED
Personal saving rate	Personal saving as a percentage of disposable personal income (DPI), frequently referred to as “the personal saving rate,” is calculated as the ratio of personal saving to DPI.	Return	FRED
Payrolls	All Employees: Total Nonfarm Payrolls.	Return	FRED
Unemployment	Unemployment	Return	FRED
Initial claims	Initial claims	Return	FRED
Housing Starts	Housing Starts	Return	FRED
Capacity utilization	Capacity utilization	Return	FRED
Dollar Index	Trade Weighted U.S. Dollar Index	Return	FRED

in Appendix B. In the sequel, each time series is transformed in order to eliminate trends and achieve its stationarity. Table A2 and Table A3 in Appendix B also contain information on considered data transformations. Further, we consider three factor models: separately for the two groups of the panel data, and one joint model for all monthly indicators. Thereby, we aim to illustrate that modeling nonlinear dependence between estimated factors of different groups of panel data with COPAR may lead to a better asset allocation.

We consider the following three DFMs for $i=fin,macro,all$:

$$\begin{array}{ccc}\hfill {\mathit{X}}_t^{\left(i\right)}& =& {\Lambda }^{\left(i\right)}{\mathit{F}}_t^{\left(i\right)}+{\mathit{\epsilon }}_t^{\left(i\right)}\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill {\mathit{F}}_t^{\left(i\right)}& =& A^{\left(i\right)}{\mathit{F}}_{t-1}^{\left(i\right)}+{\mathit{u}}_t^{\left(i\right)},\hfill \end{array}$$

(8)

where ${\mathit{X}}_t^{\left(i\right)}\in {\mathbb{R}}^{m_i\times 1}$ collects observed macroeconomic data and ${\mathit{F}}_t^{\left(i\right)}\in {\mathbb{R}}^{q_i\times 1}$ is the vector of factors. The dimension $m_i$ of the panel data for $i=fin,macro$ and $all$ is equal to $9,13$ and 22, respectively.

In the first step, we estimate three DFMs—one for each group (macro and financial) and for the full panel data. The starting time frame is from January 1986 to December 2005, and expands successively by one month until November 2016 is reached. For the three DFMs, we apply the EM-Algorithm from Section 2 to the panel data from each expanding time window and obtain a monthly sequence of estimated factors for each month of the considered time period. For $i=fin,macro$, and $all$, the EM-Algorithm requires the factor dimension $q_i$, which is not known. In what follows, we perform the model selection for the factor dimension.

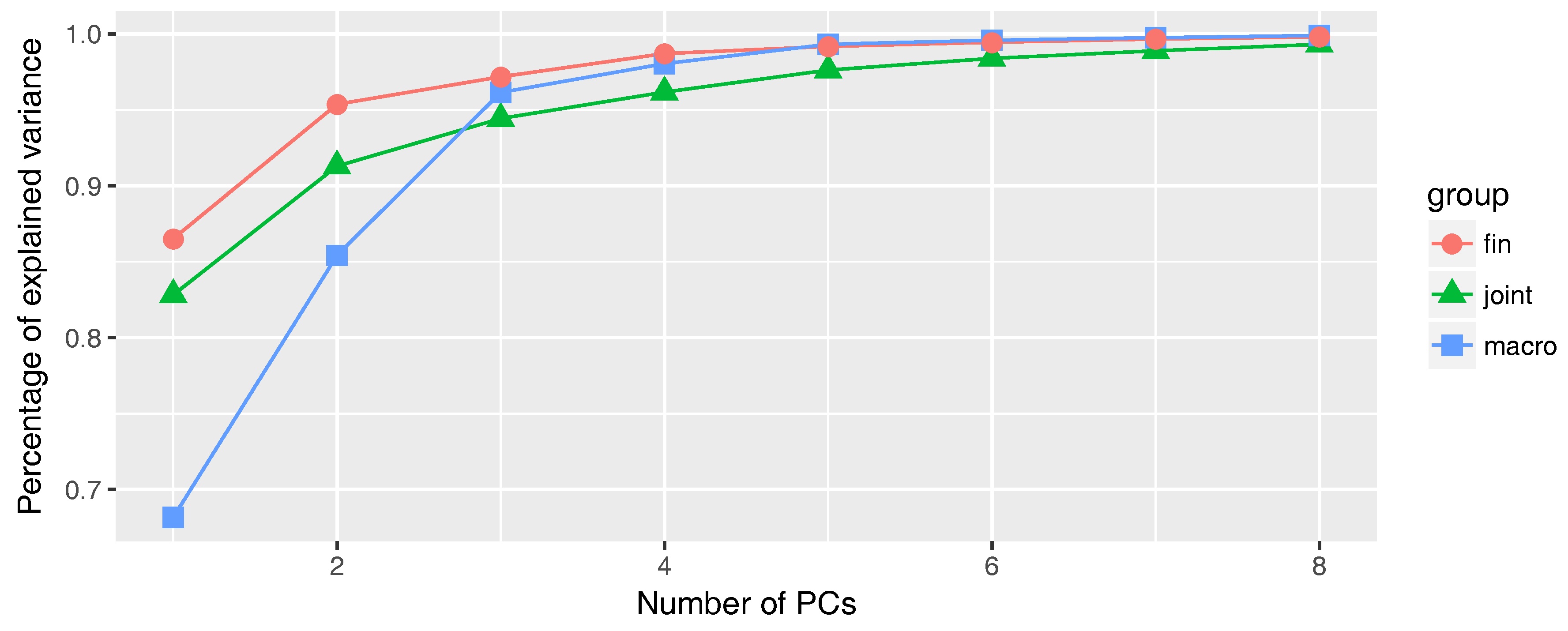
The dimension of factors is selected using principal components analysis (see Jolliffe 2002). We choose the number of principal components (PCs) such that we capture more than 95% of the empirical data variance, based on the initial time frame from January 1986 to December 2005. Figure 4 illustrates the fraction of variance captured by eight or fewer PCs for the considered time window. Thus, two factors are sufficient for the financial group to capture 95.4% of the corresponding data variability. For macroeconomic indicators, we need three factors (96.5% of variability), while four factors are enough for the whole panel data (96.2% of variability).

In general, the latent factors of DFMs may follow a VAR model of order p. Initiated by a referee’s comment, we also consider autoregressive order $p=2$ for the joint DFM with all monthly indicators and compare its forecasting performance for $p=1$ and $p=2$. Our decision criterion is based on the root-mean-square error (RMSE) of point predictions defined for univariate observations $x_1,\dots ,x_{T^{*}}$ as

$$RMSE=\sqrt{\frac{{\sum }_{t=1}^{T^{*}}{\left(x_t-{\widehat{x}}_t\right)}^2}{T^{*}}},$$

where ${\widehat{x}}_1,\dots ,{\widehat{x}}_{T^{*}}$ are predicted values. Thus, we compute the RMSE for each time series and take their average value. Thereby, our first prediction is done for January 2006 and ends in November 2016, resulting in 131 point forecasts. The averaged values of the RMSE for $p=1$ and for $p=2$ are $0.0302$ and $0.0306$, respectively. Therefore, our initial choice of $p=1$ is justified.

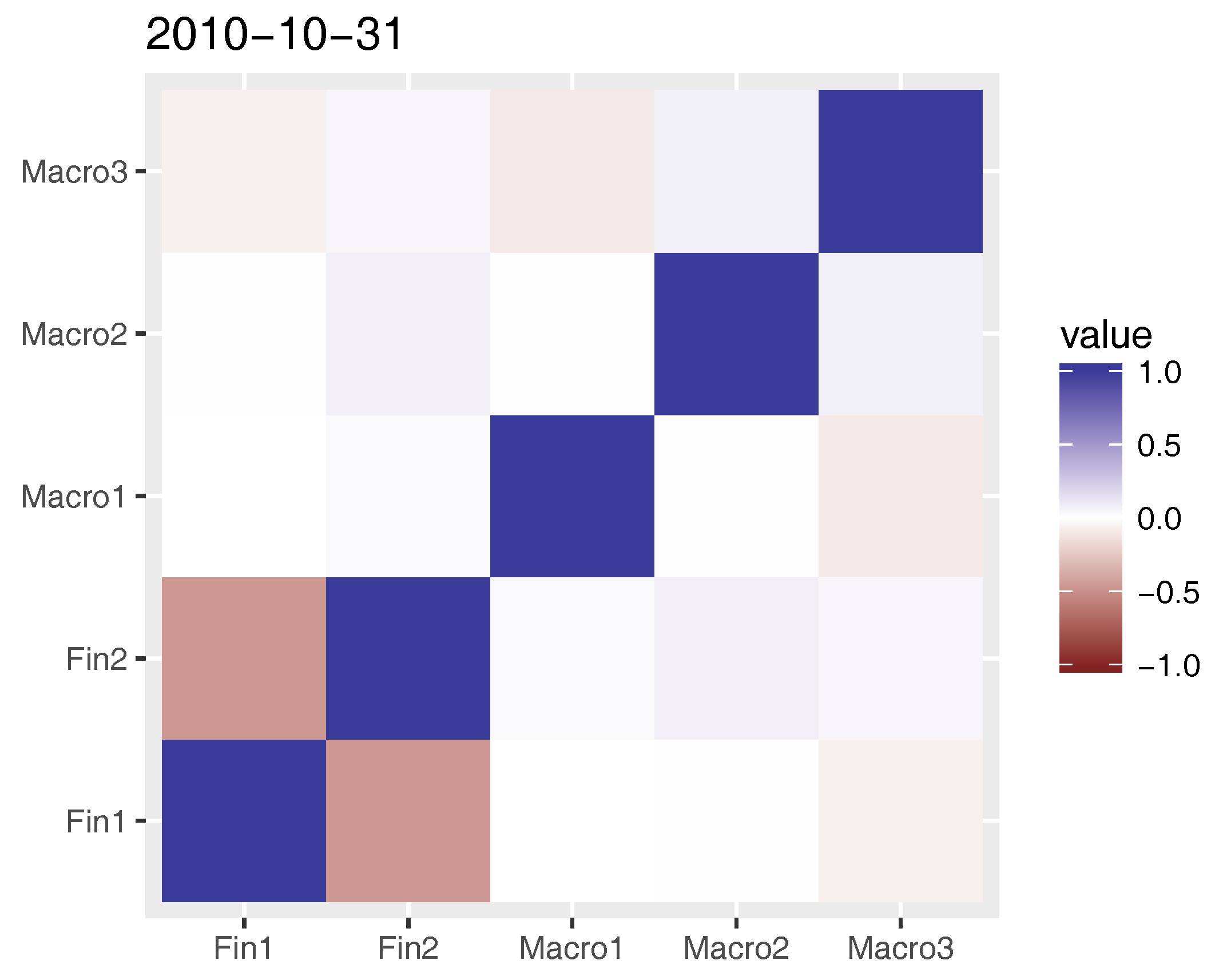
Figure 5 illustrates the correlation coefficients of the financial and macro factors filtered from data up to October 2010. The estimated factors show some moderate linear dependence within groups and a weak linear dependence between groups. Note that dynamic factor models assume factors to be multivariate normally distributed. Nevertheless, the estimated factors could exhibit non-Gaussian dependence, which we aim to capture using the COPAR model.

To improve the joint forecasting of asset returns at month t, for a subsequent month, we link the two factor models; namely, we capture the dependence structure of the estimated factors with a COPAR model. Thereby, we combine the estimated factors from two groups as a single five-dimensional vector for each data time window. We put the financial factors first, then the macroeconomic. Using fitted marginal normal distribution functions, the filtered factors are translated to copula data.

We consider a COPAR(1) model, since the transition equation of the DFMs is supposed to be a VAR(1). Further, Brechmann and Czado (2015) discuss a sophisticated copula family selection procedure for two time series. Here, we follow a more simple approach consisting of three steps. In the first step, the selection of copulas for contemporaneous cross-sectional dependence of the filtered factors is done by neglecting serial dependence. Note that the cross-sectional dependence is described by a C-vine with fixed order of variables. Therefore, we only have to select copula families of pair-copulas. Thus, we consider the estimated five-dimensional factors as iid data and perform sequential selection of copula families for each pair-copula using Akaike information criterion. Copula families for the pair-copulas associated with the first tree of the C-vine are selected first, then with the second tree, and so on. For more details on model selection for C-vines, we refer to Czado et al. (2012). Equation (9) presents the selected copula families for cross-sectional dependence in R-vine matrix notation until December 2005 (for copula families in (9), see Appendix C):

$$\begin{array}{ccc}\hfill \mathrm{Families}& =& \left(\begin{array}{c}*\\ 2& *\\ 5& 2& *\\ 16& 3& 2& *\\ 16& 2& 36& 2& *\end{array}\right).\hfill \end{array}$$

(9)

It is remarkable that none of the selected copula families in (9) is Gaussian. Moreover, only 0.5% of families selected for cross-sectional dependence for all expending time windows are the Gaussian copula.

In the second step, we use the Gaussian copulas as conditional pair-copulas to model the temporal dependence of the filtered factors. Note that this simple approach does not imply that the joint distribution of the time-shifted factors is Gaussian except for the first component of ${\mathit{F}}_t^{\left(fin\right)}$; i.e., $F_{1,t_1}^{\left(fin\right)},F_{1,t_2}^{\left(fin\right)},\dots ,F_{1,t_k}^{\left(fin\right)}$. Non-Gaussian pair-copulas for cross-sectional dependence destroy the Gaussianity of the time-shifted factors, and only the joint distribution of the first component of ${\mathit{F}}_t^{\left(fin\right)}$ remains Gaussian. In the third step, the R-vine matrix of the COPAR(1) model for the estimated factors ${\left({\mathit{F}}_t^{{\left(fin\right)}^{\prime }},{\mathit{F}}_t^{{\left(macro\right)}^{\prime }}\right)}^{\prime }$ is constructed, and the maximum likelihood estimation is performed. Copula selection and parameter estimation of the COPAR model for the factors is done for every expanding window of data; that is, as soon as the DFMs for both groups are estimated and the latent factors are filtered out. Finally, note that we also test Granger causality between components of the multivariate time series ${\left({\mathit{F}}_t^{{\left(fin\right)}^{\prime }},{\mathit{F}}_t^{{\left(macro\right)}^{\prime }}\right)}^{\prime }$ in the whole time period, and can confirm it. For this, we regress univariate series of ${\left({\mathit{F}}_t^{{\left(fin\right)}^{\prime }},{\mathit{F}}_t^{{\left(macro\right)}^{\prime }}\right)}^{\prime }$ on the lagged values of ${\left({\mathit{F}}_{t-1}^{{\left(fin\right)}^{\prime }},{\mathit{F}}_{t-1}^{{\left(macro\right)}^{\prime }}\right)}^{\prime }$.

Table A11. Summary of linear regressions for testing Granger causality. Columns contain estimate of regression coefficients, and their standard errors are given in brackets.

	Dependent Variable:
	y
	${\mathit{F}}_{\mathbf{1},\mathit{t}}^{\mathit{fin}}$	${\mathit{F}}_{\mathbf{2},\mathit{t}}^{\mathit{fin}}$	${\mathit{F}}_{\mathbf{1},\mathit{t}}^{\mathit{macro}}$	${\mathit{F}}_{\mathbf{2},\mathit{t}}^{\mathit{macro}}$	${\mathit{F}}_{\mathbf{3},\mathit{t}}^{\mathit{macro}}$
	(1)	(2)	(3)	(4)	(5)
$F_{1,t-1}^{fin}$	0.216 ***	0.655 ***	−0.189 ***	0.076	−0.094 *
	(0.054)	(0.060)	(0.053)	(0.056)	(0.055)
$F_{2,t-1}^{fin}$	0.086 **	0.214 ***	0.052	−0.056	0.048
	(0.041)	(0.045)	(0.040)	(0.042)	(0.042)
$F_{1,t-1}^{macro}$	0.076	0.009	−0.385 ***	0.037	−0.104 **
	(0.047)	(0.052)	(0.046)	(0.048)	(0.048)
$F_{2,t-1}^{macro}$	0.077 *	−0.006	0.020	−0.456 ***	0.024
	(0.046)	(0.051)	(0.045)	(0.047)	(0.047)
$F_{3,t-1}^{macro}$	−0.009	0.065	0.192 ***	−0.045	−0.554 ***
	(0.043)	(0.047)	(0.042)	(0.044)	(0.044)
Constant	0.003	0.002	−0.0005	0.003	0.0002
	(0.052)	(0.058)	(0.051)	(0.054)	(0.053)
Observations	369	369	369	369	369
R${}^2$	0.093	0.369	0.236	0.215	0.315
Adjusted R${}^2$	0.080	0.360	0.225	0.204	0.305
Residual Std. Error (df = 363)	1.003	1.109	0.981	1.030	1.026
F Statistic (df = 5; 363)	7.428 ***	42.464 ***	22.408 ***	19.893 ***	33.339 ***

Note: * p-value < 0.1; ** p-value < 0.05; *** p-value < 0.01.

in Appendix F summarizes all five linear regressions. For example, the first component of ${\left\{{\mathit{F}}_t^{\left(fin\right)}\right\}}_{t=1,\dots ,T}$ Granger causes almost all other univariate time series at least at $10\%$ of significance level with the exception of the second component of ${\left\{{\mathit{F}}_t^{\left(macro\right)}\right\}}_{t=1,\dots ,T}$.

Next, we present a conditional method for forecasting using COPAR, which follows Brechmann and Czado (2015) with a small modification. For a prediction time point, we simulate factors from the estimated COPAR model, but conditioned on the past values of the factors. The sampled factors are further used to forecast assets returns and to construct an optimal mean-variance portfolio. Since we assume an autoregressive order of one, it is enough to condition only on the last value of factors; i.e., we condition only on ${{\widehat{\mathit{F}}}_T}^{\left(fin\right)}$ and ${{\widehat{\mathit{F}}}_T}^{\left(macro\right)}$ to make a forecast for time point $T+1$. The full algorithm for both markets is given in Algorithm 1, employing notation ${\overline{\mathit{F}}}_{1:0,t}=\varnothing$.

Algorithm 1: Conditional method of forecasting using COPAR.

Estimate COPAR model based on the first T observations and get factor estimates ${\widehat{\mathit{F}}}_t={\left({{\widehat{\mathit{F}}}_t}^{{\left(fin\right)}^{\prime }},{{\widehat{\mathit{F}}}_t}^{{\left(macro\right)}^{\prime }}\right)}^{\prime }$ ; Set $j=1$; Repeat the following steps (a) If $j=q+1$ then Stop; (b) Determine the estimated conditional density of $F_{j,T+1}\mid {\widehat{\mathit{F}}}_{1:q,T},{\overline{\mathit{F}}}_{1:(j-1),T+1}$ on the equidistant grid on $(0,1)$ with step $\Delta ={10}^{-4}$, i.e., for $u=\frac{n}{10000}$, $n=1,\dots ,9999$; $$\frac{c\left({\mathsf{\Phi }}_1\left({\overline{F}}_{1,T+1}\right),\dots ,{\mathsf{\Phi }}_{j-1}\left({\overline{F}}_{j-1,T+1}\right),u,{\mathsf{\Phi }}_1\left({\widehat{F}}_{1,T}\right),\dots ,{\mathsf{\Phi }}_q\left({\widehat{F}}_{q,T}\right)\right)}{f\left({\overline{F}}_{1,T+1},\dots ,{\overline{F}}_{j-1,T+1},{\widehat{F}}_{1,T},\dots ,{\widehat{F}}_{q,T}\right)}$$ $$·\prod _{k=1}^{j-1}{\varphi }_k\left({\overline{F}}_{k,T+1}\right)·{\varphi }_j\left({\mathsf{\Phi }}_j^{-1}\left(u\right)\right)·\prod _{k=1}^q{\varphi }_k\left({\widehat{F}}_{k,T}\right),$$ where ${\varphi }_k$ and ${\mathsf{\Phi }}_k$ are the estimated Gaussian density and distribution function of latent factor $F_{k,t}^{\left(i\right)}$; (c) Determine the estimated conditional cumulative distribution function on the above grid; (d) Simulate 10,000 ${\tilde{F}}_{j,T+1}$ from the estimated conditional cumulative distribution function and set forecast ${\overline{F}}_{j,T+1}$ to their empirical mean; (e) Set $j=j+1$ and go to (a);

To illustrate the idea behind this method, we consider a small-scale example of two variables $G_t$ and $H_t$. Let us assume that we observe some values of these two random variables at time point t; i.e., $G_t={\widehat{G}}_t$, $H_t={\widehat{H}}_t$. We want to find the distribution of $G_{t+1}$ and $H_{t+1}$ conditioned on the observed values that we have observed. For this purpose, we consider the decomposition of the conditional distribution of $G_{t+1},H_{t+1}\mid G_t={\widehat{G}}_t,H_t={\widehat{H}}_t$ given by

$$\begin{array}{c}F\left(G_{t+1},H_{t+1}\mid G_t={\widehat{G}}_t,H_t={\widehat{H}}_t\right)\hfill \\ \hfill =F\left(G_{t+1}\mid G_t={\widehat{G}}_t,H_t={\widehat{H}}_t\right)F\left(H_{t+1}\mid G_t={\widehat{G}}_t,H_t={\widehat{H}}_t,G_{t+1}={\overline{G}}_{t+1}\right),\end{array}$$

where ${\overline{G}}_{t+1}$ is some forecast. One has a free choice for forecast methods for $G_{t+1}$. As Brechmann and Czado (2015), we opt for the conditional mean estimated by the sample mean. Next, we first estimate the conditional density, and then, the conditional distribution function. For this simple case of two variables $G_t$ and $H_t$, the estimated density $\widehat{f}$ of $G_{t+1}\mid G_t={\widehat{G}}_t,H_t={\widehat{H}}_t$ on a grid from 0 to 1 with step 0.0001 is estimated. Then, we search for the estimated distribution function $\widehat{F}$. With $\widehat{f}$ and $\widehat{F}$, one can estimate the mean.

In the next step, we use the estimated factors to model the asset returns of 35 industrial stocks from S&P 500 and the sampled factors to construct an optimal portfolio in the mean-variance framework for each expanding time window starting from January 2006 up to November 2016. We consider and estimate the following model for each asset return $j=1,\dots ,35$:

$$r_{j,t}={\alpha }_{j,0}+{\alpha }_{j,1}{r}_{j,t-1}+{\Gamma }_j^{\prime }{\widehat{\mathit{F}}}_t+v_{j,t},$$

(10)

where the constants ${\alpha }_{j,0}$, ${\alpha }_{j,1}$, and the vector ${\Gamma }_j$ constitute unknown regression parameters and the errors $v_{j,t}$ are assumed to be iid Gaussian with respect to t. The error terms $v_{j,t}$ are assumed to be independent across j due to the dimensionality of the error covariance matrix. Moreover, we treat all linear regression separately for each asset j due to the dimensionality of regression parameters and couple them with the common estimated factors. In Section 2, we have pointed out that the estimated factors are unique up to a rotation with an orthogonal matrix R; i.e., $R{R}^{\prime }=R^{\prime }R$ is an identity matrix. Since ${\Gamma }_j^{\prime }\widehat{{\mathit{F}}_t}={\Gamma }_j^{\prime }{R}^{\prime }R{\widehat{\mathit{F}}}_t$ holds, the impact of the rotated and unrotated estimated factors together with their regression coefficients on asset returns remains the same.

To construct an optimal portfolio in the mean-variance framework, we determine portfolio weights $\mathbf{w}$ at month t by solving the following optimization problem with respect to $\mathbf{w}$:

$$\begin{array}{c}max{\mathbf{w}}^{\prime }·\mathbb{E}\left[{\mathbf{r}}_{t+1}\right]\\ s.t.\\ 1^T·\mathbf{w}=1,\mathbf{w}\ge 0,\\ {\mathbf{w}}^{\prime }·\mathbb{V}ar\left[{\mathbf{r}}_{t+1}\right]·\mathbf{w}\le {\sigma }_{monthly}^2,\end{array}$$

where ${\mathbf{r}}_t={(r_{1,t},\dots ,r_{35,t})}^{\prime }$ is a vector of asset returns at t, $\mathbb{E}\left[{\mathbf{r}}_{t+1}\right]$ and $\mathbb{V}ar\left[{\mathbf{r}}_{t+1}\right]$ are the expectation and covariance matrix of ${\mathbf{r}}_{t+1}$. Thus, our optimal portfolio does not allow short-selling.

Since $\mathbb{E}\left[{\mathbf{r}}_{t+1}\right]$ and $\mathbb{V}ar\left[{\mathbf{r}}_{t+1}\right]$ are unknown at month t, we estimate them with four different methods, resulting in four portfolios. The first portfolio is the COPAR portfolio, which is constructed using asset returns modeled with (10). In this case, $\mathbb{E}\left[{\mathbf{r}}_{t+1}\right]$ and $\mathbb{V}ar\left[{\mathbf{r}}_{t+1}\right]$ are empirically estimated at time point t based on 10,000 sampled factors from the COPAR model and 10,000 sampled errors from the estimated univariate Gaussian distribution. The second portfolio is the DFM portfolio similarly constructed with sampled factors from the estimated stationary distribution (1) for (7)–(8) and $i=all$ (i.e., the DFM for the full panel data). The third portfolio—called independent DFM—uses sampled factors from the estimated stationary distribution (1) for (7)–(8) and $i=fin,macro$; i.e., assets returns are driven by ${\left({\mathit{F}}_t^{{\left(fin\right)}^{\prime }},{\mathit{F}}_t^{{\left(macro\right)}^{\prime }}\right)}^{\prime }$. The fourth portfolio is the historical portfolio, which employs the empirical mean and covariance matrix based on the data up to time t. We consider the historical portfolio as a benchmark. Finally note that the comparison of these four portfolios enables the assessment of the economic relevance of factors.

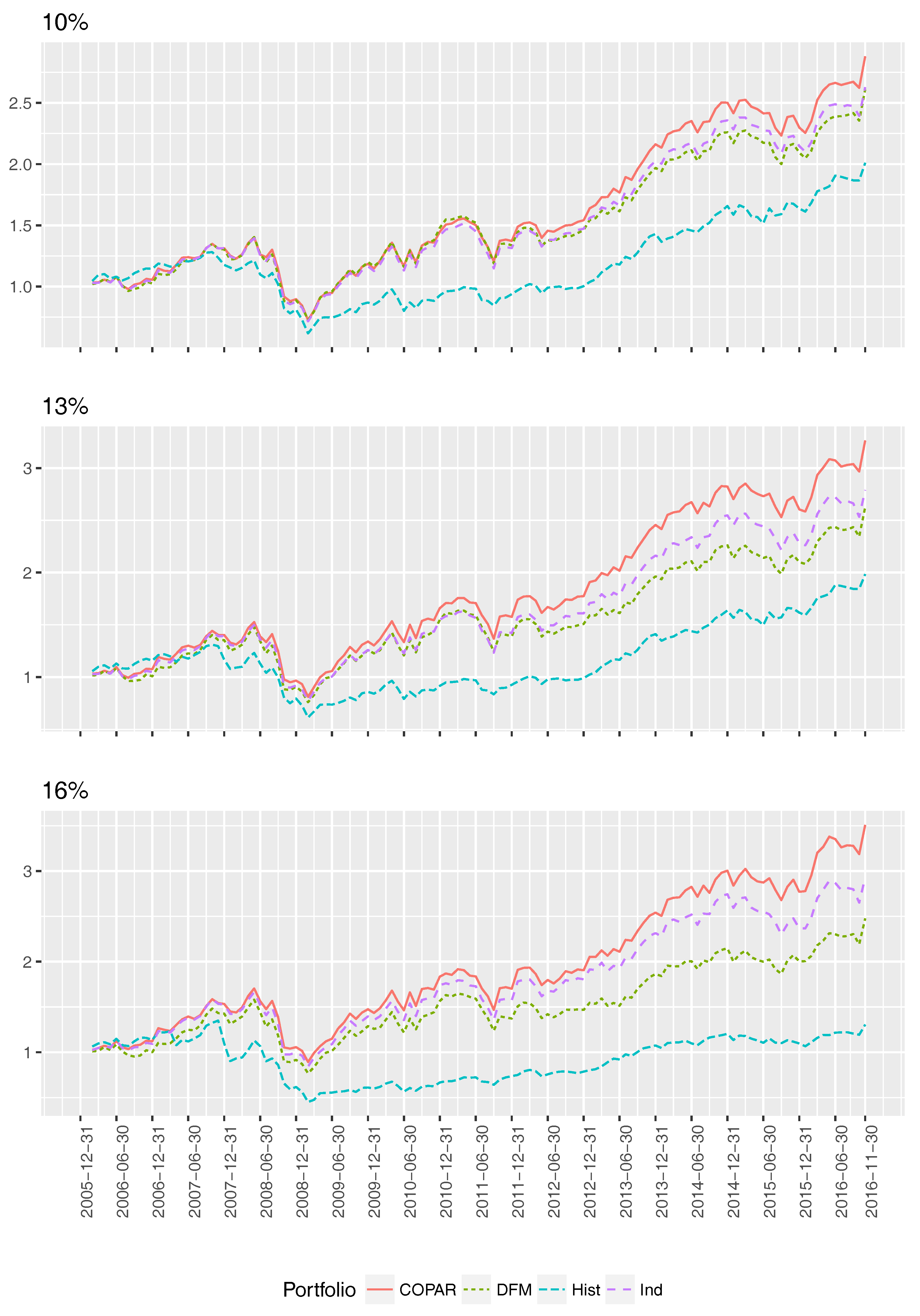
For the above mean-variance optimization problem, we choose three monthly volatilities ${\sigma }_{monthly}=2.89\%,3.75\%,4.62\%$, which correspond to annual volatilities of $\sigma =10\%,13\%,16\%$. These choices of $\sigma$’s are practically reasonable, and the optimizer diversifies the portfolio for them. For higher values of $\sigma$, the optimal portfolio consists of only one stock, if no constraints on maximal weights are imposed. We start to determine an optimal portfolio for the panel data up to January 2006. Then, we sequentially expand the time window by one month and find optimal weights for the considered four portfolios and chosen level of volatilities. The performance of the four portfolios with initial investment of 1 USD during the out-of-sample time period up to November 2016 is illustrated in Figure 6.

We observe that the COPAR portfolio outperforms the DFM, independent DFM, and historical portfolios. Further, two portfolios based on DFMs deliver a higher overall return than the historical portfolio, and the independent DFM (abbreviated in Figures and Tables as ind) is preferred over the DFM portfolio.

To compare the four portfolios, we consider several portfolio performance and risk measures summarized in Appendix D. First, note that observed standard deviations of portfolio returns are higher than prespecified ones. This is natural due to the prediction error. According to the Sharpe and Omega ratio, the COPAR portfolio is preferred over all remaining portfolios. For both risk measures, the independent DFM portfolio outperforms the DFM portfolio. We explain this finding with a fortunate split of the panel data. Further, if we consider $95\%$ Value at Risk (VaR) and $95\%$ Conditional Value at Risk (CVaR), then the historical portfolio outperforms the others except for one case. For $\sigma =16\%$ and $95\%$ VaR, the COPAR portfolio is slightly superior.

To statistically assess the differences in the Sharpe ratios, we perform the Jobson–Korkie Test from Jobson and Korkie (1981). The null hypothesis of this test is that the Sharpe ratios of the two considered portfolios are equal. The normalized and centered test statistics are asymptotically Gaussian distributed with mean 0 and variance 1 under the null hypothesis. If the null hypothesis is rejected, then there is significant statistical evidence for different Sharpe ratios. Appendix E presents results of the Jobson–Korkie Test for all pairs of portfolios and $\sigma =10\%,13\%,16\%$. The COPAR portfolio significantly outperforms the independent DFM portfolio, and this advocates our approach to model estimated factors with a COPAR model. For $\sigma =10\%$ and $\sigma =13\%$, we do not see a statistically significant difference in Sharpe ratios for historical and COPAR portfolios. We explain this finding with lower standard deviations of the historical portfolio returns.

6. Conclusions and Final Remarks

This paper applies copulas to capture the dependence structure of estimated latent factors from dynamic factor models. The proposed modeling approach is especially convenient when several factor models under consideration are estimated separately. In this context, we combine the filtered latent factors with the COPAR model of Brechmann and Czado (2015), which results in a non-Gaussian dependence between the factors. The gained flexibility of the factor dependence is then used for modeling asset returns and building optimal mean-variance portfolios.

In our empirical study, we consider U.S. panel data consisting of 9 financial and 13 macroeconomic monthly observable indicators. The nature of indicators suggests the consideration of two separate dynamic factor models. We also treat a joint dynamic factor model for all indicators. Estimated factors from the considered DFMs are used to model returns of 35 industrial stocks from S&P500. Then, factors’ predictions from different models spanning almost 11 years are employed for portfolio optimization in the mean-variance framework.

Our main contribution is a performance improvement of portfolios based on DFMs. For this, we propose to capture the dependence structure of filtered factors from DFMs with a COPAR model. This allows us to sample factor forecasts from the estimated COPAR model conditionally on past values of estimated factors. The gained factor predictions are then utilized to construct an optimal mean-variance portfolio. Thus, we compare the COPAR-based portfolio with two portfolios derived from DFMs, as well as with the classical mean-variance approach utilizing empirical means and covariance matrices. For the considered panel data and industrial stocks, we observe the outperformance of the COPAR portfolio in terms of the total return, the Sharpe and Omega ratio. The superiority of the COPAR-portfolio in terms of the Sharpe ratio is even statistically significant for several portfolio comparisons.

A possible improvement of the proposed approach is its extension with a model selection criterion for a general R-vine, which best captures the cross-sectional and temporal dependence. Thus, one departs from the COPAR model and generalizes it as well as the copula based multivariate time series models of Beare and Seo (2015) and Smith (2015). In general, one can completely revise our approach and alternatively develop dynamic versions of copula factor models as proposed by Krupskii and Joe (2013) and Oh and Patton (2017) for iid data. The first methodology in this direction is provided by Oh and Patton (2016), who capture cross-sectional dependence with time-varying copulas. These points are the subject of further research.