Between Institutions and Global Forces: Norwegian Wage Formation Since Industrialisation †
Abstract
:In the days of Manchester liberalism, the wage contract was a matter between the individual worker and employer. Any “wage policies”, either by the society or by the organizations, were non-existent. Luckily, this has been changed.Ragnar Frisch (Arbeiderbladet 30 August 1945) [1].
1. Introduction
2. A Century Plus of Labour Market Change
2.1. The Norwegian Economy at the Start of the 20th Century
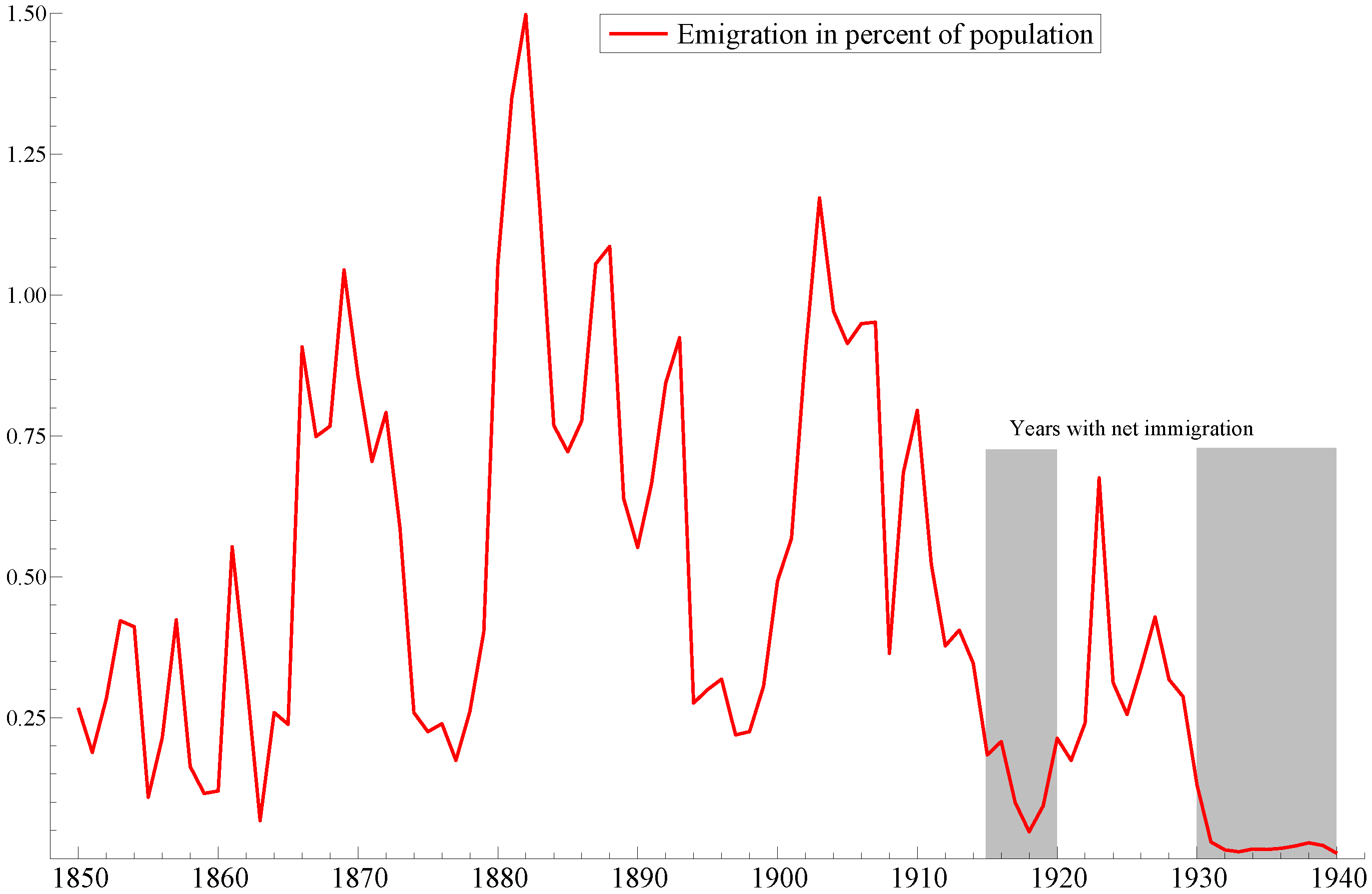
2.2. The End of Mass Emigration
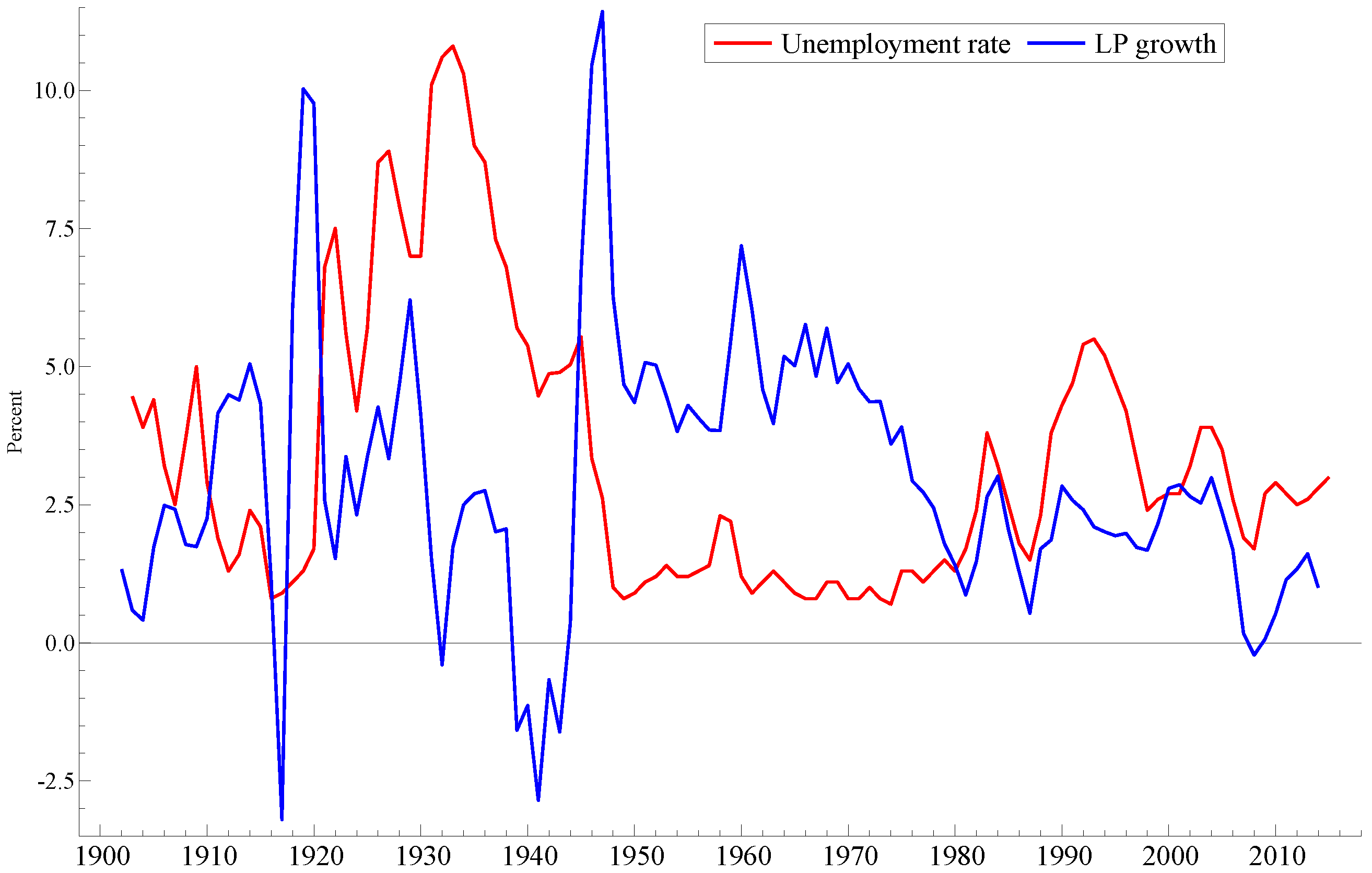
2.3. Unemployment and Productivity
2.4. Labour Market Regulation
2.5. Coordination
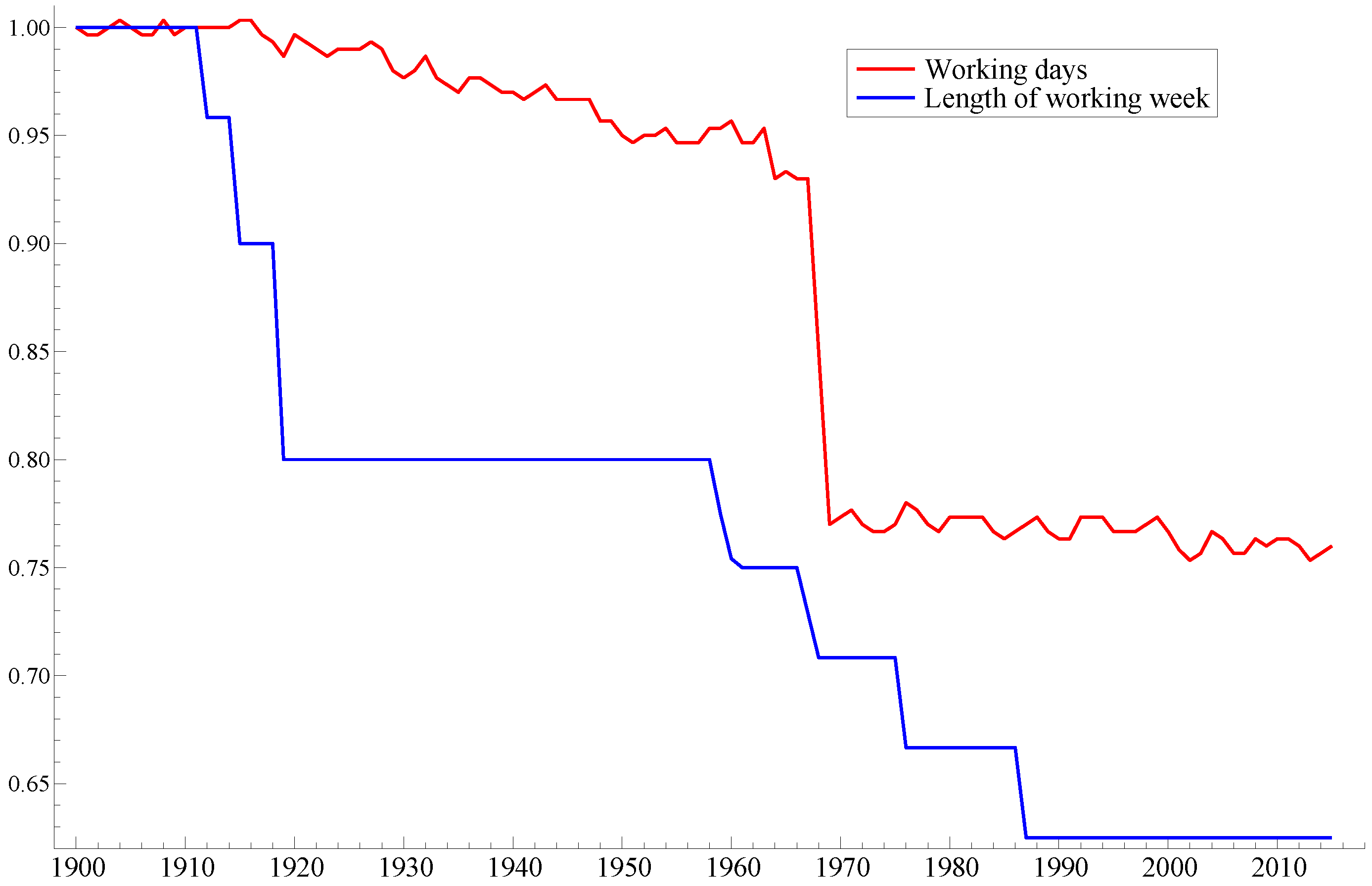
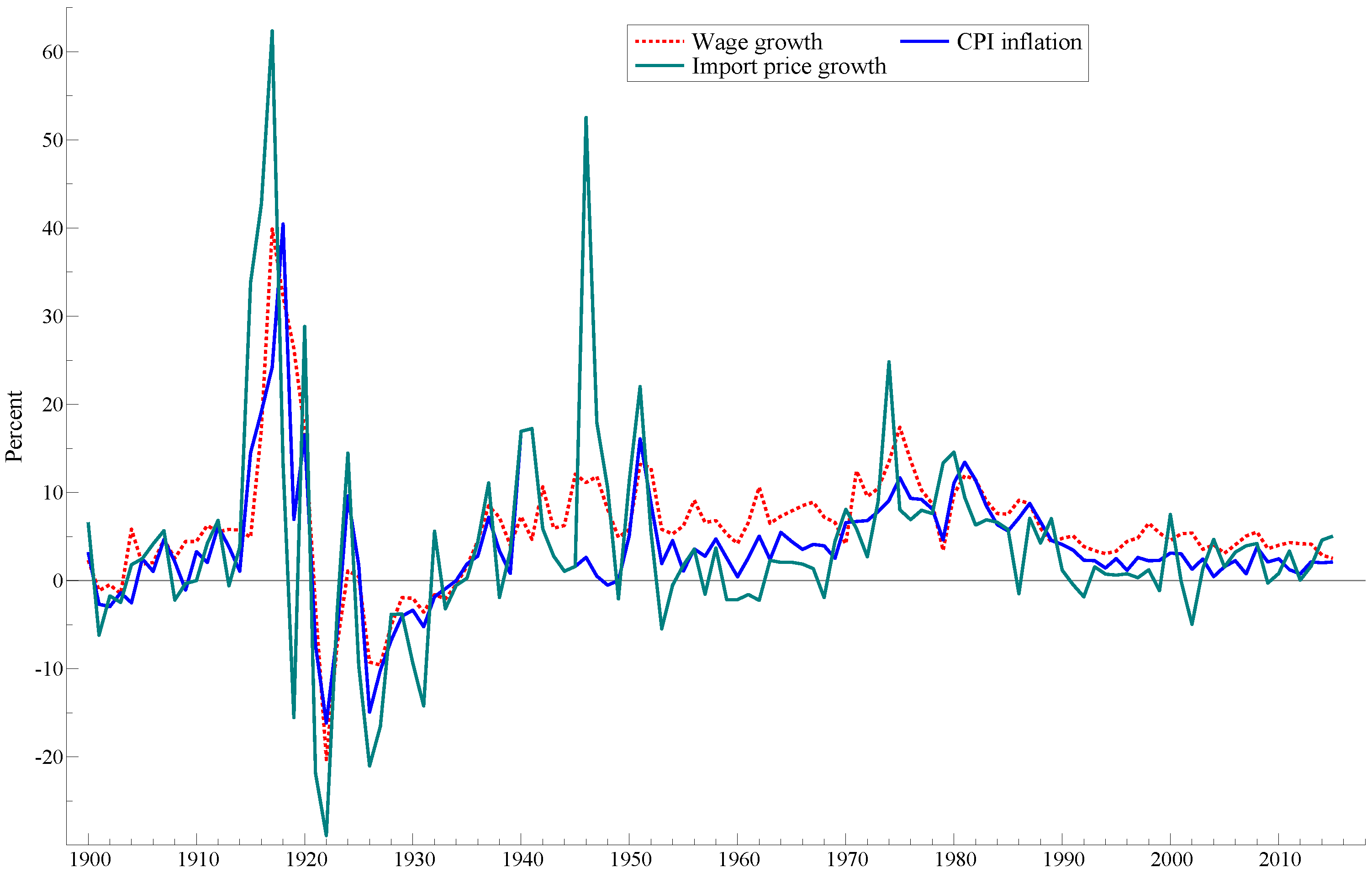
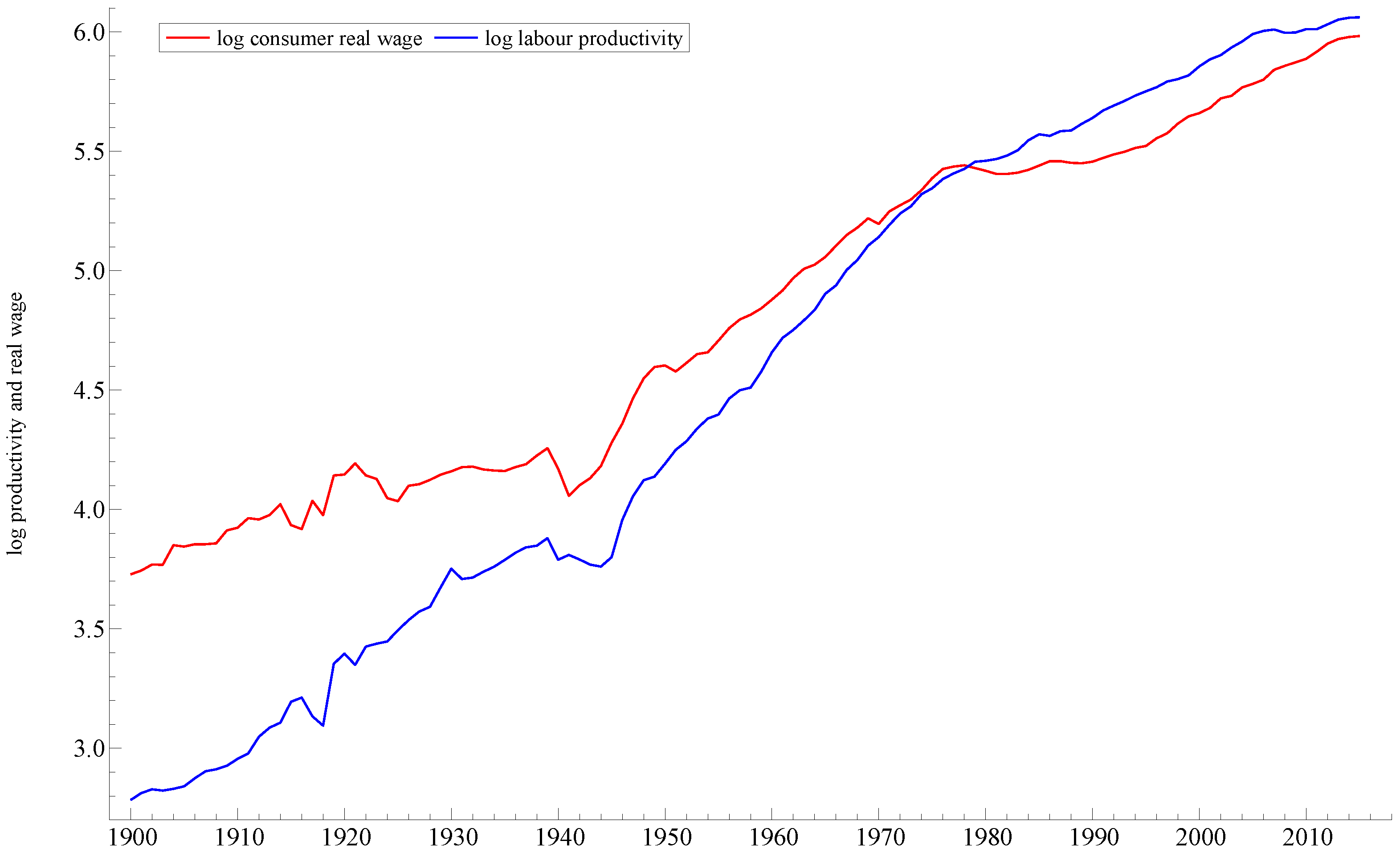
2.6. Development of Working Time and Wages
3. Modelling: Theory
3.1. Theory of Wages and the Development of Wage Modelling
At the same time as we find it challenging to determine wages theoretically, we also observe that actual wage bargains are struck year after year, and that they are rationalized by considerations of profits, actual and required (to attract investments), cost of living and relative wages (fairness). These observed regularities, that were documented early by for example Dunlop (1944) [65], give reason to believe that wage formation can be subject to econometric treatment.[wage formation]...depends on psychology, politics, and thousands of other intangible factors. As far as the economist is concerned, the final outcome is indeterminate—almost as indeterminate as the haggling between two millionaires over the price paid for a rare oil painting.
3.2. Change and Continuity
3.3. A Dynamic Model for Trends in Wage-and-Price Setting
3.3.1. Nominal and Real Trends
3.3.2. Wage-Price Spiral
3.3.3. VAR Formulation
3.3.4. Conditions for Global Asymptotic Stability
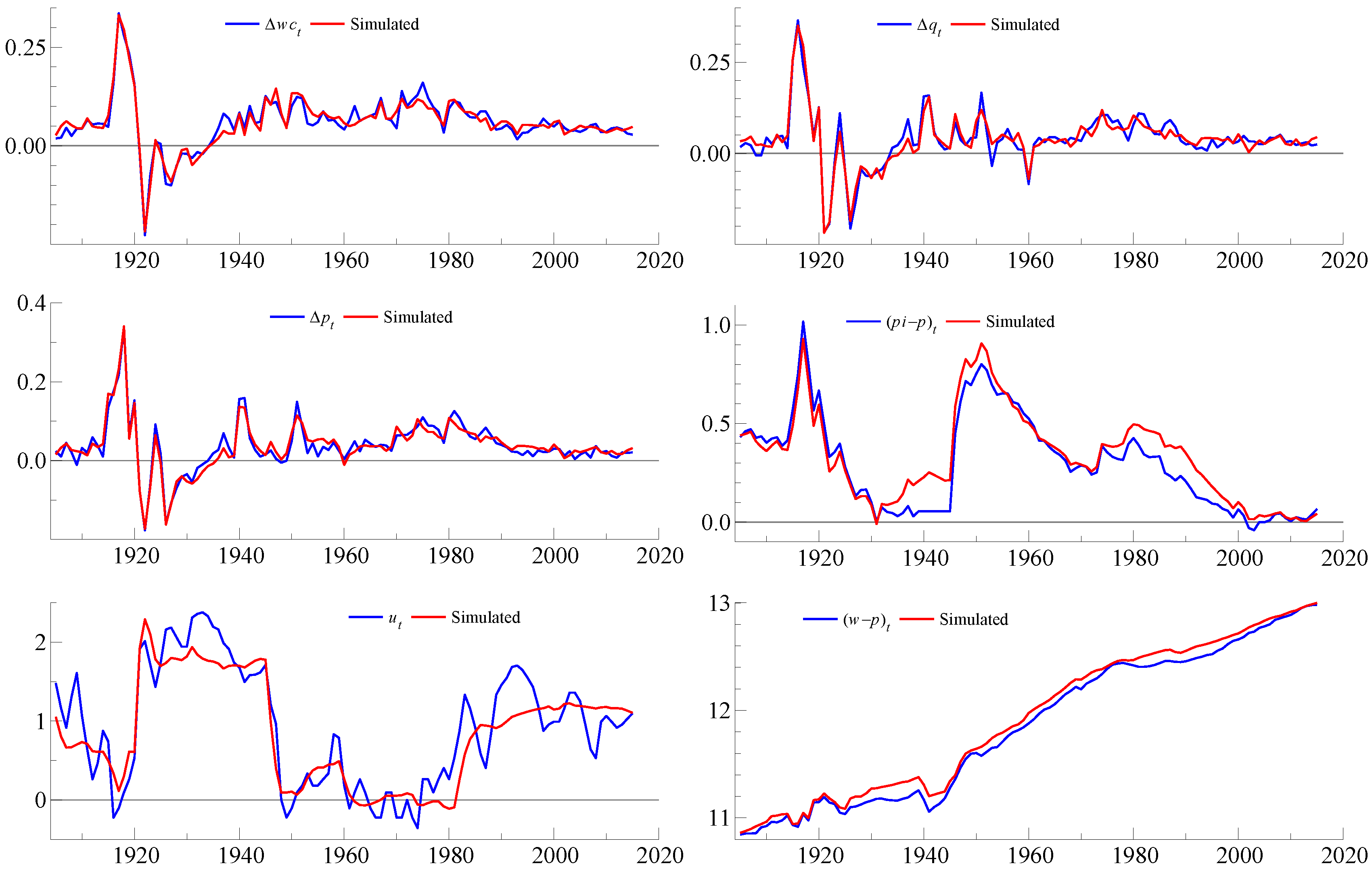
3.3.5. Numerical Simulation of the Theory Model
4. Empirical Models
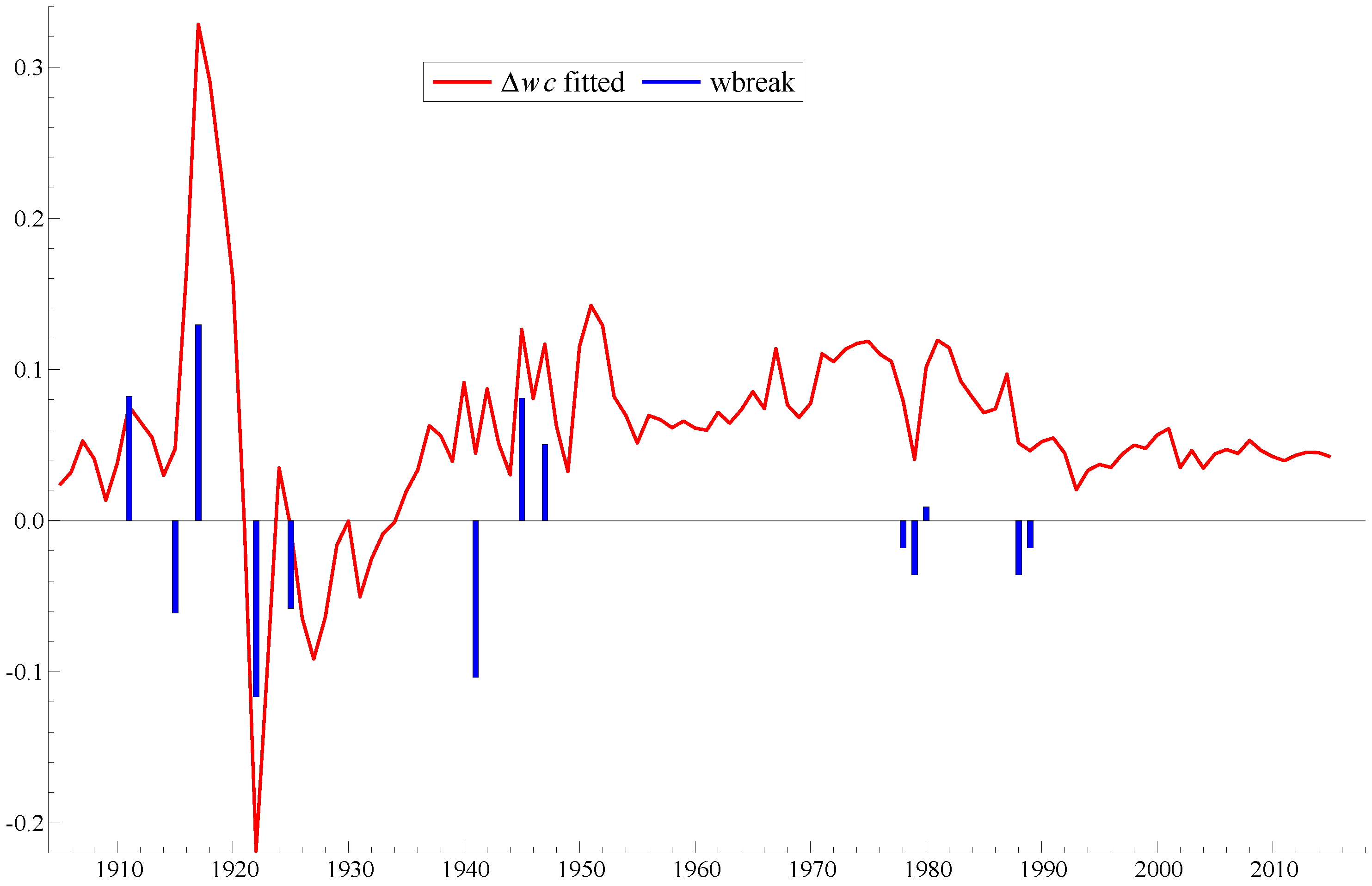
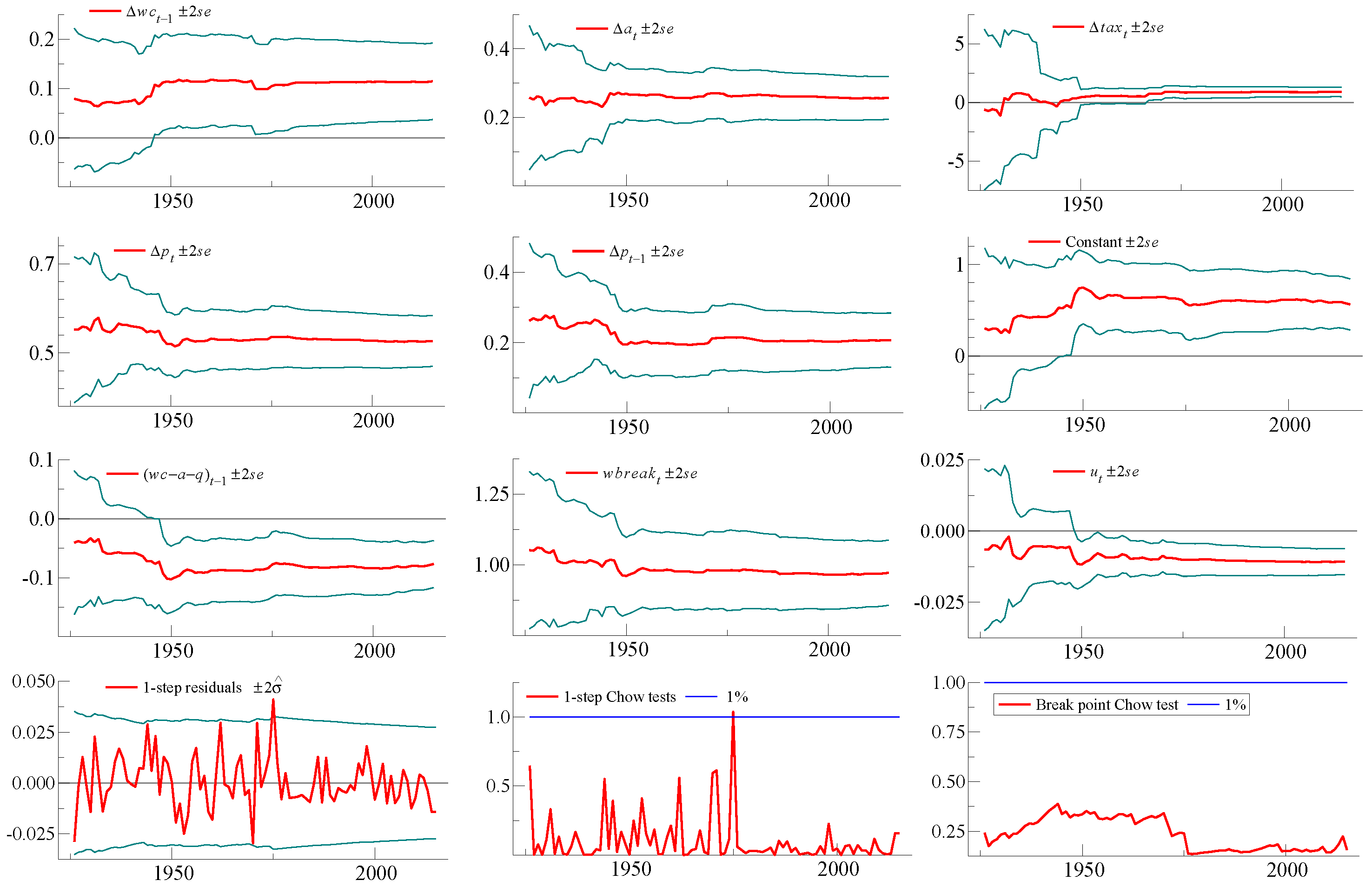
4.1. Robust Estimation with Structural Breaks
4.2. Reduced form VAR and Long-Run Wage Equation
4.3. Single-Equation Modelling
4.4. Multiple-Equation Modelling
4.4.1. Identificaton of Wage and Price
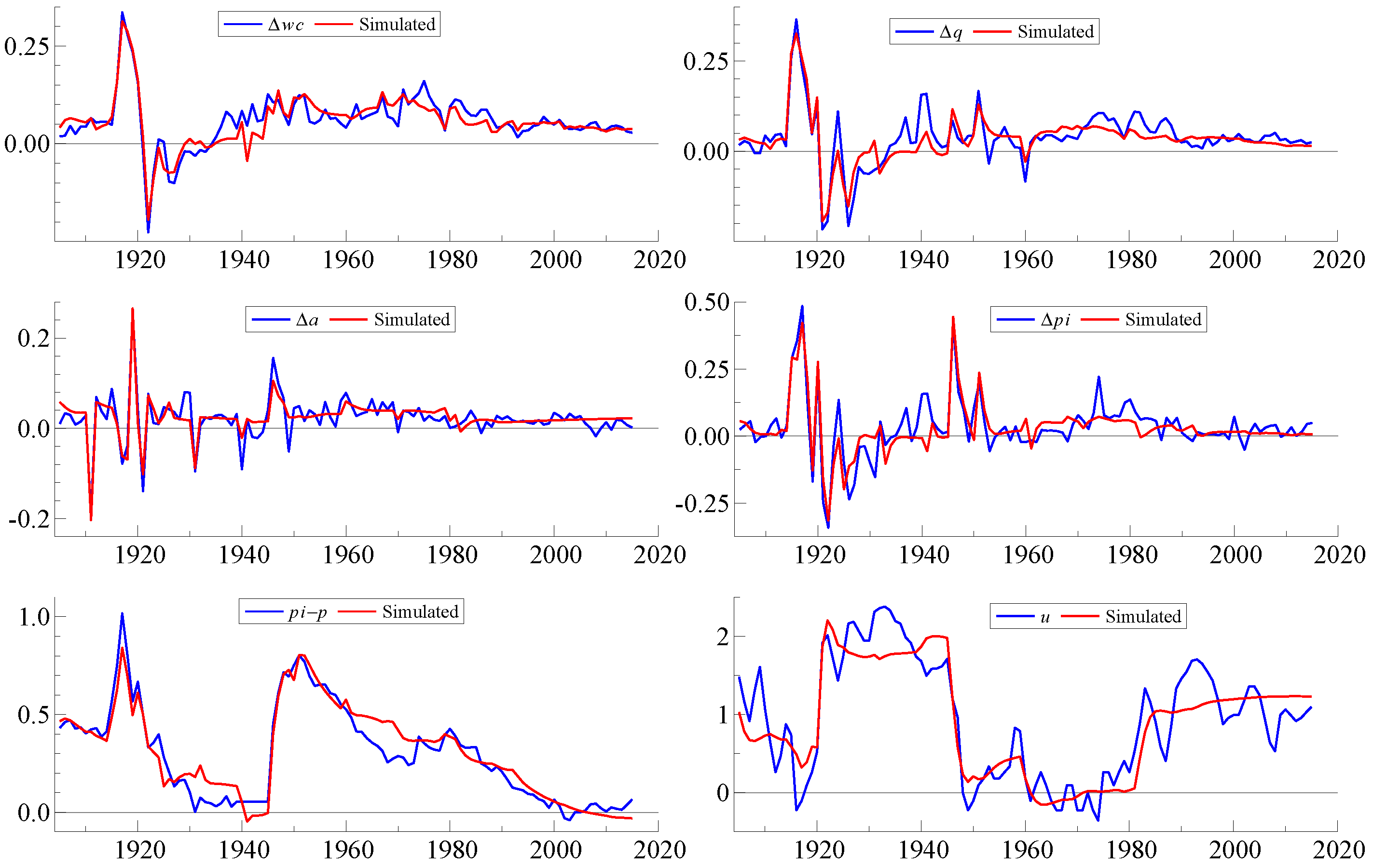
4.4.2. Reduced Form Estimates
4.4.3. FIML Estimates of Structural Model
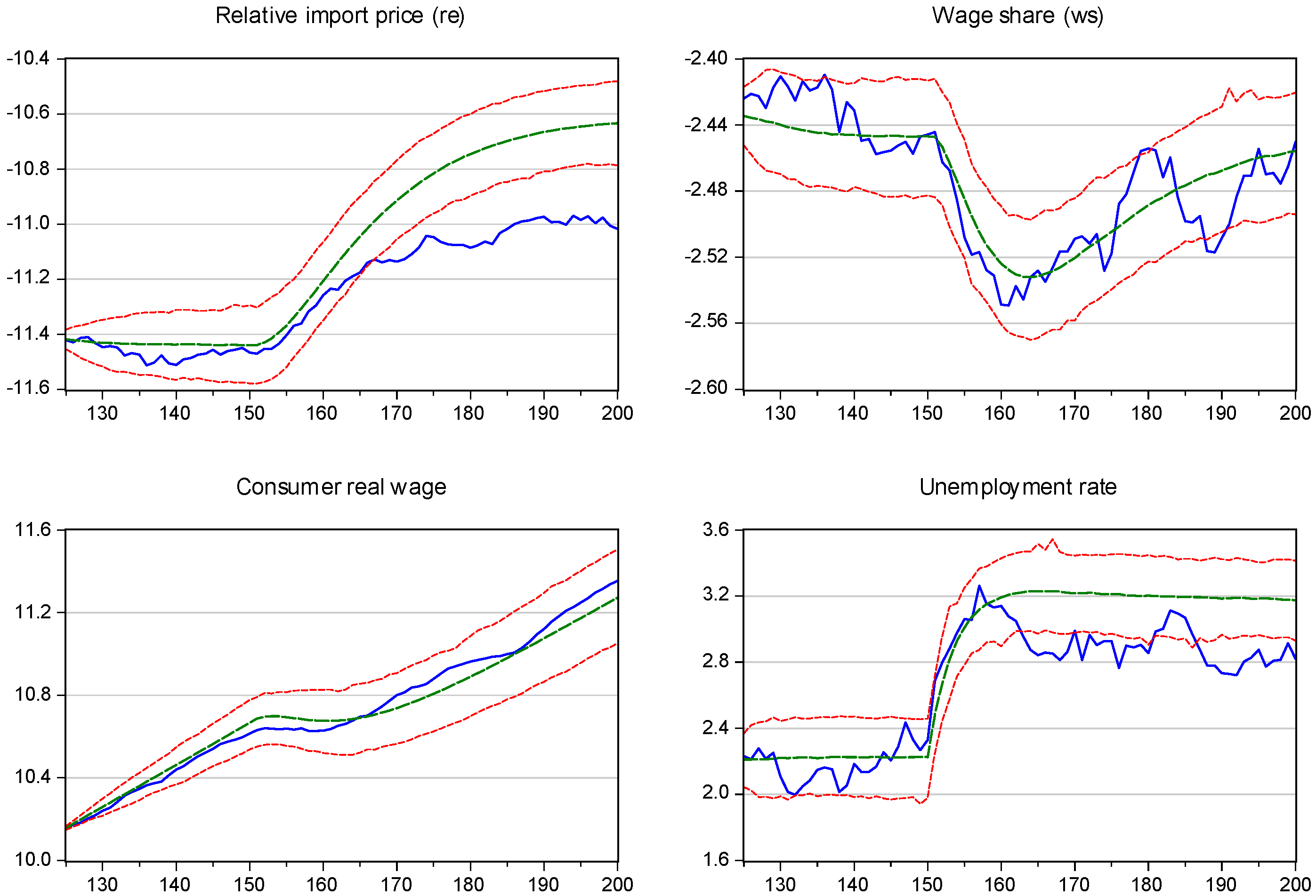
4.5. Simulation and Closing of the Model
4.6. Constancy and Invariance of the Coefficients of the Wage Equation, Lucas Citique
5. Summary and Discussion
Conflicts of Interest
Appendix A. Data Definitions and Sources
Wages Level
Consumer Price Index

Price Indices for Imports and GDP
Price Index, Mainland Norway GDP
GDP Fixed Prices
GDP Fixed Prices per Capita
Man-Hours for Mainland Norway
GDP Fixed Prices for Mainland Norway
Man-Years for Mainland Norway
GDP per Man Hour for Mainland Norway

GDP per Man Hour (Wage Earners) for Mainland Norway
GDP per Man-Year for Mainland-Norway
Payroll-Tax Rate
Unemployment Rate

Number of Working Days and Length of the Working Week
Working Hours Lost in Labour Conflicts
- 1.Ragnar Frisch was professor at the University of Oslo from 1931 to 1965, a founder of The Econometric Society and was awarded the first Nobel Prize in economics in 1969. Frisch seems to have been deeply influenced by observing at close range the impact of deflationary policies in Norway in the 1920s and by the Great Depression in the 1930s. His scientific work was motivated by the need for social improvements as much as an intellectual interest, Bjerkholt (2014) [2] (p. 299) and Bjerkholt and Qin (2011) [3] (p. 11). All quotes from the newspaper article (and the correspondence that it led to) have been translated by the author.
- 2.Frisch’s newspaper article is interesting also because it led to a correspondence with his pre-war assistant and colleague Trygve Haavelmo, who was still in USA, where he had been exiled during the war. Haavelmo opened by saying that he was “very interested in the problems” that Frisch had analysed in the article, and then went on to present a detailed note with comments (and improvements). Frisch, who wanted Haavelmo to come back to the University of Oslo, wrote back with enthusiasm and said that it was of the “greatest importance” that Haavelmo committed himself intellectually to this “all important field”, the theory of rational wage setting.
- 3.See Olstad (2009) [4], in particular chapter 5, and the concluding chapter.
- 4.Britain is an interesting case for historical comparison. At the time when the industrial unrest of the late 1960s was more of a nuisance than an unmanageable problem, Labour party minister Barbara Castle became frustrated by the unions’ lack of understanding that living in a liberalised market economy had consequences for how the unions could act. She mothered the ill fated White Paper In place of Strife in 1969, which in retrospect defined a turning point in the history of labour market regulation in Britain, see Sandbrook (2006) [5] (pp. 709–710).
- 5.The number is for 1903 which is the earliest year with data, cf. Appendix A.
- 6.Fixed 1990 International Geary-Khamis dollars, Maddison project database: http://www.ggdc.net/maddison/maddison-project/data.htm.
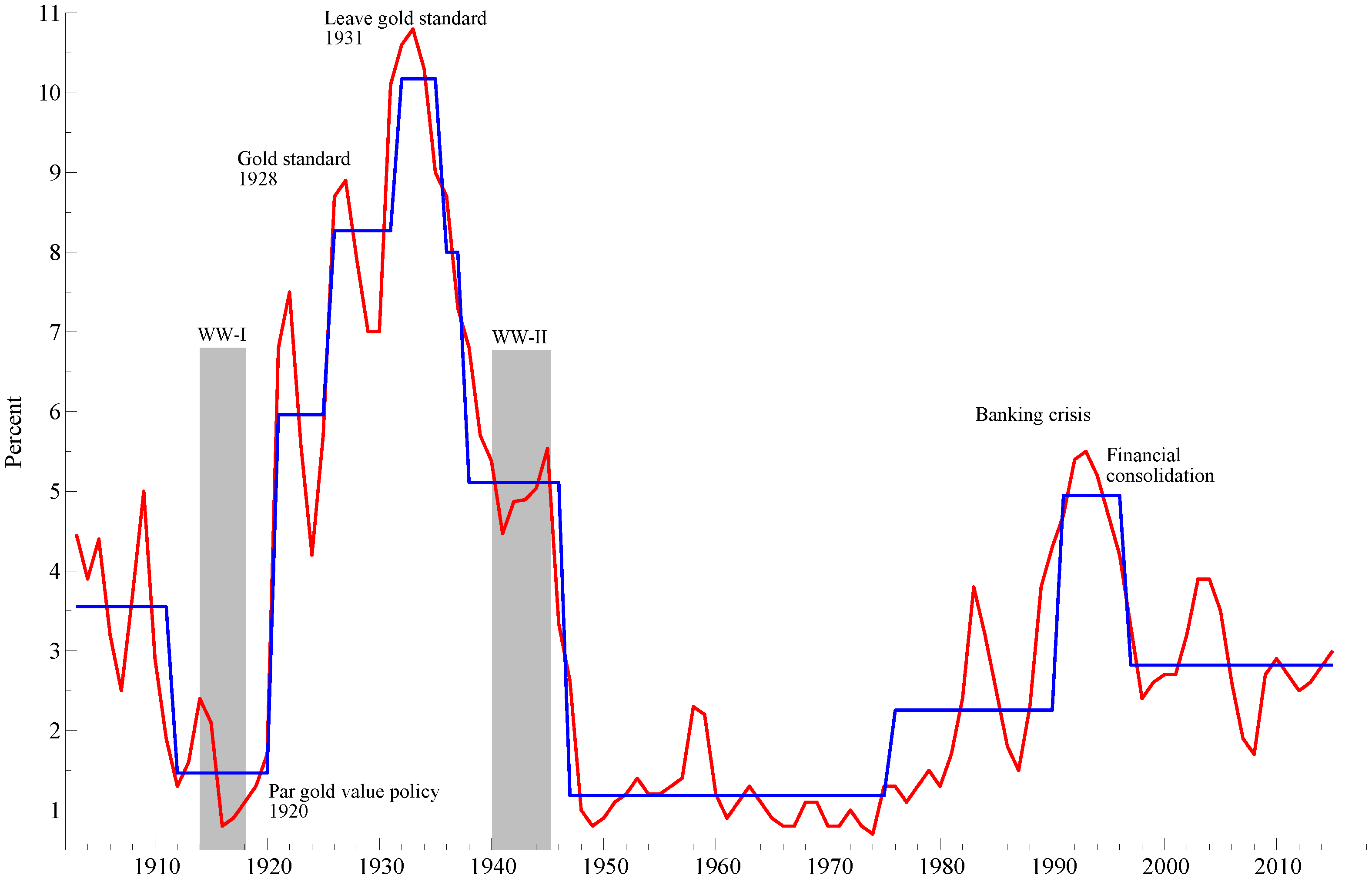
- 7.Norway left the Gold standard in 1914, even though it was a neutral country with no war efforts to finance, cf. Lie (2012) [15] (pp. 32,33). Norges Bank’s monetary expansion during the first two years of the war was related to international trade flows. However, during the two last war years another part of the monetary expansion was result of credit to domestic borowers, Værholm and Øksendal (2010) [16].
- 8.There was more than 25,000 immigrants in total in 1917, while only 2500 left Norway, Søbye (2014) [14] (Tables 4 and 15).
- 9.The Norwegian economy was affected by the Korean war of 1951–1952, but mainly in the form of a spurt of imported inflation, SSB (1965) [20] (pp. 385–392). The increase in unemployment in 1957 and 1958 may have been jointly caused by weak development in export markets, and unintended deflationary effects of fiscal policy, SSB (1965) [20] (pp. 406–408). The increase in unemployment in 1983 and 1984 had background in the weak development of the international economy and structural problems in Norway. It was first tackled by expansionary fiscal policy, which however was switched-off, primarily because the projected international recovery did not materialize. The large balance of payment deficits in the period with expansionary policy gave rise to concern about a possible loss of “economic scope for maneuvre”, SSB (1985) [21] (p. 97).
- 10.See Lie (2012) [15] (pp. 15–23).
- 11.The increased number of labour disputes, also illegal (“wild cat”) strikes, in the 1960s and 1970s is often seen as a “British disease”. However, in the 1960s and 1970s United Kingdom finished a mere seventh and sixth in a league table of working days lost per 1000 workers, with Canada, Italy, Australia, United States and Ireland all recording more strikes in those two decades. Even during the 1980s, United Kingdom finished third, behind Canada and Australia, cf. Wrigley (2002) [25] (Table 4.4), Sandbrook (2011) [26] (p. 98).
- 12.The data used by Bårdsen and Klovland is a panel data set of individual firms.
- 13.Olstad (2009) [4] (p. 419).
- 14.Reiersen (2015) [30] is an interesting analysis of the mental re-orientation during the 1920s and 1930, which probably was needed on both sides in order to break the deadlock marked by strife and industrial unrest. Reiersen’s view is that the main step was to move from a situation of distrust, and hence conflict as the main strategy on both sides, to a situation with sufficient trust so that the mutual strategy became one of compromise and cooperation.
- 15.As the interesting spat between Sæther and Eriksen (2014) [32] and Bjerkholt (2014) [2] shows, the “economic planning” of Norwegian post-war economy may have been misunderstood by some commentaries, or wrongly presented, as directives. The plans set out in the annual National Budget were expectations and intentions, not directives, Bjerkholt (2014) [2] (p. 301). The outcome depended on the international development in particular, as well as on economic control measures. In the early reconstruction years, the monitoring of the economy took place at a detailed level, and so did the use of control measures. However, the approach was more a reflection of pragmatism and an unorthodox view on policy instruments, than a principal position against product market liberalisation and consumer sovereignty SSB (1965) [20] (pp. 369,370).
- 16.The TCC had its origin in two important reports from 1966 about the system of wage and income formation, which we refer to in Section 2.5, see Longva (1994) [33].
- 17.In the period 1980–2010, Denmark, Finland and Sweden had higher union densities well above 70% for most of the time.
- 18.Again there may be an interesting parallel to Germany, where employer organisations were instrumental in operating the system of pattern bargaining, Soskice (1990) [39] (pp. 43–46).
- 19.An example of the relevance of this point is found in the contentious issues in shipyards’ regulation and the “STX-case”, where EFTA court advisory has collided with the Norwegian High Court domestic conception of public policy, see Evju (2014) [27].
- 20.On the role of the main-course model in Norwegian economic planning, see Bjerkholt (1998) [45].
- 21.Forder (2014) [42] (p. 31).
- 22.Hatton (1988) [72] (p. 84) concluded along the same lines for the British labour market: It did not change from “one where wages were set by atomistic competition to one in which the process was entirely institutional. Institutional wage setting was well established before 1914, though it became increasingly centralized until the late 1960s”.
- 23.We do not introduce explicit notation for firms’ expected wage, because with zero mean expectation errors, it will not have any implications for co-integration (or not) between the variables. However, it is understood that in (4) is an expected variable, and that p and q in (5) likewise denote expected prices in this context.
- 24.For the coefficients , and , , the non-negative signs are standard in economic models. Negative values of and , can give rise to explosive dynamics in wages and prices (hyperinflation), which is different from the low to moderately high inflation scenario that we have in mind for this paper.
- 25.Later theoretical derivations in the literature, using the Nash-solution, agree that is implied by collective bargaining, but also find to be equally theoretically important, and even purge the compensation for cost-of-living increases from the short-run dynamics, see Forslund et al. (2008) [82].
- 26.An alternative is to define a “productivity corrected producer real wage”:
- 27.Since is included as unrestricted, has four columns, against three in the theoretical section. The VAR includes an unrestricted constant and a restricted trend. The of no cointegration is rejected at the 1 percent level using the trace-test and the critical values in Table 13 in Doornik (2003) [92]. Also the hypothesis of one cointegrating vector against the alternative of two can be formally rejected. Accepting two long-run relationships, the joint hypothesis that the trend has zero coefficients in both co-integration relationships cannot be rejected at the 1 percent level.
- 28.In the IV column the Likelihood-ratio test statistic for the restriction becomes with p-value i brackets. The OLS results are: .
- 29.That is, the joint hypothesis of and the coefficients of the three nominal growth rates summing to one.
- 30.Corresponding to in the theoretical model.
- 31.Their Equation (21).
- 32.As long as the covariance matrix of the disturbances (which are omitted in the notation for simplicity) is unrestricted.
- 33.The first test (marking the start of the graph) tests the stability of the relationship over the period from 1926 to 2015. The second uses data to 1926 for estimation, and tests stability over the 1927–2015 period. Hence the number of out-of-sample periods are decreasing as we move from left to right along this graph.
- 34.Holden and Nymoen (2002) [110] concluded on the basis of results for Denmark, Finland, Norway and Sweden, for samples that started in the early 1960s and ended in 1994
- 36.Column labelled “Sysselsatte personer” in “Vedlegg 2 Table, page 35–37.
- 37.The numbers are revised, not much, compared to Grytten (1995) [118].
- 39.Galenson and Zellner (1957) [121], who included Norway in their comparison of unemployment data, used this source for a longer period of data.
- 40.“Norge hører til de land som har hatt bort imot permanent full sysselsetting i nesten hele etterkrigstiden, og der konjunkturelle bølgebevegelser produksjon og sysselsetting har vært lite merkbare ” SSB (1965) [20] (p. 352).
References
- R. Frisch. “Rasjonell lønnspolitikk [Rational Wage Policy].” Arbeiderbladet, 30 and 31 August 1945. [Google Scholar]
- O. Bjerkholt. “Ragnar Frisch and the Postwar Nowegian Economy: A Critical Comment on Sæther and Eriksen.” Econ J. Watch 11 (2014): 297–312. [Google Scholar]
- O. Bjerkholt, and D. Qin. Teaching Economics as a Science: The Yale Letcures of Ragnar Frisch. Milton Park, Abington, UK: Routledge, 2011. [Google Scholar]
- F. Olstad. Med Knyttet Neve. LOs Historie 1899–1935. Oslo, Norway: Pax Forlag, 2009. [Google Scholar]
- D. Sandbrook. White Heat. A Historry of Britain in the Swinging Sixties. London, UK: Abacus, 2006. [Google Scholar]
- D. Kolsrud, and R. Nymoen. “Macroeconomic Stability or Cycles? The Role of the Wage-Price Spiral.” Aust. Econ. Pap. 53 (2014): 41–68. [Google Scholar] [CrossRef]
- D. Kolsrud, and R. Nymoen. “Heuristic vs formal dynamics of the wage- and price-curve model of equilibrium unemployment.” J. Econ. Stud. 42 (2015): 186–206. [Google Scholar] [CrossRef]
- D.F. Hendry. “Deciding Between Alternative Approaches in Macroeconomics.” Int. J. Forecast., 2017. forthcoming. [Google Scholar]
- Norges Bank. Inflation Report. Technol Report 3; Oslo, Norway: Norges Bank, 2002. [Google Scholar]
- A.J. Isachsen. “Jarle Bergo: A professional monetary policymaker steps down.” Economic Bulletin. pp. 4–9, Norges Bank. Available online: http://static.norges-bank.no/pages/66487/Jarle_Bergo_Economic_Bulletin_1_2008.pdf?v=3/17/201415043PM&ft=.pdf (accessed on 10 November 2016).
- T. Skoglund. “Fra jordbruk til tjenester.” Økonomiske Anal. 2013 (2013): 53–55. [Google Scholar]
- C. Lindsay. “A Century of Labour Market Change.” Labour Market Trends, 2003, 133–144. [Google Scholar]
- K. Bævre, C. Riis, and T. Thonstad. “Norwegian Cohort Emigration.” J. Polpulation Econ. 14 (2001): 473–489. [Google Scholar] [CrossRef]
- E. Søbye. Folkemengdens Bevegelse 1735–2014; Oslo: Oktober Forlag, 2014. Available online: https://www.ssb.no/befolkning/artikler-og-publikasjoner/folkemengdens-bevegelse-1735-2014 (accessed on 12 April 2016).
- E. Lie. Norsk økonomisk Politikk etter 1905. Oslo, Norway: Universitetsforlaget, 2012. [Google Scholar]
- M. Værholm, and L.F. Øksendal. Letting the Anchor Go: Monetary Policy in Neutral Norway During World War I. Norges Banks Bicentenary Project; Working Paper 28; Oslo, Norway: Norges Bank, 2010. [Google Scholar]
- O.H. Grytten. “Why Was the Great Depression not so Great in the Nordic Countries? Economic Policy and Unemployment.” J. Eur. Econ. Hist. 37 (2008): 369–393, 395–403. [Google Scholar]
- F. Hodne, and O.H. Grytten. Norsk økonomi i det 20. århundre. Bergen, Norway: Fagbokforlaget, 2002. [Google Scholar]
- I. Bjørnhaug, and T. Halvorsen. Medlemsmakt og Samfunnsansvar. LOs Historie 1935–1969. Oslo, Norway: Pax Forlag, 2009. [Google Scholar]
- Statistisk Sentralbyrå (SSB). Norges økonomi etter krigen. [The Norwegian Post-War Economy]. No. 12 in Samfunnsøkonomiske Studier; Oslo, Norway: Statistisk Sentralbyrå [Central Bureau of Statistics Norway], 1965. [Google Scholar]
- Statistisk Sentralbyrå (SSB). Økonomisk utsyn over året 1984. [Economic Survey 1984]. NOS; Oslo, Norway: Statistisk Sentralbyrå, 1985. [Google Scholar]
- E. Barth, K.O. Moene, and F. Willumsen. “The Scandinavian Model—An Interpretation.” J. Publ. Econ. 117 (2014): 60–72. [Google Scholar] [CrossRef]
- E. Barth, and K.O. Moene. “Innovasjon, Kunnskap og Omstilling—Reell Versus Ideel Konkurranse.” Notat Skrevet til Produktivitetskommisjonen, Produktivitetskommisjonen. 2015. Available online: http://produktivitetskommisjonen.no/notater/ (accessed on 7 February 2016).
- A. Bergeaud, G. Cette, and R. Lecat. “Productivity Trends in Advanced Countries between 1890 and 2012.” Rev. Income Wealth, 2015. [Google Scholar] [CrossRef]
- C. Wrigley. British Trade Unions Since 1933. Cambridge, MA, USA: Cambridge University Press, 2002. [Google Scholar]
- D. Sandbrook. State of Emergency. The Way We Were: Britain 1970–1974. London, UK: Penguin Books, 2011. [Google Scholar]
- S. Evju. “Norway.” In Viking, Laval and Beyond. Edited by M. Freedland and D. Prassl. Oxford, UK: Portland, OR, USA: Hart Publishing, 2014, Chapter 12; pp. 211–228. [Google Scholar]
- G.J.A.D. Bårdsen, and J.T. Klovland. “Wage Formation and Bargaining Power During the Great Depression.” Scand. J. Econ. 112 (2010): 211–233. [Google Scholar] [CrossRef]
- M. Leiserson. Wages and Economic Control in Norway: 1945–1957. Cambridge, MA, USA: Harvard University Press, 1959. [Google Scholar]
- J. Reiersen, and Department of Business and Management, Buskerud and Vestfold University College. “From Conflict to Cooperation. Norwegian Labor Market Institutions in The Making.” Unpublished work. 2015. [Google Scholar]
- E. Barth, and K.O. Moene. “When Institutions Reciprocate.” In European Social Models from Crisis to Crisis. Edited by J.E. Dølvik and A. Martin. Oxford, UK: Oxford University Press, 2015, Chapter 10; pp. 306–324. [Google Scholar]
- A. Sæther, and I.E. Eriksen. “Ragnar Frisch and the Postwar Norwegian Economy.” Econ J. Watch 11 (2014): 46–80. [Google Scholar]
- S. Longva. “Beregningsutvalg og lønnsoppgjør.” In Stabilitet og langsiktighet. Festskrift til Hermod Skånland. Oslo, Norway: Aschehoug, 1994, pp. 335–346. [Google Scholar]
- J.M. Dyrstad. “Resource Curse Avoidance: Government Intervention and Wage Formation in the Norwegian Petroleum Sector.” Oxf. Econ. Pap., 2016. forthcoming. [Google Scholar] [CrossRef]
- E. Lie, and C. Venneslan. Over Evne. Finansdepartementet 1965–1992. Oslo, Norway: Pax Forlag, 2010. [Google Scholar]
- T. Bergh. LOs Historie. Kollektiv Fornuft.Bind 3 1969–2009. Oslo, Norway: Pax Forlag, 2009. [Google Scholar]
- T.A. Stokke, S. Nergaard, and S. Evju. Det kollektive Arbeidslivet, 2nd ed. Oslo, Norway: Universitetsforlaget, 2013. [Google Scholar]
- K. Nergaard. “Organisasjonsgrader, Tariffavtaledekning og Arbeidskonfliket 2013.” Fafo-notat 2014-14, FAFO. 2014. Available online: http://www.fafo.no/index.php/nb/zoo-publikasjoner/fafo-notater/item/organisasjonsgrader-tariffavtaledekning-og-arbeidskonflikter-2013 (accessed on 10 October 2016).
- D. Soskice. “Wage Determination: The Changing Role of Institutions in Advanced Industrialized Countries.” Oxf. Rev. Econ. Policy 6 (1990): 36–61. [Google Scholar] [CrossRef]
- B. Ruoff. “Labor Market Developments in Germany: Tales of Decency and Stability.” Working Paper 39; Berlin, Germany: Global Labour University, 2016. [Google Scholar]
- S. Evju. “Norway. Supreme Court. Rt 2013 p. 258.” Int. Labour Law Rep. 33 (2014): 3–29. [Google Scholar]
- J. Forder. Macroeconomics and the Phillips Curve Myth. Oxford Studies in the History of Economics; Oxford, UK: Oxford University Press, 2014. [Google Scholar]
- O. Aukrust. “Inflation in the Open Economy. A Norwegian Model.” In World Wide Inflation. Theory and Recent Experience. Edited by L.B. Klein and W.S. Sâlant. Washington, DC, USA: Brookings, 1977. [Google Scholar]
- G. Edgren, K.O. Faxén, and C.E. Odher. “Wages, Growth and Distribution of Income.” Swed. J. Econ. 71 (1969): 133–160. [Google Scholar] [CrossRef]
- O. Bjerkholt. “Interaction Between Model Builders and Policy Makers in the Norwegian Tradition.” Econ. Model. 15 (1998): 317–339. [Google Scholar] [CrossRef]
- H. Skånland. Inntektspolitikkens dilemma–kan det løses? Oslo, Norway: Cappelen Forlag, 1981. [Google Scholar]
- J. Llewellyn. “Can a Small Open Economy Attain Full Employment in the 1990s? ” In Stabilitet og langsiktighet. Festskrift til Hermod Skånland. Oslo, Norway: Aschehoug, 1994, pp. 313–334. [Google Scholar]
- S. Holden. “Wage Drift and Bargainig: Evidence from Norway.” Economica 56 (1989): 419–432. [Google Scholar] [CrossRef]
- NOU. “Lønnsdannelsen og Utfordringer for Norsk økonomi.” Norges Offentlige Utredninger 2013:13. Oslo Official Nowegian Reports (NOUs). : Departementenes Servicesenter, Informasjonsforvaltningen, 2013. Available online: https://www.regjeringen.no/no/dokumenter/nou-2013-13/id747181/ (accessed on 15 March 2016).
- R. Nymoen. “Wages and the Length of the Working Day. A Empirical Test Based on Norwegian Quarterly Manufacturing Data.” Scand. J. Econ. 91 (1989): 599–612. [Google Scholar] [CrossRef]
- A. Anundsen. “Oljepris og Lønnsutvikling i K-Sektor.” Oslo, Norway: Norges Bank, 29 April 2016. [Google Scholar]
- A.G. Haldane, Labour’s Share, and Speech, Bank of England. “Speech Given by Andrew G. Haldane, Chief Economist, Bank of England, Trades Union Congress, London.” 12 November 2015. Available online: http://www.bankofengland.co.uk/publications/Documents/speeches/2015/speech864.pdf (accessed on 6 May 2016).
- G. Bårdsen, and R. U.S. Nymoen. “Natural Rate Dynamics Reconsidered.” In The Methodology and Practise of Econometrics. A Festschrift in Honour of David F. Hendry. Edited by J. Castle and N. Shephard. Oxford, UK: Oxford University Press, 2009, Chapter 16; pp. 389–414. [Google Scholar]
- P.A. Samuelson. “Economic Theory and Wages.” In The Impact of the Union. Edited by D. Wright. New York, NY, USA: Harcourt Brace & Company, 1951, pp. 312–343. [Google Scholar]
- J. Hicks. “Economic Foundations of Wages Policy.” Econ. J. 65 (1955): 388–404. [Google Scholar] [CrossRef]
- R.E. Hall. “Employment Fluctuations with Equilibrium Wage Stickiness.” Am. Econ. Rev. 95 (2005): 50–65. [Google Scholar] [CrossRef]
- M. Gertler, and A. Trigari. “Unemployment Fluctuations with Staggered Nash Wage Bargaining.” J. Polit. Econ. 177 (2009): 38–86. [Google Scholar] [CrossRef]
- G. Calvo. “Staggered Prices in a Utility Maximizing Framework.” J. Monet. Econ. 12 (1983): 383–398. [Google Scholar] [CrossRef]
- O. Blanchard, and J. Galí. “Labor Markets and Monetary Policy: A New Keynesian Model with Unemployment.” Am. Econ. J. Macroecon. 2 (2010): 1–30. [Google Scholar] [CrossRef]
- T.S. Krogh. “Real wage rigidity and the unemployment volatility puzzle in small open economies.” Oxf. Econ. Pap. 68 (2016): 131–151. [Google Scholar] [CrossRef]
- S.J. Nickell, and M. Andrews. “Unions, Real-Wages and Employment in Britain 1951–79.” Oxf. Econ. Pap. 35 (1983): 183–206. [Google Scholar]
- S. Nickell. “Error Correction, Partial Adjustment: and all that:: An expostionary Note.” Oxf. Bull. Econ. Stat. 47 (1985): 119–129. [Google Scholar] [CrossRef]
- D. Usher. “Bargaining Unexplained.” Publ. Choice 151 (2012): 23–41. [Google Scholar] [CrossRef]
- P.A. Samuelson. Economics. Oxford Studies in the History of Economics; McCraw-Hill, Cambridge, MA, USA: Oxford University Press, 1955. [Google Scholar]
- J. Dunlop. Wage Determination under Trade Unions. Reprints of Economic Classic, 1966; New York, NY, USA: Augustus M. Kelley Publishers, 1944. [Google Scholar]
- A.W. Phillips. “The Relationship Between Unemployment and the Rate of Unemployment and the Rate of Change of Money Wage Rates in the U.K., 1861–1957.” Economica 25 (1958): 283–299. [Google Scholar]
- R.G. Lipsey. “The Relationship Between Unemployment and the Rate of Change in Money Wages in the United Kingdom 1862–1957: A Further Analysis.” Economica 27 (1960): 1–31. [Google Scholar] [CrossRef]
- G. Bårdsen, Ø. Eitrheim, E.S. Jansen, and R. Nymoen. The Econometrics of Macroeconomic Modelling. Oxford, UK: Oxford University Press, 2005. [Google Scholar]
- J.D. Sargan. “Wages and Prices in the United Kingdom: A Study of Econometric Methodology.” In Econometric Analysis for National Economic Planning. Edited by P.E. Hart, G. Mills and J.K. Whitaker. London, UK: Butterworth Co., 1964, pp. 25–63. [Google Scholar]
- J.D. Sargan. “A Study of Wages and Prices in the U.K. 1949–1968.” In The Current Inflation. Edited by H.G. Johnson and A.R. Nobay. London, UK: MacMillan, 1971, Chapter 4; pp. 52–71. [Google Scholar]
- J.D. Sargan. “A Model of Wage-Price Inflation.” Rev. Econ. Stud. 47 (1980): 113–135. [Google Scholar] [CrossRef]
- T. Hatton. “Institutional Change and Wage Rigidity in the U.K. 1880–1985.” Oxf. Rev. Econ. Policy 4 (1988): 74–86. [Google Scholar] [CrossRef]
- E. Bowitz, and Å. Cappelen. “Modelling Incomes Policies: Some Norwegian experiences 1973–1993.” Econ. Model. 18 (2001): 349–379. [Google Scholar] [CrossRef]
- D. Kolsrud, and R. Nymoen. “Unemployment and the Open Economy Wage-Price Spiral.” J. Econ. Stud. 25 (1998): 450–467. [Google Scholar] [CrossRef]
- G. Bårdsen, and R. Nymoen. “Testing Steady-State Implications for the NAIRU.” Rev. Econ. Stat. 85 (2003): 1070–1075. [Google Scholar] [CrossRef]
- G. Bårdsen, and R. Nymoen. “Macroeconometric Modelling for Policy.” In Palgrave Handbook of Econometrics Volume 2. Edited by T. Mills and K. Patterson. Basingstoke, UK: Palgrave Mac-Millan, 2009, Chapter 17; pp. 851–916. [Google Scholar]
- Q.F. Akram, and R. Nymoen. “Model Selection for Monetary Policy Analysis—How Important is Empirical Validity? ” Oxf. Bull. Econ. Stat. 71 (2009): 35–68. [Google Scholar] [CrossRef]
- G. Bårdsen, A. Reijer, P. Jonasson, and R. Nymoen. “MOSES: Model for studying the economy of Sweden.” Econ. Model. 29 (2012): 2566–2582. [Google Scholar] [CrossRef]
- R. Nymoen, and A. Rødseth. “Explaining Unemployment: Some Lessons from Nordic Wage Formation.” Labour Econ. 10 (2003): 1–29. [Google Scholar] [CrossRef]
- A. Rødseth. Open Economy Macroeconomics. Cambridge, MA, USA: Cambridge University Press, 2000. [Google Scholar]
- R.F. Engle, and C.W.J. Granger. “Co-integration and Error Correction: Representation, Estimation and Testing.” Econometrica 55 (1987): 251–276. [Google Scholar] [CrossRef]
- A. Forslund, N. Gottfries, and A. Westermark. “Prices, Productivity and Wage Bargaining in Open Economies.” Scand. J. Econ. 110 (2008): 169–195. [Google Scholar] [CrossRef]
- A.K. Anundsen, T.S. Krogh, R. Nymoen, and J. Vislie. “The macroeconomics of Trygve Haavelmo.” Nord. J. Polit. Econ. 37 (2012): 2. [Google Scholar]
- J.M. Keynes. The General Theory of Employment, Interest and Money, 1973rd ed. Volume VII of The Collected Writings of John Meynard Keynes; London, UK: MacMillan, 1936. [Google Scholar]
- M.P. Clements, and D.F. Hendry. Forecasting Non-Stationary Economic Time Series. Cambridge, MA, USA: The MIT Press, 1999. [Google Scholar]
- S. Johansen, and B. Nielsen. “Analysis of the Indicator Saturation Estimator as a Robust Regression Estimator.” In The Methodology and Practise of Econometrics. Edited by J.L. Castle and N. Shephard. Oxford, UK: Oxford University Press, 2009. [Google Scholar]
- D.F. Hendry, S. Johansen, and C. Santos. “Automatic Selection of Indicators in a Fully Saturated Regression.” Comput. Stat. 23 (2008): 317–335, 337–339. [Google Scholar] [CrossRef]
- J.A. Doornik. “Autometrics.” In The Methodology and Practice of Econometrics. Edited by J. Castle and N. Shephard. Oxford, UK: Oxford University Press, 2009, Chapter 8; pp. 88–121. [Google Scholar]
- R. Nymoen. Faulty Watch Towers: Structural Models in Norwegian Monetary Policy Analysis. Technol Report; Oslo, Norway: Department of Economics, University of Oslo, 2002. [Google Scholar]
- Ø. Eitrheim, E.S. Jansen, and R. Nymoen. “Progress from Forecast Failure: The Norwegian Consumption Function.” Econom. J. 5 (2002): 40–64. [Google Scholar]
- J. Doornik. “Approximations to the Asymptotic Distribution of cointegration Tests.” J. Econ. Surv. 12 (1998): 573–593. [Google Scholar] [CrossRef]
- J. Doornik. Asymptotic Tables for Cointegration Tests Based on the Gamma-Distribution. Technol Report; Oxford, UK: Nuffield College, University of Oxford, 2003. [Google Scholar]
- R. Davidson, and J.G. MacKinnon. Econometric Theory and Methods. Oxford, UK: Oxford University Press, 2004. [Google Scholar]
- K. Johansen. “Norwegian Wage Curves.” Oxf. Bull. Econ. Stat. 57 (1995): 229–247. [Google Scholar] [CrossRef]
- N.R. Ericsson, E. Maasoumi, and G. Mizon. “A Retrospective on J. Denis Sargan and His Contributions to Econometrics.” Econom. Rev. 20 (2001): 132–158. [Google Scholar] [CrossRef]
- J.L. Castle, and D.F. Hendry. “Semi-Automatic Non-Linear Model Selection.” In Essays in Non-Linear Time Series Econometrics. Edited by N. Haldrup and P. Saikkonen. Oxford, UK: Oxford Univeristy Press, 2014, pp. 163–197. [Google Scholar]
- J.L. Castle, and D.F. Hendry. “The long-run determinants of UK wages, 1860–2004.” J. Macroecon. 31 (2009): 5–28. [Google Scholar] [CrossRef]
- C. Hsiao. “Cointegration and Dynamic Simultaneous Equations Model.” Econometrica 65 (1997): 647–670. [Google Scholar] [CrossRef]
- J.A. Doornik, and D.F. Hendry. Modelling Dynamic Systems PcGive 14. Volume 2. London, UK: Timberlake Consultants, 2013. [Google Scholar]
- D.F. Hendry. “On Detectable and Non-detectable Structural Change.” Struct. Chang. Econ. Dyn. 11 (2000): 45–65. [Google Scholar] [CrossRef]
- R.F. Engle, D.F. Hendry, and J.-F. Richard. “Exogeneity.” Econometrica 51 (1983): 277–304. [Google Scholar] [CrossRef]
- J.A. Doornik, and D.F. Hendry. Empirical Econometric Modelling PcGive 13. Volume 1. London, UK: Timberlake Consultants, 2009. [Google Scholar]
- B. Nielsen, and A. Whitby. “A Joint Chow Test for Structural Instability.” Econometrics 3 (2015): 156–186. [Google Scholar] [CrossRef]
- R.F. Engle, and D.F. Hendry. “Testing Super Exogeneity and Invariance in Regression Models.” J. Econom. 56 (1993): 119–139. [Google Scholar] [CrossRef]
- R.E. Lucas Jr. “Econometric Policy Evaluation: A Critique.” Carnegie-Rochester Conf. Ser. Public Policy 1 (1976): 19–46. [Google Scholar] [CrossRef]
- D.F. Hendry. “The Encompassing Implications of Feedback verus Feedforward Mechanisms in Econometrics.” Oxf. Econ. Pap. 40 (1988): 132–149. [Google Scholar]
- C. Favero, and D.F. Hendry. “Testing the Lucas Critique: A Review.” Econom. Rev. 11 (1992): 265–306. [Google Scholar] [CrossRef]
- J. Elmeskov, and M. MacFarland. “Unemployment Persistence.” OECD Econ.Stud. 21 (1993): 59–88. [Google Scholar]
- J. Elmeskov. “Nordic Unemployment in a European Perspective.” Swed. Econ. Policy Rev. 1 (1994): 27–70. [Google Scholar]
- S. Holden, and R. Nymoen. “Measuring Structural Unemployment: NAWRU Estimates in the Nordic Countries.” Scand. J. Econ. 104 (2002): 87–104. [Google Scholar] [CrossRef]
- O.H. Grytten. “Norwegian wages 1726–2006 classified by industry.” In Historical Monetary Statistics for Norway-Part II. Volmue 38 of Occasional Papers; Edited by J.K.Ø. Eitrheim and J. Qvigstad. Oslo, Norway: Norges Bank, 2007, Chapter 6; pp. 343–383. [Google Scholar]
- O.H. Grytten. “The gross domestic product for Norway 1830–2003.” In Historical Monetary Statistics for Norway 1830–2003. Volume 35 of Occasional Papers; Edited by J.K.Ø. Eitrheim and J. Qvigstad. Oslo, Norway: Norges Bank, 2004, Chapter 6; pp. 241–288. [Google Scholar]
- S. Hansen, and T. Skoglund. “Sysselsetting og Lønn i Historisk Nasjonalregnskap.Beregninger for 1949–1969.” Notater 2009/38. Oslo, Norway: Statistisk Sentralbyr, 2005. [Google Scholar]
- S. Hansen, and T. Skoglund. “Sysselsetting og Lønn i Historisk Nasjonalregnskap.Beregninger for 1949–1969.” Notater 2008/54. Oslo, Norway: Statistisk Sentralbyr, 2008. [Google Scholar]
- S. Hansen, and T. Skoglund. “Sysselsetting og Lønn i Historisk Nasjonalregnskap.Beregninger for 1900–1930.” Notater 2009/38. Oslo, Norway: Statistisk Sentralbyr, 2009. [Google Scholar]
- A. Maddison. The World Economy. a Millenian Perspective. Paris, France: OECD Publishing, 2001. [Google Scholar]
- Statistisk Sentralbyrå (SSB). Statistiske Oversikter 1926. Det Statistiske Centralbyrå. Available online: http://www.ssb.no/a/histstat/hs1926.pdf (accessed on 12 April 2016).
- O.H. Grytten. “The Scale of Norwegian Interwar Unemployment in International perspective.” Scand. Econ. Hist. Rev. 43 (1995): 226–250. [Google Scholar] [CrossRef]
- Statistisk Sentralbyrå (SSB). Statistical Surveys 1948. Volume Oslo of NOS; Oslo, Norway: The Central Bureau of Statistics of Norway, 1948. [Google Scholar]
- Statistisk Sentralbyrå (SSB). Statistical Surveys 1958. Volume Oslo of NOS; Oslo, Norway: The Central Bureau of Statistics of Norway, 1958. [Google Scholar]
- W. Galenson, and A. Zellner. “International Comparison of Unemployment Rates.” In The Measurement and Behavior of Unemployment. Cambridge, MA, USA: NBER, 1957, pp. 439–584. [Google Scholar]
- Statistisk Sentralbyrå (SSB). Historisk Statistikk 1968. Oslo, Norway: Statistisk Sentralbyrå, 1969. [Google Scholar]
- Statistisk Sentralbyrå (SSB). Historisk Statistikk 1978. Oslo, Norway: Statistisk Sentralbyrå, 1978. [Google Scholar]
- Statistisk Sentralbyrå (SSB). Historisk Statistikk 1994. Oslo, Norway: Statistisk Sentralbyrå, 1994. [Google Scholar]






| Unionization Rate | Employer Organization | |
|---|---|---|
| 1948 | 50% | |
| 1972 | 51% | |
| 1990 | 57% | 50 % |
| 2005 | 53% | 60 % |
| 2013 | 52% | 65 % |
| Private Sector | Production of Goods | Service | |
|---|---|---|---|
| 1998 | 63% | 71% | 58% |
| 2004 | 60% | 63% | 58% |
| 2005 | 59% | 64% | 56% |
| 2008 | 59% | 65% | 55% |
| 2013 | 58% | 62% | 56% |
| OLS | GIVE | ||
|---|---|---|---|
| (0.03) | (0.11) | ||
| (0.005) | (0.03) | ||
| (0.03) | (0.074) | ||
| (0.04) | (0.04) | ||
| (0.26) | (0.26) | ||
| (0.04) | (0.04) | ||
| (0.02) | (0.03) | ||
| (0.002) | (0.003) | ||
| Constant | |||
| (0.14) | (0.19) | ||
| (0.06) | (0.08) | ||
| Sample: 1905–2015 | |||
| Sargan IV-test | |||
| , , | |||
| w-p ecm | 5.5 * | 30.8 ** | 17.8 * | |
| Breaks | 207 ** | 254 ** | 340 ** | 34 ** |
| Vector mis-spesification tests: | ||||
| 1.8 ** | ||||
| W-P ECM | 16.1 ** | 33.2 ** |
| 1904–1934 | 1935–2015 | 1904–2015 | |
|---|---|---|---|
| (0.06) | (0.06) | (0.03) | |
| (0.08) | (0.06) | (0.03) | |
| (0.08) | (0.07) | (0.04) | |
| (2.67) | (0.21) | (0.20) | |
| (0.06) | (0.07) | (0.03) | |
| (0.05) | (0.03) | (0.02) | |
| (0.008) | (0.002) | (0.002) | |
| Constant | |||
| (0.30) | (0.27) | (0.14) | |
| (0.11) | (0.10) | (0.06) | |
| Chow test | |||
© 2017 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nymoen, R. Between Institutions and Global Forces: Norwegian Wage Formation Since Industrialisation. Econometrics 2017, 5, 6. https://doi.org/10.3390/econometrics5010006
Nymoen R. Between Institutions and Global Forces: Norwegian Wage Formation Since Industrialisation. Econometrics. 2017; 5(1):6. https://doi.org/10.3390/econometrics5010006
Chicago/Turabian StyleNymoen, Ragnar. 2017. "Between Institutions and Global Forces: Norwegian Wage Formation Since Industrialisation" Econometrics 5, no. 1: 6. https://doi.org/10.3390/econometrics5010006
APA StyleNymoen, R. (2017). Between Institutions and Global Forces: Norwegian Wage Formation Since Industrialisation. Econometrics, 5(1), 6. https://doi.org/10.3390/econometrics5010006





