Abstract
We consider the problem of testing for a structural break in the spatial lag parameter in a panel model (spatial autoregressive). We propose a likelihood ratio test of the null hypothesis of no break against the alternative hypothesis of a single break. The limiting distribution of the test is derived under the null when both the number of individual units N and the number of time periods T is large or N is fixed and T is large. The asymptotic critical values of the test statistic can be obtained analytically. We also propose a break-date estimator that can be employed to determine the location of the break point following evidence against the null hypothesis. We present Monte Carlo evidence to show that the proposed procedure performs well in finite samples. Finally, we consider an empirical application of the test on budget spillovers and interdependence in fiscal policy within the U.S. states.
JEL Classification:
C01; C22; C23; H72
1. Introduction
Spatial dependence represents a situation where values observed at one location or region depend on the values of neighboring observations at nearby locations. One may ask two questions: first, does this dependence stay the same over time; and second, what might cause the dependence to change? This paper answers the first question by proposing a likelihood ratio test of the null hypothesis of no change against the alternative hypothesis of a one-time change. In case there is evidence against the null hypothesis, the paper consequently proposes a break-date estimator. The second question has been reflected upon through an empirical application of budget spillovers in the U.S. states.
In the setup of spatial panel models with N individual units (geographic locations, such as countries and zip codes, or network units, like firms and individuals) observed over T number of periods, where the outcome of each unit depends on its “neighbor’s” outcome, there exists a problem of endogeneity. Hence, such models are estimated using maximum likelihood or the generalized method of moments. Similar to the univariate time series case, in this paper a sup LR test is proposed, and the asymptotics are derived for large T cases.
In comparison to the vast literature on the change point for univariate series, the corresponding literature for panel data is quite small. One of the most popular and early tests in the univariate literature is the popular F test of Chow (1960) [1], which has been modified for cases of unknown and multiple break dates in Andrews (1993) [2], Andrews and Ploberger (1994) [3], and Bai and Perron (1998) [4], among others. Bai (1997) [5], Bai et al. (1998) [6], and Qu and Perron (2007) [7] have extended the single equation break models to multiple ones. They show that using multiple system improves the estimation precision of the break dates and the power of the tests. Perron (2006) [8] provides a survey of the literature.
In the panel data literature, Bai (2010) [9] establishes the consistency of the estimated common break point, achievable even if there is a single observation in a regime. The paper proposes a new framework for developing the limiting distribution for the estimated break point and lays down steps to construct confidence intervals. The least squares method is used for estimating breaks in means. Feng et al. (2009) [10] study a multiple regression model in a panel setting where a break occurs at an unknown common date. They establish the consistency and rate of convergence both for a fixed time horizon and large panels. In Feng et al. (2009) [10], the limiting distribution is derived without the assumption of shrinking magnitude of break. Liao (2008) [11] uses the Bayesian method for estimation and inference about structural breaks in a panel.
Han and Park (1989) [12] develop a multivariate CUSUM test in order to test for a structural break in panel data, and they apply the test to U.S. manufacturing goods trade data. Kao (2000) [13] proposes two classes of test statistics for detecting a break at an unknown date in panel data models with the time trend. The first is a fluctuation test, while the second is based on the mean and exponential Wald statistics of Andrews and Ploberger (1994) [3] and the maximum Wald statistic of Andrews (1993) [2]. De Wachter and Tzavalis (2012) [14] develop a break detecting testing procedure for the AR(p) linear panel data with exogenous or pre-determined regressors. The method accommodates structural break in the slope parameters, as well as fixed effects, and no assumption is imposed on the homogeneity of cross-sectional fixed effects. Pauwels et al. (2012) [15] provide a structural break test for heterogeneous panel data models, where the break affects some, but not all cross-section units in the panel. The test is robust to auto-correlated errors. The test statistic is based on comparing pre- and post-break sample statistics as in Chow (1960) [1].
A higher availability of geocoded socio-economic datasets has led to a vast expansion of the study of spatial interaction between economics agents. Moreover, the recursive relationship between agents in a network can be modeled using spatial econometric methods. Spatial dependence represents the transmission of developments across “neighboring” agents. Elhorst (2010) [16] provides detailed methodologies for estimating spatial panels and to compare competing models. The above tests in the panel literature do not explicitly consider the endogeneity problem in the model, which arises from the spatial dependence. We consider a spatial autoregressive model and provide a test for a break in the spatial lag parameter. To test for a change in the spatial dependence parameter, we propose a sup LR test similar to Bai (1999) [17]. Yu et al. (2008) [18] and Lee and Yu (2010) [19] provide the asymptotic properties of quasi-maximum likelihood estimators for spatial autoregressive panel data models with fixed effects. The results from Yu et al. (2008) [18] are used to derive the limit distribution of the sup LR test for large T. An estimator for the break date is proposed that can be employed once evidence against no break in the spatial lag parameter is obtained. The performance of this estimator, as well as the proposed test statistic in small samples is evaluated via a Monte Carlo study. Wied (2013) [20] develops a CUSUM-type test for time-varying parameters in a spatial autoregressive model for stock returns.
Case et al. (1993) [21] show that a state’s budget expenditure depends on the spending of similar1 states. Therefore, a rise in a “neighboring” state’s expenditure results in an increase in the state’s own expenditure. As an empirical application, we apply the likelihood ratio test to the budget dependence of U.S. states over time. The data consist of annual observations for the continental United States during the period 1960–2011. States that are economically similar are defined as neighbors. The test result shows that the null hypothesis of no break in the spatial dependence parameter is rejected, and the break date is estimated as 1982. The budget spillover is more pronounced post-break. Details of the results and intuitions on why there might be a break are discussed.
The paper is organized as follows: in Section 2, the spatial lag model is presented and discussed. Section 3 provides motivating examples where the test can be applied. We propose a sup LR test, which is described in Section 4. The limiting distribution of the test is stated in Section 5. The outline of the proof is also provided in this section (details are in the Appendix A). In the event of a rejection of the null hypothesis, we propose a break date estimator in Section 6. The finite sample properties of the test and the estimator are discussed in Section 7. Finally, we apply the test to budget spillovers in U.S. states, in Section 8. It shows that there was a change in the budget dependence between similar income states. In Section 9, we provide the conclusion and possible next steps in research.
2. Spatial Lag Model
Let us consider a simple pooled linear regression model
where i is an index of cross-sectional dimension, with i = 1,..., N, and t is an index for the time dimension, with t = 1,..., T. We discuss all of the results using “time” as the second dimension; however, for a general spatial lag model, the second dimension could very well reflect another cross-sectional characteristic, such as the industry sector or the number of classes or groups. is an observation on the dependent variable at i and t, a vector of observations on the (exogenous) explanatory variables including the intercept, β a matching K × 1 vector of regression coefficients and an error term. In stacked form, the simple pooled regression can be written as
with y a × 1 vector, X a × K matrix and ϵ a × 1 vector. In general, spatial dependence is present whenever the correlation across cross-sectional units is non-zero, and the pattern of non-zero correlations conforms to a specified neighbor relation. When the spatial correlation pertains to the dependent variable, it is known as a spatial lag model. The neighbor relation is expressed by means of a spatial weight matrix.
A spatial weights matrix W is a positive matrix in which the rows and columns correspond to the cross-sectional observations. An element of the matrix expresses the prior strength of the interaction between location i (in the row of the matrix) and location j (column). This can be interpreted as the presence and strength of a link between nodes (the observations) in a network representation that matches the spatial weights’ structure. In the simplest case, the weights matrix is binary, with = 1 when i and j are neighbors and = 0 when they are not. The choice of the weights is typically driven by geographic criteria, such as contiguity (sharing a common border) or distance. However, generalizations that incorporate notions of “economic” distance are increasingly being used, as well. By convention, the diagonal elements = 0. For computational simplicity and to aid the interpretation of the spatial variables, the weights are almost always standardized, such that the elements in each row sum to one, or = . Using the subscript to designate the matrix dimension, with as the weights for the cross-sectional dimension and the observations stacked, the full weights matrix becomes: , with an identity matrix of dimension T.
Unlike the time series case, where “neighboring” observations are directly incorporated into a model specification through a shift operator (example ), in the spatial literature, the neighboring observations are included in the model specification by applying a spatial lag operator (W) to the dependent variable. A spatial lag operator constructs a new variable, which consists of the weighted average of the neighboring observations, with the weights as specified in W. The spatial lag model or mixed regressive spatial autoregressive model includes a spatially-lagged dependent variable as an explanatory variable in the regression specification. The word “spatial lag” is used to specify the inclusion of the neighboring observations. Similar to the time series “lag operator”, emphasizes the first-order location lag in the dependent variable. The spatial lag model can be written as
where ρ is the spatial autoregressive parameter and the parameter of interest in this paper.
2.1. Endogeneity Problem
The problem in the estimation of the model (3) is that, unlike the time series case, the spatial lag term is endogenous. This is the result of the two-directionality of the neighbor relation in space (“I am my neighbor’s neighbor”), in contrast to the one-directionality in time dependence. Rewriting equation (3) in a reduced form:
indicating that the joint determination of the values of the dependent variable in the spatial system is a function of the explanatory variables and error terms at all locations in the system. The presence of the spatially lagged errors in the reduced form illustrates the joint dependence of and in each cross-section. In model estimation, the simultaneity is usually accounted for through instrumentation (IV and GMM estimation) or by specifying a complete distributional model (maximum likelihood estimation). In this paper, we use maximum likelihood estimation.
2.2. Maximum Likelihood Estimation
Assuming a Gaussian distribution for the error term, with ), the log-likelihood can be written as:
where and is the Jacobian of the spatial transformation. To avoid singularity or explosive processes, the parameter space for the true spatial autoregressive parameter ρ is compact, and is in the interior of .
Lee (2004) [22] discusses the asymptotic properties of the maximum likelihood estimators for the cross-section case. Yu et al. (2008) [18] and Lee and Yu (2010) [19] derive the properties for the spatial panel model with fixed effects. We use the properties of the maximum likelihood estimators to derive the asymptotic distribution of the test statistic.
3. Motivation
We consider the following model in a spatial lag model:
≠ means there is a change at an unknown date . We propose a sup LR test of the null hypothesis of = against the alternative hypothesis of a change: . The test detects a structural break in the spatial dependence parameter. Following are some empirical models where the test can be applied, providing motivation for the test.
3.1. Sectoral Output
Acemoglu et al. (2012) [23] look into the intersectoral input-output linkages in the U.S. and shows how microeconomic idiosyncratic fluctuations lead to aggregate fluctuations. Defining the sectoral production function as,
where is the output of sector i, is the amount of labor hired by the sector, α ∈ (0,1) is the share of labor, is the amount of commodity j used in the production of good i and is the idiosyncratic productivity shock to sector i. The exponent ≥ 0 designates the share of good j in the total intermediate input use of firms in sector i. In particular, = 0 if sector i does not use good j as input for production.
Acemoglu et al. (2012) [23] assume that the input shares of all sectors add up to one, so = 1. With the assumption of market clearing, equation (7) can be rewritten (taking the log on both sides) as equation (3). In this case, labor will be an exogenous variable, and ≠ would mean changes in the Cobb-Douglas parameter over time.
3.2. Cigarette Sales
Baltagi and Li (2004) [24] estimate a demand model for cigarettes based on a panel from 46 U.S. states and defining W based on the neighboring states:
where is real per capita sales of cigarettes by persons of smoking age (14 years and older). This is measured in packs of cigarettes per capita. is the average retail price of a pack of cigarettes measured in real terms. is real per capita disposable income. The spatial autocorrelation parameter shows the dependence of cigarette sales in the neighboring states. The tax policy on per packet cigarette differs by states, and this leads to substantial cross-state sales. However, over time, tax per packet has become more homogeneous, and hence, one could expect the parameter ρ to change over time. By testing the hypothesis that = against the alternative hypothesis of , we can check if the dependence on neighboring states has changed over time.
3.3. Budget Spillovers
Case et al. (1993) [21] showed that the U.S. states’ budget expenditure depends on the spending of similar states:
where is the per capita real government expenditure of state i in year t, includes relevant control variables, income and demographic and > 0 if a state is the “neighbor” of another state. Case et al. (1993) [21] define “neighbor” in three different ways in the paper: (1) neighbors in location; (2) states having similar income and (3) states having similar racial composition. They found that if the neighboring state increases its budget spending by a dollar, then the state increases its budget expenditure by 70 cents. Policies have changed over the years, and one might be interested in testing if the spillover effect remains the same.
3.4. Other Network Motivations
In many of the network studies, the impact of the network is usually estimated by including in the model, where W is the weighting matrix defining the network and y is the variable of concern. For example, a weighted average of the math test scores of students sitting beside student i determines student i’s test score.
With increasing network data availability, we could have repeated samples from such network experiments and then be curious to know how the impact of the network changes over time. Our structural break test could be used in this respect.
4. Test
In this section, we describe the test statistic. The spatial lag model is given by:
where ). We want to test the null hypothesis:
H0:
and and against the alternative
H1:
and , but there is an integer , , such that .
Rewriting the panel model with a change point at in the parameter ρ,
where ≠ means there is a change at an unknown date . The problem can be described as testing against .
Let us write twice the likelihood ratio as
where
- is the log-likelihood defined for the sample that includes the observations
- is the log-likelihood defined for the sample that includes the observations
- is the log-likelihood defined for the sample that includes the observations
As is unknown, we use a maximally selected likelihood ratio and reject if
is large, where , typically a small number is the trimming and [.] denotes the largest integer that is less than or equal to the argument. Therefore, the suggested test is to calculate the difference between the log-likelihood under an alternative hypothesis and the log-likelihood under null for every , and then, the test statistic is the maximum difference between them.
5. Limiting Distribution
In this section, we derive the asymptotic distribution of the test statistic. However, before that we specify the assumptions.
5.1. Assumptions
Assumptions on :
Assumption 1.
, for the off-diagonal elements of the spatial weight matrix and its diagonal elements satisfy for i = 1,..,N.
Assumption 2.
is uniformly bounded in both row and column sums.
Assumption 3.
is invertible for all ; moreover, is compact, and is in the interior of .
Assumptions on X and ϵ:
Assumption 4.
are iid across i and t with ) and for some .
Assumption 5.
The matrices and have minimum eigenvalues bounded away from zero in probability for large j. Furthermore, it is assumed that .
Assumption on N and T:
Assumption 6.
N is a non-decreasing function of T and
The following assumption is made to establish the theoretical result of the paper.
Assumption 7.
Let and then and .
Assumption 1 is a standard normalization assumption in spatial econometrics, while Assumption 2 is also used in Lee (2004) [22] and Yu et al. (2008) [18]. Assumption 3 guarantees that Model (4) is valid. Furthermore, compactness is a condition for the theoretical analysis. In empirical applications, where is row-normalized, one just searches over (−1,1). Assumption 4 provides regularity assumptions for . The normality assumption on errors is used to construct the likelihood function. However, the limit result does not depend on it. The result only needs quasi-maximum likelihood estimation (QMLE). Assumption 5 makes sure that the regressors are asymptotically stationary. Assumption 6 allows two cases: (i) as , such that , for , and (ii) N is fixed as .
Theorem 1.
Let ⟹ denote weak convergence in the distribution under the Skorokhod topology. Under Assumptions 1–6 and , the limiting distribution of is:
where , is a standard Brownian bridge and u, the trimming parameter, is a small positive number.
For a known break :
Proof of Theorem 1.
To prove the result, we first take a Taylor approximation of around the true parameter . It is found that the approximations involve partial sums of Gaussian random vectors that are independently and identically distributed. Using results from the maximum likelihood estimation of the spatial panel model, we obtain uniform convergence to Wiener processes. As a next step, the partials sums are manipulated to obtain a Brownian bridge distribution. For a fixed k, it is then easy to show that the asymptotic distribution is chi-square. The detailed proof is provided in the Appendix A. ☐
The intuition as to why the asymptotic distribution from the univariate time series test (Cörgö and Horváth (1997) [25]) is still valid in this case is because the spatial dependence is contained in time; the dependent variable of unit i only depends on the contemporaneous dependent variable of the neighboring units. Therefore, the endogeneity does not spread over time, and hence, the distribution is similar to the one found in the univariate time series case.
There is an explicit form of the distribution function of the limit random variable. The critical values are provided in Kiefer (1959) [26] (p. 438). Some of the relevant critical values are for size , 1.4978; for size , 1.8444 and for size , it is 2.649 for a 5% trimming.
6. Estimation
Following evidence against the null hypothesis, it is important to determine the location of the break date. The proposed estimator of the break date is the one that maximizes the likelihood under the alternative hypothesis,
where is the log likelihood under the alternative defined as: where
where is the log-likelihood defined for and is the log-likelihood for the sample that includes the observations .
The asymptotic properties of the estimator, including the consistency, rate of convergence and limit distribution, are currently under investigation. Simulation evidence, presented is Section 7, shows that the estimator performs very well in small samples in terms of bias and root mean squared error. The root mean squared error is shown to decrease as the sample size increases, thereby suggesting that the estimator is indeed consistent.
7. Monte Carlo Results
To evaluate the finite sample performance of the LR test and the performance of the estimator, this section reports the results of a limited set of sampling experiments. All results reported are for 1000 simulations. We consider the data generating process:
where from and from .
We first look into the power of the proposed test. Let , and the actual break date is in each of the cases. We find that the test has high power even with N and T = 50, as seen in Table 1. The power increases with increases in N and/or T (see Table 2).

Table 1.
Power of the test: I.

Table 2.
Power of the test: II.
Next, we look into graphical comparisons between empirical and asymptotic distributions of the test presented in Figure 1. The continuous lines are the asymptotic distributions, and the dotted lines are the empirical CDF. It is found that even with a small T, there is no size distortion, and the empirical distribution matches closely the asymptotic distribution. As T increases, the two distributions overlap.
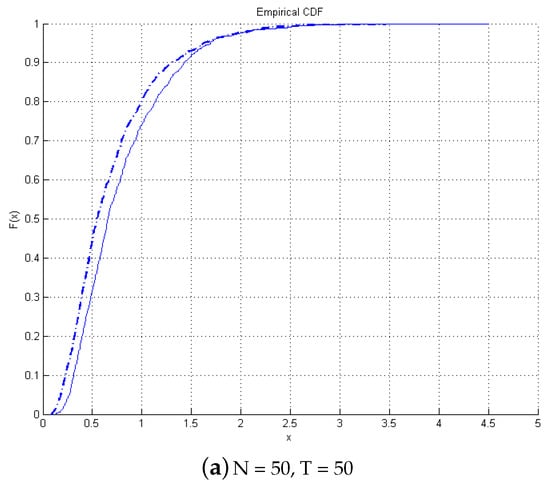
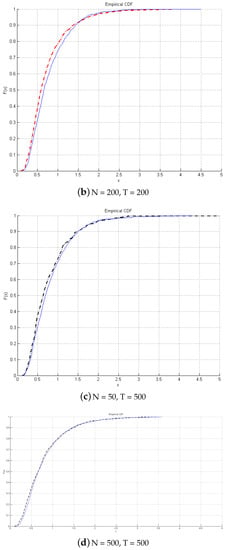
Figure 1.
Emprical versus Asymptotic Distribution of the test.
For a known break date, the asymptotic distribution is chi-square with one degree of freedom. The graphical comparison presented in Figure 2 shows that even with N = 50, T = 50, with a known break date, the empirical distribution is very close to the asymptotic chi-square distribution.
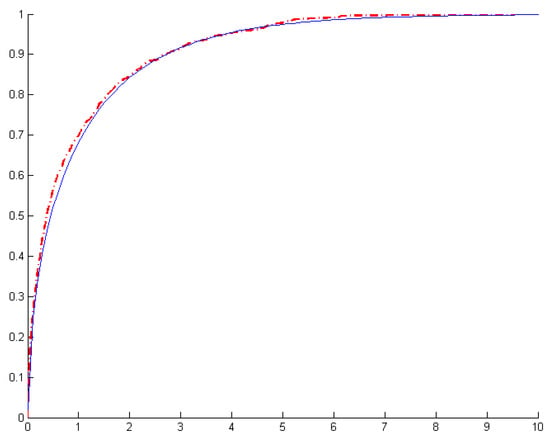
Figure 2.
CDF plot for empirical distribution with a known break.
Next, we compare the performance of the break-date estimator (see Table 3). The bias is almost negligible. The root mean square decreases with increases in N. With increases in T, the standard deviation does not go down. This is a well-known result in the univariate time series literature: only the break fraction can be consistently estimated, not the break date.

Table 3.
Estimator performance: likelihood method.
Furthermore, we make a quick comparison with the ordinary least squares residuals-based method (see Table 4), with the estimator defined by

Table 4.
Estimator performance: OLS residuals.
Here, is the sum of squared residuals of the model under the alternative assuming a break at date k. The bias is comparable in the two cases, but the standard deviation and root mean square are higher for the OLS residual-based estimate of break date.
Looking at the tables closely, an interesting pattern is observed: there is an asymmetry in the behavior of the estimator and the power of the test. When , the power of the test is lower compared to that when . Similarly, the break date estimator has a lower standard deviation and root mean square when the post-break parameter is increasing () as compared to a comparable reduction in the post-break parameter (). An explanation for such behavior could be that, when the post-break parameter is increasing (), there is a higher signal of spatial dependence. This leads to reduction in the variance and makes it easier to assess whether a break is present and locate it. However, when the post-break parameter is comparably lower (), the signal is lower, giving rise to more variation and making it more difficult to assess whether a break is present and to locate it.
The proposed likelihood-based estimator performs well in a finite sample. As N increases, the root mean square error decreases, suggesting that the estimator is consistent.
8. Budget Spillovers
Case et al. (1993) [21] showed how a U.S. state’s budget expenditure depends on the spending of similar states. Quoting Arkansas state Senator Doug Brandon (1989)2 describing his state’s budgetary policy as
“We do everything everyone else does.”
The proposed sup LR test is used to check the hypothesis that a state’s dependence on another’s budget remained the same in the U.S. or has changed over time. The data consists of an annual panel of U.S. states from 1960–2011. All dollar figures are calculated on a per capita basis and deflated using the GDP deflator (the base year being 2009). The dependent variable is the government expenditure of state i in the year t (). The budget expenditure is the sum of the direct spending of state and local governments. The variables included in other than the intercept are: the real per-capita personal income (Y), income squared (), real per capita total intergovernmental federal revenue to state and local governments (F), population density (), proportion of the population at least 65 years old (), proportion of the population between five and 14 years old () and proportion of the population that is black (). The income and revenue are the resources the state government can use. The square of the income picks up possible non-linear effects of changing resources. The population density captures the possibility that there are potential congestion effects and scale economies in the provision of state and local government services. States with different age and racial structures may have different demands for publicly-provided goods. Hence, demographic variables are included.
The model can be written as:
where X includes all of the control variables. We consider T = 52 from 1960–2011 and N = 49 states in the U.S. Case et al. (1993) [21] use three different ways to define the weight matrix. We define the elements of the weight matrix as = , where is the mean income over the sample period and is the sum . According to this definition of the weight matrix, rich states are neighbors to rich states, and poor states are neighbors to poor states. The full model (1960–2011) estimation results are presented in Table 5.

Table 5.
Full model estimate.
All of the test results are based on tests with size . We reject the null hypothesis of no break, implying evidence for a break. The break date is estimated at 1982. The pre-break budget spillover coefficient is estimated as 0.0229, while the post-break budget spillover coefficient is estimated as 0.1056. As to why there might be a break, there could be two reasons: (1) in 1981, Ronald Reagan became the president of the United States and advocated many different policies across the U.S. states (also known as Reagonomics); (2) the number of Democratic governors in the U.S. started decreasing post-1983, suggesting synchronized Republican economic policies in different states.
To differentiate between trend behaviors and fluctuations, a Hodrick-Prescott filter is applied on all of the dollar value variables to closely look into idiosyncratic budget spillovers in the U.S. states. We reject the null hypothesis of no break. The break date is then estimated to be in 1977. The pre-break ρ coefficient is 0.5718, and the post-break ρ coefficient is 0.3746. Firstly, this suggests that the idiosyncrasy in budget expenditure for a state depends on “similarly”-situated states. Secondly, the dependence goes down post-break. This can be attributed to more power given to the governors in the 1980s. For the federal government (central planner), the budget policies for each state will be similar; compared to individual governors in each state who will adjust the budget expenditures for their states based on individual needs. Therefore, overall, even though the spillovers increase (capturing overall trend in the economy), the budget spillovers in the case of idiosyncracies reduce over time.
9. Conclusions
We consider the problem of structural break in the spatial dependence parameter in a panel model and provide a likelihood ratio test.
We first describe the spatial panel model and the interpretation of the spatial lag or spatial autoregressive parameter. Next we motivate the problem of structural break in such parameter. The sup LR test statistic is proposed, and under large T, the limiting distribution is derived. The test is easy to implement, and the critical values can be analytically obtained.
In case there is evidence to reject the null hypothesis, we propose a break date estimator based on the argument that maximizes the likelihood ratio. The finite sample properties of the test and the break-date estimator are provided. The Monte Carlo simulations show that the test has good power even in small samples. The estimator of the break date shows negligible bias, and the root mean square decreases with increases in N, suggesting a consistent break-date estimator for a panel model.
We then consider the problem of budget spillovers across the U.S. states and the change in the spatial dependence over time. The test rejects the null hypothesis of no break in budget spillovers for (1) the spillover in the overall budget expenditure of the U.S. states and (2) the spillover in the fluctuations of budget expenditure. The overall trend of spatial dependence in budget expenditure is found to have increased post-break, but the idiosyncrasies in budget expenditure are less spatially dependent post-break.
The following extensions to the paper are being considered: (1) the asymptotic limit distribution of the test statistic for large N; (2) proving the consistency of the break date estimator and deriving the limiting distribution; and (3) extending the test to multiple structural breaks.
Acknowledgments
I am grateful to my advisors Pierre Perron, Zhongjun Qu, and Hiroaki Kaido for their guidance, support and encouragement. I would also like to thank Iván Fernández-Val, Jushan Bai, Laurent Pauwels, Qu Feng, Hide Ichimura, Fan Zhuo, Anindya Chakrabarti and seminar participants at Boston University for useful conversations and feedback. I am also grateful to the two anonymous reviewers and the editor for their feedback and suggestions. I am thankful to Satadru Sengupta for introducing me to Spatial Econometrics. All errors are my own.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CDF | Cumulative distribution function |
| FCLT | Functional central limit theorem |
| GMM | Generalized method of moments |
| IV | Instrumental variable |
| LR | Likelihood ratio |
| MLE | Maximum likelihood estimation |
| OLS | Ordinary least squares |
| QMLE | Quasi-maximum likelihood estimation |
| RMSE | Root mean square error |
Appendix A. Proof of Theorem
Let θ = . Then,
Denoting , and ; furthermore, defining as the MLE estimate for the pre-break regime under the alternative, as the MLE estimate for the post-break regime under the alternative and as the MLE estimate under the null. Taking a Taylor expansion of 2[] around the true value and denoting that by
Now, . Therefore, can be rewritten as:
From Lee (2004) [22] and Yu et al. (2008) [18] under Assumptions 1–6
Using these relationships and rearranging the terms, can be rewritten as:
Let , then
where .
Let, . Then, by Assumption 7, and .
Furthermore,
Now, . As , by the FCLT, we get:
where is a standard Wiener process. Thus, if we let , then by the FCLT,
Hence, we get:
Let
Rearranging the terms, we get:
where is a Brownian bridge.
For known , , the limit distribution of is .
References
- G.C. Chow. “Test of equality between sets of coefficients in two linear regressions.” Econometrica 28 (1960): 591–605. [Google Scholar] [CrossRef]
- D.W.K. Andrews. “Tests for parameter instability and structural change with unknown change point.” Econometrica 61 (1993): 821–856. [Google Scholar] [CrossRef]
- D.W.K. Andrews, and W. Ploberger. “Optimal tests when a nuisance parameter is present only under the alternative.” Econometrica 62 (1994): 1383–1414. [Google Scholar] [CrossRef]
- J. Bai, and P. Perron. “Estimating and testing linear models with multiple structural changes.” Econometrica 66 (1998): 47–78. [Google Scholar] [CrossRef]
- J. Bai. “Estimation of a change point in multiple regressions models.” Rev. Econ. Stat. 79 (1997): 551–563. [Google Scholar] [CrossRef]
- J. Bai, R. Lumsdaine, and J. Stock. “Testing and dating common breaks in multivariate time series.” Rev. Econ. Stud. 65 (1998): 395–432. [Google Scholar] [CrossRef]
- Z. Qu, and P. Perron. “Estimating and testing structural changes in multivariate regressions.” Econometrica 75 (2007): 459–502. [Google Scholar] [CrossRef]
- P. Perron. “Dealing with structural breaks.” In Palgrave Handbook of Econometrics. Edited by H. Hassani, T.C. Mills and K. Patterson. Basingstoke, UK: Palgrave Macmillan, 2006, Volume 1, pp. 278–352. [Google Scholar]
- J. Bai. “Common breaks in means and variances for panel data.” J. Econom. 157 (2010): 78–92. [Google Scholar] [CrossRef]
- Q. Feng, C. Kao, and S. Lazarova. Estimation of Change Points in Panel Models. New York, NY, USA: Mimeo, Center for Policy Research, 2009. [Google Scholar]
- W. Liao. “Structural Breaks in Panel Data Models: A New Approach.” Ph.D. Thesis, New York University, New York, NY, USA, 2008. [Google Scholar]
- A.K. Han, and D. Park. “Testing for structural change in panel data: Application to a study of U.S. foreign trade in manufacturing goods.” Rev. Econ. Stat. 71 (1989): 135–142. [Google Scholar] [CrossRef]
- J. Emerson, and C. Kao. Testing for Structural Change of a Time Trend Regression in Panel Data. Working Paper 15; New York, NY, USA: Center for Policy Research, 2000. [Google Scholar]
- S. De Wachter, and E. Tzavalis. “Detection of structural breaks in linear dynamic panel data models.” Comput. Stat. Data Anal. 56 (2012): 3020–3034. [Google Scholar] [CrossRef]
- L.L. Pauwels, F. Chan, and T.M. Griffoli. “Testing for structural change in heterogeneous panels with an application to the euro’s trade effect.” J. Time Ser. Econom. 4 (2012). [Google Scholar] [CrossRef]
- J. Elhorst. “Spatial panel data models.” In Handbook of Applied Spatial Analysis. Edited by M.M. Fischer and A. Getis. Berlin/Heidelberg, Germany: Springer, 2010, pp. 377–407. [Google Scholar]
- J. Bai. “Likelihood ratio tests for multiple structural changes.” J. Econom. 91 (1999): 299–323. [Google Scholar] [CrossRef]
- J. Yu, R. Jong, and L. Lee. “Quasi-maximum likelihood estimators for spatial dynamic panel data with fixed effects when both n and T are large.” J. Econom. 146 (2008): 118–134. [Google Scholar] [CrossRef]
- L. Lee, and J. Yu. “Estimation of spatial autoregressive panel data models with fixed effects.” J. Econom. 154 (2010): 165–185. [Google Scholar] [CrossRef]
- D. Wied. “Cusum-type testing for changing parameters in a spatial autoregressive model for stock returns.” J. Time Ser. Anal. 34 (2013): 221–229. [Google Scholar] [CrossRef]
- A.C. Case, and H.S. Rosen. “Budget spillovers and fiscal policy interdependence: Evidence from the states.” J. Public Econ. 52 (1993): 285–307. [Google Scholar] [CrossRef]
- L. Lee. “Asymptotic distributions of quasi-maximum likelihood estimators for spatial autoregressive models.” Econometrica 72 (2004): 1899–1925. [Google Scholar] [CrossRef]
- D. Acemoglu, V.M. Carvalho, A. Ozdaglar, and A. Tahbaz-Salehi. “The network origins of aggregate fluctuations.” Econometrica 80 (2012): 1977–2016. [Google Scholar] [CrossRef]
- B.H. Baltagi, and D. Li. “Prediction in the panel data model with spatial correlation.” In Advances in Spatial Econometrics. Edited by L. Anselin, R. Florax and S. Rey. Berlin/Heidelberg, Germany: Springer, 2004, pp. 283–295. [Google Scholar]
- M. Csörgö, and L. Horváth. Limit Theorems in Change-Point Analysis. New York, NY, USA: Wiley, 1997. [Google Scholar]
- J. Kiefer. “K-Sample Analogues of the Kolmogorov-Smirnov and Cramer-V. Mises tests.” Ann. Math. Stat. 30 (1959): 420–447. [Google Scholar] [CrossRef]
- 1Case et al. (1993) [21] defines similar states in three different ways: (1) similar in location, (2) similar in income and (3) similar in racial composition.
- 2Applebome, P. (1989), “Governors in the South Seek to Lift Their States”, New York Times, 12 Feb, L26.
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).